Recent rigidity results for graphs with prescribed mean curvature

1.   Introduction

Chemotaxis, the migration of cells along the chemical concentration gradient, plays a central role in a wide spectrum of physiological and pathological processes, such as embryo development, wounding healing, immunity, and cancer metastasis, and so on. This paper is concerned with the following Keller-Segel type chemotaxis system with logistic source

for $x \in \mathbb{R}$ and $t\geq 0$, where $u(x, t)$ and $c(x, t)$ denote the cell density and chemical concentration, respectively. $D > 0$ and $\epsilon\ge 0$ represent the cell and chemical diffusion rates, respectively, $\chi > 0$ is the chemotactic coefficient and $\mu\geq 0$ denotes the cell growth rate.

When $\chi = 0$ (no chemotaxis), $u$ and $c$ decouple and the first equation of (1.1) reduces to the following well-known Fisher-KPP equation ^[1,2]

The Fisher-KPP equation (1.2) has been widely considered as the most fundamental mathematical model in mathematical biology and population dynamics and there are huge amounts of results available (see a survey paper ^[3] and references therein). One of the most prominent results is that (1.2) admits a minimal wave speed $c_0 = 2\sqrt{\mu D}$ in $\mathbb{R}$, which is also the spreading speed when the initial value is compactly supported (cf. ^[4]).

When $\mu = 0$ (no cell growth), the system (1.1) is well-known as the singular Keller-Segel model originally proposed in ^[5] to describe the traveling band formation of bacterial chemotaxis towards the oxygen absorbed by the bacteria. It was also used to describe the chemotactic movement of motile aerobic bacterial toward oxygen ^[6,7], and to describe the directed movement of endothelial cells toward the signaling molecule vascular endothelial growth factor (VEGF) during the initiation of blood vessel network formation (cf. ^[8,9,10,11]). In many of these works, the chemical diffusion $\epsilon$ has been assumed to be small or zero (see ^[5,9,11] for biological relevance). A challenging issue in the analysis of (1.1) is the singularity at $c = 0$. Luckily it can be resolved by a Cole-Hopf type transformation (cf. ^[9,12])

which transforms system (1.1) into equations without singularity:

The transformed system (1.4) with $\mu = 0$ has been extensively studied and abundant results have obtained on the existence/stability of traveling wave solutions and global well-posedness and asymptotic behavior of solutions. We refer readers to ^{[13,14,15,16,17,18,19,20,21,22]} for $\epsilon = 0$, and ^{[12,17,23,24,25,26,27,28]} for $\epsilon > 0$. The zero chemical diffusion limit and associated boundary-layer solutions as $\epsilon\rightarrow 0$ were investigated in ^{[17,29,30,31,32,33,34]}.

The model (1.4) with $\mu > 0$ has received attentions recently and the existence of traveling wave solutions with a minimal wave speed was obtained in ^[35] for $x \in \mathbb{R}$ for $\epsilon > 0$. The global existence and large-time behavior of solutions as well as the convergence of $\epsilon \to 0$ have been established in ^[36,37] if the initial datum is a small perturbation around constant equilibria with finite energy for $x\in \mathbb{R}$. The nonlinear stability of diffusive contact wave in $\mathbb{R}$ was obtained in ^[38]. The purpose of this paper is to investigate the existence and stability/instability of traveling wave solutions to the singular Keller-Segel system (1.1) with $\epsilon\geq 0$ and to prove the convergence of traveling wave solutions as $\epsilon\to 0$.

Since singularity will arise in the first equation of (1.1) as $c$ approach to zero, it is challenging to study (1.1) directly. Instead we shall study traveling wave solutions of the transformed system (1.4) and then transfer the results of (1.4) back to (1.1) through the Cole-Hopf transformation (1.3). The system (1.4) is a system coupling a reaction-diffusion equation with a nonlinear conserved equation. It is well-known that the reaction-diffusion equations usually admit infinitely many wave speeds with a minimal wave speed (cf. ^[4]), while the equations of conservation laws have unique traveling wave speed for given far-field states (cf. ^[39]), as shown for (1.4) with $\mu = 0$ in ^[23,28]. Therefore a natural question is whether the traveling wave speed of (1.4) is unique or not. The answer is by no means easy or straightforward. Previously, by constructing a three-dimensional invariant set, the authors of ^[35] established the existence of traveling wave solutions with a minimal wave speed to system (1.4) with $\epsilon > 0$ under certain conditions, where a range for the minimal wave speed was estimated without explicit identification. The results for $\epsilon = 0$ remain unknown since the analysis of ^[35] requires the condition $\epsilon > 0$. We also mention that the traveling wave solutions and spreading speed of a chemotaxis model with logistic source were studied in ^[40,41] for weak chemotaxis, where the model considered therein was very different from (1.1) by assuming that there is no singularity (i.e., linear chemotactic sensitivity) and the chemical was elicited from instead of consumed by cells. Apart from this, in this paper, we do not require the chemotaxis to be weak.

In this paper, we first explore the traveling wave solutions of (1.4) with $\epsilon = 0$ for $(x, t)\in \mathbb{R}\times [0, \infty)$. Using the phase plane analysis, we find that (1.4) with $\epsilon = 0$ admits a minimal wave speed which is the same as that of the Fisher-KPP equation if the chemotaxis is weak (i.e., $\chi\leq\mu D$), while if chemotaxis is strong (i.e., $\chi > \mu D$), we show that (1.4) with $\epsilon = 0$ admits traveling wave solutions whenever $s\geq \sqrt{2\chi+4\mu D}$. Using the singular perturbation method ^[42,43], we establish the existence of traveling wave solutions of (1.4) when $\epsilon > 0$ is small. We then establish the vanishing diffusion limit of traveling wave solutions of (1.4) as $\epsilon\rightarrow 0$. By computing the essential spectrum of linearized operator, we show that traveling wave solutions of (1.4) with $\epsilon\geq 0$ are linearly (or spectrally) unstable in the Sobolev space $H^1(\mathbb{R}) \times H^2(\mathbb{R})$. Finally we use numerical simulations to demonstrate the stabilization of traveling wave solutions with fast decay initial data and explore effect of system parameters on the wave propagation dynamics.

2.   Statement of main results

The main results of this paper are associated with the traveling wave solutions of (1.1) with $\epsilon = 0$. It is easy to see that (1.1) has two equilibria $(1, 0)$ and $(0, c_+)$ where $c_+\geq 0$ is a constant. Hence we expect the system (1.1) with $(x, t) \in \mathbb{R} \times [0, \infty)$ admits traveling wave solutions in the form

connecting $(1, 0)$ and $(0, c_+)$, namely satisfying

with far-field (i.e., asymptotic) states

where $' = \frac{d}{dz}$ denotes the differentiation with respect to $z$ and $s\in \mathbb{R}$ is called the wave speed. Note that $U$ and $C$ are non-negative biologically. Then from the second equation of (2.1), we see that $s\ne 0$ since otherwise $UC\equiv0$ if $\epsilon = 0$ or $C'' = \frac{1}{\epsilon}UC\geq 0$ if $\epsilon > 0$, and consequently the solutions are not traveling wave profiles. Without loss of generality, hereafter we only consider the case $s > 0$ (i.e., right-moving waves) and similar analysis is directly extendable to the case $s < 0$. When $s > 0$, from the second equation of (2.1), we find $C' = \frac{U C}{s}\geq 0$ if $\epsilon = 0$ or $C' = \frac{1}{\epsilon} \int_{-\infty}^z e^{\frac{s}{\epsilon}(\xi-z)}U(\xi)C(\xi)d\xi > 0$ if $\epsilon > 0$, which indicates that $c_+ > 0$.

Studying (2.1) directly for both $\epsilon = 0$ and $\epsilon > 0$ is difficult since $C$ may be zero asymptotically, which causes a possible singularity. Therefore we resort to the Cole-Hopf transformation (1.3) and consider the transformed system (1.4). That is, we let

and then the traveling wave profile $(U, V)(z)$ of (1.4) satisfies

with far-field states

We note that $v_- = -\frac{C'}{C}\leq 0$ since $C_z\geq0$.

For the convenience of stating our results, in what follows, we always assume

Then our first result concerning the existence of traveling wave solutions to the transformed system (1.4) with $\epsilon = 0$ is given below.

Theorem 2.1. Let $D, \mu, \chi > 0$. If $s < 2\sqrt{\mu D}$, then the system (1.4) with $\epsilon = 0$ does not admit any nonnegative traveling wave solutions. If the wave speed $s$ satisfies $(2.5)$, then the system (1.4) with $\epsilon = 0$ has a unique (up to a translation) traveling wave solution $(U, V)(z)$ satisfying $(2.4)$ and $U' < 0, V' > 0$, where $v_- = -\frac{1}{s}$.Moreover$(U, V)(z)$ converges to its far field states $(u_\pm, v_\pm)$ exponentially as $z \to \pm \infty$.

Next result is concerned with the existence of traveling wave solutions to the system (1.4) with small $\epsilon > 0$ and convergence as $\epsilon \to 0$.

Theorem 2.2. Let $(U^0, V^0)(z)$ be the solution of (1.4) with $\epsilon = 0$ obtained in Theorem 2.1.Then there exists some $\epsilon_0 > 0$ such that for any $0 < \epsilon < \epsilon_0$, the system(1.4) with $\epsilon > 0$ has a solution $(U^{\epsilon}, V^{\epsilon})(z)$ satisfying

Moreover, for all $0 < \epsilon < \epsilon_0$, $(U^{\epsilon}, V^{\epsilon})$ converges to the far-field states $(u_\pm, v_\pm)$exponentially as $z \to \pm\infty$.

Remark 2.1. It was proved in [35,Theorem 1.1] that the system (1.4) with any $\epsilon > 0$ admits a unique (up to a translation) traveling wave solution with a minimal wave speed $c_*$, where a range of $c_*$ was given but the exact value of $c_*$ was not determined. Here we can assert that $2\sqrt{\mu D}$ is precisely the minimal wave speed if $\varepsilon > 0$ is sufficiently small and $\chi < \mu D$. This is an improvement of ^[35]. But our results are valid only for sufficiently small $\varepsilon > 0$ or $\varepsilon = 0$. When $\chi > \mu D$, the results of this paper are not directly comparable with [35,Theorem 1.1] since the bounds of $c_*$ therein depend on $\varepsilon$.

By the Cole-Hopf transformation (1.3), we get the corresponding results on the traveling wave solutions to the pre-transformed Keller-Segel system (1.1).

Theorem 2.3. Let $D, \mu, \chi > 0$. Then we have the following results.

(1) If $s$ satisfies $(2.5)$, then the system (1.1) with $\epsilon = 0$ has a unique (up to a translation) monotone traveling wave solution $(u(x, t), c(x, t)) = (U(z), C(z))$ satisfying $(2.2)$ and $U' < 0, \ C' > 0$. Moreover, $(U, C)$ converges to its far-field states $(u_\pm, c_\pm)$ exponentially as $z \to \pm\infty$. If $s < 2\sqrt{\mu D}$, there is no traveling wave solution to the system (1.1) with $\epsilon = 0$.

(2) There exists an $\epsilon_0 > 0$ such that for any $0 < \epsilon < \epsilon_0$, the system (1.4) with $\epsilon > 0$ has a unique (up to a translation) traveling wave solution $(U^{\epsilon}, C^{\epsilon})(z)$ satisfying $(2.2)$ and

provided that $C^\epsilon(0) = C^0(0)$, where $(U^0, C^0)$ is the traveling wave solution of system (1.1)with $\epsilon = 0$ obtained in (1). Moreover, for all $0 < \epsilon < \epsilon_0$, $(U^{\epsilon}, C^{\epsilon})$ converges to the far-field states$(u_\pm, c_\pm)$ exponentially as $z \to \pm\infty$.

The results of Theorem 2.1 assert that if chemotaxis is weak so that $\chi < \mu D$, then the system (1.4) with $\epsilon = 0$ has a minimal wave speed $s_0 = 2\sqrt{\mu D}$ which is the same as that of the Fisher-KPP equation. If $\chi = \mu D$, the wave speed $s_0 = 2\sqrt{\mu D}$ is a critical wave speed where the traveling wave solutions do not exist whenever $s < s_0$ while exist for any $s > s_0$, but whether traveling wave solutions exist for $s = s_0$ remains unknown in this paper. If chemotaxis is strong (i.e., $\chi > \mu D$), we can show that traveling wave solutions exist whenever $s > \sqrt{2\chi +4\mu D}$, but whether $\sqrt{2\chi +4\mu D}$ is a possible minimal wave speed is unknown. One thing that is observed in the numerical simulations shown in Section 5 is that chemotaxis will increase the wave speed when it is strong. In other words, when chemotaxis is strong, the minimal wave speed is greater than $s_0 = 2\sqrt{\mu D}$.

The last result of this paper is about the instability of traveling wave solutions.

Theorem 2.4. Let $(U, V)(z)$, $z = x-st$, be the traveling wave solution of system (1.4) with $\epsilon\geq 0$ satisfying (2.4).Then the essential spectrum of the linearized operator at the traveling wave solution$(U, V)$, denoted by $\sigma(L)$, satisfies

In particular, the traveling wave solution $(U, V)(z)$ is linearly unstable if $\epsilon > 0$ and spectrally unstable if $\epsilon = 0$.

The rest of this paper is organized as follows. The existence of traveling wave solutions of (1.4) with $\epsilon = 0$ is proved in Section 3. Furthermore we provide an explicit representation for traveling wave solutions with large wave speed in this section. In Section 4, we establish the existence of traveling wave solutions of (1.4) when $\epsilon > 0$ is small. We then establish the vanishing diffusion limit of traveling wave solutions of (1.4) as $\epsilon\rightarrow 0$. We prove the linear instability of traveling wave solutions to the system (1.4) in Section 5. Finally we show some numerical simulations to explore the effect of system parameters on the wave propagation dynamics in Section 6.

3.   Existence of traveling wave solutions when $\epsilon=0$

In this section, we prove Theorem 2.1, namely, the existence of traveling wave solutions to systems (1.4) and (1.1) with $\epsilon = 0$. Furthermore we shall provide an explicit representation for traveling wave solutions with large wave speeds.

3.1.   Existence of traveling wave solutions

We start with the traveling wave equations of the transform system (1.4) with $\epsilon = 0$, which satisfy (2.3) and (2.4) that

with far-field (i.e., asymptotic) states as $z \to \pm \infty$:

From the second equation of (3.1), we have

where $\beta$ is an integration constant satisfying

The boundary conditions (3.2) entail that $\beta = -v_+-\frac{u_+}{s} = 0$ which in turns yields

Substituting (3.3) into the first equation of (3.1), we derive that $U$ satisfies a second order differential equation

where $U\geq 0$ for all $z \in \mathbb{R}$.

Setting $U' = W$, we obtain a system of first order differential equations as follows

The system (3.6) admits two critical points $(0, 0)$ and $(1, 0)$. To prove the existence of traveling wave solutions of (3.6), it suffices to find a heteroclinic trajectory joining the two critical points such that $W = U'\leq 0$ for all $U\in [0, 1]$.

Proposition 3.1. Let $D, \mu, \chi > 0$ and $(2.5)$ hold.Then the system (3.6) has a heteroclinic solution $(U, W)(z)$ with $U' < 0$, which is unique up to a translation and satisfiesthe following boundary conditions

Moreover, the solution $(U, W)$ converges to the far-field states $(u_{\pm}, w_{\pm})$ exponentially as $z \to \pm\infty$.

Proof. We prove Proposition 3.1 by constructing an invariant region in the phase plane. The proof consists of several steps.

Step 1. Linear stability of critical points

We calculate the Jacobian matrix of system (3.6) at the critical point $(1, 0)$

where the eigenvalue $\sigma$ of $M_1$ satisfies characteristic equation

which has two real roots with opposite signs,

where

Therefore $(1, 0)$ is a saddle point. The eigenvector corresponding to $\sigma_2 > 0$ is

Next we calculate the Jacobian matrix at the critical point $(0, 0)$

where

The eigenvalues of $M_2$ are

If $\gamma = 0$, i.e., $s = 0,$ then $(0, 0)$ is a center, and there is no trajectory connecting the saddle point $(1, 0)$ and the center $(0, 0)$.

If $\gamma < 0$ and $\gamma^2-\frac{4\mu}{D} < 0$, then $0 < s < s_1$ where

In this case, $(0, 0)$ is a stable focus and thus the heteroclinic trajectory converges to the origin. As the curve spirals, $U$ possess negative values which is not physically meaningful for the cell density. Hence there are no nonnegative traveling wave solutions for the system (3.6) when $0 < s < s_1$.

Finally, if $\gamma < 0$ and $\gamma^2-\frac{4\mu}{D}\geq 0$, then $s\geq s_1$. It is straightforward to check that

Thus $(0, 0)$ is a stable node if $s\geq s_1$.

Therefore, if $s\geq s_1$, it is possible that there is a heteroclinic trajectory emanating from the saddle point $(1, 0)$ and entering the stable node $(0, 0)$. In the next step, we prove the existence of such a heteroclinic trajectory by the phase plane analysis where an invariant region will be constructed provided that $s\geq s_1$.

Step 2. Construction of an invariant region

We now construct an invariant region for the system (3.6) and (3.7) in the $U$-$W$ phase plane under some sufficient conditions including $s\geq s_1$. The nullclines of the system (3.6) consist of

and

The nullclines intersect at critical points $(0, 0)$ and $(1, 0)$. Since $W = U'\leq 0$ for all $U\in [0, 1]$, from (3.14) we derive that $-s^2+2\chi U < 0$ for all $U\in (0, 1)$, which is ensured by $s > s_2$ where

Assume that $s > s_2$. Then

It is straightforward to calculate from (3.14) that

Then $g'(U) = 0$ leads to

If $s > s_2$, we find that (3.18) has two distinctive real roots denoted by $U_m$ and $U_M$, where $U_m < U_M$ and $U_m = \frac{1}{2}\Big(\frac{s^2}{\chi}-\sqrt{\big(\frac{s^2}{\chi})^2-\frac{2s^2}{\chi}}\Big)$.

It is easy to check from (3.18) that

From (3.17) and (3.18) we derive that $g'(U_m) = 0$ and that

Hence $g(U)$ has a minimum point $U_m\in (0, 1)$

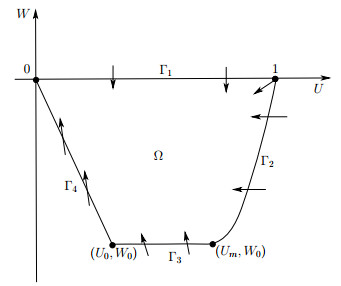
We define $\Omega$ to be a region bounded by the following curves in the phase plane, see Figure 1

where $h > 0$ is a constant to be determined and $(U_0, W_0)$ is the intersection point of $\Gamma_3$ and $\Gamma_4$ satisfying $0 < U_0\leq U_m$ and $W_0 = g(U_m)$.

We shall show that under some sufficient conditions $h > 0$ can be chosen such that $\Omega$ is an invariant region of (3.6). First we have the following direct observations.

(i) On the top boundary $\Gamma_1$ of $\Omega$, we derive from (3.6) that $W' = -\frac{\mu}{D}U(1-U) < 0$ for all $U \in (0, 1)$, and the flow points downward towards the interior of $\Omega$.

(ii) Along the right boundary $\Gamma_2$ of $\Omega$, which is part of the nullcline $W = g(U)$ for $U_m < U < 1$, the flow points leftward towards the interior of $\Omega$ in that $U' = W < 0$ and $W' = 0$.

(iii) On the bottom boundary $\Gamma_3$ of $\Omega$, since the nullcline $W = g(U)$ lies above $\Gamma_3$ and so $W' = \frac{W}{Ds}(-s^2+2\chi U)-\frac{\mu}{D}U(1-U) > \frac{g(U)}{Ds}(-s^2+2\chi U)-\frac{\mu}{D}U(1-U) = 0$, then the flow points upper left towards the interior of $\Omega$.

To show that $\Omega$ is an invariant region of (3.6), it remains to prove

(iv) There exists some $h > 0$ such that along the straight line $W = -h U$ for $0\leq U < U_0$, the flow points left upward towards the interior of $\Omega$ along $\Gamma_4$.

To this end, we consider the inner product of the inward normal vector of the line $W = -h U$ with the vector field of system (3.6) for $0 < U < U_0\leq U_m$

We want to find an $h > 0$ such that along $\Gamma_4: W = -h U$ for $0\leq U < U_0\leq U_m < 1$ it has

Clearly (3.21) is ensured if we can find some $h > 0$ such that

where we have used $\gamma = -\frac{s}{D}$. We proceed with two cases.

Case 1: $\chi\leq\mu D$. For convenience, we rewrite $Q(h)$ as

where $Q_1(h) = h^2-\frac{s}{D}h+\frac{\mu}{D}, Q_2(h) = \frac{2\chi}{Ds}h-\frac{\mu}{D}$. Under the condition $s\geq s_1 = 2\sqrt{\mu D}$, setting $h_0 = \frac{s}{2D}$, one can easily check that

and

By choosing $h = h_0 = \frac{s}{2D}$, we get

If $\chi < \mu D$, then $s_2 = \sqrt{2\chi} < s_1 = 2\sqrt{\mu D}$. Hence if $s\geq s_1$, from (3.24)–(3.26), we find that

That is, (3.22) is fulfilled by choosing $h = h_0$ and $s\geq s_1$.

In the case $\chi = \mu D$, it is clear that $Q(h_0) < 0$ for all $0 < U < U_0\leq U_m < 1$ if $s > s_1 = 2\sqrt{\mu D}$ and hence (3.22) is satisfied.

Case 2: $\chi > \mu D$. In this case, first note we have $-\frac{s}{D}+\frac{2\chi}{Ds}U = -\frac{1}{Ds}(s^2-2\chi U) < 0$ under the condition $s\geq s_2 = \sqrt{2\chi}$ and $0\leq U < U_0 < U_m < 1$. Hence the equation $Q(h) = 0$ has two positive roots if and only if

which also provides the necessary and sufficient condition for some $h > 0$ satisfying (3.22). A direct computation shows that (3.27) is equivalent to the following condition given that $s\geq s_2 = \sqrt{2\chi}$

Since $0\leq U < U_0\leq U_m$, (3.28) is guaranteed if

which holds if and only if

since $U_m = \frac{1}{2}\Big(\frac{s^2}{\chi}-\sqrt{\big(\frac{s^2}{\chi})^2-\frac{2s^2}{\chi}}\Big)$, where $s_3 > \max\{s_1, s_2\}$ for any $\chi, \mu, D > 0$.

In summary, we prove (3.22) holds if one of the following conditions hold: (a) $\chi < \mu D$ and $s\geq s_1 = 2\sqrt{\mu D}$; (b) $\chi = \mu D$ and $s > s_1 = 2\sqrt{\mu D}$; (c) $\chi > \mu D$ and $s\geq s_3 = \sqrt{2\chi+2\mu D}$, as defined in (2.5).

Under (3.22), we get (3.21) which implies that the angle between the flow direction and inward normal vector of line $W = -hU$ is acute. Hence the flow along $\Gamma_4$ generated by system (3.6) points left upward and towards the interior of $\Omega$ as illustrated in Figure 1. This finishes the proof of (iv).

Step 3. Existence of a heteroclinic solution

Now we show that there is a heteroclinic trajectory of (3.6) joining the two critical points $(0, 0)$ and $(1, 0)$ under the condition (2.5) in Proposition 3.1. To this end, it suffices to show that the unstable manifold of the system (3.6) emanating from the saddle $(1, 0)$ points inside the invariant region.

Indeed, the slope of the nullcline $\Gamma_2$ at $(1, 0)$, denoted by $\frac{dW}{dU}\Big|^{\Gamma_2}_{(1, 0)}$, is

On the other hand, from (3.8)–(3.10) we see that the slope of the unstable manifold of (3.6) at $(1, 0)$ is

By (3.16) which holds true under condition (2.5), $\frac{2\chi}{s}-s = D\theta < 0$, it is straightforward to verify that

Thus, under the conditions (a)–(c), the unstable manifold emanating from the saddle $(1, 0)$ enters and is trapped inside the invariant region $\Omega$ and the heteroclinic trajectory eventually converge to the stable node $(0, 0)$ as $z \to \infty$ by the Poincaré-Bendixson theorem. Since the unstable manifold at the saddle $(1, 0)$ is one-dimensional, the heteroclinic solution to the system (3.6) with (3.7) is unique up to a translation.

Moreover, under the conditions (a)–(c) in Proposition 3.1, $\sigma_2 > 0$ and $\lambda_1 < \lambda_2 < 0$, see (3.8) and (3.13). Therefore the trajectory converges to its far-field states $(1, 0)$ and $(0, 0)$ exponentially as $z \to \pm\infty$. Thus the proof of Proposition 3.1 is completed.

Proof of Theorem 2.1. The existence of $U$ is given by Proposition 3.1, and $V$ is obtained directly from (3.3). This proves Theorem 2.1.

3.2.   Large wave speed analysis

From the results of Theorem 2.1, we see that the traveling wave solutions with large wave speed always exist. Next we shall explore to find an explicit approximation of the heteroclinic orbit for (3.6) in the phase-plane and the traveling wave profile for large wave speeds.

The heteroclinic trajectory obtained in Proposition 3.1 satisfies

If we let

Equation (3.29) can be rewritten as

where

When $s$ is large, $\varepsilon$ is a small parameter and we may expand $y$ as a power series in $\varepsilon$

After substituting this expansion into Eq (3.30) and match powers of $\varepsilon$, we get

and so on, where prime now denotes the differentiation with respect to $U$. Hence the heteroclinic trajectory can be approximated by

which can also be rewritten, in terms of the original variables $W$ and $U$, as

which gives an approximation of explicit heteroclinic solution of (3.6) obtained in Proposition 3.1 for large wave speeds.

Next we are more interested in the traveling wave solution in the physical plane. For this, we need to return to the Eq (3.5). Setting

Equation (3.5) takes the form

where prime now indicates differentiation with respect to $\xi$. When $s > 0$ is large, we again think of $\varepsilon$ as a small parameter and expand $U$ in powers of $\varepsilon$:

Substituting the above expansion into Eq (3.31) and match powers of $\varepsilon$, we get

and so on. Notice that both Eq (3.32) and our traveling wave solutions are invariant to translation in the independent variable $\xi$. Hence without loss of generality, we may take $\xi = 0$ to be the point where $U = 1/2$ for all $\varepsilon$. In other words, we supplement the equations in (3.32) with the conditions

The solution of the first equation of (3.32) subject to condition (3.33) has a simple form

Then substituting this solution into the second equation of (3.32) and solving the resulting equation with condition (3.33), we obtain

Hence in terms of the original variable $z$, when the wave speed $s > 0$ is large, an explicit traveling wave profile $(U, V)$ of (3.1) and (3.2) can be approximated as

and $V(z, s) = -\frac{U(z, s)}{s}$ from (3.4).

4.   Vanishing diffusion limit

In this section, we establish the existence of traveling wave solutions of (1.4) when $\epsilon > 0$ is small. We then establish the vanishing diffusion limit of traveling wave solutions of (1.4) as $\epsilon\rightarrow 0$.

We note that the traveling waves solution $(U, V)(z)$ of (1.4) satisfies (2.3) and (2.4). For convenience, we rewrite them below

with boundary conditions

Integrating the second equation of (4.1) from $-\infty$ to $\infty$ and using (4.2), we have

Solving (4.3) for $s$, we obtain

Moreover, from (4.2) we have

Then substituting $\eta = 0$ into (4.3) and solving for $s$ in terms of $v_-$ and $u_- = 1$, we have

This shows that the wave speed of (1.4) is convergent as $\epsilon \to 0$ and hence gives a necessary condition to show the convergence of traveling wave solutions of (1.4) as $\epsilon \to 0$.

Now we are in a position to prove Theorem 2.2.

Proof of Theorem 2.2. We shall employ the geometric singular perturbation theory ^[33,42,43] to prove Theorem 2.2. Setting $U' = W$ and $V' = Z$ where $' = \frac{d}{d z}$, we obtain a system of first order differential equations from (4.1) as follows

with boundary conditions (4.2) and $W(-\infty) = W(+\infty) = 0$, $Z(-\infty) = Z(+\infty) = 0$. The system (4.5) is referred to as the slow system ^[43]. The solution of (4.1) and (4.2) is that of (4.5) with the above boundary conditions.

Setting $\epsilon = 0$ in the fourth equation of (4.5), we obtain an invariant manifold $M_0$ defined by

Hence the equations on the invariant manifold $M_0$ satisfies

The first two equations of (4.6) are nothing but (3.6). It has been shown in Proposition 3.1 that under the condition (2.5), (4.6) with (3.7) has a solution $(U^0, W^0)$ which is unique up to a translation. Therefore (4.5) with $\epsilon = 0$ subject to (4.2) has a unique traveling wave solution $(U^0, W^0, V^0, Z^0)$ up to a translation, where $Z^0 = -\frac{W^0}{s}, V^0 = -\frac{U^0}{s}$.

Now we define the rescaling $\tau = \frac{z}{\epsilon}$, and convert the system (4.5) into a fast system

where $\dot{f} = \frac{df}{d \tau}$. Note that at any point on $M_0$, $\frac{\partial G}{\partial Z}|_{\epsilon = 0} = -s \ne 0$. Hence $M_0$ is normally hyperbolic for the fast system (4.7) with $\epsilon = 0$. By Fenichel's invariant manifold theorem ^[43], for $\epsilon > 0$ sufficiently small, there is a slow manifold $M_{\epsilon}$ that lies within $O(\epsilon)$ neighborhood of $M_0$ and is diffeomorphic to $M_0$. Moreover it is locally invariant under the flow of (4.7) and can be written as

Then the slow system (4.5) on $M_{\epsilon}$ can be written as

which is a regular perturbation of (4.6).

Noting that the third equation of (4.8) is decoupled from the first two equations, we only need to solve the first two equations and hence get $V$ directly from the third equation. It has been shown in Proposition 3.1 that (4.6) subject to (4.2) has a one-dimensional unstable manifold near $u_-$, denoted by $\mathcal{U}^-$, and a one-dimensional stable manifold near $u_+$, denoted by $\mathcal{S}^+$. The transversal intersection $\mathcal{U}^- \cap \mathcal{S}^+$ gives the heteroclinic orbit $(U^0(z), W^0(z))$. Then by the geometric singular perturbation theory(see ^[42] or ^[43]), for sufficiently small $\epsilon > 0$, there is a heteroclinic orbit $(U^{\epsilon}, W^{\epsilon})$ of (4.5) on $M_{\epsilon}$, which is a small perturbation of $(U^0, W^0)$, satisfying

Moreover, since it was shown in Proposition 3.1 that $(U^0, W^0)$ converges to its far-field states $(u_\pm, w_\pm)$ exponentially as $z \to \pm\infty$, then for sufficiently small $\epsilon > 0$, the orbit $(U^{\epsilon}, W^{\epsilon})$, obtained from the above geometric singular perturbation method, also converges to the far-field states $(u_\pm, w_\pm)$ exponentially as $z \to \pm\infty$.

Note that on $M_{\epsilon}$, $V^{\epsilon}(z) = -\frac{U^{\epsilon}(z)}{s}+O(\epsilon) = -\frac{U^0(z)}{s}+O(\epsilon) = V^0(z)+O(\epsilon)$. It is evident that

and $V^{\epsilon}$ also converges to the far-field states $v_\pm$ exponentially as $z \to \pm\infty$ in that $V^0$ does so. This completes the proof of Theorem 2.2.

Proof of Theorem 2.3. The existence of $U$ has been given in Theorem 2.1. By (1.3), we have

which yields that

where $C(0) > 0$. By (1.3) and (3.4), we have $s = \frac{C}{C'}(-\infty)$.

Since $V(z) \leq 0$ and $V(-\infty) = v_- < 0$, then $-\int_0^z V(y)dy \to -\infty$ as $z \to -\infty$ and hence $C(-\infty) = c_- = 0$. Moreover $-\int_0^{\infty} V(y)dy$ is bounded since $V(z) \to v_+ = 0$ exponentially as $z \to \infty$. Let $-\int_0^{\infty} V(y)dy = M$. Then $C(\infty) = c_+ = C(0)e^M > 0$. We obtain a uniformly bounded traveling wave solution $C$ satisfying (2.2)

The monotonicity of $C$ is derived from $C' = -V C > 0$ where $V < 0$ and $C > 0$ for all $z \in \mathbb{R}$. This finishes the proof of Theorem 2.3 (1).

We proceed to prove Theorem 2.3 (2). Using Theorem 2.2 and the Cole-Hopf transformation (1.3), we prove, for small $\epsilon > 0$, the existence of traveling wave solution $C^{\epsilon}$ and its convergence to the far-field states exponentially as $z \to \pm\infty$ as in (1). We are left only to prove the convergence of $C^{\epsilon}$ as $\epsilon\rightarrow 0$, as the convergence of $U^\epsilon$ as $\epsilon\rightarrow 0$ has been given in Theorem 2.2. Indeed, it follows from (1.3) that

provided that $C^{\epsilon}(0) = C^0(0)$. From Theorem 2.1, we know that $-\int_0^{\infty} V^0(y)dy$ is bounded since $V^0(z) \to 0$ exponentially as $z \to \infty$. Thus $C^0$ is monotone and tends to the far-field states exponentially as $z \to \pm\infty$. Then (4.11) alongside (4.10) yields

This completes the proof of Theorem 2.3.

5.   Proof of Theorem 2.4

In this section, we study the stability of traveling wave solutions $(U(x-st), V(x-st))$ of the system (1.4) obtained in Theorem 2.4. To this end, we consider the Cauchy problem of (1.4) in the moving coordinate $z = x-st$

with initial data

where $(u_0, v_0)(z)$ is a perturbation of the traveling wave solution $(U(z), V(z))$.

Since the second equation of (5.1) is in conservative form, the technique of taking anti-derivative is used for the perturbation (cf. ^[20]). Therefore the solution to the Cauchy problem of (5.1) can be decomposed as

where $\phi = u-U$ denotes the perturbation of $u$ away from the traveling wave profile $U$ and $\psi$ is the antiderivatives of the perturbation $v-V$.

We consider $(\phi, \psi)$ in the Sobolev space

Since $v_+-v_-\neq 0$ and the second equation in (5.1) is a conservation law, there is a translation constant $z_0$ such that

which leads to

Let

Then $\psi(\pm \infty, 0) = 0.$ From the second equation in (5.1) it follows that

Now substituting (5.2) into (5.1) and then integrating the second equation with respect to $z$, we derive that the perturbation function $(\phi(z, t), \psi(z, t))$ satisfies

For simplicity of notations, we assume the shift $z_0 = 0$ in what follows. The linear part of the system (5.4) yields

where $L$ is a closed operator defined by

with

We can rewrite the linear operator $L$ as

where

Note that $A_1(z)$ and $A_2(z)$ are exponentially convergent as $z\to \pm \infty$ since $U, V,$ and $V'$ are exponentially convergent. If $\epsilon > 0$, then ${\bf d}$ is a positive definite matrix, and as a consequence the operator $L$ is sectorial and generates an analytic semigroup (see page 83 of ^[44]). In this case, the spectral stability (reps. instability) implies linear stability (resp. instability), cf. ^[45].

By the standard spectral theory ^[46], the boundary of the essential spectrum of $L$ can be described by that of limiting operator $L^\pm$ as $z\rightarrow \pm \infty$

The boundary of the essential spectrum of $L$ is described by the following curves

where

Evaluating $(u_{+}, v_{+}) = (0, v_+)$ in $A^{+}(\tau)$, $\lambda \in S^{+}$ satisfies

Since $\mu$ is positive, $Re(\lambda_2) = -D \tau^{2} + \mu > 0$ for some $\tau \in \mathbb{R}$. Therefore

Hence the traveling wave solutions of (1.4) with $\epsilon > 0$ are linearly unstable against perturbations.

However, when $\epsilon = 0$, we are unable to show the linearized operator $L$ generates an analytical semigroup, and hence we only can conclude that the traveling wave solutions are spectrally unstable. The proof of Theorem 2.4 is completed.

6.   Simulations and discussion

In this paper, we prove the existence of traveling wave solutions to the singular Keller-Segel system (1.1) with the logistic growth. To avoid the singularity, we first establish the existence of traveling wave solutions to the transformed system (1.4) with $\epsilon = 0$ by the phase-plane analysis and then transfer the results to (1.1) via the Cole-Hopf transformation (1.3). By the geometric singular perturbation theory, we study the convergence of traveling wave solutions of (1.1) as $\epsilon\rightarrow 0$. Moreover, we show that traveling wave solutions of (1.4) are linearly unstable if $\epsilon > 0$ and spectrally unstable if $\epsilon = 0$ in the Sobolev space $X = H^1(\mathbb{R}) \times H^2(\mathbb{R})$. The instability is mainly caused by the cell growth at the right far-field state as observed from the essential spectrum given in (5.5). This is similar to the Fisher-KPP equation. It is known that the traveling wave solution of the Fisher-KPP equation is asymptotically stable to small perturbation of compact support (cf. ^[47]) or initial value with fast decaying in the far field (cf. ^[48]). Hence naturally we ask whether the traveling wave solutions of (1.1) will have similar stability properties to the Fisher-KPP equation. However this question is much harder than the Fisher-KPP equation to investigate in that (1.1) is a strongly coupled system with singularity. Below we shall use numerical simulations to illustrate the traveling wave profiles degenerated by the singular Keller-Segel system (1.1) is stable if the initial data decay fast. Similar to the analysis, we shall not simulate (1.1) directly due to the singularity, and instead we employ the Cole-Hopf transformation (1.3) and simulate the reformulated system

with initial data

where $v_0(x) = -(\log c_0)_x = -\frac{c_{0x}}{c_0}$ and the values of $u_\pm, v_\pm, c_\pm$ are given in (2.2) and (2.4). Since the traveling wave solutions converge to the asymptotic states exponentially as $x \to \pm\infty$, the domain $\mathbb{R}$ can be effectively approximated by a finite interval with a suitably large length. In simulations, we approximate the boundary conditions by Dirichlet boundary conditions to comply with the initial data. The Matlab PDE solver based on finite difference scheme is implemented to perform the numerical computations. We first construct an approximate traveling wave profile $(U, C)(x)$ for (6.1) as

where $v_- < 0$ is the far-field state of $V$ at $-\infty$. By the transformation (1.3), the traveling wave profile satisfying (2.4) for $V(x)$ is

Thus the left and right asymptotic states of the traveling wave profile $(U, V, C)$ satisfy $u_+ = c_- = v_+ = 0$, where $c_+ > 0$ can be arbitrarily chosen and we set $c_+ = 1$ in our simulations. We remark that the value of $v_-$ can not be arbitrary since it is related to the wave speed $s$, where $v_- = -\frac{1}{s}$ as $\epsilon = 0$ (see (3.4)). The virtue wave speed $s$ may depend on $D, \chi, \mu$ or initial values and remains unknown. But it can be numerically approximated. Next we choose appropriate perturbations. Note that instability shown in Theorem 2.4 is caused by the linear growth at the far-field state $(1, 0)$, hence we shall impose exponentially (fast) decay initial function, and assume the initial value is a small perturbation of $(U, V, C)$ with exponential decay as $x \to \infty$. Precisely for numerical simulations we set the initial value $(u_0, v_0, c_0$) as

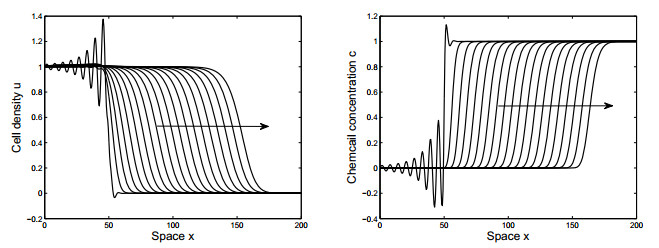
In simulations, we first numerically find the approximate value of $v_-$ and then plug it into (6.3). The numerical propagating wave profiles of (1.1) with $\epsilon = 0$ are plotted in Figure 2 for $\chi < \mu D$ and in Figure 3 for $\chi > \mu D$, where we do observe that solutions stabilize into stable traveling wave profiles. This indicates that traveling wave solutions of (1.1) are stable if the initial data decay fast (like exponential decay) at far field and leave an interesting question to explore in the future.

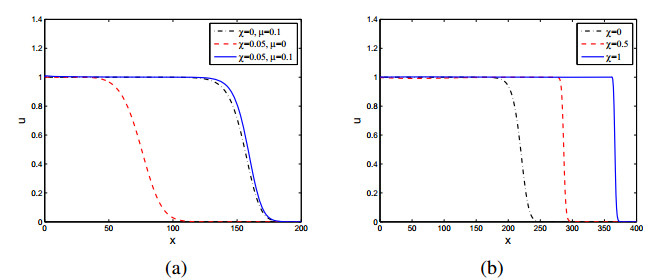
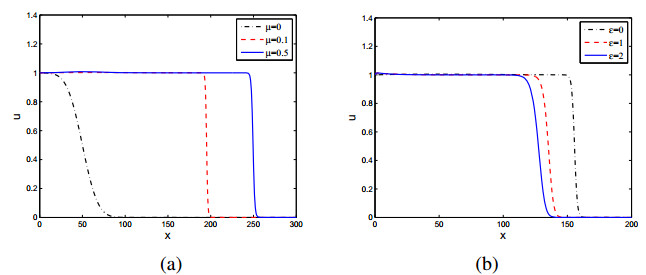
In the present paper, how the system parameters affect the wave propagation dynamics like spreading speed is not examined. We first explore the effect of chemotaxis intensity on the wave propagation. When $\chi < \mu D$, our analytical results in Theorem 2.3 shows that the Keller-Segel system (1.1) with $\epsilon = 0$ has the same minimal wave speed $2\sqrt{\mu D}$ as the Fisher-KPP equation. We underline that although the existence of minimal wave speed of (1.1) with $\epsilon > 0$ was proved in [35,Theorem 1.1], the exact minimal wave speed was not found. In this paper, we identify the minimal wave speed in the case of weak chemotaxis for (1.1) with $\epsilon = 0$. Our numerical simulations shown in Figure 4(a) confirm this analytical result, where we see that the traveling wave fronts for both $\mu = 0$ and $\mu > 0$ touch zero at the same location at the same time. This also indicates that if $\chi$ is small so that $\chi < \mu D$, the chemotaxis will not reduce nor increase the spreading speed, which leaves another interesting question for future studies. If we increase the chemotaxis intensity, we find that the wave propagation properties will change. In particular, the chemotaxis obviously increases the wave propagation speed by comparing the plots in Figure 4(b) for different values of $\chi$. How to show that the strong chemotaxis increases the propagating (or spreading) speed imposes a fascinating open question to investigate. From both Figure 4(a), (b), we also observe that the propagating (or spreading) speed of the Keller-Segel model without logistic source (i.e., $\mu = 0)$ can be smaller or larger than the Fisher-KPP equation (i.e., $\chi = 0$) depending on the intensity of chemotaxis (compare the red and black curves). From the numerical simulations shown in Figure 5(a), we find that the logistic source may increase the wave propagation speed. From both Figures 4(b) and 5(a), we observe that both chemotaxis and logistic source may increase the wave propagation speed and hence favor the species invasion. Lastly we investigate the effect of the chemical diffusion rate on the wave propagation. The numerical simulations shown in Figure 5 indicate that the chemical diffusion rate $\epsilon$ will decrease the wave propagation speed, in contrast to the classical reaction-diffusion equation (like the Fisher-KPP equation) in which diffusion usually enhances the wave propagation speed.

Acknowledgments

We are grateful to the two referees for their careful reading and valuable comments which help us considerably improve the precision and exposition of this paper. The research of Zhi-An Wang was partially supported by the Hong Kong RGC GRF grant No. PolyU 153055/18P (Project P0005472) and PolyU 15304720 (Project P0032967).

Conflict of interest

The authors declare there is no conflict of interest.