To Alberto Farina, with esteem and affection.
1.
Introduction
The main result of this paper concerns the validity of the comparison principle
when u and v are viscosity solutions of variable coefficient second order gradient free differential inclusions
where Ω⊂RN is a bounded domain and Θ:Ω⊸R×S(N) is a suitable set valued map. We will show that the comparison principle holds if Θ is a proper elliptic map which is Hausdorff continuous (see Theorem 1.1 below). Proper ellipticity of the map means that Θ takes values in the proper elliptic subsets of R×S(N). As formalized in Definition 2.1, this means that each Θ(x) is a non empty, closed, and proper subset of R×S(N) which is Q-monotone; that is,
where S(N) denotes the space of symmetric N×N matrices with its natural partial ordering. Hausdorff continuity just means that Θ is continuous as a map from Euclidian space into the metric space of closed subsets of R×S(N) equipped with the Hausdorff distance (see Definition 3.1 and the remarks which follow). For proper elliptic maps, we will show in Proposition 3.4 that this (locally uniform) continuity is equivalent to the statement that: for each Ω′⊂⊂Ω and η>0, there exists δ=δ(η,Ω′)>0 such that for each x,y∈Ω′
Our main result will then be used to establish the validity of the comparison principle for second order gradient-free fully nonlinear PDEs of the form
where F is a continuous function of its arguments. The Eq (1.5) we treat will be proper elliptic in a sense which is inspired by Krylov's general notion of ellipticity [18]. More precisely, one shifts attention from the Eq (1.5) to the differential inclusion
where one requires that
If Θ is a proper elliptic map, then the inclusion (1.7) is called a proper elliptic branch of the Eq (1.5). We will give sufficient conditions on the operator F which ensure the existence of a continuous proper elliptic map Θ such that the branch condition (1.7) holds and for which viscosity solutions u,v of the differential inclusion (1.2) correspond to admissible viscosity subsolutions, supersolutions of the differential equation. In this way, the comparison principle for the Eq (1.5) follows from the validity of the comparison principle for (1.2).
In order to carry out this program, we will treat operators F which are proper elliptic in the sense that
where either
or
The notion of admissibility mentioned above uses Φ as an additional constraint on the test functions (or test jets) used in the viscosity formulation of subsolutions and supersolutions. In the unconstrained case (1.10), this constraint is silent and one recovers the classical viscosity formulations. On the other hand, the constrained case (1.9) arises in situations where F(x,⋅,⋅) is suitably monotone only on proper subsets Φ(x)⊊R×S(N), and the admissibility constraint is essential. Treating such situations in a general and coherent way is a main motivation of the present work.
Before giving additional details of the possible applications to PDEs, we discuss the comparison principle (1.1) in the framework of nonlinear potential theory: given a Θ-subharmonic function u and a Θ-superharmonic function v; that is, upper semicontinuous and lower semicontinuous functions u and v on ¯Ω satisfying (1.2) in a viscosity sense (see Definition 2.4), we look for monotonicity and regularity properties on Θ that guarantee the validity of (1.1). This program was initiated systematically in the groundbreaking work of Harvey and Lawson [12] for differential inclusions
that is, in the context of a pure second order constant coefficient potential theory in which the elliptic map appearing in the inclusion does not depend on the x variable. Such a potential theory might come from a purely second order operator of interest. In this situation, which corresponds to Θ(x)=R×Θ on Ω in (1.2), it has been proven that the mere monotonicity assumption Θ+P⊂Θ for all P≥0 is sufficient for the comparison principle to hold. The introduction of a genuine x-dependence and further constraints on (u(x),Du(x)) poses then the natural question of what are minimal conditions on the map Θ that guarantee the validity of the comparison principle. An important step in this program has been settled in a subsequent work [13] for general differential inclusions involving the full 2-jet of u on Riemannian manifolds; the approach in [13] is based on the reduction of the x-dependent case to a constant map (called constant coefficient subequation) of the form (u(x),Du(x),D2u(x))∈F⊂R×RN×S(N), for which a general theory is developed. We mention that in the case of constant maps F on Euclidean space, further generalizations in the direction of minimal monotonicity assumptions on F are a work in progress [7]. While the general approach of [13] covers a wide variety of situations, it requires implicit assumptions on the x-dependence in the problem. In partial contrast, [8] has been devoted to the search for more explicit conditions in the special case of (u,Du)-independent inclusions D2u(x)∈Ψ(x)⊂S(N), with a particular focus placed on the minimal assumptions on the set-valued map Ψ needed for the comparison principle. A main aim of the present work is to generalize results of [8] to Du-independent inclusions of the form (1.2), which also allow for constraints on u(x), and again with the purpose of identifying monotonicity and regularity properties of Θ as a set-valued map that lead to comparison principles. We finally mention that a recent work [15] addresses similar (and additional) issues for maps of the form F(x)={(u,p,A):F(u,p,A)≥f(x)}, namely for maps F that are given by superlevel sets of a proper elliptic operator. For gradient-free operators, results obtained in [15] fit into our theory.
We now explain how we aim to prove the comparison principle (1.1) for a variable coefficient gradient-free potential theory determined by Θ. We follow the approach initiated in [12] as continued in [8]. There are three main ingredients in this approach: monotonicity, duality and continuity. The natural monotonicity in this context is to require that Θ(x) in Q-monotone in the sense (1.3). For the PDE applications, when Θ is suitably associated to a differential operator F=F(x,r,A), this Q-monotonicity reflects the typical monotonicity properties of properness (decreasing in r) and degenerate ellipticity (increasing in A) for F. The natural notion of duality involves the Dirichet dual ˜Θ of Θ, defined pointwise by
and introduced by Harvey and Lawson in [12]. The dual map ˜Θ is proper elliptic if and only if Θ is. Moreover, v is Θ-superharmonic if and only if ˜u=−v is ˜Θ-subharmonic. The first step in the monotonicity-duality approach for comparison (1.1) is to prove the relevant subharmonic addition theorem, which in this setting means (see Theorem 5.2): given a Θ-subharmonic function u and a Θ-superharmonic function v
It is worth noting that ˜Q is a constant map, even when Θ and ˜Θ are not. The subharmonic addition theorem reduces the comparison principle (1.1) to the validity of the zero maximum principle (see Theorem 4.1): for every w which is ˜Q-subharmonic on Ω
Our proof of (1.13) exploits the following characterization of ˜Q-subharmonics as those functions w whose positive part satisfies a comparison principle with respect to affine functions a: for all open subsets X of Ω,
The proof of the fundamental subharmonic addition theorem (1.12) relies on a reduction to semi-convex functions. To perform this reduction, based on sup-convolution approximations, one needs some control on how the proper elliptic sets Θ(x) behave as x varies in Ω. In particular, one needs to control the distance between Θ(x) and Θ(y) as subsets of R×S(N). We will prove that a sufficient regularity condition is to requires the Hausdorff continuity of Θ taking values in the closed subsets of R×S(N), thus generalizing the analogous condition in [8] for maps with values in the closed subsets of S(N). Once the reduction to semi-convex functions is available, the subharmonic addition theorem is obtained by means of Dirichlet duality and a Jensen-type lemma on the passage of almost everywhere to everywhere information (see Lemma 5.4). Our main comparison result, generalizing the one in [8] for set-valued maps in S(N), is the following result (see Theorem 5.1 for the proof).
Theorem 1.1(Comparison principle: potential theoretic version). Let Θ be a Hausdorff continuous proper elliptic map on Ω. Then the comparison principle holds; that is, if u∈USC(¯Ω) and v∈LSC(¯Ω) are Θ-subharmonic and Θ-superharmonic respectively in Ω (in the sense of Definition 2.4), then
We now return to the discussion of some possible applications of our potential theoretic result to fully nonlinear PDE. There is an extensive literature for treating general fully nonlinear elliptic equations via viscosity methods, and several attempts to restate or relax standard structural conditions (such as those stated in [9]) have been proposed. For example, when the equation lacks of strict monotonicity in the u-variable, as in u-independent equations, one can rely on some strict monotonicity (in some direction) with respect to the Hessian variable, see e.g., [2,3,17]. As noted above, we are particularly interested in the constrained case where F(x,⋅,⋅) is proper elliptic only when restricted to some admissibility constraint set Φ(x)⊊R×S(N). By exploiting Krylov's idea of shifting the focus to the level sets of the operator F, the potential theoretic approach of Harvey and Lawson furnishes an elegant and unified framework to treat viscosity solutions with admissibility constraints in many situations that would otherwise require ad-hoc adjustments for a given operator F of interest.
In the constrained case, a first general application to PDEs based on the comparison principle for differential inclusions developed here, is a comparison principle for the Eq (1.5) under the following assumptions on F: there exists a proper elliptic map Φ:Ω→℘(R×S(N)) such that for each x∈Ω one has
and for each Ω′⊂⊂Ω and each η>0 there exists δ=δ(η,Ω′) such that
The condition (1.15) states that F(x,⋅,⋅) is proper elliptic if restricted to Φ(x). The conditions (1.16) and (1.17) guarantee that the constraint Φ(x) is compatible with the zero locus of the operator F, so that the map defined by
is proper elliptic and defines a proper elliptic branch of (1.5) (see Theorem 6.3). The condition (1.18) is a sufficient condition for Θ to be a Hausdorff continuous proper elliptic map, so that the comparison principle of Theorem 1.1 for Θ-sub/superharmonic functions can be applied (see Theorem 6.8). One then obtains the comparison principle for admissible viscosity solutions to the PDE (see Definition 6.4), provided that a mild non-degeneracy assumption on F holds (see formula (6.21) in the correspondence principle of Theorem 6.5). The resulting comparison principle is stated in the main Theorem 6.13, which also covers the unconstrained case where Φ(x)=R×S(N) for all x∈Ω.
Remark 1.2. Our main structural condition (1.18) reflects a precise geometrical property of the associated map Θ, which, in some cases, is weaker than the general classical conditions in [9] (as will be noted for the Eq (1.21) below). Such improvements using our method were also seen for the reduced class of equations F(x,D2u)=0 (see Remark 5.1 of [8]). The condition (1.18) can be regarded as a joint strict monotonicity with respect to (r,A) and regularity with respect to the x variable. On the other hand, the structural condition (1.18) is not necessary for Θ to be continuous. Moreover, in some cases it may be easier to check directly the continuity of Θ by using Remark 6.9. An important example where this occurs is given below in (1.22).
We now discuss various illustrations of our approach, in both constrained and unconstrained cases, where we will apply our method to two interesting model equations and their generalizations. An interesting feature of the methods presented here is how both situations can be placed into the same general framework.
In the constrained case, we will prove a comparison principle for equations arising in the study of hyperbolic affine hyperspheres. The relevant equation can be written in the form
where h≥0 is the negative of the curvature (when constant). These equations are proper elliptic on Φ:=Q and are particularly degenerate (a lack of strict monotonicity properties) for vanishing curvatures. The comparison principle for (1.20) is given in Theorem 6.14. This result is then generalized in Theorem 6.16 to the following class of perturbed Monge-Ampère equations
where g,m,M are continuous functions, and g(⋅) is increasing and positive on some open interval (r0,∞). For a perturbation matrix M which is merely continuous, the Eq (1.21) does not, in general, satisfy the standard structural condition (3.14) of Crandall-Ishii-Lions [9].
In the unconstrained case, we present a new comparison principle for the special Lagrangian potential equation
where {λi(A)}Ni=1 are the eigenvalues of A∈S(N) and the phase h takes values in the interval I:=(−Nπ/2,Nπ/2). This equation for h fixed is proper elliptic (but possibly highly degenerate) on all of Φ:=R×S(N). The Eq (1.22) with constant phases h(x)≡θ was introduced by Harvey-Lawson [11] in the study of calibrated geometries and existence and uniqueness of viscosity solutions in this case is known from their work (see [12] and [16]). The inhomogeneous equation also has a natural geometric interpretation (see, for example the discussion in [16]), but it is less well understood. A key feature in the theory is played by the special phase values
which determine the phase intervals
In Theorem 6.18, we show that the comparison principle holds if h is continuous and takes values in any one of the phase intervals (1.24); that is, if
Our proof involves a delicate argument to show that the natural proper elliptic map
is Hausdorff continuous if (1.25) holds and hence the comparison principle for (1.22) follows from Theorem 1.1.
It is important to note that the comparison principle (and much more) is known in the special case for h taking values in the top phase interval I1=((N−2)π/2,Nπ/2) as shown in Dinew, Do and Tô [10]. An alternate proof is given by Harvey and Lawson [16] which makes use of the notion of tameness of the operator G(A):=∑Ni=1arctan(λi(A)) on the subequation G(θ):={A∈S(N):G(A)≥θ}).
It is also important to note that while the operator
is proper elliptic on all of Φ=R×S(N), it fails to satisfy our regularity condition (1.18) if h takes on any of the special values θk in (1.23). Indeed, we will show that the proper elliptic map Θ in (1.26) fails to be Hausdorff continuous if any continuous (and non constant) h takes on any of the special values (see Proposition 6.17). This leaves open the question whether comparison also holds for continuous h which takes on a special phase value (see Open Question on page 23 of [16]).
We have focused attention on proper elliptic pairs (F,Θ) which are compatible in the sense that (see Remark 6.6):
This ensures the correspondence between Θ subharmonics/superharmonics and admissible viscosity subsolutions/supersolutions of the equation determined by the operator F. Hence, given F one can pass to the potential theory determined by Θ and then "come back" to the admissible viscosity formulation for the operator F. However, in situations in which (F,Θ) are a proper elliptic pair, but the compatibility (1.28) fails, one could decide to use the potential theory determined by Θ as a replacement for a viscosity solution treatment of the equation. In the constrained case, compatibility fails if the non-degeneracy condition (6.21) fails.
As a final introductory remark, we have limited the present investigation to the validity of the comparison principle (1.1). Our comparison principles would yield uniqueness results for the Dirichlet problem on Ω in both the PDE and potential theoretic settings. In particular, we leave the important and interesting question of existence for the Dirichlet problem for a future work. An important feature of the methods pioneered by Harvey and Lawson is the determination (in terms of Θ) of the suitable boundary convexity needed to obtain existence. The reader might wish to consult [8,12,13,15] for the use of a Perron method for existence in many situations which would cover some of the equations and potential theories considered here. Finally, the use of viscosity solutions with admissibility constraints has been extended to include some elements of nonlinear spectral theory in [4], including characterization of principal eigenvalues and existence of associated principal eigenfunctions by maximum principle methods.
2.
Proper elliptic maps and their subharmonics
In all that follows, Ω⊂⊂RN will be a bounded open connected set and S(N) will denote the space of symmetric N×N matrices, which carries the usual partial ordering of the associated quadratic forms and λ1(A)≤⋯≤λN(A) denote the ordered eigenvalues of A∈S(N). We will denote by ℘(R×S(N)):={Φ:Φ⊂R×S(N)} and use the notations ¯Φ,Φ∘ and Φc for the closure, interior and complement of Φ∈℘(R×S(N)). We will also make use of spaces of semicontinuous functions
and
2.1. Proper elliptic maps and their duals
We begin with the definition of the class of set valued maps we will use, where we denote by
and
Definition 2.1. A map Θ:Ω→℘(R×S(N)) is said to be a proper elliptic map if for each x∈Ω, one has
and
that is, if (r,A)∈Θ then (r+s,A+P)∈Θ(x) for each s≤0 and P≥0. We will also say that Θ(x) is Q-monotone if (2.5) holds.
If E:={Φ⊂R×S(N):Φ is closed, non empty and proper with Φ+Q⊂Φ} , then a proper elliptic map is just a set valued map taking values in E, the collection of proper elliptic sets. Note that a proper elliptic map is strict as a set-valued map, namely it satisfies Θ(x)≠∅ for each x∈Ω (see Chapter 1 of Aubin and Cellina [1] for the elementary notions concerning set-valued maps).
An important example is provided by the constant map Θ(x)=Q for all x∈Ω with Q defined by (2.3). Clearly the Q-monotonicity (2.5) is related to the monotonicity properties of F(x,r,A) for proper and degenerate elliptic Eq (1.5). Notice that if Θ=Θ(x,A) independent of r∈R then we can identify Θ with an elliptic map in the sense of [8] and if Θ=Θ(A) is also independent of x we can identify Θ with an elliptic set (Dirichlet set) in the sense of [12].
A class of dual maps using the Dirichlet dual, introduced by Harvey-Lawson [12], plays an essential role in this theory.
Definition 2.2. Let Θ:Ω→℘(R×S(N)) be a proper elliptic map. The dual map ˜Θ:Ω→℘(R×S(N)) is defined pointwise by
An essential example is given by the dual to constant map Q, which is the constant map ˜Θ(x)=˜Q for each x∈Ω where
and
as a simple calculation shows. We record the following elementary properties which will be used throughout.
Proposition 2.3. Let Θ:Ω→℘(R×S(N)) be a proper elliptic map. Then the following properties hold.
(a) The dual ˜Θ:Ω→℘(R×S(N)) is a proper elliptic map. Moreover an arbitrary map Θ will be a proper elliptic map if its dual map is.
(b) The dual of ˜Θ is the map Θ.
(c) The sum of Θ and ˜Θ satisfies
Moreover, (r,A)∈Θ(x) if and only if (r+s,A+B)∈˜Q for each (s,B)∈˜Θ(x).
(d) For each x∈Ω one has
(e) For each x∈Ω one has
Proof. The claims (b) and (d) follow directly from the pointwise definition of the dual map (2.6). For the claim (e), recall that by definition the set Θ(x) is closed in the natural topology of R×S(N) for each x∈Ω, where Θ(x) has non empty interior. Each (r,A)∈Θ(x) can be written as the limit as ε→0+ of (r−ε,A+εI)∈Θ(x)+(N∘×P∘), and Θ(x)+(N∘×P∘)=[Θ(x)]∘. The claims (a) and (c) make use of various known identities for elliptic sets and elliptic maps as presented in [12] and [8].
2.2. Weakly subharmonic functions associated to proper elliptic maps
The main concept in this paper concerns the Θ-subharmonic functions on a domain Ω which are determined by a proper elliptic map Θ on Ω. These upper semicontinuous functions are defined in a pointwise and viscosity sense by requiring that the relevant second order subdifferential lies in Θ(x). Following the approach of Harvey and Lawson, the natural class of Θ-superharmonic functions will be characterized in terms of the ˜Θ-subharmonic functions with respect to the dual map (see Definition 2.4 and Remark 2.7). For u twice differentiable, to be Θ-subharmonic on Ω means that
that is; that the (reduced) 2-jet Jxu lies in the constraint set Θ(x) for each x∈Ω. We will say that u is strictly Θ-subharmonic in Ω if Jxu∈[Θ(x)]∘ for all x∈Ω. For u∈USC(Ω), one makes use of a viscosity definition. To this end, for each fixed x0∈Ω, consider the upper test jets
and the lower test jets
Definition 2.4. Let Θ be a proper elliptic map on Ω and x0∈Ω.
(a) A function u∈USC(Ω) will be called Θ-subharmonic in x0 if
and u is said to be Θ-subharmonic in Ω if (2.15) holds for each x0. The spaces of all such functions will be denoted by ΘSH(x0) and ΘSH(Ω) respectively.
(b) A function u∈LSC(Ω) will be called Θ-superharmonic in x0 if
(a) A function u∈C(Ω) will be called Θ-harmonic in Ω if it is both Θ-subharmonic and Θ-superharmonic in Ω.
A few remarks about Definition 2.4 are in order.
Remark 2.5. In the differential inclusion (2.15) there is no constraint made in the gradient variable, which corresponds to the gradient free equations that we treat here. If one denotes by J2=R×RN×S(N) the space of 2-jets with jet coordinates J=(r,p,A)∈J2, then the inclusion (2.15) is equivalent to
with a constraint set
that is a subset of the (full) 2-jet space and where
is the set of second order superjets. The reduced formulation (2.15) will be used throughout to simplify notation and to emphasize the gradient independent nature of the equations we consider.
Remark 2.6. Many equivalent choices for the upper/lower test functions φ which compete in (2.13), (2.14) could be used in Definition 2.4. For example, one could use upper test jets J+x0u corresponding to φ=Q a quadratic polynomial. One could also assume that (u−Q) has a strict maximum (of zero) in x0 where for some ε>0
or assume that
In all cases, the resulting spaces ΘSH(x0) and ΘSH(Ω) remain the same. For a proof, see Lemma C.1 of [7] which treats general pointwise inclusions in the form (2.17).
Remark 2.7. Since [Θ(x0)∘]c=−˜Θ(x0) and J+x0(−u)=−J−x0u, one has
that is, Θ-superharmonicity can be expressed in terms of subharmonicity for the dual map.
Remark 2.8. The following coherence principle for the classical and weak notions of Θ-subharmonicity holds: let u∈USC(Ω) be twice differentiable in x0∈Ω *. Then
* u(x)=u(x0)+⟨p,x−x0⟩+12⟨A(x−x0),x−x0⟩+o(|x−x0|2) as x→x0 for some (p,A)∈RN×S(N). Hence u is differentiable in x0 with p=Du(x0) and we denote by D2u(x0) the matrix A.
The forward implication makes use of the Taylor expansion for u and the fact (2.11), while the reverse implication uses only the positivity property Θ(x)+({0}×P)⊂Θ(x) for each x∈Ω, which is contained in (2.5). For more details see Remark 2.7 of [7].
We will now give a useful alternate characterization of the spaces of Θ-subharmonic functions which exploits a pointwise characterization of subaffine functions. We recall that if X⊂RN is open, w∈USC(X) is said to be subaffine on X if for each domain Ω⊂⊂X and each affine function a one has
If (2.22) holds for each Ω, we write w∈SA(X), where one knows that for w∈USC(X)
which means that for each Ω⊂⊂X and for each x0∈Ω and for each upper test function φ for w at x0 one must have
One also knows that w∈SA(X) if and only if for each x0∈X there is no triple (ε,ρ,a) with ε,ρ>0 and a affine such that
We will write w∈SA(x0) if (2.25) holds.
The following lemma gives a pointwise characterization of the space ˜QSH(Ω). Additional characterizations and properties of ˜QSH(Ω) will be briefly discussed in Section 4.
Lemma 2.9. Given w∈USC(Ω) and x0∈Ω, one has w∈˜QSH(x0) if and only if
Proof. Assume that w∈˜QSH(x0) but that (2.26) fails; that is,
and
Combining (2.28) with the pointwise characterization (2.25) one must have a triple (ε,ρ,a) such that
The function φ(⋅):=a(⋅)−ε|⋅−x0|2 is then a C2 upper test function for w at x0 and hence by (2.27) one must have
but r=a(x0)>0 by (2.29) and λN(−2εI)<0 so A=−2εI∉˜P, a contradiction.
On the other hand, if (2.26) holds, but w∈˜QSH(x0) fails, there must be an upper test function φ for w at x0 which is C2 near x0 and satisfies
with
that is,
One has w(x0)=φ(x0)>0 by the first condition in (2.30) and (2.32). Hence (2.26) implies that w∈SA(x0) and hence D2φ(x0)∈˜P by (2.23) (and in particular (2.24)), but this contradicts the second condition in (2.32).
We are now ready for the alternate characterization.
Theorem 2.10. Let Θ be a proper elliptic map on Ω.
(a) A function u∈USC(Ω) is Θ-subharmonic in x0∈Ω if and only if
(b) A function u∈LSC(Ω) is Θ-superharmonic in x0∈Ω if and only if
Proof. Since (b) is equivalent to the statement that −u∈˜ΘSH(x0), claim (b) follows from claim (a) by duality since the dual of ˜Q(x0) is Q(x0). We argue by contradiction.
Assume first that u∈ΘSH(x0) but that (2.33) fails; that is, one has
but there exists v which is C2 near x0 satisfying
where the last condition in (2.36) means that there is a triple (ε0,ρ,a) with
where (2.37) also holds with ε in place of ε0 for each ε∈(0,ε0]. For each such ε>0, consider the function vε defined by
Since Jx0v∈˜Θ(x0) by (2.36) one has for every ε>0
while
and using (2.37) with the affine function aε:=a−ε one has
Hence with 0<ε<(u+v)(x0), the function φε:=−vε+aε is an upper test function for u at x0 and satisfies
by (2.35). However, since a(x0)>0 by (2.36) and (2.37), then (2.39) yields
which means Jx0v∈−[Θ(x0)]∘=˜Θ(x0)c which contradicts the first condition in (2.36).
On the other hand, if (2.33) holds, but u∉ΘSH(x0), then there exists φ which is C2 near x0 and satisfies for some ρ>0
and
For each ε>0 consider the function vε:=−φ+ε−εQx0 with Qx0 as in (2.38). These vε are C2 near x0 and satisfy
where, by (2.42), one has −Jx0φ∈−[Θ(x0)]c=[˜Θ(x0)]∘ and hence
However, using (2.41) and the definitions of vε and Qx0, one has
and
The formulas (2.46)–(2.47) with the triple (ε/2,ρ,ε) show that (u+vε)∉˜QSH(x0), which combined with (2.45) says that u+vε∉˜Q(x0) and hence (2.44) contradicts (2.33) for the function vε with ε>0 and small.
We will often use this characterization to show that that u∈USC(Ω) belongs to ΘSH(Ω) by using an argument by contradiction. We formalize this in the following remark.
Remark 2.11. Given u∈USC(Ω) and x0∈Ω. If u∉ΘSH(x0) then there exists a function v which is C2 near x0 with Jx0v∈˜Θ(x0) and there exists a triple (ε,ρ,a) such that
since (2.48) is the meaning of u+v∉˜QSH(x0) (see Lemma 2.9 and (2.25)). Moreover, by reducing ε and altering the affine function a if need be, we can assume that v satisfies the stronger condition
by considering the perturbation vε:=v+εQx0−ε used in the proof of Theorem 2.10.
3.
Continuity of proper elliptic maps
In preparation for the comparison principle for proper elliptic maps and their applications to comparison principles for admissible viscosity solutions for proper elliptic branches of second order gradient free fully nonlinear Eq (1.5), we present a few elementary properties of Θ-subharmonic functions associated to proper elliptic maps. These properties will be needed in the proof of the subharmonic addition theorem (1.12) (which is stated in Theorem 5.2) and these properties depend on various degrees of continuity of the proper elliptic maps Θ.
We begin with describing the notion continuity that we will require, that of Hausdorff continuity. Given Φ⊂R×S(N) and ε>0 we will denote by
the ε-enlargement of the subset Φ where ||(r,A)||:=max{|r|,max1≤i≤N|λi(A)|} gives a norm on R×S(N). Proper elliptic maps take values in E⊂K(R×S(N)), where K(R×S(N)) are the closed subsets of R×S(N). One knows that (K(R×S(N)),dH) is a complete metric space with respect to the Hausdorff distance defined by
See Proposition 7.3.3 and Proposition 7.3.7 of Burago, Burago and Ivanov [5] for details on this structure, where we note that since the subsets of R×S(N) need not be bounded, the metric can take on the value +∞; in particular, one has
and with J:=R×S(N) one has
Definition 3.1. An arbitrary map Θ:Ω→K(R×S(N)) will be called Hausdorff continuous on Ω if for each x∈Ω and η>0 there exists δ=δ(x,η)>0 such that
The following (elementary) remark will have important consequences for the continuity of proper elliptic maps.
Remark 3.2. An arbitrary map Θ:Ω→K(R×S(N)) is Hausdorff continuous on Ω if and only if Ω is locally uniformly Hausdorff continuous; that is, for any Ω′⊂⊂Ω:
Indeed, if Θ is continuous on Ω⊂RN taking values in the metric space (K(R×S(N)),dH), the Heine-Cantor theorem gives the uniform continuity of Θ on ¯Ω′ compact (and hence on Ω′). On the other hand, with x∈Ω arbitrary, it is enough to consider Ω′=Bρ(x)(x)⊂⊂Ω to find the continuity of Θ at x.
Remark 3.3. From here on, we will use the shorter term continuous in place of Hausdorff continuous for maps Θ:Ω→K(R×S(N)).
For proper elliptic maps, (local) uniform continuity has useful equivalent formulations.
Proposition 3.4. Let Θ be a proper elliptic map on Ω and let Ω′⊆Ω. Then the following are equivalent:
(a) Θ is uniformly continuous on Ω′, that is (3.5) holds;
(b) For for each η>0 there exists δ=δ(η,Ω′)>0 such that
(c) For for each η>0 there exists δ=δ(η,Ω′)>0 such that for each x,y∈Ω′
The proof follows easily from the definitions of proper ellipticity and continuity for maps Θ:Ω→K(R×S(N)). See the proof of Proposition 3.3 in [8] for the analogous result for uniformly continuous elliptic maps Θ, which take values in K(S(N)). Notice by interchanging the roles of x and y in (3.7), one also must have Θ(y)+(−η,ηI)⊂Θ(x) if |x−y|<δ.
Remark 3.5. Property (b) of Proposition 3.4 is precisely the notion that the set valued map Θ:Ω′→℘(R×S(N)) is uniformly upper semicontinuous on Ω′ (see Chapter 1 of Aubin and Cellina [1] for the elementary notions concerning set-valued maps, including their semi-continuity). Hence, Proposition 3.4 says that for proper elliptic maps the (local) uniform upper semicontinuity of Θ as a set-valued map is equivalent to the (local) uniform continuity of the function Θ taking values in the metric space (K(R×S(N)),dH). Property (c) in terms of translations by multiples of (−1,I) is the form in which we will normally use the (local) uniform continuity.
We now show that continuity of Θ passes to the dual map and that uniform continuity extends to the boundary.
Proposition 3.6. Let Θ:Ω→E⊂K(R×S(N)) be an elliptic map. Then,
(a) Θ is (uniformly) continuous on Ω if and only the dual map ˜Θ is (uniformly) continuous on Ω.
(b) If Θ is uniformly continuous on Ω, then Θ extends to a uniformly continuous elliptic map on ¯Ω.
Proof. A straightforward adaptation of Proposition 3.5 of [8], which can be proven using the formulation (3.7), shows that Θ is uniformly continuous on Ω if and only the dual map ˜Θ is. It is worth noting that the δ,η relation is the same for Θ and its dual. Finally, a map that is merely continuous on Ω is uniformly continuous on ¯Ω′, for any Ω′⊂⊂Ω, thus its dual ˜Θ is continuous on Ω, which completes part (a).
Part (b) can be proven using the argument in [8,Proposition 3.10]; that is, for any x0∈∂Ω, define Θ(x0) in the usual way as the limiting set of the Cauchy sequence {Θ(xk)}, where {xk}⊂Ω is an arbitrary sequence converging to x0. Then, one can verify that properties (2.4) and (2.5) pass to the limit.
We conclude this section with the elementary properties of Θ-subharmonic functions associated to continuous proper elliptic maps.
Proposition 3.7. Let Θ be a continuous elliptic map on Ω.
(1) (Maximum Property) u,v∈ΘSH(Ω) ⇒ max{u,v}∈ΘSH(Ω);
(2) (Sliding Property) u∈ΘSH(Ω) ⇒ u−m∈ΘSH(Ω) for each constant m≥0;
(3) (Families Locally Bounded Above Property)
Let F⊂ΘSH(Ω) be a non empty family of functions which are locally uniformly bounded from above. Then the upper envelope u:=supf∈Ff has upper semicontinuous regularization † u∗∈ΘSH(Ω).
† We recall that u∗(x):=lim supr→0+{u(y):y∈Ω∩¯Br(x)} for each x∈Ω.
If, in addition, Θ is uniformly continuous on Ω,
(4) (Uniform Translation Property) All sufficiently small translates of u∈ΘSH(Ω) have a fixed small quadratic perturbation which is Θ-subharmonic on the domain of the translate. In particular, for each η>0 if δ=δ(η)>0 is chosen as in the formulation (3.7) of uniform continuity then ‡.
‡If Θ is a constant elliptic map, then a stronger consequence than (4) follows, namely uy=u(⋅−y)∈ΘSH(Ωδ) for all y∈Bδ(0). This property plays a key role in [12] but may fail if Θ is not constant.
with
(5) (Existence of Bounded Θ-harmonics) There exist smooth bounded Θ-harmonic functions on Ω of the form
for each sufficiently large τ.
Moreover, one also has the properties (1)–(5) for ˜Θ-subharmonic functions since ˜Θ is (uniformly) continuous if Θ is by Proposition 3.6
Proof. We will make use of the characterization formula (2.33) and argue by contradiction (as discussed in Remark 2.11) to prove the Maximum Property (1) and the Sliding Property (2). If (1) were false, then w:=max{u,v}∉ΘSH(x0) for some x0∈Ω and there exist φ which is C2 near x0 with Jx0φ∈˜Θ(x0) and a triple (ε,ρ,a) such that
Since u,v≤w everywhere, in (3.10) we can replace w with u when w(x0)=u(x0) or w with v when w(x0)=v(x0) to contradict u,v∈ΘSH(x0).
Similarly, if (2) were false, then for some x0∈Ω there exist φ which is C2 near x0 with Jx0φ∈˜Θ(x0) and a triple (ε,ρ,a) such that
Setting ˜φ:=φ−m in (3.11) gives a contradiction to u∈ΘSH(x0) since Jx0˜φ=Jx0φ+(−m,0)∈˜Θ(x0).
For the Families locally Bounded Above Property (3), using the characterization (2.33), it suffices to show that for each fixed x0∈Ω and each fixed v which is C2 near x0 with Jx0v∈˜Θ(x0) one has
where w∗(x)=(u+v)∗(x) for all x∈Ω by the continuity of v. We will use an argument by contradiction to show that (3.12) holds.
First, we will show that there is a family of quadratic perturbations of w∗ which are ˜Q-subharmonic in each x0∈Ω fixed. Using the local uniform continuity of ˜Θ with any sequence {εj}j∈N such that εj↘0 as j→+∞, one has the existence of δj=δj(εj/2) for which
Take δj even smaller (if necessary) so that the C2 function satisfies
With Qx0(⋅):=12|⋅−x0|2, consider the sequence of functions
For each j∈N and each f∈F⊂ΘSH(Ω) fixed, the characterization (2.33) says that the function f+v+εjQx0−εj (competing in the defintion of wj) is ˜Q-subharmonic in Bδj(x0)) provided that
which does hold. In fact,
which can be written as the sum
which by (3.13) and (3.14) belongs to ˜Θ(x)+Q⊂˜Θ(x) for each x∈Bδj(x0). Hence (3.16) holds and each wj is the sup over a family of ˜Q-subharmonic functions. Property (3) for the constant coefficient gradient free proper elliptic map ˜Q on the open set Bδj(x0) then gives (see Proposition D.1 (G) of [7]):
and hence by (3.15) and (3.12) one has
We are now ready to prove that (3.12) holds. If (3.12) were false, then there exists a triple (ε,ρ,a) such that
Take j∗ large enough to ensure that
so that
and with the affine function ˜a(⋅):=a(⋅)−εj∗ one has
The relations in (3.21) and (3.22) say that w∗j∗∉SA(x0) which contradicts (3.17).
For the Uniform Translation Property (4), we begin by noting that uy;η is well defined and upper-semicontinuous on Ωδ for each η>0 and y∈Bδ(0). It remains to show that for each x0∈Ωδ if v∈C2(Ω) satisfies
then
Define the test function ˆvy;η by ˆvy;η(x):=v(x−y)+η2(|x−y|2−ω) with ω as in (3.8)–(3.9). Notice that
where η2(|x0|2−ω)≤−η. Hence (3.25) yields
and hence for each η>0,y∈Bδ(0) one has
by the uniform continuity of ˜Θ and the non positivity of η2(|x0|2−ω)+η. In addition one has
where the positivity comes from (3.23). Since x0+y∈Ω, one has u∈ΘSH(x0+y) and hence (3.26) and (3.27) give u+ˆvy;η∈SA(x0+y) and hence
However, using the definitions
and hence (3.28) gives the needed conclusion (3.24).
For the existence of bounded Θ-harmonic functions in (5), it suffices to show that there exists τ such that
Moreover, it suffices to construct τ such that (−τ,τI)∈Θ(x) holds, since a corresponding ˜τ can be constructed for ˜Θ (which is also uniformly continuous by Proposition 3.6 (a)) and hence one can take the maximum of τ and ˜τ by the monotonicity of proper elliptic maps.
Note that Θ extends to a uniformly continuous map on ¯Ω by Proposition 3.6 (b), which is compact. Since Θ(y) is a proper elliptic set for each y∈¯Ω, there exists ty such that
Indeed, pick any (ry,Ay)∈Θ(y) and define ty:=max{−ry,λN(Ay)} and one has
Using the uniform continuity of Θ with η=1, there exists δ=δ(1)>0 such that
Since ¯Ω is compact there exists a finite open covering {Bδ(yk)}nk=1 with yk∈¯Ω. Combining (3.30) and (3.31), one has for each x∈¯Ω
Picking τ=1+T yields the desired conclusion (−τ,τI)∈Θ(x).
A pair of remarks are in order concerning the properties (1)–(5) of Proposition 3.7.
Remark 3.8. The properties (1) and (2) hold for arbitrary proper elliptic maps Θ since they are purely pointwise statements that require no regularity of Θ. The argument used for property (3) does not really require continuity (3.4). It would suffice to ask that there exists δj=δj(εj,x0,D2v(x0)) such that (3.13) holds. This is because the argument in purely local near each fixed x0, and fixed element of ˜Θ(x0). On the other hand, uniform continuity is really used for properties (4) and (5).
Remark 3.9. The maximum property (1), sliding property (2) and the bounded Θ,˜Θ-subharmonics in property (5) will be used to make suitable truncations in the reduction of the Subharmonic Addition Theorem for semi-continuous functions to the case in which the functions are bounded from below (see Lemma 5.5 below). On the other hand, the families locally bounded above property (3) and the uniform translation property (4) will be used in the proof of the Subharmonic Addition Theorem in the case of functions which are bounded from below (see Lemma 5.6 below).
4.
A maximum principle for ˜Q-subharmonic functions
In this section, we discuss some fundamental properties of the space of ˜Q-subharmonic functions which play a key role in our treatment of the comparison principle. We begin by noting that the space ˜QSH(X) with X⊆RN open has also been studied in [7] in the context of constant coefficient (and gradient free) subequation constraint sets. There one finds additional characterizations such as
where w+ is the positive part of w, SA(X) are the subaffine functions satisfying the comparison principle (2.22) for each Ω⊂⊂X and each affine function a. The space SA+(X) consists of the subaffine plus functions on X in which one uses positive affine functions a in the comparison principle (2.22); that is, w∈USC(X) is subaffine plus on X if for each Ω⊂⊂X and each affine function a which is non-negative on ¯Ω, one has
The equivalence (4.1) is discussed and proven in [7] (see Theorem 9.7).
An important property of subaffine plus functions is the validity of the following zero maximum principle, which is a comparison principle between the subaffine plus functions w and 0.
Theorem 4.1. For each w∈USC(¯Ω)∩˜QSH(Ω), one has
Proof. Once the equivalence (4.1) is established, it is sufficient to observe that since w∈USC(¯Ω) and w≤0 on ¯Ω, by a standard compactness argument one has that for all ε>0 there exists δ=δ(ε)>0 such that w≤ε in a neighborhood of ∂Ω. Then, since w is subaffine plus on Ω, the comparison principle with the affine function a≡ε holds, hence w≤ε on Ω. Letting ε→0 gives the result.
Remark 4.2. Combining Theorem 4.1 with Theorem 2.10(a) immediately gives the following comparison result for proper elliptic maps Θ on Ω between viscosity subharmonics and classical superharmonics: for each pair u∈USC(¯Ω)∩ΘSH(Ω) and v∈C2(Ω)∩C(¯Ω)∩˜ΘSH(Ω) one has
since w:=u+v∈USC(¯Ω)∩˜QSH(Ω). The main result of this paper will be to show that a continuity property on Θ ensures that (4.3) continues to hold if v is merely USC(¯Ω)∩˜ΘSH(Ω).
Finally, we note that since the constant proper elliptic map ˜Q is trivially uniformly continuous on Ω, we have the validity of all of the properties of Proposition 3.7. In addition, one has the following property for decreasing limits, which plays a key role in the proof of the comparison principle in the next section.
Lemma 4.3. If {wn}n∈N⊂˜QSH(Ω) is a decreasing sequence, then
Proof. This is a special case of Proposition B.1 (E) of [7] for the constant coefficient gradient free subequation constraint set
5.
The comparison principle for continuous proper elliptic maps
The purpose of this section is to prove the following comparison principle in nonlinear variable coefficient gradient-free potential theory.
Theorem 5.1(Comparison principle: potential theoretic version). Let Θ be a continuous proper elliptic map on Ω. Then the comparison principle holds; that is, if u∈USC(¯Ω) and v∈LSC(¯Ω) are Θ-subharmonic and Θ-superharmonic respectively in Ω, then
Proof. By exploiting Harvey-Lawson duality and the zero maximum principle for ˜Q-subharmonic functions (Theorem 4.1), the proof of Theorem 5.1 reduces to the proof of the following result. Recall that v is Θ superharmonic if and only if ˜u=−v is ˜Θ-subharmonic.
Theorem 5.2(Subharmonic Addition). Let Θ be a uniformly continuous proper elliptic map on an open set X⊂⊂RN. For each pair of functions, u,˜u∈USC(¯X) one has
Indeed, let u and v be as in the statement of Theorem 5.1 and assume the validity of Theorem 5.2. Set ˜u:=−v∈USC(¯Ω)∩˜ΘSH(Ω). The comparison principle (5.1) is then equivalent to
Now set w:=u+˜u, and consider an arbitrary open set X⊂⊂Ω. Since Θ is uniformly continuous on ¯X, one has that w∈˜QSH(X) by Theorem 5.2. Since X⊂⊂Ω is arbitrary, w∈˜QSH(Ω), and (5.3) is a consequence of the zero maximum principle Theorem 4.1 for w. This completes the proof of Theorem 5.1, modulo the proof of Theorem 5.2.
Proof of Theorem 5.2. The proof involves three steps:
1). prove (5.2) under the additional assumption that u,˜u are semi-convex and hence almost everywhere twice differentiable (Lemma 5.3 and Lemma 5.4);
2). reduce the general case to the case of u,˜u bounded from below by suitable truncations and limit procedures (Lemma 5.5);
3). prove (5.2) for u,˜u semi-continuous and bounded below by taking decreasing limits of suitable quadratic perturbations of sup-convolution approximations which are semi-convex and locally subharmonic (Lemma 5.6).
Step 1: Prove (5.2) in the special case of u,˜u semi-convex on X⊂⊂RN for an arbitrary proper elliptic map (not necessarily continuous).
Recall that if λ>0, a function u:X→R is said to be λ-semi-convex if u+λQ0 is a convex function, where Q0(x)=12|x|2.
Lemma 5.3. Let Θ be a proper elliptic map on X⊂⊂RN. If u,˜u∈USC(¯X) are λ-semi-convex, then (5.2) holds; that is,
Moreover, one has the comparison principle (5.1) on X for u and v:=−˜u∈LSC(¯X) which is Θ-superharmonic in X.
Proof. The functions u,˜u and u+˜u are all semi-convex and hence twice differentiable almost everywhere in X by Alexandroff's theorem. Since u∈ΘSH(X) and ˜u∈˜ΘSH(X), the coherence property of Remark 2.8 yields
Property (2.9) of Proposition 2.3 then gives §
§ The formula Θ(x0)+˜Θ(x0)⊂˜Q for each x0 is known as the jet addition theorem which follows from Harvey-Lawson duality and the invariance property Θ(x0)+Q⊂Θ(x0) (see Section 6 of [7]).
The desired conclusion (5.4) is reached by applying the following lemma to w:=u+˜u, which is a version of Jensen's lemma on the passage of almost everywhere to everywhere information  .
.
 See [14] for a discussion on the equivalence of the Slodkowski and Jensen lemmas.
See [14] for a discussion on the equivalence of the Slodkowski and Jensen lemmas.
Lemma 5.4. Let w∈USC(X) be 2λ-semi-convex. Then w∈˜QSH(X) provided that
Proof. By the pointwise characterization of Lemma 2.9, one needs only to show that
Define X+:={x∈X: w(x)>0}, which is open since w is continuous, and it suffices to show that
Since w is twice differentiable almost everywhere, the hypothesis (5.6) yields
and hence one has
For w∈USC(X+) and semi-convex, the condition (5.9) gives the needed property (5.8) by applying Lemma 7.3 of [12] (see also Lemma 4.10 of [8]). We note only that the main idea is to pass a lower bound on the largest eigenvalue from a set of full measure to the entire domain X+, where the condition D2w(x)∈˜P means precisely λN(D2w(x))≥0 and the tool used is Slodkowski's largest eigenvalue theorem [19].
Step 2: For upper semi-continuous u,˜u and Θ uniformly continuous on X, reduce to the special case of u,˜u bounded from below.
Lemma 5.5. Let Θ be a uniformly continuous proper elliptic map on X. If the subharmonic addition theorem
holds for each pair u,˜u∈USC(¯X) which are bounded from below, then (5.10) holds for each pair u,˜u∈USC(¯X).
Proof. If either u or ˜u is not bounded from below on ¯X, consider the sequences in USC(¯X)
where φ is the bounded Θ-harmonic function constructed in Proposition 3.7 (5). These sequences will be bounded from below since φ and −φ are. By parts (1) and (2) of Proposition 3.7, one has um∈ΘSH(X) and ˜um∈˜ΘSH(X) for each m∈N. Assuming the (5.10) holds for pairs which are bounded below, one has
but wm↘w:=u+˜u as m→+∞ and hence u+˜u∈˜QSH(X) by the Decreasing Limit Property of Lemma 4.3 for ˜QSH(X).
Step 3: Prove (5.2) for u,˜u∈USC(¯X) which are bounded below with Θ uniformly continuous on X.
The idea of the proof is to use the sup convolution and suitable quadratic perturbations to build regularizing sequences for u and ˜u which are semi-convex and locally Θ and ˜Θ-subharmonic respectively. The subharmonic addition theorem holds along the approximating sequences which tend to u+˜u∈˜QSH(X) by the Decreasing Limit Property of Lemma 4.3.
We begin by recalling that if u∈USC(X) and bounded on X, for each ε>0, one defines the sup-convolution uε by
where one extends u to be −∞ outside of X. The function defined in (5.13) satisfies the following well-known properties (cf. Theorem 8.2 of [12], for example):
and
For u∈ΘSH(X) bounded with |u|≤M on X, consider the family of quadratic perturbations uε(⋅)+η(|⋅|2−ω) with η>0 small and ω:=2+supx∈X|x|2 is the parameter introduced in (3.8)–(3.9).
Lemma 5.6. For every η>0 there exists ¯ε=¯ε(η)>0 such that
where
Proof. Indeed, the Uniform Translation Property (4) of Proposition 3.7 says that for each η>0 there exists δ=δ(2η)>0 such that
Moreover, as noted in Proposition 3.6, the η,δ relation is the same for the dual map ˜Θ and hence there is an analogous family {˜uz,η}z∈Bδ(0) associated to ˜u which will be ˜Θ-subharmonic.
Now, for ε>0, consider the collection
Since −1ε|z|2≤0 for each z, Proposition 3.7 (2) gives F⊂ΘSH(Xδ) and the collection is locally uniformly bounded from above. By Proposition 3.7 (3), the Perron function defined for x∈Xδ by
will admit an upper semicontinuous regularization [uεη]∗ which belongs to ΘSH(Xδ).
It is not hard to see that for small ε one has that uεη is semi-convex and hence continuous so that uεη=[uεη]∗∈ΘSH(Xδ) and the claim (5.14) follows. Indeed, by choosing ε∈(0,δ2(η)/2M) the values of z with |z|≥δ do not compete in the sup which defines the sup-convolution uε in (5.13) and hence the first term in (5.17) is uε(x) and one has the following identity on Xδ(η):
which gives the semi-convexity and continuity of uεη.
Armed with Lemma 5.6, we complete Step 3 of the proof of Theorem 5.2 by fixing a sequence {ηj}j∈N with ηj→0 as j→+∞ and select εj:=min{ηj,ˉε(ηj)} so that δj:=δ(εj)=√2εjM→0+ and Ωδj↗Ω. The corresponding approximating sequences {uεjηj} and {˜uεηj} defined by (5.18) are 2/εj-semi-convex and Θ,˜Θ-subharmonic in Ωδj. By Lemma 5.3 one has wj:=uεjηj+˜uεηj∈˜QSH(Ωj). By construction wj↘u+˜u and Ωδj↗Ω and hence u+˜u∈˜QSH(Ω) by applying the Decreasing Limit Property of Lemma 4.3.
5.1. Comparison with local continuity in r
We conclude the section by observing that in order to prove comparison, our continuity demands on Θ can be slightly reformulated in ways that might be useful for applications. Recall that by Proposition 3.4 (c), uniform continuity of Θ on X⊂⊂Ω is equivalent to the following property: for all η>0, ∃δ=δ(η,X) such that
Assume now that Θ satisfies for each X⊂⊂Ω
Theorem 5.7. Let Θ be a proper elliptic map on Ω that satisfies (5.20) for each X⊂⊂Ω. Then the comparison principle holds; that is, if u∈USC(¯Ω) and v∈LSC(¯Ω) are Θ-subharmonic and Θ-superharmonic respectively in Ω, then
This comparison principle might be useful in order to obtain comparison principles fro certain PDEs; for example, see Remark 6.21. Its proof is based on two observations. First, under the assumption (5.20), one can define for all M>0 a uniformly continuous map ΘM on X⊂⊂Ω that agrees with Θ for values in [−M,M]×S(N) in the codomain. Second, Θ-subharmonic functions that are bounded in the sup-norm by M are ΘM-subharmonic. One then concludes by a standard truncation argument and the comparison principle for continuous elliptic maps on Ω, which are locally uniformly continuous.
Let
where
By the fact that ψM is continuous and odd, it is straightforward to check that
Lemma 5.8. For all M>0 large, ΘM defined above is a proper and uniformly continuous elliptic map on each X⊂⊂Ω.
Proof. First, we observe that ΘM(x) is non-empty. Indeed, by Proposition 3.7 (5), there exists τ>0 such that (−τ,τI)∈Θ(x) for all x∈X. Hence, for all M≥τ, ψM(−τ)=−τ, so (−τ,τI)∈ΘM(x) for all x. To prove that ΘM(x)≠R×S(N), one argues similarly via a couple (r,A)∉Θ(x) for all x. Proper ellipticity easily follows from the monotonicity of ψM and the degenerate ellipticity of Θ(x).
Continuity of Θ can be obtained by the alternative characterization stated in Proposition 3.4. Fix any η>0, and from (5.20) let δ=δ(R,η) be such that
Let (r,A)∈ΘM(x), so (ψM(r),A)∈Θ(x). Note that |ψM(r)|≤M, so (ψM(r),A)∈Θ(x)∩([−R,R]×S(N)). Hence, for |x−y|<δ,
that in turn gives (r,A+ηI)∈ΘM(y). By ellipticity of ΘM(y), one has (r−η,A+ηI)∈ΘM(y), that finally yields ΘM(x)+(−η,ηI)⊂ΘM(y) for all |x−y|<δ.
Lemma 5.9. Let u∈USC(¯X) be such that |u|≤R for some R>0. If u is Θ-subharmonic (˜Θ-subharmonic), then u is ΘR-subharmonic (~ΘR-subharmonic).
Proof. Fix any x0∈X, and let φ be C2 near x0, φ(x0)=u(x0), and u−φ have a local maximum at x0. Since |u(x0)|≤R, φ(x0)=ψR(φ(x0)), hence
that gives J+x0u⊂ΘR(x). The proof for ~ΘR-subharmonic functions is completely analogous.
We conclude with the proof of the comparison principle.
Proof of Theorem 5.7. Arguing as in Lemma 5.5, with X⊂⊂Ω arbitrary, it is enough to consider a pair of functions u,v∈USC(¯X) which are bounded from below (and above). Hence, we assume that for some R>0, |u|,|v|≤R on Ω. By Lemma 5.9, u and v are ΘR-subharmonic and ~ΘR-subharmonic respectively. Since ΘR is a uniformly continuous elliptic map on X by Lemma 5.8, by the subharmonic addition theorem 5.2 u−v∈˜QSH(X) for each X⊂⊂Ω and hence u−v∈˜QSH(Ω). The comparison principle for u,v on Ω then follows from the zero maximum principle (Theorem 4.1).
6.
Comparison principles for admissible solutions of proper elliptic PDEs
Armed with the potential theoretic comparison principle for continuous proper elliptic maps developed in previous sections, we derive comparison principles for some fully nonlinear second order PDEs. The equations we treat will have variable coefficients and will be gradient-free and proper elliptic (which, in general, may require the imposition of an admissibility constraint in order to ensure the needed monotonicity). The strategy we employ will be to determine structural conditions on the defining operator F for the PDE which allow us to define a proper elliptic map Θ whose subharmonics/superharmonics correspond to viscosity subsolutions/supersolutions of the PDE (with perhaps admissibility constraints on the upper and lower test jets used in the viscosity formulation). We call this the correspondence principle (see Theorem 6.5). That being done, an additional condition will be placed on the operator F in order to ensure that Θ is continuous. This additional structural condition involves some mild regularity and strict monotonicity assumptions on F (see property (6.35)). Hence the comparison principle for the PDE follows directly from the comparison principle for continuous proper elliptic maps Θ given in Theorem 5.1.
While we have no complete recipe to associate a (continuous) proper elliptic map Θ to any given operator F, we are able to complete the program described above for a large class of equations that enjoy suitable monotonicity properties on proper elliptic subsets of R×S(N). We call this the constrained case and this will be developed in Section 6.1 below. Moreover, in the unconstrained case, when no admissibility constraint is needed, we will show that a natural choice of Θ can be made so that the correspondence principle holds without admissibility constraints on the upper and lower test jets in the (standard) viscosity formulation (see Remark 6.7). Finally, we will present some comparison principles for two examples of fully nonlinear PDEs (one constrained and one unconstrained), to illustrate how our general theory applies in specific situations.
6.1. Proper elliptic branches and admissible viscosity solutions of PDEs
We begin with the notion of proper ellipticity for a nonlinear equation
where F:Ω×R×S(N)→R is a continuous function satisfying
We will call such an F a gradient-free operator.
Definition 6.1. Let F be a gradient-free operator. The equation (6.1) determined by F is said to be proper elliptic if there exists a proper elliptic map Θ:Ω→℘(R×S(N)) such that
In that case one calls the differential inclusion
a proper elliptic branch of the equation (6.1) defined by Θ.
Notice that the definition depends only on the sets Γ(x) and not on the particular form of the operator F, which was the insight of Krylov [18] for his general notion of ellipticity. Recall that Θ is a proper elliptic map if for each x∈Ω
and
For gradient-free equations, ellipticity in the sense of Krylov requires only the weaker monotonicity assumption Θ(x)+({0}×P)⊂Θ(x) for each x∈Ω. Notice also that a given F may admit many branches as Θ need not be unique. See section 2 of [18] for a discussion of this point.
Next, we turn to the question of structural conditions on F for which proper elliptic branches can be defined. We will start by asking that at least some proper elliptic map Φ exists along which F is proper elliptic (Q-monotone). One might think of the maximal such proper elliptic map Φ. Subsequently, we will examine further conditions on the pair (F,Φ) for which there is a natural proper elliptic map Θ which determines a proper elliptic branch of the Eq (6.1).
Definition 6.2. Let F be a gradient-free operator. We say that F is proper elliptic if there exists a proper elliptic map Φ:Ω→℘(R×S(N)) such that
In this case (F,Φ) will be called a proper elliptic pair.
Given a proper elliptic pair (F,Φ), in general, Φ will not satisfy the branch condition ∂Φ(x)⊂Γ(x). We will examine one general situation in which a suitable subset Θ(x) of Φ(x) for each x∈Ω does indeed determine a proper elliptic branch of (6.1).
Before stating a general result, a simple example is instructive. Consider the following Monge-Ampère equation
where f is continuous and nonnegative. The operator F(x,r,A)=−rdet(A)−f(x) is clearly Q monotone on all of Q=N×P; that is, for each x∈Ω,(r,A)∈Q and (s,P)∈Q one has
Hence for the proper elliptic map defined by Φ(x)=Q for each x∈Ω one has that (F,Φ) is a proper elliptic pair. In addition, it is clear that this constant map Φ is the maximal map for which F restricted to Φ is Q-monotone. Now, for each x∈Ω one has
while
and hence F(x,r,A)=f(x) for each (r,A)∈∂Φ(x) and the branch condition ∂Φ(x)⊂Γ(x) holds only at points where f(x)=0. This suggests reducing Φ to
where one easily checks that (F,Θ) is a proper elliptic pair and that ∂Θ(x)⊂Γ(x) so that Θ defines an elliptic branch of (6.8).
We now give the general statement suggested by this example, where we recall that Γ(x)={(r,A)∈R×S(N):F(x,r,A)=0}.
Theorem 6.3(Proper elliptic branches). Let (F,Φ) be a proper elliptic pair; that is, the gradient-free operator is Q-monotone when restricted to the proper elliptic map Φ in the sense (6.7). Assume that the following two conditions hold:
Then, the map Θ:Ω→℘(R×S(N)) defined by
is a proper elliptic map and Θ defines a proper elliptic branch of the PDE (6.1) determined by F; that is,
Proof. This is a generalization of [8,Proposition 5.1]. For each x∈Ω, Θ(x)≠∅ by the first condition (6.9) and is not all of R×S(N) since Φ(x) is a proper subset (by Definition 2.1). Moreover Θ(x) is closed since Φ(x) is closed and F is continuous, where it would suffice to have F(x,⋅,⋅) upper semicontinuous for each x fixed. Hence Θ satisfies the property (2.4) of a proper elliptic map. For the Q-monotonicity condition (2.5), notice that for each x∈Ω and for each (r,A)∈Θ(x)⊂Φ(x) one has
by the Q-monotonicity property of Φ. Using the Q-monotonicity of F restricted to Φ (6.7) and the definition (6.11) of Θ one has
and hence Θ is a proper elliptic map.
It remains only to check that Θ defines a branch; that is, that (6.12) holds. One easily checks that ∂Θ(x) is the union of two sets
and
which yields (6.12) if the branch condition (6.10) holds since Φ(x) is closed by definition.
In addition to the equation (6.8) mentioned above, examples of equations for which this proposition applies include elliptic equations with F=F(x,A) independent of r as treated in [8]. Additional examples, where one also has the comparison principle, will be given in the next subsection.
Now that a proper elliptic branch of the PDE (constrained by Φ) is defined by the map Θ in (6.11), we turn to the definition of Φ-admissible viscosity sub/supersolutions to the equation (6.1), with the idea of establishing the equivalence between such admissible sub/supersolutions and Θ-sub/superharmonics (Definition 2.4) for the map Θ. We will again make use of the upper and lower test jets, which we recall are defined for each fixed x0∈Ω by
and
Definition 6.4. Let F:Ω×R×S(N)→R be continuous and Φ:Ω→℘(R×S(N)) a proper elliptic map.
(a) One says that u∈USC(Ω) is a Φ-admissible viscosity subsolution of (6.1) in Ω if for every x0∈Ω one has
(b) One says that u∈LSC(Ω) is a Φ-admissible viscosity supersolution of (6.1) in Ω if for every x0∈Ω one has
One says that u∈C(Ω) a Φ-admissible viscosity solution of (6.1) in Ω if both conditions (a) and (b) hold.
Notice that for Θ(x):={(r,A)∈Φ(x): F(x,r,A)≥0}, the Φ-admissible subsolution condition (6.17) is equivalent to
which defines u∈USC(Ω) being Θ-subharmonic in x0 (see Definition 6.4). On the other hand, recall that u∈LSC(Ω) is Θ-superharmonic in x0 if
Under an additional hypothesis of non degeneracy, the condition (6.20) is equivalent to the condition (6.18).
Theorem 6.5(Correspondence principle). Let (F,Φ) be a proper elliptic pair and let Θ be the corresponding proper elliptic map defined by (6.11); that is,
Then the following equivalences hold.
(a) A function u∈USC(Ω) is a Φ-admissible viscosity subsolution of (6.1) in Ω if and only if u∈ΘSH(Ω) (u is Θ-subharmonic in Ω).
(b) A function u∈LSC(Ω) is a Φ-admissible viscosity supersolution of (6.1) in Ω if and only if −u∈˜ΘSH(Ω) (u is Θ-superharmonic in Ω) provided that the following non-degeneracy condition is satisfied:
Proof. The equivalence of part (a) has been noted above. For the equivalence of part (b), notice that the Φ-admissible supersolution condition (6.17) is clearly equivalent to
and by comparing (6.22) with (6.19), it suffices to show that for each fixed x∈Ω one has
Making use of the duality ˜Θ(x):=−([Θ(x)]∘)c, by negating the elements in (6.23), it suffices to show that
We calculate directly the dual ˜Θ(x) using the property [˜Θ(x)]∘=−[Θ(x)]c which follows from the reflexivity of Θ(x). By definition, we have
and hence
Hence
which yields
Now we take the closure in R×S using the property (2.11) for the proper elliptic maps ˜Θ and ˜Φ to conclude
We just need to check now that Ψ(x) as defined in (6.24) equals Θ(x) as calculated in (6.25). By the continuity of F one clearly has ˜Θ(x)⊂Ψ(x). For the reverse inclusion it suffices to show that
By the non degeneracy condition (6.21), (−r,−A)∉[Θ(x)]∘ which by duality means (r,A)∈−([Θ(x)]∘)c=˜Θ(x), as needed.
A few observations about this correspondence principle are in order.
Remark 6.6. For F,Φ and Θ as in Theorem 6.5, if one also assumes the branch condition (6.10), then Θ defines a proper elliptic branch of the PDE (6.1) by Theorem 6.3. Moreover, by adding in the non degeneracy condition (6.21) (which is not required for the Correspondence Principle of 6.5) it follows that
and
Hence, borrowing the terminology of [7] in the constant coefficient setting, we can say that (F,Θ) is a (constrained case) compatible proper elliptic pair for which the correspondence principle holds.
Next, we briefly discuss the "standard" case in which there is no a priori need to impose admissibility constraints. In this case we will derive a correspondence principle between standard viscosity subsolutions (supersolutions) of proper elliptic operators and Θ-subharmonic (superharmonic) functions under mild non-degeneracy conditions (see (6.29) and (6.30)).
Remark 6.7(The unconstrained case). If F is a gradient-free operator (F continuous with Γ(x)≠∅) which is proper elliptic on all of R×S(N); that is,
then there is no need to constrain F to some proper subset of the gradient-free jet space J:=R×S(N) in order for F to be Q-monotone. In this case, by letting Φ=J in Definition 6.4 one recovers usual notion of viscosity subsolutions and supersolutions since the condition (r,A)∈J in (6.17) holds trivially and the possibility (r,A)∉[J]∘=J cannot occur. We will say that (F,J) is an (unconstrained case) compatible proper elliptic pair.
Now, if one defines the map Θ:Ω→℘(R×S(N)) as before with Φ≡J; that is,
then Θ(x) will be closed by the continuity of F and non empty as Γ(x)≠∅. In addition, Θ(x) will be a proper subset of J if
Hence Θ will be a proper elliptic map since for each x∈Ω, the Q-monotonicity of F on all of J yields the Q-monotonicity of Θ(x). Finally, in this case, the non-degeneracy condition (6.21) becomes
and so (F,Θ) is a compatible pair in the sense (6.27)–(6.28). Hence one has correspondence principle between Θ-superharmonic functions and standard (unconstrained) viscosity supersolutions of the PDE (6.1).
6.2. Comparison principles for PDEs from potential theoretic comparison
In the previous subsection, we have discussed fiberwise properties (i.e., for x∈Ω fixed) of the operator F(x,⋅,⋅) that ensure that the map Θ (defined by (6.11) in the constrained case and by (6.29) in the unconstrained case) is: 1) proper elliptic, 2) defines a proper elliptic branch of the PDE (6.1) and 3) satisfies the correspondence principle (of Theorem (6.5) in the constrained case and of Remark 6.7 in the unconstrained case). We now discuss structural conditions on F as x varies which will ensure that the associated proper elliptic map Θ is continuous. Combining this continuity with the correspondence principle of Theorem 6.5 will then yield the validity of the comparison principle for (Φ-admissible) viscosity solutions of the PDE (6.1), by applying the potential theoretic version of comparison (Theorem 5.1) for continuous proper elliptic maps.
Theorem 6.8 (Continuity of proper elliptic maps). Let F∈C(Ω×R×S(N)) be a gradient-free operator and Θ:Ω→℘(R×S(N)) be a proper elliptic map of the form
where either
or
Assume that the pair (F,Φ) satisfies the following regularity condition: for every Ω′⊂⊂Ω and for every η>0, there exists δ=δ(η,Ω′)>0 such that
Then, the proper elliptic map Θ is continuous.
Proof. We will show that Θ is locally uniformly continuous. Since Θ is assumed to be proper elliptic, by Proposition 3.4, it suffices to show that for every fixed Ω′⊂⊂Ω and for every fixed η>0, there exists δΘ=δΘ(η,Ω′)>0 such that for each x,y∈Ω′
In the constrained case (6.33), we have the validity of (6.36) with Φ in place of Θ for some δΦ=δΦ(η,Ω). It suffices to choose δΘ=min{δΦ,δ}. Indeed, for each pair x,y∈Ω′ with |x−y|<δΘ, pick an arbitrary (r,A)∈Θ(x) so that (r,A)∈Φ(x) and F(x,r,A)≥0, which by the continuity of Φ and the regularity property (6.35) yields
which yields the inclusion in (6.36).
In the unconstrained case (6.34), the constant map Φ≡J is trivially continuous ((6.36) for Φ holds for every δΦ>0 and hence it suffices to choose δΘ=δ and use the regularity condition (6.35)).
Before moving on to comparison principles, a few remarks are in order.
Remark 6.9. In Theorem 6.8, the structural condition (6.35) on F is merely sufficient to ensure that a proper elliptic map Θ given by (6.32) is continuous. The (locally uniform) continuity of Θ is equivalent to the statement that: for every Ω′⊂⊂Ω and for every η>0, there exists δ=δ(η,Ω′)>0 such that ∀x,y∈Ω′ with |x−y|<δ one has
This condition is weaker, in general, than the structural condition (6.35) and hence useful to keep in mind for specific applications (see, for example, the proof of Theorem 6.18). On the other hand, the structural condition (6.35) can be more easily compared to other structural conditions on F present in the literature.
Remark 6.10. In Theorem 6.8 we have assumed that Θ defined by (6.32) is a proper elliptic map. By what we have done previously, we have sufficient conditions which guarantee that Θ is indeed proper elliptic. In particular, it is enough to assume that
in order to ensure the needed Q-monotonicity of each Θ(x). Each Θ(x) will be closed (by the continuity of F) and non-empty provided
The remaining condition Θ(x)⊊R×S(N) is always satisfied in the constrained case (Θ(x)⊂Φ(x)⊊R×S(N)). In the unconstrained case, one need only assume
Remark 6.11. The importance of having Θ be proper elliptic on Ω is twofold. On the one hand, we can exploit the formulation (3.7) for proper elliptic maps, which makes the regularity condition (6.35) a natural one. On the other hand, proper ellipticity on all of Ω rules out the possibility that Θ(x)=R×S(N) on some proper subset Ω′ of Ω but with Θ proper elliptic on Ω∖Ω′. In such a case, by picking any x∈Ω′ and y∈Ω∖Ω′, since Θ(y)⊊R×S(N), dH(R×S(N),Θ(y))=+∞, as noted in (3.3). This holds for pairs x,y which are arbitrarily close.
Remark 6.12. As a final comment, we note that when the pair (F,Φ) is proper elliptic, the condition (6.35) is restrictive only for η>0 small. Indeed, if for some η∗>0, and for each η∈(0,η∗], there exists δ=δ(η,Ω)>0 such that (6.35) holds, the proper ellipticity (6.39) implies that (6.35) continues to hold for each η>η∗ by taking δ(η,Ω′)=δ(η∗,Ω′).
We conclude this subsection by stating a comparison principle for viscosity solutions of PDE (6.1) in both constrained and unconstrained cases.
Theorem 6.13(Comparison principle: PDE version). Given F∈C(Ω×R×S(N),R) and Φ:Ω→℘(R×S(N)) where either
or
and let Θ:Ω→℘(R×S(N)) be defined by
Assume that F restricted to Φ is proper elliptic; that is,
and that the pair (F,Φ) satisfies the regularity property (6.35); that is, for every Ω′⊂⊂Ω and for every η>0, there exists δ=δ(η,Ω′)>0 such that
Assume the non-empty condition (6.9); that is,
and the non-degeneracy condition (6.21); that is,
Moreover, in the constrained case (6.42) assume the branch condition (6.10); that is,
and in the unconstrained case (6.43) assume the properness condition (6.30); that is,
Then, the map Θ is a continuous proper elliptic map and defines a proper elliptic branch of the PDE (6.1); that is,
and for every bounded domain Ω the comparison principle for the PDE (6.51) holds; that is,
if u is a Φ-admissible viscosity subsolution of (6.51) in Ω and u is a Φ-admissible viscosity supersolution of (6.51) in Ω.
Proof. In the constrained case (6.42), the map Θ defined by (6.44) is a proper elliptic map and defines a proper elliptic branch of (6.51) by applying Theorem 6.3, where one uses (6.45), (6.47) and (6.49). The non-degeneracy condition (6.48) then yields the correspondence principle of Theorem 6.5. Hence the comparison principle (6.52) follows from the potential theoretic version of comparison (Theorem 5.1).
In the unconstrained case (6.43), the map Θ defined by (6.44) is proper elliptic, as discussed in Remark 6.7, where one uses (6.45), (6.47) with Φ(x)=J for each x∈Ω and the properness condition (6.50). Using the non-degeneracy condition (6.48), which in this case means (6.31), one has the correspondence principle between Θ subharmonics/superharmonics and standard viscosity subsolutions/supersolutions of the PDE (6.51) (as noted in Remark 6.7). Hence, again, comparison for the PDE (6.51) reduces to the validity of Theorem 5.1.
6.3. Comparison in the constrained case
We now focus our attention on specific examples. We consider first the validity of the comparison principle for an interesting prototype equation that is defined by an operator that is proper elliptic only when constrained to certain proper subsets of R×S(N). We will consider the equation
where
When h is positive constant, this kind of Monge-Ampère equation is important in the question of the completeness of the affine metric of hyperbolic affine spheres as treated by Cheng and Yau in [6]. In particular, for any negative constant L, a necessary and sufficient condition for the graph of v to be a hyperbolic affine sphere with affine mean curvature L and center at the origin is that its Legendre transform u=v∗ satisfies (see section 5 of [6]):
which is equivalent to (6.53) for u>0 with L=−h<0. Here, we consider the case of h being a function of the x variable, possibly vanishing on Ω. Clearly,
fails to satisfy proper ellipticity conditions on the whole R×S(N). Still, F restricted to Q=N×P satisfies (6.45). We can prove the following comparison result.
Theorem 6.14. Suppose that h satisfies (6.54). Then, the map Θ:Ω→℘(R×S(N)) defined by
is a continuous proper elliptic map and defines a proper elliptic branch of (6.53). Moreover, for any Q-admissible viscosity subsolution u and any Q-admissible viscosity supersolution v of (6.53) (in the sense of Definition 6.4),
Proof. To show that the comparison principle holds, it is sufficient to check all the assumptions of Theorem 6.13 in the constrained case. First, Q is x-independent, so it is clearly Hausdorff continuous. The monotonicity condition (6.45) is easily verified: F(x,r,A) is decreasing in r and increasing in A if r≤0 and A≥0; that is, if (r,A)∈Q. For all x∈Ω, (r,A)=(−(h(x))1N+2,I)∈Q satisfies F(x,r,A)=0, hence the non-empty condition (6.47) holds. Moreover, since ∂Q=({0}×P)∪(N×∂P), F(x,⋅,⋅)≤0 on ∂Q for each x, we have the branch condition (6.49). To check the regularity condition (6.46), note that for η>0,
for all (r,A)∈Q and y∈Ω. For any fixed Ω′⊂⊂Ω, by the uniform continuity of h on Ω′, it is sufficient to pick |x−y|<δ and δ=δ(η,Ω′)>0 small enough to have η2N+2−h(y)+h(x)≥0. Similarly, the non-degeneracy condition (6.48) is satisfied. Indeed, for any (r,A)∈[Θ(x)]∘, (r+η,A−ηI)∈Θ(x) for small η>0. As before,
The comparison principle thus follows from Theorem 6.13.
Remark 6.15. Note that Θ(x)={F(x,⋅,⋅)≥0}∩(N×S(N))∩(R×P), in other words
Moreover, it can be easily checked that Q-admissible viscosity subsolutions and supersolutions of (6.53) are equivalent to standard viscosity subsolutions and supersolutions (i.e., with no additional restrictions on the upper and lower test functions φ) of
which can be seen as a Bellman equation, or an obstacle problem for the fully non-linear equation (6.53). Indeed, classical solutions to min{F(x,u,D2u),−u,λ1(D2u)}=0 are actually (convex) solutions to min{F(x,u,D2u),−u}=0.
Of course, the Eq (6.53) is just a prototype of equations for which the product structure is amenable to our methods. For example, one can obtain comparison principles for equations of the form g(x,u)F(x,D2u)=h(x), assuming that g(x,⋅) is decreasing and and that F(x,⋅) is increasing, with some strictness in at least one of the two variables, to guarantee the validity of (6.35). General examples of such F can be found in [8,Section 5]. In particular, our methods naturally cover more general equations of the form
where g,m,M are continuous functions, and g(⋅) is increasing and positive on some open interval (r0,∞). We stress that mere continuity with respect to x for g,m,M is sufficient here, while the application of general arguments in [15] involving jet-equivalence may require further regularity properties of data, as Lipschitz continuity. See Definition 2.9 of [15]. Note also that the Eq (6.55) is a generalized version of an example discussed in [8]HY__HY, Remark 5.10], where it is pointed out that condition (6.35) allows one to treat some cases in which the standard Crandall-Ishii-Lions condition (see [9,Condition (3.14)]) does not hold.
Theorem 6.16. Suppose that h∈C(Ω) is non-negative, m∈C(Ω), M∈C(Ω;S(N)) and g∈C(R) satisfies
Then, the map Θ:Ω→℘(R×S(N)) defined by
where
is a continuous proper elliptic map and defines a proper elliptic branch of (6.55). Moreover, for any Φ-admissible viscosity subsolution u and any Φ-admissible viscosity supersolution v of (6.55) (in the sense of Definition 6.4),
Proof. We apply Theorem 6.13 in the constrained case, where one needs to check that the needed conditions hold. First, one easily checks that Φ defined by (6.58) a proper elliptic map; that is, each Φ(x) is a non-empty, closed proper subset of R×S(N) which is Q-monotone, where we note that
so that (r,A)∈Φ(x) yields (r+s,A+P)∈Φ(x) for each s≤0 and P≥0. The proper elliptic map Φ is continuous, as one sees by using the local uniform continuity of m and M to show the local uniform continuity of Φ in the sense of (3.7) in the characterization of Proposition 3.4. Hence (6.42) holds.
Next, the operator F defined by
is Q-monotone in the sense (6.45) since (r,A)∈Φ(x) and (s,P)∈Q=N×P yields
as g is increasing and non-negative on [r0,+∞) by (6.56), while
The non-empty condition (6.47) holds since for each x∈Ω, the element
gives
where g(r0+1)>0 in view of the positivity assumption in (6.56).
For the branch condition (6.49), since Φ(x)=(N+m(x)−r0)×(P−M(x)), one has
and hence F(x,⋅,⋅)≤0 on ∂Φ(x) for each x.
For the regularity property (6.46); that is, for Ω′⊂⊂Ω and η>0 arbitrary, there exists δ=δ(η,Ω′)>0 such that
one makes use of the local uniform continuity of m,M and g together with the monotonicity of g and det on Φ(x). Indeed, pick δ=δ(η,Ω′)>0 so that for each x,y∈Ω′ with |x−y|<δ one has:
where g(r0+η/2)>0 by (6.56). Since g is increasing on [r0,+∞), the first condition in (6.62) together with m(x)−r≥r0 if (r,A)∈Φ(x) yields
Similarly, since det is increasing on P, the second condition in (6.62) together with A+M(x)∈P for (r,A)∈Φ(x) yields
Using (6.63), (6.64) and the inequality det(A+B)≥det(A)+det(B) for A,B≥0, one finds
where we have also used the third condition in (6.62) in the last inequality.
Finally, the non-degeneracy condition (6.48) follows from the structure of F(x,⋅,⋅) on Θ(x). Indeed, if (r,A)∈[Θ(x)]∘, one must have both
and
Consequently, in the equation
if (r,A)∈[Θ(x)]∘, then one must have h(x)>0. However, in this case by the positivity in (6.65) and the strict monotonicity of det on P∘ one cannot preserve F(x,⋅,⋅)≥0 in a neighborhood of (r,A)∈[Θ(x)]∘.
6.4. Comparison in the unconstrained case
As a final illustration of our method, we will prove a new comparison principle for the inhomogeneous special Lagrangian potential equation
where
are the ordered eigenvalues of A∈S(N) and h∈C(Ω). As noted in the introduction, while this equation is proper elliptic on all of R×S(N), its treatment is delicate due to the degeneracies when the operator G:S(N)→I=(−Nπ/2,Nπ/2) defined by
takes on one of the special phase values
which determine the phase intervals
As discussed in the introduction, we will make a contribution to the following Open Question (page 23 of [16]): does the comparison principle hold for each continuous phase function h taking values in I? For h taking values in the top phase interval I1, this is known (see [10] or [16]). We will show that the comparison principle holds if h takes values in any one of the phase intervals Ik with k∈{1,…,N}. We will also show that our method breaks down if h takes on one of the special phase values θk.
We begin by embedding the PDE (6.68) into its natural potential theoretic framework. For the pure second order operator (1.27) consider the map Θ:Ω→℘(R×S(N)) defined by
One easily checks that Θ is a proper elliptic map and defines a proper elliptic branch of (6.68). Indeed, each Θ(x) is closed by the continuity of G and h, Θ(x) is non-empty since
and Θ(x)⊊R×S(N) since one easily finds (r,A) such that G(A)−h(x)<0 by using the monotonicity of G on all of S(N). The operator F(x,r,A):=G(A)−h(x) is clearly proper elliptic on R×S(N) so that Θ(x) is Q-monotone. Finally, Θ defines a branch of (6.68) since
Having embedded the PDE problem into its natural potential theoretic framework, the main point is to verify the continuity of the map Θ. This is delicate since the operator G degenerates on level sets {A∈S(N): G(A)=θk} for each k=1,…,N−1. We will show that Θ is continuous if h avoids the special phase values θk and hence the comparison principle follows from Theorem 5.1. The key idea in the proof is that if h∈C(Ω) avoids each special phase value, then h maps compact subsets of Ω into a compact subset Σ of some open phase interval Ik, which yields a locally uniform bound on at least one eigenvalue of A∈G−1(Σ) (see Lemma 6.19 below). It is perhaps instructive to first show how continuity fails nearby a point x0 where h (non constant) does take on a special phase value, and hence our method breaks down.
Proposition 6.17(Failure of continuity). Let h∈C(Ω) and suppose that there exists a convergent sequence {xn}n∈N⊂Ω with limit x0∈Ω such that for some k=1,…,N−1
and
Then the proper elliptic map Θ is not continuous.
Proof. By Proposition 3.4(c) with Ω′ any neighborhood of x0 and η=1, it suffices to show that either
or
We treat first the case h(xn)>θk. By the definition of Θ, in order to show (6.77) it suffices to exhibit a sequence {An}⊂S(N) such that
One such sequence is provided by the block diagonal matrices
where Ik∈S(k) is the identity matrix and an,bn>0 are to be chosen suitably large, but are constrained to satisfy
so that the first condition in (6.79) holds. By making use of the mean value theorem one finds ξn∈(−an,−an+1) and ηn∈(bn,bn+1) such that
which by (6.81) yields
If one sends an to +∞ then by (6.81) and the definition of θk one must have
and hence also bn goes to +∞. This also forces ξ2n and η2n to infinity. Hence by choosing an large enough one can make the right hand side of (6.82) smaller than h(xn), where h(xn)>θk by hypothesis.
Similarly, in the case h(xn)<θk, one can show that (6.78) holds by exhibiting a sequence {An}n∈N⊂S(N) such that
Again we take An of the form (6.80) with the constraint (6.81) replaced by
so that the first condition in (6.83) holds. By choosing an and bn large enough, the same mean value argument used above gives
so that the second condition in (6.83) holds, which completes the proof.
On the other hand, if h avoids the special phase values, then the proper elliptic map Θ is continuous.
Theorem 6.18. Suppose that h∈C(Ω) satisfies
Then, the proper elliptic map Θ defined in (6.73) is continuous, and defines a proper elliptic branch of (6.68). Moreover, for any viscosity subsolution u and any viscosity supersolution v of (6.68),
Proof. We have already discussed the claims that Θ is proper elliptic and defines a proper elliptic branch of (6.68). Moreover, the branch condition (6.74) is precisely the needed non-degeneracy condition (6.31) which ensures the correspondence principle between viscosity supersolutions and Θ-superharmonic functions (as discussed in Remark 6.7).
Hence, in order to have the comparison principle for Θ-sub/superharmonic functions, it suffices to verify that Θ is a continuous map (in order to apply the potential theoretic comparison Theorem 5.1).
To prove that Θ is indeed continuous, one can argue as follows. By Remark 3.2 and Proposition 3.4(c), the proper elliptic map Θ will be continuous on Ω if for each Ω′⊂⊂Ω and each η>0 there exists δ(η,Ω′)>0 such that for each x,y∈Ω′ with |x−y|<δ
which in terms of the special Lagrangian potential operator G requires showing that for each η>0 and each pair x,y∈Ω′ with |x−y|<δ one has the implication
Notice that the continuity of h and condition (6.85) shows that h(¯Ω′) is a compact subset of the open set Ik and hence
Hence there exists ε>0 (depending on Ω′ and h) such
There are two cases to consider for the pair (x,A) in (6.87); namely,
In the first case of (6.90), using the monotonicity of G and the uniform continuity of h on ¯Ω′, one has
for each x,y∈Ω′ with |x−y|≤δ=δ(Ω′), but independent of η>0.
For the second case of (6.90), we make use of the following fact. See Figure 1 which represents the case of dimension N=2 for the interval I1=(0,π).
Lemma 6.19. For any Σ compact in Ik open, the set G−1(Σ)={A∈S(N): G(A)∈Σ} satisfies the following property: there exists C=C(Σ)>0 such that
We postpone the proof of the Lemma, proceeding with the analysis of the remaining case h(x)≤G(A)≤h(x)+ε; that is,
By (6.89), we have [h(x),h(x)+ε]⊂⋃γ∈[0,ε]{h(¯Ω′)+γ}=:Σ is compact in Ik open and hence by Lemma 6.19 we have λjA(A)≤C=C(Σ) for some jA∈{1,…,N}. The mean value theorem then implies
for some ξ∈(λjA,λjA+η). We have |ξ|≤C+η by (6.91) and hence for η≤η∗:=C we have (1+ξ2)−1≥(1+4C2)−1. Therefore, for η∈(0,η∗) by the monotonicity of arctan and (6.92) we have
for all x,y∈Ω′ with |x−y|<δ(η,Ω′) to ensure |h(x)−h(y)|<(1+4C2)η, which we can do by the local uniform continuity of h. The same δ also works for η>η∗ as G is increasing. This completes the proof of the continuity (6.86) modulo the proof of Lemma 6.19.
Proof of Lemma 6.19. We argue by contradiction. Let {An}n∈N⊂G−1(Σ) be a sequence such that |λj(An)|→+∞ for all j=1,…,N. The set of all possible accumulation points of {G(An)}n∈N is {(N−2k)π/2: k=0,1,…,N}, which correspond to subsequences with
Since such accumulation points do not belong to Ik⊃Σ, they also do not belong to Σ, and therefore G(An)∉Σ for n large enough, which contradicts An∈G−1(Σ).
We conclude with a pair or remarks concerning possible generalizations.
Remark 6.20. Note that (6.68) is u-independent. It is still interesting to observe how non-degeneracy properties of the operator G and regularity of the inhomogeneous term affect continuity of the associated elliptic map Θ. We also point out that our comparison results could be easily extended to cover more general u-dependent equations of the form
under the assumption that h is continuous, monotone in the second variable, and satisfies h(Ω×R)⊂Ik for some k.
Remark 6.21. The comparison principle stated in Theorem 5.7, that uses a slightly relaxed version of Hausdorff continuity (5.20), might be useful in situations where terms of the form g(x,u) appear in the equation. For c∈C(¯Ω), c≥0, consider for example the proper elliptic map
which defines a proper elliptic branch of the linear PDE
To check Hausdorff continuity, for any given η>0, and (r,A)∈Θ(x),
Then, one has for general c that [c(y)−c(x)]r+η(N+c(y))≥0 for x close to y, that is (r−η,A+ηI)∈Θ(y), only if r lies in a bounded subset of R. This is precisely what (5.20) requires, while Θ would fail to satisfy the stronger Hausdorff continuity (unless c is constant over Ω).
Acknowledgments
The authors wish to thank Reese Harvey for many elucidating discussions and constructive criticism, especially concerning the application given here to the special Lagrangian potential equation. In addition, the authors wish to thank an anonymous referee for the careful reading of the original manuscript.
Cirant partially supported by the Fondazione CaRiPaRo Project "Nonlinear Partial Differential Equations: Asymptotic Problems and Mean-Field Games" and the Programme "FIL-Quota Incentivante" of University of Parma, co-sponsored by Fondazione Cariparma. Payne partially supported by the Gruppo Nazionale per l'Analisi Matematica, la Probabilità e le loro Applicazioni (GNAMPA) of the Istituto Nazionale di Alta Matematica (INdAM) and the projects: GNAMPA 2017 "Viscosity solution methods for fully nonlinear degenerate elliptic equations", GNAMPA 2018 "Costanti critiche e problemi asintotici per equazioni completamente non lineari" e GNAMPA 2019 "Problemi differenziali per operatori fully nonlinear fortemente degeneri".
Conflict of interest
The authors declare no conflict of interest.
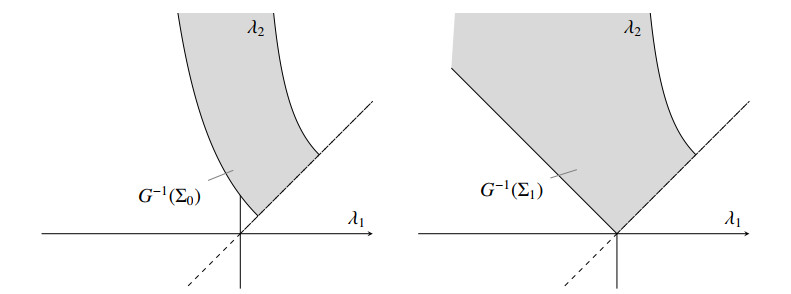









 .
. DownLoad:
DownLoad:



