1.
Introduction
In [16] a mathematical result about the separability of spatial and chromatic features of natural images has been established under two hypothesis: Second order stationarity and commutativity of the so-called spatiochromatic covariance matrices. Among other consequences, this result guarantees the well-posedness of several image codification models.
The closest representation of physical irradiance of a visual scene can be obtained through multispectral and high dynamic range (HDR) techniques. Unfortunately, nowadays technology permits the acquisition of artifact-free multispectral and HDR images only for still-life scenes, thus constraining too much the available data-set that can be used for statistical purposes. For this reason, knowing that we are considering a rough approximation of the true irradiance, we were forced to build our datasets by using Raw images obtained via RGB cameras.
In [16] it has been shown that spatiochromatic covariance matrices of raw images do not commute perfectly. However, the commutativity properties improve considerably if the information carried by raw images is modified according to an important transformation called Michaelis-Menten formula that can be written like this: uμ(x)↦uγμ(x)/(uγμ(x)+mγμ), where u is the RGB raw image function, x is the pixel location, μ is one of the RGB chromatic channel, so that uμ(x) is the image intensity in the pixel x and in the chromatic channel μ and m represents the average value. More specifically, we want to investigate the influence of the parameter γ on the commutativity.
The reason why we consider this formula instead of others is that it has been empirically discovered in [20] that it fits the behavior of retinal cones in the transduction processed from light radiance to neuronal electric potential. Thus, the transformed images after the application of the Michaelis-Menten formula can be considered as a good approximation of the first signal input for the visual chain of events that characterize the human visual system.
We stress that the mathematical theory developed in this paper is aimed at formalizing and extending the results of [16], with the hope that they may be useful for vision scientists to refine their models.
The paper is structured as follows. In section 2, we recall the most important information that we need from the state of the art about statistics of natural images in order to introduce our work. In section 3, we discuss an estimation strategy of spatiochromatic covariance matrices of images, followed by a measure of their commutativity. In section 4.1, we present the image database that we used in our research. Most importantly, we introduce a crucial pre-processing filtering tool in our procedure: the sky classifier. In section 5, we discuss some result about the commutativity change after the application of the Michaelis-Menten transformation. Finally, in section 6 we resume our contributions and put our work in perspective.
2.
Spatiochromatic features of natural images
There is a general agreement about the fact that the Human Visual System (HVS from now on) has evolved in order to optimize the elaboration of visual signals coming from scenes of the natural world (which will be shorten with natural scenes from now on, following the traditional nomenclature). Attneave [1], MacKay [11] and Barlow [2] pioneered the idea that the HVS may optimize the processing of natural signals by performing a redundancy reduction, however they did not quantify these ideas with a computational theory that can provide a coding for natural images.
Two kind of redundancies can be distinguished in the interaction between humans and the natural environment: Firstly, natural scenes have plenty of homogeneous areas and the light reflected from spatial locations belonging to those areas will be interpreted as the same visual information, this implies a strong spatial correlation. Secondly, light signals are absorbed by the three L,M,S-type cones in the retina, whose sensitivity is not independent because they are highly overlapping. This implies a strong chromatic correlation. When both effects are taken into account, one speaks about spatiochromatic correlation.
The literature about natural image statistics is vast and its exhaustive presentation is far beyond the scope of this paper. Here we will deal only with the statistical information gathered by considering the spatial representation of the image and emphasizing the results from [4] and [19], which are essential to understand the development of our paper.
Before describing the results of [4] and [19], let us recall that when principal component analysis (PCA) is performed on small natural image patches, the basic features that result are Fourier descriptors, see for instance [13]). This fact is a consequence of spatial stationarity.
2.1. Chromatic redundancy in natural images
The first statistical information about chromatic redundancy has been experimentally obtained in [12] in the framework of color segmentation of RGB images. For each picture of a database of 8 RGB images, the authors computed the covariance matrix C of the distribution of the values of R, G and B at each pixel. They found that the eigenvectors of the covariance matrix are approximately the following ones for each image of the database: v1=(13,13,13)t, v2=(12,0,−12)t, v3=(−14,12,−14)t. These vectors correspond to the three following uncorrelated color features: X1=R+G+B3, X2=R−B2, X3=2G−(R+B)4.
This shows that the feature related to the largest variance is the luminance X1 (or achromatic channel) and the other two features are described by the opponent channels X2 (red-blue) and X3 (green-violet).
Buchsbaum and Gottshalk approached in [4] the problem of finding uncorrelated color features from a purely theoretical point of view. They considered the abstract ensemble of all possible visual stimuli (radiances) S≡{S(λ),λ∈L}, where L is the spectrum of visible wavelengths. From a given representative S(λ)∈S, a weighted integration of S(λ) over the visual spectrum, with weights given by the Vos-Walraven spectral sensitivity functions L(λ),M(λ),S(λ), yields the three cone activation values L=∫LS(λ)L(λ)dλ, M=∫LS(λ)M(λ)dλ, S=∫LS(λ)S(λ)dλ.
Assuming that the stimulus S(λ) (coming from a fixed point ˉx of a scene) is a random variable, a covariance matrix can be build from the three random variables L,M,S. This matrix, called the chromatic covariance matrix is defined as:
where CLL≡E[L⋅L]−(E[L])2, CLM≡E[L⋅M]−E[L]E[M]=CML, and so on, E being the expectation operator.
Let K(λ,μ)=E[S(λ)S(μ)]−E[S(λ)]⋅E[S(μ)] be the covariance function, then the entries of the covariance matrix can be written as CLL=∬L2K(λ,μ)L(λ)L(μ)dλdμ, and so on.
To be able to perform explicit calculations, the analytical form of the covariance function K(λ,μ) must be specified. In the absence of a database of multispectral images, Buchsbaum and Gottschalk used abstract non-realistic data, i.e., they chose the easiest covariance function corresponding to visual stimuli maximally uncorrelated with respect to their energy at different wavelengths, i.e., K(λ,μ)=δ(λ−μ), δ being the Dirac distribution. As the authors themselves observe, this condition is satisfied only if the ensemble S is made of monochromatic signals.
With this choice, the entries of the covariance matrix C are all positives and they can be written as CLL=∫LL2(λ)dλ, CLM=∫LL(λ)M(λ)dλ, and so on. C is also real and symmetric, so it has three positive eigenvalues λ1≥λ2≥λ3 with corresponding eigenvectors vi, i=1,2,3. If W is the matrix whose columns are the eigenvectors of C, i.e., W=[v1|v2|v3], then the diagonalization of C is given by Λ=WtCW=diag(λ1,λ2,λ3).
The eigenvector transformation of the cone excitation values L,M,S, in the special case of monochromatic stimuli, is then
The transformed values A,P,Q are uncorrelated and their covariance matrix is Λ. A is the achromatic channel, while P and Q are associated to the opponent chromatic channels.
The key point in Buchsbaum and Gottschalk's theory is the application of the Perron-Frobenius theorem (see e.g., [3] for more details), which assures that positive matrices, i.e., matrices whose entries are all strictly greater than zero, have one and only one eigenvector whose entries have all the positive sign, and this eigenvector corresponds to the largest eigenvalue, i.e., λ1. So, only the transformed A channel will be a linear combination of the cone activation values L,M,S with positive coefficients, while the channels P and Q will show opponency. This is the theoretical reason underlying the evidence of post-retinal chromatic opponent behavior, following Buchsbaum and Gottschalk.
Using the data obtained above, Buchsbaum and Gottschalk could write explicitly the transformation from (L,M,S) to (A,P,Q) as follows:
More information about the relationship between Buchsbaum and Gottschalk's theory and other well-known color spaces can be found in [10].
2.2. Spatiochromatic redundancy in natural images
The most influential paper about spatiochromatic feature is [19], where Ruderman, Cronin and Chiao proposed a patch-based spatiochromatic coding and tested Buchsbaum-Gottschalk's theory on a database of 12 multispectral natural images of foliage. The authors have shown that the scatterplots in the LM and LS planes of the L,M,S cone activations values (corresponding to 1000 pixels randomly selected in the database) show a high degree of correlation but also asymmetry. So, they decided to study these data by first reducing their asymmetry: They modified the LMS values by taking their decimal logarithm and then they subtracted the average image value in the logarithmic domain. They obtained the so-called Ruderman-Cronin-Chiao coordinates, i.e., ˜L=LogL−⟨LogL⟩, ˜M=LogM−⟨LogM⟩ and ˜S=LogS−⟨LogS⟩. Following [19], if ˜L, ˜M, ˜S are the basis vectors in the logarithmically-transformed space, then the application of the PCA gives the following three principal axes:
The color space spanned by these three principal axes is called ℓαβ space.
The key point of the paper is the idea to study spatiochromatic features by considering 3×3 patches, with each pixel containing a 3-vector color information, so that every patch is converted in a vector with 27 components that were analyzed with the PCA. The principal axes of these small patches in the logarithmic space show that the first fluctuations are in the achromatic channel, followed by blue-yellow fluctuations in the α direction and red-green ones in the β direction.
The spatial axes are largely symmetrical and can be represented by Fourier features, in line with the translation-invariance of natural images, as argued in [5]. It is important to stress that no pixel within the patches appear other than the primary gray, blue-yellow or red-green colors, i.e., no mixing of ℓ,α,β has been found in any 3×3 patch. This means that not only the single-pixel principal axes ℓ,α,β, but also the spatially-dependent principal axes ℓ(x),α(x),β(x), viewed as functions of the spatial coordinate x inside the patches, are decorrelated. These results have been confirmed by [14].
2.3. Second order stationarity
Let us now analyze the consequence of second order stationarity in natural images on their decorrelated spatiochromatic features. For the sake of clarity, we will first start with the simplest case of gray-level images, where stationarity implies that the principal components are Fourier basis functions. We will then extend this result to the color case and show that a supplementary hypothesis on color covariance matrices yields principal components given by the tensor product between Fourier basis functions on one side, and achromatic plus opponent color coordinates on the other.
2.4. The gray-level case
Let I be a gray-level natural image of dimension W×H. We denote the H rows of I as r0,…,rH−1 and the position of each pixel of I row-wise as follows* :
* To avoid cumbersome repetitions of the indexes variability, from now on, we will suppose that j,j′∈{0,…H−1} and k,k′∈{0,…W−1}, unless otherwise specified.
Each row rj=(rj0,…,rjW−1) will be interpreted as a W-dimensional random vector and each component rjk as a random variable.
Let us define the spatial covariance of the two random variables rjk, rj′k′:
Due to the symmetry of covariance we have cj,j′k,k′=cj′,jk′,k. We write the spatial covariance matrix of the two random vectors rj, rj′ as cov(rj,rj′)≡Cj,j′, where Cj,j′ is the W×W matrix:
Finally, the spatial covariance matrix C of the image I can be written as:
Notice that C is a HW×HW matrix because each sub-matrix Cj,j′ is a W×W matrix.
Hypothesis 1. From now on, the covariance of I is assumed to be invariant under translations of the row and column index, i.e., cj,j′k,k′=c|j−j′||k−k′|.
Hypothesis 1 is weaker than the typical definition of second order stationarity because here we do not assume the translation invariance of the mean. Alongside this hypothesis, we add a technical requirement on the geometry of digital images which is implicitly assumed every time the Fourier transform is considered, i.e., we will consider a symmetrized spatial domain with a toroidal distance, which means that we will perform the identification rjk=rj′k′ when j≡j′ (mod H) and k≡k′ (mod W), i.e., every time there exist a,b∈Z such that j′−j=aH and k′−k=bW.
As a covariance matrix, C is real, symmetric and positive-definite. Now, as a consequence of the previous hypotheses, the matrix C is also block-circulant with circulant blocks. Indeed, the Cj,j′ are circulant matrices, i.e., matrices where each row vector is rotated one element to the right relative to the preceding row vector†, or, equivalently, each column vector is rotated one element down with respect to the preceding column vector. If we use the convenient shorthand notation 'circ()' to denote a circulant matrix, by specifying only the first row (or, equivalently, the first column, due to symmetry) between the round brackets, then Cj,j′ can be written as follows:
† This can be easily verified by noticing that cj,j′k,k′=cj,j′k+1,k′+1.
Now, if we write Cj≡C0,j, j=0,…,H−1 it is straightforward to see that the covariance matrix C is block-circulant and can be explicitly written as:
It is well known that an n×n circulant matrix has n eigenvalues corresponding to the components of the DFT of the finite sequence given by the first row of the matrix itself, and its eigenvectors are the Fourier basis functions, see e.g., [6] or [8].
Let us apply this general result to the W×W circulant matrices Cj. The set of eigenvalue equations Cjem=λjmem, λj∈ C and e∈ C W, m=0,…,W−1, can be written as the following matrix equation CjEW=ΛjEW, where‡:
‡ We have used the simplified notation cjm≡c0,j0,m to denote the matrix element of position m in the first row of the matrix Cj≡C0,j, m=0,…,W−1.
and EW is the Vandermonde matrix which implements the DFT, i.e., the so-called Sylvester matrix :
The following remark will help us understanding how to extend the previous diagonalization procedure to the whole matrix C.
Remark 1. Let M=circ(M0,…,MH−1) be a block-circulant matrix and let us assume that the blocks Mj can be diagonalized on the same basis B. If we write EH=[e0|e1|⋯|eH−1], with the vectors ej defined as in Eq. (2.12) for all j=0,…,H−1, then it can be verified by direct computation that EH⊗B is a basis of eigenvectors of M, where ⊗ denotes the Kronecker product.
In the case of our spatial covariance matrix C, all the submatrices Cj have the same basis of eigenvectors EW, thus the result stated in the previous remark can be directly applied on the matric C to guarantee that
for m=0,…,W−1, and l=0,…,H−1 provides a basis of eigenvectors for the matrix C.
Actually, due to the symmetry of covariance matrices, the complex parts of the exponentials cancel out (see [8]) and so the 2D cosine Fourier basis also constitutes a basis of eigenvectors of C:
2.5. The color case
Let us consider now an RGB image function u:Ω→[0,255]3, where Ω is the spatial domain, and, for all (j,k)∈Ω, u(j,k)=(R(j,k),G(j,k),B(j,k)) is the vector whose components are the red, green and blue intensity values of the pixel defined by the coordinates (j,k).
We define the spatiochromatic covariance matrix among two pixels of position (j,k) and (j′,k′) by extending Eq. (2.6) as follows:
where we defined cj,j′k,k′(R,R)=E[R(j,k)R(j′,k′)]−E[R(j,k)]E[R(j′,k′)], cj,j′k,k′(R,G)=E[R(j,k)G(j′,k′)]−E[R(j,k)]E[G(j′,k′)], and similarly for the remaining matrix elements. Of course the matrix cj,j′k,k′ is symmetric because cj,j′k,k′(G,R)=E[G(j,k)R(j′,k′)]−E[G(j,k)]E[R(j′,k′)]=cj,j′k,k′(R,G), and similarly for all the other off-diagonal elements.
Naturally, we can extend Hypothesis 1 to RGB image case, as follows.
Hypothesis 1 (RGB case). The spatiochromatic covariance of u of the chromatic channels μ,ν is assumed to be invariant under translations of row and column index, i.e., cj,j′k,k′(μ,ν)=c|j−j′||k−k′|(μ,ν), for all μ,ν∈R,G,B.
With the same technical requirements, we know that C(μ,ν) is also block-circulant with circulant blocks.
In the particular case defined by j′=j and k′=k, we will call cj,j′k,k′ 'chromatic autocovariance' and denote it simply as c0. Notice that the matrix analyzed in [4] is the chromatic autocovariance of the LMS values.
We then define the spatiochromatic covariance matrix Cj,j′ among the two random vectors rj, rj′ given by the j-th and j′-the rows of the spatial support of u by extending Eq. (2.7) as follows:
Finally, we define the spatiochromatic covariance matrix C of the RGB image u by extending Eq. (2.8) to the 3HW×3HW matrix defined in this way:
Now, supposing that all the elements of the matrices (2.15) are positive, thanks to the Perron-Frobenius theorem we can assure that each of these cj,j′k,k′ matrices has a basis of eigenvectors that can be written as a triad of achromatic plus opponent chromatic channels.
{If we further assume that the matrices (2.15) can be diagonalized on the same basis of eigenvectors (A,P,Q), then, thanks to Remark 1, we have that the eigenvectors of the spatiochromatic covariance matrix C(R,G,B) can be written as the following Kronecker product:}
which is precisely the type of eigenvectors that have been exhibited experimentally in [18]. A standard result of linear algebra guarantees that a set of matrices can be diagonalized on the same basis of eigenvectors if and only if they commute§. Thanks to the hypothesis of translation invariance of covariance, this is verified if and only if the generic covariance matrix cj,j′k,k′ commutes with the chromatic autocovariance matrix c0.
§ We recall that, given two generic matrices A and B for which the products AB and BA is well defined, [A,B]≡AB−BA is called the 'commutator' between them. Of course A and B commute if and only if [A,B]=0.
The following proposition holds true [16].
Proposition 1. Let u:Ω→[0,255]3 be an RGB image function, with a periodized spatial domain Ω, and suppose that
1. All matrices cj,j′k,k′ are positive, i.e., their elements are strictly greater than 0;
2. The spatiochromatic covariance matrices cj,j′k,k′ defined in (2.15) depend only on the distances |j−j′|, |k−k′|, i.e., the covariance of u is stationary;
3. The following commutation property holds:
Then, the eigenvectors of the spatiochromatic covariance matrix C defined in (2.17) can be written as the Kronecker product (A,P,Q)⊗em,l, where (A,P,Q) is the achromatic plus opponent color channels triad and em,l is the 2D cosine Fourier basis defined in Eq. (2.14).
Proposition 1 defines a mathematical framework where the empirical result of Ruderman et al. can be formalized and understood in terms of statistical properties of natural images. In [16], the hypotheses of the proposition above have been checked thanks to simulations performed on databases of natural images: The first two hypotheses have been confirmed, while the third will be discussed in detail in the following part of the paper.
2.6. Commutativity and exponential decay of covariance matrices
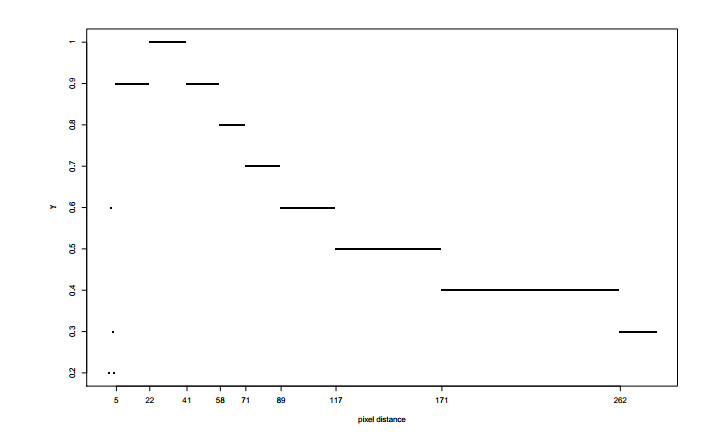
The experiments conducted in [16] empirically discovered a linear relationship in the semi-logarithmic scale between spatiochromatic covariance cj,j′k,k′(μ,ν) and pixel distance d=√(j−j′)2+(k−k′)2:
This, of course, implies an exponential decay for spatiochromatic covariance that corrected the power-law decay that was commonly supposed to hold true. These analytic expressions will allow us performing a theoretical analysis of the covariance estimators ˆcdμν, which will play an important role in the discussion of commutativity.
It must be underlined that the exponential decay of cdμν holds true with a great amount of precision only for an intermediate pixel distance range and it slightly deviates from it when d is very small or very large. These deviations are to be expected, because of two different reasons. When d is small, noise and the convolution kernel used by image sensors [15] introduce non linearity between irradiance and pixel intensities; when d is large, the sensor response is altered by optical phenomena as vignetting [7] or an incorrect camera aperture.
This is the reason why, in papers dealing with databases of natural images (see, e.g., [19]), it is common to consider a reduced range of distances to compute statistical features. We will follow the same convention while dealing with experiments. However, for the theoretical part of the paper, we will allow the validity of the exponential decay for any distance d≥0.
3.
Estimation of spatiochromatic covariances
In this section, we will propose a reliable method to estimate the spatiochromatic covariances and then we will analyze their properties.
3.1. Construction of covariance estimators
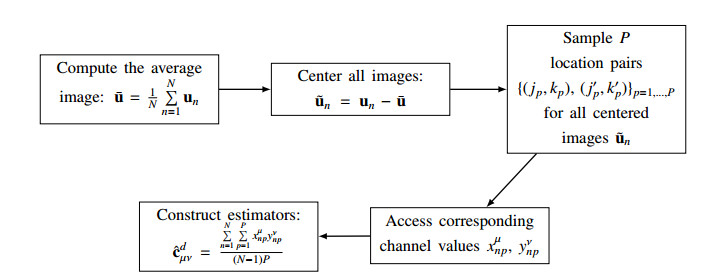
Let us start by introducing some notation and nomenclature. un:Ω→[0,1]3, n=1,2,…,N, is the n-th RGB image function with spatial support Ω (common to all images). For each fixed pixel location x∈Ω, un(x)=(Rn(x),Gn(x),Bn(x)) is the RGB value of x in the three chromatic channels. The values {un(x),x∈Ω}n=1,…,N are i.i.d. image samples with finite population mean and covariance. First of all, we compute the average image ˉu=1NN∑n=1un=(ˉR,ˉG,ˉB) and subtract it from each image to get centered images ˜un=un−ˉu=(Rn−ˉR,Gn−ˉG,Bn−ˉB). The μ-channel of the n-th centered image will be written as ˜uμ,n.
The main task that we must perform is to estimate the coefficients βμν in Eq. (2.20). For this, we decided to use the classical ordinary least squares (OLS) estimation [17], which requires the samples in the regression model to be independent. However, in practice, we face the problem that the number of raw images that we have at disposal in our database (and, in general, in the databases publicly available) is not sufficient to provide enough independent samples.
To have a quantitative idea, the final image samples that we have for empirical studies of covariance are 701, suppose that we build a regression model according to the exponential decay and we fit it with the OLS estimation. Suppose also that the distance d ranges from 0 to 100 with step 1 and μ,ν∈{R,G,B}, this implies the need of 909 covariance independent estimators given by log(ˆcdμν).
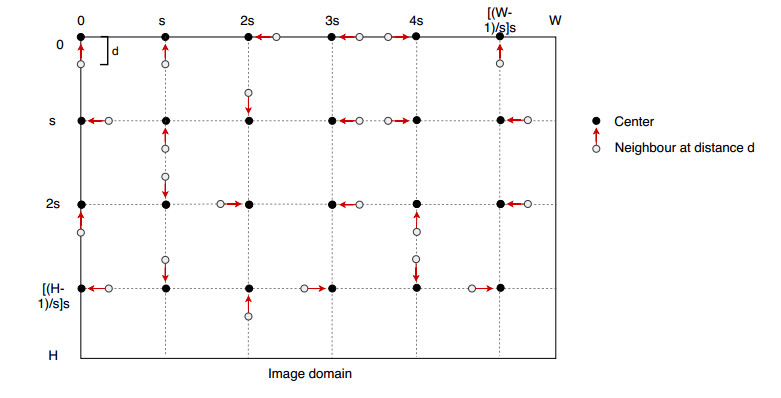
Let us describe how we have computed the estimators accordingly to the OLS prescriptions and overcame this problem. In each centered image, we sample P location pairs given by a center and its neighbor with a fixed step size s.
Centers are fixed in each image and their locations have coordinates
where, P=([H−1s]+1)([W−1s]+1), and [] takes the floor. Neighbours are also fixed throughout all images, while we do not restrict their locations as long as their distance from the centers remains d, for each fixed value of d. We write their locations as (j′p,k′p), with the same range variability as (jp,kp).
We notice that the set of centers can be identified with a downsampled version of the original image, so that we can consider the stationary hypothesis and its consequences to hold true also for the set of centers.
Finally, we estimate cdμν as follows:
To simplify the notation, let us write xμnp=˜uμ,n(jp,kp) for the centers and yνnp=˜uν,n(j′p,k′p) for the neighbors.
Finally, the estimators of spatiochromatic covariance matrices are:
We resume this construction in the scheme visualized in Figures 1 and 2.
3.2. Properties of ˆcdμν
Let us now discuss the properties of the estimators that we have built in the previous section. First of all, ˆcdμν are unbiased: in fact E(˜un)=0, and cov(˜un)=N−1Ncov(un), thus E(ˆcdμν)=∑Nn=1∑Pp=1E(xunpyvnp)(N−1)P=cdμν.
Then, we observe that, during the construction process to compute the estimators, we will keep introducing covariance values. Nevertheless, thanks to the covariance exponential decay, this accumulation will not cause a large variance of the estimators. In fact, we can prove that it exists an upper bound for cov(cdμν,cd′μ′ν′), where μ,ν,d and μ′,ν′,d′ are two different set of parameters, and that this quantity decreases with P, the number of samples.
In order to do that, we first notice that, by direct computation, it can be verified that if C is a block-circulant matrix with circulant blocks, i.e., Cj,j′=circ(cj,j′0,0,cj,j′0,1,...,cj,j′0,W−1) and C=circ(C0,C1,...,CH−1), then H−1∑j,j′=0W−1∑k,k′=0cj,j′k,k′=HWH−1∑j=0W−1∑k=0c0,j0,k.
Since the centers {xμnp}p constitute a downsampled version of the image uμ,n, its spatiochromatic covariance is also endowed with properties mentioned in section 2, as well as the one above, thus
thus
Moreover, since yμnp≤1 and yν′np′≤1, then |E(xμnpyνnpxμ′np′yν′np′)|≤|E(xμnpxμ′np′)|=N−1Ncdist[(jp,kp),(jp′,kp′)]μμ′.
Therefore P∑p=1P∑p′=1|E(xμnpyνnpxμ′np′yν′np′)|≤N−1NP∑p=1P∑p′=1cdist[(jp,kp),(jp′,kp′)]μμ′. From the remark above about circulant block matrices and from Hypothesis 1 (RGB case), it follows that:
Since βμν<0, then:
Moreover, since P=([H−1s]+1)([W−1s]+1), we can get:
therefore:
but H−1s−1<[H−1s]≤H−1s, thus, if we plug the previous inequality into the upper bound in Eq. (3.8), then we get:
So we get an upper bound for the covariances and, furthermore, when the set of parameters μ,ν,d is equal to the set μ′,ν′,d′, then we automatically have upper bound for the variances of the estimators.
Following an analogous procedure, we can get another upper bound w.r.t to the dimension W, i.e.,
This upper bound implies that the estimators are under control. Since βμμ′<0, this upper bound increases monotonically w.r.t s and thus it decreases w.r.t P. So, it makes sense for us to sample more pairs even in one image.
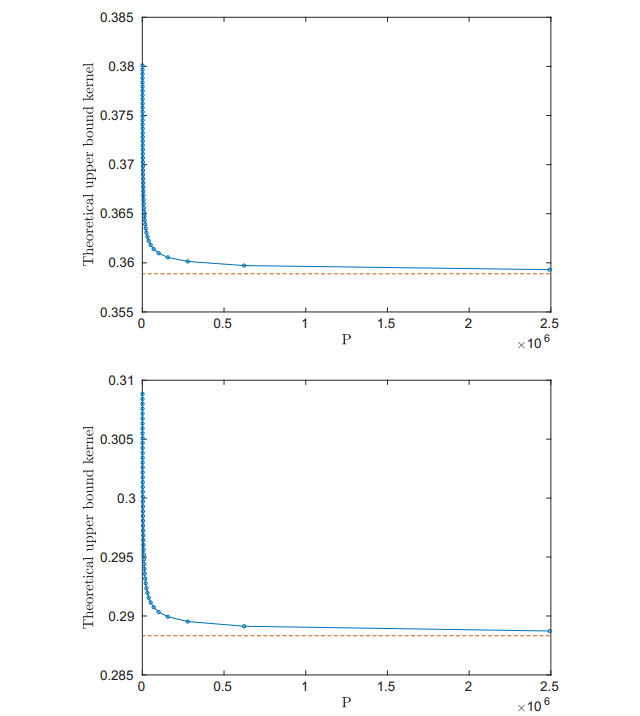
Let us compute the limit of the upper bound when P tends to infinity. The only part of it that depends on P is the kernel 1−eβμμ′(H−1+s)(1−eβμμ′s)(H−1s), thus we confine the computation on it:
In Figure 3, we show the behavior of the kernel w.r.t. P for the image dimensions of our database and for some β values of the same magnitude of those reported in [16].
We can notice an asymptotic behavior of the upper bound w.r.t. P, which implies that the error introduced in the computation by limiting ourselves to a value of P that can be managed by an ordinary computer is negligible.
We conclude this section with two remarks. The first one is that, if we set (μ,ν,d)=(μ′,ν′,d′), then, by Eqs. (3.9) and (3.10), then the covariance cov(ˆcdμν,ˆcd′μ′ν′) becomes the variance var(ˆcdμν) and so, when N→+∞, the upper bounds tend to 0 and thus the variance will tend to 0 as well.
The second remark is that, the previous information plus the unbiasedness of the estimators imply that the estimators ˆcdμν converge to cdμν in L2 sense, so that they are √N-consistent. Furthermore, because of the dedicated sampling strategy, ˆcdμν are asymptotically normal estimators. By the delta method, we get that log(ˆcdμν) is also a √N-consistent estimator of log(cdμν), for every strictly positive cdμν.
3.3. Regression
We now pass to the analysis of the regression step in order to estimate the slopes βμν with the OLS technique, as previously mentioned, which can be written as follows:
where d ranges in the intermediate pixel range mentioned in section 2.6. We will denote the OLS estimators of the slopes βμν as ˆβOLSμν.
We start by pointing out two problems related with the use of log(ˆcdμν): The first one is that they are correlated, so that the noise terms ϵdμν are correlated too. The second one is that log(ˆcdμν) is likely to be biased because of the non-linearity of the logarithmic function.
As we will now underline, these two problems will have a limited impact on our computation.
Actually, in spite of the fact that the noise terms are correlated, the OLS estimators are still unbiased, the only adverse effect of correlation is that the variance of ˆβOLSμν will become larger. Formally speaking, the ˆβOLSμν will not be the so-called BLUE, which stands for Best Linear Unbiased Estimators.
Passing to the second problem, even if log(ˆcdμν) is biased w.r.t log(cdμν), as we previously mentioned, it remains √N-consistent. By definition of consistency, if we observe a tiny variance of log(ˆcdμν), then its biasedness can be ignored.
As we will show in more detail in section 5, the variance of log(ˆcdμν) that we measured in practice is almost null and so is the variance of ˆβOLSμν, thus biasedness is not a problem for our computations.
4.
Analysis of spatiochromatic covariance matrices commutativity
To study the commutativity of spatiochromatic covariance matrices quantitatively, we need to select a measure. Let us report here some standard definition that will be useful in this section.
Quoting [9], we call a set F⊂M(n,R) of matrices a commuting family of matrices if every pair of matrices in F commutes. F is said to be simultaneously diagonalizable if there is a single non-singular matrix V∈M(n,R) such that V−1AV is diagonal for every A∈F.
From classical linear algebra, it is well known that F⊂M(n,R) is a commuting family if and only if it is a simultaneously diagonalizable family. Moreover, for any given A∈F and for any given ordering λ1,…,λn of the eigenvalues of A, there is a non-singular matrix V∈M(n,R) such that V−1AV= diag(λ1,…,λn). Finally, if A is symmetric, then V is orthogonal, i.e., V−1=VT, the transposed of V.
These considerations allow us the possibility to measure the commutativity properties of the set of estimates {ˆcd}d without having to compute all the commutators. Instead, we will compute the matrix V which best simultaneously diagonalizes the family of matrix estimates and we will measure the lack of commutativity by this value:
where JD-obj stands for joint diagonalisability objective and it is the sum of the square off-diagonal elements of VTˆcdV, where d runs from 0 to some maximal distance value used compute the covariances. Of course, in the case of perfect commutativity, JD-obj would be zero while, for an almost-commuting family, the value of JD-obj will be small but not perfectly null.
4.1. Dataset description
The database we used consists of 732 raw images, of size 1288×1936, taken by a Canon 400D. In order to explore the largest possible variety of visual content of natural scenes, we have diversified as much as possible the pictures that we have taken. In Each 4-neighborhood of pixels in a raw image contains two pixels corresponding to the R and B channels and two pixels corresponding to the G channel. Each RAW image was demosaicked to build a subsampled sRGB image simply by keeping unaltered the R and B information and averaging the G channel.
The advantage of raw images is that they are free from post-processing operations such as gamma correction, white balance or compression, thus, modulo camera noise, they provide a much better approximation of irradiance than other images, as e.g., jpeg ones. An excerpt of this database is provided in Figure 4.
However, we found out that the proportion of images containing large areas of the sky (called sky images hereafter) dominates the semantic content of the database. Too many sky images will cluster a subset, which will have a different covariance structure than the rest. Therefore, prior to the numeric studies, we need to filter part of sky images out, to balance the database.
For this purpose, we have developed a sky classifier, that we will describe in detail in the appendix.
After filtering, there are 701 images left.
4.2. Implementation
The only hyperparameter that we need to assign beforehand is the step size s. In practice, we have approximately min(H,W) options for s. Since we need to decrease the variance as much as possible, considering the execution time, we chose s=2 (P=623392).
The computational complexity of Eq. (3.1) is O(NP). We use Matlab 9.4 ¶ to implement the method. In the case of our database, it takes around 14 hours to compute 281 (pixel distances) × 9 (channel combinations) estimates for raw images, while it needs 23 to 24 hours to perform a Michaelis-Menten transformation and the same estimation.
¶ Codes to reproduce our experiments are available at https://github.com/yiyej/spatiochromatic_cov.
5.
Numeric results
In this section we present and discuss the numerical results that we have obtained through our simulations.
5.1. Validations of estimators' properties
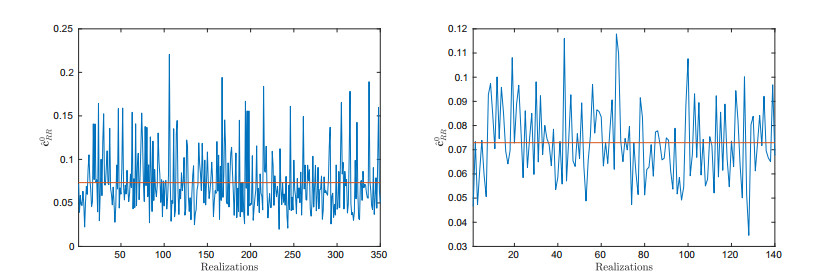
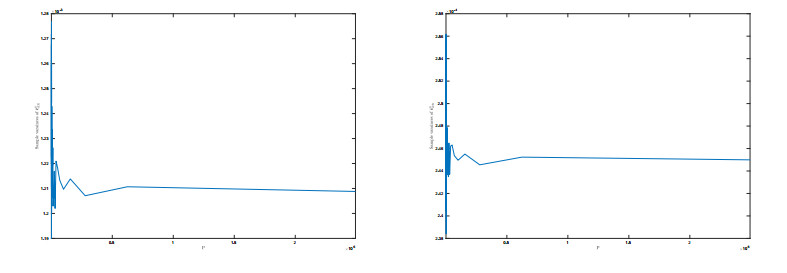
To validate the properties of estimator ˆcdμν, we group n0 images to mimic once realization. So we have Nn0 realizations in total. Figure 5 shows the unbiasedness of ˆcdμν. Figure 6 shows the empirical upper bounds of var(ˆcdμν).
5.2. Exponential decay of spatio-chromatic covariance of raw images
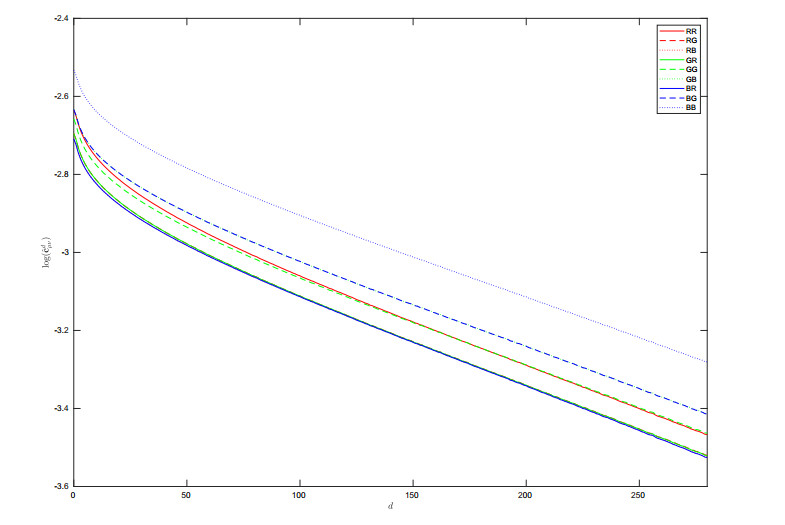
In Figure 7 we show the decay of log(ˆcdμν) computed for the raw images of our database, after the sky classifier, with respect to d. Since we find a linear relationship, the exponential decay holds. We built the regression model and fit it with OLS. Estimates of the slopes are provided in Table 1. Notice that, up to the accuracy 10−4, the straight lines relative to the combinations of chromatic channels RR, RG (GR), RB (BR) are parallel and the same is true for those relatives to the combinations GG and GB (BG). All the straight lines are parallel up to the accuracy 10−3.
5.3. Effects of the Michaelis-Menten transformation on commutativity
In this subsection, we will be focusing on the effects of the Michaelis-Menten transformation, uμ(x)↦uγμ(x)/(uγμ(x)+mγμ) on the commutativity properties of spatio-chromatic covariance matrices.
Firstly, we compute the JD-obj measure, Eq. (4.1) for the original raw images of our database after the action of the sky classifier. Then, we transform the raw images applying the Michaelis-Menten formula with 9 different γ values, ranging from 0.2 to 1 with step 0.1 and we compute again the JD-obj measure.
It is clear that, if γ→0, then the Michaelis-Menten formula will turn all the image pixels to 1/2, thus leaving with constant images and all spatiochromatic covariance matrices would be identical and perfectly commuting. Since we want to avoid this trivial situation, we remain far from the value γ=0 by starting with γ=0.2.
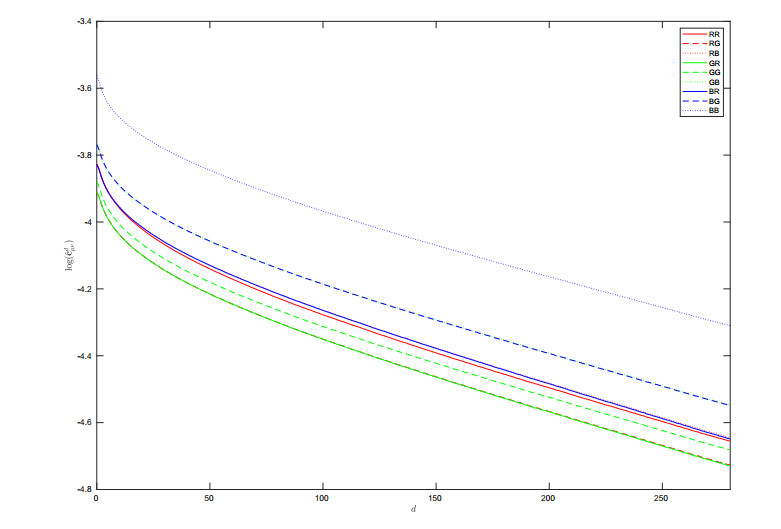
In Figure 8 it can be seen that also after the Michaelis-Menten transformation the exponential decay of covariance holds true||.
|| It is worth mentioning that the Michaelis-Menten transformation interchanges the position of some straight lines. For example, when γ=0.7, the lines RB(BR) and RR are shifted up w.r.t RG(GR) and GG, respectively.
Let us now discuss the quantitative results about the commutativity measure, i.e., the JD-obj values. For the sake of clarity, let us write JD-obj(raw) and JD-obj(MM) for the JD-obj values obtained with the original raw images and the transformed ones, with the Michaelis-Menten transformation, respectively.
We have performed experiments to compute these values on the family of matrices {ˆcd}d=0,…,dM by changing the value of γ.
One interesting result is that for all dM and for all γ greater than 0.5 JD-obj(MM)< JD-obj(raw). This remains true also for some values of γ smaller than 0.5 but, in this case, the relationship between JD-obj(MM) and JD-obj(raw) depends on dM.
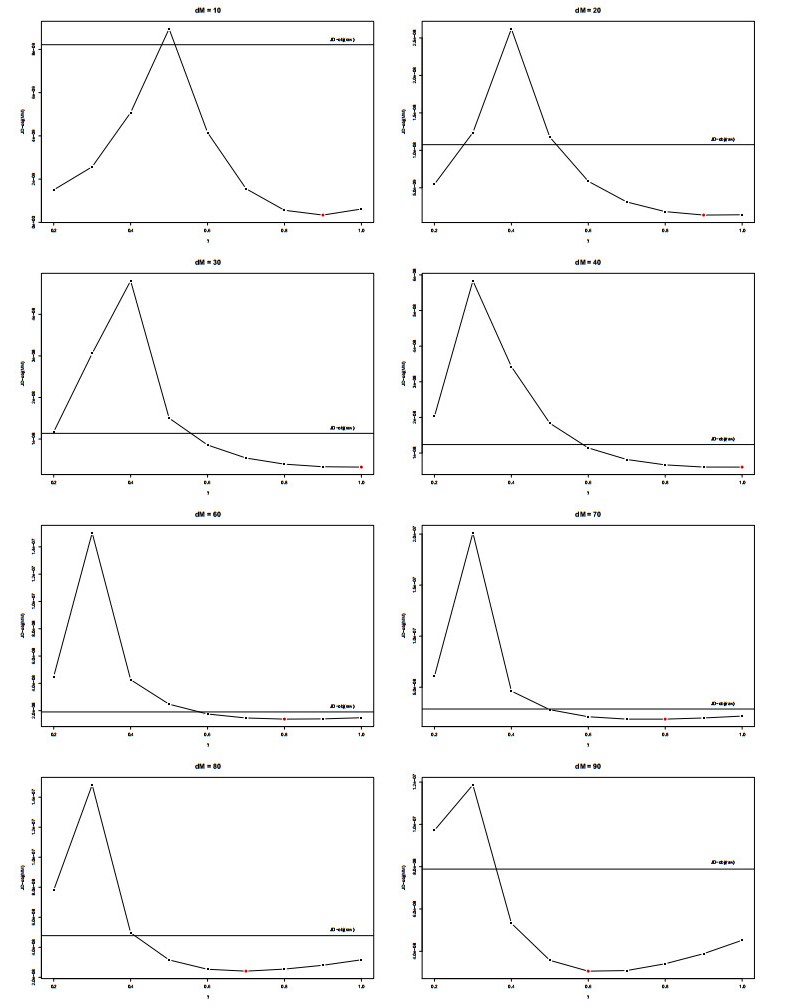
In Figure 9 we show the JD-obj(MM) with different γ parameters and with dM ranging from 10 to 90. The horizontal line is JD-obj(raw). For all these distance values, we empirically verified that when γ≥0.6, then the Michaelis-Menten transformation improves the commutativity of the family {ˆcd}d=0,…,75, whilst, for γ≤0.5, the Michaelis-Menten transformation may improve or not the commutativity.
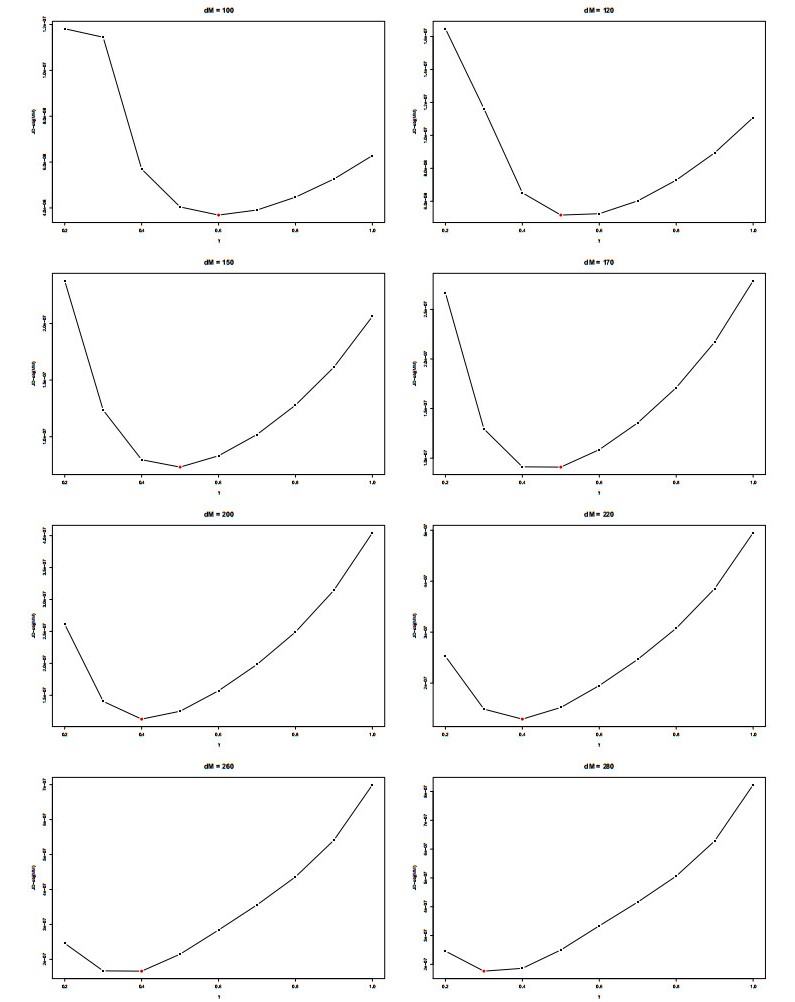
In Figure 10 we show the JD-obj(MM) with different γ parameters and with dM ranging from 100 to 280. Here there is no horizontal line showing JD-obj(raw) because, for all these distance values and for all γ the Michaelis-Menten transformation improves the commutativity of the family {ˆcd}d=0,…,75. However, we can notice that the optimal value of γ, corresponding the absolute minimum of the curve representing JD-obj(MM), gradually shifts towards 0. One explanation for this behavior is the following: When a large number of matrices is considered, much more noise will be introduced in the computation, in this case, very small values of γ tend to make the family of matrices more homogeneous, thus improving commutativity. Plus, if these matrices do not really commute, then the best way of forcing them to commute is to make them having more homogeneous values.
We believe that, focusing on small dM will help revealing the true information about the action of the Michaelis-Menten transformation. Interestingly, 0.9 is the first value of γ to be best, before γ decreases back to small values.
In Figure 11 we indicate the best γ value with respect to commutativity for all the distances from 1 to 280.
6.
Conclusions and perspectives
The work of this paper is inspired by the analysis of spatiochromatic features of natural images provided in [16]. Our contributions to the improvements of this paper are the following.
First of all, we constructed a collection of estimators for spatiochromatic covariance matrices that is reliable from the perspectives of unbiasedness and consistency. This construction is based on a method that permits to exploit as much as possible the information of each image, thus allowing the use of relatively small databases of images, as those typically available for raw or multispectral natural images. Our proposal is general and may be applied to reduces the amount of sample needed by any image statistics model.
Moreover, we devised a sky classifier which allowed us to remove from our database images with statistically redundant information about the sky.
We also verified with great accuracy the exponential decay of spatiochromatic covariance for raw images, showing that, up to a 10−3 accuracy, the exponential decay coefficient is the same for each combination of chromatic channels, if we avoid the very first distances which are affected by noise and errors introduced by the convolution kernel of cameras. The consequence is that, up to this accuracy, spatio-chromatic covariance matrices commute and the results of paper [16] about the possibility to separate the codification of spatial and chromatic visual signals into a tensor product hold true.
Finally, we have analyzed the consequences of the application of the Michaelis-Menten transformation to our raw data. If raw data can be associated to the radiance of a visual scene, their Michaelis-Menten transformed can be associated with the output of retinal cones after the absorption of light.
So, it is natural to test if the Michaelis-Menten transformation has an effect on the commutativity of spatio-chromatic covariance matrices, allowing a more precise and efficient tensor product codification of spatial and chromatic visual signals by the optical neurons.
The Michaelis-Menten transformation depends on a parameter γ, which has been measured as 0.74 for the retina of a rhesus monkey. Our tests have confirmed that the exponential decay is retained after the application of the Michaelis-Menten transformation and, remarkably, that, when γ ranges between 0.6 and 1, the commutativity of spatio-chromatic covariance matrices is actually improved with respect to the original raw image values.
The results that we have obtained are very promising and confirm the conjectures of paper [16] about the importance of the Michaelis-Menten transformation. However, for a full proof of these assumptions a database of natural mulispectral images should be built and analyzed with the techniques described in this paper. Technological limitations of multispectral cameras do not allow this for the moment when movement (e.g., leaves moved by the wind or people walking) is considered.
Acknowledgments
Jérémie Bigot is a member of Institut Universitaire de France (IUF), and this work has been carried out with financial support from the IUF. Edoardo Provenzi acknowledges a partial support from the CNRS grant 80primes.
Conflict of interest
The authors declare no conflict of interest.
Appendix
Sky classifier
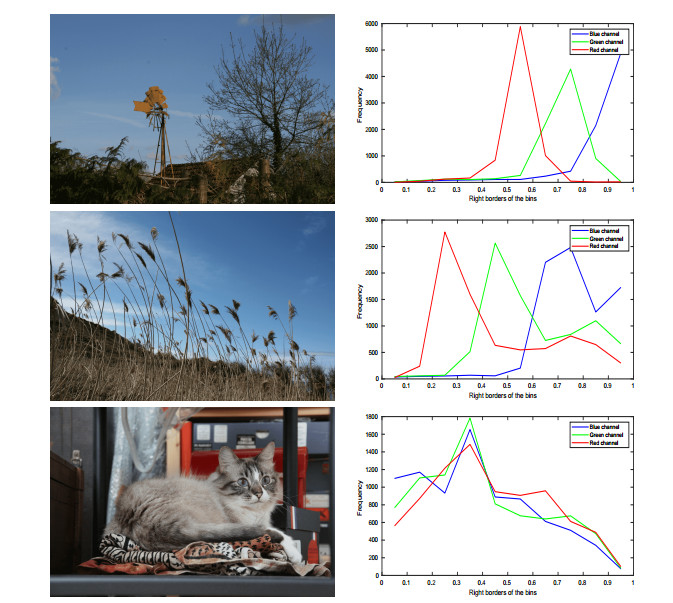
The key point of this classifier is to control the distribution mass of blue channel and red channel. After a statistical analysis of our database, we found out that, in general, the objects appearing in the pictures are characterized by high values of red, while, of course, the sky is always characterized by high values of blue.
We only consider sky in the daylight. Figure 12 shows one common distribution of daylight sky. We can see that the mass of blue channel distribution of the sky area is located in the high-valued range, so that there is an enough number of pixels capable of exhibiting `bright blue'. Also, the mass of red channel is located out of the high-valued range. Thus, most of pixels in sky images in our database are characterized by a simultaneous presence of large amount of high-valued blue pixels and a relatively small amount of high-valued red pixels.
Inspired by the analysis above, we defined the Boolean variable that labels sky in our classifier as follows:
where, Quantileμ(pμ) is the quantile of the probability pμ for the pixel value distribution of the chromatic channels μ=B or R and θB should be located in the high-valued range, θR should be located out of high-valued range.
%By requiring this, we can assure that the mass of blue channel is located in high-valued range and that the mass of red channel is located out of high-valued range.
If our database contained only horizontal images, we could limit our sky classifier only to the upper 1/3 part of an image. However, as can be seen from Figure 4, we also have to deal with rotated vertical images, thus, in order to take into account both image geometries, we apply our algorithm only on the top right part of the images. More specifically, we considered the pixels belonging to the top-right part of the image, i.e., the sub-image with coordinates (x,y), x≥(1−λ)W and 0≤y≤λH.
We then compute Quantileμ(pμ) in each sub-image and the label variable. If the label turns out to be 1, then we take the image out of our database.
Notice that pictures with a significant amount of clouds in the sky will, correctly, not be removed, because in this case there will be a significant amount of bright red pixels.
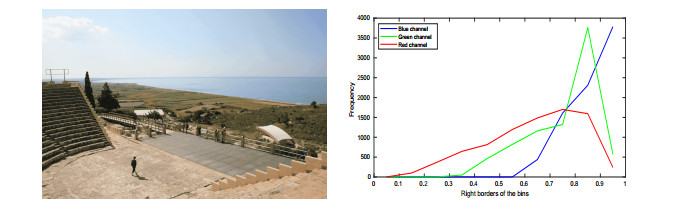
Moreover, if there is a sufficient amount of detail in the sky, as shown by Figure 13, the classifier will not remove the image from the database.
By correctly tuning the parameters of the classifier, we can control the proportion of sky images to be taken out. The tuning for our database gave this parameter selection: λ=0.4, pB = 0.4, pR = 0.6, θB = 0.6, θR = 0.6 which classified 31 pictures as sky images over 732, reported in Figure 14.









 DownLoad:
DownLoad: