Pellet diameter of Ganoderma lucidum in a repeated-batch fermentation for the trio total production of biomass-exopolysaccharide-endopolysaccharide and its anti-oral cancer beta-glucan response

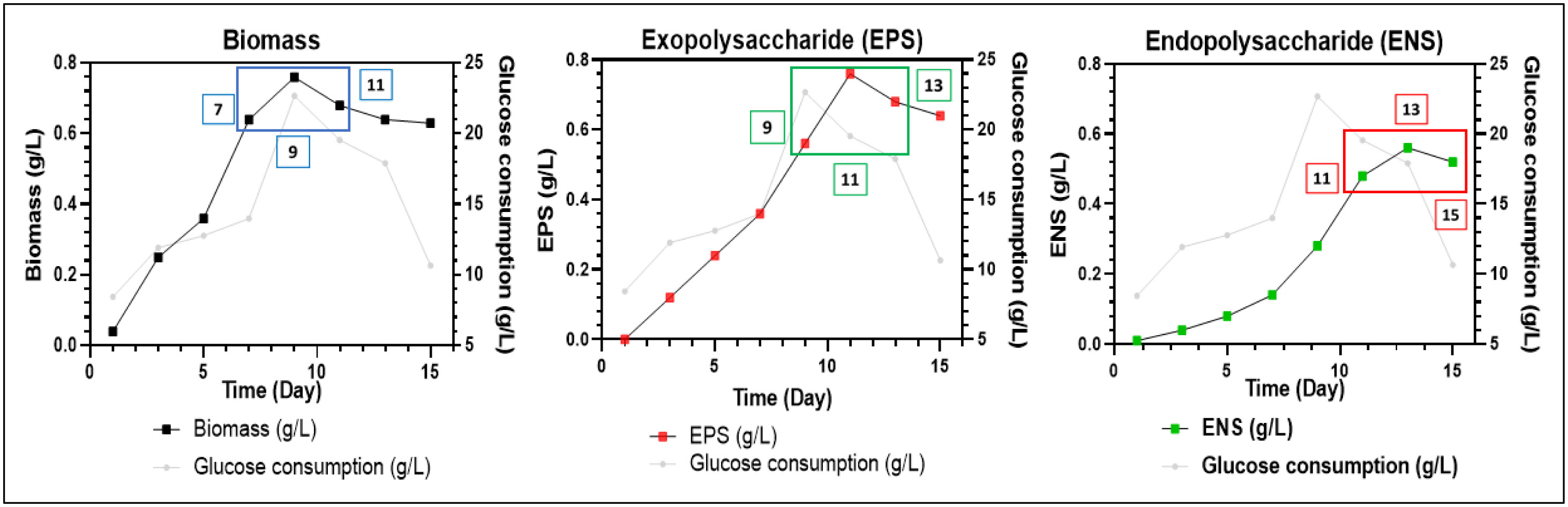
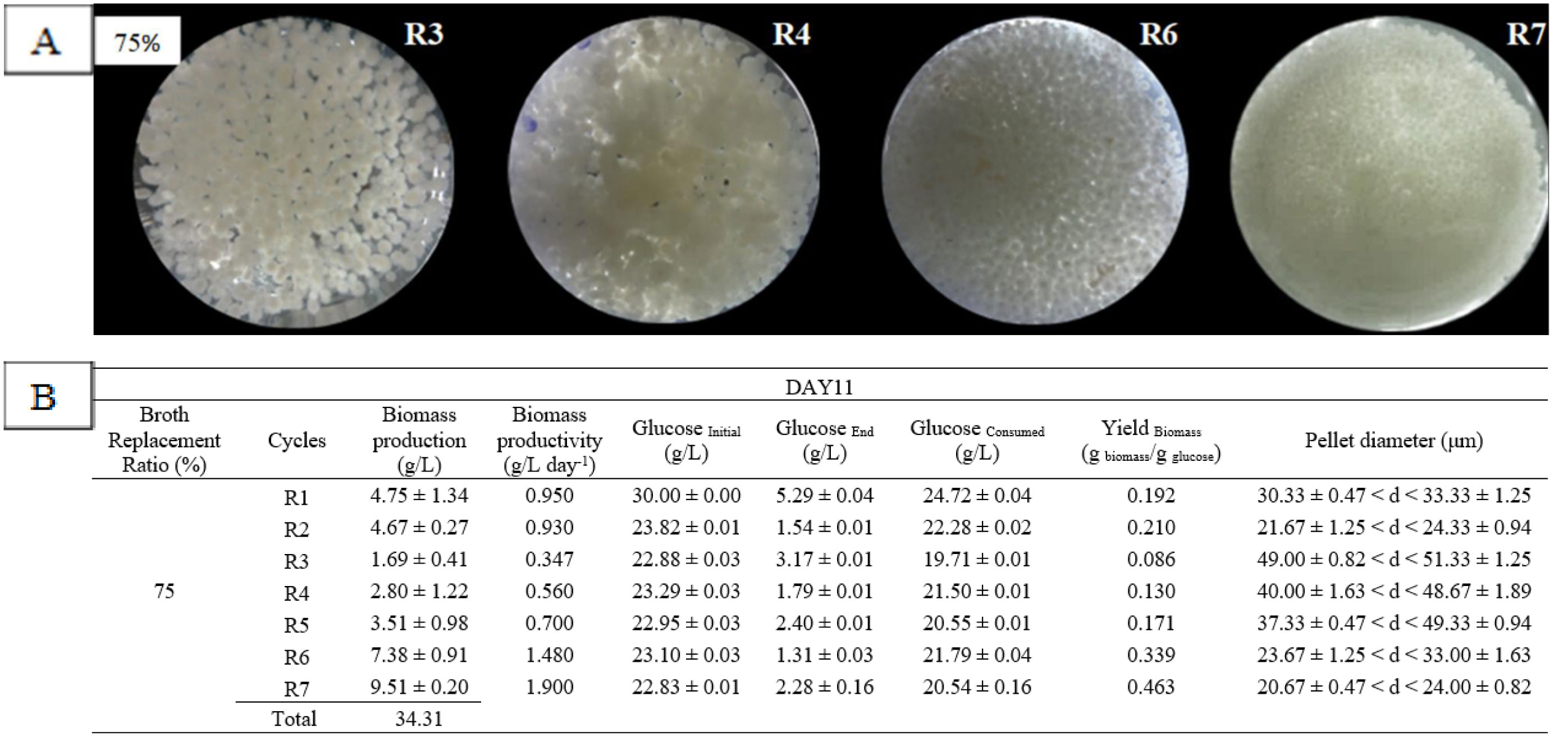
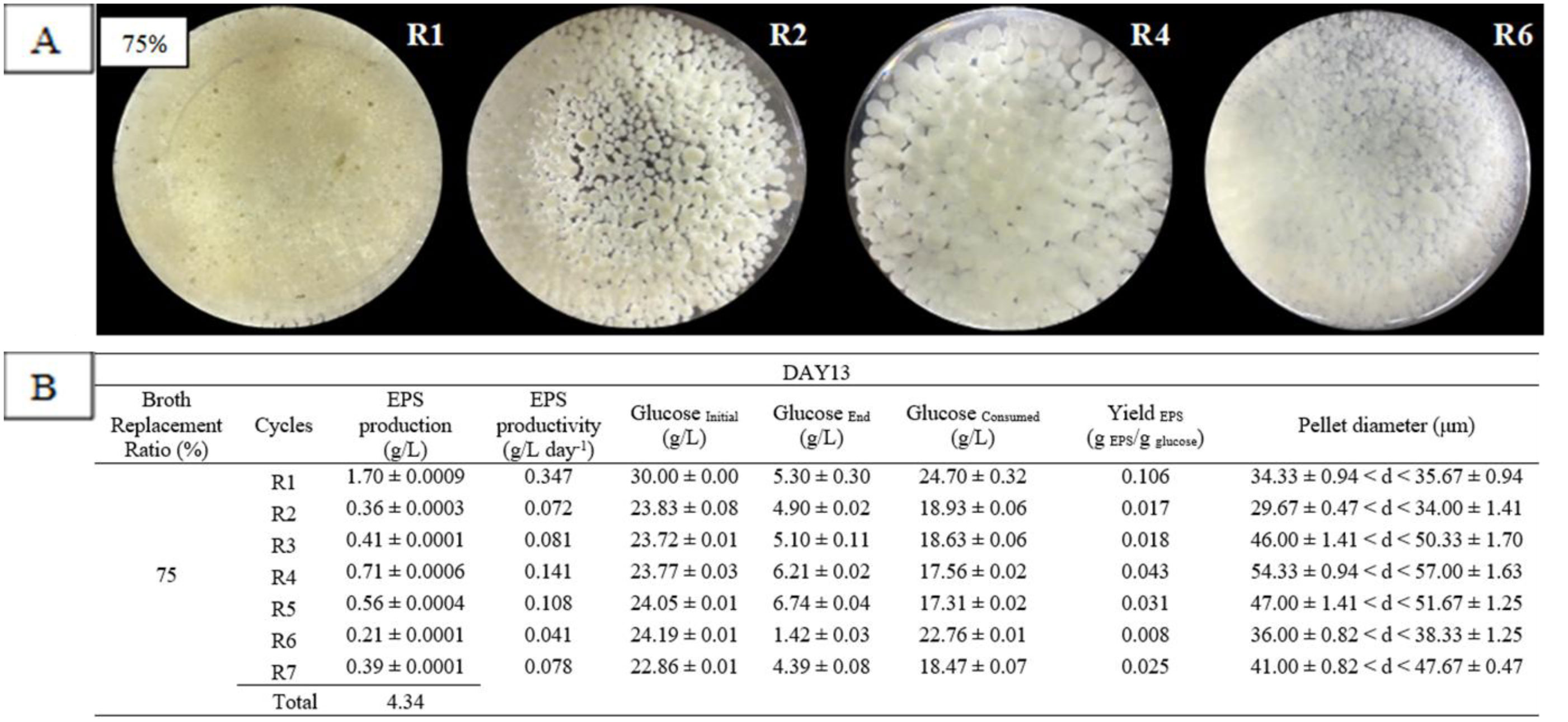
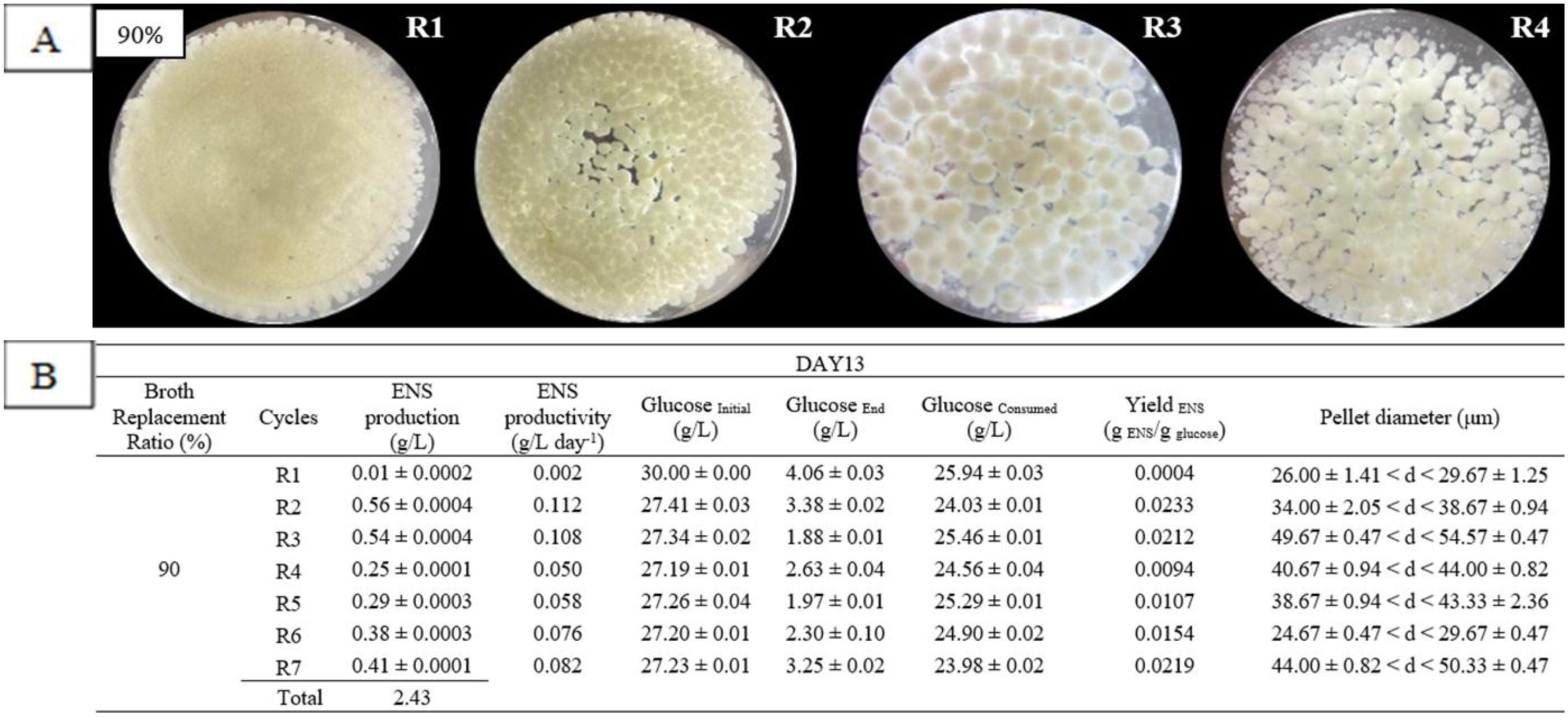
Dedicated to our friend Giuseppe (Rosario) Mingione on his 50th birthday.

1.   Introduction

Let us consider the functional

where $v:\Omega \subset \mathbb{R}^n \to \mathbb{R}^n$, $n\geq 2$, $\Omega$ a bounded open set, $p > 1,$ $r > 0$.

It is well known that, if $u$ is a minimizer for $\mathcal{F} (v)$, the maximum principle holds, namely, each component $u^{\alpha}$ of $u = (u^1, ..., u^n)$ satisfies the following condition

Indeed, maximum principle holds true, in general, for minimizers of the class of functionals

where the integrand $\Psi(s, \, t)$ is such that $s\to \Psi(s, \, t)$ strictly increases, and $t\to \Psi(s, \, t)$ is increasing (see ^[39]).

What happens when we only have that $s\to \Psi(s, \, t)$ is increasing and not necessarily strictly increasing? Two examples are $\Psi(s, \, t)\, = \, |t|$ that gives

and $\Psi(s, \, t)\, = \, \max \{|s|^p\, -\, 1;\, 0\}\, +\, |t|^r$ that gives

with $p > 1$ and $r > 0$. Maximum principle fails. Namely, consider $n = 2$, $\Omega\subset \mathbb{R}^2$ is the ball $B(0;\, \pi)$ centered in the origin and with radius $\pi$.

The map $u: = (1, \, 1+\, \sin|x|)$ has gradient

$\det Du = 0$, and $|Du|^2\, = \, \cos^2|x|\, \leq \, 1$. It minimizes both the functionals (1.2) and (1.3). Moreover, the

second component $u^2 = 1\, +\, \sin|x|$ equals $1$ on the boundary of $\Omega$, and is strictly greater than $1$ inside. Therefore, the second component of the minimizer $u$ does not satisfy the maximum principle. This example was given to the last author by V. Sverak a few years ago. F. Leonetti gladly takes the opportunity to thank V. Sverak for his kindness.

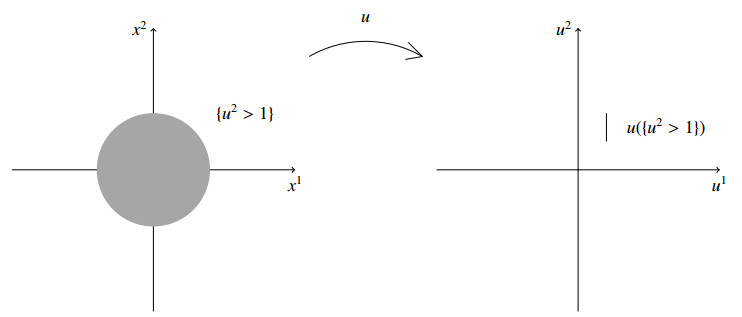
Furthermore, regarding the previous example, it is worth pointing out that the level set $\{x\in \Omega :\, u^2 (x)\, > \, 1 = \, u^2_{\partial \Omega}\}$ has positive measure

on the other hand, the measure of the image of the same level set, by means of $u$, is zero

see Figure 1.

Figure 1.  Image of the level set.

DownLoad: Full-Size Img PowerPoint

We ask ourselves whether the previous example shows a common feature to all minimizers when $t \to \Psi(s, t)$ strictly increases.

In this paper, we give a positive answer to previous question obtaining a modified version of maximum principle in the case the integrand $\Psi (s, \, t)$ of the functional (1.1) strictly increases only with respect to the second variable $t$.

We will suppose $p > n$ in order to ensure semicontinuity property and consequent existence of minimizers (see ^[17]), and also to apply the area formula, that reveals to be a key tool in our proof.

In addition, we can still get a similar maximum principle by using a version of the area formula for $u\in W^{1, \, 1}(\Omega, \, \mathbb{R}^n)$, see ^[34,35], provided a suitable negligible set $S\, = \Omega\setminus \cal A_D$ is removed (see definition 2.1).

Let us come back to the functional (1.3): coercivity holds true with exponent $p$ and growth from above with exponent $q = :nr$ that could be different from $p$. When we deal with functionals with different growth, regularity for minimizers is usually obtained when the two exponents of growth and coercivity are not too far apart, see ^{[3,6,10,11,12,13,18,32,49,50]}. In our case, we do not assume anything on the distance between the two exponents $p$ and $q$. This is not in contradiction with the counterexamples in the double phase case ^[22,25], since our functional (1.3) is autonomous, neither is in contrast with counterexamples in the autonomous case ^{[33,38,47,48]}, since they show blow up along a line that intersects the boundary of $\Omega$ while, in our case, minimizers are bounded on $\partial \Omega$.

With regard to the regularity of minimizers $u$ of (1.1), let us mention partial regularity results in ^{[9,23,26,27,28,30,36,52]}. Everywhere regularity results can be found in ^[7,19,29,31], for $n = 2$. We also mention global $L^\infty$ bounds in ^{[4,5,21,39,40,41,42,43,44]}, and local $L^\infty$ regularity in ^{[8,14,15,16,20]}. Furthermore, concerning nonlinear elasticity, we cite, in particular, the results in ^{[1,37,45,46,51]}.

In the next section 2 we write some preliminaries. In section 3 we state our result and we give the proof.

2.   Preliminaries

In order to obtain our result, we need that the area formula holds. Therefore, let us recall the following

Definition 2.1. Let $u : \mathbb{R}^n \rightarrow \mathbb{R}^n$ be a map which is almost everywhere approximately differentiable and let $A$ be a measurable subset of $\mathbb{R}^n$. We define the Banach indicatrix of $u$ by

where

and the theorem

Theorem 2.2. (see Theorem 1 in section 1.5, chapter 3, at page 220 of ^[35]) Let $\Omega$ be an open subset of $\mathbb{R}^n$ and u be an almost everywhere approximately differentiable map, in particular let $u\in W^{1, 1}(\Omega; \mathbb{R}^n)$. Then for any measurable subset $A$ of $\Omega$ we have that $N(u, A, \cdot)$ is measurable and

holds.

Furthermore, a related condition we will refer to is the Lusin property (N) that is so defined

Definition 2.3. (Lusin property (N)) Let $\Omega \subset \mathbb{R}^n$ be an open set and $f: \Omega \rightarrow \mathbb{R}^n$ a mapping. We say that f satisfies Lusin property (N) if the implication

holds for each subset $E \subset\Omega$.

3.   Main results

Let $\Psi:[0, +\infty) \times [0, +\infty) \rightarrow \mathbb{R}$ be a continuous non negative function such that

and let us denote $\Omega\subset \mathbb{R}^n$ a bounded open set. We will consider integral functional of the type

Definition 3.1. Let $p\geq 1$ and $u\in W^{1, p}(\Omega; \mathbb{R}^n)$ such that $\mathcal{F}(u) < \infty$. We will say that $u$ is a minimizer of $\mathcal{F}$ in $\Omega$, if and only if

The main result is the following

Theorem 3.2. Let $u\in W^{1, p}(\Omega; \mathbb{R}^n)$, $p > n$, be the continuous representative of a minimizer of the functional (3.1), under assumptions $(H1)$ and $(H2)$. Fix $\alpha \in \{1, \dots, n\}$, and let us denote

$B_{L_{\alpha}}$ is the set of points in $\Omega$ where the maximum principle is violated, then

Proof. Let us define

It results that $v$ is a good test function in $(3.2)$, namely $u-v\in W_0^{1, p}(\Omega; \mathbb{R}^n)$, then we deduce that

Let us denote

and let us split the integrals in $(3.4)$ on the sets $G_{L_{\alpha}}$ and $B_{L_{\alpha}}$. Observing that $Du\equiv Dv$ on the set $G_{L_{\alpha}}$ we can get rid of the common part in (3.4) thus obtaining

Now we observe that on $B_{L_{\alpha}}$, $Dv^{\alpha} = 0$ and $\det Dv = 0$, then

Now, argue by contradiction, by assuming that

At this stage, we recall that $|Dv|\leq |Du|$ on $B_{L_{\alpha}}$, and we use the strict monotonicity of $\Psi$ with respect to the second argument $(H2)$, and hypothesis $(H1)$, to deduce

thus reaching a contradiction. The previous argument shows that

Using the area formula $(2.1)$ we conclude

To conclude the proof we recall that the condition $p > n$ ensures that $u:\Omega\rightarrow \mathbb{R}^n$ satisfies the Lusin property (N), that is $\mathcal{L}^n (u(E)) = 0$ whenever $E\subset \Omega$ and $\mathcal{L}^n (E) = 0$. In particular $\mathcal{L}^n (B_{L_{\alpha}}\setminus \mathcal{A}_{D}(u)) = 0$ and this implies that

Connecting $(3.7)$ and $(3.10)$ we get $(3.3)$.

It is worth pointing out some comments concerning the hypotheses in Theorem 3.2.

As a matter of fact, assuming $u\in W^{1, p}(\Omega; \mathbb{R}^n)$ for $p > n$ ensures some fundamental conditions.

The first point concerns the existence of minimizers of the functional $(3.1)$. Assuming that $p > n$ guarantees not only that $\det Du\in L^1$, but more that the map

is sequentially continuous with respect to the weak topology (see Theorem 8.20 in ^[17]). The aforementioned property, that is no longer true for $p < n$, see ^[2], is one of the main ingredients to prove the lower semicontinuity of the functional $(3.1)$. The second main ingredient to deduce the existence of minimizers of the functional $(3.1)$ is a kind of convexity assumption on the function $\Psi$. Precisely, we have that if the function

is convex and

then the functional $(3.1)$ is weakly lower semicontinuous and coercive in $W^{1, p}(\Omega; \mathbb{R}^n)$. The existence of minimizers of the functional (3.1) follows for any fixed boundary datum $u\in W^{1, p}(\Omega; \mathbb{R}^n)$ such that $\mathcal{F}(u) < +\infty$ (see Theorem 8.31 in ^[17]; see also ^[24]).

The second main point, where the assumption $p > n$ is crucial, concerns the Lusin property (N) quoted in the Definition 2.3. It is known that the Lusin property (N) still holds true for $u\in W^{1, n}(\Omega; \mathbb{R}^n)$, if $u$ is a homeomorphism. Moreover, there are also other results about the validity of the Lusin property (N) for suitable $p < n$, or with integrability rate close to $n$ under particular assumptions, but, beyond that, the Lusin property (N) is no longer true, in general, for $u\in W^{1, p}(\Omega; \mathbb{R}^n)$ with $p\leq n$. In this case we can carry on the proof of Theorem 3.2 as before, but we can not conclude in the same way because we do not have any information regarding the set $\mathcal{L}^n(u(B_{L_{\alpha}}\setminus \mathcal{A}_{D}(u)))$. Nevertheless we can state the Theorem 3.2 in a weaker form. We need to stress the dependence of the level set $B_{L_{\alpha}}\, = \, \{x\in\Omega\, :\, u^{\alpha}(x) > L_{\alpha}\}\, = \, B_{L_{\alpha}}(u)$ on the considered representative $u$ of the minimizer.

Theorem 3.3. Let $u\in W^{1, p}(\Omega; \mathbb{R}^n)$, $p \geq 1$, be a minimizer of the functional (3.1) under assumptions $(H1)$ and $(H2)$. Fix $\alpha \in \{1, \dots, n\}$, then

Remark 3.4. We note that (3.9) holds true for every representative $u$ of a $W^{1, p}$- minimizer (see section 1.5, chapter 3 of ^[35]). Moreover, in accordance with Corollary 1, chapter 3 of ^[35], if we consider a Lusin representative $u$, it satisfies Lusin property (N) in whole $\Omega$ so that

holds, and for such a representative we come to the conclusion that

Acknowledgments

We acknowledge support by GNAMPA, INdAM, MUR, UNIVAQ, UNISA, UNISANNIO, Università di Napoli "Parthenope" through the Project CoRNDiS, DM MUR 737/2021, CUP I55F21003620001.

Conflict of interest

The authors declare no conflict of interest.