1.
Introduction
The Lotka-Volterra equations that represent the system of continuous-time non-linear differential equations whose solution is deterministic, evolved to determine the dynamics of biological systems. This system is a more generalized version of the Kolmogorov model because it only focuses on the predator-prey interactions but ignores competition, disease and mutualism, which the Kolmogorov model includes. As compared with other mathematical model, following assumptions are made in order to formulate the Lotka-Volterra equations:
(i) For the prey population there is no shortage of food.
(ii) The amount of food supplied to the prey is directly related to the size of the prey population.
(iii) The rate of change of population is directly proportional to its size.
(iv) The environment is constant and genetic adaptation is not assumed to be negligible.
(v) Predators will never stop eating.
Based on said assumptions a continuous-time, two-species Lotka-Volterra system takes the following form [1,2,3]:
where x and y respectively denotes the number of prey and predator. The quantities: dxdt and dydt respectively denotes the instantaneous rates of prey and predator, and a, b, c and d are positive real parameters. In 1st equation of system (1.1), ax represent that prey are reproduced exponentially whereas bxy shows that the rate at which the predator kills prey. So, if there is no population of prey or no population of predator, no decrease in the population of prey can occur. The equation for prey can be summed up as the rate at which new prey is born, minus the rate at which prey is killed off. Now in 2nd equation of system (1.1), cxy represent the rate at which predators kill prey except that a different constant is used to describe this relationship since the rate at which predators kill and the rate at which they reproduce are not identical. Also, dy is assumed to be an exponential decay, which mean that prey cannot kill the predators and that the decrease in predator population is due to natural death or emigration.
It is anticipated that as compared to continuous-time system, discrete-time system designated by difference equations are widely explored because these models are more reasonable, if populations have non-overlapping generations, as compared to differential type models, and also one can obtain more accurate numerical simulations [4,5,6]. During the last few years, discrete-time predator-prey models have been extensively investigated by studying fixed points, local and global dynamical properties, existence of possible bifurcation and chaos [7,8,9] and references cited therein. So, in this work, we explore the local dynamics, bifurcations and hybrid control in a 3×3 discrete-time predator-prey model, i.e., two prey and one predator, representing by the following system of difference equations [10]:
where xn, yn and zn respectively denotes population densities of prey and predator respectively, and a,b,c,d,e,f and r are real positive parameters. More precisely, r is the net reproductive rate of the prey population, a denotes the intrinsic rate of growth the prey, b is the rate of conversion of a consumed prey to a predator, c is the per capita rate of predation of the predator, d is death rate of the predator, e is the rate of conversion of a consumed prey to a predator and f is the per-capita rate of predation of the predator.
It is important here to mention that in 2013 Sagayaraj et al. [10] studied the local dynamics about three boundary fixed points only: P000(0,0,0), P0y0(0,r−1r,0) and P0yz(0,df,rf−f−drcf), out of five fixed points including the unique positive fixed point. So for the interested readers, these results regarding the local dynamics about fixed points: P000(0,0,0), P0y0(0,r−1r,0) and P0yz(0,df,rf−f−drcf) are summarized in Table 1.
From the Table 1, it is clear that for the said fixed points: P000(0,0,0), P0y0(0,r−1r,0) and P0yz(0,df,rf−f−drcf), Sagayaraj et al. [10] cannot give complete local dynamical classifications to interested readers, which is still further consideration and improvements towards local dynamical properties along with topological classifications and bifurcation analysis for the model under consideration. So, in this paper we will study the local dynamics about fixed points, bifurcations like fold bifurcation, Neimark-Sacker or Hopf bifurcation, supercritical or subcritical Neimark-Sacker bifurcation, period-doubling or flip bifurcation, supercritical or subcritical period-doubling bifurcation, and hybrid control in the model (1.2). More precisely, our key contributions in this paper are as follows:
● To explore the local dynamical properties along with different topological classifications about fixed points of the under consideration model.
● To explore the existence of prime period and periodic points of the model (1.2).
● To explore the existence of possible bifurcations about fixed points of 3×3 model.
● Presentation of numerical simulation to verify theoretical results.
● To control the N-S and P-D bifurcations about the positive fixed point by Hybrid control strategy.
This paper is structured as follows: In Section 2, we explored the existence of fixed points of the model (1.2) algebraically. The linearized form of the model (1.2) is presented in Section 3. In Section 4, we explored the local dynamics about boundary fixed points and unique positive fixed point of the model. Existence of prime period and periodic points of the model (1.2) are explored in Section 5. In Section 6, we explored the existence of bifurcations about boundary fixed points of the model (1.2) whereas detailed bifurcation analysis about boundary fixed points and unique positive fixed point of the model (1.2) are given in Section 7. Theoretical results are verified numerically in Section 8. In Section 9, the hybrid control strategy is presented to control the N-S and P-D bifurcations about the unique fixed point of the model while a brief summary of the paper is presented in Section 10.
2.
Existence of fixed points of the model (1.2)
The existence of fixed points in the interior of R3+ is explored in this Section. The result regarding the existence of fixed points for the 3×3 discrete-time model (1.2) can be summarized as a following Lemma:
Lemma 2.1. In the interior of R3+, model (1.2) has four boundary fixed points and a unique positive fixed point. Precisely
(i) ∀ a,b,c,d,e,f,r, P000(0,0,0) is a boundary fixed point of model (1.2);
(ii) P0y0(0,r−1r,0) is a boundary fixed point of the model (1.2) if r>1;
(iii) P0yz(0,df,rf−f−drcf) is a boundary fixed point of the model (1.2) if f>drr−1 where r>1;
(iv) Px0z(de,0,ab) is also boundary fixed point of the model (1.2), ∀ a,b,c,d>0;
(v) P+xyz(br(d−f)+f(b+ac)ber,br−b−acbr,ab) is the unique positive fixed point of (1.2) if d>bf(r−1)−afcbr and b>acr−1 where r>1.
Proof. If Pxyz(x,y,z) is a fixed point of model (1.2) then
Since for P000(0,0,0), P0y0(0,r−1r,0), P0yz(0,df,rf−f−drcf) and Px0z(de,0,ab), Eq (2.1) satisfied identically, and hence P000(0,0,0), P0y0(0,r−1r,0), P0yz(0,df,rf−f−drcf) and Px0z(de,0,ab) are boundary fixed points of the model (1.2). In order for the existence of the unique positive fixed point one need to solve the following equation simultaneously:
From first equation of system (2.2) one gets:
From second equation of system (2.2) and Eq (2.3), one gets:
Finally, from third equation of system (2.2) and Eq (2.4), one gets:
In view of Eqs (2.3)–(2.5) one can conclude that Pxyz(br(d−f)+f(b+ac)ber,br−b−acbr,ab) is the interior fixed point of model (1.2). Additionally, P+xyz(br(d−f)+f(b+ac)ber,br−b−acbr,ab) is the unique positive fixed point of the model (1.2) if d>bf(r−1)−afcbr and b>acr−1 where r>1.
3.
Linearized form of the model (1.2)
The linearized form of 3×3 model (1.2) about fixed point Pxyz(x,y,z) is explored in this Section. So we have the following map to create the corresponding linearized form of model (1.2):
where
Finally, J|Pxyz(x,y,z) about Pxyz(x,y,z) under the map, which is depicted in Eq (3.1), is
4.
Local dynamical properties about fixed points of the model (1.2)
Local dynamical properties along with topological classifications about fixed points: P000(0,0,0), P0y0(0,r−1r,0), P0yz(0,df,rf−f−drcf), Px0z(de,0,ab) and P+xyz(br(d−f)+f(b+ac)ber,br−b−acbr,ab) of 3×3 model (1.2) are explored in this section.
4.1. Local dynamical properties about P000(0,0,0)
The J|P000(0,0,0) about P000(0,0,0) is
The eigenvalues of J|P000(0,0,0) about P000(0,0,0) are
So by stability theory [11], the local dynamics of 3×3 model (1.2) about P000(0,0,0) can be conclude as follows.
Lemma 4.1. For P000(0,0,0) following conditions hold:
(i) P000(0,0,0) is never sink;
(ii) P000(0,0,0) is a source if
(iii) P000(0,0,0) is a saddle if
(iv) P000(0,0,0) is non-hyperbolic if
or
4.2. Local dynamical properties about P0y0(0,r−1r,0)
The J|P0y0(0,r−1r,0) about P0y0(0,r−1r,0) is
The eigenvalues of J|P0y0(0,r−1r,0) about P0y0(0,r−1r,0) are
We also summarized the local dynamics of 3×3 model (1.2) about P0y0(0,r−1r,0) as follows:
Lemma 4.2. For P0y0(0,r−1r,0), following statements hold:
(i) P0y0(0,r−1r,0) is never sink;
(ii) P0y0(0,r−1r,0) is a source if
(iii) P0y0(0,r−1r,0) is a saddle if
(iv) P0y0(0,r−1r,0) is non-hyperbolic if
or
4.3. Local dynamical properties about P0yz(0,df,rf−f−drcf)
The J|P0yz(0,df,rf−f−drcf) about P0yz(0,df,rf−f−drcf) is
The eigenvalues of J|P0yz(0,df,rf−f−drcf) about P0yz(0,df,rf−f−drcf) are
where
In the following Lemmas, we give the topological classifications about P0yz(0,df,rf−f−drcf) if Δ≥0 (resp. Δ<0) by existing literature [9,12].
Lemma 4.3. If Δ=4d2fr+d2r2−4drf2+4d2frf2≥0 then for P0yz(0,df,rf−f−drcf) of model (1.2), following statements hold:
(i) P0yz(0,df,rf−f−drcf) is a stable node if
(ii) P0yz(0,df,rf−f−drcf) is an unstable node if
(iii) P0yz(0,df,rf−f−drcf) is saddle node if
or
(iv) P0yz(0,df,rf−f−drcf) is non-hyperbolic if
or
Lemma 4.4. If Δ=4d2fr+d2r2−4drf2+4d2frf2<0 then for P0yz(0,df,rf−f−drcf) of model (1.2), following statements hold:
(i) P0yz(0,df,rf−f−drcf) is stable focus-node if
(ii) P0yz(0,df,rf−f−drcf) is an unstable focus-node if
(iii) P0yz(0,df,rf−f−drcf) is saddle focus-node if
or
(iv) P0yz(0,df,rf−f−drcf) is non-hyperbolic if
or
4.4. Local dynamical properties about Px0z(de,0,ab)
The J|Px0z(de,0,ab) about Px0z(de,0,ab) is
The eigenvalues of J|Px0z(de,0,ab) about Px0z(de,0,ab) are
Lemma 4.5. For Px0z(de,0,ab), following statements hold:
(i) Px0z(de,0,ab) is never stable focus-node;
(ii) Px0z(de,0,ab) is an unstable focus-node if
(iii) Px0z(de,0,ab) is a saddle focus-node if
(iv) Px0z(de,0,ab) is non-hyperbolic if
4.5. Local dynamical properties about P+xyz(br(d−f)+f(b+ac)ber,br−b−acbr,ab)
The J|P+xyz(br(d−f)+f(b+ac)ber,br−b−acbr,ab) about P+xyz(br(d−f)+f(b+ac)ber,br−b−acbr,ab) is
The characteristic equation of J|P+xyz(br(d−f)+f(b+ac)ber,br−b−acbr,ab) about P+xyz(br(d−f)+f(b+ac)ber,br−b−acbr,ab) is
where
Now in the following lemma, we explore the necessary and sufficient condition under which the roots of (4.34) lies on open unit disk by utilizing Theorem 1.4 of [11].
Lemma 4.6. P+xyz(br(d−f)+f(b+ac)ber,br−b−acbr,ab) of 3×3 model (1.2) is a sink iff the following conditions hold:
where δ1,δ2 and δ3 are depicted in (4.35).
5.
Existence of prime period and periodic points of the model (1.2)
We explore that the fixed points: P000(0,0,0), P0y0(0,r−1r,0), P0yz(0,df,rf−f−drcf), Px0z(de,0,ab) and P+xyz(br(d−f)+f(b+ac)ber,br−b−acbr,ab) of the model (1.2) are periodic points of prime period- 1. Additionally, we also explore that P000(0,0,0), P0y0(0,r−1r,0), P0yz(0,df,rf−f−drcf), Px0z(de,0,ab) and P+xyz(br(d−f)+f(b+ac)ber,br−b−acbr,ab) of the model (1.2) are periodic points having period- 2,3,⋯,n, by existing Literature [13,14,15].
Theorem 5.1. Fixed points: P000(0,0,0), P0y0(0,r−1r,0), P0yz(0,df,rf−f−drcf), Px0z(de,0,ab) and P+xyz(br(d−f)+f(b+ac)ber,br−b−acbr,ab) of model (1.2) are periodic points of prime period- 1.
Proof. From model (1.2), one has
where f,g and h are represented in system (3.2). After straightforward computation, from Eq (5.1) one gets:
From Eq (5.2), one can conclude that P000(0,0,0), P0y0(0,r−1r,0), P0yz(0,df,rf−f−drcf), Px0z(de,0,ab) and P+xyz(br(d−f)+f(b+ac)ber,br−b−acbr,ab) of model (1.2) is a periodic point of prime period- 1.
Hereafter we proved that fixed points: P000(0,0,0), P0y0(0,r−1r,0), P0yz(0,df,rf−f−drcf), Px0z(de,0,ab) and P+xyz(br(d−f)+f(b+ac)ber,br−b−acbr,ab) of 3×3 model (1.2) are periodic points having period- 2,3,⋯,n.
Theorem 5.2. The fixed point: P000(0,0,0) of 3×3 model (1.2) is a periodic point of period- 2,3,⋯,n.
Proof. From Eq (5.1), one has
Thus Eq (5.3) indicates that P000(0,0,0) of model (1.2) is a periodic point of period-2,3,⋯,n.
Theorem 5.3. The fixed points: P0y0(0,r−1r,0), P0yz(0,df,rf−f−drcf), Px0z(de,0,ab) and P+xyz(br(d−f)+f(b+ac)ber,br−b−acbr,ab) of 3×3 model (1.2) are periodic points of period- 2,3,⋯,n.
Proof. Same as the proof of Theorem 5.2.
6.
Existence of bifurcations about fixed points of the 3×3 model (1.2)
Existence of bifurcations about boundary fixed points: P000(0,0,0), P0y0(0,r−1r,0), P0yz(0,df,rf−f−drcf) and Px0z(de,0,ab) are explored in this Section. Moreover occurrence of bifurcations about boundary fixed points can be summarized as follows:
(i) About P000(0,0,0), one of the eigenvalues λ2|(4.5)=1 but λ1,3=1+a,1−d≠1 or −1. So 3×3 model (1.2) may undergoes a fold bifurcation if parameters Λ=(a,b,c,d,e,f,r) goes through the following curve:
For the interested readers, it is important here to mention that we have introduced new notation like λ2|(4.5) which stands that we have evaluated the eigenvalue λ2 at non-hyperbolic condition, which is depicted in Eq (4.5). Similarly we use such notation for same purpose in the rest of the paper.
Moreover, about P000(0,0,0), one of the eigenvalues λ3|(4.6)=−1 but λ1,2=1+a,r≠1 or −1. So 3×3 model (1.2) may undergoes a P-D bifurcation if parameters Λ goes through the following curve:
It is noted that for d=2 the predator leaves a negative number of offspring, i.e., in the absence of prey and therefore its no make sense biology. Thus we will exclude this case from further study.
(ii) About P0y0(0,r−1r,0), one of the eigenvalues λ2|(4.11)=−1 but λ1,3=1+a,1−d+f(r−1)r≠1 or −1. So 3×3 model (1.2) undergoes a P-D bifurcation if parameters Λ goes through the following curve:
Also P0y0(0,r−1r,0), one of the eigenvalues λ3|(4.12)=−1 but λ1,2=1+a,2−r≠1 or −1. So 3×3 model (1.2) undergoes a P-D bifurcation if Λ goes through the following curve:
(iii) About P0yz(0,df,rf−f−drcf), pair of complex conjugate eigenvalues |λ2,3|(4.26)=1 but λ1=1+a+bc(1−r+drf)≠1 or −1. So 3×3 model (1.2) undergoes a N-S bifurcation if parameters Λ goes through the following curve:
(iv) About Px0z(de,0,ab), λ1|(4.32)=−1 but |λ2,3|=1+ad>1. So 3×3 model (1.2) may undergoes P-D bifurcation if Λ goes through the following curve:
7.
Detailed bifurcation analysis about fixed points of the model (1.2)
For the completeness of this Section, the detailed bifurcation analysis about fixed points of the model (1.2) is presented as follows:
7.1. Fold bifurcation about P000(0,0,0)
About P000(0,0,0), 3×3 model (1.2) undergoes a fold bifurcation when parameters Λ goes through the curve, which is depicted in Eq (6.1). But by computation, fold bifurcation do not occur and therefore P000(0,0,0) is degenerate with high co-dimension for the original parameters Λ of 3×3 model (1.2).
7.2. P-D bifurcation about P0y0(0,r−1r,0)
About P0y0(0,r−1r,0), 3×3 model (1.2) undergoes P-D bifurcation when Λ goes through the curve, which is depicted in Eq (6.3). Since model (1.2) is invariant w.r.t x=z=0 then we can restrict the model (1.2) on x=z=0, to determine the bifurcation, where model (1.2) takes the form:
Also the map corresponds to Eq (7.1) takes the form:
Denote r=r∗=3, y=y∗=r−1r. By computation one gets: fy|r=r∗=3, y=y∗=r−1r=−1 which is non-hyperbolic condition for P-D bifurcation. Moreover, the non-degenerate conditions: fyy|r=r∗=3, y=y∗=r−1r=−6≠0 and fr|r=r∗=3, y=y∗=r−1r=29≠0 hold, which implies that 3×3 model (1.2) undergoes the P-D bifurcation when Λ goes through the curve, which is depicted in Eq (6.3). Additionally, (fyyfr+2fyr)(2fyyy+3f2yy)|r=r∗=3, y=y∗=r−1r=−81<0, and hence by existing literature [15,16,17] model (1.2) undergoes the supercritical P-D bifurcation.
7.3. N-S bifurcation about P0yz(0,df,rf−f−drcf)
In this Subsection, N-S bifurcation of the 3×3 model (1.2) is explored about P0yz(0,df,rf−f−drcf), if Λ goes through the curve, which is depicted in Eq (6.5) by assuming that r≠f(2c+ac+b)b(f−d). Let
then 3×3 model (1.2) takes the form:
whose linear part is same as J|P0yz(0,df,rf−f−drcf), which is depicted in Eq (4.13). Moreover at Eq (4.26), following non-degenerate conditions hold:
and additionally it is require that λm2,3≠1 where m=1,2,3,4 which also true by computation. Now using the transformation:
Equation (7.4) takes the following form:
where
and
Hereafter, we have the system (7.7) on the center manifold, i.e.,
where
In view of Eqs (7.10) and (7.7) becomes:
After some manipulation, from Eq (7.12) one gets: α1=α2=α3=0. So, the system (7.7) restricted to Wc(0) becomes
where
In order for Eq (7.13) to undergoes a N-S bifurcation, one require that the following discriminatory quantity σ should be non-zero [12,18,19]:
where
After straightforward calculation, one gets:
Based on N-S bifurcation analysis about P0yz(0,df,rf−f−drcf), one has
Theorem 7.1. 3×3 model (1.2) undergoes a N-S bifurcation at P0yz(0,df,rf−f−drcf) if σ≠0. Moreover, if σ<0 (resp. σ>0), then an attracting (resp. repelling) closed curve bifurcates from P0yz(0,df,rf−f−drcf). Finally Supercritical (resp. subcritical) N-S bifurcation take place if σ<0 (resp. σ>0).
Remark 1: Recall that about Px0z(de,0,ab), 3×3 model (1.2) may undergoes P-D bifurcation if Λ goes through the curve, which is depicted in Eq (6.6). But by computation, P-D bifurcation do not occur and therefore Px0z(de,0,ab) is degenerate with high co-dimension.
Hereafter, we explore the N-S as well as P-D bifurcations of the 3×3 model (1.2) without calculating the eigenvalues of J|P+xyz(br(d−f)+f(b+ac)ber,br−b−acbr,ab) about P+xyz(br(d−f)+f(b+ac)ber,br−b−acbr,ab). Precisely, in the following two theorems, we explore N-S and P-D bifurcations by utilizing explicit criteria, i.e., the criteria which is formulated by using a set of inequalities or equalities that contain the coefficients of the characteristic equation derived from J|P+xyz(br(d−f)+f(b+ac)ber,br−b−acbr,ab) about the unique positive fixed point [20,21,22].
7.4. N-S and P-D bifurcations about P+xyz(br(d−f)+f(b+ac)ber,br−b−acbr,ab)
Theorem 7.2. If
then 3×3 model (1.2) undergoes a N-S bifurcation about P+xyz(br(d−f)+f(b+ac)ber,br−b−acbr,ab), where δ1,δ2 and δ3 are depicted in Eq (4.35).
Proof. By utilizing explicit criterion, which is depicted in [20,21], for n=3 one gets:
Finally
Theorem 7.3. If
then 3×3 model (1.2) undergoes a P-D bifurcation about P+xyz(br(d−f)+f(b+ac)ber,br−b−acbr,ab).
Proof. By utilizing explicit criterion, which is depicted in [21,22], for n=3 one gets:
Finally
8.
Numerical simulations
Theoretical results are illustrated numerically in this Section. In this regard, following cases are presented to discuss the correctness of obtained theoretical results about fixed points for the 3×3 model (1.2):
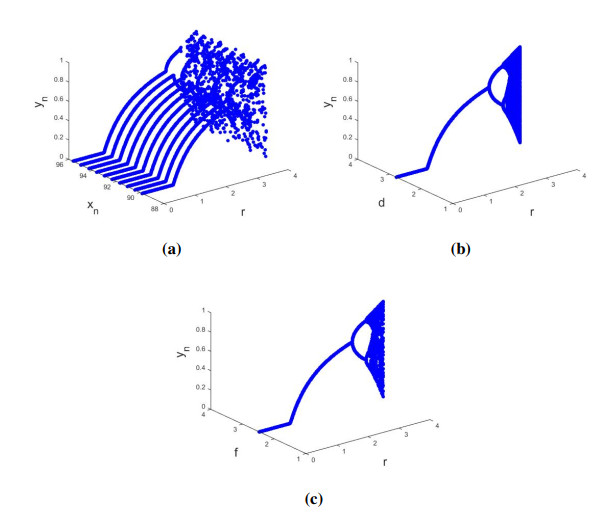
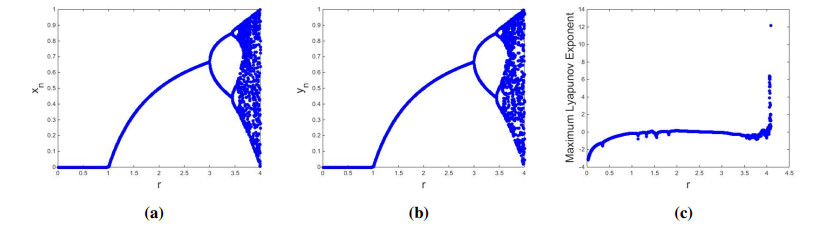
Case I: If a=0.007,b=0.001,c=0.1,d=0.39,e=0.5,f=2.7 and varying r∈[1.2,10.4] then Figure 1a clearly indicates that about P0y0(0,0.6884735202492211,0), model (1.2) undergoes P-D bifurcation, which correctness the theoretical discussion in Subsection 7.2. More 3D bifurcation diagrams are plotted and depicted in Figure 1b, 1c.
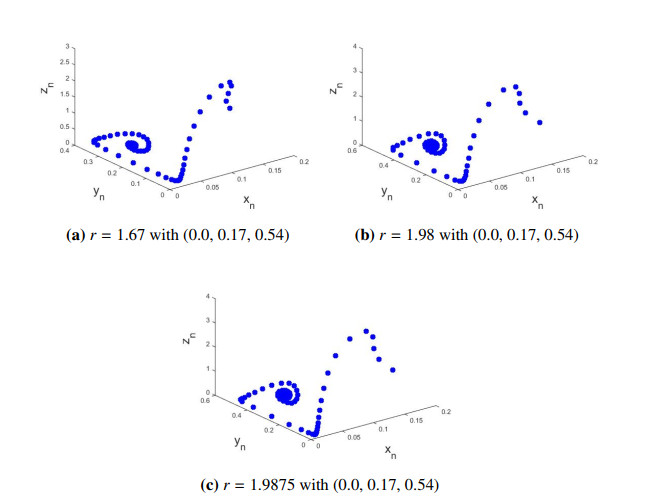
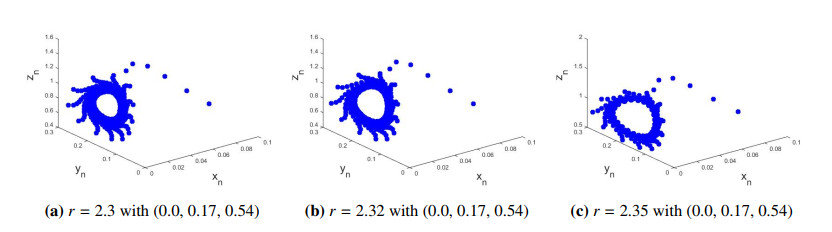
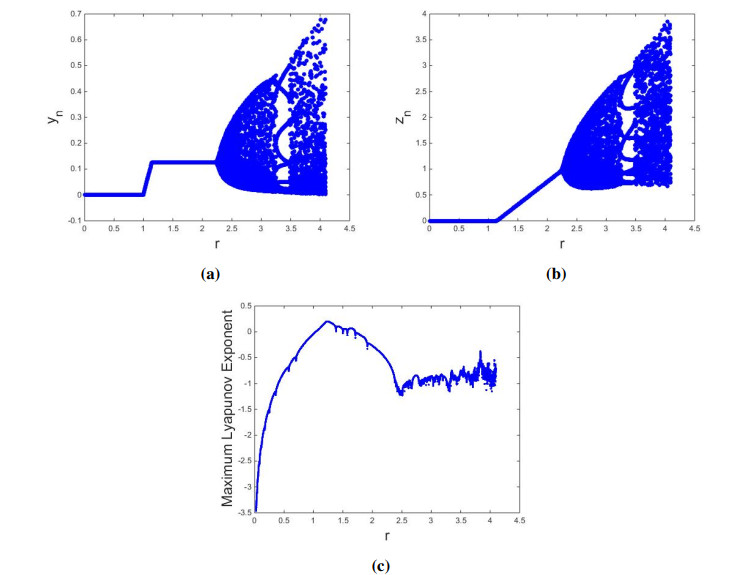
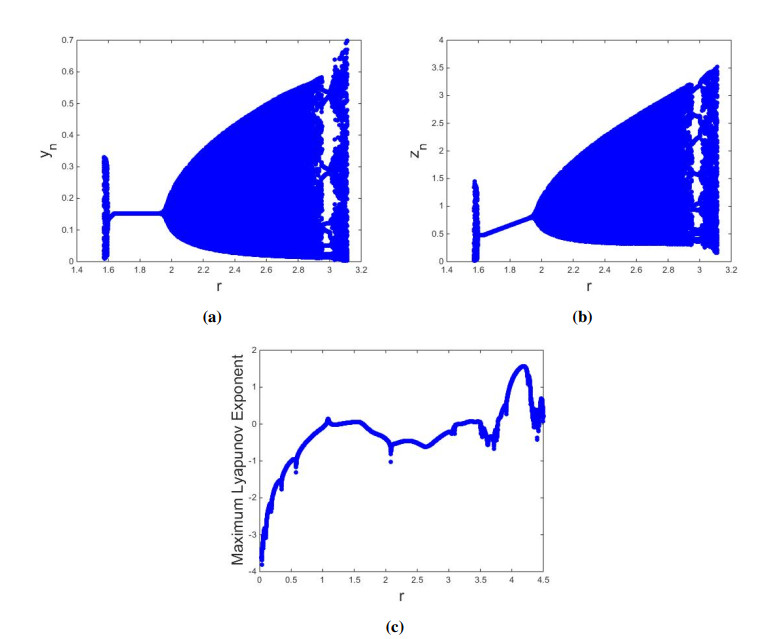
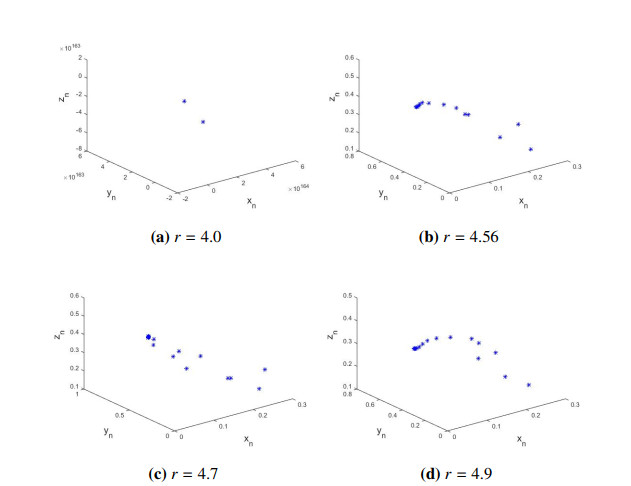
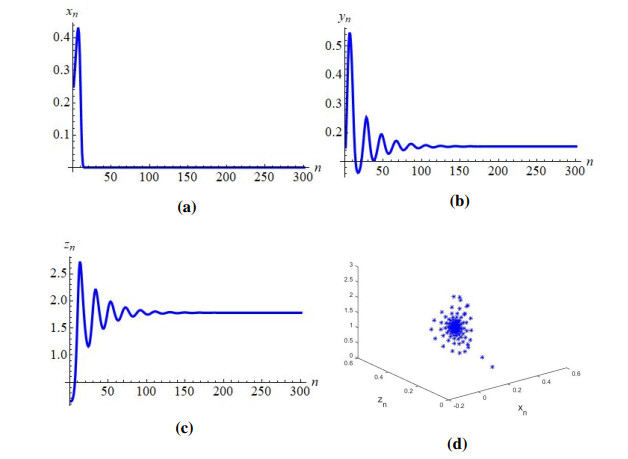
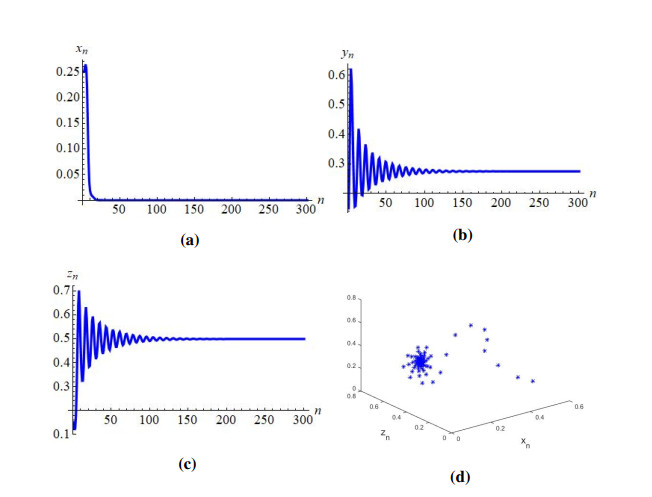
Case II: If a=0.45, b=0.9,c=0.99,d=0.29,e=0.3,f=2.3 then from Eq (4.26) one gets: r=2.2772277227722775. By Lemma 4.4, P0yz(0,df,rf−f−drcf) is locally asymptotically focus if r<2.2772277227722775, exchange of stability if r=2.2772277227722775, and unstable focus if r>2.2772277227722775. For instance, if r=1.4<2.2772277227722775 then it is clear from Figure 2a that P0yz(0,0.12608695652173912,0.2257356170399649) of model (1.2) is locally asymptotically focus. Similarly others values of r, if r<2.2772277227722775 then P0yz(0,df,rf−f−drcf) of model (1.2) is also locally asymptotically focus (Figure 2b, 2c). But if r>2.2772277227722775 then discrete-time model (1.2) loss its stability and meanwhile stable closed curve appears (Figure 3a, 3c). The appearance of these closed curve implies that model (1.2) undergoes supercritical N-S bifurcation when parameters goes through the curve, which is depicted in Eq (6.5). This correctness of theoretical results obtain in Subsection 7.3. Finally, the bifurcation diagrams along with Maximum Lyapunov Exponent in this case, are plotted and drawn in Figure 4.
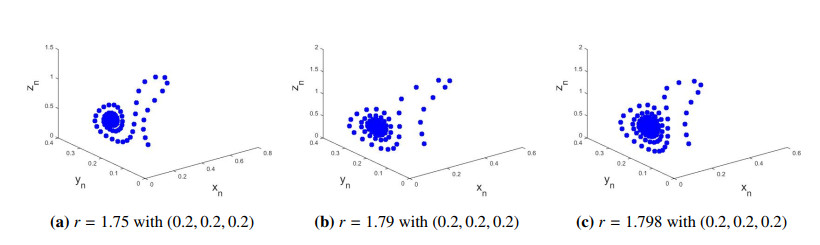
Case III: If a=0.45, b=0.93,c=0.8,d=0.95,e=0.15,f=0.45 and parameter r vary from 1.23 to 10.4, i.e., r∈[1.23,10.4] then at r=2.86317 the P+xyz(br(d−f)+f(b+ac)ber,br−b−acbr,ab) loss its stability. That means that P+xyz(br(d−f)+f(b+ac)ber,br−b−acbr,ab) is locally stable if r<2.86317. For instance, if r=1.75<2.86317 then it is clear from Figure 5a that unique positive fixed point P+xyz(19.044546850998465,0.2737327188940094,0.48387096774193544) of model (1.2) is locally stable. Similarly others values of r, if r<2.86317 then P+xyz(br(d−f)+f(b+ac)ber,br−b−acbr,ab) of model (1.2) is also locally stable (Figure 5b, 5c). Also if a=0.45,b=0.93,c=0.8,d=0.95,e=0.15,f=0.45,r=2.86317 then Eq (4.34) along with Eq (4.35) takes the following form:
By computer computation, from Eq (8.1) one gets:
with
This grantee that for above parametric values, discrete-time model (1.2) undergoes N-S bifurcation when parameter r goes through the bifurcation values, i.e., r=2.86317. Moreover the parametric conditions, which are depicted in Eq (7.18), under which the model (1.2) undergoes a N-S bifurcation hold, i.e.,
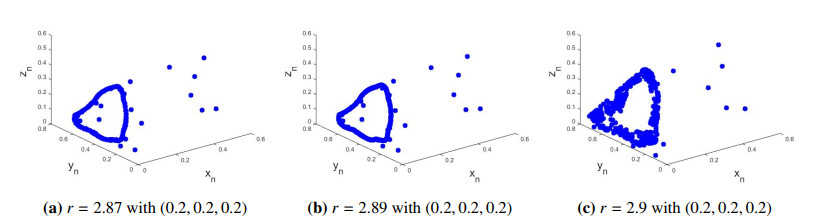
which again grantee that model (1.2) undergoes a N-S bifurcation if parameters goes through the bifurcation value. Hence if r>2.86317 then discrete-time model (1.2) loss its stability and meanwhile stable closed curve appears (Figure 6a–6c). The appearance of these closed curve implies that model (1.2) undergoes supercritical N-S bifurcation when parameters goes through r>2.86317. This correctness of theoretical results obtain in Subsection 7.4. Finally, the bifurcation diagrams along with Maximum Lyapunov Exponent in this case, are plotted and drawn in Figure 7.
Case IV: If a=0.3, b=1.99,c=3.75,d=0.75,e=0.235,f=1.0305 and parameter r vary from 1.6 to 5.2, i.e., r∈[1.6,5.2] then at r=3.9603484492658967 the P+xyz(br(d−f)+f(b+ac)ber,br−b−acbr,ab) loss its stability. That means that P+xyz(br(d−f)+f(b+ac)ber,br−b−acbr,ab) is stable if r<3.9603484492658967, unstable if r=3.9603484492658967 and P-D bifurcation appears if r>3.9603484492658967. For instance, if a=0.3,b=1.99,c=3.75,d=0.75,e=0.235,f=1.0305,r=3.97 then Eq (4.34) along with Eq (4.35) takes the following form:
From Eq (8.2) one gets:
with
This grantee that for above parametric values, discrete-time model (1.2) undergoes P-D bifurcation when parameter r goes through the bifurcation values, i.e., r=3.9603484492658967. Moreover the parametric conditions, which are depicted in Eq (7.20), under which the model (1.2) undergoes a P-D bifurcation hold, i.e.,
which again grantee that model (1.2) undergoes a P-D bifurcation. The bifurcation diagrams along with Maximum Lyapunov Exponent in this case, are plotted and drawn in Figure 8. More figure are plotted and drawn in Figure 9 that indicates that model (1.2) complex dynamics of period-2, 10, 11, 12 respectively. For the qualitative behavior of the continuous-time model, we refer the reader [23,24,25] and references cited therein.
9.
Hybrid control of bifurcations
In discrete-time models, chaos control can be obtained using various methods, some of them are the state feedback method, pole-placement technique and hybrid control method. Among all these methods, hybrid control technique is the simplest to implement. Moreover this method can be implemented for controlling chaos under the influence of both N-S and P-D bifurcations. To control the chaos in model (1.2), we will utilize Hybrid control strategy to control the N-S and P-D bifurcations about the positive fixed point: P+xyz(br(d−f)+f(b+ac)ber,br−b−acbr,ab). For more detailed study about the Hybrid control strategy, we refer the reader to [26,27,28] and reference cited therein.
9.1. Control of N-S bifurcation
The Hybrid control strategy is applied for control of N-S bifurcation in this Subsection. Recall that if the uncontrolled discrete-time model (1.2) undergoes a N-S bifurcation about P+xyz(br(d−f)+f(b+ac)ber,br−b−acbr,ab) then the controlled discrete-time model correspond to model (1.2) becomes:
where 0<α<1. Here it is noted that control model (9.1) reduces to model (1.2) if α=1, and chaos for model (9.1) can be delayed, advance or even completely eliminate by choosing the suitable choice of the parametric value of α. Now if one reconsider the Case Ⅲ of Section 8 then J|P+xyz(19.044546850998465,0.20737327188940094,0.48387096774193544) about P+xyz(19.044546850998465,0.20737327188940094,0.48387096774193544) for the controlled system (9.1) becomes
The characteristic polynomial of Eq (9.2) becomes
whose roots lies in an open disk |λ|<1 iff α∈(0,0.66675). For instance, if α=0.56 the phase portraits for controlled system (9.1) are plotted and drawn in Figure 10.
9.2. Control of P-D bifurcation
Recall that if Case Ⅳ of Section 8 hold then J|P+xyz(13.30555251494148,0.604750275583457,0.1507537688442211) about P+xyz(13.30555251494148,0.604750275583457,0.1507537688442211) for the controlled system, which is depiction in system (9.1), becomes
The characteristic polynomial of Eq (9.4) becomes
whose roots lies in an open disk |λ|<1 iff α∈(0,0.543543). For instance, if α=0.50 the phase portraits for controlled system (9.1) are plotted and drawn in Figure 11.
10.
Conclusions and future work
This work deals with the study of local dynamics along with different topological classifications, bifurcations and Hybrid control of the model (1.2) in R3+. In the interior of R3+, it is explored that the model has boundary fixed points: P000(0,0,0), P0y0(0,r−1r,0), P0yz(0,df,rf−f−drcf), Px0z(de,0,ab) and a unique positive fixed point: P+xyz(br(d−f)+f(b+ac)ber,br−b−acbr,ab) under certain parametric conditions. We have explored the local dynamics along with different topological classifications about fixed points: P000(0,0,0), P0y0(0,r−1r,0), P0yz(0,df,rf−f−drcf) and Px0z(de,0,ab) by applying the method of Linearization and stability theory, and conclusions are presented in Table 2. We have also investigated the local dynamics about positive fixed point: P+xyz(br(d−f)+f(b+ac)ber,br−b−acbr,ab), and proved that it is a sink if and only if Eq (4.36) along with Eq (4.35) hold. We have also investigated the existence of prime period and periodic points for the model (1.2). Further, about each fixed point of the under consideration model, we have discussed the possible bifurcation scenarios. In general, bifurcation theory is the mathematical study of changes in the qualitative or topological structure of a given family, such as the integral curves of a family of vector fields and the solutions of family of differential equations. It is most commonly applied to the mathematical study of dynamical systems, a bifurcation occurs when a small smooth change made to the parameter values namely the bifurcation parameters of the system causes a sudden qualitative or topological change in its behavior. So, in the current study, we proved that about P000(0,0,0) there exist a fold bifurcation as well as P-D bifurcation if Λ respectively goes through the curves: FB|P000(0,0,0)={Λ:r=1} and PDB|P000(0,0,0)={Λ:d=2}. But by computation it goes to degenerate to high dimension and hence there does not such bifurcations about P000(0,0,0). About P0y0(0,r−1r,0), it is proved that there exist a P-D bifurcation when Λ goes through the curve: PDB|P0y0(0,r−1r,0)={Λ:r=3}. We have also proved that about P0yz(0,df,rf−f−drcf) the model (1.2) undergoes a N-S bifurcation when Λ goes through the curve: NSB|P0yz(0,df,rf−f−drcf)={4d2fr+d2r2−4drf2+4d2frf2<0, r=ff−1−d}. By explicit criterion(without finding eigenvalues) it is proved that about P+xyz(br(d−f)+f(b+ac)ber,br−b−acbr,ab) the model (1.2) undergoes N-S as well as P-D bifurcations. Numerical simulations are presented to verify theoretical results. Further, we have computed maximum Lyapunov exponents numerically. At the end, hybrid control strategy is applied to stabilize chaos existing in the model (1.2). Global dynamics about fixed points: P000(0,0,0), P0y0(0,r−1r,0), P0yz(0,df,rf−f−drcf), Px0z(de,0,ab) and P+xyz(br(d−f)+f(b+ac)ber,br−b−acbr,ab), existence of global bifurcations and construction of forbidden set for the model (1.2) are our next aim to study.
Acknowledgments
This research is partially supported by the Higher Education Commission of Pakistan.
Conflict of interest
The authors declare that they have no conflicts of interest regarding the publication of this paper.









 DownLoad:
DownLoad: