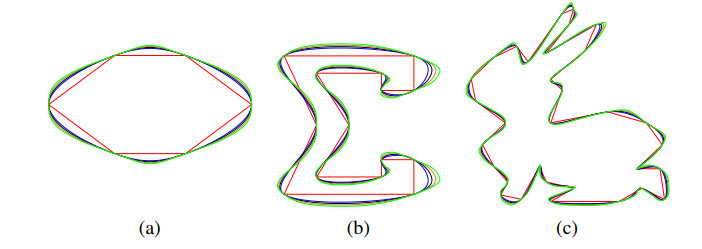In this paper, we first present a 6-point binary interpolating subdivision scheme (BISS) which produces a C2 continuous curve and 4th order of approximation. Then as an application of the scheme, we develop an iterative algorithm for the solution of 2nd order nonlinear singularly per-turbed boundary value problems (NSPBVP). The convergence of an iterative algorithm has also been presented. The 2nd order NSPBVP arising from combustion, chemical reactor theory, nuclear engi-neering, control theory, elasticity, and fluid mechanics can be solved by an iterative algorithm with 4th order of approximation.
1.
Introduction
The Computer Aided Geometric Design (CAGD) is an attractive field of mathematics to deal with algorithms for the construction of smooth curves and surfaces. In this field, we present mathematical formulation of shapes which are used in computer graphics, manufacturing or analysis. It has applications in different field of mathematics such as numerical geometry, numerical analysis, theory of approximation, computer graphics, and computer algebra. CAGD gains importance due to its use in different industrial areas and engineering. One of the most important area in CAGD is "subdivision schemes". The subdivision schemes are very useful for the construction of smooth curve and surface. Here we give short review on 6-point BISS. The first 6-point BISS was introduced by [1] in 1989. Weissman [2] introduced this scheme in his Master thesis in 1990. Lee et al. [3] also introduced this scheme in 2006. Ko et al. [4] and Lian [5] introduced schemes in 2007 and 2008 respectively. Later on, 6-point BISS was introduced by [6,7].
The 6-point BISS take a polygon as an input and produce the refined polygon as an output. In order to get refined polygon, 6-point BISS use six points of coarse polygon to find one point corresponding to each edge of the polygon while carry on the points of coarse polygon. The 6-point BISS schemes introduced by above authors are different due to the different coefficients used in an affine combination of six points. All the above authors, have presented the applications of 6-point BISS in curve/surface modeling. But in this paper, we present its application for the curve modeling as well as for the solution of 2nd order NSPBVP. Especially, we find the solution of the following type of 2nd order NSPBVP:
with boundary conditions
where 0<ϵ≤1. This type of 2nd order NSPBVP arises in the different area of engineering and other sciences. Particularly, these problems arises in the field of nuclear engineering, chemical reaction theory, physics and many other fields of sciences. Since the too small coefficient of 2nd order derivative causes the derivative approaches to zero. Therefore it is difficult to handle such type of problems. In literature, subdivision based algorithms were developed only for linear [8,9,10,11,12] and nonlinear [13,14,15] boundary value problems. The solution of linear singularly perturbed boundary value problems was presented by [16]. The solution of 2nd order NSPBVP of the type presented in (1.1) by subdivision scheme based iterative algorithm is not find yet. This motivate us to introduce the algorithm for the solution of this type of problems. The distribution of the rest of the paper is as follows:
In Section 2, we present a 6-point BISS and discuss some of its properties. In Section 3, we construct BISS based iterative algorithm for the approximate solution of NSPBVP. The convergence and error estimation of the algorithm are also presented in this section. In Section 4, the solutions of some of NSPBVP are presented. The Section 5 is reserved for the conclusion.
2.
Binary subdivision scheme
If p0={p0i,i∈Z} is the initial sketch (i.e., polygon) of some shape then to get the refined sketch pk+1={pk+1i,i∈Z,k>0}, we suggest the following 6-point BISS
where w is a parameter. The points pki are related with the diadic mesh points tki=i/2k.
2.1. Continuity of the scheme
In this section, by using the techniques of Dyn [17], we see that the scheme produces the curvature continuous curves.
Theorem 2.1. The 6-point BISS is C2-continuous for the parametric interval 0<w<0.042 i.e., scheme produces the limit curve with 2-degree of smoothness.
Proof. If we arrange the points involved in odd and even rules of (2.1) as
then the sequence of coefficients of these points in odd and even rules is
This sequence can be represented in terms of the following Laurent polynomial
Or equivalently
By multiplying it with the factor 2z1+z, we get
Again multiplying it with the same factor, we get
Further multiplying, we get
Let Sα, Sα1, Sα2, Sα3, be the schemes corresponding to the Laurent polynomials α(z), α1(z), α2(z), α3(z) respectively then
This implies
Since ‖(12Sα1)‖∞<1 for w∈(−1348,348), therefore the scheme Sα1 is contractive and the scheme Sα is C0-continuous. Since
therefore ‖(12Sα2)‖∞<1 for w∈(−116,316),(−332,132). Hence the scheme Sα2 is contractive and the scheme Sα is C1-continuous. Again
so ‖(12Sα3)‖∞<1 for w∈(0,116). Thus the scheme Sα3 is contractive and the scheme Sα is C2-continuous for the parametric interval 0<w<0.042.
2.2. Approximation order of the scheme
Here we compute the approximation order of the scheme. If α(1)(z) denotes first derivative of α(z), τ=α(1)(1)2=0 and tki=−τ+i+τ2k=i+02k=i2k then by Conti and Hormann [18], the scheme (2.1) has primal parametrization. The scheme generates polynomial of degree 3 because
where
Lemma 1. The 6-point BISS reproduces up to 3rd degree polynomials w.r.t. the primal parameterizations (i.e., for τ=0).
Proof. If α(i)(z), i=0,1,2,3 denote the derivative of α(z) then following can be verified:
but
and
This implies that
Thus
This completes the proof.
Since by Lemma 1, scheme produces polynomial of degree 3 therefore by Dyn [17] it has approximation order 4.
2.3. Eigenvalues and normalized eigenvectors
Here first we find the subdivision matrix then we compute its eigenvalues and left & right normalized eigenvectors corresponding to these eigenvalues. If we take
then by taking i=−2,−1,0 and 1 in even and odd rules and i=2 in just even rule of (2.1), we get a system of equations.
where
pj+1=(pj+1−4,pj+1−3,pj+1−2,pj+1−1,pj+10,pj+11,pj+12,pj+13,pj+14)T, and pj=(pj−4,pj−3,pj−2, pj−1,pj0,pj1,pj2,pj3,pj4)T. Here S is called the subdivision matrix of the scheme. Its eigenvalues are: λ=1,12,14,β3,β4,β5,β6,β7,β8, where β0=1,β1=12,β2=14, while the other eigenvalues β3...β8 and their corresponding eigenvectors are not needed in rest of the paper, so we do not write their values. It has been noticed that the some of eigenvalues and eigenvectors of the subdivision matrix are complex. The right normalized eigenvectors ξβi and left normalized eigenvectors ηβi, for i=1,2 corresponding to the eigenvalues β1 and β2 are
where
2.4. Applications of the scheme for curve modeling
Here, we show the applications of the 6-point BISS by presenting different shapes. We also show that how the parameter controls the shape of limiting curves. Red sketches are the initial structures made by 2D data points while other sketches are produced by the scheme at different values of parameter. Here we use w=0.01,0.02,0.03 and 0.04.
3.
Applications of the scheme for approximate solutions of NSPBVP
Here we gather some necessary stuff to establish a subdivision based iterative algorithm to find the approximate solution of NSPBVP.
Lemma 2. [10,14] The fundamental solution define as
is twice continuously differentiable and cardinally supported on Δ=(−5,5) and zero outside the Δ.
Lemma 3. [9] The Cardinal basis θ(t) is twice continuously differentiable on (−5,5) and its first and second derivatives are obtained by using the left eigenvectors of (2.3) corresponding to the eigenvalues β1=12 and β2=14 respectively. The derivatives values are
where
and
Hence, the first and second derivatives of (3.1) are
To construct the iterative algorithm, we only need the right and left normalized eigenvectors corresponding to the eigenvalues β1 and β2. Since the parameter w is involved in these eigenvectors. Therefore, for simplicity, we take the randem value of w=125 from the C2- continuity of the parametric interval of the scheme. So the left and right normalized eigenvectors corresponding to the eigenvalues β1 and β2 are:
Similarly, from (3.2), we get
In coming section, we introduce 6-point BISS based iterative algorithm for the solution of 2nd order NSPBVP.
3.1. Algorithm for the approximate solution of 2nd order NSPBVP
Let N≥4, h=1N, ϵ<h and ti=ih,i=0,1,2,⋯,N. Let
with the property G(ti)=gi be an approximate solution of (1.1). The unknowns {gi} will be determined. From (1.1) and (3.4), we get
where
The following N+1 system of equations can by obtained by substituting (3.4) and (3.6) in (3.5).
Theorem 3.1. The system of equations (3.7) reduces to
where j=0,1,2,⋯,N and θ″j=θ″(j).
Proof. Let j=0 then by (3.7)
For tj=jh,j=0,1,2,⋯,N, this implies
Since the support of θ(t) is (−5,5) therefore θ″(t)=0 beyond the interval (−5,5), so by (3.1) and (3.2), we get
If θ″(j)=θ″j, then
The expansion of (3.7) gives
For tj=jh,j=1,2,⋯,N, we get
If θ″(j)=θ″j, for j=1,2,⋯,N, then
Hence combining equations (3.9) and (3.10), we get (3.8).
The system of N+1 equations (3.8) with N+9 unknowns gi can be written as:
where the (N+1)×(N+9) ordered matrix
the (N+9)×1 ordered matrix
and the (N+1)×1 ordered matrix
3.2. Boundary conditions
Since the number of equations (i.e., N+1) are less than the number of unknowns (i.e., N+9) in the system (3.11). So there are 8 degree of freedoms to get unique solution. Two degree of freedoms are given in (1.2), i.e.
Since 6-point BISS reproduces 3rd degree polynomial with 4th order of approximation so we suggest the boundary conditions of order four for solution. The values of the left end points g−3,g−2,g−1 and right end points gN+1,gN+2,gN+3 can be computed by using the polynomial A(t) of degree three by interpolating it at (ti,gi), 0≤i≤3. Let
where
Since G(ti)=gi then by replacing ti=−ti for i=1,2,3, we have
We suggest the following boundary conditions to find the values of the left end points
Similarly for the right end points, we may define gi=A(ti), i=N+1,N+2,N+3 where
Similarly, we suggest the following conditions to find the values of the right end points
So we get 6 degree of freedoms from (3.16) and (3.17). Finally, we get the system of (N+9)×(N+9) nonlinear equations:
where the coefficient matrix J=(JT0,WT,JT1)T, W is defined in (3.12). To obtain matrix J0, first three rows of J0 comes from equation (3.16) and 4th row of J0 comes from (3.15) at g0=β,
Similarly for J1, first row of J1 comes from (3.15) at gN=γ and remaining rows come from (3.17),
And G and R(g) are defined as
Now, we see whether or not the system (3.18) is nonsingular. In this system the matrix J is neither diagonally dominant nor symmetric. For the time being, if we ignore the first and last three rows and columns of the matrix J then it is symmetric. We consider the symmetric part of it of order (N+1)×(N+1) for sufficiently large N.
It can be easily seen that the matrix C is nonsingular for N≤1000. While the determinant of J is also non zero. Its determinant increases as N increases for N≤1000. This implies that J is nonsingular. In other way, the eigenvalues of J for N≤1000 are nonzero therefore it is also nonsingular by [19]. Hence the system (3.18) is nonsingular for N≤1000.
3.3. The iterative algorithm
The iterative algorithm based on 6-point BISS can be summarized in three steps.
Step-1. Initial approximation:
First of all choose the initial approximation G0 for the system of linear equations:
where
Here F0 is the linear approximation of R(g).
Step-2. Iterative scheme:
Follow the following iterative scheme for rest of the approximations
Step-3. Stoping criteria:
If ϵtol is error tolerance then repeat Step-2 until any one of the following inequality is satisfied
3.4. Convergence of iterative algorithm
The following theorem guaranteed the convergence of iterative algorithm.
Proposition 1. If L0 & L1 and h are Lipschitz constants and mesh size respectively then the solution at kth iteration {G(k)} converges linearly to the solution G∗ of the nonlinear system (3.18) with the condition that Lipschitz constants and mesh size are small enough i.e.,
Proof. For small values of h and ϵ<h, we have JG∗=F(G∗) and JG(k+1)=F(G(k)). Then the error vector E(k)=G(k)−G∗ satisfies the following
For i=1,2,⋯,N−1, we get the following by Mean Value Theorem
where the difference operators D1 and D2 are defined below
Since Ei=EN−i=0,i=0,−1,−2,−3,−4, therefore
This implies
This further implies
Since
therefore
This completes the proof. In following theorem, we see that the power of approximation of iterative algorithm is at least O(h4). Its proof is similar to the proof of Proposition in [14].
Theorem 3.2. let y(t) be the exact and G(t) be the numerical solutions of the problem (2.1) then
4.
Solution of 2nd order NSPBVP
Here we present the solutions of two 2nd order NSPBVPs obtained by our iterative algorithm.
Example 4.1. Consider the 2nd order NSPBVP
with exact solution
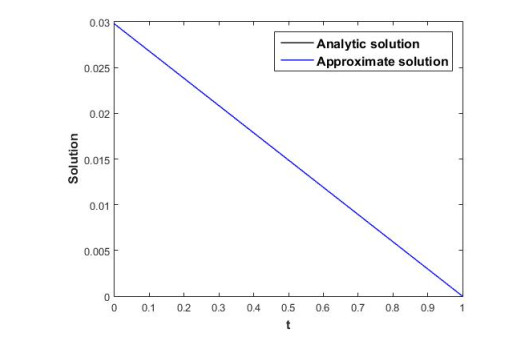
We find the approximate solution of above problem by iterative algorithm with parameters: ϵ=(0.244)2, N = 10 and tolϵ=10−6. We see that the maximum absolute error (MAE) is 2.55676×10−6 after third iteration. The comparison between approximate and exact solutions is given in Table 1 and Figure 2.
Example 4.2. Consider the 2nd order NSPBVP
with exact solution
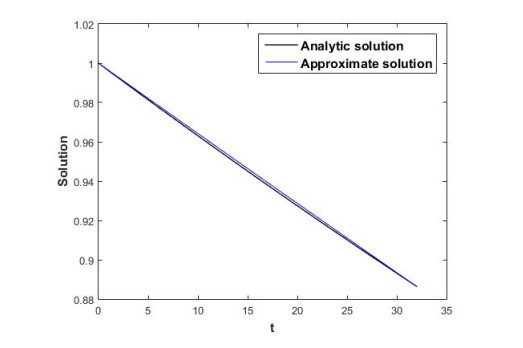
We find the approximate solutions of above problem by iterative algorithm with parameters: ϵ=(0.244)2, (0.244)4&(0.244)5, N = 32 and tol=10−6 and MAE are 0.51×10−2, 0.34×10−3 & 0.85×10−4 obtained after third iteration respectively. The comparison between approximate and exact solutions is given in Tables 2, 3 & 4 and Figure 3. From these tables, we have observed that for very smaller value of ϵ (i.e. ϵ→0) more accurate results can be achieved.
5.
Conclusion
In this paper, we have presented a 6-point BISS which produces a curvature continuous curve with 4th order of approximation. Firstly, we have explored its qualities for curve modeling. Secondly, we have used this scheme to develop an iterative algorithm for the solution of 2nd order NSPBVP arising from different physical phenomenon. The convergence of an iterative algorithm has also been presented. The approximate solutions of 2nd order NSPBVP obtained by our iterative algorithm has approximation order ≤O(h4).
Availability of data and material
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
Author's contributions
The authors have contributed equally to this manuscript. They read and approved the final manuscript.
Acknowledgement
We thanks the anonymous reviewers for careful reading of our manuscript and their many insightful comments and suggestions.
Conflict of interest
The authors declare that they have no competing interests









 DownLoad:
DownLoad: