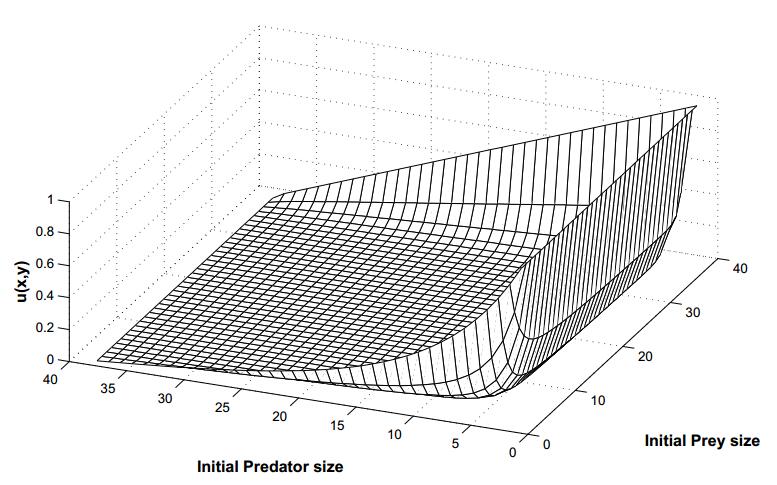
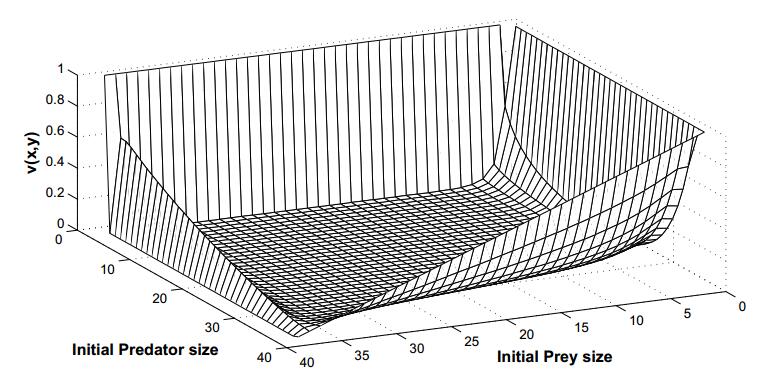
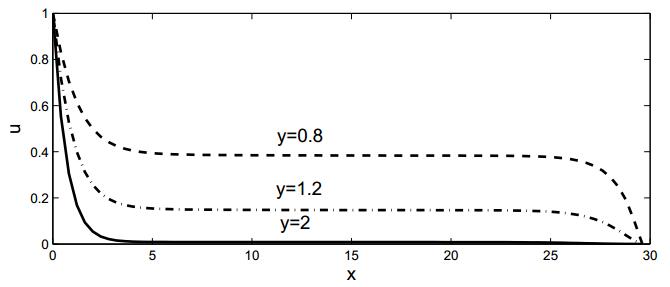
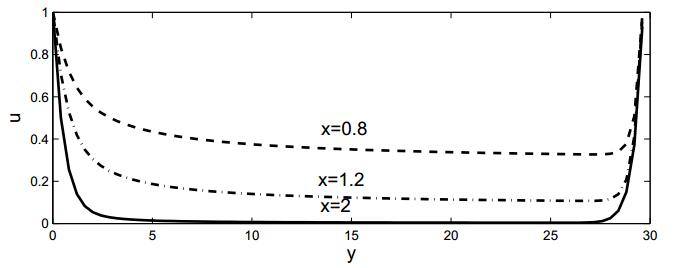
|
[1]
|
J. Liu, H. Dang, X. W. Wang, The significance of intertumor and intratumor heterogeneity in liver cancer, Exp. Mol. Med., 50 (2018), e416.
|
|
[2]
|
T. M. Grzywa, W. Paskal, P. K. Włodarski, Intratumor and intertumor heterogeneity in melanoma, Transl. Oncol., 10 (2017), 956-975. doi: 10.1016/j.tranon.2017.09.007

|
|
[3]
|
K. Anderson, C. Lutz, F. W. Van Delft, C. M. Bateman, Y. Guo, S. M. Colman, et al., Genetic variegation of clonal architecture and propagating cells in leukaemia, Nature, 469 (2011), 356-361.
|
|
[4]
|
S. Li, F. E. Garrett-Bakelman, S. S. Chung, M. A. Sanders, T. Hricik, F. Rapaport, et al., Distinct evolution and dynamics of epigenetic and genetic heterogeneity in acute myeloid leukemia, Nat. Med., 22 (2016), 792-799.
|
|
[5]
|
G. C. Webb, D. D. Chaplin, Genetic variability at the human tumor necrosis factor loci., J. Immunol., 145 (1990), 1278-1285.
|
|
[6]
|
A. Marusyk, K. Polyak, Tumor heterogeneity: Causes and consequences, Biochim. Biophys. Acta, Rev. Cancer, 1805 (2010), 105-117. doi: 10.1016/j.bbcan.2009.11.002

|
|
[7]
|
A. A. Alizadeh, V. Aranda, A. Bardelli, C. Blanpain, C. Bock, C. Borowski, et al., Toward understanding and exploiting tumor heterogeneity, Nat. Med., 21 (2015), 846-853.
|
|
[8]
|
M. Lee, G. T. Chen, E. Puttock, K. Wang, R. A. Edwards, M. L. Waterman, et al., Mathematical modeling links wnt signaling to emergent patterns of metabolism in colon cancer, Mol. Syst. Biol., 13 (2017), 912.
|
|
[9]
|
S. Terry, S. Buart, S. Chouaib, Hypoxic stress-induced tumor and immune plasticity, suppression, and impact on tumor heterogeneity, Front. Immunol., 8 (2017), 1625. doi: 10.3389/fimmu.2017.01625

|
|
[10]
|
S. Akgul, A.-M. Patch, R. C. J. D'Souza, P. Mukhopadhyay, K. Nones, S. Kempe, et al., ¨ Intratumoural heterogeneity underlies distinct therapy responses and treatment resistance in glioblastoma, Cancers, 11 (2019), 190.
|
|
[11]
|
T. D. Laajala, T. Gerke, S. Tyekucheva, J. C. Costello, Modeling genetic heterogeneity of drug response and resistance in cancer, Curr. Opin. Syst. Biol., 17 (2019), 8-14. doi: 10.1016/j.coisb.2019.09.003

|
|
[12]
|
X. Ma, J. Huang, Predicting clinical outcome of therapy-resistant prostate cancer, Proc. Natl. Acad. Sci., 116 (2019), 11090-11092. doi: 10.1073/pnas.1906812116

|
|
[13]
|
A. M. Stein, T. Demuth, D. Mobley, M. Berens, L. M. Sander, A mathematical model of glioblastoma tumor spheroid invasion in a three-dimensional in vitro experiment, Biophys. J., 92 (2007), 356-365. doi: 10.1529/biophysj.106.093468

|
|
[14]
|
T. L. Stepien, E. M. Rutter, Y. Kuang, Traveling waves of a go-or-grow model of glioma growth, SIAM J. Appl. Math., 78 (2018), 1778-1801. doi: 10.1137/17M1146257

|
|
[15]
|
A. Martínez-González, G. F. Calvo, L. A. P. Romasanta, V. M. Pérez-García, Hypoxic cell waves around necrotic cores in glioblastoma: A biomathematical model and its therapeutic implications, Bull. Math. Biol., 74 (2012), 2875-2896. doi: 10.1007/s11538-012-9786-1

|
|
[16]
|
H. Hatzikirou, D. Basanta, M. Simon, K. Schaller, A. Deutsch, 'Go or grow': The key to the emergence of invasion in tumour progression?, Math. Med. Biol.: A J. IMA, 29 (2012), 49-65. doi: 10.1093/imammb/dqq011

|
|
[17]
|
Z. Husain, P. Seth, V. P. Sukhatme, Tumor-derived lactate and myeloid-derived suppressor cells: Linking metabolism to cancer immunology, Oncoimmunology, 2 (2013), e26383. doi: 10.4161/onci.26383

|
|
[18]
|
A. N. Mendler, B. Hu, P. U. Prinz, M. Kreutz, E. Gottfried, E. Noessner, Tumor lactic acidosis suppresses CTL function by inhibition of p38 and JNK/c-Jun activation, Int. J. Cancer, 131 (2012), 633-640. doi: 10.1002/ijc.26410

|
|
[19]
|
K. Fischer, P. Hoffmann, S. Voelkl, N. Meidenbauer, J. Ammer, M. Edinger, et al., Inhibitory effect of tumor cell-derived lactic acid on human T cells, Blood, 109 (2007), 3812-3819.
|
|
[20]
|
E. C. Fiedler, M. T. Hemann, Aiding and abetting: How the tumor microenvironment protects cancer from chemotherapy, Annu. Rev. Cancer Biol., 3 (2019), 409-428. doi: 10.1146/annurev-cancerbio-030518-055524

|
|
[21]
|
J. K. Saggar, M. Yu, Q. Tan, I. F. Tannock, The tumor microenvironment and strategies to improve drug distribution, Front. Oncol., 3 (2013), 154.
|
|
[22]
|
A. I. Minchinton, I. F. Tannock, Drug penetration in solid tumours, Nat. Rev. Cancer, 6 (2006), 583-592. doi: 10.1038/nrc1893

|
|
[23]
|
A. Baldock, R. Rockne, A. Boone, M. Neal, C. Bridge, L. Guyman, et al., From patient-specific mathematical neuro-oncology to precision medicine, Front. Oncol., 3 (2013), 62.
|
|
[24]
|
A. L. Baldock, S. Ahn, R. Rockne, S. Johnston, M. Neal, D. Corwin, et al., Patient-specific metrics of invasiveness reveal significant prognostic benefit of resection in a predictable subset of gliomas, PLoS One, 9 (2014), e99057.
|
|
[25]
|
S. Barish, M. F. Ochs, E. D. Sontag, J. L. Gevertz, Evaluating optimal therapy robustness by virtual expansion of a sample population, with a case study in cancer immunotherapy, Proc. Nati. Acad. Sci., 114 (2017), E6277-E6286. doi: 10.1073/pnas.1703355114

|
|
[26]
|
J. C. L. Alfonso, L. Berk, Modeling the effect of intratumoral heterogeneity of radiosensitivity on tumor response over the course of fractionated radiation therapy, Radiat. Oncol., 14 (2019), 88.
|
|
[27]
|
F. Forouzannia, H. Enderling, M. Kohandel, Mathematical modeling of the effects of tumor heterogeneity on the efficiency of radiation treatment schedule, Bull. Math. Biol., 80 (2018), 283-293. doi: 10.1007/s11538-017-0371-5

|
|
[28]
|
C. H. Morrell, J. D. Pearson, H. B. Carter, L. J. Brant, Estimating unknown transition times using a piecewise nonlinear mixed-effects model in men with prostate cancer, J. Am. Stat. Assoc., 90 (1995), 45-53. doi: 10.1080/01621459.1995.10476487

|
|
[29]
|
N. Hartung, S. Mollard, D. Barbolosi, A. Benabdallah, G. Chapuisat, G. Henry, et al., Mathematical modeling of tumor growth and metastatic spreading: Validation in tumor-bearing mice, Cancer Res., 74 (2014), 6397-6407.
|
|
[30]
|
J. Poleszczuk, R. Walker, E. G. Moros, K. Latifi, J. J. Caudell, H. Enderling, Predicting patientspecific radiotherapy protocols based on mathematical model choice for proliferation-saturation index, Bull. Math. Biol., 80 (2018), 1195-1206. doi: 10.1007/s11538-017-0279-0

|
|
[31]
|
A. Rafii, C. Touboul, H. A. Thani, K. Suhre, J. A. Malek, Where cancer genomics should go next: a clinician's perspective, Hum. Mol. Genet., 23 (2014), R69-R75.
|
|
[32]
|
D. Zardavas, A. Irrthum, C. Swanton, M. Piccart, Clinical management of breast cancer heterogeneity, Nat. Rev. Clin. Oncol., 12 (2015), 381-394. doi: 10.1038/nrclinonc.2015.73

|
|
[33]
|
A. D. Barker, C. C. Sigman, G. J. Kelloff, N. M. Hylton, D. A. Berry, L. J. Esserman, I-spy 2: an adaptive breast cancer trial design in the setting of neoadjuvant chemotherapy, Clin. Pharmacol. Ther., 86 (2009), 97-100. doi: 10.1038/clpt.2009.68

|
|
[34]
|
A. S. Meyer, L. M. Heiser, Systems biology approaches to measure and model phenotypic heterogeneity in cancer, Curr. Opin. Syst. Biol., 17 (2019), 35-40. doi: 10.1016/j.coisb.2019.09.002

|
|
[35]
|
R. A. Gatenby, E. T. Gawlinski, A reaction-diffusion model of cancer invasion, Cancer Res., 56 (1996), 5745-5753.
|
|
[36]
|
P. Tracqui, G. C. Cruywagen, D. E. Woodward, G. T. Bartoo, J. D. Murray, E. Alvord Jr, A mathematical model of glioma growth: the effect of chemotherapy on spatio-temporal growth, Cell Proliferation, 28 (1995), 17-31. doi: 10.1111/j.1365-2184.1995.tb00036.x

|
|
[37]
|
M. A. J. Chaplain, Reaction-diffusion prepatterning and its potential role in tumour invasion, J. Biol. Syst., 3 (1995), 929-936. doi: 10.1142/S0218339095000824

|
|
[38]
|
H. L. Harpold, E. C. Alvord Jr, K. R. Swanson, The evolution of mathematical modeling of glioma proliferation and invasion, J. Neuropathol. Exp. Neurol., 66 (2007), 1-9. doi: 10.1097/nen.0b013e31802d9000

|
|
[39]
|
R. Rockne, J. K. Rockhill, M. Mrugala, A. M. Spence, I. Kalet, K. Hendrickson, et al., Predicting the efficacy of radiotherapy in individual glioblastoma patients in vivo: a mathematical modeling approach, Phys. Med. Biol., 55 (2010), 3271.
|
|
[40]
|
T. E. Yankeelov, N. Atuegwu, D. Hormuth, J. A. Weis, S. L. Barnes, M. I. Miga, et al., Clinically relevant modeling of tumor growth and treatment response, Sci. Transl. Med., 5 (2013), 187ps9-187ps9.
|
|
[41]
|
D. A. Hormuth II, J. A. Weis, S. L. Barnes, M. I. Miga, E. C. Rericha, V. Quaranta, et al., Predicting in vivo glioma growth with the reaction diffusion equation constrained by quantitative magnetic resonance imaging data, Phys. Biol., 12 (2015), 046006.
|
|
[42]
|
K. R. Swanson, R. C. Rostomily, E. C. Alvord Jr, A mathematical modelling tool for predicting survival of individual patients following resection of glioblastoma: A proof of principle, Br. J. Cancer, 98 (2008), 113-119. doi: 10.1038/sj.bjc.6604125

|
|
[43]
|
S. Prokopiou, E. G. Moros, J. Poleszczuk, J. Caudell, J. F. Torres-Roca, K. Latifi, et al., A proliferation saturation index to predict radiation response and personalize radiotherapy fractionation, Radiat. Oncol., 10 (2015), 159.
|
|
[44]
|
C. Vaghi, A. Rodallec, R. Fanciullino, J. Ciccolini, J. Mochel, M. Mastri, et al., Population modeling of tumor growth curves, the reduced Gompertz model and prediction of the age of a tumor, in Mathematical and Computational Oncology (eds. G. Bebis, T. Benos, K. Chen, K. Jahn, E. Lima), Lecture Notes in Computer Science, Springer International Publishing, Cham, (2019), 87-97.
|
|
[45]
|
T. J. Sullivan, Introduction to Uncertainty Quantification, Springer, 2015.
|
|
[46]
|
G. J. Lord, C. E. Powell, T. Shardlow, Introduction to Computational Stochastic PDEs, Cambridge, 2014.
|
|
[47]
|
R. Smith, Uncertainty Quantification: Theory, Implementation, and Applications, SIAM, 2014.
|
|
[48]
|
N. Henscheid, E. Clarkson, K. J. Myers, H. H. Barrett, Physiological random processes in precision cancer therapy, PLoS One, 13 (2018), e0199823.
|
|
[49]
|
J. P. O'Connor, C. J. Rose, J. C. Waterton, R. A. Carano, G. J. Parker, A. Jackson, Imaging intratumor heterogeneity: Role in therapy response, resistance, and clinical outcome, Clin. Cancer Res., 21 (2015), 249-257. doi: 10.1158/1078-0432.CCR-14-0990

|
|
[50]
|
R. J. Allen, T. R. Rieger, C. J. Musante, Efficient generation and selection of virtual populations in quantitative systems pharmacology models, CPT: Pharmacometrics Syst. Pharmacol., 5 (2016), 140-146. doi: 10.1002/psp4.12063

|
|
[51]
|
T. R. Rieger, R. J. Allen, L. Bystricky, Y. Chen, G. W. Colopy, Y. Cui, et al., Improving the generation and selection of virtual populations in quantitative systems pharmacology models, Prog. Biophys. Mol. Biol., 139 (2018), 15-22.
|
|
[52]
|
D. J. Klinke, Integrating epidemiological data into a mechanistic model of type 2 diabetes: Validating the prevalence of virtual patients, Ann. Biomed. Eng., 36 (2008), 321-334. doi: 10.1007/s10439-007-9410-y

|
|
[53]
|
B. J. Schmidt, F. P. Casey, T. Paterson, J. R. Chan, Alternate virtual populations elucidate the type i interferon signature predictive of the response to rituximab in rheumatoid arthritis, BMC Bioinf., 14 (2013), 221. doi: 10.1186/1471-2105-14-221

|
|
[54]
|
J. Bassaganya-Riera, Accelerated Path to Cures, Springer, 2018.
|
|
[55]
|
N. Henscheid, Quantifying Uncertainties in Imaging-Based Precision Medicine, Ph.D thesis, University of Arizona, 2018.
|
|
[56]
|
J. G. Albeck, J. M. Burke, S. L. Spencer, D. A. Lauffenburger, P. K. Sorger, Modeling a snapaction, variable-delay switch controlling extrinsic cell death, PLoS Biol., 6 (2008), e299.
|
|
[57]
|
Q. Wu, S. D. Finley, Predictive model identifies strategies to enhance tsp1-mediated apoptosis signaling, Cell Commun. Signaling, 15 (2017), 53. doi: 10.1186/s12964-017-0207-9

|
|
[58]
|
M. R. Birtwistle, J. Rauch, A. Kiyatkin, E. Aksamitiene, M. Dobrzyński, J. B. Hoek, et al., Emergence of bimodal cell population responses from the interplay between analog single-cell signaling and protein expression noise, BMC Syst. Biol., 6 (2012), 109.
|
|
[59]
|
D. Brown, R. A. Namas, K. Almahmoud, A. Zaaqoq, J. Sarkar, D. A. Barclay, et al., Trauma in silico: Individual-specific mathematical models and virtual clinical populations, Sci. Transl. Med., 7 (2015), 285ra61-285ra61.
|
|
[60]
|
A. Badano, C. G. Graff, A. Badal, D. Sharma, R. Zeng, F. W. Samuelson, et al., Evaluation of digital breast tomosynthesis as replacement of full-field digital mammography using an in silico imaging trial, JAMA Net. Open, 1 (2018), e185474-e185474.
|
|
[61]
|
W. Kainz, E. Neufeld, W. E. Bolch, C. G. Graff, C. H. Kim, N. Kuster, et al., Advances in computational human phantoms and their applications in biomedical engineering—a topical review, IEEE Trans. Radiat. Plasma Med. Sci., 3 (2019), 1-23.
|
|
[62]
|
E. Roelofs, M. Engelsman, C. Rasch, L. Persoon, S. Qamhiyeh, D. De Ruysscher, et al., Results of a multicentric in silico clinical trial (rococo): Comparing radiotherapy with photons and protons for non-small cell lung cancer, J. Thorac. Oncol., 7 (2012), 165-176.
|
|
[63]
|
J. K. Birnbaum, F. O. Ademuyiwa, J. J. Carlson, L. Mallinger, M. W. Mason, R. Etzioni, Comparative effectiveness of biomarkers to target cancer treatment: Modeling implications for survival and costs, Med. Decis. Making, 36 (2016), 594-603. doi: 10.1177/0272989X15601998

|
|
[64]
|
D. Li, S. D. Finley, The impact of tumor receptor heterogeneity on the response to anti-angiogenic cancer treatment, Integr. Biol., 10 (2018), 253-269. doi: 10.1039/C8IB00019K

|
|
[65]
|
K. Mustapha, Q. Gilli, J.-M. Frayret, N. Lahrichi, E. Karimi, Agent-based simulation patient model for colon and colorectal cancer care trajectory, Procedia Comput. Sci., 100 (2016), 188-197. doi: 10.1016/j.procs.2016.09.140

|
|
[66]
|
J. P. Rolland, H. H. Barrett, Effect of random background inhomogeneity on observer detection performance, J. Opt. Soc. Am. A, 9 (1992), 649-658. doi: 10.1364/JOSAA.9.000649

|
|
[67]
|
H. H. Barrett, K. J. Myers, Foundations of Image Science, NY: John Wiley and Sons, New York, 2004.
|
|
[68]
|
M. A. Kupinski, E. Clarkson, J. W. Hoppin, L. Chen, H. H. Barrett, Experimental determination of object statistics from noisy images, JOSA A, 20 (2003), 421-429. doi: 10.1364/JOSAA.20.000421

|
|
[69]
|
F. Bochud, C. Abbey, M. Eckstein, Statistical texture synthesis of mammographic images with clustered lumpy backgrounds, Opt. Express, 4 (1999), 33-42. doi: 10.1364/OE.4.000033

|
|
[70]
|
N. Henscheid, Generating patient-specific virtual tumor populations with reaction-diffusion models and molecular imaging data, Math. Biosci. Eng., Submitted.
|
|
[71]
|
W. Hundsdorfer, J. G. Verwer, Numerical solution of time-dependent advection-diffusion-reaction equations, Springer Science and Business Media, 2013.
|
|
[72]
|
S. KM, M. Prah, Data from brain-tumor-progression, The Cancer Imaging Archive, 2018.
|
|
[73]
|
M. Davidian, D. M. Giltinan, Nonlinear models for repeated measurement data: An overview and update, J. Agric., Biol., and Environ. Stat., 8 (2003), 387-419. doi: 10.1198/1085711032697

|
|
[74]
|
K. Clark, B. Vendt, K. Smith, J. Freymann, J. Kirby, P. Koppel, et al., The cancer imaging archive (tcia): maintaining and operating a public information repository, J. Digital Imaging, 26 (2013), 1045-1057.
|
|
[75]
|
S. Desmée, F. Mentré, C. Veyrat-Follet, J. Guedj, Nonlinear mixed-effect models for prostatespecific antigen kinetics and link with survival in the context of metastatic prostate cancer: A comparison by simulation of two-stage and joint approaches, Am. Assoc. Pharm. Sci. J., 17 (2015), 691-699.
|
|
[76]
|
A. Król, C. Tournigand, S. Michiels, V. Rondeau, Multivariate joint frailty model for the analysis of nonlinear tumor kinetics and dynamic predictions of death, Stat. Med., 37 (2018), 2148-2161. doi: 10.1002/sim.7640

|
|
[77]
|
E. Grenier, V. Louvet, P. Vigneaux, Parameter estimation in non-linear mixed effects models with SAEM algorithm: extension from ODE to PDE, ESAIM: Math. Modell. Numer. Anal., 48 (2014), 1303-1329. doi: 10.1051/m2an/2013140

|
|
[78]
|
H. Liang, Modeling antitumor activity in xenograft tumor treatment, Biom. J.: J. Math. Methods Biosci., 47 (2005), 358-368.
|
|
[79]
|
H. Liang, N. Sha, Modeling antitumor activity by using a non-linear mixed-effects model, Math. Biosci., 189 (2004), 61-73. doi: 10.1016/j.mbs.2004.01.002

|
|
[80]
|
A. M. Stein, D. Bottino, V. Modur, S. Branford, J. Kaeda, J. M. Goldman, et al., Bcr-abl transcript dynamics support the hypothesis that leukemic stem cells are reduced during imatinib treatment, Clin. Cancer Res., 17 (2011), 6812-6821.
|
|
[81]
|
T. Ferenci, J. Sápi, L. Kovács, Modelling tumor growth under angiogenesis inhibition with mixed-effects models, Acta Polytech. Hung., 14 (2017), 221-234.
|
|
[82]
|
B. Ribba, G. Kaloshi, M. Peyre, D. Ricard, V. Calvez, M. Tod, et al., A tumor growth inhibition model for low-grade glioma treated with chemotherapy or radiotherapy, Clin. Cancer Res., 18 (2012), 5071-5080.
|
|
[83]
|
B. Ribba, N. H. Holford, P. Magni, I. Trocóniz, I. Gueorguieva, P. Girard, et al., A review of mixed-effects models of tumor growth and effects of anticancer drug treatment used in population analysis, CPT: Pharmacometrics Syst. Pharmacol., 3 (2014), 1-10.
|
|
[84]
|
N. W. Shock, R. C. Greulich, R. Andres, D. Arenberg, P. T. Costa, E. G. Lakatta, et al., Normal human aging. the baltimore longituidinal study of aging, U.S. Government Printing Office Publication.
|
|
[85]
|
https://www.mathworks.com/help/stats/nlmefit.html, accessed November 16, 2019.
|
|
[86]
|
H. T. Banks, V. A. Bokil, S. Hu, A. K. Dhar, R. A. Bullis, C. L. Browdy, et al., Modeling shrimp biomass and viral infection for production of biological countermeasures, Math. Biosci. Eng., 3 (2006), 635-660.
|
|
[87]
|
H. T. Banks, J. L. Davis, A comparison of approximation methods for the estimation of probability distributions on parameters, Appl. Numer. Math., 57 (2007), 753-777. doi: 10.1016/j.apnum.2006.07.016

|
|
[88]
|
M. Sirlanci, S. E. Luczak, C. E. Fairbairn, D. Kang, R. Pan, X. Yu, et al., Estimating the distribution of random parameters in a diffusion equation forward model for a transdermal alcohol biosensor, Automatica, 106 (2019), 101-109.
|
|
[89]
|
E. M. Rutter, H. T. Banks, K. B. Flores, Estimating intratumoral heterogeneity from spatiotemporal data, J. Math. Biol., 77 (2018), 1999-2022. doi: 10.1007/s00285-018-1238-6

|
|
[90]
|
H. T. Banks, K. B. Flores, I. G. Rosen, E. M. Rutter, M. Sirlanci, W. C. Thompson, The prohorov metric framework and aggregate data inverse problems for random pdes, Commun. Appl. Anal., 22 (2018), 415-446.
|
|
[91]
|
H. T. Banks, W. C. Thompson, Existence and consistency of a nonparametric estimator of probability measures in the prohorov metric framework, Int. J. Pure Appl. Math., 103 (2015), 819-843.
|
|
[92]
|
H. Akaike, A new look at the statistical model identification, in Selected Papers of Hirotugu Akaike (eds. E. Parzen, K. Tanabe, G. Kitagawa), Springer New York, New York, (1998), 215-222.
|
|
[93]
|
R. Ullrich, H. Backes, H. Li, L. Kracht, H. Miletic, K. Kesper, et al., Glioma proliferation as assessed by 3-fluoro-3-deoxy-l-thymidine positron emission tomography in patients with newly diagnosed high-grade glioma, Clin. Cancer Res., 14 (2008), 2049-2055.
|
|
[94]
|
E. Stretton, E. Geremia, B. Menze, H. Delingette, N. Ayache, Importance of patient dti's to accurately model glioma growth using the reaction diffusion equation, in 2013 IEEE 10th Int. Symp. Biomed. Imaging, IEEE, 2013, 1142-1145.
|
|
[95]
|
N. C. Atuegwu, D. C. Colvin, M. E. Loveless, L. Xu, J. C. Gore, T. E. Yankeelov, Incorporation of diffusion-weighted magnetic resonance imaging data into a simple mathematical model of tumor growth, Phys. Med. Biol., 57 (2011), 225-240.
|
|
[96]
|
J. Lipková, P. Angelikopoulos, S. Wu, E. Alberts, B. Wiestler, C. Diehl, et al., Personalized radiotherapy design for glioblastoma: Integrating mathematical tumor models, multimodal scans, and bayesian inference, IEEE Trans. Med. Imaging, 38 (2019), 1875-1884.
|
|
[97]
|
J. Kaipio, E. Somersalo, Statistical and Computational Inverse Problems, Springer Science and Business Media, 2006.
|
|
[98]
|
A. M. Stuart, Inverse problems: a bayesian perspective, Acta Numer., 19 (2010), 451-559. doi: 10.1017/S0962492910000061

|
|
[99]
|
P. R. Jackson, J. Juliano, A. Hawkins-Daarud, R. C. Rockne, K. R. Swanson, Patient-specific mathematical neuro-oncology: using a simple proliferation and invasion tumor model to inform clinical practice, Bull. Math. Biol., 77 (2015), 846-856. doi: 10.1007/s11538-015-0067-7

|
|
[100]
|
J. Oden, Cse 397 Lecture Notes: Foundations of Predictive Computational Science, 2017. Available from: https://www.oden.utexas.edu/media/reports/2017/1701.pdf.
|
|
[101]
|
J. Collis, A. J. Connor, M. Paczkowski, P. Kannan, J. Pitt-Francis, H. M. Byrne, et al., Bayesian calibration, validation and uncertainty quantification for predictive modelling of tumour growth: A tutorial, Bull. Math. Biol., 79 (2017), 939-974.
|
|
[102]
|
E. J. Kostelich, Y. Kuang, J. M. McDaniel, N. Z. Moore, N. L. Martirosyan, M. C. Preul, Accurate state estimation from uncertain data and models: An application of data assimilation to mathematical models of human brain tumors, Biol. Direct, 6 (2011), 64. doi: 10.1186/1745-6150-6-64

|
|
[103]
|
A. Hawkins-Daarud, S. Prudhomme, K. G. van der Zee, J. T. Oden, Bayesian calibration, validation, and uncertainty quantification of diffuse interface models of tumor growth, J. Math. Biol., 67 (2013), 1457-1485.
|
|
[104]
|
I. Babuška, F. Nobile, R. Tempone, A systematic approach to model validation based on bayesian updates and prediction related rejection criteria, Comput. Methods Appl. Mech. Eng., 197 (2008), 2517-2539. doi: 10.1016/j.cma.2007.08.031

|
|
[105]
|
J. T. Oden, E. A. B. F. Lima, R. C. Almeida, Y. Feng, M. N. Rylander, D. Fuentes, et al., Toward predictive multiscale modeling of vascular tumor growth, Arch. Comput. Methods Eng., 23 (2016), 735-779.
|
|
[106]
|
M. Lê, H. Delingette, J. Kalpathy-Cramer, E. R. Gerstner, T. Batchelor, J. Unkelbach, et al., MRI based bayesian personalization of a tumor growth model, IEEE Trans. Med. Imaging, 35 (2016), 2329-2339.
|
|
[107]
|
A. Hawkins-Daarud, S. K. Johnston, K. R. Swanson, Quantifying uncertainty and robustness in a biomathematical model-based patient-specific response metric for glioblastoma, JCO Clin. Cancer Inf., 3 (2019), 1-8.
|
|
[108]
|
I. M. Sobol, Sensitivity estimates for nonlinear mathematical models, Math. Modell. Comput. Exp., 1 (1993), 407-414.
|
|
[109]
|
P. Constantine, Active Subspaces: Emerging Ideas for Dimension Reduction in Parameter Studies, SIAM, 2015.
|
|
[110]
|
M. D. Morris, Factorial sampling plans for preliminary computational experiments, Technometrics, 33 (1991), 161-174. doi: 10.1080/00401706.1991.10484804

|
|
[111]
|
C. Rasumssen, C. Williams, Gaussian Processes for Machine Learning, MIT Press, 2006.
|
|
[112]
|
X. Zhu, M. Welling, F. Jin, J. Lowengrub, Predicting simulation parameters of biological systems using a gaussian process model, Stat. Anal. Data Mining: ASA Data Sci. J., 5 (2012), 509-522. doi: 10.1002/sam.11163

|
|
[113]
|
M. C. Kennedy, A. O'Hagan, Bayesian calibration of computer models, J. R. Stat. Soc.: S. B (Stat. Method., 63 (2001), 425-464.
|
|
[114]
|
Y. LeCun, L. Bottou, Y. Bengio, P. Haffner, et al., Gradient-based learning applied to document recognition, Proc. IEEE, 86 (1998), 2278-2324.
|
|
[115]
|
A. Krizhevsky, I. Sutskever, G. E. Hinton, Imagenet classification with deep convolutional neural networks, in Advances in Neural Information Processing Systems (eds. F. Pereira, C. J. C. Burges, L. Bottou, K. Q. Weinberger), Curran Associates, (2012), 1097-1105.
|
|
[116]
|
O. Ronneberger, P. Fischer, T. Brox, U-net: Convolutional networks for biomedical image segmentation, in Medical Image Computing and Computer-Assisted Intervention (eds. N. Navab, J. Hornegger, W. M. Wells, A. F. Frangi), Springer International Publishing, Cham, (2015), 234-241.
|
|
[117]
|
A. Esteva, A. Robicquet, B. Ramsundar, V. Kuleshov, M. DePristo, K. Chou, et al., A guide to deep learning in healthcare, Nat. Med., 25 (2019), 24-29.
|
|
[118]
|
Z. Cao, L. Duan, G. Yang, T. Yue, Q. Chen, An experimental study on breast lesion detection and classification from ultrasound images using deep learning architectures, BMC Med. Imaging, 19 (2019), 51.
|
|
[119]
|
D. Ribli, A. Horváth, Z. Unger, P. Pollner, I. Csabai, Detecting and classifying lesions in mammograms with deep learning, Sci. Rep., 8 (2018), 4165. doi: 10.1038/s41598-018-29025-1

|
|
[120]
|
E. M. Rutter, J. H. Lagergren, K. B. Flores, Automated object tracing for biomedical image segmentation using a deep convolutional neural network, in Medical Image Computing and Computer Assisted Intervention (eds. A. F. Frangi, J. A. Schnabel, C. Davatzikos, C. Alberola López & G. Fichtinger), Springer International Publishing, Cham, (2018), 686-694.
|
|
[121]
|
S. Bakas, M. Reyes, A. Jakab, S. Bauer, M. Rempfler, A. Crimi, et al., Identifying the best machine learning algorithms for brain tumor segmentation, progression assessment, and overall survival prediction in the BRATS challenge, preprint, arXiv: 1811.02629.
|
|
[122]
|
M. Havaei, A. Davy, D. Warde-Farley, A. Biard, A. Courville, Y. Bengio, et al., Brain tumor segmentation with deep neural networks, Med. Image Anal., 35 (2017), 18-31.
|
|
[123]
|
Q. Xie, K. Faust, R. Van Ommeren, A. Sheikh, U. Djuric, P. Diamandis, Deep learning for image analysis: Personalizing medicine closer to the point of care, Crit. Rev. Clin. Lab. Sci., 56 (2019), 61-73. doi: 10.1080/10408363.2018.1536111

|
|
[124]
|
X. Feng, N. Tustison, C. Meyer, Brain tumor segmentation using an ensemble of 3d U-nets and overall survival prediction using radiomic features, in Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries (eds. A. Crimi, S. Bakas, H. Kuijf, F. Keyvan, M. Reyes, T. van Walsum), Springer International Publishing, Cham, (2019), 279-288.
|
|
[125]
|
E. Puybareau, G. Tochon, J. Chazalon, J. Fabrizio, Segmentation of gliomas and prediction of patient overall survival: A simple and fast procedure, in Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries (eds. A. Crimi, S. Bakas, H. Kuijf, F. Keyvan, M. Reyes & T. van Walsum), Springer International Publishing, Cham, (2019), 199-209.
|
|
[126]
|
L. Sun, S. Zhang, L. Luo, Tumor segmentation and survival prediction in glioma with deep learning, in Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries (eds. A. Crimi, S. Bakas, H. Kuijf, F. Keyvan, M. Reyes & T. van Walsum), Springer International Publishing, Cham, (2019), 83-93.
|
|
[127]
|
B. Lyu, A. Haque, Deep learning based tumor type classification using gene expression data, in Proceedings of the 2018 ACM International Conference on Bioinformatics, Computational Biology, and Health Informatics, ACM, New York, (2018), 89-96.
|
|
[128]
|
P. Mobadersany, S. Yousefi, M. Amgad, D. A. Gutman, J. S. Barnholtz-Sloan, J. E. V. Vega, et al., Predicting cancer outcomes from histology and genomics using convolutional networks, Proc. Natl. Acad. Sci., 115 (2018), E2970-E2979.
|
|
[129]
|
J. Zou, M. Huss, A. Abid, P. Mohammadi, A. Torkamani, A. Telenti, A primer on deep learning in genomics, Nat. Genet., 12-18.
|
|
[130]
|
B. Shickel, P. J. Tighe, A. Bihorac & P. Rashidi, Deep EHR: A survey of recent advances in deep learning techniques for electronic health record (EHR) analysis, IEEE J. Biomed. Health Inf., 22 (2017), 1589-1604.
|
|
[131]
|
R. A. Taylor, J. R. Pare, A. K. Venkatesh, H. Mowafi, E. R. Melnick, W. Fleischman, et al., Prediction of in-hospital mortality in emergency department patients with sepsis: a local big data-driven, machine learning approach, Academic Emerg. Med., 23 (2016), 269-278.
|
|
[132]
|
T. Zheng, W. Xie, L. Xu, X. He, Y. Zhang, M. You, et al., A machine learning-based framework to identify type 2 diabetes through electronic health records, Int. J. Med. Inf., 97 (2017), 120-127.
|
|
[133]
|
H. Xu, Z. Fu, A. Shah, Y. Chen, N. B. Peterson, Q. Chen, et al., Extracting and integrating data from entire electronic health records for detecting colorectal cancer cases, in AMIA Annual Symposium Proceedings, American Medical Informatics Association, (2011), 1564.
|
|
[134]
|
D. Zhao, C. Weng, Combining pubmed knowledge and ehr data to develop a weighted bayesian network for pancreatic cancer prediction, J. Biomed. Inf., 44 (2011), 859-868. doi: 10.1016/j.jbi.2011.05.004

|
|
[135]
|
R. Caruana, Multitask learning, Mach. Learn., 28 (1997), 41-75. doi: 10.1023/A:1007379606734

|
|
[136]
|
S. Ruder, An overview of multi-task learning in deep neural networks, preprint, arXiv: 1706.05098.
|
|
[137]
|
N. Jaques, S. Taylor, E. Nosakhare, A. Sano, R. Picard, Multi-task learning for predicting health, stress, and happiness, in NIPS Workshop on Machine Learning for Healthcare, 2016.
|
|
[138]
|
R. C. Rockne, A. Hawkins-Daarud, K. R. Swanson, J. P. Sluka, J. A. Glazier, P. Macklin, et al., The 2019 mathematical oncology roadmap, Phys. Biol., 16 (2019), 041005.
|
|
[139]
|
M. Raissi, P. Perdikaris, G. E. Karniadakis, Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations, J. Comput. Phys., 378 (2019), 686-707. doi: 10.1016/j.jcp.2018.10.045

|
|
[140]
|
S. H. Rudy, S. L. Brunton, J. L. Proctor, J. N. Kutz, Data-driven discovery of partial differential equations, Sci. Adv., 3 (2017), e1602614. doi: 10.1126/sciadv.1602614

|
|
[141]
|
J. H. Lagregren, J. T. Nardini, G. M. Lavigne, E. M. Rutter, K. B. Flores, Learning partial differential equations for biological transport models from noisy spatiotemporal data, preprint, arXiv: 1902.04733.
|
|
[142]
|
F. Hamilton, A. L. Lloyd, K. B. Flores, Hybrid modeling and prediction of dynamical systems, PLoS Comput. Biol., 13 (2017), e1005655. doi: 10.1371/journal.pcbi.1005655

|
|
[143]
|
J. Lagergren, A. Reeder, F. Hamilton, R. C. Smith, K. B. Flores, Forecasting and uncertainty quantification using a hybrid of mechanistic and non-mechanistic models for an age-structured population model, Bull. Math. Biol., 80 (2018), 1578-1595. doi: 10.1007/s11538-018-0421-7

|
|
[144]
|
N. Gaw, A. Hawkins-Daarud, L. S. Hu, H. Yoon, L. Wang, Y. Xu, et al., Integration of machine learning and mechanistic models accurately predicts variation in cell density of glioblastoma using multiparametric MRI, Sci. Rep., 9 (2019), 10063.
|
|
[145]
|
D. P. Kingma, M. Welling, Auto-encoding variational bayes, preprint,, arXiv: 1312.6114.
|
|
[146]
|
C. Doersch, Tutorial on variational autoencoders, preprint, arXiv: 1606.05908.
|
|
[147]
|
A. Myronenko, 3d mri brain tumor segmentation using autoencoder regularization, in Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries (eds. A. Crimi, S. Bakas, H. Kuijf, F. Keyvan, M. Reyes, T. van Walsum), Springer International Publishing, Cham, (2019), 311-320.
|
|
[148]
|
J. Xu, L. Xiang, Q. Liu, H. Gilmore, J. Wu, J. Tang, et al., Stacked sparse autoencoder (ssae) for nuclei detection on breast cancer histopathology images, IEEE Trans. Med. Imaging, 35 (2015), 119-130.
|
|
[149]
|
I. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. Warde-Farley, S. Ozair, et al., Generative adversarial nets, in Advances in Neural Information Processing Systems (eds. Z. Ghahramani, M. Welling, C. Cortes, N. D. Lawrence, K. Q. Weinberger), Curran Associates, (2014), 2672-2680.
|
|
[150]
|
L. Metz, B. Poole, D. Pfau, J. Sohl-Dickstein, Unrolled generative adversarial networks, preprint, arXiv: 1611.02163.
|
|
[151]
|
M. Arjovsky, L. Bottou, Towards principled methods for training generative adversarial networks, preprint, arXiv: 1701.04862.
|
|
[152]
|
A. Radford, L. Metz, S. Chintala, Unsupervised representation learning with deep convolutional generative adversarial networks, preprint, arXiv: 1511.06434.
|
|
[153]
|
M. Frid-Adar, I. Diamant, E. Klang, M. Amitai, J. Goldberger, H. Greenspan, GANbased synthetic medical image augmentation for increased CNN performance in liver lesion classification, Neurocomputing, 321 (2018), 321-331. doi: 10.1016/j.neucom.2018.09.013

|
|
[154]
|
H.-C. Shin, N. A. Tenenholtz, J. K. Rogers, C. G. Schwarz, M. L. Senjem, J. L. Gunter, et al., Medical image synthesis for data augmentation and anonymization using generative adversarial networks, in Simulation and Synthesis in Medical Imaging (eds. A. Gooya, O. Goksel, I. Oguz, N. Burgos), Springer International Publishing, Cham, (2018), 1-11.
|
|
[155]
|
J.-Y. Zhu, T. Park, P. Isola, A. A. Efros, Unpaired image-to-image translation using cycleconsistent adversarial networks, in The IEEE International Conference on Computer Vision (ICCV), 2017.
|
|
[156]
|
Y. Zhang, S. Miao, T. Mansi, R. Liao, Task driven generative modeling for unsupervised domain adaptation: Application to x-ray image segmentation, in Medical Image Computing and Computer Assisted Intervention (eds. A. F. Frangi, J. A. Schnabel, C. Davatzikos, C. Alberola-López, G. Fichtinger), Springer International Publishing, Cham, (2018), 599-607.
|
|
[157]
|
C. E. Gast, A. D. Silk, L. Zarour, L. Riegler, J. G. Burkhart, K. T. Gustafson, et al., Cell fusion potentiates tumor heterogeneity and reveals circulating hybrid cells that correlate with stage and survival, Sci. Adv., 4 (2018), eaat7828.
|
|
[158]
|
K. Mitamura, Y. Yamamoto, N. Kudomi, Y. Maeda, T. Norikane, K. Miyake, et al., Intratumoral heterogeneity of 18f-FLT uptake predicts proliferation and survival in patients with newly diagnosed gliomas, Ann. Nucl. Med., 31 (2017), 46-52.
|
|
[159]
|
D. A. Hormuth II, J. A. Weis, S. L. Barnes, M. I. Miga, V. Quaranta, T. E. Yankeelov, Biophysical modeling of in vivo glioma response after whole-brain radiation therapy in a murine model of brain cancer, Int. J. Radiat. Oncol. Biol. Phys., 100 (2018), 1270-1279. doi: 10.1016/j.ijrobp.2017.12.004

|
|
[160]
|
E. M. Rutter, T. L. Stepien, B. J. Anderies, J. D. Plasencia, E. C. Woolf, A. C. Scheck, et al., Mathematical analysis of glioma growth in a murine model, Sci. Rep., 7 (2017), 2508.
|
|
[161]
|
S. Benzekry, C. Lamont, J. Weremowicz, A. Beheshti, L. Hlatky, P. Hahnfeldt, Tumor growth kinetics of subcutaneously implanted Lewis Lung carcinoma cells, 2019. Available from: https://zenodo.org/record/3572401#.Xqt0TlNKjRZ.
|
|
[162]
|
M. Mastri, A. Tracz, J. M. L. Ebos, Tumor growth kinetics of human LM2-4LUC+ triple negative breast carcinoma cells, 2019. Available from: https://zenodo.org/record/3574531#.Xqtzv1NKjRZ.
|
|
[163]
|
A. Rodallec, S. Giocometti, J. Ciccolini, R. Fanciullino, Tumor growth kinetics of human MDA-MB-231 cells transfected with dTomato lentivirus, 2019. Available from: https://zenodo.org/record/3593919#.Xqt0PlNKjRZ.
|









 DownLoad:
DownLoad: