1.
Introduction
Understanding the rich diversity or coexistence of populations observed in the nature is a main goal in many ecological research activities. The major interactions among community of populations are competition and predation which were the focuses of the classical book on mathematical models of population ecology authored by Freedman in 1980 [1]. In a theoretical setting where populations competing for a single resource, only one population can persist. This theoretical finding is often termed as the competitive exclusion principle [2]. Indeed, Gause observed that two species competing for the same limiting resource cannot coexist at constant population values [3]. Pure predator-prey interactions give rise to predator-prey communities called simple food chains. A simple food chain often consists of only a few species in ecological settings which prevents it to be the framework to host many species. However, predator-prey interaction often results in oscillatory population densities which may provide variable resources levels to enable the coexistence of many competing species [4]. Therefore coexistence of many species is mostly likely the consequence of concurrent competition and predation interactions among species.
In a remarkable effort of dissecting how density-mediated (indirect competition) and trait-mediated (selective predation) interactions among species may have contributed to the coexistence of species, van Veen et. al. studied an insect community consisting of two aphid species (Acyrthosiphon pisum and Megoura viciae) and a specialist parasitoid (Aphidius ervi) that attacks only one of the aphids (A. pisum). In extensive experiments, they found that the two aphid species alone were unable to coexist, with A. pisum competitively excluding M. viciae. Moreover, they observed that the interaction between A. pisum and the parasitoid was unstable. However, the three-species community persisted for at least 50 weeks [5]. It is observed that parasitoid attack on the susceptible host reduces the interspecific competition experienced by the non-host (a density-mediated effect), and the presence of the non-host reduces the searching efficiency of the parasitoid (a trait-mediated effect). To study this experiment analytically, van Veen et. al. [5] proposed the following three-species interaction dynamic model:
where N1 and N2 are numbers of the two aphid species, A. pisum and M. viciae, respectively. P denotes the number of the specialist parasitoid, A. ervi, which attacks only N1. The parameter ri is the per capita growth rate (or the intrinsic rate of increase) of aphid species i, i=1,2. The parameter αii is the intraspecific competition coefficient (also be interpreted as the reciprocal of carrying capacity) and αij,i≠j, is the interspecific competition coefficient, i,j=1,2. 1/μ represents the average lifespan of the parasitoid. Parameter α1p is the parasitoid per capita attack rate of N1, while b1 is the parameter controlling the reduction in parasitoid attack rate with increasing host number (N1), which may be interpreted as correlated with the searching and handling time, and b2 can be interpreted as the time wasted when a parasitoid encounters an unsuitable aphid (N2), which is equivalent to the "recognition time" in classical diet models from foraging theory. s is the parasitoid sex ratio, and c denotes the effect of parasitoid number on parasitoid recruitment. All these parameters are positive constants.
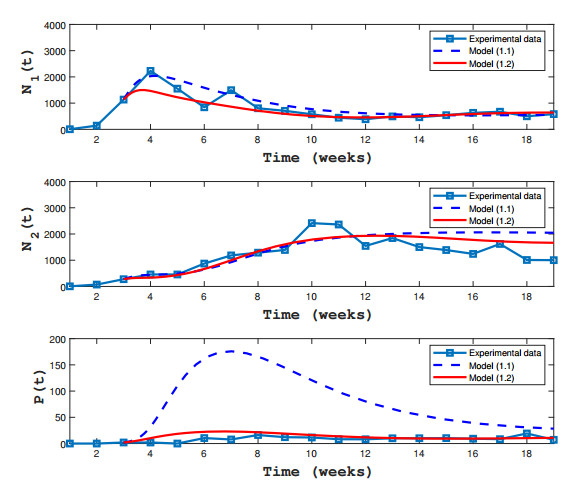
Note that the functional response and incidence functions of parasitoid are not proportional in model (1.1), i.e., they don't obey the usual conservation law of mass. While proportionality is not a must in reality, the lack of it implies the conservation of some weighted sum of masses is lost which may artificially add complexity to an already complicated population growth process. In addition, Figure 1 shows that there is a big discrepancy between the fitted population trajectories of (1.1) and the experimental data sets in [5]. In particular, parasitoid numbers are sometimes much larger. In fact, from the full three-species cage experiments in [5], people can infer that parasitoid (A. ervi) have to search for the susceptible host (A. pisum), and the other aphids (M. viciae) may interfere the search of parasitoid at the same time. In an effort to reduce this discrepancy, we employ a standard incidence function to represent both the functional response and incidence functions of parasitoid. This yields the following modified model:
From Table 1, we observe that the model (1.2) provides a better fitting than that of model (1.1) in Figure 1. Most noteworthy is the sharp reduction of the aforementioned big discrepancy between the data and the model (1.2) fitting of the parasitoid numbers compare to that of the data and the model (1.1) fitting of the parasitoid. Thus, (1.2) may be more suitable to describe the full three-species cage experiments in [5]. In the present paper, we will study the dynamics of model (1.2) with a focus on the local and global stabilities of its nonnegative steady states. Observe that the function
is not defined at (0,0,0). However, lim(N1,N1,P)→(0+,0+,0+)R(N1,N1,P)=α1p/c. Hence, in the following, we define R(0,0,0)=α1p/c. With this definition, we see that (0,0,0) is a steady state of model (1.2). However, the model is not differentiable at (0,0,0). Indeed, model (1.2) is a ratio-dependent model with two preys and one specialist predator. A ratio-dependent model with one prey and two predators was studied in [6] while a ratio-dependent food chain was studied in [7]. In these studies, through a nonlinear transformation (blow-up transformation), the authors were able to reveal the rich dynamics often observed in ratio-dependent models due to the non-smoothness of the trivial steady state (0,0,0). Indeed, rich dynamics, such as global stability, limit cycles and extinction, was also found in ratio-dependent models with only two populations [8,9,10,11].
2.
Dissipativity
Since we are interested in the long term dynamics of the population interactions, we assume that the initial condition of (1.2) has the form
We also assume that parameters of (1.2) are all positive. It is easy to see that the right hand side functions of the equations of (1.2) are uniformly Lipschitzian and hence the solution of model (1.2) with initial conditions (2.1) is unique and exist for all t>0 [12]. We first show that that model (1.2) produces solutions that are biologically plausible. Mathematically, this is equivalent to establish the following proposition.
Proposition 2.1.
For model (1.2), solutions with initial conditions (2.1) are positive and eventually uniformly bounded.
Before proving the above proposition, we would like to establish the following general result.
Lemma 2.1. Assume the function F(t,x) is uniformly Lipschitzian with respect to x and there is a continuous function C(t) such that F(t,x)≥C(t)x for x≥0. Then the solution of
exists, is unique and positive for all t>0.
Proof. The existence and uniqueness follow from the uniform Lipschitzian property of the function F(t,x) and Theorem 5.2 in [12]. Since F(t,x)≥C(t)x for x≥0 we see that dxdt≥C(t)x which implies that for all t>0, we have x(t)≥x(0)e∫t0C(s)ds>0.
We are now in a position to prove the Proposition 2.1.
Proof. We first establish the positiviness of P(t). Notice that dPdt=FP(N1,N2,P)=PfP(N1,N2,P) where fP(N1,N2,P)≥−μ for positive values of N1(t),N2(t) and P(t). By Lemma 2.1 with C(t)=−μ, we see that P(t) stays positive.
We now consider the positivity of N1(t). Observe that
where
Note that α1pPb1N1+b2N2+cP≤α1pc is always valid because all variables are nonnegative. As a result, we have
By Lemma 2.1 with C(t)=C1(t), we see that N1(t) stays positive. The positivity of N2(t) can be established similarly.
Now we present the arguments for ultimate boundedness of solutions of (1.2) in R3+. Since all components of a solution of (1.2) are positive, using the first and second equations of (1.2), we have
As a result, we have lim supt→+∞N1(t)≤1/α11≡N∞1 and lim supt→+∞N2(t)≤1/α22≡N∞2, respectively.
Using the monotonicity of sα1pN1Pb1N1+cP on N1 and above analysis, we have
Thus, using the third equation of (1.2), we have
As a result, we have lim supt→+∞P(t)≤sα1p−b1μcμ≡P∞ if sα1p−b1μ>0, and limt→+∞P(t)=0 if sα1p−b1μ≤0.
A hallmark of the rich dynamics of ratio-dependent population models is the possibility of the origin as an attractor, implying the collapse of the population community [7,10,11,13]. Contrast to many ratio-dependent population models, it is easy to see from the N2 equation that the origin as an equilibrium of model (1.2) can not be an attractor. This maybe intuitive biologically since the parasitoid species only attack one of the species which may indirectly help the persistence of the other aphid species. In addition, we have the following much stronger result.
Proposition 2.2. Assume that α1p<cr1 or α1p≤b1μ/s. If (N1(t),N2(t),P(t)) is a solution of model (1.2) with initial conditions (2.1), then
Proof. We have two cases to consider: 1) α1p<cr1 and 2) α1p≤b1μ/s. In the following, we let Z(t)≡N1(t)+N2(t).
Consider first case 1. We prove it by contradiction. If the proposition is false, then there is a strictly increasing sequence of positive values ti such that Z(ti)<1/i is a strictly decreasing sequence and Z′(ti)≤0, i=1,2,.... Since all components of the solution stay positive, we have
Hence
Since α1p≤cr1, we see for large enough values of i, we will have both 1−α1pcr1−α11N1−α12N2>0 and 1−α21N1−α22N2>0. Hence dZ(ti)dt>0 which contradicts the fact that ti is selected to have Z′(ti)≤0.
Consider now the case 2 with α1p≤b1μ/s. From the proof of the case 1, the conclusion of the proposition is true if α1p<cr1. Hence we assume below that cr1≤α1p≤b1μ/s. The proof of Proposition 2.1 shows that α1p<b1μ/s implies limt→+∞P(t)=0. Hence for any δ>0 there is a time tδ>0 such that t>tδ implies that P(t)<δ. Let
and δ be so small such that
We claim that if for some t0>tδ such that Z(t0)≥δ0, then Z(t)≥δ0 for all t>t0. If this claim is false, then there is a t1≥to such that Z(t1)=δ0 and Z′(t1)≤0. Observe that
However,
This is a contradiction which proves our claim. Clearly this claim implies the conclusion of the proposition.
If the statement that Z(t0)≥δ0 for some t0>tδ is not true, then Z(t)<δ0 for all t≥tδ. In this situation, we have
This implies that for all t≥tδ, we have Z(t)>N2(t)>N2(tδ)egt where g=1−(α21+α22)δ0>0. Therefore Z(t) will be unbounded which contradicts the statement that Z(t)<δ0 for all t≥tδ. The proof of the proposition is now complete.
The proof of the second case for the Proposition 2.2 implies that if limt→+∞P(t)=0, then the Proposition 2.2 hold. Hence we have the following result.
Theorem 2.1. If (N1(t),N2(t),P(t)) is a solution of model (1.2) with initial conditions (2.1), then
We conjecture that Proposition 2.2 remains true even if the condition α1p<cr1 or α1p≤b1μ/s is removed.
Since sα1p−b1μ≤0 implies limt→+∞P(t)=0, this together with Proposition 2.2 imply that if α1p<b1μ/s in system (1.2), then its limit system is
System (2.7) is the well studied Lotka-Volterra competition model (see related sections in [1], [12] or [14]). Let D1=α22−α12,D2=α11−α21 and D=α11α22−α12α21. We have the following global results for system (1.2).
Proposition 2.3. Suppose that α1p<b1μ/s in system (1.2), then limt→+∞P(t)=0 and the following statements are true.
(i) When α11<α21 and α22>α12, equilibrium E1=(1α11,0,0) is globally asymptotically stable and E2=(0,1α22,0) is unstable.
(ii) When α11>α21 and α22<α12, system (1.2) has no coexist equilibrium, equilibrium E1 is always unstable and E2 is globally asymptotically stable.
(iii) When α11>α21 and α22>α12, system (1.2) has a unique coexist equilibrium E12=(D1D,D2D,0), which is globally asymptotically stable, both equilibria E1 and E2 are unstable.
(iv) When α11<α21 and α22<α12, the unique coexist equilibrium E12 is a saddle, both equilibria E1 and E2 are stable, i.e., the bistability phenomenon of initial value dependence will occur.
In the rest of this paper, we assume that sα1p−b1μ>0 is valid in system (1.2).
3.
Equilibria of system (1.2)
In this section, we study the existence, location and numbers of equilibrium of system (1.2). Let
It is easy to see that system (1.2) has boundary equilibria E0=(0,0,0),E1=(1/α11,0,0) and E2=(0,1/α22,0). Recall that D1=α22−α12,D2=α11−α21 and D=α11α22−α12α21. After straightforward algebraic manipulation on (3.1), we obtain the following results.
Proposition 3.1. The following are true for system (1.2).
(i) When D1,D2 and D have the same sign, i.e., α11>α21 and α22>α12, or α11<α21 and α22<α12, equilibrium E12=(D1D,D2D,0) exists.
(ii) When r1s>sα1p−b1μc, equilibrium E13=(˜N∗1,0,˜P∗) exists, and
Now, we consider the existence of positive equilibrium of system (1.2). According to (3.1), we know that the positive equilibrium must be the solution of the following algebraic equations
For (3.2), substituting the second and third equations into the first equation, and substituting the second equation into the third equation, we have
where
According φ1(N1)=φ2(N1), we have
Note that △=(r1sθ1−ω1)2+4r1sθω2 is the discriminant of (3.4). According to the formula of roots of a quadric equation, we know the roots of (3.4) are
Furthermore, we have
Combining (3.3), (3.4) and (3.5), similar to Proposition 2.3, we split the analysis into four subsections.
3.1. α11<α21 and α22>α12
In this case, we know D1>0, i.e., θ1>0, but the sign of θ is undetermined.
When θ>0, we know △>|r1sθ1−ω1| is always valid. So N1∗1>0 and N2∗1<0 in (3.5), i.e., N1∗1 is the unique positive root of (3.4). Note that θ1/θ>1/α21 due to α11<α21. We know ω2ω1<N1∗1<1α21 can ensure ϕ(N1∗1)>0,φ1(N1∗1)>0 and φ2(N1∗1)>0.
When θ<0, we will analyze the existence of positive equilibrium of system (1.2) according to the sign of △ and r1sθ1−ω1. If △<0 or r1sθ1−ω1>0, it is clear that there is no positive equilibrium in system (1.2). If △=0 and r1sθ1−ω1<0, we have N1∗1=N2∗1=r1sθ1−ω12r1sθ≡N12∗1>0. To ensure ϕ(N12∗1)>0,φ1(N12∗1)>0 and φ2(N12∗1)>0, we also need ω2ω1<N12∗1<1α21. If △>0 and r1sθ1−ω1<0, we know N1∗1>0,N2∗1>0 in (3.5). Similarly, we know ϕ(Nk∗1)>0,φ1(Nk∗1)>0 and φ2(Nk∗1)>0 if ω2ω1<Nk∗1<1α21,k=1,2.
Summarize the above analyses, we have
Proposition 3.2. Suppose that sα1p−b1μ>0,α11<α21 and α22>α12.
(i) If θ>0 and ω2ω1<N1∗1<1α21, then system (1.2) has a unique positive equilibrium E+=(N1∗1,N∗2,P∗), in which N∗2=ϕ(N1∗1),P∗=φ1(N1∗1)μ. Otherwise, there is no positive equilibrium in system (1.2).
(ii) If θ<0,△=0 and r1sθ1−ω1<0, then system (1.2) has a unique positive equilibrium E+=(N12∗1,N∗2,P∗) when ω2ω1<N12∗1<1α21, in which N∗2=ϕ(N12∗1),P∗=φ1(N12∗1)μ. If θ<0,△>0 and r1sθ1−ω1<0, system (1.2) may have two positive equilibria Ek+=(Nk∗1,Nk∗2,Pk∗), which depends on whether ω2ω1<Nk∗1<1α21 is satisfied, here Nk∗2=ϕ(Nk∗1),Pk∗=φ1(Nk∗1)μ,k=1,2. Otherwise, there is no positive equilibrium in system (1.2).
3.2. α11>α21 and α22<α12
In this case, we know D1<0, i.e., θ1<0, but the sign of θ is also undetermined.
When θ>0, similar to the above analyses, we know N1∗1 is the unique positive root of (3.4). However, because φ1(x)<0 is always valid for x>0 if θ1<0 and θ>0, there is no positive equilibrium in system (1.2).
When θ<0, since r1sθ1−ω1<0 is always valid, we will analyze the existence of positive equilibrium of system (1.2) according to the sign of △. If △<0, it is clear that there is no positive equilibrium in system (1.2). If △=0, we have N1∗1=N2∗1=r1sθ1−ω12r1sθ≡N12∗1>0. Note that θ1/θ>1/α21 due to α11>α21 and the sign of θ,θ1. We know ω2ω1<N12∗1<1α21 can ensure ϕ(N12∗1)>0,φ1(N12∗1)>0 and φ2(N12∗1)>0. If △>0, we know N1∗1>0,N2∗1>0 in (3.5). Similarly, we know ϕ(Nk∗1)>0,φ1(Nk∗1)>0 and φ2(Nk∗1)>0 if ω2ω1<Nk∗1<1α21,k=1,2.
Summarize the above analyses, we have
Proposition 3.3. Suppose that sα1p−b1μ>0,α11>α21 and α22<α12.
(i) If θ>0, then there is no positive equilibrium in system (1.2).
(ii) If θ<0 and △=0, then system (1.2) has a unique positive equilibrium E+=(N12∗1,N∗2,P∗) when ω2ω1<N12∗1<1α21, in which N∗2=ϕ(N12∗1),P∗=φ1(N12∗1)μ. If θ<0 and △>0, system (1.2) may have two positive equilibria Ek+=(Nk∗1,Nk∗2,Pk∗), which depends on whether ω2ω1<Nk∗1<1α21 is satisfied, here Nk∗2=ϕ(Nk∗1),Pk∗=φ1(Nk∗1)μ,k=1,2. Otherwise, there is no positive equilibrium in system (1.2).
3.3. α11>α21 and α22>α12
In this case, we know D1>0,D>0, i.e., θ1>0,θ>0. Thus, △>|r1sθ1−ω1| is always valid, and N1∗1 is the unique positive root of (3.4). Note that θ1/θ<1/α21 in this case. We know ω2ω1<N1∗1<θ1θ can ensure ϕ(N1∗1)>0,φ1(N1∗1)>0 and φ2(N1∗1)>0. As a result, we have
Proposition 3.4. Suppose that sα1p−b1μ>0,α11>α21 and α22>α12. If ω2ω1<N1∗1<θ1θ, then system (1.2) has a unique positive equilibrium E+=(N1∗1,N∗2,P∗), in which N∗2=ϕ(N1∗1),P∗=φ1(N1∗1)μ. Otherwise, there is no positive equilibrium in system (1.2).
3.4. α11<α21 and α22<α12
In this case, we know D1<0,D<0, i.e., θ1<0,θ<0. Since r1sθ1−ω1<0 is always true, we will analyze the existence of positive equilibrium of system (1.2) according to the sign of △. If △<0, it is clear that there is no positive equilibrium in system (1.2). If △=0, we have N1∗1=N2∗1=r1sθ1−ω12r1sθ≡N12∗1>0. Note that θ1/θ<1/α21 in this case. We know ω2ω1<N12∗1<θ1θ can ensure ϕ(N12∗1)>0,φ1(N12∗1)>0 and φ2(N12∗1)>0. If △>0, we have N1∗1>0,N2∗1>0 in (3.5). Similarly, we know ϕ(Nk∗1)>0,φ1(Nk∗1)>0 and φ2(Nk∗1)>0 if ω2ω1<Nk∗1<θ1θ,k=1,2.
Summarize the above analyses, we have
Proposition 3.5. Suppose that sα1p−b1μ>0,α11<α21 and α22<α12. If △=0, then system (1.2) has a unique positive equilibrium E+=(N12∗1,N∗2,P∗) when ω2ω1<N12∗1<1α21, in which N∗2=ϕ(N12∗1),P∗=φ1(N12∗1)μ. If △>0, then system (1.2) may have two positive equilibria Ek+=(Nk∗1,Nk∗2,Pk∗), which depends on whether ω2ω1<Nk∗1<1α21 is satisfied, here Nk∗2=ϕ(Nk∗1),Pk∗=φ1(Nk∗1)μ,k=1,2. Otherwise, there is no positive equilibrium in system (1.2).
4.
Stability of non-origin equilibria
In order to gain a global understanding of the rich and complex dynamics of (1.2), we would like to study the stability of all its equilibria. Note that (1.2) is not differentiable at origin equilibrium E0, and the standard linearization approach cannot be used at E0. To avoid this difficulty for now, this section will focus on the non-origin equilibria, including boundary equilibria E1,E2,E12,E13 in Proposition 3.1, and the possible positive equilibria E+,Ek+,k=1,2.
The Jacobian matrix of (1.2) at E1 and E2 are
and
respectively. Note that the eigenvalues of (4.1) and (4.2) lie on the diagonal. Hence, we have the following results.
Proposition 4.1. Suppose that sα1p−b1μ>0 in (1.2).
(i) Equilibrium E1 is a saddle.
(ii) Equilibrium E2 is locally asymptotically stable if α22<α12.
The Jacobian matrix of (1.2) at E12 is
Clearly, the element in the lower right-hand corner of (4.3) is one of eigenvalue of (4.3). When sα1p−b1μ>0, (sα1p−b1μ)D1−b2μD2b1D1+b2D2<0 is equivalent to sα1p−b1μb2μ<D2D1. Furthermore, recall D=α11α22−α12α21, we can conclude that the trace of the upper left-hand 2×2 matrix is always negative and its determinant is positive if all D1,D2,D are positive. Thus, we have
Proposition 4.2. Suppose that sα1p−b1μ>0 in (1.2). Equilibrium E12 is locally asymptotically stable if D1>0,D2>0,D>0 and sα1p−b1μb2μ<D2D1.
The Jacobian matrix of (1.2) at E13 is
Here
Clearly, λ1=r2(1−α21˜N∗1) is one of eigenvalue of (4.4), and the other two eigenvalues of (4.4) satisfying
Here
According to the existence of E13 in Proposition 3.1, we know
As a result,
Thus, when r1=(sα1p−b1μ)(b1μ+sα1p−scμ)s2cα1p≡r∗1, we have A1=0. In addition, ∂A1∂r1=1≠0 is always valid.
Note that λ1<0 is equivalent to ˜N∗1>1α21. Using the expression of ˜N∗1 in Proposition 3.1, we have
i.e., r1sc−(sα1p−b1μ)>r1scα11α21, which is equivalent to r1>−α21(sα1p−b1μ)scD2≡r∗∗1 if D2<0. As a result, according to the Routh-Hurwitz criteria (rephrased to be user-friendly for the cases of polynomial of lower orders in Kuang et al. [15]) we have
Proposition 4.3. Assume that r1>sα1p−b1μsc and α11<α21 in (1.2). E13 is locally asymptotically stable if r1>max{r∗1,r∗∗1}.
According to the the criterion in [16] (which was rephrased to be user-friendly and employed in the work of Beretta and Kuang [13]), without using eigenvalues, we obtain
Proposition 4.4. Assume that r1>sα1p−b1μsc and α11<α21 in (1.2). If r∗1>r∗∗1, there is a simple Hopf bifurcation at r1=r∗1.
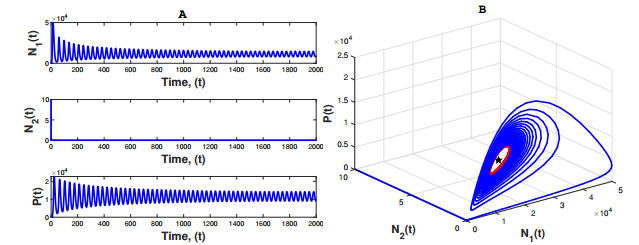
Remark 4.1. For three-species interaction model (1.2) in full-community experiment, Proposition 12 indicates that fluctuation scenarios can be found in host-parasitoid plane (N1-P plane) under some suitable parameters. In fact, taking r2=2.82,α11=1.82×10−5,α12=3.70×102,α21=3.97×102,α22=3.82×10−4,α1p=5.81,μ=0.5,b1=5.2925,b2=6.4178×10−5,c=3.7527 and s=7.9556×10−1 artificially, we have r∗1=0.8270,r∗∗1=0.6619. Let r1=0.8270. Figure 2 shows that the patterns of fluctuation is indeed on the N1-P plane.
Now, we study the stability of positive equilibrium of (1.2). For the convenience of notation, we record the positive equilibrium as E+=(N∗1,N∗2,P∗). Based on (3.2), after a series of calculations, the Jacobian matrix at E+ is given by
Here
Furthermore, the characteristic equation of (4.7) is given by
in which
According to the Routh-Hurwitz criteria [15], we have
Proposition 4.5. Suppose that sα1p−b1μ>0 and the positive equilibrium E+ exists in (1.2). E+ is asymptotically stable if and if C2>0,C3>0 and △≡C1C2−C3>0.
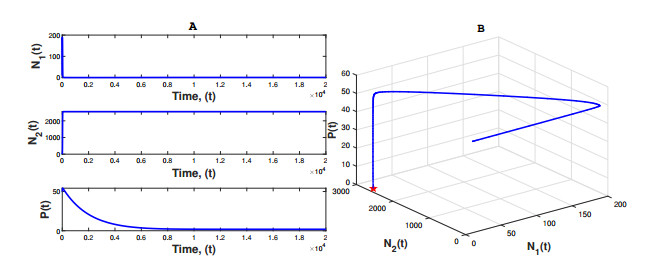
Remark 4.2. For three-species interaction model (1.2) in full-community experiment, Proposition 4.5 indicates that coexistence scenarios can be found under some suitable parameters, which is consistent with the experimental results in [5]. In fact, taking r1=2.90,r2=2.82×10−1,α11=4.92×10−3,α12=3.70×10−4,α21=3.97×10−4,α22=3.92×10−4,α1p=2.81,μ=0.50×10−3,b1=2.2925×10−5,b2=6.4178×10−5,c=1.7527 and s=7.9556×10−3 artificially, we have positive equilibrium E+=(7.6586×10−1,2.5502×103,1.8603), and Figure 3 shows that E+ is stable.
According to the criterion in [16], we have
Proposition 4.6. Suppose that sα1p−b1μ>0 and the positive equilibrium E+ exists. If existing a parameter value, note as θ0, such that C2(θ0)>0,C3(θ0)>0,△(θ0)=0 and d△(theta)dθ|θ=θ0≠0, then a simple Hopf bifurcation occurs at θ=θ0.
5.
Dynamics near the origin equilibrium E0
As mentioned previously, the origin equilibrium E0 in (1.2) can not be asymptotically stable since no positive solution can tend to it due to the N2 equation. Since the system is not differentiable at E0, the standard linearized techniques cannot be used to study the solution properties near it. To overcome this difficulty, we apply the technique of ratio-dependent transformations (also referred as blow-up transformations) which were effectively used in [9,10,17]. Even in the case of much simpler ratio-dependent predator-prey models, the origin is known as the source and difficulty in revealing and understanding its rich and complex dynamics [9,10,13].
We first perform the transformation (N1,N2,P)→(y1,y2,y3) where y1=N1N2,y2=N2 and y3=PN2. This transforms (1.2) to the following system:
The equilibria of the transformed system (5.1) include the following boundary equilibria
and possible positive equilibrium V4=(N∗1N∗2,N∗2,P∗N∗2) under corresponding conditions. Here N∗1,N∗2,P∗ are given in Proposition 3.2-3.5. Interestingly, there is a singular line r1sy1−(r2+μ)y3=0 in system (5.1), and all the points on it are the steady states (V1) of the system. Clearly, V2,V3 and V4 correspond to the E2,E12 and E+ of system (1.2) respectively, while E0 has been blown up into infinite equilibria: V0 and points (V1) on the singular line.
The variational matrix of (5.1) evaluated at V0 is
Note that there are two eigenvalues λ1=r1>0,λ2=r2>0. V0 is always unstable. Clearly, the y3-axis is the stable manifold of V0 while the y1y2 plane is the unstable manifold of V0.
We can see that solution starting near the y3-axis and close to the origin will decline along y3-axis and leave the origin in a fashion tangent to the y1y2-plane.
The variational matrix of (5.1) evaluated at V1 is
Here
Clearly, λ1=r2>0 is one of eigenvalue of (5.2). Hence V1 is also always unstable.
The second transformation is (N1,N2,P)→(z1,z2,z3) where z1=N1P,y2=N2P and y3=P. This transforms (1.2) to the following system:
The equilibria of the transformed system (5.3) include the following boundary equilibria
and possible positive equilibrium W4=(N∗1P∗,N∗2P∗,P∗) under corresponding conditions. Here ˆz1=c(r1+μ)−α1psα1p−b1μ−r1b1, ˜N∗1,˜P∗ are given in Proposition 3.1, N∗1,N∗2,P∗ are given in Proposition 3.2-3.5. Interestingly, there is also a singular line c+b1z1+b2z2=α1pr1−r2 in system (5.3), and all the points on it are the steady states (W2) of the system. Clearly, W3 corresponds to the E13 of system (1.2), while E0 has been blown up into infinite equilibria: W0,W1 and points (W2) on the singular line.
The variational matrix of (5.3) evaluated at W0 is
Note that one of eigenvalues λ1=r2+μ>0. W0 is always unstable.
The variational matrix of (5.3) evaluated at W1 is
and three corresponding eigenvalues of (5.4) are
In order to make all eigenvalues of (5.4) are negative, combining with the nonnegativity of ˆz1, we split the analysis into two cases based on the precondition of sα1p−b1μ>0.
(i) Suppose that sc−b1>0. According to the expressions, we know ˆz1>0,A1<0,A2<0 and A3<0 means
or
(ii) Suppose that sc−b1<0. According to the expressions, we know ˆz1>0,A1<0,A2<0 and A3<0 means
or
However, after some analyses, we find that conditions (5.5)-(5.6) and (5.7)-(5.8) are contradict to the assumptions sc−b1>0 and sc−b1<0 respectively. Thus, W1 is always unstable.
The variational matrix of (5.3) evaluated at W2 is
Here
and A7=−μ+sα1p˜z1c+b1˜z1+b2˜z2=r2 based on the expression of W2. Clearly, λ1=r2>0 is one of eigenvalue of (5.9). W2 is also always unstable.
6.
Discussion
The main purposes of this paper includes 1) the formulation and validation of a biologically more realistic and mathematically more coherent model (1.2) and 2) an initial attempt in studying the rich dynamics of model (1.2).
As mentioned in the introduction, a main focus of population ecology studies is to identify some plausible mechanisms that leading to the extinction and coexistence of community populations. This includes total extinction or the collapse of all populations in a community. Unfortunately, existing food web models that based on prey-dependent functional response functions totally excludes the possibility of the extinction of all community populations as the bottom prey or produce population will never go extinct in those models. The key assumption of ratio-dependent models is that the growth of consumer species is a function of per-capita resource level instead of the total resource level assumed in most prey-dependent models [1,13,18]. Admittedly, ratio-dependent models are often less tractable than prey-dependent models due to the fact the origin is a non-smooth equilibrium. For this reason, there are many remaining mathematical open questions related to the global and nonlinear dynamics of model (1.2).
An even more realistic but mathematically less tractable model of a given community population growth and interactions may involve time delays in population growth [19,20,21,22]. A first attempt on systematic studying of a special delayed ratio-dependent population model based on classic delay-independent parameter method was presented in Beretta and Kuang [23]. Realistic population models with time delays often include survival rate parameters which are usually functions of time delays [21,22]. For these delay models, most popular traditional methods of studying characteristic equations for delay models no longer effective and their study require the applications of the geometric stability switch method or its extensions presented in [20]. Not surprisingly, for the experimental results of van Veen et al. [5], we were able to show numerically that a delayed version of model (1.2) can improve the model fitting. We hope to present a mathematical study of such delayed model in the future.
Per capita growth rate often correlates negatively with population density. The well known logistic equation for the growth of a single species incorporates this intraspecific competition. Multi-trophic models often ignore self-limitation of the consumers leading to the survival of only the fittest species. Kuang et al. found that intraspecific competition can account for the stable coexistence of many consumer species on a single resource in a homogeneous environment and resource growth rates may also play an important role in promoting coexistence of consumer species [24].
In nature, a single resource species may contain many limiting nutrients for consumer species. In addition, producer and consumer may competing for the same essential chemical elements such as carbon, nitrogen and phosphorous [25]. These limiting nutrient contents can vary over time which affect the resource quality and hence impact the consumer growth in a complicated manner [26,27,28]. Population growth models that incorporating both resource quantity and quality are likely better match experimental observations, generating richer dynamics and promote population coexistence [29,30,31]. Such models are often termed stoichiometric population models, especially when limiting nutrients are chemical elements [32,33]. One promising and timely direction of extending the current work is to incorporating the quality dynamics of the aphid species as resource to the parasitoid.
Acknowledgments
Yang Kuang's research is partially supported by NSF grants DMS-1615879, DEB-1930728 and an NIH grant 5R01GM131405-02. Kaifa Wang's research is partially supported by an NSFC grant 11771448.
Conflict of interest
The authors declare that they have no competing interests.









 DownLoad:
DownLoad: