Extinction and stationary distribution of a competition system with distributed delays and higher order coupled noises

1.   Introduction

In the last few decades, the mathematical models, which describe the effect of competition caused by limited resources on the growth of species, have been established and explored extensively ^[1,2,3,4,5]. On the other hand, time delay accompanies the whole process of species population survival and reproduction. Because of the variety of delay between different individuals of the same species or the cumulative effect of the past history of a system, it is more appropriate to establish model with distributed delay ^[6,7,8]. Cushing ^[9] and MacDonald ^[10] introduced the weak kernel and the strong kernel functions to describe the distributed delay, later on, these two kinds of kernels have been investigated by many scholars (see ^{[11,12,13,14]}).

With the idea of the weak kernel functions, we formulate the following competitive system with distributed delays

where $x$ and $y$ measure the population densities of two competing species. $\alpha_ie^{-\alpha_it}(\alpha_i > 0)$ are the weak kernel functions. The delays are the time passing between the intra-specific competition at a given instant and its effect, at a later time, on the dynamics of the two species. The coefficients $r_i$, $b_i$, $c_i\ (i = 1, 2)$ are positive constants, and represent the intrinsic growth rates, the intra-specific competitive rates and the inter-specific competitive rates, respectively. The term $c_1y/(1+y)$ (or $c_2x/(1+x)$) is an increasing function with respect to $y$ (or $x$) and has a saturation value for large enough $y$ (or $x$).

There are many related ecology and investigations of system (1.1). Especially, for system (1.1) without delays, Wang and Liu ^[15] analyzed the existence and global stability of almost periodic solutions of system, Li et al. ^[16] investigated the stability and Turing pattern of system with self- and cross-diffusion effect, Hu and Liu ^[17] took two coupling noise sources into account and obtained the sufficient conditions for survival results of system. On the other hand, for system (1.1) with discrete delays, Chen and Ho ^[18] discussed the persistence and global stability of system, Liu et al.^[19] studied the existence of positive periodic solutions of system with impulsive perturbations. Obviously, it can be seen from the above literatures that they did not consider system with distributed delays. To reveal the effect of distributed delays we propose system (1.1).

Denote

By applying the linear chain technique, system (1.1) transforms into the following equivalent four-dimensional system

Due to environmental noise, the birth rate and other parameters involved in a system can reflect random fluctuation to some extent^[20,21,22]. Some researches indicate that random interference cannot be ignored for competitive ecological models ^[23,24,25]. In addition, many researchers also introduced higher order perturbations into the system when the random perturbations may depend on the population's density^[26,27]. Therefore, in this paper, similarly to ^[17,28] we further incorporate two noise sources in the system (1.3), that is, one noise source not only has influence on the intrinsic growth rate of one species but also on that of the other species. Strongly inspired by the above arguments, we assume that the white noises affect $r_i (i = 1, 2)$ mainly according to

and obtain the following stochastic system which corresponds to the deterministic system (1.3)

Here, for convenience' sake, let $x = x(t)$, $y = y(t)$, $u = u(t)$, $v = v(t)$, and $dB_i = dB_i(t)(i = 1, 2)$. $B_i$ are the independent standard Brownian motions defined on the complete probability space $(\Omega, \mathcal{F}, \mathbb{P})$ with a filtration $\{\mathcal{F}\}_{t\geq0}$ satisfying the usual conditions, that is $B_i$ are normally distributed with mean $0$ and variance $t$ (see ^[29]), and $\sigma_{ij}^2(i, j = 1, 2)$ denote the intensities of the white noises.

The rest of this paper is arranged as follows. Section 2 focuses on exploring the unique global positive solution to system (1.5). Sufficient conditions for extinction of the species and the existence of a stationary distribution of the positive solutions to system (1.5) are obtained in section 3 and section 4, respectively. In section 5, several examples are demonstrated to verify our results and a brief discussion is given.

2.   Global positive solution

Assign

Theorem 2.1. For any given initial value $(x(0), y(0), u(0), v(0))\in \mathbb{R}_+^4$, system $(1.5)$ has a unique global positive solution for any $t\geq0$.

Proof. Obviously, for any initial value $(x(0), y(0), u(0), v(0))\in \mathbb{R}_+^4$, there is a unique local solution $(x(t), y(t), u(t), v(t))\in\mathbb{R}_+^4$ on $t\in [0, \tau_\varrho)$, where $\tau_\varrho$ denotes the explosion time. To complete the proof, we only need to show that $\tau_\varrho = +\infty$ a.s. Similarly to ^[29], we construct a nonnegative $C^2$–function $V: \mathbb{R}_+^4\rightarrow \mathbb{R}_+$ satisfying

where $O_n = (\frac{1}{n}, n)\times (\frac{1}{n}, n)\times(\frac{1}{n}, n)\times(\frac{1}{n}, n)$ and $n > 1$ is a sufficiently large integer and $K$ is a positive constant. Let $0 < p < 1$, we assign

Since $-\ln z\rightarrow+\infty\ {\rm as}\ z\rightarrow0, \ {\rm and}\ \frac{z^p}{p}-\ln z\rightarrow+\infty\ {\rm as}\ z\rightarrow+\infty, \ {\rm where}\ p > 0$, we can obtain that $\liminf_{n\rightarrow+\infty, (x, y, u, v)\in\mathbb{R}_+^4\backslash O_n}V(x, y, u, v) = +\infty$. In the following, we will verify that $LV(x, y, u, v)\leq K$. An application of Itô's formula shows that

where

The rest proof is similar to Theorem 2.1 in ^[30] and hence we omit it here.

3.   Extinction

Theorem 3.1. If $r_1 < \frac{1}{2}(\sigma_{11}^2+\sigma_{12}^2)$, $r_2 < \frac{1}{2}(\sigma_{21}^2+\sigma_{22}^2)$, then both $x(t)$ and $y(t)$ will be extinct exponentially.

Proof. Using Itô's formula in the first equation of system (1.5), one can show that

Integrating from $0$ to $t$ and dividing by $t$ on both sides of the above equality lead to

Denote $Z_i(t) = \sigma_{1i}\int_0^tx(s)dB_i(s)$, so that its quadratic variation is

Using the exponential martingale inequality and the Borel-Cantell lemma, similar to ^[27,31], we have that for almost all $\omega\in \Omega$, there is a random integer $l_0 = l_0(\omega)$ such that for $l\geq l_0$,

For all $0\leq l-1\leq t\leq l$, $l\geq l_0$, substituting (3.3) to (3.2), we have

The strong law of local martingales implies that

Taking the superior limit on both sides we get

Similarly, one can obtain that

The proof is completed.

4.   Existence of stationary distribution

Consider the integral equation

where $\sigma_r(s, X(s))$ and $B_\xi(s)$ are vectors.

Lemma 4.1. ^[32] Suppose that the coefficients of $(4.1)$ are independent of $t$ and satisfy the following conditions for some constant $N$

in $O_R\subset \mathbb{R}_+^d$ for every $R > 0$ and there exists a nonnegative $C^2-$function $W(x)$ in $\mathbb{R}_+^d$ such that $LW(x)\leq -1$ outside some compact set. Then the system (4.1) exists a solution which is a stationary distribution.

Remark 4.1. The condition (4.2) in Lemma 4.1 can be replaced by the global existence of the solution of (4.1) in view of Remark 5 in Xu ^[33].

Assign

Theorem 4.1. If $\beta_i > 0 (i = 1, 2)$, then there exists a positive solution $(x(t), y(t), u(t), v(t))$ of the system $(1.5)$ which is a stationary Markov process.

Proof. Since we have obtained the existence of the global positive solution of system (1.5) in Theorem 2.1, from Remark 4.1, we only need to consider a nonnegative $C^2-$function $W(x, y, u, v)$ and a closed set $O\subset \mathbb{R}_+^4$ satisfying

One derives from system (1.5), by Itô's formula, that

and for the constant $0 < p < 1$, we have

Define

where $M_i = \frac{2}{\beta_i}\max\{2, J_i\}$, $J_i\ (i = 1, 2)$ are positive constants which will be determined later. Since $\widetilde{W}(x, y, u, v)$ is a continuous function, there exists a minimum point $(\hat{x}, \hat{y}, \hat{u}, \hat{v})$ in the interior of $\mathbb{R}_+^4$. Then we can choose the following $C^2$–function $W:\mathbb{R}_+^4\rightarrow \mathbb{R}_+\cup\{0\}$

which, together with (4.4)–(4.5), leads to

Let $\epsilon > 0$ be sufficiently small such that

Define the bounded closed set

Assign

Case 1. When $(x, y, u, v)\in O_1^\epsilon$, it follows from (4.8) that

where

Since $M_1 = \frac{2}{\beta_1}\max\{2, J_1\}$, one can see that $\frac{M_1\beta_1}{4}\geq 1$. Then we have from (4.9) that

Similarly, for any $(x, y, u, v)\in O_3^\epsilon$,

where

Since $M_2 = \frac{2}{\beta_2}\max\{2, J_2\}$, we have $\frac{M_2\beta_2}{4}\geq 1$. It follows from (4.9) that

Recalling (4.8), we can calculate that

where

Case 2. When $(x, y, u, v)\in O_2^\epsilon$, by (4.9) we can derive that

Similar, if $(x, y, u, v)\in O_4^\epsilon$, then we have

Case 3. When $(x, y, u, v)\in O_5^\epsilon$ or $(x, y, u, v)\in O_7^\epsilon$, we have from (4.9) that

Case 4. When $(x, y, u, v)\in O_6^\epsilon$ or $(x, y, u, v)\in O_8^\epsilon$, it follows from (4.9) that

The above analysis shows that there is a closed set $O^\epsilon$ defined by (4.10) such that

The proof is completed.

5.   Numerical simulations and discussions

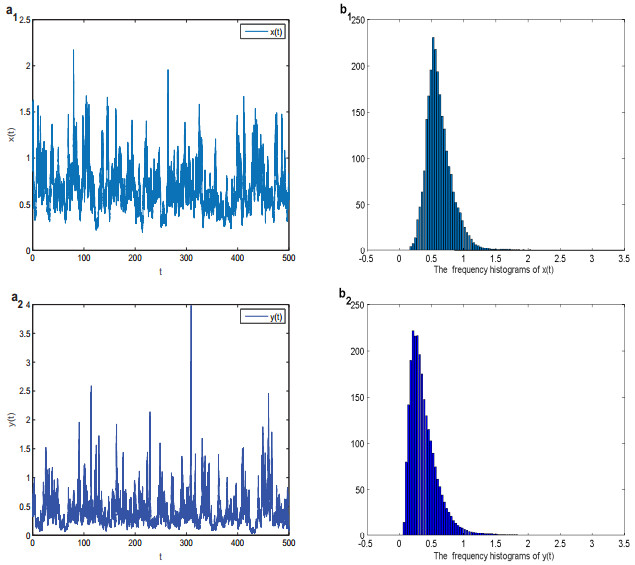
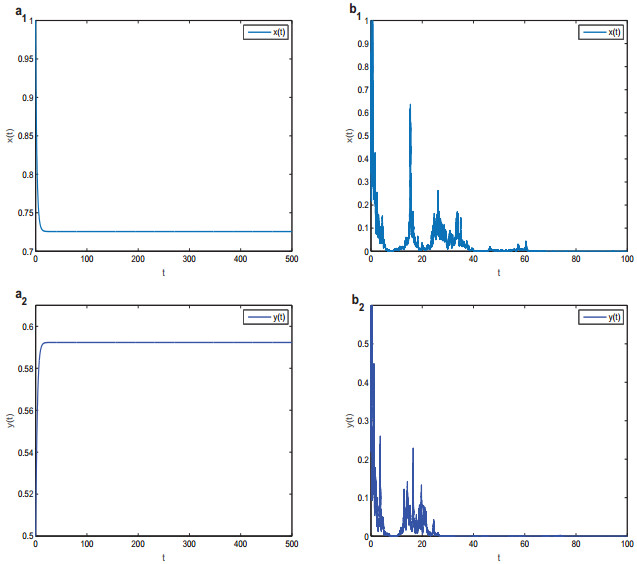
To illustrate our theoretical results, we will perform several specific numerical simulations. We first fix $r_1 = 0.4$, $r_2 = 0.6$, $b_1 = 0.5$, $b_2 = 0.8$, $c_1 = 0.1$, $c_2 = 0.3$, $\alpha_1 = 0.1$, $\alpha_2 = 0.2$. Let $\sigma_{11} = \sigma_{12} = \sigma_{21} = \sigma_{22}\equiv 0$, and we find that both of two species are persistent (see Figure 1(a$_1$)–(a$_2$)). However, if $\sigma_{11} = 0.9$, $\sigma_{12} = 0.5$, $\sigma_{21} = 1$, $\sigma_{22} = 0.8$, then we have from Theorem 3.1 that $x(t)$ and $y(t)$ will be extinct exponentially (see Figure 1(b$_1$)–(b$_2$)). When we choose $\sigma_{11} = 0.1$, $\sigma_{12} = 0.15$, $\sigma_{21} = 0.3$, $\sigma_{22} = 0.25$, it follows from Theorem 4.1 that the system (1.5) has a stationary distribution (see Figure 2).

Our theoretical results and the above numerical examples reveal that the coupling noises can change the asymptotic properties of system (1.5).

(Ⅰ) For ecosystems, it is important to analyze the survival of species. It can be seen from Figure 1(a$_1$)–(a$_2$) that the two competing species can survive if the competitive system is not affected by environmental noise. However, two species will go to extinction if the coupling noises are suitable large (see Figrue 1(b$_1$)–(b$_2$)).

(Ⅱ) To analyze the statistic characteristic of the long-term behaviors of the sample trajectories, a useful approach is to study the stationary distribution. Figure 2 implies that the relatively small coupling noises can ensure the existence of a stationary distribution.

Acknowledgments

The authors thank the editor and referees for their careful reading and valuable comments. The work is supported by the National Natural Science Foundation of China (Nos.11871201, 11961023), and Natural Science Foundation of Hubei Province, China (No.2019CFB241).

Conflict of interest

The authors declare there is no conflict of interest.