In this paper, we propose a predator-prey model with genetic differentiation both in the predator and prey. First, we analyze two special cases: a model without the predators and a model with one genotype in both the predator and prey, and for each model show that the positive equilibria are always globally stable when they exist, while the boundary equilibria are always unstable. Then, for the newly proposed model, we give the results that the positive equilibrium is always local stable when it exists, the boundary equilibrium at the origin is always unstable, and the stability of another boundary equilibrium is determined by the existence of the positive equilibrium. Moreover, our discussions show the existence of local center manifolds near the equilibria. Finally, we give some examples to illustrate our results.
1.
Introduction
Since Lotka and Volterra [1,2] proposed the classical Lotka-Volterra predator-prey model, it has received much attention in studying the relationships between the predator and prey [3,4,5,6,7]. In the meaning of biology, the population cannot grow unrestrictedly. However, the prey grows infinitely in the absence of the predator for the original Lotka-Volterra predator-prey model. To correct this unrealistic defect, the modified Lotka-Volterra predator-prey model with the finite environment carrying capacity for prey is considered and studied (refer to May [8] for a detailed model construction), which is in the form
where R and K are the per capita growth rate and the carrying capacity of the prey x, h and d are the hunting ability and the death rate of the predator y, respectively. As part of the subsystem of the proposed model in this article, more specific analysis and results for model (1.1) will be given in Section 3.
Recently, Mobilia et al. [9] expanded Lotka-Volterra predator-prey model and studied the effects of the spatial constraints and stochastic noise on the properties of the predator-prey systems. Considering the spatial constraints and stochastic noise, Mobilia et al. [9] formulated a predator-prey model similar to model (1.1), and a stochastic lattice Lotka-Volterra model (SLLVM). They obtained a lot of important and interesting results differing from those of the classical (unrestricted) deterministic Lotka-Volterra predator-prey model by a suitable mean-field approach, field-theoretic arguments and Monte Carlo simulations. In the topical review [10], from the historical overview of population dynamics to the stochastic lattice Lotka-Volterra predator-prey models, Dobramysl et al. focused on spatially extended population dynamics models and the role of fluctuations and correlations in biological systems induced by the demographic noise. Also, they demonstrated the cyclic dominance of three-species populations and multiple species competition networks. The models in the above two articles are the improvements of the Lotka-Volterra predator-prey by considering the finite carrying capacity and incorporating the stochastic noise, spatial constraints and spatial extension.
The Lotka-Volterra predator-prey models have been explored and expanded widely in the aspects of the diffusion, time delay, harvesting, switching and herd behavior [11,12,13,14,15,16,17,18,19,20,21], etc. However, considering the effect of the population interactions for different genotypes on the ecosystem is a research hotspot that has only been developed in recent years.
Taking into account the fact that the prey is genetically distinguishable and assuming that the prey is divided into two subpopulations with two different genotypes x and y, Venturino [22] proposed an ecogenetic model
where z represents the predator, R is the reproduction rate of the prey, p and q=1−p are the fractions of the newborns for the two genotypes x and y, a and b are the population pressures of the two genotypes of the prey, h and g are the predators' different hunting ability to prey on the two genotypes of food, respectively; m is the mortality rate of the predator, 0<e<1 is the conversion rates of the prey into the predator's newborns. The author showed that if the predator invasion number is greater than 1 then the predator is permanent and the model is persistent. Furthermore, model (1.2) could be persistent oscillatory under some conditions. Reference [23] also proposed an eco-genetic model with distinguishable genotypes happened in the prey. Supposed that the genetically distinguishable species are the predator with two different genotypes y and z, Viberti and Venturino [24] introduced a model
where R and K are the reproduction rate and the environment's carrying capacity of the prey x, respectively, and all other parameters have the similar meaning to those in model (1.2). Then authors investigated the extinction of the predator, the permanence of the prey and the coexistence of the two species. However, model (1.3) does not allow persistent oscillation, which is the main difference between models (1.2) and (1.3). Similar to model (1.3), Viberti and Venturino [25] proposed a predator-prey model with Holling Ⅱ response function in describing the dynamics of two different genotypes predator.
Motivated by [22,24,25], we propose a predator-prey model in which the genetic differentiation both happened in the predator and prey. The model is presented in the form as follows
where the two genotypes population x and y of the prey have the same reproduction rate R, the two genotypes population u and v of the predator have the same conversion rates 0<e<1; p1 and q1=1−p1 are the fractions of the newborns of the prey x and y respectively, p2 and q2=1−p2 are the fractions of the newborns of the predator u and v respectively, a and b are the different pressures felt by the two types of prey population, k and l are the mortality rates of u and v respectively; we also assume that the predator u has the same hunting ability to prey x and prey y, which is denoted by m; Similarly, the hunting ability of predator v to prey x and prey y is denoted by n. All coefficients in model (1.4) are positive. Assuming that both the two types of predators have different hunting abilities to the two types of the prey, Castellino et al. [26] gave a more general predator-prey model with both species genetically distinguishable. However, they only roughly analyzed the stability of the boundary equilibria and showed some results by numerical simulations. In this paper, we shall give a detailed analysis of the model (1.4).
In order to simplify calculations, we first nondimensionalize model (1.4) by letting t=eτ, x(τ)=αX(t), y(τ)=αY(t), u(τ)=γU(t), v(τ)=γV(t). Then it becomes
Let α=Rp1a, γ=em, and define new parameters r=Rp1e, c=nm, w=q1p1, s=ba, p=p2mRp1a, q=q2mRp1a, g=ke, d=le. Then the above model can be further simplified into
It is clear that all of models (1.2), (1.3), (1.4), and (1.5) have more than one predator or one prey, and are generalizations of Lotka-Volterra predator-prey model apparently.
Azzali et al. [27] studied a competitive model with genetically distinguishable species. In fact, model (1.4) is similar to the ecoepidemiology model, i.e., the population model with diseases spreading in the species. Earlier researches on the ecoepidemiology models can be found from [28,29], and influences of diseases on the predator-prey models and competitive models can refer to the articles [30,31,32,33,34,35,36,37,38,39,40].
The rest of this paper is organised as follows. In Sections 2 and 3, we shall analyze model (1.5) without predators and model (1.5) with one genotype in both the predator and prey, respectively. The full model of (1.5) will be discussed in Section 4. Some examples to illustrate our main results will be given in Section 5. In Section 6, we shall give our conclusions and discussions.
2.
Stability of model (1.5) without the predators
Without the predators, model (1.5) becomes
It is easy to know that (0,0) and (1,ws) are two equilibria of the model. And we can obtain the following two lemmas.
Lemma 2.1. For model (2.1), the boundary equilibrium (0,0) is unstable, and the positive equilibrium (1,ws) is locally stable.
Proof. The Jacobian matrix of (2.1) is
Then the characteristic polynomial of J1 at (0,0) is λ2−(r+wr)λ, which has two eigenvalues λ1=0, λ2=r(1+w)>0. So, the origin (0,0) is unstable.
Similarly, at (1,ws) the characteristic polynomial is (λ+r+wrs)(λ+wr+sr), resulting in two negative eigenvalues λ1=−r(1+ws), λ2=−r(s+w). Therefore, equilibrium (1,ws) is locally stable.
Lemma 2.2. Model (2.1) does not admit any periodic solution.
Proof. Let
it is easy to know that B1(X,Y) is a continuously differentiable function in the first quadrant. We get that
Then the Bendixson-Dulac criterion ([41], Proposition 1.195) implies our result here.
Then, Lemmas 2.1 and 2.2 yield the following global behavior of model (2.1).
Theorem 2.1. Positive equilibrium (1,ws) of model (2.1) is globally asymptotically stable.
Remark 2.1. In the biological sense, Theorem 2.1 means that two genotypes of the prey will always coexist without the predators. This is consistent with the Hardy-Weinberg law [42], which shows that the gene and genotype frequencies in a species will remain constant from the first daughter generation onwards.
3.
Stability of model (1.5) with one genotype in both the predator and prey
When both the predator and prey have only one genotype, model (1.5) becomes the nondimensionalization of the Lotka-Volterra predator-prey model (1.1), which is in the following form
It is easy to obtain that the model always has two boundary equilibria (0,0) and (1,0), and has a positive equilibrium (gp,r(p−g)p) if p>g. The positive equilibrium (gp,r(p−g)p) approaches to the boundary equilibrium (1,0) as p→g.
Next, by using Jacobin matrix and center manifold theory, we have Lemma 3.1 and 3.2 as shown in the following.
Lemma 3.1. For model (3.1), boundary equilibrium (0,0) is always unstable, and the other boundary equilibrium (1,0)
(a) is stable when p<g;
(b) is unstable when p>g;
(c) has a local center manifold
when p=g, where K is a small neighborhood of the origin, and
Proof. The Jacobian matrix of (3.1) is
The characteristic polynomial of matrix J2 at (0,0) is (λ−r)(λ+g), which has two eigenvalues λ1=r, λ2=−g. Therefore, equilibrium (0,0) is a saddle point.
The characteristic polynomial of matrix J2 at (1,0) is (λ+r)(λ+g−p), which has two eigenvalues λ1=−r<0, λ2=p−g. We have the following three cases.
(a) If p<g, then λ2<0, implying equilibrium (1,0) is locally stable.
(b) If p>g, then λ2>0. Thus, equilibrium (1,0) is a saddle point. Hence, unstable accordingly.
(c) If p=g, then λ2=0. By the center manifold theory [43,44], there is a local center manifold at equilibrium (1,0), which is calculated as follows. Let x1=X−1, u1=U. Model (3.1) becomes
where
Equilibrium (1,0) of model (1.5) becomes equilibrium (0,0) of (3.2). The eigenvalues of A are the same as those of matrix J2 at(1,0), which are λ1=−r, λ2=0. By the center manifold theory, equilibrium (0,0) has a one-dimensional center subspace and a one-dimensional stable subspace. The eigenvectors of A with respect to λ1 and λ2 are
respectively. Let P=(e1,e2), then P−1AP=B, where B=diag(λ1,λ2). Therefore, Let
then
The local center manifold at (0,0) is described by an approximation function ψ:span{e2}→span{e1}. Since ψ(0)=Dψ(0)=0, we set the Taylor expansion near (0,0) as
By the center manifold approximation theorem, we have
Simplifying the above equation and comparing the coefficients of the two sides, we get
Thus, the center manifold at (0,0) is
where K is a small neighborhood of the origin, and
Lemma 3.2. If p>g, then model (3.1) has a stable positive equilibrium (gp,r(p−g)p).
Proof. From the above discussion, the positive equilibrium (gp,r(p−g)p) exists if and only if p>g. For model (3.1), the characteristic polynomial of Jacobian matrix at (gp,r(p−g)p) is f(λ)=λ2+θ1λ+σ1, where θ1=rgp, σ1=rgp−gp. It is clear that σ1>0. Let Δ1=θ21−4σ1, then Δ1<θ21. The roots of f(λ) are λ1,2=−θ1±√Δ12. Then, we only need to discuss the real parts of λ1,2.
1. If Δ1≥0, then both λ1,2 are negative, and positive equilibrium (gp,r(p−g)p) is stable accordingly.
2. If Δ1<0, then λ1,2 are two conjugate complex numbers with negative real part, and positive equilibrium (gp,r(p−g)p) is stable accordingly.
Above discussion indicates the local behavior of equilibria in model (3.1), next we illustrate the global dynamical behaviors of these equilibria. First, we need to discuss the existence of periodic solution in model (3.1).
Lemma 3.3. For model (3.1), there is no periodic solution.
Proof. Let
It is easy to know that B2(X,U) is a continuous differentiable function in the first quadrant. Then, in the first quadrant
By the Bendixson-Dulac criterion, model (3.1) has no periodic solution.
From Lemmas 3.1, 3.2 and 3.3, we know the global behavior of model (3.1).
Theorem 3.1. For model (3.1), boundary equilibrium (0,0) is always unstable, and
(a) if p>g, then boundary equilibrium (1,0) is unstable and positive equilibrium (gp,r(p−g)p) is globally asymptotically stable;
(b) if p<g, then boundary equilibrium (1,0) is globally asymptotically stable and there is no positive equilibrium.
From Theorem 3.1, we know that if the death rate of predator is bigger than its conversion rate, then the predator will be extinct while the prey will be permanent; if the death rate of predators is smaller than the conversion rate, then the predator and the prey will coexist permanently.
4.
The dynamics of model (1.5)
4.1. Existence of the equilibria
It is easy to find that the origin E0(0,0,0,0) and E1(1,ws,0,0) are two boundary equilibria of model (1.5). If
has a positive solution, then it is the positive equilibrium of model (1.5). Let (X∗,Y∗,U∗,V∗) is a solution of Eq (4.1), then
where h=gdpd+cqg.
If 0<X∗<1, 0<Y∗<ws, U∗>0, V∗>0, then (X∗,Y∗,U∗,V∗) is a positive solution of (4.1), which means it is the positive equilibrium of model (1.5).
From the first two equations of (4.2), we get
Let Δ2=[w+1−(1−s)h]2+4wh(1−s), then Δ2=[w−1+(1−s)h]2+4w>0. Let
then f(ws)>0 if h<1+ws, and f(ws)≤0 if h≥1+ws.
Next, we shall prove that h<1+ws is the necessary and sufficient condition for the existence of positive equilibrium of model (1.5). First, we shall prove that if h<1+ws then 0<X∗<1, 0<Y∗<ws, U∗>0, V∗>0, and model (1.5) has a positive equilibrium E∗(X∗,Y∗,U∗,V∗) accordingly. Three cases are considered.
Case 1. When s=1, we get Y∗=whw+1 from (4.3). So, by (4.2),
If h<1+w, then 0<X∗<1, 0<Y∗=whw+1<w1+w(1+w)=w, U∗>0, V∗>0.
Case 2. When s<1, i.e., 1−s>0, it is easy to find that the parabola f(Y) is opening up and the curve intersects vertical axis at point (0,−wh). Thus, (4.3) has one positive root
By (4.2) and the above equation, we get
If h<1+ws, then f(ws)>0. From the image of parabola f(Y), we know that f(Y∗)=0 and f(Y)<0 as Y∈(0,Y∗). So 0<Y∗<ws. By the first equation of (4.2), we have 0<X∗<1. Accordingly, U∗>0 and V∗>0.
Case 3. When s>1, i.e., 1−s<0, the parabola f(Y) is opening down and the curve intersects vertical axis at point (0,−wh). Since 1−s<0 and w+1−(1−s)h>0, we know the center shaft of the parabola is positive. So, f(Y) has two positive roots
which means
from Eq (4.2). By f(ws)>0 as h<1+ws, f(Y)>0 as Y∈(Y∗1,Y∗2) and f(Y)<0 as Y∉[Y∗1,Y∗2], we get that ws∈(Y∗1,Y∗2), which means 0<Y∗1<ws<Y∗2. The same reason as that of Case 2 gives 0<X∗1<1. Accordingly, U∗1>0, V∗1>0.
By the same analysis as the above three cases, we have that if h≥1+ws then Y∗≥ws for Case 1 and 2, and both Y∗2>Y∗1>ws for Case 3. From the second equation of (4.1), we know that Eqs (4.1) have no positive solutions. Therefore, model (1.5) has no positive equilibria.
From the above discussion, we get the following results.
Theorem 4.1. Model (1.5) always has two boundary equilibria E0(0,0,0,0) and E1(1,ws,0,0). Furthermore, h<1+ws is the necessary and sufficient condition for the existence of an unique positive equilibrium E∗(X∗,Y∗,U∗,V∗) of model (1.5), where 0<X∗<1, 0<Y∗<ws, U∗>0 and V∗>0.
4.2. Stability of the boundary equilibria
The Jacobian matrix of model (1.5) at E0 is
The characteristic polynomial of J(E0) is λ(λ−r−wr)(λ+g)(λ+d), which has four eigenvalues λ1=0, λ2=r+rw, λ3=−g and λ4=−d. Since λ2>0, E0 is unstable.
Theorem 4.2. The boundary equilibrium E0 of (1.5) is unstable.
The Jacobian matrix of model (1.5) at E1 is
The characteristic polynomial of J(E1) is
J(E1) has two negative eigenvalues λ1=−r−rws and λ2=−rw−rs. The other two eigenvalues of J(E1) are the roots of polynomial f1(λ)=λ2−θλ+σ, where
The two roots of f1(λ) are
Let Δ3=θ2−4σ, then
It is easy to find that
so,
Now, we discuss the stability of E1 from three cases.
Case 1. If h>1+ws, then
By (4.6) and σ>0, we have θ<0 and Δ3=θ2−4σ<θ2, respectively. Therefore, both λ3,4 have negative real parts, E1 is stable accordingly.
Case 2. If h<1+ws, then
and Δ3=θ2−4σ>θ2 accordingly. For any θ, (4.5) shows that one of λ3,4 is negative and the other is positive. Therefore, E1 is unstable.
Case 3. If h=1+ws, then
So, Δ3=θ2−4σ=θ2. Because (4.6) means θ<0, (4.5) shows that one of λ3,4 is θ and the other is 0. Thus, the Jacobian matrix J(E1) has one zero eigenvalue and three negative eigenvalues. By the center manifold theory, there exist a one-dimensional center manifold and a three-dimensional stable subspace at E1.
From the above discussion, we get the following results.
Theorem 4.3. Equilibrium E1 of model (1.5) is stable if h>1+ws, and unstable if h<1+ws.
By Theorems 4.2 and 4.3, we know that if h>1+ws then model (1.5) has no positive equilibrium and E1 is stable. Since the axes are invariant sets of model (1.5), boundary equilibrium E1 is globally stable when h>1+ws.
Theorem 4.4. If h>1+ws, then the boundary equilibrium E1 is globally stable.
Theorem 4.5 gives a local center manifold at E1 for Case 3 of the above discussion.
Theorem 4.5. For boundary equilibrium E1, if h=1+ws, then there is a local center manifold
where K1 is a small neighborhood of the origin,
and
with
Proof. First, we take a matrix transformation. Let x1=X−1, y1=Y−ws, u1=U and v1=V, then model (1.5) becomes
where
The eigenvalues of J(E1) are λ1=−r(1+ws), λ2=−rs(1+ws), λ3=θ, λ4=0. By the center manifold theory, (0,0,0,0) has a one-dimensional center subspace and a three-dimensional stable subspace. The eigenvectors of J(E1) with respect to λ1, λ2, λ3 and λ4 are
respectively, where
Let P=(e1,e2,e3,e4), then P−1J(E1)P=B, where B=diag(λ1,λ2,λ3,λ4). Let
then,
where
and
with
The local center manifold is described by a approximation function η:span{e4}→span{e1,e2,e3}, which we set
Since η(0)=Dη(0)=0, the Taylor expansion at the origin is
By the center manifold approximation theory, we have
Simplifying the above equations and comparing the coefficients of the the same order terms in both sides, we get
Thus, we get the center manifold as follow
where K1 is a small neighborhood of the origin, and
4.3. Stability of the positive equilibrium
In this section, we consider the stability of E∗.
Theorem 4.6. If h<1+ws, then the unique positive equilibrium E∗ of model (1.5) is stable.
Proof. The Jacobian matrix of model (1.5) at E∗ is
Let j=cqg2+pd2pd+cqg, the characteristic polynomial of J∗ is
where
a3=r(s+1)(X∗+Y∗)+(U∗+cV∗)+j,
a2=r2s(X∗+Y∗)2+r2(X∗+Y∗)[s(w−sY∗)+(1−X∗)]+(d+g)(U∗+cV∗)+r(s+1)j(X∗+Y∗),
a1=r(p+cq)(sX∗+Y∗)(X∗+Y∗)(U+cV∗)+r2(X∗+Y∗)j[s(w−sY∗+(1−X∗))]+gd(U+cV∗)+(p+cq)(X∗+Y∗)(U+cV∗)2+r2sj(X∗+Y∗)2,
a0=gd[(U+cV∗)+r(sX∗+Y∗)](U∗+cV∗).
For 0<X∗<1, 0<Y∗<ws, we know a3>0, a2>0, a1>0 and a0>0. According to the Routh-Hurwitz stability criterion, if
also holds, then positive equilibrium E∗ is stable.
Next, we prove that (4.8) is satisfied. Let g(r)=a2a3−a1. Substituting the values of U∗ and V∗ into g(r), we get that g(r)=b2r3+b1r2+b0r, where
b2=(X∗+Y∗)(sX∗+Y∗+w+1)[s(w−sY∗)+(1−X∗)+s(X∗+Y∗)],
b1=(s+1)2(X∗+Y∗)2j+(w−sY∗+1−X∗)(2sX∗+2Y∗+1+w)j,
b0=(s+1)(X∗+Y∗)j2+(w−sY∗+1−X∗)[(d+g)j−dg].
From (4.2), we know that X∗ and Y∗ do not depend on r, and b2>0, b1>0. Since
we have b0>0. So, g(r)>0, i.e., (4.8) holds. Therefore, (4.8) and Theorem 4.1 mean that E∗ is stable.
Remark 4.1. Theorem 4.1 and 4.6 mean h<1+ws is the necessary and sufficient condition for the existence and stability of the unique positive equilibrium E∗ of model (1.5).
Remark 4.2. By Theorems 4.1, 4.3 and 4.6, we know that if h>1+ws then model (1.5) has no positive equilibrium and E1 is stable, and if h<1+ws then the unique positive equilibrium of model (1.5) is stable and E1 is unstable. Therefore, there is a transcritical bifurcation in model (1.5).
5.
Examples
In this section, some examples are given to illustrate our main results. Furthermore, we get some strategies for species protection by insight into the examples.
From the discussion in Section 4, we know that the boundary equilibrium E1 is stable when h>1+ws, and the positive equilibrium E∗ appears and becomes stable when h<1+ws. In order to testify our analyzed results, we take some examples by simulation. For convenience, fix
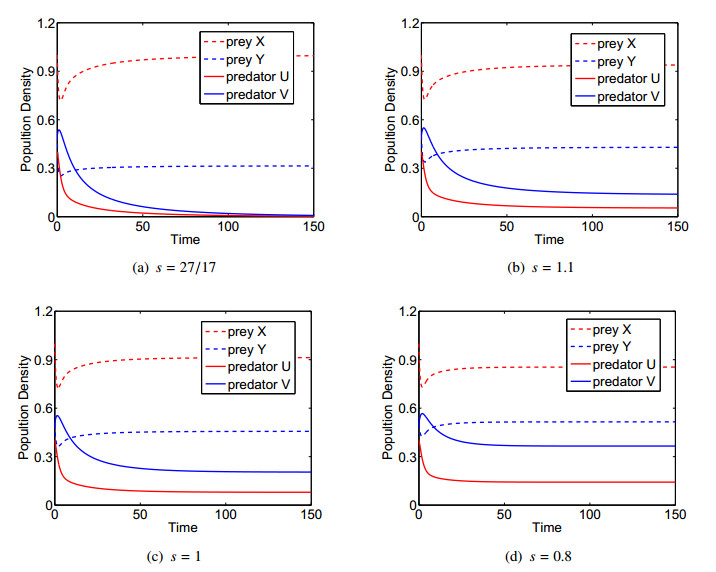
and the initial condition (0.3,0.5,0.4,0.8). Next, we observe the time series diagrams of the four populations with four different values of s (see Figure 1). In this figure, the red dotted line represents the size of prey X, the blue dotted line represents the size of prey Y, the red solid line represents the size of predator U, the blue solid line represents the size of predator V.
In Figure 1(a), we choose s=27/17 which satisfies the equality h>1+ws. According to Theorem 4.3 and Remark 4.1, in this case the boundary equilibrium E1(1,1754,0,0) is stable while the positive equilibrium doesn't exist. In the figure, the size of two prey populations X and Y approach to 1 and 0.31≈1754 respectively as the time increases, while the two predator populations U and V both tend to zero. This shows that E1 is stable, which verify our results.
In Figure 1(b), we choose s=1.1 which satisfies the equality h<1+ws. According to Theorem 4.3 and Remark 4.1, in this case the boundary equilibrium E1(1,511,0,0) is unstable while the positive equilibrium E∗(0.96,0.41,0.04,0.09) is stable. In the figure, the size of two prey populations X and Y approach to 0.96 and 0.41, and the two predator populations U and V both tend to 0.04 and 0.09 respectively as the time increases. This shows that E∗ is stable, which verify our results.
In Figure 1(c), we choose s=1 which satisfies the equality h<1+ws. According to Theorem 4.3 and Remark 4.1, in this case the boundary equilibrium E1(1,12,0,0) is unstable while the positive equilibrium E∗(0.91,0.46,0.08,0.20) is stable. In the figure, the size of two prey populations X and Y approach to 0.91 and 0.46, and the two predator populations U and V both tend to 0.08 and 0.20 respectively as the time increases. This verifies our results.
In Figure 1(d), we choose s=0.8 which satisfies the equality h<1+ws. According to Theorem 4.3 and Remark 4.1, in this case the boundary equilibrium E1(1,58,0,0) is unstable while the positive equilibrium E∗(0.86,0.51,0.14,0.35) is stable. In the figure, the size of two prey populations X and Y approach to 0.86 and 0.51, and the two predator populations U and V both tend to 0.14 and 0.35 respectively as the time increases. This verifies our results.
From the biological point of view, the decrease of s can be regarded as the decrease in the ratio of the survival pressure of population Y to the survival pressure of population X. In the process of decreasing, the population Y has more advantages in survival than population X, which leads to an increase in the population density. Conversely, the density of population X decreases due to the stronger stress in the same environment. At the same time, both the densities of predator U and V are increased. It is worth noting that, with the change of s in the above examples, the total amount of two prey populations remains unchanged, while the total density of two predator populations expands. This result gives us two implications for model (1.5): First, the balance of two prey groups can be adjusted by controlling the environmental pressure experienced by one of the prey population; Second, endangered predator populations can be saved by controlling the survival pressure of the prey population.
6.
Conclusions and discussions
In this paper, a predator-prey model with genetic differentiation both happened in the predator and prey is studied, and some interesting results are obtained.
For model (1.5) without the predators, by the qualitative analysis and the Bendixson-Dulac criterion, we get that the boundary equilibrium (0,0) is unstable, and the positive equilibrium (1,ws) is global asymptotical stability. These indicate that the two genotypes of the prey will be permanent.
Model (1.5) with one genotype of the predator and prey has two boundary equilibria (0,0) and (1,0), and a positive equilibrium (gp,r(p−g)p) when p>g. The boundary equilibrium (0,0) is always unstable. The boundary equilibrium (1,0) is stable when p<g, unstable when p>g, and there is a stable local center manifold at (1,0) when p=g. The positive equilibrium (gp,r(p−g)p) is always stable if it exists. We also show that there is no periodic solution in the model by using Bendixson-Dulac criterion. Therefore, the global dynamics of the model is clear as follows: boundary equilibrium (1,0) is globally stable when p<g, positive equilibrium (gp,r(p−g)p) is globally stable when p>g, and there is a transcritical bifurcation in the model when p=g.
Model (1.5) has two boundary equilibria E0(0,0,0,0), E1(1,ws,0,0), and a positive equilibrium E∗ if and only if h<1+ws. The boundary equilibrium E0 is always unstable. Another boundary equilibrium E1 is stable when h>1+ws, unstable when h<1+ws, and there is a stable local center manifold at (1,0) when h=1+ws. The positive equilibrium E∗ is stable if it exists. Furthermore, there is a transcritical bifurcation in the model when h=1+ws.
If h>1+ws, then model (1.5) has no positive equilibrium, an unstable E0 and a stable E1. Since the axes are invariant with respect to model (1.5), boundary equilibrium E1 is globally stable when h>1+ws. This means that the prey will be permanent and the predators will be extinct, which is similar to the principle of competitive exclusion for two competitive species [45]. However, if h<1+ws then model (1.5) has a local positive equilibrium and two unstable boundary equilibria. The global stability of the positive equilibrium needs to be further analyzed.
Acknowledgments
The authors would like to thank the referees for their valuable comments and helpful suggestions.
The research was supported by the Visiting Scholar Program of Ludong University. The corresponding author would like to thank Department of Mathematics and Statistics at Memorial University of Newfoundland for kindly hosting during his visiting.
Conflict of interest
The authors declare that they have no conflict of interest.









 DownLoad:
DownLoad:


