A novel group decision making method for airport operational risk management

1.   Introduction

As one of the four sub-systems in the civil aviation, the operational risk of an airport directly affects the security level of civil aviation. The existing work of airport operation safety majorly focuses the analysis of cause and the prevention of aviation accidents, which pays a very weak role in improving the safety level of civil aviation. If the risk factors can be analyzed and evaluated in advance, the relevant departments can take a series of measures in time to reduce the risk level of the airport operation. Therefore, it is of great significance to conduct a scientific and reasonable risk assessment of the airport operation, in order to improve the security level of civil aviation ^[1,2,3].

Actually, many uncertain factors, such as weather and traffic control, affect the safety of civil aviation operation. They can be quantified by using the stochastic, fuzzy, gray and language etc. Each has its own advantages and disadvantages. Compared with other uncertain techniques, fuzzy sets can be used to describe their uncertainty more accurately based on expert experience, in the absence of statistical data. The concept of fuzzy sets was introduced by Zadeh and later Atanassov generalized this idea to intuitionistic fuzzy sets ^[4]. Intuitionistic fuzzy sets with the membership, non-membership, and hesitation function is a powerful tool to deal with vagueness in many areas of engineering ^[5,6]. Hence, intuitionistic fuzzy sets would be used to characterize uncertain factors of civil aviation operation risk.

Besides, these intuitionistic fuzzy values may contain some certain (i.e., membership function) and uncertain information (i.e., non-membership function), where hesitation function depending on the attitude of the decision maker, aims at adjusting degree of uncertainty. Obviously, both certainty and uncertainty of different indicators play a role in the risk evaluation of the airport operation. Hence, it's very important for transit authorities to investigate how the interaction between them affects the evaluation results. Set pair analysis was firstly introduced by Zhao ^[7], which was used to solve such problem well. However, related studies are rare ^[8,9].

Another contribution of this study was to present a group decision making model to reveal how does the perception bias of different decision makers on the same scheme affects the risk ranking of civil aviation operation ^[10,11]. Because each decision maker is very different from each other, the results of this method are more accurate, comprehensive, objective, and scientific, compared with the traditional evaluation method of single decision maker ^[12,13,14].

The main work of this study was to extend the research of the intuitionistic fuzzy group decision making model by integrating set pair analysis to reveal how the change between the certainty and uncertainty affects the evaluation results. The research focused on the following critical research tasks: (1) Building a multi-criteria evaluation indicator, with an integration of human, equipment, management and environment levels in the framework; (2) Designing a novel uncertain group decision making model, integrating intuitionistic fuzzy set and set pair analysis. The model was applied to a real-world case which aims to evaluate the operation risk ranking of several Chinese airports. Sensitivity analyses were also performed to investigate the impact of degree of uncertainty on the model performance.

The remainder of the manuscript is organized as follows. Section 2 summarizes the status and deficiency of the current research. Section 3 describes the evaluation framework for airport operation risk. Section 4 provides a numerical experiment and analysis of the sensitivity. Finally, Section 5 discusses the results and possible future work.

2.   Review of literature

In recent years, more and more attention has been paid to handle the problems of risk assessment of the airport operation, due to the development of the Chinese aviation industry and the increasing pressure of security airport operation. These literature about this risk assessment can be categorized into two major classes, namely the methods based on safe indicators, and mathematical models and methodologies for safe evaluation.

The methods based on safe indicators normally consider the four groups indicators related to human, equipment, management and environment. Heinrich's accident causation theory suggested that human factors leads to the occurrence of an accident. Shi and Luo ^[15] used the complex scientific theory to construct the human safety risk evaluation index system of the airport flight zone. Jin et al. ^[16] further studied the human factors and classification system to analyze the unsafe events that occurred in the airport operational field. Chang et al. ^[17] also applied a Shello model to categorize the human risk factors associated with pilots in runway incursions. Netjasov and Janic ^[1] presented a safety assessment model to reveal optimal relation between causal for aircraft and air traffic control/management operations, collision risk, human factor error and third-party risk. Hofer and Wetter ^[18] developed a new airport security technology by taking into human factor issues as well as different operational aspects into account. Li et al. ^[19] analyzed the different utilization modes of the lateral runway and adjacent parallel runway to evaluate their green efficiency. Mostafaee et al. ^[20] investigated the effect of airport noise on the employees of Ground Safety department at Mehrabad airport to evaluate the Sound Pressure Level (SPL). Luo and Chen ^[21] applied AHP and fuzzy comprehensive evaluation method to obtain the risk level under the condition of RNP technology operation into Nyingchi airport from the four aspects of human risk factor, equipment risk factor, environment risk factor and management risk factor. Although the previous research has been of great help in reducing the risk level of accidents involving people, it is still confined to the study of individual factors. These indicators were divided into three levels including incident level, the other occurrence level and process monitoring level ^{[1,2,15,16,17,18,19,20,21]}.

In terms of evaluation methodologies, the multi-criteria ranking methods are generally used for performance analysis and evaluation. The premise of above-mentioned risk assessment of the airport operation is an assumption of deterministic data environment, which can be accurately obtained through big data analysis or manual investigation. Sun et al. ^[22] introduced the Bow-tie risk technology, through recognition and the appraisal of risk, the analysis of risk factor, the establishment of risk barrier, adopting the risk control and mitigation, and restoring the measure. Liu et al. ^[23] built a risk entropy model and synthetically computed the weights for evaluation indexes by using the analytic hierarchy process (AHP) method and the entropy-weight method. Rezaee and Yousefi ^[24] analyzed the causality of airport risk and proposed a new decision-making method for optimizing the airport risk by using the cognitive map and data envelopment method. Wong et al. ^[25] presented an approach which was not only taking into account risk factors previously ignored by standard risk assessments but also considering the operational and traffic characteristics of the runway concerned.

However, above-mentioned data driven models so far consider deterministic information. On the one hand, the values of indicators are also changing dynamically due to environmental changes, which lead to random evaluation based on statistical characteristics of indicators is more practical in real world. In this case, Nie al et. ^[26] considered the separate grouping of every class of passengers to minimize overall false alarm probability and maintain the overall false clear probability within specifications set by a security authority. On the other hand, when data is missing, fuzzy or grey evaluation is a feasible method and technique. Hadjimichael ^[27] analyzed a risk modeling methodology which represents the risk factors and their interrelationships in a fuzzy expert system. Qin and Luo ^[28] used the catas-trophe theory and fuzzy set to assess the safety risk of the airport flight area. Hofer et al. ^[18] and Tang et al. ^[29] tried to use grey cluster theory to evaluate airport runway incursion's human risk.

By summarizing and summarizing the existing research work, following critical issues deserve further investigations:

1) Although some of the studies focus on the risk evaluation of airport operation, few of them consider the uncertainties of the indicators in the evaluation model ^{[1,2,15,16,17,18,19,20,21]}. Especially, the existing studies have neglected how the interaction between the certainty and uncertainty of the thing itself affects the evaluation results. In the absence of complete data ^{[4,5,6,7,8,9]}, a combination of intuitionistic fuzziness and set-pair analysis is a widely used mathematical theory that deals with the determination and uncertainty of the system, which deserves a further extension and enhancement of existing mathematical models and methodologies to avoid insufficient for airport risk evaluation.

2) Although a few literatures have studied the group decision evaluation model of airport operation risk assessment ^[12,13,14], the existing studies ignore the uncertainty in the consistency degree of any two experts on the same airport operation risk. Therefore, the uncertain group decision making base on intuitionistic fuzzy set and set pair analysis can effectively solve this problem ^[4,7].

3.   Methodology

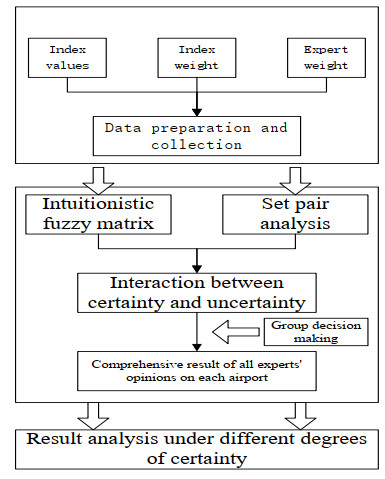
The core work of this study is to construct the index system of airport operation risk and design its evaluation model. Based on the conclusions of previous research ^[1,30,31], a multi-criteria evaluation approach, with an integration of human, equipment, management and environment levels in the framework, was demonstrated to evaluate airport operation risk. This evaluation model, integrating the intuitionistic fuzzy sets, set pair analysis and group decision making method, features in scientifically and objectively solving uncertain evaluation problem in the absence of data, with the help of expert experience knowledge. The flowchart of this methodology is graphically illustrated in Figure 1 to get an in-depth understanding of the evaluation process of related operation with input and output elements, in which: airport-related performance data collection, involving index and weight values, were mainly collected from the government and transportation agencies in first stage; the calculation process of the operation risk of each airport was implemented under interaction between certainty and uncertainty in the second stage; result analysis was implemented in third stage to obtain stable airport risk ranking in different situations and the reasons for the changes in the rankings among different airports.

Figure 1.  Methodological framework.

DownLoad: Full-Size Img PowerPoint

3.1.   Evaluation criteria establishment of airport operation risk

To enable the interaction between the four policy levels, the integration weights were used to determine different levels of importance on various technical criteria. Each policy level had several technical levels. As shown in Table 1, the primary indicator 'Human' includes professional quality, work error rate, staff and post matching degree, and awareness of executive responsibility; the indicator 'Equipment' includes the equipment reliability, maintenance level, degree of configuration integrity and degree of automation; the 'Management' indicator includes the risk control capability, operation monitoring level, personnel training level, and integrity of risk management plan; and the 'Environment' includes the traffic demand handling capacity, the ability to deal with weather, collaborative atmosphere, and the ability of bird/animal invasion prevention.

Table 1.  The evaluation framework of airport operation risk.

Primary Indicators	Secondary Indicators	Indicator Type
		Cost ype	Value ype
C1: Human	C-1-1: Professional quality		√
	C-1-2: Work error rate	√
	C-1-3: Staff and post matching degree		√
	C-1-4: Awareness of executive responsibility		√
C2: Equipment	C-2-1: Equipment reliability		√
	C-2-2: Maintenance level		√
	C-2-3: The degree of configuration integrity		√
	C-2-4: Degree of automation		√
C3: Management	C-3-1: Risk control capability		√
	C-3-2: Operation monitoring level		√
	C-3-3: Personnel training level		√
	C-3-4: The integrity of risk management plan		√
C4: Environment	C-4-1: Traffic demand handling capacity		√
	C-4-2: The ability to deal with weather		√
	C-4-3: Collaborative atmosphere		√
	C-4-4: The ability of Bird/animal invasion prevention		√

---

 | Show Table

DownLoad: CSV

3.2.   Intuitionistic fuzzy group decision making model for evaluating airport operation risk

It can be seen from above that airport operation risk involves many factors that affect each other, and different decision makers have their own preferences for these indicators of the same airport, which everyone ranks the airport operation risk differently. Furthermore, many of these factors are uncertain. It is very necessary to analyze the impact of their certainty and uncertainty on the result ranking. Therefore, the combination of group decision making method, intuitionistic fuzzy set and set pair analysis is one of the most effective methods to solve these problems.

3.2.1.   Basic concepts of ternary connection numbers based on intuitionistic fuzzy value

3.2.1.1.   Conversion of intuitionistic fuzzy value and ternary connection number

The intuitionist fuzzy value was first proposed by Bulgarian scholar Atanassov ^[4,5], who denoted as $F = \{ < x, {t_F}(x), {f_F}(x) > |x \in P\}$, where ${\rm{P}}$ is a non-empty set. ${t_F}(x)$ and${f_F}(x)$ are the membership degree and non-membership degree of element ${\rm{x}}$ in ${\rm{P}}$, such that the expression $0 \leqslant {t_F}(x) + {f_F}(x) \leqslant 1$ is satisfied. Let ${\pi _F}(x) = {\rm{1}} - {t_F}(x) - {f_F}(x)$ denote the hesitation of element ${\rm{x}}$ in ${\rm{P}}$, satisfying $0 \leqslant {\pi _F}(x) \leqslant 1$. Obviously, if ${\pi _F}(x) = {\rm{0}}$, $F$ would be degenerated to the traditional fuzzy number. ${\pi _F}(x)$ is the intuitive indicator of element ${\rm{x}}$ in ${\rm{P}}$.

Connection number is a structural function proposed by Zhao ^[7], which reflects the structural relations of various systems under different conditions. Let A, B and C be real numbers, and let ${\rm{u}} = {\rm{A}} + Bi + Cj$represent a ternary connection number, where $j = - 1$, $i \in [-1, 1]$. A, B and C represent the same degree, difference degree and opposition degree of the research object, respectively. By corresponding the degree of membership, the degree of non-membership and the degree of hesitation of intuitionistic fuzzy number with the degree of same degree, degree of opposition and degree of difference of the connection number, intuitionistic fuzzy number can be converted into three-dimensional connection number.

Thus, ${\rm{u}} = {\rm{A}} + Bi + Cj = {t_F}(x) + (1 - {t_F}(x) - {f_F}(x))i + {f_F}(x){\rm{j}}$;

where, ${\rm{A}} = {t_F}(x)$, ${\rm{B}} = (1 - {t_F}(x) - {f_F}(x))$, ${\rm{C}} = {f_F}(x)$.

3.2.1.2.   Operation rule of ternary connection number

Take three ternary connection numbers ${\rm{u}} = {\rm{A}} + Bi + Cj$, ${{\rm{u}}_{\rm{1}}} = {{\rm{A}}_{\rm{1}}} + {B_{\rm{1}}}i + {C_{\rm{1}}}j$ and ${{\rm{u}}_{\rm{2}}} = {{\rm{A}}_{\rm{2}}} + {B_{\rm{2}}}i + {C_{\rm{2}}}j$ as examples. Since j = 1, the ternary connection number ${\rm{u}} = {\rm{A}} + Bi + Cj$ can be converted to a binary connection number${\rm{u}} = {\rm{A}} + {\rm{C}} + Bi$. Four operation rules for addition, subtraction, multiplication, and division of${u_1}$and${u_2}$are defined as follows.

(1) Addition: Let where, $A = {A_{\rm{1}}} + {A_{\rm{2}}} + {C_{\rm{1}}} + {C_{\rm{2}}}$, $B = {B_{\rm{1}}} + {B_{\rm{2}}}$.

(2) Subtraction: Let where, $A = {A_{\rm{1}}}{\rm{ - }}{A_{\rm{2}}} + {C_{\rm{1}}}{\rm{ - }}{C_{\rm{2}}}$, $B = {B_{\rm{1}}}{\rm{ - }}{B_{\rm{2}}}$.

(3) Multiplication: Let ${\rm{u}} = {{\rm{u}}_{\rm{1}}} \cdot {{\rm{u}}_{\rm{2}}} = ({{\rm{A}}_{\rm{1}}} + {B_{\rm{1}}}i + {C_{\rm{1}}}j)({{\rm{A}}_{\rm{2}}} + {B_{\rm{2}}}i + {C_{\rm{2}}}j) = {\rm{A}} + Bi$ where, $A = ({A_{\rm{1}}} + {C_{\rm{1}}}{\rm{)}} \cdot ({A_{\rm{2}}} + {C_{\rm{2}}}{\rm{)}}$, $B = ({A_{\rm{1}}} + {C_{\rm{1}}}{\rm{)}} \cdot {B_{\rm{2}}} + ({A_{\rm{2}}} + {C_{\rm{2}}}{\rm{)}} \cdot {B_{\rm{1}}}$.

(4) Division: Let ${\rm{u}} = \frac{{{{\rm{u}}_{\rm{1}}}}}{{{{\rm{u}}_{\rm{2}}}}} = \frac{{{{\rm{A}}_{\rm{1}}} + {B_{\rm{1}}}i + {C_{\rm{1}}}j}}{{{{\rm{A}}_{\rm{2}}} + {B_{\rm{2}}}i + {C_{\rm{2}}}j}} = {\rm{A}} + Bi$ where, $A = \frac{{{A_{\rm{1}}} + {C_{\rm{1}}}}}{{{A_{\rm{2}}} + {C_{\rm{2}}}}}$, .

3.2.2.   Intuitionistic fuzzy group decision making model of airport operation risk based on ternary connection number

In the case of multi-attribute group decision making, it often happens that experts' opinions conflict and consensus exist. An important problem to be solved in group decision-making models is to effectively resolve the consistency and conflict of opinions among the experts and agammaegate individual opinions into consistent opinions that can reflect the expert groups. Due to the lack of data to analyze the variation characteristics of indicator values, an intuitionistic fuzzy set based on expert experience and knowledge was used to characterize them. However, these models ignore the certainty and uncertainty of the indicators, which cannot reveal the influence of the ranking change of them on the evaluation result. Further, the ternary connection numbers were proposed to characterize their certainty and uncertainty to unify different decision makers on the uncertain evaluation of airport operation risk, which is related to the degree of contact.

The set of $m$ experts was denoted as $E = \{ {e_1}, {e_2}, ..., {e_m}\}$. There was a total $r$ of airport $A = \{ {a_1}, {a_2}, ..., {a_r}\}$ needed to evaluate their operation risk. Risk of airport operation involved a total n of hybrid-type indicators $C = \{ {c_1}, {c_2}, ..., {c_n}\}$. According to the experience and personal preference of each expert, the intuitionistic fuzzy value $p_{ij}^k = (t_{ij}^k, f_{ij}^k, \pi _{ij}^k)$ made by the kth expert on the jth indicator of ith airport was used to characterize their uncertainties. On this basis, the kth expert's intuitionistic fuzzy matrix for evaluating operation risk of all airports is denoted by the matrix in Equation 1.

where, i = 1, 2, …, r; j = 1, 2, …, n; k = 1, 2, …, m.

The intuitionistic fuzzy value $p_{ij}^k = (t_{ij}^k, f_{ij}^k, \pi _{ij}^k)$ could be converted to ternary connection number$p_{ij}^k = t_{ij}^k + \pi _{ij}^ki + f_{ij}^kj$, and the intuitionistic fuzzy matrix is equivalent to the following matrix given by Equation 2.

where, i = 1, 2, …, r; j = 1, 2, …, n; k = 1, 2, …, m.

When the weight vector of these indicators $C = \{ {c_1}, {c_2}, ..., {c_n}\}$ is denoted as $W = \{ {w_1}, {w_2}, ..., {w_n}\}$ ($\sum\limits_{j = 1}^n {{w_j} = 1}$), the intuitionistic fuzzy distance between any two experts k and t for evaluating operation risk of airport i can be calculated based on haiming distance using the Equation 3.

where, $\alpha$, $\beta$and $\delta$ describe degree of membership, non-membership and hesitation of intuitionistic fuzzy number of influence on evaluation results, respectively.

This distance related to the degree of contact, reflects the degree of agreement among each pair $(k, t)$ of experts on evaluating operation risk of airport i. As seen from the above formulas,

(1) if two experts had identical opinions on evaluating operation risk of airport i, the intuitionistic fuzzy distance equals 0;

(2) if two experts had completely opposite opinions on evaluating operation risk of airport i, their intuitionistic fuzzy distance equals 1;

(3) if two experts had different opinions on evaluating operation risk of airport i to some extent, the intuitionistic fuzzy distance was a value in [0, 1].

According to the consistency degree of the operation risk of airport i between any two pairs of n experts, the consensus degree matrix of evaluating operation risk of airport i can be constructed as showed in Equation 4.

If $k \ne j$, $e_i^{kj} = e_i^{jk}$; otherwise, $e_i^{kj} = 0$. For evaluating operation risk of airport i, average consistency degree of expert k ($k$ = 1, 2, …, m) can be denoted from Equation 5.

Similarly, relative uniformity of expert $k$ ($k$ = 1, 2, …, m) can be seen from Equation 6.

It can be seen from the above that the final comprehensive consensus degree of all experts' opinions on evaluating operation risk of airport i is denoted in Equation 7.

where, ${R_k}$ denotes the relative importance of each expert$k$($k$ = 1, 2, …, m). Obviously, the relative importance of each expert was different, and the opinion of some experts was more important than that of others. The determination method of the relative important weight of experts was as follows:

Initially, the most important expert from all the experts was selected and assigned the weight equal to 1.

Then, the $k$th expert with the most important expert was compared to get the relative weight of that expert, i.e., ${r_k}$ ($k$ = 1, 2, …, m)

Finally, the relative important weight of each expert was determined by Equation 8.

If each expert was of equal importance, then ${R_1} = {R_2} = ..., = {R_m} = \frac{1}{m}$.

According to the values of ${e_i}$in the order from small to large, the operation risk of airport i with the smallest value indicated the degree of consistency in the expert group on evaluation result, and the opinions of the experts were not much different.

4.   Case study

Four airports in Tianjin(A1), Shijiazhuang(A2), Beijing(A3) and Qinhuangdao(A4) city in China were selected for evaluating the uncertain airport operational risk management as examples. According to the individual opinions of three airport risk managers (e1–e3) on the alternative plans, the consistency degree of expert group's opinions was analyzed to obtain weight of evaluation criteria, i.e., ${w_j} = \frac{1}{{16}}$(j = 1, 2, …, n); in addition, the intuitionistic fuzzy matrix of these experts for alternative plans is seen from Table 2.

Table 2.  Intuitionistic fuzzy value on operational risk for different airports.

Indicator		Intuitionistic fuzzy value $p_{ij}^k = (t_{ij}^k, f_{ij}^k, \pi _{ij}^k)$ of each expert on plans
		e1				e2				e3
		A1	A2	A3	A4	A1	A2	A3	A4	A1	A2	A3	A4
C1	C11	0.2190, 0.4942, 0.2868	0.6793, 0.2210, 0.0997	0.5194, 0.4587, 0.0219	0.0535, 0.5087, 0.4378	0.0470, 0.4187, 0.5343	0.9347, 0.0459, 0.0194	0.8310, 0.1439, 0.0251	0.5297, 0.2419, 0.2284	0.6789, 0.2648, 0.0563	0.3835, 0.6086, 0.0079	0.0346, 0.2793, 0.6861	0.6711, 0.0340, 0.2948
	C12	0.0077, 0.4108, 0.5815	0.4175, 0.2563, 0.3262	0.9304, 0.0498, 0.0198	0.0920, 0.6735, 0.2345	0.3834, 0.3556, 0.2610	0.6868, 0.2286, 0.0847	0.8462, 0.1232, 0.0307	0.6539, 0.0066, 0.3395	0.0668, 0.8180, 0.1152	0.5890, 0.3573, 0.0537	0.5269, 0.3342, 0.1388	0.4160, 0.5174, 0.0666
	C13	0.7012, 0.1569, 0.1419	0.2625, 0.5262, 0.2114	0.3282, 0.4582, 0.2136	0.9910, 0.0078, 0.0012	0.9103, 0.0416, 0.0481	0.0475, 0.4657, 0.4868	0.6326, 0.0733, 0.2941	0.3653, 0.5649, 0.0698	0.7622, 0.0155, 0.2223	0.7361, 0.1762, 0.0877	0.7564, 0.2233, 0.0203	0.2470, 0.4096, 0.3434
	C14	0.9826, 0.0024, 0.0150	0.6515, 0.0751, 0.2734	0.8847, 0.0593, 0.0560	0.7665, 0.1092, 0.1243	0.7227, 0.1249, 0.1524	0.0727, 0.4136, 0.5137	0.2727, 0.6411, 0.0862	0.4777, 0.4213, 0.1010	0.7534, 0.2440, 0.0026	0.6316, 0.1163, 0.2521	0.4364, 0.2478, 0.3158	0.2378, 0.2783, 0.4839
C2	C21	0.2749, 0.1534, 0.5717	0.4865, 0.3237, 0.1897	0.0606, 0.0008, 0.9386	0.5163, 0.1544, 0.3293	0.3593, 0.6402, 0.0006	0.8977, 0.0631, 0.0393	0.9047, 0.0737, 0.0216	0.3190, 0.2845, 0.3965	0.1665, 0.1280, 0.7055	0.9092, 0.0001, 0.0907	0.5045, 0.3604, 0.1351	0.9866, 0.0091, 0.0042
	C22	0.4940, 0.3444, 0.1616	0.9478, 0.0370, 0.0152	0.3841, 0.0503, 0.5655	0.5297, 0.1006, 0.3697	0.2661, 0.1506, 0.5832	0.0737, 0.7676, 0.1587	0.2771, 0.5523, 0.1706	0.4644, 0.1144, 0.4212	0.0907, 0.7605, 0.1487	0.5007, 0.0472, 0.4521	0.9138, 0.0543, 0.0319	0.9410, 0.0048, 0.0542
	C23	0.0501, 0.3693, 0.5806	0.8278, 0.0671, 0.1051	0.6885, 0.0885, 0.2231	0.7362, 0.1114, 0.1523	0.7615, 0.2271, 0.0114	0.1254, 0.2355, 0.6392	0.8682, 0.1024, 0.0294	0.7254, 0.0775, 0.1971	0.7702, 0.2177, 0.0121	0.0159, 0.6812, 0.3029	0.6295, 0.2904, 0.0801	0.9995, 0.0001, 0.0004
	C24	0.8886, 0.0013, 0.1102	0.3510, 0.1584, 0.4906	0.8460, 0.0613, 0.0927	0.2693, 0.6053, 0.1254	0.2332, 0.1471, 0.6197	0.5133, 0.3990, 0.0877	0.4121, 0.3533, 0.2346	0.4154, 0.0922, 0.4924	0.3063, 0.6820, 0.0116	0.5911, 0.0558, 0.3531	0.8415, 0.0280, 0.1305	0.5373, 0.4571, 0.0056
C3	C31	0.4679, 0.1368, 0.3952	0.1537, 0.1857, 0.6606	0.0331, 0.7685, 0.1984	0.9554, 0.0299, 0.0148	0.2872, 0.1665, 0.5463	0.5717, 0.2719, 0.1565	0.5344, 0.3241, 0.1414	0.7483, 0.1594, 0.0923	0.1783, 0.0835, 0.7382	0.8024, 0.1375, 0.0601	0.4985, 0.3776, 0.1239	0.5546, 0.0251, 0.4203
	C32	0.8907, 0.0654, 0.0439	0.1598, 0.5880, 0.2522	0.1304, 0.4575, 0.4121	0.0030, 0.3287, 0.6683	0.6248, 0.0852, 0.2900	0.2128, 0.0925, 0.6948	0.0910, 0.5035, 0.4055	0.4143, 0.4117, 0.1740	0.8420, 0.0504, 0.1076	0.7147, 0.2176, 0.0677	0.2746, 0.4265, 0.2989	0.0269, 0.1392, 0.8339
	C33	0.7098, 0.0469, 0.2433	0.1809, 0.6661, 0.1530	0.6521, 0.1100, 0.2380	0.3858, 0.1909, 0.4233	0.9379, 0.0301, 0.0320	0.3175, 0.3800, 0.3024	0.1503, 0.1150, 0.7347	0.3877, 0.3601, 0.2522	0.2399, 0.6538, 0.1062	0.8870, 0.0835, 0.0295	0.6813, 0.1684, 0.1502	0.4997, 0.2592, 0.2411
	C34	0.1475, 0.3673, 0.4852	0.5901, 0.1611, 0.2488	0.1482, 0.3304, 0.5215	0.1418, 0.3173, 0.5409	0.5872, 0.1069, 0.3060	0.9554, 0.0199, 0.0247	0.9833, 0.0047, 0.0120	0.5649, 0.1105, 0.3246	0.8456, 0.0572, 0.0973	0.5561, 0.2112, 0.2326	0.4088, 0.0463, 0.5450	0.2521, 0.5024, 0.2455
C4	C41	0.4885, 0.3459, 0.1656	0.1260, 0.6299, 0.2440	0.6293, 0.3485, 0.0222	0.6216, 0.1957, 0.1827	0.4640, 0.2755, 0.2605	0.1998, 0.7560, 0.0442	0.1267, 0.2808, 0.5925	0.8031, 0.1302, 0.0667	0.9611, 0.0283, 0.0106	0.3192, 0.3136, 0.3671	0.6513, 0.1606, 0.1882	0.2478, 0.3022, 0.4499
	C42	0.4764, 0.3171, 0.2065	0.0284, 0.6511, 0.3205	0.1420, 0.4486, 0.4094	0.1312, 0.2382, 0.6306	0.3893, 0.6024, 0.0082	0.9017, 0.0338, 0.0645	0.9475, 0.0435, 0.0090	0.8856, 0.0735, 0.0408	0.2033, 0.1198, 0.6769	0.4265, 0.3107, 0.2628	0.4103, 0.0088, 0.5809	0.0922, 0.4958, 0.4120
	C43	0.1622, 0.7690, 0.0688	0.2531, 0.1843, 0.5626	0.4553, 0.2482, 0.2964	0.8089, 0.0307, 0.1603	0.0711, 0.2477, 0.6813	0.1351, 0.7299, 0.1349	0.3495, 0.5315, 0.1190	0.9317, 0.0483, 0.0200	0.3653, 0.6157, 0.0190	0.7832, 0.1505, 0.0663	0.4523, 0.0121, 0.5356	0.6516, 0.2466, 0.1018
	C44	0.2152, 0.3427, 0.4421	0.2501, 0.7435, 0.0063	0.5060, 0.3724, 0.1216	0.7558, 0.1210, 0.1231	0.6796, 0.1866, 0.1338	0.8609, 0.0968, 0.0423	0.6004, 0.0684, 0.3312	0.4622, 0.0430, 0.4948	0.9089, 0.0685, 0.0226	0.4713, 0.1478, 0.3809	0.8176, 0.0008, 0.1817	0.9514, 0.0079, 0.0407

---

 | Show Table

DownLoad: CSV

In order to rank the operational risk of airports, the ternary connection numbers, seen from Table 3, were used to transform them into the same dimension one according to Equation 2, which further revealed the influence of the certainty and uncertainty of the thing itself on the risk ranking of the airport.

Table 3.  Ternary connection numbers on operational risk for different airports.

Indicator		Intuitionistic fuzzy value $p_{ij}^k = (t_{ij}^k, f_{ij}^k, \pi _{ij}^k)$ of each expert on plans
		e1					e2					e3
		A1	A2	A3	A4	A1		A2	A3	A4	A1		A2	A3	A4
C1	C11	0.2190+ 0.4942j+ 0.2868i	0.6793+ 0.2210j+0.0997i	0.5194+ 0.4587j+0.0219i	0.0535+ 0.5087j+0.4378i	0.0470+ 0.4187j+0.5343i		0.9347+ 0.0459j+0.0194i	0.8310+ 0.1439j+0.0251i	0.5297+ 0.2419j+0.2284i	0.6789+ 0.2648j+0.0563i		0.3835+ 0.6086j+0.0079 i	0.0346+ 0.2793j+0.6861i	0.6711+ 0.0340j+0.2948i
	C12	0.0077+ 0.4108j+0.5815i	0.4175+ 0.2563j+0.3262 i	0.9304+ 0.0498j+0.0198 i	0.0920+ 0.6735j+0.2345 i	0.3834+ 0.3556j+0.2610 i		0.6868+ 0.2286j+0.0847 i	0.8462+ 0.1232j+0.0307 i	0.6539+ 0.0066j+0.3395 i	0.0668+ 0.8180j+0.1152 i		0.5890+ 0.3573j+0.0537 i	0.5269+ 0.3342j+0.1388 i	0.4160+ 0.5174j+0.0666 i
	C13	0.7012+ 0.1569j+0.1419 i	0.2625+ 0.5262j+0.2114 i	0.3282+ 0.4582j+0.2136 i	0.9910+ 0.0078j+0.0012 i	0.9103+ 0.0416j+0.0481 i		0.0475+ 0.4657j+0.4868 i	0.6326+ 0.0733j+0.2941 i	0.3653+ 0.5649j+0.0698 i	0.7622+ 0.0155j+0.2223 i		0.7361+ 0.1762j+0.0877 i	0.7564+ 0.2233j+0.0203 i	0.2470+ 0.4096j+0.3434 i
	C14	0.9826+ 0.0024j+0.0150 i	0.6515+ 0.0751j+0.2734 i	0.8847+ 0.0593j+0.0560 i	0.7665+ 0.1092j+0.1243 i	0.7227+ 0.1249j+0.1524 i		0.0727+ 0.4136j+0.5137 i	0.2727+ 0.6411j+0.0862 i	0.4777+ 0.4213j+0.1010 i	0.7534+ 0.2440j+0.0026 i		0.6316+ 0.1163j+0.2521 i	0.4364+ 0.2478j+0.3158 i	0.2378+ 0.2783j+0.4839 i
C2	C21	0.2749+ 0.1534j+0.5717 i	0.4865+ 0.3237j+0.1897 i	0.0606+ 0.0008j+0.9386 i	0.5163+ 0.1544j+0.3293 i	0.3593+ 0.6402j+0.0006 i		0.8977+ 0.0631j+0.0393 i	0.9047+ 0.0737j+0.0216 i	0.3190+ 0.2845j+0.3965 i	0.1665+ 0.1280j+0.7055 i		0.9092+ 0.0001j+0.0907 i	0.5045+ 0.3604j+0.1351 i	0.9866+ 0.0091j+0.0042 i
	C22	0.4940+ 0.3444j+0.1616 i	0.9478+ 0.0370j+0.0152 i	0.3841+ 0.0503j+0.5655 i	0.5297+ 0.1006j+0.3697 i	0.2661+ 0.1506j+0.5832 i		0.0737+ 0.7676j+0.1587 i	0.2771+ 0.5523j+0.1706 i	0.4644+ 0.1144j+0.4212 i	0.0907+ 0.7605j+0.1487 i		0.5007+ 0.0472j+0.4521 i	0.9138+ 0.0543j+0.0319 i	0.9410+ 0.0048j+0.0542 i
	C23	0.0501+ 0.3693j+0.5806 i	0.8278+ 0.0671j+0.1051 i	0.6885+ 0.0885j+0.2231 i	0.7362+ 0.1114j+0.1523 i	0.7615+ 0.2271j+0.0114 i		0.1254+ 0.2355j+0.6392 i	0.8682+ 0.1024j+0.0294 i	0.7254+ 0.0775j+0.1971 i	0.7702+ 0.2177j+0.0121 i		0.0159+ 0.6812j+0.3029 i	0.6295+ 0.2904j+0.0801 i	0.9995+ 0.0001j+0.0004 i
	C24	0.8886+0.0013j+0.1102 i	0.3510+ 0.1584j+0.4906 i	0.8460+ 0.0613j+0.0927 i	0.2693+ 0.6053j+0.1254 i	0.2332+ 0.1471j+0.6197 i		0.5133+ 0.3990j+0.0877 i	0.4121+ 0.3533j+0.2346 i	0.4154+ 0.0922j+0.4924 i	0.3063+ 0.6820j+0.0116 i		0.5911+ 0.0558j+0.3531 i	0.8415+ 0.0280j+0.1305 i	0.5373+ 0.4571j+0.0056 i
C3	C31	0.4679+ 0.1368j+0.3952 i	0.1537+ 0.1857j+0.6606 i	0.0331+ 0.7685j+0.1984 i	0.9554+ 0.0299j+0.0148 i	0.2872+ 0.1665j+0.5463 i		0.5717+ 0.2719j+0.1565 i	0.5344+ 0.3241j+0.1414 i	0.7483+ 0.1594j+0.0923 i	0.1783+ 0.0835j+0.7382 i		0.8024+ 0.1375j+0.0601 i	0.4985+ 0.3776j+0.1239 i	0.5546+ 0.0251j+0.4203 i
	C32	0.8907+ 0.0654j+0.0439 i	0.1598+ 0.5880j+0.2522 i	0.1304+ 0.4575j+0.4121 i	0.0030+ 0.3287j+0.6683 i	0.6248+ 0.0852j+0.2900 i		0.2128+ 0.0925j+0.6948 i	0.0910+ 0.5035j+0.4055 i	0.4143+ 0.4117j+0.1740 i	0.8420+ 0.0504j+0.1076 i		0.7147+ 0.2176j+0.0677 i	0.2746+ 0.4265j+0.2989 i	0.0269+ 0.1392j+0.8339 i
	C33	0.7098+ 0.0469j+0.2433 i	0.1809+ 0.6661j+0.1530 i	0.6521+ 0.1100j+0.2380 i	0.3858+ 0.1909j+0.4233 i	0.9379+ 0.0301j+0.0320 i		0.3175+ 0.3800j+0.3024 i	0.1503+ 0.1150j+0.7347 i	0.3877+ 0.3601j+0.2522	0.2399+ 0.6538j+0.1062 i		0.8870+ 0.0835j+0.0295 i	0.6813+ 0.1684j+0.1502 i	0.4997+ 0.2592j+0.2411 i
	C34	0.1475+ 0.3673j+0.4852 i	0.5901+ 0.1611j+0.2488 i	0.1482+ 0.3304j+0.5215 i	0.1418+ 0.3173j+0.5409 i	0.5872+ 0.1069j+0.3060 i		0.9554+ 0.0199j+0.0247 i	0.9833+ 0.0047j+0.0120 i	0.5649+ 0.1105j+0.3246 i	0.8456+ 0.0572j+0.0973 i		0.5561+ 0.2112j+0.2326 i	0.4088+ 0.0463j+0.5450 i	0.2521+ 0.5024j+0.2455 i
C4	C41	0.4885+ 0.3459j+0.1656 i	0.1260+ 0.6299j+0.2440 i	0.6293+ 0.3485j+0.0222 i	0.6216+ 0.1957j+0.1827 i	0.4640+ 0.2755j+0.2605 i		0.1998+ 0.7560j+0.0442 i	0.1267+ 0.2808j+0.5925 i	0.8031+ 0.1302j+0.0667 i	0.9611+ 0.0283j+0.0106 i		0.3192+ 0.3136j+0.3671 i	0.6513+ 0.1606j+0.1882 i	0.2478+ 0.3022j+0.4499 i
	C42	0.4764+ 0.3171j+0.2065 i	0.0284+ 0.6511j+0.3205 i	0.1420+ 0.4486j+0.4094 i	0.1312+ 0.2382j+0.6306 i	0.3893+ 0.6024j+0.0082 i		0.9017+ 0.0338j+0.0645 i	0.9475+ 0.0435j+0.0090 i	0.8856+ 0.0735j+0.0408 i	0.2033+ 0.1198j+0.6769 i		0.4265+ 0.3107j+0.2628 i	0.4103+ 0.0088j+0.5809 i	0.0922+ 0.4958j+0.4120 i
	C43	0.1622+ 0.7690j+0.0688 i	0.2531+ 0.1843j+0.5626 i	0.4553+ 0.2482j+0.2964 i	0.8089+ 0.0307j+0.1603 i	0.0711+ 0.2477j+0.6813 i		0.1351+ 0.7299j+0.1349 i	0.3495+ 0.5315j+0.1190 i	0.9317+ 0.0483j+0.0200 i	0.3653+ 0.6157j+0.0190 i		0.7832+ 0.1505j+0.0663 i	0.4523+ 0.0121j+0.5356 i	0.6516+ 0.2466j+0.1018 i
	C44	0.2152+ 0.3427j+0.4421 i	0.2501+ 0.7435j+0.0063 i	0.5060+ 0.3724j+0.1216 i	0.7558+ 0.1210j+0.1231 i	0.6796+ 0.1866j+0.1338 i		0.8609+ 0.0968j+0.0423 i	0.6004+ 0.0684j+0.3312 i	0.4622+ 0.0430j+0.4948 i	0.9089+ 0.0685j+0.0226 i		0.4713+ 0.1478j+0.3809 i	0.8176+ 0.0008j+0.1817 i	0.9514+ 0.0079j+0.0407 i

---

 | Show Table

DownLoad: CSV

Based on Equation 3, the distance of each pair $(k, t)$ of experts to airport i was obtained in Table 4, when $\alpha$, $\beta$ and $\delta$ when $\alpha$, $\beta$ and $\delta$ were set to 10, 5, 5, respectively, and the consensus degree matrix of all experts evaluating operation risk of airport i was constructed as follows.

Table 4.  Distance of pair $(k, t)$ of experts on each airport.

	Pair $(k, t)$ of experts
	$e_i^{1, 2}$	$e_i^{1, 3}$	$e_i^{2, 3}$
A1	0.1749+ 0.0952 i + 0.0527 j	0.2255+0.0709 i + 0.0824 j	0.1588+0.0985 i +0.0866 j
A2	0.2389+ 0.0841 i + 0.0966 j	0.2410+ 0.0656 i +0.0834 j	0.2288+ 0.0739 i +0.0966 j
A3	0.2446+0.0820 i +0.0804 j	0.1682+0.0721 i + 0.0681 j	0.2271+0.0872 i + 0.0616 j
A4	0.1862+ 0.0608 i + 0.0666 j	0.1969+0.0703 i +0.0555 j	0.2110+0.0939 i +0.0698 j

---

 | Show Table

DownLoad: CSV

Let the importance of the three experts be ${r_1}$ = 1, ${r_2}$ = 0.6, ${r_3}$ = 0.8. Then, their relative importance weights were ${R_1}$ = 0.42, ${R_2}$ = 0.25 and ${R_3}$ = 0.33, respectively. To evaluate operation risk of each airport, its average consistency degree and relative uniformity of each expert was calculated, and the evaluation result by considering the different expert opinions was obtained, as seen from Table 5.

Table 5.  Uncertain evaluation result based on ternary connection numbers.

	Opinion of each expert on an airport						${e_i}$
	${R_1}$= 0.42		${R_2}$= 0.25		${R_3}$= 0.33
	$A(e_i^1)$	$RAD(e_i^1)$	$A(e_i^2)$	$RAD(e_i^2)$	$A(e_i^3)$	$RAD(e_i^3)$
A1	0.2002+0.0830i+0.0676j	0.3428-0.0080 i	0.1669+ 0.0968i+ 0.0696j	0.3029+0.0175i	0.1922+ 0.0847i+0.0845j	0.3543-0.0094i
A2	0.2400+0.0749i+0.0900j	0.3349-0.0000i	0.2338+0.0790i+0.0966j	0.3354+0.0049i	0.2349+0.0697i+0.0900j	0.3297-0.0048i
A3	0.2064+0.0770i+0.0742j	0.3302-0.0028i	0.2359+0.0846i+0.0710j	0.3610-0.0027i	0.1977+0.0796i+0.0649j	0.3088+0.0056i
A4	0.1916+0.0656i+0.0610j	0.3214+0.0068i	0.1986+0.0774i+0.0682j	0.3394+0.0010i	0.2040+0.0821i+0.0626j	0.3392+0.0058i

---

 | Show Table

DownLoad: CSV

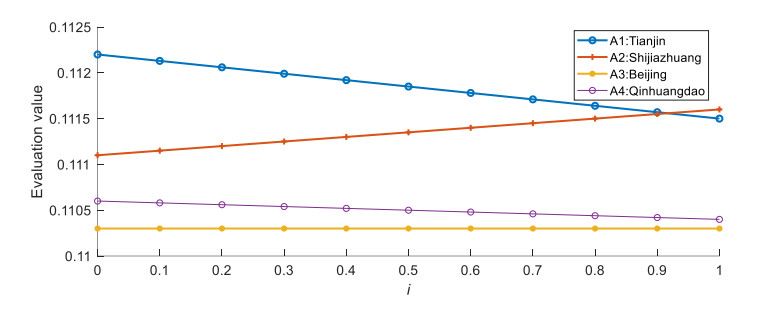
As seen from Table 5, the evaluation value of the airport operation risk was a binary connection number $u = A + Bi$, in which the information of certainty was related with the degree of membership and non-membership of all indicators and uncertainty was related with degree of hesitation. Its value changed as contact degree i fluctuated from 0 to 1, as shown in Figure 2. In the case, the more hesitant the experts were, the more volatile would be the evaluation results. Operation risk value of airport in Beijing remained the same because the experts had no hesitation, while for that of Tianjin and Qinhuangdao decreased due to the hesitation in the experts was counterproductive to the results. In the same way, for Shijiazhuang a gradual increase was observed because the hesitation of the experts had a positive effect on the results. When i was set as 0, the value was only decided by their determined information, and operation risk ranking of four airports was A1, A2, A4, A3. When i was set as 1, the value was also affected by all of their uncertainty information, and operation risk ranking of four airports was A2, A1, A4, A3.

Figure 2.  Evaluation values on airport operation risk with changes in contact degree i.

DownLoad: Full-Size Img PowerPoint

5.   Conclusions

This study presented a novel intuitionistic fuzzy group decision making model for airport operation risk assessment. The main contributions of this paper were as follows : (1) A multi-criteria evaluation criteria, with an integration of human, equipment, management and environment levels, was demonstrated to analyze airport operation risk; (2) A novel group decision making model with an integration of set pair analysis and intuitionistic fuzzy set was designed to reveal the influence of the certainty and uncertainty of thing itself on the risk ranking change of the airport operation. The feasibility and applicability of the proposed model were illustrated by a real-world example on four airports in China. The results show that: (1) The evaluation value of the airport operation risk was a changed one, and its ranking was related to the fact that whether the certain part of all attribute indicators played an important role in evaluation result than that of the uncertain part or not; (2) If operation risk ranking of two airport changed, their threshold contact degrees were found; (3) If operation risk ranking of two airport always remained the same, the uncertainty exhibited a limited influence on the evaluation rank. Therefore, the proposed model could pave a way to overcome the shortcomings of the traditional methods in quantitatively analyzing the impact of uncertainty of attributes on the ranking of airport operation risk.

Note that these values of main indicators in this paper were assumed to be time-independent variables. Many factors affect them, varying over time from year to year. Extending this evaluation model to an explicitly dynamic setting with time-varying value of indicators is a worthwhile direction for further work and future research.

Acknowledgements

This paper is funded by the Humanities and Social Sciences Foundation of the Ministry of Education in China (16YJCZH086); Nantong Science and Technology Innovation Program (MS22018012); the Six Talent Peaks Project of Jiangsu Province, China (SZCY-009); Key science and technology projects in the transportation industry in China (2018-MS3-083); the Natural Science Foundation of Tianjin in China (17JCQNJC08600); CAAC Key laboratory of General Aviation Operation (Civil Aviation Management Institute of China)(CAMICKFJJ-2019-03); the central college basic scientific research operating expenses fund in civil aviation university of China (3122019126).

Conflict of interest

The authors declare there is no conflict of interest.