1.
Introduction
According to US government statistics, the attendance rate for otitis media in children under 2 years old increased by 224% from 1975 to 1990, and 80% of children under 10 years old experienced otitis media [1,2]. Acute otitis media causes not only pain and fever but also complications such as hearing loss or cholesteatoma [3]. Previous studies revealed that otitis media was strongly correlated with infection of the upper airway, as well as allergy, obstruction, and neoplasm, which result in dysfunction of the Eustachian tube [4,5]. As the deep location of the middle ear impedes direct observation and measurement, there have been efforts to determine its elaborate structure by indirect means.
During the past decades, several studies have investigated the correlations between the anatomy and function of the Eustachian tube. Tympanogram curvature types were used to evaluate the function of the Eustachian tube, and radiography was used to examine its structure [6]. Owing to advances in computer technology, computed tomography (CT) and magnetic resonance imaging became the main techniques for medical imaging of Eustachian tube-related diseases [7,8]. Three-dimensional (3D) reconstruction based on CT images of the Eustachian tube revealed the relationships between morphological changes and secretory otitis media [9]. Similarly, 3D reconstruction of the mastoid antrum verified the correlation between the size of mastoid antrum and the incidence and prognosis of otitis media [10,11]. Recently, a 3D model of the human nasal cavity was constructed by numerical simulations to quantitatively analyze the progress and lapse of nasal diseases, in which the functional self-adaption of the nasal structure to the biomechanics of airflow was established [12]. By contrast, there are few numerical models of the entire middle ear. It is difficult to construct such a model because the biomechanical characteristics of different parts of the middle ear, including the Eustachian tube, vary greatly and are affected by nasopharyngeal lesions and body position. However, a personal 3D model of the middle ear is essential for patient-specific diagnosis and therapy. In this study, we examined the pressure-flow properties in different parts of a 3D model of the middle ear to verify its validity.
2.
Materials and methods
2.1. Geometrical model
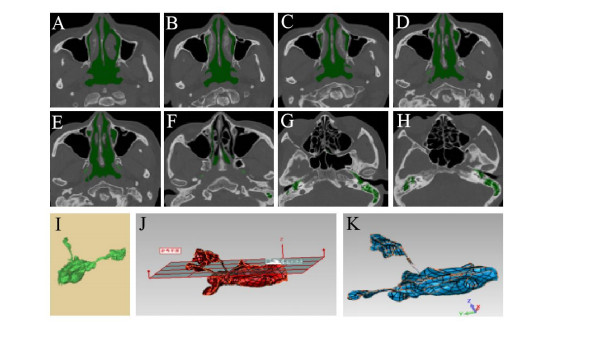
The geometrical model was constructed based on data from a 41-year-old female volunteer without any Eustachian or respiratory disease, who provided written consent to participate in the study. She had normal hearing and type A acoustic impedance. The volunteer sat quietly in the CT room for 30 minutes to adapt to the environment before scanning took place. During CT scanning, the volunteer performed a 6-second Valsalva maneuver to open the Eustachian tube. A set of high-quality tomography images of the temporal bone were acquired. A total of 66 images were used for 3D reconstruction with the Mimics 20.0 software. The different tissues in the DICOM images were distinguished by a grayscale from to -1204 to -657. Only air-containing structures, including the nasal cavity, nasopharyngeal cavity, Eustachian tube, tympanic cavity, tympanic antrum, and mastoid cavity, were used to construct the 3D model (Figure 1).
2.2. Finite element model and numerical simulation
The volume and surface mesh of the IGES file was completed by Ansys 15.0 to form the middle ear model. The model was imported into ANSYS workbench for numerical simulation of the flow field. Msc Nastran 2014 were used for the fluid-solid coupling calculations to study the interactions between air flow and the bony wall of the middle ear.
The main governing equation of fluid:
Continuity equation:
Navier-Stokes equation:
Here, ρ is the fluid density; p is the dynamic pressure of the fluid; v is the kinematic coefficient of viscosity; f is the mass force; and u is velocity vector. The accelerated velocity of a fluid micelle is given by the left-hand sides of the equations, whereas the right-hand sides of the equations give the positive pressure, the volume force, and the viscous shear force of the fluid micelle, respectively.
The governing equation of solid:
Here, ρs is the solid density; ¨ds is the structural displacement field of the solid; σs is the Cauchy stress tensor; and fs is the structural force vector of the solid.
Fluid-solid coupling boundary condition:
Here, τf and τs are the shear tensors of the mass points on the solid and fluid boundary, respectively, whereas ds and df are the displacements of the mass points in solid and fluid, respectively.
2.3. Boundary conditions and model set-up
The geometrical model was divided into 4 parts: the entrance (the right anterior nostril), the exit (the bilateral tympanic membrane), the face grid (the surface part between the entrance and the exit), and the body grid (the fluid part between the entrance and the exit). A mixed mesh consisting of three layers of prismatic boundary layers with tetrahedron as the main element was generated. Structural model of the pneumatic system in the middle ear: 522814 nodes, 22658231 elements, 692239 tetrahedra. The eardrum was made of a mesh of surface elements, and the body surface was taken from the corresponding region of the tympanic fluid to form two elliptical surface elements (the size of the ellipse is 9 mm×8 mm, the thickness is 0.10 mm, and the area is about 90 mm2).
The parameters of the materials were set as listed in Table 1 [13,14].
The Eustachian tube was considered opened on the connection with the nasopharynx. The temporal bone was fixed in all degrees of freedom except for movement of the tympanic membrane. The walls of the tympanum were fixed into the bony structure of the middle ear. Thus, the displacement of the tympanum edges was considered to be zero; however, the rotation of the edges was not restricted. The Eustachian tube and tympanum were made of homogeneous, isotropic, continuous and elastic materials, and the air in the model was regarded as a non-compressed fluid. Its physical parameters, such as density, specific heat, coefficient of viscosity, thermal conductivity, and mass diffusion coefficients, were not affected by temperature or humidity. In a healthy person, the inner and outer pressures of the tympanic membrane are both the same as atmospheric pressure. Hence, in our research, the absolute atmosphere pressure was ignored. Only the relative pressure was taken into account, that is, 3.5 KPa and 30 KPa from the right nostril. Arick used a device providing an air pressure level between 3.5 KPa and 20 KPa [15]. Streamsys, an automated device made in China, has two pressure settings: 20 KPa for children and 36 KPa for adults. In this work, we choose 3.5 KPa and 30 KPa as the input pressures. We simulated Politzerization with an automated device: pressures of 3.5 KPa and 30 KPa were exerted at the right nostril as the entry loadings, and the exit loading was set to a pressure of 0 KPa on the tympanums of both ears. The initiative pressure of the reconstructed model was set to 0 KPa. The period of the fluid-solid coupling calculation was set to 1 s. To perform status analysis of the transient turbulence, the velocities and pressures of the airflow at 0, 0.2, 0.4, 0.6, 0.8, and 1.0 s were determined after a pressure of 3.5 KPa or 30 KPa was loaded. The displacement of the right tympanum, as well as the maximal velocity and pressure of the airflow, were added to the diagram at the corresponding time points.
3.
Results
3.1. The bio-mechanical properties of the middle ear model under 3.5 KPa
3.1.1. Airflow velocity in middle ear models under 3.5 KPa
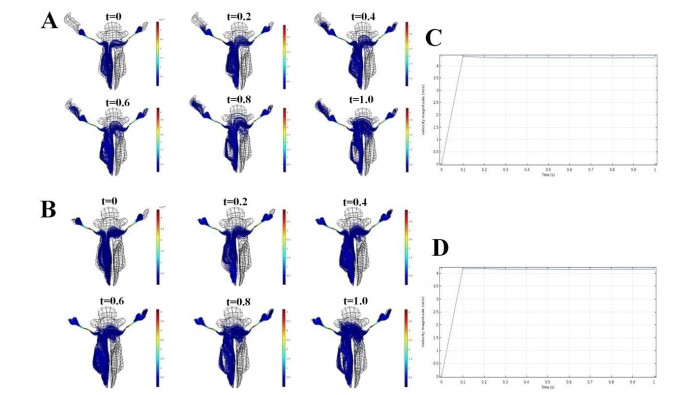
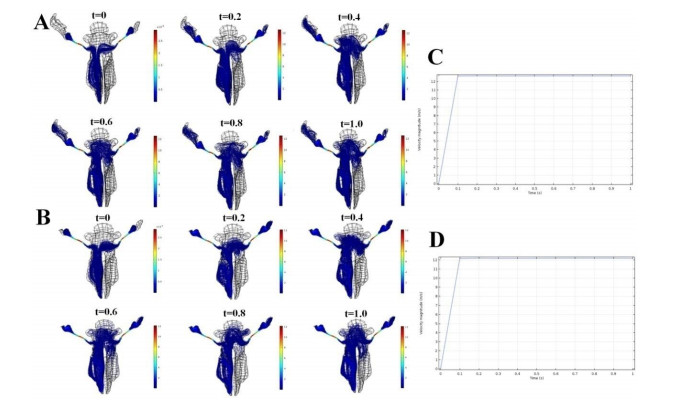
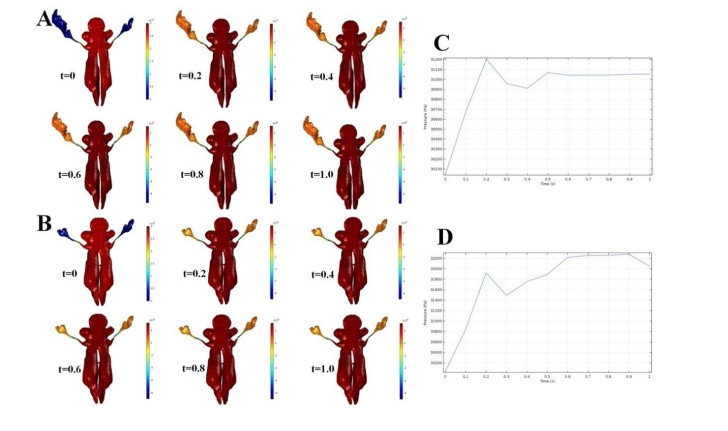
In the middle ear model, the static parameters of the Eustachian tube in an open state were as given in Table 2. To study the bio-mechanical properties of the model, air pressure was loaded from the right nostril. Under a pressure of 3.5 KPa, the velocities of the airflow at initiation (0 s) in the nasal cavity, Eustachian tube, and mastoid process were all zero (Figure 2A). At 0.2 s, there was a continuous current from the right nostril to both tympanums, but no current was detected in most of the space of the left nasal cavity. The current reached its maximal velocity of 4.2 m/s at the isthmus of the Eustachian tube and then decreased rapidly to 0.5 m/s at the tympanum (Figure 2A, C, Table 3). The current did not extend to the top area of the nasal cavity or the mastoid process until 0.4 s. When the current field was enlarged in the nasal cavity and mastoid process, most areas of the top and left nasal cavity were still devoid of currents. When the current appeared in the top nasal cavity at 0.8 s, even forming a pore in the right nasal cavity and a circuit in the mastoid process, the maximal velocity was still 4.2 m/s at the isthmus of the Eustachian tube (Figure 2A, C). The distribution of the air currents became stable at 1 s (Figure 2A).
When a 3.5 KPa entry pressure was loaded in the model without right mastoid process, the distribution of the air current differed little from that of the complete middle ear model at 0.2 s (Figure 2A, B). However, the maximal velocity in the isthmus was 4 m/s, which was reduced to 0.3 m/s at the tympanum (Figure 2B, D, Table 3). From 0.2 to 1 s, this maximal velocity was sustained and the current distribution was similar to that of the middle ear model with right mastoid process (Figure 2A, B). The curvature diagrams show that in the models with and without right mastoid process, the airflow velocities reached their maximum in 0.1 s and remained at that level until 1 s (Figure 2C, D).
3.1.2. Airflow pressure in middle ear models under 3.5 KPa
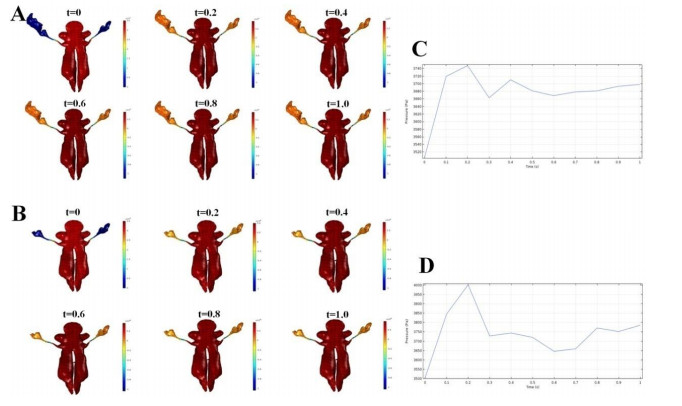
When a pressure of 3.5 KPa was loaded onto the middle ear model at the right nostril at 0 s, the pressure decreased gradually from the right nostril to the tympanum (Figure 3A). At 0.2 s, the nasal cavity was filled with an even pressure; however, in the Eustachian tube, the air pressure decreased dramatically to -10 KPa at the isthmus and returned to 0 KPa at the tympanum. This pressure distribution was maintained until 1 s (Figure 3A, Table 3).
When the right mastoid process was removed and a pressure of 3.5 KPa was loaded onto the model, the pressure from the right nostril to the tympanum also decreased gradually to zero. At 0.2 s, the minimal pressure in the isthmus was -0.8 KPa, while the pressure at tympanum was still zero. This pressure distribution was maintained until 1 s (Figure 3B, Table 3).
These results show that the air pressure in the intact middle ear model reached its maximum in 0.2 s with a non-linear tendency and then underwent a fall and rise from 0.2 to 0.6 s before stabilizing for both entry pressures (Figure 3C). By contrast, when the right mastoid process was removed, although the pressure reached its maximum at 0.2 s in a non-linear manner, the duration of the subsequent fluctuation was elongated to 0.9 s (Figure 3D).
3.1.3. Tympanum displacement under 3.5 KPa
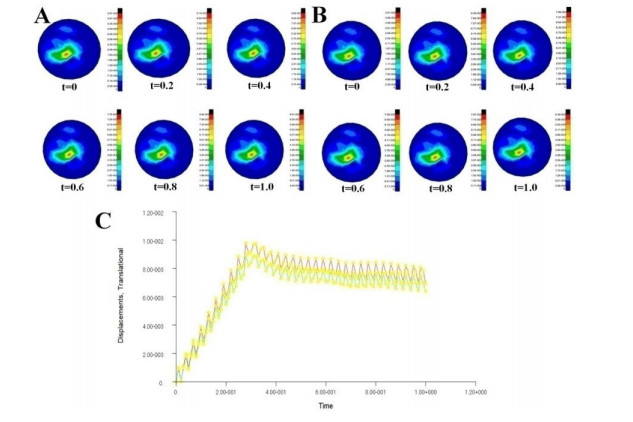
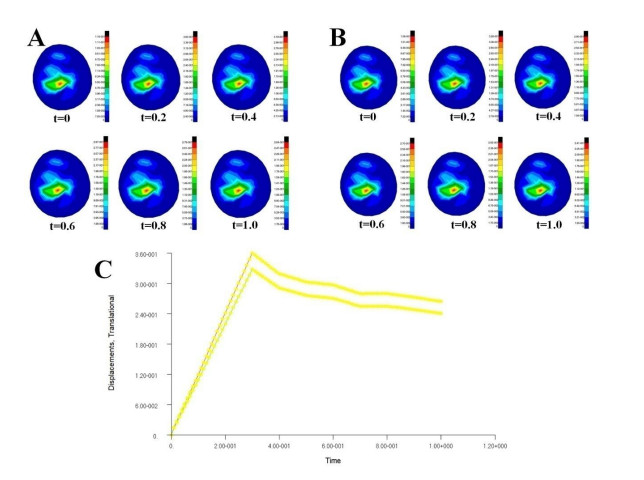
The numerical simulations showed that whether the right mastoid process was kept or removed, the displacement location of the tympanum showed little change under a pressure of 3.5 KPa (Figure 4A, B). The displacement of the right tympanum in the model with mastoid process increased gradually and reached a maximum of 9.14×10-3 mm at 0.3 s, then fell to and remained at 8.0×10-3 mm in the rest period (Figure 4C, Table 3). However, in the case without the mastoid process, although the tendency of the displacement changes seemed no different from the normal case, the maximal displacement decreased by 8.2% to 8.39×10-3 mm (Figure 4C, Table 3).
3.2. The bio-mechanical properties of the middle ear model under 30 KPa
3.2.1. Airflow velocity in the middle ear models under 30 KPa
When 30 KPa pressure was loaded onto the model from the right nostril, an initial air velocity of zero was detected in the nasal cavity, Eustachian tube, and mastoid process. The distribution of the current field at 0.2 s was similar to that in the 3.5 KPa case, except that the maximal velocity was 12.8 m/s at the isthmus of the Eustachian tube and reduced to 3 m/s at the tympanum (Figure 5A, Table 3). From 0.4 to 1 s, the air current was distributed in the top and left nasal cavities with a maximal velocity of 12.8 m/s at the isthmus of the Eustachian tube (Figure 5A, Table 3).
When the right mastoid process was removed, the distribution of the current field in the model without mastoid process was similar to that in the normal model. The maximal velocity slightly decreased to 12.1 m/s at the isthmus compared with the normal case. However, the velocity at the tympanum was 2.0 m/s, much less than that (3.0 m/s) in the normal model (Figure 5B, Table 3).
The curvature diagrams showed that the airflow velocity in the complete model of the middle ear reached its maximum value in 0.1 s and remained at this level until 1 s. Similarly, the maximal velocity in the model without mastoid process was also achieved in 0.1 s and sustained until 1 s (Figure 5C, D).
3.2.2. Airflow pressure in middle ear models under 30 KPa
When a pressure of 30 KPa was loaded at the right nostril in the middle ear model with mastoid process, the initial pressure at the tympanum was 0 Pa. At 0.2 s, the minimal pressure of -100 KPa was detected at the isthmus of the Eustachian tube; this gradually rose to 0 Pa at the tympanum. Subsequently, no change was observed in the pressure distribution (Figure 6A, Table 3).
Under an entry pressure of 30 KPa, although the maximal velocity of the air current in the model without mastoid process was only slightly reduced, the minimal pressure increased remarkably to -80 KPa at 0.2 s. However, the pressure on the tympanum was still zero and the distribution of pressure showed no difference between the models with and without mastoid process (Figure 6B, Table 3).
The air pressures in the model with mastoid process reached their maximum in 0.2 s in a non-linear manner, and then underwent a fall and rise from 0.2 to 0.6 s before stabilizing for both entry pressures (Figure 6C). By contrast, the pressure changes in the model without mastoid raised dramatically in 0.2 s. After a fall during the following 0.1 s, the pressure climbed to the maximum of 32.25 KPa at 0.6 s, and then fluctuated from 0.6 to 0.9 s before becoming stable (Figure 6D, Table 3).
3.2.3. Tympanum displacement in middle ear models under 30 KPa
Under a pressure of 30 KPa, the displacement of the tympanum in both models was similar to that in the case of 3.5 KPa (Figure 7A, B). However, in models with and without the mastoid process, the displacement of the right tympanum increased gradually and reached its maximum at 0.3 s to 35×10-2 and 32×10-2 mm, respectively (Figure 7C, Table 3). During the rest period, the displacement fell to and remained at 26×10-2 and 24×10-2 mm, respectively (Figure 7C, Table 3). Thus, the loss of the mastoid process resulted in an 11% decrease in tympanum displacement.
4.
Discussion
As the middle ear is an air-containing organ, its function relies on the mechanical characteristics of the air current. However, the complicated anatomical structure of middle ear makes the mechanical characteristics vary among its different parts, especially in the Eustachian tube. The deep location of the middle ear also makes it difficult to obtain precise measurements of anatomic structure. Several numerical models have been developed to determine the anatomical structure of middle ear, none of which reflected the varying characteristics of the airflow in different physiological and pathological states of the middle ear. In our study, an infinite element model and fluid-solid coupling simulations were used to construct a model of the middle ear in which the mechanical characteristics of the air flow in different parts could be evaluated.
The Eustachian tube resembles a Venturi tube, which is composed of two broader spaces and a narrow connection. According to Bernoulli’s law, which states that fluid velocity increases at the expense of pressure, the fluid velocity in a Venturi tube decreases with increasing cross-sectional area. Thus, in the Eustachian tube, the velocity and pressure of the air current should be maximal and minimal, respectively, at the isthmus. In our middle ear model, the maximal velocity and the minimal pressure were indeed detected at the isthmus of the Eustachian tube, and their absolute values increased with increasing entry pressure (Table 3). These results indicate that this model recapitulated the biomechanical characteristics of the real middle ear. We also found that with increasing air pressure at the pharyngeal ostium of the Eustachian tube (entry pressure), the pressure at the isthmus (exit pressure) decreased, although the velocity increased. When the difference between the entry and exit pressures increased, the possibility of collapse in the isthmus also increased. This result is consistent with the clinical finding that the Valsalva maneuver often fails to re-open the closed Eustachian tube in patients with middle ear effusion. However, once the pressure at the isthmus has been increased by auripuncture, and the pressure difference between entry and exit has also decreased, the collapsed Eustachian tube is more easily re-opened by the Valsalva maneuver. Therefore, our model not only theoretically explains why and how the Valsalva maneuver can re-open the collapsed Eustachian tube but also suggests the clinical use of early auripuncture in the case of hydrotympanum.
We further evaluated the influence of the mastoid process on the function of the Eustachian tube by simulation of pressure-flow changes in the model. It is well known that otitis media impairs the development of mastoid air cells, which results in reduced cell volume and buffer capability of air pressure [15,16]. Dysfunction of the Eustachian tube also reduces the pressure and causes accumulation of effusions in the tympanic cavity, triggering recurrent otitis media. A sufficient volume of the mastoid air cell is also crucial for sonic conduction [17]. The fluid-solid coupling simulation indicated that loss of the mastoid process decreased the maximal velocity and tympanum displacement, but the time to stabilization and the minimal pressure were increased (Table 3). These results demonstrate that loss of the mastoid process weakened the buffering capability of the Eustachian tube, as well as the sonic conduction. This conclusion is consistent with the clinical observation that increasing the volume of the mastoid air cell ameliorates refractory secretory otitis media.
Clinically, the diagnosis and treatment of otitis media are hindered by the inaccessibility of the middle ear. Thus, many clinicians and scientists have attempted to build numerical models via CT scanning and 3D reconstruction to directly reflect anatomical and functional disorders of the middle ear. However, such attempts were unsuitable for clinical use because of their high time cost and the low resolution of the reconstructed model [18]. Benefiting from advances in software, we developed a method to rapidly build an individual middle ear model for a specific patient. Combined with measurements of the air flow in the model, it was feasible to assess the anatomical and functional characteristics of the individual middle ear. Therefore, the model established by our approach will benefit the diagnosis and treatment of dysfunctions of the middle ear.
Although our 3D model of the middle ear provides a key tool for diagnosis and therapy [19], further development is required. For example, the musculi levator veli palatini and tensor veli palatini were assumed to be in contraction, and the Eustachian tube was modeled as a rigid body. However, a previous study suggested that the musculi levator veli palatini and tensor veli palatini control the Eustachian tube [20]. Sudon found that the contraction of the musculi levator veli palatini rotated the posterior wall of the Eustachian tube to open its anterior end [21]. Therefore, in future 3D reconstruction and clinical practice, the status of the musculi levator veli palatini and tensor veli palatini will be taken into account to more accurately simulate the bio-mechanical properties of the middle ear.
5.
Conclusion
In this study, we developed a procedure to construct a model of the middle ear, and examined the validity of the resulting model using numerical simulations. Fluid-solid coupling calculations were used to evaluate the airflow characteristics of the model. In this model, the pressure-flow properties under different air pressures and the buffer capability of the mastoid process were consistent with clinical findings. Therefore, our model is able to simulate the real middle ear, and will provide a practical approach to detect and evaluate middle ear diseases.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (Grant Nos: 31500764, 11472074, 11572079 and 11772087). This study was approved by the Ethics Committee of the 2nd Affiliated Hospital to Dalian Medical University.
Conflict of interest
No potential conflicts of interests were reported by the authors.









 DownLoad:
DownLoad: