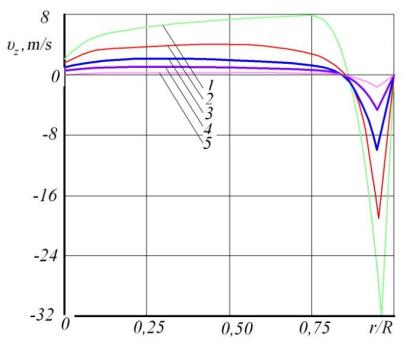
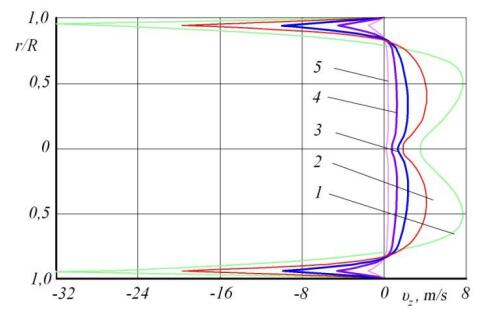
This is an analytical solution of the two-dimensional non-isothermal mathematical model describing the change in the velocity profile of a cylindrical extrusion die. This solution is based on the following assumptions. The two-dimensional melt flow is asymmetric. A melt viscosity anomaly may take place. Heat generated by viscous friction is a factor affecting the melt flow. The melt flow moving towards the metering section is in a steady state. Neither mass forces nor inertia forces are present. Velocity gradients along the channel are neglected. The mathematical model was built up from the incompressibility equation, motion equations, energy equation, and the rheological equation. This model depicted a non-isothermal flow of rheological fluid moving through the cylindrical extrusion die. A diagram was drawn. It depicts the melt velocities at a die entrance in different cross-sectional views. Computer testing was performed to verify the obtained solutions and compare them with the real extrusion process. Difference between calculated and experimental data was below 14%. Results allow concluding a matching of numerical results with experimental data, and so the possibility of using a built-up model in an extrusion die design for single-screw extruders.
1.
Introduction
A problem is to improve the calculation theory and methods that are applied to extrusion equipment. If solved, it can ensure the optimal design of extruder sections for the production of food of required quality [1,2,3,4]. From this perspective, mathematical modelling of extrusion process is of critical need.
Because the quality of extruded article, as well as the extrusion machine operation, is largely dependent upon the function of a metering section, the analysis will touch upon the mathematical models of extrusion at the metering section.
A common choice for the viscosity function is the power-law equation. It is easy to make calculations of flow and stress fields with the constitutive equation of the power-law generalized Newtonian fluid. For many polymer melts, < 1 values of the power-law index correctly capture the flow behaviour at high rates of deformation [5]. The overall predictions of the power-law generalized Newtonian fluid are found to be adequate when the information about the pressure drop and the flow rate is desired. This choice is even more relevant because the target parameters in this study do not include memory effects, relaxation time, or other elasticity effects.
Based on the isothermal Newtonian flow model, James M. McKelvey derived an expression for the volumetric flow rate in the metering zone, m3/sec [6]:
Where: Q–volume rate of flow in the metering zone, m3/sec; Uz–velocity component of barrel in z-axis direction (z-axis is oriented along the axis of a screw channel), m/sec; h–screw channel depth, m; W–channel width, m; μH–Newtonian fluid viscosity, Pa s; ∂P/∂P∂z∂z–pressure gradient along z-axis, Pa/m; Fd,Fp–dimensionless shape factors concerning with the effect of h/hWWon the flow ratio distribution.
Solution to this flow problem generated an equation for productivity in metering zone. However, despite the ease of solving the equation, some shortcomings do not allow getting a full picture of a melt flow through the channel in the metering zone. These shortcomings are the accepted Newtonian flow, the focus just on the problem of one-dimensional isothermal flow, the neglected convective heat transfer, the quality of extruded article, etc.
Rheological models provide the most accurate physical picture of the extrusion process [7,8,9]. The first close attempt to solve this problem was made by Z. Tadmor, R.V. Torner, et al. [10,11,12]. They introduced mathematical models for one-dimensional isothermal flow of a power-law fluid:
Where: Q–specific volumetric flow rate, m3/(sec·m); Vo–velocity in the direction parallel to the moving plate, m/sec; H–screw channel depth, m; G–dimensionless pressure gradient; s=1/1nn (or 1/1mm)–reciprocal of exponent in power-law flow; sign–sign of the function signG=G/G|G||G|; λ–dimensionless longitudinal coordinate.
Where: Q–volume rate of flow, m3/sec; ηo–dimensionless coordinate with zero shear stress; ηo=yo/yohh; yo–coordinate of cross-section with zero shear stress, m; dP/dPdxdx–pressure gradient, Pa/m.
These models have a common drawback–no evaluation is implied for the quality of polymer melt and for the quality of extruded article, accordingly. Improving the quality of extruded article is a step essential for the improvement of processing operations. This problem can be solved by stabilising the key process parameters (volumetric flow rate, pressure, and temperature).
The problem of a polymer melt flow in single-screw extruders was considered in a range of papers with due account for the effect of melt leaking out through the gaps [9,13,14]. This resulted in an analytical expression for the volumetric flow rate in the metering zone that takes into account die leakages.
Where: N–screw rotation speed, rpm; S–screw pitch, m; φ–screw helix angle; δ–flight clearance, m; Bz–dimensionless pressure gradient in forward flow; χ–ratio referring to pressure gradients acting in circulation flow.
Even though viscosity anomaly was taken into account in model (4), it does not involve pressure drops in the channel and in the radial clearance.
Tadmor made the following assumptions to simplify the model. The given process is stationary. The polymer tube is uniform. The polymer travels through the channel at a constant speed. The melting point is clearly defined. The channel curvature is not a factor to consider. A melting problem is reduced to a one-dimensional problem of heat and mass transfer [12]. However, such solution does not provide an adequate examination of convective and diffusion mechanisms of heat transfer.
Chang Dae Han suggested that the main reason for the difference between the calculated and the experimental data is the Tadmor's assumption about the infinite depth of a solid bed. According to Chang, his assumption entailed a misassessment of the temperature profile [15]. Therefore, he considered a solid bed between the barrel and the screw root. With this approach, he found the temperature distribution in the film mass (exponential law), and assumed that it does not change at melting. Hence, he was able to determine the screw temperature using the heat transfer equation.
Papers considered above are devoted to the problem of one-dimensional flow, but this approach does not allow taking into account the effect of mixing and the effect of convective heat transfer.
R.V. Torner introduced an iterative procedure of solving equations for melt in a melt zone. This practice was suggested as an addition to the already existing calculation method, which was applied to plasticizing extruders with conical units. Thus, he obtained a model of the two-dimensional non-isothermal flow of a pseudo-plastic fluid [12]:
Where: k(l)–polytropic efficiency dependent upon the location of a cross section on the flight axis; l–longitudinal coordinate of standard cross section, varying within 0≤l≤l∂; μo–material constant, Pa s; A=(π⋅D)1+1/n⋅[(t−i⋅e)/(t−i⋅e)h1/n⋅Э1+e/eδ1/nδ1/nh1/n⋅Э1+e/eδ1/nδ1/n]⋅i⋅ctgϕ; Э1–dimensionless criterion, Э1=[(1−ηo)(cosφ)1+1/n+χ(1−ηoц)(sinφ)1+1/n]⋅Bz(n+1)1/n; ηoц–dimensionless coordinate with zero shear stress in circulation flow; l∂–actual length of metering zone, m; b–temperature coefficient of viscosity, 1/deg; R=eb(T−To); T–melt temperature, ℃; ρ–melt density, kg/m3; cp–specific heat of melt, J/(kg×K).
The solution of the two-dimensional problem only cannot give the extruder characteristics that will work or a temperature profile of the melt down the screw.
V.V. Skachkov reviewed the existing methods of solving equations for melt in a melt zone [10]. The introduced parameter was the apparent melting heat. This parameter took into account that extra energy necessary to heat the melt to the average film temperature. The flow rate was found to be the strongest factor affecting the melting process; its effect was stronger than the effect of the number of rotations and effect of the barrel temperature.
Pervadchuk V.P. coined a theory of polymeric materials melting in the plasticizing extruders. According to this theory, one has to solve complete equations for the conservation of mass, momentum, and energy [16,17]. Piecewise constant approximation of changes in longitudinal velocity allows reducing the solution of the three-dimensional stationary problem to the two-dimensional non-stationary one. The qualitatively new characteristics of melting were obtained. By qualitatively new, one should understand the shape of a solid film mass, velocity and temperature profiles, etc. However, the problem that was solved applies only to the Newtonian fluid and to a constant screw channel height.
Therefore, in the single-screw extrusion, one of the most important issues is to build a mathematical model that would allow him/her to predict the quality of extruded article and to take into account the required quality indicators when calculating or selecting the geometry of a screw. Yet, melt behaviour in the forming channels of a die and in the metering section is insufficiently studied. Therefore, it is essential to build mathematical models of extrusion that would describe the change in temperature/pressure and in the average velocity of the fluid travel in the zone. This necessity rises from the fact that these parameters have the direct effect on the quality of a finished product and on the quality of the extruder operation.
The purpose of this article is to present an analytical solution to the two-dimensional non-isothermal mathematical model describing the change in velocity profile of a cylindrical extrusion die.
2.
Materials and methods
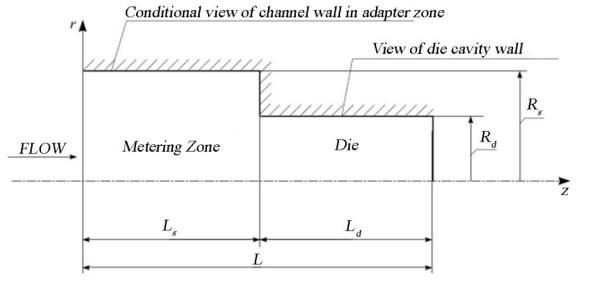
Rheological melt flow is pushed through the channel to the metering section of a die, and then it is pressed out through the die cavities. To study the melt flow in the cavity of a die, let us consider the flow of a fluid in a stepped cylindrical channel (dimensions: length l1 and diameter d1; length l2 and diameter d2. d1 > d2). Let the melt flow in the die body to be known and stationary.
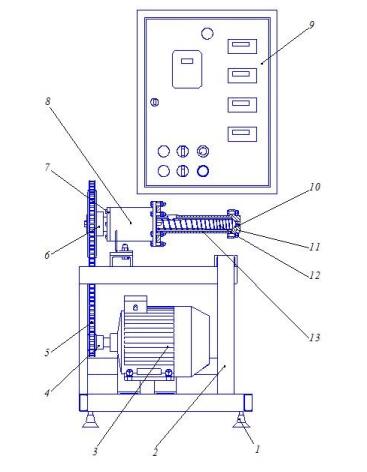
Extrusion process was investigated on grain crops in the single-screw extruder KMZ (Figure 1).
The investigation over complex mixtures was performed using the experimental single screw extruder EUM-1 (Figure 2).
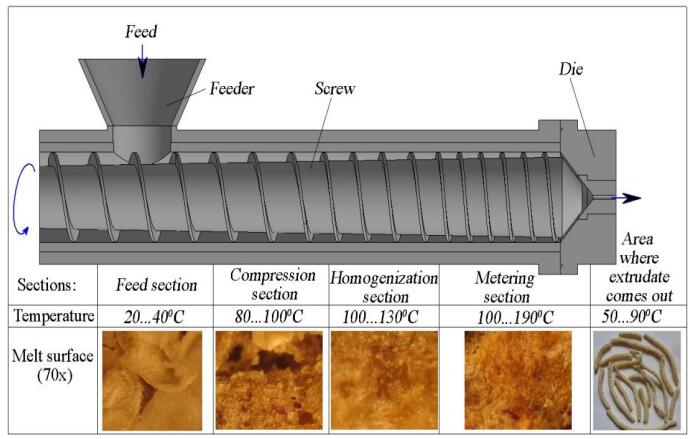
To assess the nature of changes that occur in the structure of material at extrusion, the focus was laid on the qualitative changes that emerge in crops along the work chamber of the single-screw extruder (Figure 3).
The pre-moistened raw material enters the feed section, where it is mixed to thickening. When this happens, air between the particles of the product is squeezed out to some extent. In the feed section, coarse-grained particles have voids between them. In the compression section, particles are under significant mechanical stress that causes them to deform throughout the volume. At the same time, internal stress increases in a stepwise manner. When it reaches the point above the compressive strength, the fracture of biopolymers and cellular particles becomes stronger, enabling the compaction and the beginning of melt formation.
In the homogenization zone, a homogeneous melt is formed with a small number of particles that have not yet melted.
In the metering section, which has the pressure stabilisation and pressurization function, with temperature maintained at 120 to 190 ℃, the product becomes plastic (homogenization completed). The insignificant traces of unmelted starch kernel are associated with the incomplete denaturation of protein molecules, especially globular ones. Thus, the properties of an extruded product depend on both the starch phase and the protein phase. The product that came out of the extruder was porous, with a slight decrease in mechanical strength.
Histological studies of the extruded material structure revealed that in the heating zone, where the heating elements are located, physicochemical parameters of initial mixtures did not significantly change. Large particles were dense, with uneven edges, while smaller particles were more spherical in shape.
A system of differential equations for non-isothermal flow can be applied to each k-th channel. For an asymmetric flow, modelled as the two-dimensional flow, tangential velocity component equals to zero. Because the melt flow is stationary, the viscosity anomaly is present, and the melt itself is incompressible, the differential equations (if small mass forces are ignored) can be written in the cylindrical coordinate system as:
Incompressibility equation [13]:
Motion equation:
Energy equation:
Where: Ф–dissipation function, characterizing the conversion of kinetic energy into heat energy:
Where: τzz=2η(I2,T)∂ϑz∂z; τrr=2η(I2,T)∂ϑr∂r; τθθ=2η(I2,T)ϑrr;
τzr=τrz=η(I2,T)(∂ϑr∂z+∂ϑz∂r)–stress tensor components.
For a continuous flow, a rheological equation was used, expressed through a generalized power law:
Where: ηо, m–material constants; β–temperature coefficient of viscosity; I2–quadratic strain rate tensor,
To reduce the order, (1)–(7) were expressed as the alternating current φ
and vorticity ω:
Then, incompressibility Eq (1) will be accomplished automatically.
Let us transform motion equations using vorticity and current variables. For this purpose, Eq (7) was differentiated with respect to z, and Eq (8)–with respect to r. Results from the differentiation of Eq (8) was subtracted from the results that were obtained in differentiation of Eq (7).
Expression on the left of (6) will be:
By subtracting (15) from (16), one will get:
Expressions on the right of (6) and (7) were done by analogy:
Equation (18) was transformed by grouping:
Where:
Thus, in current and vorticity coordinates, motion equation will take the following form:
Where: Sω is determined by (20).
In new coordinates, energy equation will be as follows:
Where:
Equations (19) and (22) were complemented by equation for vorticity ω, which in a cylindrical coordinate system:
Thus, a system was built up from three Eqs (19), (22) and (23)—equations for current ψ, vorticity ω and temperature Т that require boundary conditions:
Where: Т0–barrel wall temperature, v0– inlet velocity.
Initial melt temperature is assumed to be distributed across the cross-section uniformly and to be equal to Т0
Aside from that, symmetry condition was given for functions ϑz, ϑr, and T:
For current and vorticity variables in (24–28), conditions are as follows:
At channel inlet
At inside barrel wall
For vorticity, boundary condition can be determined from equation for a current:
It was assumed true for the zone before the boundary.
To determine vorticity at the boundary, ∂ψ∂r|r=Re=0condition of melt adhesion should be met. This can be accomplished using a finite difference scheme for a system of equations:
Conditions along the axis of symmetry
With new variables
and with new values of velocity ϑ0, pressure P0, temperature Т0 and viscosity η0, dimensionless values
can be determined.
With (33) and (34), Eqs (21) and (22) and boundary conditions (29)–(32) can be written in a dimensionless form:
Equation for a current function (general equation of motion)
Where:
energy equation
vorticity equation
temperature boundary conditions
current boundary conditions
vorticity boundary conditions
conditions along the axis of symmetry
Thus, a mathematical model was built for a non-isothermal flow of rheological fluid in a cylindrical channel. Expressions assume Re=ϑ0RЭρ/η0(Reynolds number); Ec=ϑ20/ϑ20(T0c)(T0c) (Eckert's number); Pe=ρcϑ0RЭ/λ (Peclet number).
In (37), functionˉΦ is as follows:
Where:
In Eq (35), ˉSω function is nonlinear and contains terms with first and second order derivatives of viscosity function η that characterizes viscosity profile of the melt. The structure of ˉSω function can be selected by modelling the melt flow in the channel using (35)–(43).
When fluid flows out of an adapter channel with a larger diameter into a die cavity of a smaller diameter, a flow forms at a relatively large distance before entering the die. With a certain velocity profile, fluid flow that is entering the metering section transforms into a parabolic one in a stepwise fashion. It is a common case when the melt accumulates in dead spots and flows in circulatory motion, forming vortices.
As can be seen from the mathematical model (35)–(43), process patterns depend on many parameters: Rheological characteristics of melt, channel size, and geometry, thermal, physical and hydraulic properties of the melt, and parameters affecting the process flow (boundary and initial conditions). The flow rate profiles of the melt at a die exit can also be calculated.
Because the mathematical model of a melt flow includes (35)–(43), the finite difference method was applied for numerical implementation. This method was the one settled on because the analytical solution is very difficult to generate and numerical methods are applied mainly to rheological melts [13,14,18].
With the axis of symmetry of the channel, the following system can be drawn (Figure 1).
Figure 4 depicts some channel that is followed by the die inlet. This channel has some radius Rc and some length Lc. To analyze the formation of dead spots near the die, we assumed that the velocity profile of a melt flow in the section is uniform. Such an approach can be applied if the condition Rc > > Rd (3–5-fold, approximately) is met [7,8,19].
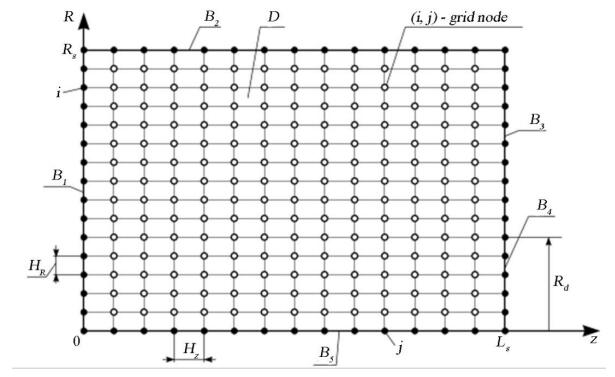
The problem-solving algorithm was considered on a uniform grid. Some domain D was gridded uniformly (grid step Hz and HR with respect to z and R, respectively) (Figure 5).
Let rd be the radius of a die cavity, and lc, rc be the channel length and radius in the metering section. The radius of a die cavity Re was taken as an equivalent to rd in order to solve the problem:
Thus, dimensionless geometry of a channel in the metering section can be found:
For definiteness, let us assume that channel radius rв is tied to the radius of a die cavity: rв = KR rм, where KR–integer (proportionality factor).
Let us determine the grid domain D:
Where:
Where: nz–number of grid steps along the Z-axis; nR–number of grid steps along the R-axis, divides channel radius.
Figure 2 shows boundaries of domain D, which may take the corresponding boundary conditions:
At B1–initial conditions (temperature, vorticity, and current);
At B2. B3–first-order boundary conditions, conditions related to adhesion, or the lack of adhesion, at rheological melt/channel wall interface;
At B4 –condition characterizing melt flow in the channel through the die;
At B5–starting point for setting symmetry conditions for flow parameters.
For discretisation, (35)–(38) were re-written as follows:
Equation for current function
Where:
energy equation
Where: εr=1/Pe;
vorticity equation
Where: ˉη is determined by (46), ˉΦ–by (36) and (44), respectively.
Let us introduce the grid functions Ωij,ψij,andθij into the (i, j) node (Figure 2) (functions correspond to ˉω∗,ˉψi,andˉT):
Below are designations for discretisation of derivatives:
For the second-order derivatives, expressions are the following:
For mixed derivatives, designations are as follows:
In (59)–(61), u can take one of the following values, "Ω","ψ",or"θ" (u∈{"Ω","ψ","θ"}). Formula (61) is used to calculate ˉSω.
With designations (57)–(61) given for internal nodes {i=¯2,Nz−1,j=¯2,NR−1}, Eqs (48)–(51) may be written as:
Steady-state equations, such as (62)–(64), are solved using an interactive method [7,17], which requires the introduction of some definitions.
θij is given at B1, B2. and B3 (Figure 2):
Where: {B1∪B2∪B3}– set of nodes of B1, B2 and B3.
Let θijbe=1 in other points of a grid model, namely on the domain, including boundaries:
At channel inlet, boundary conditions are given as follows:
At channel border:
plus symmetry condition
Let us assume
in all internal points of D.
To determine the vorticity boundary conditions, boundary conditions for a vorticity function were approximated [14]:
Let Ωijbe=0 in all internal points of D.
At free boundary (at the channel exit, B4):
To solve (62)–(64), alternating direction method was used [9,14]. Let us explain its general structure on the example of two-dimensional operator steady-state equation
Let us change (75) to non-steady-state equation
Where: σ-iteration parameter, analogous to time period. Below is the alternative directions scheme:
Where: S–iteration index; σRS, σzS–iteration parameters that differ in direction.
Thus, (75) was reduced to two tridiagonal systems of algebraic equations that can be solved by tridiagonal matrix algorithm. In (77) and (78), ˜u=un+1/122, and ˆu=un+1, so at the first run, fractional solution un+1/122 is found and put in the second run (run in other direction) to find desired solution un+1.
With (77) and (78) in use, solution accuracy can be guided by the absolute criterion
or the fractional criterion
Thus, solution accuracy depends on grid parameters σ and ε. Experimental calculations confirm the existence of grid parameters that are close to those optimal for small Reynolds numbers. These parameters allow obtaining an approximate solution with the least time [14]. They are selected by computer-based experiments. There are methods for calculating the optimal set of parameters for some problems [14].
Let us write equations with the alternative directions for vorticity fields, current function and energy in the internal points of D.
Ⅰ. System of vorticity Eq (7):
Ⅱ.
Where: σSΩz,σSΩR–iteration parameters.
Equations (81) and (82), regrouped by transfer of unknown terms to the left, as well as known terms to the right, are as follows:
Where:
With (59)–(61), Eqs (83) and (84) may be written through Ωij:
or as a tridiagonal system of linear algebraic equations:
Where:
Ⅰ. System of equations for vorticity function (64):
Where: σSψz,σψR–iteration parameters.
With unknown terms of (93) and (94) regrouped to the left and known terms regrouped to the right, transformation will be as follows:
Where:
With (59)–(61), Eqs (95) and (97) may be written through ψij
or as a tridiagonal system of linear algebraic equations:
Where:
Ⅱ. System of energy Eq (63):
Where: σSθz,σSθR–iteration parameters.
With unknown terms of (105), and (106) regrouped to the left, and known terms regrouped to the right, transformation will be as follows:
Where:
With (59)–(61), Eqs (109) and (110) may be written through θij
or as a tridiagonal system of linear algebraic equations:
Where:
3.
Results and Discussions
In this article, a flow of a biopolymer melt is considered a continuous medium. The change in the viscosity of such an anomalously viscous and incompressible fluid is described by the rheological Eq (11) and the description is accurate enough. The Eq (11) is expressed as a generalized power law. This model is intended to describe the movement of a pseudo-plastic fluid the shear stress for which is a parameter defined by the power rheology law. For these pseudo-plastic fluids, viscosity decreases with the increase in the velocity gradient. The verification of obtained solution showed high adequacy: The resulting model allows calculating the flow rates of the rheological fluid melt in different sections near the die cavity with the accuracy sufficient for engineering calculations (± 10%). Therein, the viscosity of a rheological fluid η changes. It decreases by 7%.
The schemes of alternative directions were created to model vorticity fields (89–90), current function (99–100), and energy (113–114). These schemes were presented as a system of algebraic equations. For solving the problem, these equations must be supplemented with boundary conditions (67)–(74).
The problem of melt flow in the metering section was presented in the form of the finite-difference equations for vorticity, current function and energy (89), (90), (99), (100), (113), and (114). Because this problem is a large-scale problem, then solving it requires an iterative method or a sequence of steps.
To model the flow of a rheological melt, Model 1 program was developed in Turbo Pascal 7.0 under Windows 10. This program includes Ris and Glob modules.
The Glob module is designed to set constants and variables used in the program. The Ris module is to display graphs on the monitor, namely, graphs of velocities along the channel axis in various cross-sections.
The key module, Model 1, calculates parameters of rheological melt flow in the metering section.
Block 1 implies the initialization of variables and arrays, as well as the calculation of Re, Pe, Ec, K1, criteria of a difference grid step. Initial values are assigned to grid functions.
At the iterative process start, temperature is assumed to be constant throughout the entire zone. The melt flows with initial velocity through the zone in a non-vortical motion, so the temperature was taken as
Where: Qwall,Qinlet–temperature of channel wall and flow at the channel inlet, respectively;
vorticity as Omij=0,(i,j)∈D,
current as Fmij=0,(i,j)∈D.
Calculation results from model. rez file were used as input data in subsequent modelling.
Block 2 implies the calculation of melt flow rate at channel inlet, which result is assigned to a switching variable.
Blocks 3, 4, and 5 imply the melt flow determination. First, melt flow is determined in metering section, then vorticity and energy are determined. In any case, determination ends when accuracy criteria (79) and (80) are met at Eps = 1·10-6 and σθz=σθR=10000, σΩz=σΩR=σϕz=σϕR=1000.
Block 6 implies the calculation of the volume rate of flow Rashs though the die cavity.
Block 7 implies the analysis of calculations: calculation either continues (return to Block 3), or is finished (move on to Block 8). Calculation is finished if the volume rate of flow through the die cavity overstrives that at the channel inlet.
Block 8 implies the display of results on the monitor and the transfer of calculation results to the model. rez file. The velocity profiles for various sections of the channel are recorded in this file. The velocity profiles of various zones in the channel near the die cavity were displayed on the monitor.
Calculations were made for the rheological melt in a channel, which length was L = 12 mm, which diameter was D = 12 mm, and which die cavities had diameter (d) of 4 mm. The total number of difference grid nodes in D was NzR = 1875. The number of nodes in z-direction was 75, in R-direction–25. The z-coordinate increment was Δz = 0.027, while the r-coordinate increment was ΔR = 0.0417. The melt flow rate at channel inlet was Rashs = 0.0905 m3/s, while at die cavity, it takes the value of Rashs = 0.0926 m3/s, so the error is
Viscosity profile of rheological fluid η dropped from 265 to 248, down about 7%. Initial data and calculation results are given in Tables 1 and 2. Diagrams depicting velocities of rheological melt in various zones near the die cavity are shown in Figures 3 and 4.
Obtained model allows calculating the flow rate of rheological melt in various zones near the die cavity with sufficient accuracy (± 10%).
4.
Conclusions
This article provides a mathematical model of non-isothermal rheological fluid in a cylindrical channel of a die. Computer testing verified the obtained solutions for the compliance with a real extrusion process. Results allow concluding a possibility of using the built-up model in matrix design for single-screw extruders [20,21]. The single-screw extruder is commonly used in polymer processing where the performance of the mixing section is significant in determining the quality of the final product. It is therefore of great interest to simulate the flow field in the single-screw extruder. The mixing performance of the extruder considerably influences the quality and morphology of the final product. For this reason, the flow field in the mixing section has been studied by a number of authors to gain a better understanding of the process. As an example of such work, you can give a link to the work [22]. Our work is different in that in the construction of our model we used more stringent boundary conditions, taking into account the biological nature of the polymer, implying the need for further use of the biopolymer extrudate as a food product.
Acknowledgements
This article was done within the framework of 2018–2020 R & D project "Development of Technology for Pasta Production from Non-Traditional Poly-Grass Raw Materials" (State Registration Number 0118RK00310) funded by the grand of the Ministry of Education and Science of the Republic of Kazakhstan.
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: