1. Introduction
The polymer matrix composites (PMCs) are commonly used in construction, automotive, and aerospace mainly because of high strength to weight ratio [1]. In PMCs, thermosetting epoxy is the most commonly used matrix [2]. The damage tolerance and fracture toughness of epoxy can be enhanced with the incorporation of (nano-) fillers such as metallic oxides [3,4,5], clays [6,7,8], carbon nanotubes (CNTs) [9,10,11], and other carbonaceous materials [12,13,14,15,16]. Various theoretical and computational approaches have been employed to explore the effect of graphene as reinforcement on the performance of polymer nanocomposites including but not limited to, quantum mechanical-based methods [17], Continuum Mechanics (CM) [18], Molecular Mechanics (MM) [19], Molecular Dynamics (MD) [20], atomistic modeling [21], Density Functional Theory (DFT) [22], and multiscale modeling [23]. The mechanical, thermal, and electrical properties of graphene based polymer nanocomposites have widely been studied. Cao [24] has reviewed the atomistic studies on the mechanical properties of graphene and Allegra et al. [25] have reviewed the modeling of polymer nanocomposites reinforced with spherical nanoparticles or statistically isotropic aggregates. The high strength and stiffness of graphene significantly improve the mechanical properties of polymer nanocomposites. Cho et al. studied the mechanical properties of graphene-epoxy nanocomposites with a combination of MM and Mori-Tanaka Method (MTM) [26]. Hamdia et al. [27] used five different sensitivity analysis (SA) methods to study the influence of uncertainty input parameters on the fracture toughness of polymer clay nanocomposites (PNCs). The SA methods include, (1) PAWN, (2) EFAST, (3) Sobol, (4) Regionalized Sensitivity Analysis, and (5) Standardized Regression Coefficient methods. They reported that all methods showed that stiffness of clay, radius of curvature, and aspect ratio have marginal influence on the output with different ranking position. The stiffness of matrix was the most influential parameter, followed by concentration of clay and fracture energy of the polymer matrix.
When nano-fillers are introduced in polymers, the fracture pattern significantly changes due to the deflection of advancing cracks with strong nano-fillers. The topography of fractured surfaces can provide information about the dispersion state of nano-fillers and interfacial interactions. There are two main classifications of topography measurement methods: non-contact techniques, such as focus-follow method, and contact techniques, such as stylus method [28]. Non-contact techniques have found more applications than contact techniques. In case of fragile surfaces, non-contact techniques are especially preferred as damage to surface may occur if contacted. In both the classifications, the parameter definitions remain the same. The results obtained by two techniques are also alike. The non-contact techniques do not only keep the surface under examination intact, but also the topography can be measured easily and quickly. However, these techniques have certain limitations. For example, those regions of surface which are not in the line of sight may not be detected by some non-contact techniques resulting in artefacts. In addition, due to the non-uniform intensity of light, the focus lens may follow the surface inaccurately resulting in the erroneous results. Furthermore, as there is no external agency to interact with the surface, the topography results will be exactly the replica of the surface under examination. At one side, it is an advantage. On the other hand, it may produce artifacts in the results. For example, if the surface contains contaminations, such as dirt, the contaminations will appear in topography profile. This effect may be well pronounced at nano-scale. Therefore, the samples should be prepared meticulously for non-contact techniques.
The influence of topographical features is momentous both at micro and macro levels [29,30]. For example, Karger-Kocsis et al. [31] have rightly reported that hierarchical and hairy fillers have high surface area and capillary wetting by the polymers that can significantly improve the interfacial interactions and result in a concomitant enhancement in the mechanical properties. In addition, various attributes of the polymers can be studied from the fractography analysis of the samples [32]. The topography also becomes very important when the polymers are applied in tribological applications [33]. It is because the cracks in most of the cases originate from the surfaces [34]. The topography plays a crucial part especially in the presence of surface notches as they generate triaxial state of stress in the presence of which the polymers show a marked degradation in mechanical properties, especially when the polymers are thermosetting such as epoxy. Although micro-and nano-scale topography of polymers and polymer nanocomposites have been discussed in detail, however, the influence of macro-topography on mechanical properties of polymers has been overlooked, especially to correlate the fracture patterns with the topography of samples before fracture takes place.
In current work, multi-layered graphene (MLG)/nanoclay-epoxy nanocomposites of three different types were produced: (1) 0.5 wt% MLG-EP, (2) 0.5 wt% nanoclay-EP, and (3) 0.25 wt% MLG-0.25 wt% nanoclay-EP. The maximum enhancement in mechanical properties was recorded in 0.25 wt% MLG-0.25 wt% nanoclay-EP nanocomposites, especially when treated with 1200P abrasive paper. The second highest improvement in mechanical properties was observed in case of 0.5 wt% MLG-EP nanocomposites. However, in case of 0.5 wt% nanoclay-EP, least improvement in mechanical properties was observed. It can be attributed to the interfacial interactions and presence of agglomerates that cause stress concentration and concomitant degradation of mechanical properties [35]. The fractography analysis of the samples revealed that nano-fillers significantly influence the fracture patterns. In addition, a careful examination of the topographical features of the fractured surfaces suggests that the dispersion state of the fillers, interfacial interactions, and presence of any agglomerates of filler can be estimated based on the surface parameters such as maximum surface roughness (Rz or Rmax), surface roughness average (Ra), and root mean square parameter of roughness (Rq). For example, a high value of Rz (with low Ra value) with deep crater and/or trenches indicates the presence of filler agglomerates and concomitant poor mechanical properties of polymer nanocomposites. Similarly, a relatively high surface roughness average with low Rz value indicates uniform dispersion of the filler and simultaneously improved mechanical properties. However, it was observed that waviness average parameter (Wa) does not have any relation with the weight fraction, dispersion state, or agglomeration of the filler.
2. Materials and Method
2.1. Materials
MLG (99.2% purity, 80 m2/g specific surface area, 4.5 µm average lateral size, 12 nm average thickness) used was purchased from Graphene Supermarket, USA. Halloysite nanoclay was used as second filler and purchased from Sigma-Aldrich. The diameter of nanoclay is between 30-70 nm with length 1-4 µm and has a tube-like morphology. The density of halloysite nanoclay is 2.53 g/cm3 and surface area is 64 m2/g. The epoxy and hardeners used were based on bisphenol A-epichlorohydrin and dimethylbenzylamine isophorone diamine, respectively. The resin was purchased from Polyfibre, UK. The densities of liquid epoxy and hardener were~1.3 g/cm3 and~1.1 g/cm3, respectively.
2.2. Production of Samples
The nano-filler was dispersed in the hardener using tip sonicator (Model VC 750, Vibra-cell, USA, 750 W, 250 kHz). Although the sonication was carried out at room temperature, however, temperature of the system rose due to high energy vibration produced by tip sonicator. The resins were vacuum degassed in separate beakers for 30 min. Then, the resins were mixed manually for 10 min. The mixing ratio (by weight) of hardener:epoxy was 1:2. The mixture was again degassed for 15 min. The samples were cast in silicone molds. Two-step curing was carried out: room temperature for 6 h and post-curing at 80°C for 6 h. The top and bottom surfaces of each sample were treated with abrasive papers for 1 min on rotating wheels at rotational speed of 150 rpm.
2.3. Characterization
An Infinite focus Alicona G4 optical microscope was employed to measure topography. The working principle of the microscope is focus-follow method which is a non-contact method. ASTM Standard D792 (Equations 1 and 2) was used to measure densification. The densities of water, hardener, and epoxy were 0.9975, 1.1, and 1.3 g/cm3, respectively. Vickers microhardness was measured using Buehler Micromet II hardness tester (200 g, 10 s). Universal Testing Machine (Instron Model 3382) was used to conduct tensile test (ASTM D638, 4 mm thickness, Type-V geometry, 0.5 mm/min), three-point bending test (ASTM D790, 3×12.7×48 mm, 1.0 mm/min), and mode-I fracture toughness test (ASTM D5045, 36×6×3 mm, crack length 3 mm, 0.5 mm/min, Equations 3-5). ASTM standard D 6110 was used to measure Charpy impact toughness (specimen dimensions 64×12.7×3.2 mm with V-notch of 45°, 2.5 mm depth and 0.25 mm tip of radius) using Equation 6. The weight of impactor head was 400 g and length of impactor arm was 0.4 m.
|
$Experimental \, density = \frac{{Weight \, in \, Air}}{{Weight \, in \, Air - Weight \, in \, Water}} \times Density \, of \, water$
|
(1)
|
|
$Densification {\text{(%)}} = \frac{{Experimental Density}}{{Theoretical Density}} \times 100$
|
(2)
|
|
${K_{1C}} = \frac{{{P_{max}}f\left( {\frac{a}{w}} \right)}}{{B{W^{{\raise0.5ex\hbox{$\scriptstyle 1$}
\kern-0.1em/\kern-0.15em
\lower0.25ex\hbox{$\scriptstyle 2$}}}}}}$
|
(3)
|
|
$f({\raise0.5ex\hbox{$\scriptstyle a$}
\kern-0.1em/\kern-0.15em
\lower0.25ex\hbox{$\scriptstyle w$}}) = \frac{{\left[ {(2 + \frac{a}{w})\left\{ {0.0866 + 4.64(\frac{a}{w}) - 13.32{{(\frac{a}{w})}^2} + 14.72{{(\frac{a}{w})}^3} - 5.6{{(\frac{a}{w})}^4}} \right\}} \right]}}{{{{(1 - \frac{a}{w})}^{3/2}}}}$
|
(4)
|
|
${G_{1c}} = \frac{{K_{1c}^2(1 - {v^2})}}{E}$
|
(5)
|
|
$Impact \, toughness = \frac{{mgh(cos\beta - \cos \alpha )}}{{wt}}$
|
(6)
|
3. Results and Discussion
The mechanical properties have been summarized in Table 1. The values indicate that from the three compositions made with five surface conditions for each composition, the best combination of mechanical performance can be achieved in case of 0.25 wt% MLG-0.25 wt% nanoclay-EP nanocomposites processed with 1200P abrasive paper.
Table 1.Mechanical properties of 0.5 wt% MLG/nanoclay-EP nanocomposites.
| Sr. | Properties | As-cast | Velvet cloth | 1200P | 320P | 60P |
| 1 | Densification (%) | 99.4 ± 0.31 | 99.4 ± 0.32 | 99.3 ± 0.35 | 99.3 ± 0.38 | 99.1 ± 0.4 |
| | 99.3 ± 0.4 | 99.4 ± 0.30 | 99.5 ± 0.33 | 99.2 ± 0.31 | 99.4 ± 0.33 |
| | 99.4 ± 0.25 | 99.4 ± 0.42 | 99.3 ± 0.45 | 99.3 ± 0.36 | 99.1 ± 0.28 |
| 2 | Microhardness (HV) | 359 ± 15.2 | 372.1 ± 10.2 | 395.4 ± 11.8 | 335 ± 18.6 | 298 ± 21.7 |
| | 330.3 ± 21.6 | 362.9 ± 18.3 | 383.8 ± 9.0 | 328.5 ± 18.1 | 312.2 ± 31.4 |
| | 364.9 ± 21.2 | 378 ± 19.2 | 401.3 ± 18.8 | 340.9 ± 18.6 | 303.9 ± 21.7 |
| 3 | Young’s modulus (MPa) | 828.5 ± 29.5 | 839.8 ± 24.5 | 864.1 ± 28.5 | 792 ± 35.9 | 784.9 ± 42.6 |
| | 747.1 ± 22.1 | 780.3 ± 17.6 | 799.6 ± 23.6 | 741.1 ± 28.9 | 710.2 ± 33.8 |
| | 852.5 ± 18.9 | 863.8 ± 16.8 | 888 ± 19.5 | 816 ± 23.4 | 808.9 ± 28.6 |
| 4 | UTS (MPa) | 64.1 ± 1.5 | 66.5 ± 2.1 | 72.6 ± 1.6 | 59.6 ± 1.8 | 55.2 ± 2.5 |
| | 52.8 ± 1.1 | 56.6 ± 1.2 | 62.9 ± 1.3 | 52.3 ± 2.1 | 50.3 ± 3.6 |
| | 68 ± 1.2 | 70.3 ± 1.7 | 76.5 ± 1.9 | 63.5 ± 2.9 | 59.1 ± 3.1 |
| 5 | Tensile strain (%) | 7.9 ± 1.1 | 7.1 ± 0.9 | 7.2 ± 1.6 | 8.8 ± 1.2 | 9 ± 2.1 |
| | 10 ± 0.9 | 10.1 ± 0.8 | 11.1 ± 0.8 | 11.5 ± 1.1 | 14.7 ± 1.8 |
| | 7.7 ± 0.8 | 6.9 ± 0.9 | 7 ± 0.7 | 8.6 ± 1.3 | 8.8 ± 1.8 |
| 6 | Flex. Modulus (MPa) | 799 ± 38.3 | 887.1 ± 25.3 | 897.3 ± 30.5 | 862.9 ± 33.5 | 652.9 ± 42.6 |
| | 734.4 ± 32.7 | 833.8 ± 22.5 | 860.1 ± 33.4 | 816.4 ± 34.4 | 624.7 ± 43.4 |
| | 832 ± 31.4 | 920.1 ± 26.2 | 930.3 ± 31.4 | 895.8 ± 37.5 | 685.9 ± 32.6 |
| 7 | Flex. Strength (MPa) | 78.7 ± 6.9 | 81.5 ± 3.8 | 89.9 ± 2.9 | 75.6 ± 4.6 | 73.6 ± 8.3 |
| | 66.8 ± 5.3 | 73.9 ± 4.5 | 85.1 ± 4.4 | 71.9 ± 6.6 | 62.9 ± 8.7 |
| | 81.7 ± 3.5 | 84.5 ± 3.1 | 92.9 ± 2.6 | 80.1 ± 8.5 | 79.7 ± 10.7 |
| 8 | Flex. Strain (%) | 5.8 ± 0.06 | 5.8 ± 0.29 | 5.9 ± 0.31 | 6.2 ± 0.49 | 6.9 ± 0.4 |
| | 6.7 ± 0.08 | 6.6 ± 0.12 | 6.3 ± 0.13 | 6.9 ± 0.21 | 7.7 ± 0.29 |
| | 5.5 ± 0.05 | 5.5 ± 0.08 | 5.6 ± 0.09 | 5.9 ± 0.12 | 6.6 ± 0.19 |
| 9 | K1C (MPa·m1/2) | 1.12 ± 0.1 | 1.14 ± 0.15 | 1.14 ± 0.05 | 1.13 ± 0.1 | 1.12 ± 0.1 |
| | 0.88 ± 0.08 | 0.78 ± 0.09 | 0.92 ± 0.11 | 0.84 ± 0.13 | 0.83 ± 0.17 |
| | 1.14 ± 0.07 | 1.16 ± 0.08 | 1.17 ± 0.09 | 1.16 ± 0.11 | 1.15 ± 0.13 |
| 10 | G1C (J/m2) | 341.5 ± 51.5 | 546.6 ± 42.3 | 620.5 ± 47.9 | 684.7 ± 62.8 | 759.6 ± 69.8 |
| | 311.2 ± 31.6 | 521.3 ± 26.3 | 589.2 ± 22.3 | 637.1 ± 41.5 | 744.3 ± 48.6 |
| | 365.4 ± 29.3 | 570.6 ± 28.6 | 644.5 ± 22.6 | 708.6 ± 38.9 | 783.6 ± 43.4 |
| 11 | Charpy (kJ/m2) | 1.31 ± 0.15 | 1.45 ± 0.1 | 1.57 ± 0.09 | 1.24 ± 0.12 | 1.21 ± 0.2 |
| | 1.22 ± 0.11 | 1.42 ± 0.09 | 1.33 ± 0.09 | 1.15 ± 0.11 | 1.15 ± 0.17 |
| | 1.35 ± 0.09 | 1.49 ± 0.08 | 1.61 ± 0.1 | 1.28 ± 0.13 | 1.25 ± 0.19 |
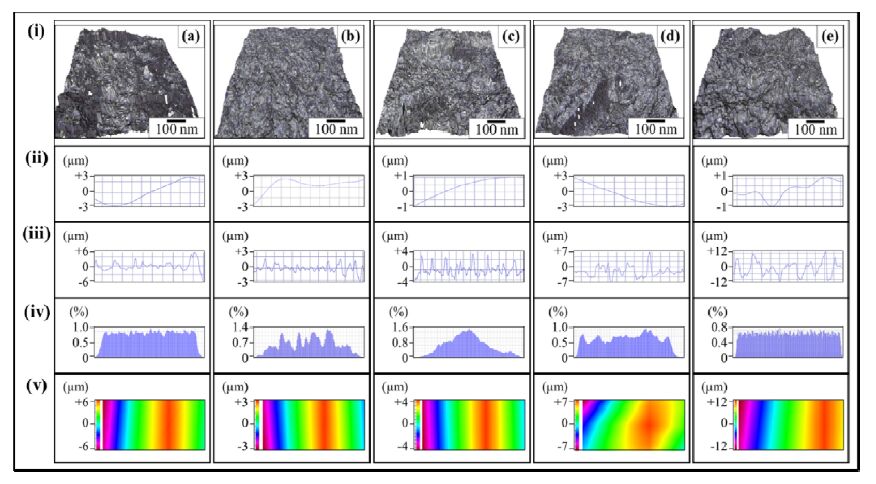
The fractography surfaces of 0.5 wt% MLG-EP nanocomposites are shown in Figure 1.
The monolithic epoxy shows straight bamboo-like fracture pattern indicating the occurrence of typical epoxy brittle fracture. However, with the incorporation of carbonaceous reinforcements, the cracks are rebounded resulting in non-linear and parabolic fracture patterns [36]. This was the reason that no specific orientation of crack propagation was observed in 3PBT specimens reinforced with MLG. The fracture became coarser when the samples were treated with 1200P abrasive paper and velvet cloth while trenches and straight and flat fracture patterns were observed when the samples were treated with 60P and 320P abrasive papers. The fracture patterns of K1C specimens differ from those of 3PBT specimens in a way that fracture was originated from the notch tip as the tip generated high levels of stress concentration. As the displacement rate is relatively low in K1C testing, the surface notches showed a significant impact on the topography of fracture surfaces. However, the influence of surface notches and topographical features on fracture patterns was marginalized in case of Charpy impact testing where the samples were suddenly impacted at the back of the notch by a heavy and pointed hammer. Sheer and straight fracture patterns were observed in Charpy impact specimens and fracture took place right from the tip of notch.
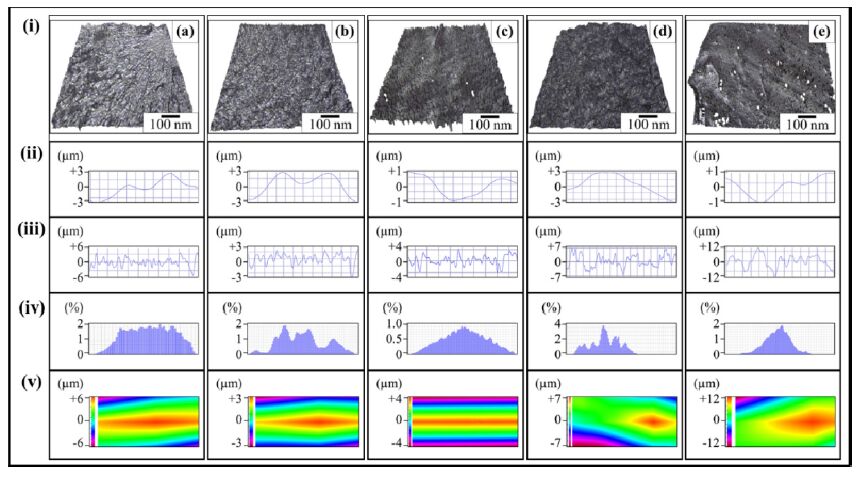
The fractography surfaces of 0.5 wt% nanoclay-EP nanocomposites are shown in Figure 2.
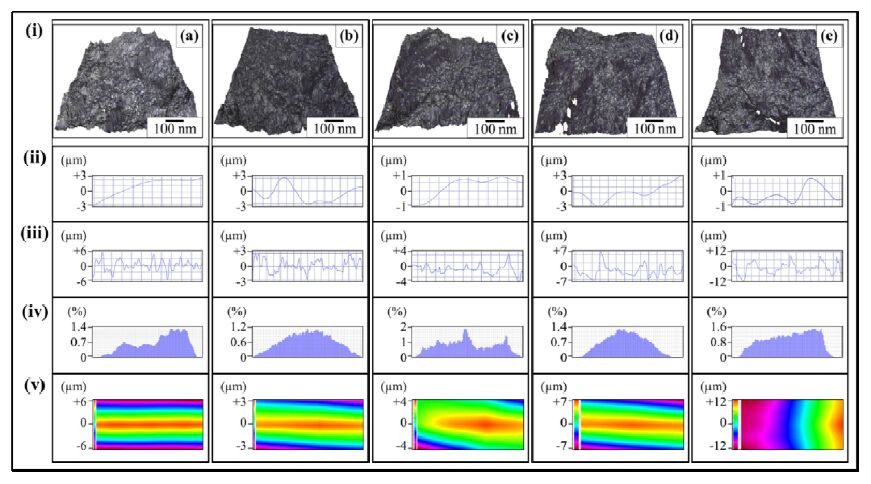
Overall, a coarser topography of fractured surfaces was observed in 0.5 wt% MLG-EP samples than in 0.5 wt% nanoclay-EP samples. No specific orientation of crack propagation was recorded in 3PBT specimens reinforced with nanoclay. As in case of 0.5 wt% MLG-EP samples, the fracture patterns of K1C specimens of 0.5 wt% nanoclay-EP samples differ from those of 3PBT specimens in a way that fracture was originated from the notch tip as the tip generated high levels of stress concentration. As the displacement rate is relatively low in K1C testing, nanoclay also showed a significant impact on the topography of fracture surfaces. However, the influence of nanoclay on fracture patterns was marginalized in case of Charpy impact testing where the samples were suddenly impacted at the back of the notch by a heavy and pointed hammer. Sheer and straight fracture patterns were observed in Charpy impact specimens and fracture took place right from the tip of notch. The fractography surfaces of 0.25 wt% MLG-0.25 wt% nanoclay-EP nanocomposites are shown in Figure 3. Overall, the coarsest topography of fractured surfaces was observed in case of 0.25 wt% MLG-0.25 wt% nanoclay-EP nanocomposites. The details of topographical features are further discussed below.
The topographical features of fracture surfaces of tensile specimen of 0.5 wt% MLG/nanoclay-EP nanocomposites are shown in Figure 4-6. The surface waviness (Figure 4-6ii) and Gaussian distribution (Figure 4-6iv) did not show a specific trend of change with the abrasive papers. It can be attributed to the multiple factors affecting the fracture pattern such as surface notches, MLG/nanoclay distribution, orientation, and interfacial interactions. Usually a specific pattern is observed in waviness due to wobbling of machining tool. On the contrary to Wa, a specific variation in surface roughness (Figure 4-6iii) was observed. The surface roughness of as-cast 0.5 wt% MLG/nanoclay-EP nanocomposites varied between±6 µm with the presence of deep crests and troughs. With the treatment with the velvet cloth, the surface roughness changed slightly which became pronounced in samples treated with 1200P abrasive paper. However, in case of samples treated with 60P and 320P abrasive papers, deep trenches can be observed in roughness patterns (Figure 4-6diii and Figure 4-6eiii) that may be attributed to the presence of large notches. The trenches can also be observed in the surface profiles (Figure 4-6dv and Figure 4-6ev).
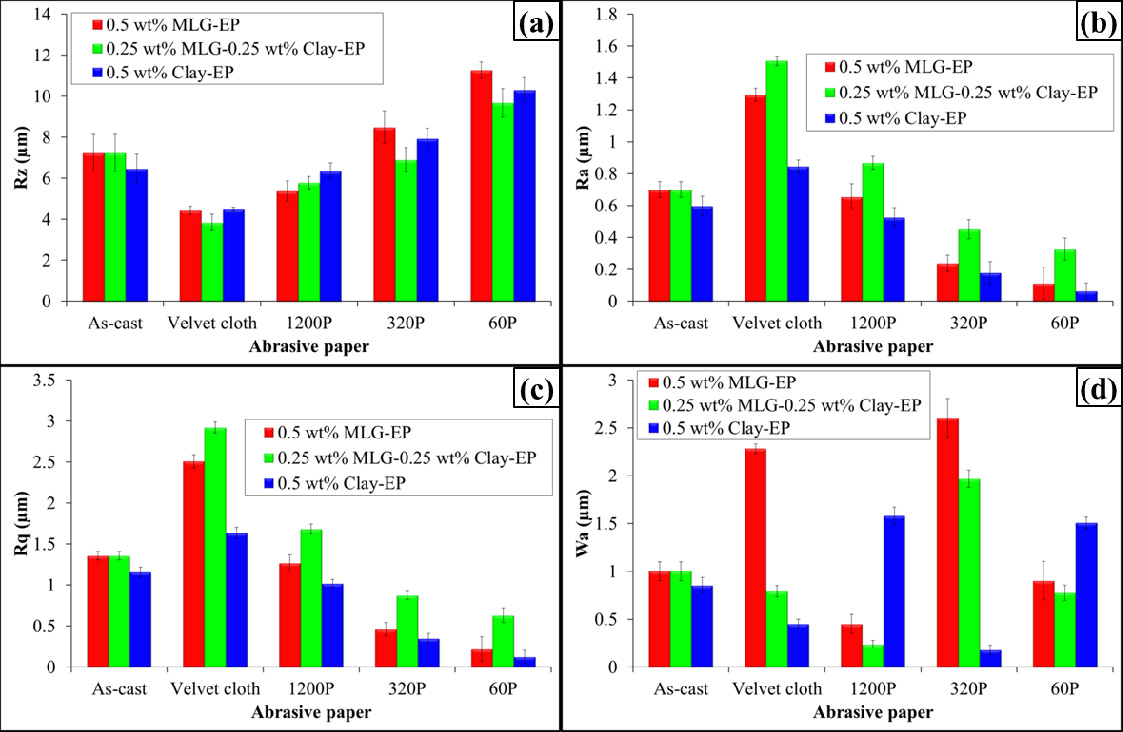
The topographical features are summarized in Figure 7. This Rz comes from the ravines formed due to brittle fracture in the thermoset. The Rz values were significantly decreased by the incorporation of nano-fillers. As ravines present in monolithic epoxy are removed with the incorporation of nano-fillers due to the diversion of advancing cracks, therefore, a decrease in Rz indicates a uniform dispersion of fillers and deflection of the cracks. In addition, an increase in mechanical properties with the incorporation of nano-fillers further corroborates the uniform dispersion of nano-fillers and energy dissipation at deflection of cracks. The variation in Rz value is in accord with the change in the mechanical properties. Therefore, Rz can be an indicator of the dispersion state of filler.
Apart from Rz, Ra is another important parameter to consider. The decrease in Ra with increasing Rz may seem contradicting however can be explained on the basis of observed fractured patterns and surface roughness charts. When treated with 1200P abrasive paper and velvet cloth, no crater was formed due to which lower Rz value was observed. In addition, cracks were deflected quite sharply resulting in sudden variation in surface roughness thereby increasing the Ra value. On the contrary, when treated with 60P and 320P abrasive papers, deep notches were present that caused fracture and increased Rz due to crater formation. However, once cracks formed, it could not deflect much and rest of the fractured surface remained flat thereby decreasing the Ra value. Therefore, a high value of Ra (with low Rz value) can be on indicator of smoother samples surfaces, absence of agglomerates and uniform dispersion of nano-fillers. On the other hand, a low value of Ra (with high Rz value) indicates the presence of deep surface notches, agglomerates, and non-uniform dispersion of nano-fillers. A similar trend was observed in Rq values as in Ra values. However, no specific trend was observed in surface waviness and may not be indicative of dispersion state of nano-fillers and topographical features.
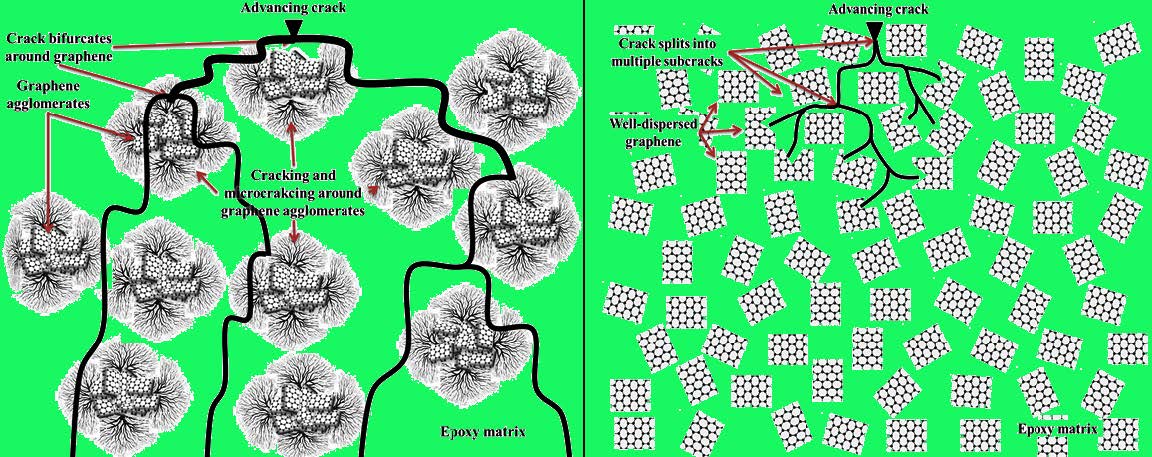
The relationship between dispersion state and nature of crack advancement is schematically shown in Figure 8.
Figure 8(a) is a schematic of poorly dispersed agglomerated graphene in epoxy matrix. As graphene sheets have stress concentration factor associated with them, (micro-) cracks are generated around the graphene agglomerates. These (micro-) cracks may propagate under the application of external load and may lead to fracture. If there is a pre-existing crack in the matrix, it will propagate when load is applied. If the crack faces the agglomerate, it will either be restrained by the agglomerate or detour/bifurcate to circumvent the agglomerate in case of higher loads. However, as graphene is present in the form of agglomerates, a major portion of the epoxy matrix is not reinforced at all. Therefore, crack can easily propagate through the brittle epoxy until fracture occurs. This is possibly the reason why poorly dispersed graphene was not found efficient in improving the fracture toughness of epoxy [37]. This poor dispersion does not only degrade the mechanical properties but also the influence can be observed in case of fractured surfaces. The advancing cracks do not deflect frequently and follow a linear path. Therefore, relatively lower Ra values were observed in case of nanoclay where low mechanical properties were recorded. On the contrary, if graphene is uniformly dispersed, it would be difficult for the crack to move. Figure 8(b) shows a schematic diagram for an ideal situation in which graphene of nearly same dimensions is homogeneously dispersed into epoxy matrix. In this case, as sheet size is relatively smaller than that of graphene agglomerate, the stress concentration factor associated with them is benign and there is almost no (micro-) cracking around individual graphene sheets. If there is a pre-existing crack in the matrix and it starts propagating under the influence of external load, it has to come across graphene sheets at each step. If the external load is high enough, each crack will split into multiple sub-cracks. There is required energy at each division and sub-division of crack to generate new surfaces. Therefore, extensive energy will be dissipated before the crack covers long displacement from its initial position to cause fracture. This will significantly improve the fracture toughness of the epoxy. Therefore, uniformly dispersed graphene is preferred to improve the fracture toughness of the epoxy-graphene nanocomposites. This uniform dispersion does not only improve the mechanical properties but also the influence can be observed in case of fractured surfaces. The advancing cracks is deflected frequently and follow a tortuous path. Therefore, a relatively higher Ra values were observed in case of MLG and MLG-nanoclay nanocomposites where improved mechanical properties were recorded.
4. Conclusion
In conclusion, the topographical features of fractured patterns of polymer nanocomposites can be used to approximate the dispersion state, interfacial interactions, and presence of agglomerates, and overall influence of the incorporation of fillers on the mechanical properties of produced nanocomposites. The highest mechanical properties were recorded in case of MLG-nanoclay-EP nanocomposites. A high value of Ra (with low Rz value) can be on indicator of smoother samples surfaces, absence of agglomerates and uniform dispersion of nano-fillers. On the other hand, a low value of Ra (with high Rz value) indicates the presence of deep surface notches, agglomerates, and non-uniform dispersion of nano-fillers. A similar trend was observed in Rq values as in Ra values. However, no specific trend was observed in surface waviness and may not be indicative of dispersion state of nano-fillers and topographical features.
Acknowledgments
The authors would like to thank the Department of Mechanical and Construction Engineering, Northumbria University, UK for the provision of research facilities, without which the analysis of relevant data was not possible.
Conflict of Interest
All authors declare no conflict of interest.









 DownLoad:
DownLoad: