Abbreviations: DHW: Domestic Hot Water; EED: Energy Efficiency Directive; EPBD: Energy Performance of Buildings Directive; EU: European Union; GHG: Greenhouse Gases; HVAC: Heating, Ventilation, and Air-Conditioning; LED: Light Emitting Diode; MS: Member States; nZE: nearly Zero Energy; nZEB: nearly Zero Energy Buildings; neZEH: nearly Zero Energy Hotels; PV: Photovoltaic; RES: Renewable Energy Sources; ROI: Return on Investment; UNWTO: World Tourism Organisation
1. Introduction
The existing building stock represents a high potential for energy savings [1,2]. Currently, there are a few successful demonstrations of nearly Zero Energy Buildings (nZEBs) in Europe to motivate and initiate replications in the private sector. Hotels in specific, represent a big challenge, since they are usually complex building systems and at the same time, energy intensive businesses [3,4]. The hotel industry is highly depended on energy, which in some luxury hotels is up to 50% of the total Operation and Maintenance cost [5], therefore their challenge is to minimize energy costs without compromising the quality of their guests' stay [6].
Indeed, the hotel industry is the most energy and resource-intensive branch of the accommodation sector. They are "comfort or service-oriented accommodations" [7] with great heterogeneity in terms of business sizes and other individual features. Major studies investigating energy efficiency in the tourism sector pointed out the high potential of energy savings as well as the lack of a systematic approach for investigating its energy use [8]. The credibility and applicability of results shown in many types of research aiming at improving the understanding of the hotel energy flows [9,10,11] are always strongly depended on a wide variety of variables. However, based on different studies [12], the idea of a "typical" hotel remains vague and is required to be linked to a bottom-up approach including hosting and non-hosting activities, as will be explained below.
Although several examples of energy saving in non-domestic buildings exist today [13,14], hotels face difficulties when undertaking energy efficiency actions, mainly due to the existing energy policies, as well as due to being unfamiliar with energy technologies [15].
Since hotels place great significance on the comfort of their guests, they can apply a variety of mechanical and passive cooling means, such as natural cooling, ventilation, shading, thermal insulation etc.
[16], providing a range of options so that architects and developers select the most sustainable strategy. It is clear that the implementation of renewable applications in the hotel/tourism sectors is case sensitive and follows different routes depending on existing needs and climate changes [17].
Studies suggest to integrate energy in the complete environmental performance of the hotels as a part of their excellence and eco-friendly policy [18]. The significant demand for Domestic Hot Water (DHW), not only for sanitary uses but also for swimming pools or spa facilities, can be covered by Renewable Energy Sources (RES), mostly with solar thermal systems [19,20].
This paper summarizes the approach and methodology of the "nearly Zero Energy Hotels" (neZEH) initiative, which is a response to the Energy Performance of Buildings Directive (EPBD) recast, 2010/31/EU [21], supporting the EU Member States (MS) in their national plans for increasing the number of nZEBs [22]. The paper aims to: (ⅰ) describe briefly the methodology for developing neZEH pilot projects; (ⅱ) present the results of energy audits in hotels located in six south European countries (Greece, Croatia, France, Romania, Italy and Spain) plus one north (Sweden) for comparison; (ⅲ) to assess how realistic is the nearly Zero Energy (nZE) vision in the hotel sector.
2. Legislative framework
2.1. European policy
In the EPBD recast (article 2) an nZEB is defined as "a building that has a very high energy performance; the nearly zero or very low amount of energy required should be covered to a very significant extent by energy from renewable sources, including energy from renewable sources produced on-site or nearby". According to the EPBD recast, by 31 December 2020 all new private buildings and after 31 December 2018, all new public buildings should be nZEBs. Even though the EPBD recast provides the framework for nZEBs, the MS should implement it in such a way to reflect their national, regional or local conditions [23].
Furthermore, article 4 of the Energy Efficiency Directive (EED) [24] stipulates that MS shall establish a long-term strategy to trigger investments in the renovation of their existing building stock, both residential and commercial, public or private.
Various reports in the past [25,26,27] have analyzed the status of nZEB transposition in national legislations. According to most recent data, the status of nZEB definition in the EU countries is as follows: 18 countries have set an official definition, in one country the definition is under approval, whereas in nine countries the definition is under development.
In 13 MS, the definition includes also the proportion of RES production. Although most MS reported a wide variety of policy measures, including financial incentives, strengthening their building regulations, communication activities and demonstrations, not in all cases is well-defined whether these measures specifically target nZEBs. Based on data from Concerted Action EPBD, the numerical definitions do not cover all building typologies in all countries; moreover, they are remarkably different in content, calculation assumptions and ambition level.
2.2. Transposition of EPBD in the selected EU countries
Within the context of the neZEH project, the national framework has been analyzed for the seven studied EU countries [6]. Most of these countries have officially introduced numerical definitions for some categories of new and refurbished buildings (Table 1).
Table 1. nZEB numerical definitions for new and refurbished buildings in the neZEH countries (status February 2016).
| Country |
New buildings |
|
Refurbished buildings |
| Status of definition |
Maximum primary energy (kWh/m2/y) |
Share of RES |
Status of definition |
Maximum primary energy (kWh/m2/y) |
| Residential |
Non-residential |
Residential |
Non-residential |
| Croatia |
✔ |
35–80 |
25–250 |
✔ 30% |
The same as for new buildings |
| France |
✔ |
40–65 [a, b] |
70–110 |
✔ Quantitative [c] |
✔ |
80 [a, b] |
60% PE [d] |
| Greece |
Under development |
- |
- |
Minimum share in current requirements for all buildings |
Under development |
- |
- |
| Italy |
✔ |
Class A1 |
50% RES for DHW + 50% RES for (DHW + heating + cooling) |
✔ As for new buildings |
| Romania |
✔ |
93–217 [a, b] |
50–192 [a, b] |
✔ Quantitative |
✔ |
120–230 [a, b] |
120–400 [a, b] |
| Spain |
Under development |
Buildings will need to comply with class A |
Minimum share in current requirements for all buildings |
Under development |
- |
- |
- |
| Sweden |
Under development |
30–75 [a, b] |
30–105 [a, b] |
All energy from RES will be excluded from the consumption values |
ND* |
- |
- |
| *ND = no data; [a] Depending on the reference building; [b] Depending on the location; [c] Requirement depending on the RES measures adopted; [d] Maximum primary energy consumption defined as a percentage of primary energy consumption (PE) of a reference building. |
Estonia has been the first MS, which defined numerical targets for the hotel type of buildings (130 kWh/m2/y of primary energy, 27% RES), including heating and cooling, ventilation, DHW, lighting and auxiliary electricity, as well as the use of appliances [28].
3. Methodology
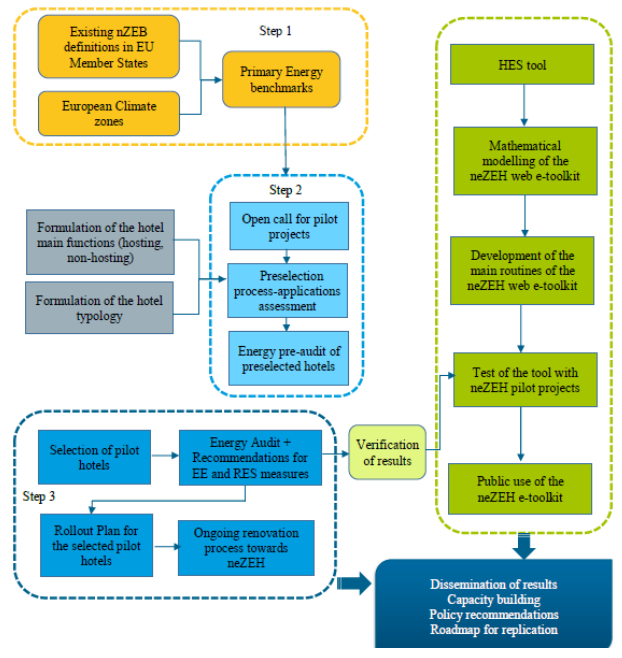
The objective of the European initiative Nearly Zero Energy Hotels [6], involving partners from the tourism and energy efficiency sectors, academia and research and organisations with worldwide impact, like the World Tourism Organisation (UNWTO), was to accelerate the rate of refurbishments of existing hotels into nZEBs. The methodology to achieve this objective consisted of: providing technical assistance to existing pilot hotels for refurbishing into nZEBs, demonstrating the sustainability of investments towards zero energy and undertaking training and capacity building activities at regional, national and EU level (Figure 1).
3.1. Benchmarking methodology
Due to the delay of national transposition of the nZEB definition and given the absence of numerical indicators for hotel buildings in the neZEH countries, there was a necessity to introduce certain benchmarks for primary energy use and RES share. The benchmarks were used as targets for the pilot projects, in the cases where the official definition was not in place.
The benchmarking took into account that hotels cannot be considered as typical non-residential buildings; their business model includes numerous energy-intensive operations related to their customers' comfort and expectations, therefore, closely linked to their competitiveness and viability [29]. Data from Spanish hotels estimate that energy use related to the non-hosting function of the hotel i.e., hotel zones where conditions other than the standard indoor environmental conditions may be required, such as swimming pool, kitchen, spa, etc., can reach to an average 35% of the total energy use [30]. Initially, the research team focused on identifying benchmarks for nZE hotels, taking into account only the typical use of the building, as defined in the EPBD.
According to EPBD recast, the typical use (heating, ventilation, cooling, lighting, DHW) must refer to the standard indoor environmental conditions, which in the case of hotels are the comfort conditions for their guests and staff, as recommended in EN15251:2007 Standard ("Indoor environmental input parameters for design and assessment of energy performance of buildings addressing indoor air quality, thermal environment, lighting and acoustics"). With these principles, the standard zones of a hotel to be considered among the hosting functions are guests' rooms, reception hall, offices, meeting rooms, bar and restaurant.
The additional energy uses of non-hosting functions, such as spas, swimming pools, saunas, gym, kitchens, laundry, etc., can be considered in the future in a "modular" benchmarking based on the results of the pilot projects.
The initial step in the benchmarks calculation was the definition of the climate zones; in this work, five European climate zones were assumed as defined by the Ecofys [31]. Each region within a country was assigned to one of these climate zones.
A reference country with existing nZEB numerical definition or relevant minimum energy performance values was chosen as representative for each of the five European climate zones, in order to have reference numerical values for each zone. The first step calculation included the energy uses of heating, cooling, DHW, HVAC auxiliaries and lighting. Since not all reference values corresponded to the same energy uses, adjustments were made to include energy uses that were missing from some reference values, so as to obtain comparable values for the five climatic zones. The primary energy indicators calculated for the five climatic zones were then increased with extra delivered energy for appliances according to Estonian regulation—which at the time, as mentioned before, was the only country that introduced nZEB numerical definition for hotels—converted into primary energy using the national primary energy factors for electricity. The results were primary energy indicators (benchmarks) for new hotels—all energy end uses included—for the seven neZEH countries, as shown in Table 2 [6]. In order to introduce benchmarks for refurbished hotels, a correction factor of 30% was applied, based on review of existing national nZEB definitions and minimum requirements in building codes with different values for new built and renovated buildings.
Table 2. Country-specific neZEH benchmarks.
| Country |
Primary energy indicator for new hotels (kWh/m2/y)a |
Primary energy indicator for refurbished hotels (kWh/m2/y)a |
| Croatia |
77 |
100 |
| France |
115 |
150 |
| Greece |
76 |
122 |
| Italy |
71 |
93 |
| Romania |
80 |
104 |
| Spain |
72 |
94 |
| Sweden |
134 |
175 |
| aincluding hosting functions + appliances. |
Primary energy indicators for existing hotels (2008 level) were also calculated to provide an insight into the energy reduction needed to be achieved to reach benchmarks for new hotels. Energy use data for existing building stock from EU level sources [32,33,34] were processed, showing that data from residential buildings are more proper to describe the hosting function of hotels than the non-residential building data. The existing residential buildings data by energy source [32] were used in combination with national primary energy parameters in order to calculate primary energy values. Adjustments for additional cooling and ventilation needs were made taking into account EN15251:2007 standard, resulting in primary energy indicators for the hosting function of hotels in each country (2008 level). The comparison of these indicators with benchmarks for new hotels showed that an average 75% energy reduction has to be achieved, a value which is in compliance with previous results [33].
3.2. The pilot projects
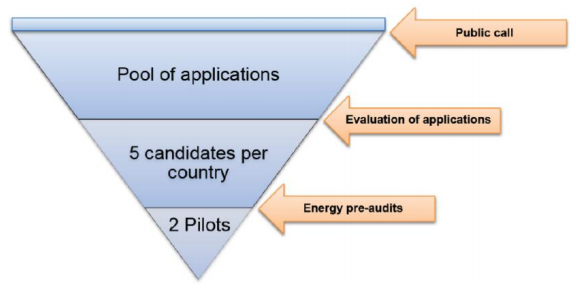
In order to demonstrate the feasibility of refurbishment interventions leading to nZEB status, neZEH supported pilot projects in the seven target countries, which were selected following a three-step process (Figure 2):
(a) Public calls per country; this initial step resulted in a pool of 85 applications.
(b) Evaluation of the candidate applications and selection of 35 hotels (five candidates per country) by applying criteria, including the hotel's commitment and maturity to achieve nZE status, the distribution of selected hotels amongst the different climate zones and the alternative typologies.
(c) Energy pre-audits: the selected hotels were pre-audited in order to assess, in an initial phase, their capability and potential to reach the nZE targets. More accurate energy and economic data helped in filtering and ranking the hotels to lead to the selection of at least two pilot hotels per country.
3.2.1. Climate zones
As mentioned previously in Section 3.1, five European climatic zones were taken into account in the benchmark calculations. These climatic zones were also used as a reference throughout the implementation of the action, meaning that outcomes should be representative per each zone, to make sure that there are replicable examples for all the regions of Europe.
3.2.2. Hotel typologies
Four hotel typologies were identified: (ⅰ) Coastal; (ⅱ) Mountain; (ⅲ) Urban; (ⅳ) Rural. Each participating country had pre-identified the hotel typologies within its region, so as the five candidates during the pre-audit phase would correspond to these typologies.
3.3. Energy audits and feasibility study
An energy audit was implemented in each pilot hotel, which included a full on-site inspection and examination of energy uses, suggesting the most appropriate solutions to reach nZE levels. In more detail the audit included:
• Data gathering and compilation (drawings, energy statistics, utility bills, etc.).
• On-site inspection (study of HVAC infrastructure, lighting status, windows and insulation standards, etc.).
• Calculation of the current energy flows (inputs and losses).
• Recommendations for proper measures ranked based on savings and future costs.
• A proposed action plan.
Following the energy audit, a detailed energy study, as well as a feasibility study were carried out, which included the most suitable technological solutions combined with a cost scenario and the calculation of the Return on Investment (ROI), to assist in the decision making. The following parameters were taken into account when proposing technological solutions:
• The specific characteristics of each hotel (site and orientation, energy consumption, seasonality, etc.).
• The improvement of the thermal comfort conditions for hotel guests, as well as other critical quality parameters for hotels, such as noise levels and overall convenience of guests.
• The cost of each solution based on real market data of each country.
• The funding opportunities, tax reliefs or credit facilities available.
• The payback period of each solution.
The hotels received advice on available funding opportunities and assistance in the tender preparation and selection of contractors for implementing the energy efficiency and RES measures. Furthermore, training was provided to the hotel owners and staff, guiding them on how to maximize their efficiency and optimize the use of the implemented solutions; training material and guides are available to other hoteliers for upscale [6]. Finally, the hotels received marketing guidelines [6] to support them in their effort to communicate their nZE profile to potential guests. The pilot hotels will continue to receive expanded visibility at national and EU level, inspiring more hoteliers to proceed in similar refurbishments and triggering more investments in nZE projects.
4. Results and discussion
The results from seven European countries are presented in this paper. The pilot hotels have been audited, gathering a set of technical and qualitative data for each. Per case, the group of experts analysed each function (hosting and non-hosting). The primary energy use was calculated from building plant characteristics and occupation schedules in relation to real consumption from bills in order to validate them. Although the energy demand for non-hosting functions (pools, bars, restaurants, conference room, spa, etc.) varies from country to country, hotel type, operation months and occupancy, in some hotels it reaches to more than three times the energy demand of the hosting functions (Table 3).
Table 3. Primary energy use and RES share before refurbishment for (a) hosting functions and (b) non-hosting functions for the 16 pilot hotels, as resulted from the energy audits.
| Hotel |
Country |
Hotel typology |
Operating months |
% Average occupancy during opening months |
Facilities |
Primary energy use (kWh/m 2/y) |
RES share (%) |
| Hosting |
Non-hosting |
Hosting |
Non-hosting |
| 1 |
Croatia |
Coastal |
May–Oct |
35 |
spa/wellness |
130 |
16 |
36 |
N/A |
| 2 |
Croatia |
Coastal |
all year |
48 |
spa, sauna, pool, gym |
66 |
60 |
64 |
N/A |
| 3 |
France |
Coastal |
all year |
83 |
lounge bar, pool, spa |
244 |
N/A |
0 |
N/A |
| 4 |
France |
Rural |
Apr–Oct |
44 |
lounge bar, pool, spa |
490 |
N/A |
8 |
N/A |
| 5 |
Greece |
Urban |
May–Oct |
84 |
kitchen, restaurant, pools |
230 |
450 |
30 |
0 |
| 6 |
Greece |
Coastal |
Apr–Oct |
78 |
pools, bars, restaurants, conference room |
250 |
293 |
26 |
20 |
| 7 |
Greece |
Urban |
all year |
80 |
Bar |
287 |
0 |
20 |
0 |
| 8 |
Italy |
Mountain |
Jun–Sep |
21 |
Spa/wellness |
100 |
66 |
74 |
0 |
| 9 |
Italy |
Urban |
all year |
76 |
kitchen, gym |
266 |
24 |
0 |
0 |
| 10 |
Romania |
Urban |
all year |
70 |
restaurant, conference room |
347 |
1,451 |
0 |
0 |
| 11 |
Romania |
Urban |
all year |
59 |
restaurant, conference room |
227 |
588 |
4 |
0 |
| 12 |
Romania |
Mountain |
all year |
20 |
spa, pool, adventure park, conference rooms, restaurant, disco, tennis |
277 |
1,460 |
0 |
0 |
| 13 |
Spain |
Rural |
all year |
22 |
spa, pool, shrine room |
278 |
253 |
9 |
0 |
| 14 |
Spain |
Coastal |
all year |
80 |
spa, restaurant, gym, sauna |
363 |
2,273 |
9 |
0 |
| 15 |
Sweden |
Urban |
all year |
56 |
kitchen, restaurant, sauna |
722 |
1,482 |
0 |
0 |
| 16 |
Sweden |
Urban |
all year |
35 |
kitchen, restaurant, sauna, gym |
151 |
1,285 |
0 |
0 |
| Averages |
|
|
|
|
277 |
727 |
18 |
2 |
Generally, in most cases, as can be concluded from the pilot project results:
• the full-year operating hotels are bigger energy consumers than the seasonal ones, when comparing within the same country.
• the rural/mountain ones have higher primary energy use than the coastal and the urban ones.
• the non-hosting activities very often impose an important burden on the energy performance of hotels.
• the use of RES is limited in most cases, which might not be expected at first.
Energy saving and RES measures were proposed per case, focusing on the energy uses with the highest energy consumption and the most inefficient parts and equipment of each hotel. The set of measures proposed for each hotel should satisfy the target of neZEH benchmarks, in terms of the eventual primary energy use for the hosting functions and the eventual RES share, always in conjunction with economic feasibility. The thermal comfort for guests and the overall improvement of indoor environmental conditions, on the basis of international and national standards (usually around 20 ℃ for winter and 26 ℃ for summer), was also an important parameter. In addition, guest convenience was taken into account, especially in the case of automatic controls, as well as the maintenance of quality and services standards.
The data gathered from the energy audits were used to optimize the simulation models for the calculations of the energy savings and renewable energy production of the proposed measures. The primary energy reduction percentage and RES share were calculated both for hosting and non-hosting functions, in order to demonstrate the energy efficiency potential of the different services of hotels. Results for the total of 16 hotels are presented in Table 4.
Table 4. Energy savings and RES share in hosting and non-hosting functions in the audited hotels.
|
Average primary energy use after suggested interventions (kWh/m2/y) |
Average reduction percentage (%) |
Average RES share after (%) |
| Hosting functions |
102 |
63 |
46 |
| Non-hosting functions |
374 |
49 |
11 |
The overwhelming majority of pilot hotels are able to achieve savings higher than 50% of their initial consumption. That is a substantial saving percentage, taking into account that most of these hotels have been already quite energy efficient. When it came to RES share, the majority of them experienced a coverage increase of at least 20%, while some others have demonstrated up to a remarkable 60%. On average, by applying the measures proposed in the energy audits, the RES share increased from an average of 18% to an average of 46% in the hosting functions.
Primary energy use for the hosting functions across all sixteen pilot hotels can decrease dramatically—from an average of 277 kWh/m2/y to an average of 102 kWh/m2/y; a reduction of 63%. At the same time, RES share for the hosting functions can be increased by an average of 18% to an average of 46%.
The non-hosting functions are, on average, much more energy intensive, therefore, extremely important for the overall performance of the hotel energy efficiency towards the nZEB concept. The primary energy use for the non-hosting functions can decrease from an average of 727 kWh/m2/y to an average of 374 kWh/m2/y, a reduction of 49%.
Amongst the measures which will improve (directly or indirectly) the energy consumption, simple interventions, offering the most attractive payback (i.e., lighting controls, sun-shading devices, shower head diffusers, etc.), are also included. In contrary, building envelope insulation, although being the first priority in terms of energy efficiency and thermal comfort of guests, remains very often less attractive, with up to 25 years payback period (Table 5).
Table 5. Measures suggested after energy audits.
| Measure |
Energy savings (%) |
Investment (€) |
Payback period (yrs) |
| Building envelope insulation |
3–35 |
30,000–350,000 |
6.4–25 |
| Installation of solar thermal collectors |
5–39 |
5,600–143,000 |
10–14 |
| Installation of photovoltaic (PV) panels |
4–23 |
8,000–300,000 |
4.5–20 |
| Installation of Building Energy Management System |
2.6–18.5 |
12,000–125,000 |
6.8–21 |
| Replacement of light bulbs with LED |
2–14 |
1,200–32,000 |
1–9 |
| Lighting controls |
1–7 |
1,300–4,000 |
0.4–2 |
| Replacement of low efficiency with high efficiency heat pumps |
1–36 |
30,000–300,000 |
5.4–11.8 |
| Adding ceiling fans and use of control systems for cooling |
17 |
95,000 |
9.5 |
| Installation of radiant heaters |
1 |
7,000 |
12 |
| Installation of geothermal heating system |
10–58 |
50,000–500,000 |
6–16 |
| Installation of sun-shading devices |
2–6 |
8,000–20,000 |
3 |
| Connection to district heating |
1–26 |
14,000–89,000 |
5–9 |
| Outdoor redesign for better microclimate |
4 |
25,000 |
4 |
| Heat recovery in ventilation |
5.7–8 |
20,000–86,000 |
8–16 |
| Install water saving taps and shower head diffusers |
4.9–7.5 |
350–1,600 |
0.16–0.3 |
| Balance the DHW network |
1 |
4,000 |
7 |
| Replacement of the minibars |
2.1 |
32,250 |
10.7 |
| Balancing and improvements of heating system |
1–21 |
800–38,000 |
1–5.7 |
| Reduce stand-by consumption |
1 |
400 |
1.4 |
5. Energy efficiency in hotels e-toolkit
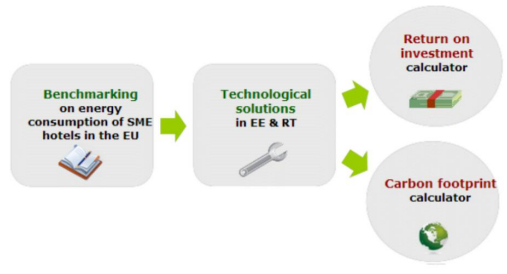
Based on the overall experience gained from the neZEH initiative and its pilot projects, a practical e-toolkit was developed to help hotel owners benchmark their energy consumption compared to the neZEH levels and to suggest appropriate measures for energy efficiency improvement and RES integration. It is designed to increase the energy efficiency capacity in the accommodation industry and to encourage hotel owners to proceed with energy renovation projects towards nZE targets. The neZEH e-toolkit [35] is based on the UNWTO Hotel Energy Solutions toolkit (also co-funded by the Intelligent Energy Programme), which—since 2011—has engaged 20,000 users worldwide and 1,500 hotels in Europe in better understanding how to become energy efficient and more competitive (Figure 3).
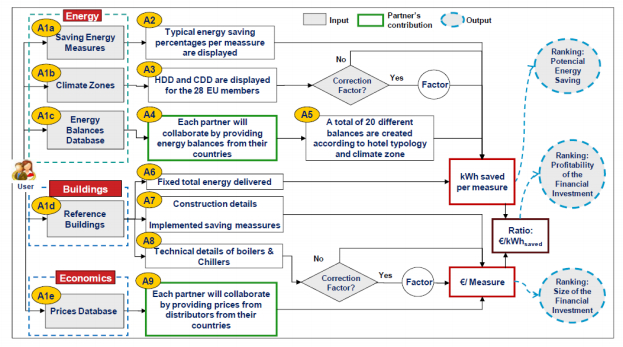
The neZEH e-toolkit uses a ranking methodology at the national level, to rank the identified solutions according to three aspects: potential energy savings, size of the financial investment and profitability of the financial investment, as per the flux diagram shown in Figure 4.
The toolkit is online since 2016 and the target users are the hotel owners or hotel technical staff. It is a user-friendly tool, which requires answers to a short questionnaire and subsequently provides hoteliers with a report assessing their current energy profile, indicating how close the hotel is to from achieving the nearly zero energy levels and providing an indicative set of appropriate renewable energy and energy efficiency measures.
6. Annex: Case study hotel
The case study of Hotel No. 6, as appears in Table 3, is presented in more detail in this Annex. The hotel actual status is calculated with the use of energy bills from all the different energy types, on-site visits and measurement of lamps, equipment, heating, cooling and hot water systems, interviews and cooperation with the hotel management and maintenance departments. The energy audit included building information and measurements, occupancy data from the hotel, description of all mechanical and equipment installations, RES, water and energy use of every building of the hotel. Table 6 shows the general data from the hotel located in a coastal location in the island of Crete. The hotel according to all the information gathered had a primary energy consumption of 250 kWh/m2/y for the hosting functions and primary energy consumption of 293 kWh/m2/y for the non-hosting functions.
Table 6. General data for the hotel case study, as derived from the energy audit performed.
| Hotel typology |
Coastal, Resort & Spa hotel |
| Category |
5 stars |
| Location |
Lasithi, Crete |
| Working season |
April–October |
| Number of beds |
1,036 |
| Mean occupancy |
78% |
| Total hotel area (m2) |
20,866 |
| Thermal zones area (m2) |
18,017 |
| Non-thermal zones area (m2) |
2,849 |
| Annual primary energy consumption (MWh) |
4,624 |
| Electricity energy consumption (kWh) |
1,311,430 |
| Biomass energy consumption (kWh) |
428,400 |
| Oil energy consumption (kWh) |
98,472 |
| LPG energy consumption (kWh) |
270,794 |
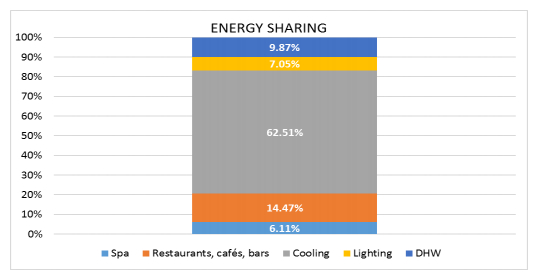
All the information is used for correlations between the occupancy and energy use for different functions of the hotel and also for constructing a simulation model of the hotel. The simulation model is validated from the selected data and is used for the selection and implementation of the proposed energy measures. All the necessary climatic data and thermal comfort boundaries are used for setting points according to the different countries. For this particular example, the simulation model included climatic data from the government database for the location in Lasithi, Crete and the thermal comfort boundaries were set at 20 ℃ for winter and 26 ℃ for summer as proposed in the Greek legislation for energy consumption in buildings. The proposed measures as presented in Table 7 are derived from the hotel necessities and installations with large energy demand, like the cooling loads, which reach to a striking 62% as can be seen in Figure 5. The measures resulted in the primary energy use for the hosting functions to drop to 99 kWh/m2/y (60% energy saving) and RES share to increase to 60%, thus reaching the neZEH benchmarks set for Greece and achieving in this way nZEB status. At the same time, the measures proposed helped the hotel reduce primary energy use for non-hosting functions to 110 kWh/m2/y (62% energy saving) and RES share to rise to 50%.
Table 7. Results of the proposed energy saving and RES measures for the hotel case study.
| Enhancement |
Yearly primary energy savings per m2 (kWh/m2/y) |
Total yearly primary energy savings (kWh/y) |
Avoided emissions (kg CO2/y) |
Simple investment payback (y) |
| Adding heat pumps for cooling and DHW |
92 |
1,667,060 |
456,118 |
5.4 |
| Installing PV modules |
34 |
609,000 |
207,690 |
6.0 |
| Adding insulation and double glazed windows in the central building |
21 |
371,161 |
126,578 |
19.2 |
| Adding solar collectors for DHW and coverage of the spa pool |
13 |
231,184 |
11,805 |
10.0 |
| Adding green for better microclimate conditions |
11 |
198,193 |
67,590 |
4.1 |
| Total |
171 |
3,076,598 |
869,781 |
9.4 |
The project rollout plan assumed a step by step approach, where the priority measures or more economically attractive measures are installed first. The insulation, which is more expensive and has a longer payback time, was set to be installed from 2020 onwards. Despite the long payback, it was decided to eventually adopt this solution as it will greatly contribute to the improvement of thermal comfort for hotel guests and have a positive impact on the hotel standards.
7. Conclusions
It is a known fact that buildings consume 40% of total energy and emit 36% of Greenhouse Gases (GHG) in the EU [37], so the existing building stock represents a high potential for energy savings. Accommodation in specific, counting for 21% of total tourism sector GHG emissions [38], represents a bigger challenge, since hotels are more complex building systems and energy intensive businesses.
This work proposes a step by step approach, starting from an energy audit and resulting in a renovation rollout plan and a marketing plan, and provides useful insights regarding the nZEB benchmarks for hotel buildings, in terms of energy indicators. A complete methodology was developed and applied in the hotel sector to support the implementation of a large-scale renovation towards nZE status. The analysis showed that:
(ⅰ) The vision of nZE in hotels is close to the reality; economically attractive interventions towards nZE are feasible in existing hotels.
(ⅱ) In most of the cases, the achievement of nZE targets is possible to be implemented in two or more phases.
(ⅲ) The non-hosting functions are more critical than the hosting ones, when targeting for high energy efficiency in hotels; this is due to the fact that hotels are not typical buildings, but resemble small communities.
(ⅳ) In most of the cases, the high-tech solutions are not always the best value for money option; low-cost interventions in selected cases could be very economically efficient.
(ⅴ) The hotel industry is very cooperative to become more competitive, but in parallel eco-friendly. Hoteliers acknowledge that they have a lot to gain by implementing energy efficiency measures, including the reduction of operational and maintenance cost, energy security on peak demands, an increase of competitiveness and improved image.
(ⅵ) A key element of the initiative's success is the commitment of the tourism stakeholders to endorse the neZEH concept in hotels, challenging, even more hotels to invest in renovation projects that achieve nΖΕ levels.
In the long-term, the neZEH project plans to support the hospitality sector to reduce operational costs and to enhance competitiveness and sustainability, contributing in parallel to the EU efforts to reach the 2020 and 2030 targets. It is estimated that the investments triggered by 2020 will be 80 M€ and will have as a result: cumulative primary energy savings to reach 42,000 toe/y, RES production of 11,000 toe/y and up to 98,000 t CO2eq/y reduction of GHG emissions.
The 16 pilot projects in Greece, Croatia, France, Italy, Romania, Spain and Sweden, will stand out as "real life" lighthouse examples in Europe and globally and inspire other hotel owners to invest in high energy performance refurbishments, including a large share of their energy needs covered by on-site or nearby RES, as requested by the EPBD recast and EED European Directives.
In line with other published reports and papers, this work would like to highlight the significance of capabilities building actions as a crucial part of the policy packages promoting nZEBs, maybe by a potential shift from subsidizing applications [39].
Additionally, the authors suggest future work should consider a "modular" benchmarking, with a specific focus on non-hosting functions, in order to provide recommendations for policy makers for dealing with hotel buildings' complexities. The parameters which affected the results, identified in this work, were the hotel typology, climate zone, offered facilities, operation seasonality. The data results obtained and presented in this paper can be used in a future study to define modular benchmarks for hotels, on the basis of the different parameters that define how much and how energy is being used in European hotels.
Acknowledgments
This work was supported by the European Commission under the Intelligent Energy Europe Programme, within the framework of the project neZEH (Nearly Energy Zero Hotels, www.nezeh.eu) [grant number IEE/12/829/SI2.644758, 01/04/2013 to 31/03/2016]. The sole responsibility for the content of this paper lies with the authors. It does not necessarily reflect the opinion of the European Union. The European Commission is not responsible for any use that may be made of the information contained therein.
The authors would like to thank the following persons for their active involvement in the project neZEH: Rodrigo Morell and Ignacio G. Hernandez (Creara Consultores S.L., Madrid, Spain), Zoritsa Urosevic (World Tourism Organization, Madrid, Spain), Cristina Nunez (Network of European Regions for Competitive and Sustainable Tourism, Brussels, Belgium), Anita Derjanecz (Federation of European Heating, Ventilation and Air-conditioning Associations, Brussels, Belgium), Camelia Rata (Agency of Braşov for Energy Management and Environment Protection, Braşov, Romania), Marko Bišćan (Energy Institute Hrvoje Požar, Zagreb, Croatia), Stephane Pouffary (ENERGIES 2050, Villeneuve-Loubet, France), Sara L. Sacerdotti (Sistemi Territoriali per l'Innovazione, Torino, Italy), Nigel Claridge (Sustainable Innovation, Stockholm, Sweden).
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: