Distributed delays in a hybrid model of tumor-Immune system interplay

1.   Introduction

The importance of fractional differential equations (FDE) needs no emphasis as they are considered to be fundamental in the analysis and modeling of numerous physical phenomena of science and engineering such as heat conduction, viscoelasticity, polarization, diffusion waves, electromagnetic waves, signal processing and control theory ADDIN EN.CITE.DATA ^[1,2,3,4,5]. Fractional dynamic systems that contains a single differential operator in the equations are sometimes found insufficient to accurately and realistically address the problems effectively, therefore, at times it is necessary to use multi-term fractional differential equations (MFDE) instead. For example, to illustrate the motion of real physical systems, the modeling of the motion of a rigid plate immersed in a Newtonian fluid and a gas in a fluid, respectively. Also the asymptotic behavior for low and high frequencies in the modeling of frequency-dependent damping materials are well described by the fractional differential equations of $1/2$-order or $3/2$-order^[6,7]. The mathematical model for such materials are elegantly modeled by a MFDE named Bagley Torvik equation (BTE), which was introduced by Bagley and Torvik in the beginning of 1980's as their work on the manifestation of fractional derivative in the behavior of viscoelastic materials and is generally given as:

where, $g\left( x \right)$ is the unknown function, ${\omega _1}$, ${\omega _2}$, ${\omega _3}$, ${\omega _4}$ and ${\omega _5}$ are the constant coefficients and $X$ is a constant representing the computational domain of the inputs $x \in \left[ {0, X} \right]$. These BTEs plays a vital role in solving numerous problems of real life and since its first appearance in 1980, it has been solved for its numerical and analytic solutions by many scholar and scientists ADDIN EN.CITE.DATA ^[8,9,10,11].

In the past few years, many heuristic and meta-heuristic algorithm have been proposed to solve various global optimization problems. By far the majority of new meta-heuristic algorithms are inspired by nature among which, the largest fraction of these nature inspired algorithms are based on some successful characteristics of a biological system. The bio-inspired meta-heuristic algorithms particularly those based on the swarm intelligence are an essential part of the modern global optimization algorithms. Over the past few decade, the swarm intelligence based (SIB) algorithms have gained strong attention of scientists and researchers due to its remarkable advantages as compared to the traditional optimization techniques used earlier ^[12,13,14]. The SIB algorithm which have been developed by drawing inspiration from the swarm intelligence system in nature includes the firefly algorithm (FFA) which is based on the flashing pattern and behavior of swarming fireflies ^[15], while the cuckoo search algorithm (CSA) uses the parasitic strategy of cuckoo species ^[16], particle swarm optimization (PSO) and its improved version known as the accelerated particle swarm optimization algorithm (APSOA) are based on the swarming behavior of birds and fishes schooling in nature ^[17,18], the ant algorithm (AA) mimics the behavior of social insects (i.e., ants) ^[19], the bat algorithm (BATA) which is one of the most powerful and extensively used meta-heuristic algorithm based on the echolocation behavior of foraging bats ^[20,21,22] and many more. On the other hand there are some meta-heuristic algorithms which are bio-inspired but are not based on the swarm intelligence such as the genetic algorithm (GA) ^[23], the differential evolution algorithm (DEA) ^[24,25] and the flower pollination algorithm (FPA) ^[26].

The BATA developed by Yang is one of the latest bio-inspired meta-heuristic algorithm which is based on the echolocation behavior of foraging microbats. The echolocation capability of microbats is very fascinating, which is used to detect prey and avoid obstacles even in complete darkness. The microbats emit loud sound pulse and sense the echo that is reflected by the surrounding objects, which enables them to determine the environment around them. This interesting process of emitting and reflecting sound waves is mimicked in Figure 1. These bats build a 3D image of the surrounding in their brains by using the deferral time of the response, time difference between the two ears and the loudness variation of echoes. The varying pulse rate of emission and loudness provides a mechanism for auto-zooming into the region where promising solutions are found. To further enhance the performance of this highly efficient and powerful algorithm many new variants of BATA algorithm have been produced which are found in the literature ADDIN EN.CITE.DATA ^{[20,21,22,27]}.

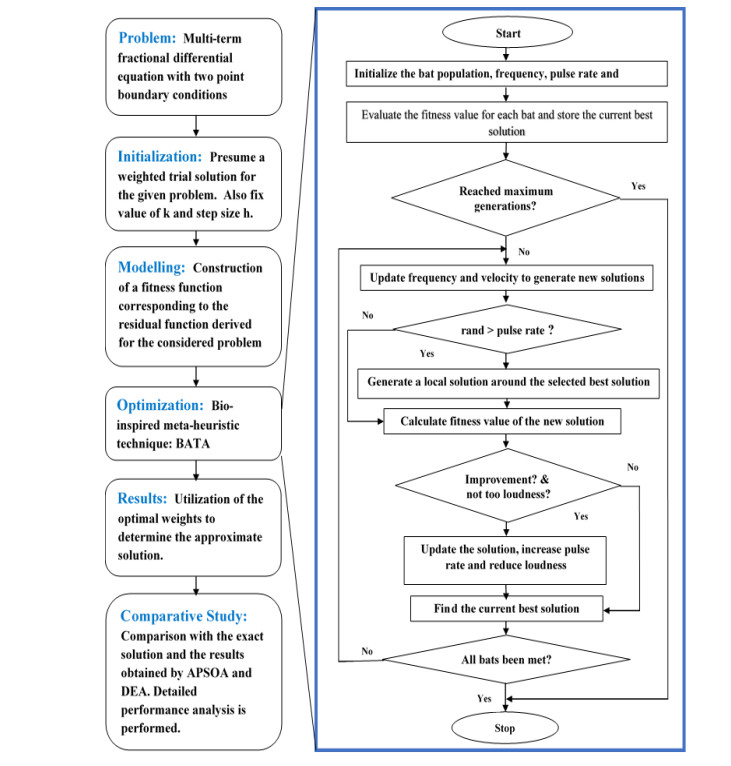
In the present study a framework is provided to solve MFDEs subject to four different variants of the two point boundary conditions, which are commonly used to solve real world problems. The residual power series method (RPSM) introduced by Arqub ^[28] in 2013 provides an efficient and practical approach for determining the analytical solution of classical differential equations (DEs). This numerical technique (RPSM) based on the generalized Taylor series formula was later modified and successfully applied to solve various types of FDEs ADDIN EN.CITE.DATA ^{[29,30,31,32]}. The new residual optimization technique (NROT) suggested in this framework is an amalgamation of the BATA with the principal idea for constructing the solution of the FDEs offered in RPSM. Moreover, the validity and accuracy of the NROT is further ratified by incorporating the idea of the RPSM with two other popular and powerful bio-inspired meta-heuristic algorithms, i.e., APSOA and DEA.

The silent features of the employed technique are summarized as:

● Developing a non-interrupted and non-iterative NROT by using the fractional approach in Caputo sense to solve MFDEs subject to a set of four elementary boundary conditions.

● Optimization of the constructed residual function to attain the optimal values of the unknown weights in the considered power series solution.

● Utilization of the BATA to achieve the desired fitness of the residual function along with two other influential and proficient optimization techniques i.e., APSOA and DEA, to ratify the accuracy and consistency of the presented scheme.

● Framing the designed methodology of the presented scheme along with the relevant parameters detailing.

● Performing numerical simulation and statistical analysis to analyze the performance indices.

A brief overview of the paper is as follows: In Section 2 fundamental definitions and theorems are presented. The designed methodology is projected in Section 3 with the learning solver described in Section 4. The mathematical formulation of the considered performance indices is displayed in Section 5 with the discussion of the attained numerical and statistical results given in Section 6. Lastly, the summary and highlight remarks are listed in Section 7.

2.   Preliminaries

This section comprises of some essential definitions and results of fractional calculus that are going to be used in the further discussion.

Definition 2.1. For a continuously differential function $f\left( x \right)$ the Caputo fractional derivative ${}^cD_0^\gamma f\left( x \right)$ for $x > 0$ is defined as ^[32,33],

While, the direct implementation of Caputo fractional derivative on a power function ${x^\varpi }$ is expressed as,

Where, $x > 0$ and $\tau - 1 < \gamma \leqslant \tau $ for $\tau \in \aleph $.

Definition 2.2. A power series (PS) expansion about $x = {\bar x_0}$ expressed in the form,

where, all constant coefficient ${w_i} \in \Re $, $x \geqslant {\bar x_0}$ and $0 \leqslant \tau - 1 < \gamma < \tau $ for $\tau \in \aleph $ is called a fractional power series (FPS) about ${\bar x_0}$ ^[34].

Theorem 2.3. Suppose that a FPS representation of a function $f\left( x \right)$ about $x = {\bar x_0}$ given by,

If ${D^{i\gamma }}f\left( x \right)$ are all continuous on $\left( {{{\bar x}_0}, {{\bar x}_0} + {R^*}} \right)$ for $i \in \aleph $ and ${R^*}$ as the radius of convergence then the constant coefficients can be expressed as,

where, ${D^{i\gamma }} = {D^\gamma } \cdot {D^\gamma } \cdot {D^\gamma }...{D^\gamma }$ (i^th times).

3.   New residual optimization technique (NROT)

Consider a non-linear multi-term fractional differential equation expressed as:

subject to the initial conditions written as:

and the boundary conditions at $x = {x_n}$ given as:

where, $\forall {\alpha _i} \in \Re , i = 1, 2, 3, ..., j$ such that $0 < {\alpha _1} < {\alpha _2} < ... < {\alpha _j} < r \in \aleph $.

Now for the proposed technique we assume the weighted trial solution of Eq. (7) is of the form:

where, $\forall {w_i};i = 0, 1, 2, ..., \aleph , $ are the unknown weights of the trial solution $\phi \left( x \right)$. Then the residual function for the k^th order approximate solution of the k^th truncated series of the weighted trial solution satisfying the boundary conditions is written as:

with

where, $R_{^{\phi , k}}^k\left( x \right)$ comprises of the $k$ unknown weights. Differentiating Eq. (10) and using $\phi \left( x \right)$ along with the defined set of possible initial and boundary conditions we obtain:

By using Eq. (13) and Eq. (14) in Eq. (10), the k^th truncated series of the refined trial solution is given by:

where, $\forall {w_i};i = 1, 2, ..., k - 1, $ are the unknown weights of the trial solution $\phi \left( x \right)$, which are to be determined. The modified residual function along with the corresponding fitness function for the considered MFDE (7) attained by the utilization of the revised trial solution (15) are given as Eq. (16) and Eq. (17), respectively.

where, ${{x}_{i}}=i{{h}^{*}}$, with the step size ${h^*} = X/v$ and $v$ as the sample size of the collocation points for the computation domain $[0,X]$. The derived fitness function (17) defined in the mean square sense comprises of $k - 2$ unknown weights which are determined in an accelerated and profitable manner by making use of an efficient and powerful optimization technique BATA. Graphical abstract of the above projected scheme (NROT) is portrayed in Figure 2.

Lemma 3.1. For problem (7) subject to the two point boundary conditions, if the trial solutions $\phi \left( x \right)$ is in the form of Eq (15), then it satisfies the conditions (8) and (9).

Lemma 3.2. Consider a continuous and integrable function $\phi \left( x \right)$ defined in some interval $\left[ {0, X} \right]$, then the series (10) converges if the remainder term defined in the weighted trial solution approaches to zero as $k$ tends to infinity.

Theorem 3.3. Suppose $\phi \left( x \right)$ be an integrable and continuous function defined in $\left[ 0,X \right]$ with ${{\left( x-{{{\bar{x}}}_{0}} \right)}^{i}}\le M$ for all $i=0,1,2,\cdots ,k$ and the optimal values of $k-2$ unknown weights achieved by the considered meta-heuristic techniques such that $\left| {{w}_{i}} \right|\le {{M}^{*}};i=1,2,\cdots ,k-1$ then the refined series solution (15) converges as $k\to \infty $.

The proof easily follows by utilizing the aforementioned Lemma 3.2.

4.   Learning solver: BATA

Bat-inspired algorithm (BATA) is a relatively new and powerful meta-heuristic algorithm based on the successful characteristics of biological system (i.e., echolocation behavior of the microbats). They emit loud sound and listen for the echo that is reflected back by the surrounding objects. Studies from the past have proved that these bats have the ability to locate and identify the target, the type of target and even the moving speed of it. Moreover, the wing flutter rate of the prey induces a Doppler effect which helps these foraging bats to discriminate between the targets. In BATA the travelling range of the emitted pulses can be adjusted by either adjusting the wavelengths $\tilde \lambda $ or the frequencies $\tilde f$ because they are related to each other in the form of the constant $\tilde \lambda \tilde f$. The three most idealized rules used for developing the code of bat-inspired algorithm are as follows:

● All bats use their echolocation capability to avoid obstacles and detect prey in the dark.

● Bats fly randomly with the velocity ${\tilde v_i}$ and frequency ${\tilde f_{\min }}$ from the current position ${\tilde x_i}$ but with varying loudness and rate of pulse ${\tilde r_i} \in \left[ {0, 1} \right]$, which depends on the proximity of the target.

● While the loudness can vary in many ways, from a minimum value ${\tilde A_{\min }}$ to a large positive value ${\tilde A_0}$ or vice versa.

After initializing the dimension ${n^*}$ and the population of bats, new solution are established by updating the velocity and frequency of the i^th bat and consuming the above rules that can be translated into the expressions given as,

where, $\hbar $ is a random number drawn from a uniform distribution, ${x^*}$ represents the current best solution and the fixed frequency range denoted by $\left[ {{{\tilde f}_{\min }}, {{\tilde f}_{\max }}} \right]$. As the iterations proceed the loudness and pulse rate for some constants ${\theta _1}$ and ${\theta _2}$ are updated by using the expressions given as follow:

with $0 < {\theta _1} < 1$ and ${\theta _2} > 0$. Here, in the implementation of BATA in the deliberated scheme (NROT) for the learning of unknown weights in the acquired fitness function (17) the parameter values are presented in Table 1.

To further ratify the correctness and efficiency of the NROT the solutions are also constructed by using the algorithm APSOA defined in ^[18] and the built-in MATHEMATICA codes for the DEA used in the software MATHEMATICA 11.0 for the optimization of the fitness function defined as Eq. (17).

5.   Performance evaluation

Performance indices based on the root mean square error ${P_{RMS}}$, mean absolute deviation ${P_{MAD}}$, Nash Sutcliffe efficiency ${P_{NSE}}$ and the Global mean fitness $GMF$ are utilized to analyze the proposed methodology in detail for the solution of linear and non-linear MFDEs subject to four different types of boundary conditions.

In reference to the solution obtained by the designed methodology, the definition of ${P_{MAD}}$ and ${P_{RMS}}$ in terms of the approximate solution $y_i^*$, exact solution $y_i^e$ and input grid point equal to $K$ are mathematically defined as:

The mathematical definition of Nash Sutcliffe efficiency, ${P_{NSE}}$ along with its error function ${P_{ENSE}}$ is given by:

and

A global operator based on the mean fitness value is written as:

where, ${\left. {E\left( x \right)} \right|^\mu }$ stands for fitness of the ${\mu ^{th}}$ run and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{K} \in \aleph $ represents the total number of independent runs of the algorithm. For an ideal system the error based indices of ${P_{RMS}}$, ${P_{MAD}}$, ${P_{NSE}}$ and $GMF$ are zero, while optimal value of ${P_{ENSE}}$ is equal to one.

6.   Simulation and results

In this section, numerical results of the suggested scheme (NROT) optimized using BATA are presented here for the assessment of linear and nonlinear non-homogenous MFDEs subject to four different variants of boundary conditions that cope a reasonable spectrum of possible cases. Furthermore, to validate the correctness and effectiveness of the deliberated scheme the results are also constructed by using the present scheme NROT in conjunction with two other powerful and efficient meta-heuristic techniques i.e., APSOA and DEA. The parameter setting for BATA, APSOA and DEA are defined in Table 1. In addition, comparative study is also conducted on the basis of performance indices formulated in the above Section 5. The reliability and accuracy of the suggested scheme NROT using the meta-heuristic solver BATA is further analyzed through the statistical results based on the large number of independent runs.

The boundary value problems for these four variants are given below:

Case Study I

Consider the following fractional non-homogenous MFDE

subject to the Neumann boundary conditions given as:

Here, the exact solution is $\phi \left( x \right) = {x^2}$. Assuming Eq. (15) as the approximate solution of Eq. (25) and by utilizing the boundary conditions (26) the truncated trial solution is obtained, which yields the residual function of ${k^{th}}$ order written as:

which automatically leads to a fitness function formulated as:

Case Study Ⅱ

Consider the following fractional order MFDE

with the Dirichlet boundary conditions written as:

The exact solution of the above formulated MFDE is $\phi \left( x \right) = {x^2} - x$. The residual function attained by the NROT is expressed as:

with the related fitness function given as:

Case Study Ⅲ

The proposed scheme is now tested on another form of MFDE with the two point boundary conditions given as:

The exact solution of the Eq. (33) is $\phi \left( x \right) = {x^2} + 1$ with the residual function accomplished by using the NROT is presented as:

which automatically leads to a fitness function written as:

Case Study Ⅳ

Consider the following non-linear MFDE,

with two point boundary conditions given as:

Here, the exact solution of Eq. (37) is $\phi \left( x \right) = {x^3}/3$ with the residual function derived using the NROT is formulated as:

By using the proposed scheme Eq (39) automatically leads to a fitness function presented as:

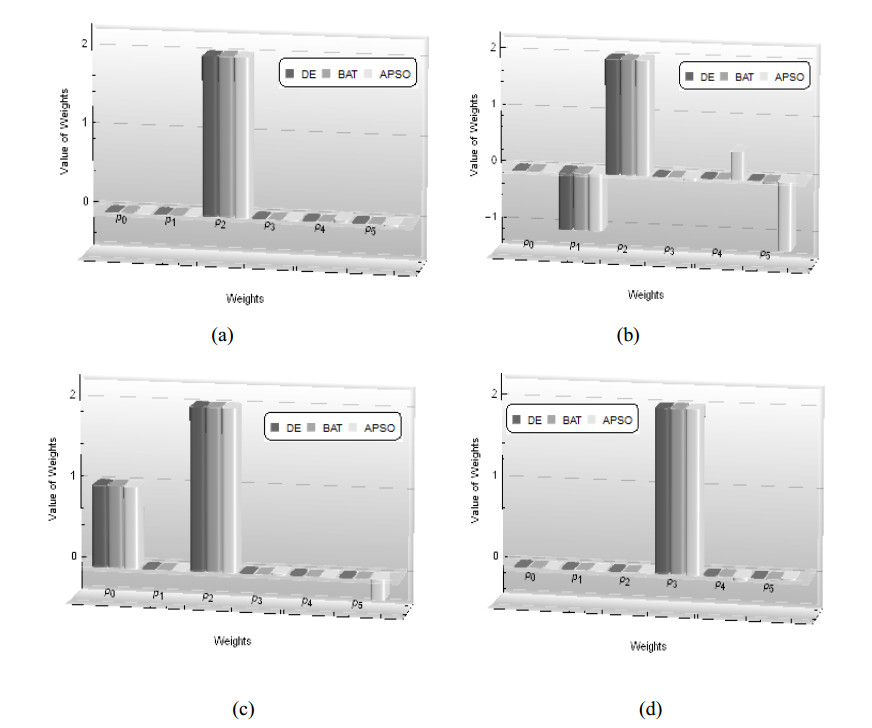
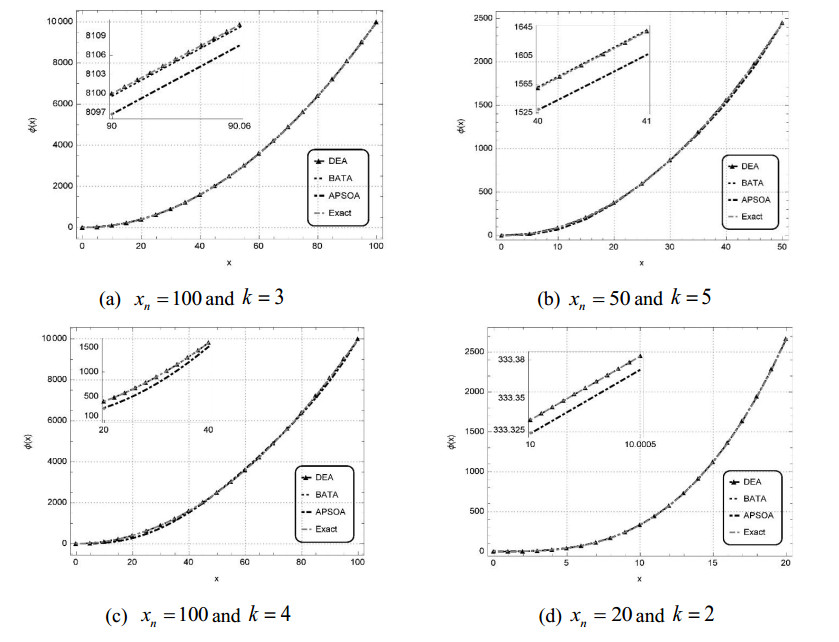
Minimization of the above given fitness functions (28), (32), (36) and (40) defined for the respective four test cases of the MFDEs is carried out by applying the proposed design methodology (NROT) using BATA, APSOA and DEA, with the parameter settings provided in Table 1. One of the best set of weights learned stochastically by using BATA, APSOA and DEA with ${x_n} = 1$ and $k = 5$ for all the cases are graphically presented in Figure 3(a-d), respectively. The numerical results attained by utilizing a particular set of weights learned stochastically using the BATA for the aforementioned cases Ⅰ–Ⅳ, which yields a fitness value (FV) $1.67350 \times {10^{ - 9}}, $ $6.07290 \times {10^{ - 9}}, $ $1.87730 \times {10^{ - 9}}$ and $2.22120 \times {10^{ - 9}}$ are presented in Tables 2–5, respectively. Analogously, the results are evaluated by the NROT incorporated with the other two very powerful and efficient optimization techniques i.e., APSOA and DEA, that are presented in Table 2 for case Ⅰ, Table 3 for case Ⅱ, Table 4 for case Ⅲ, and Table 5 for case Ⅳ, which evidently interprets about the reliability and competency of the recommended scheme. The fitness values accomplished by the NROT in combination with the APSOA and the DEA are presented in Table 6. Furthermore, these Tables 2–5 also contains the related absolute error (AE) defined as the deviation between the results obtained by the NROT in combination with three different stochastic techniques (i.e., BATA, APSOA, DEA) with the respective exact solution ${\phi _e}$ for each case. Whereas, the values of maximum absolute error (MAX-AE) accomplished by using BATA for cases (Ⅰ-Ⅳ) are $1.17878 \times {10^{ - 5}}, $ $4.08576 \times {10^{ - 6}}, $ $1.95158 \times {10^{ - 5}}$ and $9.65586 \times {10^{ - 6}}$, respectively. The accuracy and convergence of the offered scheme is further analyzed in term of the performance indices defined as Eqs. 20–24. The optimal values of root mean square error ${P_{RMS}}$, mean absolute deviation ${P_{MAD}}$ and Nash Sutcliffe effciency ${P_{NSE}}$ achieved by the implementation of the NROT in conjunction with BATA, APSOA and DEA for all the test cases are portrayed in Table 6. Similarly, the values of the error estimates achieved by the implementation of the suggested scheme incorporated with BATA for cases Ⅰ–Ⅳ with the parameter setting defined in Table 1, for a larger span (i.e., ${x_n} = 5$ ) and $k = 5$ presented in Table 7 demonstrates about its accuracy and reliability of the proposed technique. Moreover, the solution for the above cases are also constructed for a larger span by using the offered technique in combination with the APSOA and DEA. Graphical solutions portrayed in Figures 4(a-d) at different values of $k$ and $h = 0.5$ with ${x_n} = 100$ for case Ⅰ; ${x_n} = 50$ for case Ⅱ; ${x_n} = 100$ for case Ⅲ; and ${x_n} = 20$ for case Ⅳ, respectively, clearly illustrates about the constructive agreement between the exact solution and the results obtained by the NROT amalgamated with BATA, APSOA and DEA.

The above discussion validates about the correctness and accuracy of the NROT incorporated with BATA, APSOA and DEA. The numerical results also interprets about the outclass performance of the BATA in terms of accuracy and competency which outstands the APSOA. Whereas, the DEA computed results outperforms both ^[36,37]. Moreover, the deliberated scheme (NROT) is better than all the former numerical and approximate techniques defined in the literature, as it requires no linearization, integration or transformation to successfully solve the MFDEs subject to different possible variants of boundary conditions. Accuracy, competency and computational intelligence are the main attributes of the suggested scheme, which remains valid even for a larger span of the computational domain.

Statistical analysis

This section contains the results of statistical analysis in terms of mean, standard deviation and mean deviation for the fitness achieved by the execution of 100 independent runs to solve the above defined cases of the MFDEs. The reliability and accuracy of the recommended scheme are validated by this analysis.

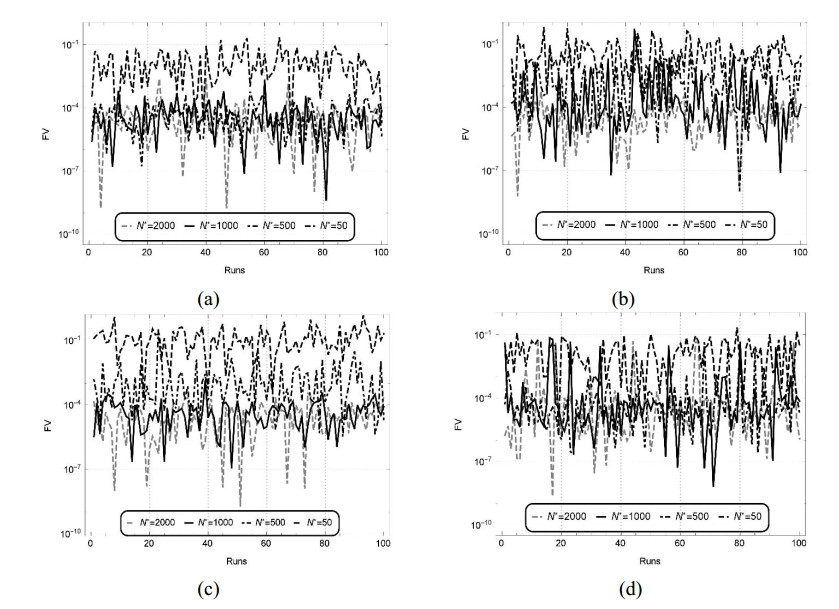
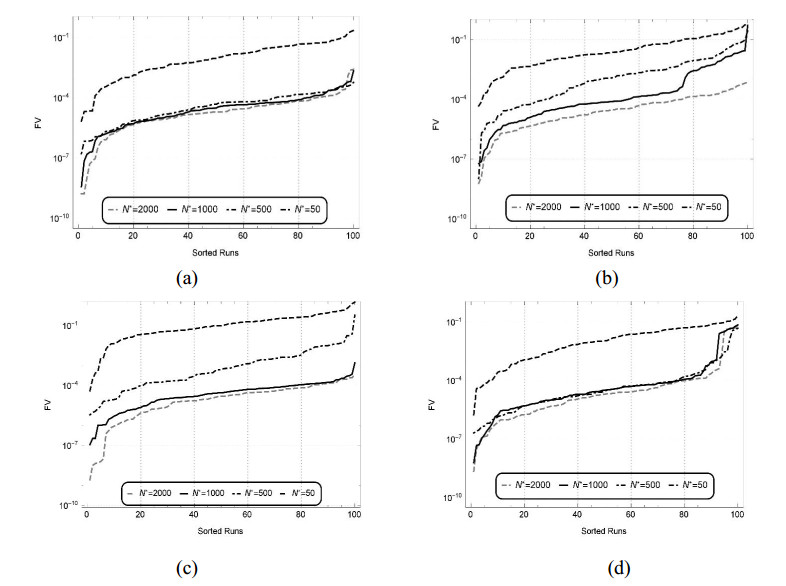
To optimize the fitness functions (28), (32), (36) and (40) defined for the test cases Ⅰ–Ⅳ respectively, 100 independent runs are carried out by using BATA for ${x_n} = 1$ and the parameter setting defined in Table 1. The results of statistical analysis for all these cases Ⅰ–Ⅳ based on the fitness values against 100 independent runs for a fifth order truncated series of the trial solution (10) at distinct values of ${N^*}$ (number of generations) are depicted in Figure 5(a-d), respectively. Next by rearranging the multiple runs on the basis of results plotted in Figure 5(a-d) and the ascending order of fitness values for ${N^*} = 50,500, 1000$ and $2000$, the sorted fitness values using semi logarithmic plot are presented in Figure 6(a-d), respectively. These Figure 6(a-d) and the comparison results for different cases depicted in Figure 4(a-d) clearly illustrates about the reliability, accuracy and convergence of the deliberated technique. Moreover, the precision of the designed methodology can be further improved by the increase in the number of generations ${N^*}$. The consistency in the correctness of the suggested technique (NROT), for $x \in \left[ {0, 1} \right]$, step size $h = 0.1$ and the number of generations ${N^*} = 2000$ at different values of $k = 5, 6$ and $7$ is scrutinized through statistics in terms of minimum fitness (MINF), maximum fitness (MAXF), global mean fitness (GMF), mean deviation fitness (MDF) and the standard deviation of the fitness (STDF) values accomplished by the fitness functions (28), (32), (36) and (40) for the respective cases Ⅰ–Ⅳ based on the hundred independent runs as tabulated in Table 8. The values of MINF achieved at contrasting values of $k$ for all the above cases lie around ${10^{ - 8}}$ to ${10^{ - 9}}$. It is seen that the respective values of MAXF, GMF, STDF and MDF attained at different values of $k \in \left\{ {5, 6, 7} \right\}$ are around ${10^{ - 2}}$ to ${10^{ - 4}}$, ${10^{ - 3}}$ to ${10^{ - 5}}$, ${10^{ - 3}}$ to ${10^{ - 5}}$ and ${10^{ - 3}}$ to ${10^{ - 5}}$ for the first three cases while, no visible variation is observed in the results of case Ⅳ. The reliability and accuracy of the deliberated scheme is further examined on percentage convergence runs through different level of fitness values, with results of 100 independent runs for the suggested scheme based on the criteria $FV \leqslant {10^{ - 3}}$, ${10^{ - 4}}$, ${10^{ - 5}}$, ${10^{ - 6}}$ and ${10^{ - 7}}$ presented in Table 9. The average convergence rate on the basis $FV \leqslant {10^{ - 3}}$ is about 100%, 97%, 98% and 90% for the cases Ⅰ–Ⅳ, respectively. Generally, the statistics show that consistently accurate results are obtained for more than 80% of the independent runs of BATA on the basis of the criterion $FV \leqslant {10^{ - 4}}$ which, clearly elucidates about the accuracy and reliability of the presented scheme. This analysis is made on Intel(R), with a 1.70 GHz Core $i3$ processor, 4.00 GB RAM, by running MATLAB version 2010a for the calculation of results.

7.   Conclusion and open problem

In this endeavor, a novel bio-inspired meta-heuristic approach based on the idea of RPSM with the BATA, is successfully applied to solve linear and non-linear MFDEs subject to different possible sets of two point boundary conditions. The competency and effectiveness of the NROT is validated by conducting numerical experiments consuming the offered scheme in combination with two other meta-heuristic techniques. A concrete inference on the performance of the offered technique in terms of accuracy and convergence is drawn by the statistical analysis based on the hundred independent runs. The contribution of the suggested scheme can be briefly narrated in form of the salient features given as:

● A competitive bio-inspired meta-heuristic solver is presented for the assessment of the MFDEs with fractional derivative defined in the Caputo sense by using BATA.

● The design methodology is well suited to solve the MFDEs for different possible variants of two point boundary conditions, even for a larger span.

● The numerical results constructed by the two other popular optimization techniques i.e., DEA and APSOA for the learning of $k - 2$ unknown weights in the derived fitness function ratifies the performance of the suggested scheme.

● Comparative study of the results computed using the NROT with the available exact solution evidences the outstanding performance of the suggested scheme in terms of accuracy, computational cost and simplicity.

● Accuracy and reliability of the deliberated scheme is validated by the accomplished near optimal values of the error indices based on the root mean square error ${P_{RMS}}$, mean absolute deviation ${P_{MAD}}$, Nash Sutcliffe efficiency ${P_{NSE}}$ and the Global fitness $GMF$.

● Statistical analysis show that consistently accurate results are obtained for more than 80% of the independent runs of BATA for all the test cases based on the criterion $FV \leqslant {10^{ - 4}}$.

In the future, one may explore the dynamics of various physical phenomena of real life interpreted in terms of the fractional partial differential equations by the implementation of the recommended technique incorporated with another new and powerful meta-heuristic optimization technique.

Conflict of interest

The authors declare no conflict of interest.