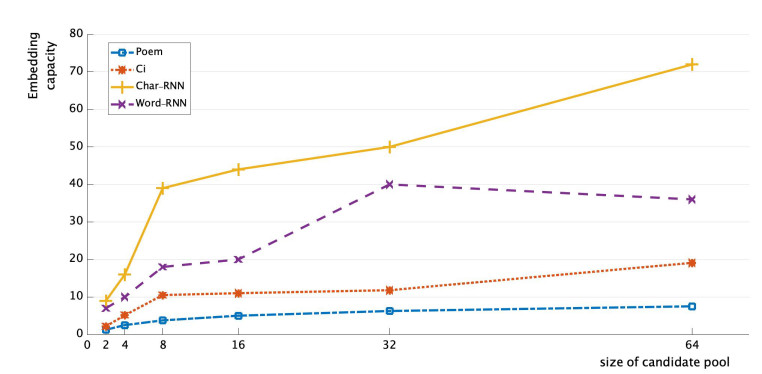In recent years many delay epidemiological models have been proposed
to study at which stage of the epidemics the delays can destabilize
the disease free equilibrium, or the endemic equilibrium, giving
rise to stability switches. One of these models is the SEIR model
with constant latency time and infectious periods [2],
for which the authors have proved that the two delays are harmless
in inducing stability switches. However, it is left open the problem
of the global asymptotic stability of the endemic equilibrium
whenever it exists. Even the Lyapunov functions approach, recently
proposed by Huang and Takeuchi to study many delay epidemiological
models, fails to work on this model. In this paper, an age-infection
model is presented for the delay SEIR epidemic model, such that the
properties of global asymptotic stability of the equilibria of the
age-infection model imply the same properties for the original
delay-differential epidemic model. By introducing suitable Lyapunov
functions to study the global stability of the disease free
equilibrium
(when $\mathcal{R}_0\leq 1$) and of the endemic equilibria (whenever $
\mathcal{R}_0>1$) of the age-infection model, we can infer the
corresponding
global properties for the equilibria of the delay SEIR model in [2], thus proving that the endemic equilibrium in
[2] is globally asymptotically stable whenever it
exists.
Furthermore, we also present a review of the SIR, SEIR epidemic
models, with and without delays, appeared in literature, that can be
seen as particular cases of the approach presented in the paper.
1.
Introduction
Information hiding, as an important research direction in the field of network security, has made great progress in recent years. Secret information is usually embedded into various multimedia carriers, such as text, images [1], audio [2] and videos [3]. Since text is the most widely used media, information hiding based on text has great value. Most traditional text steganography methods hide secret information in an existing document by exploiting its typesetting (format-based) and its lexical, syntactical, and semantical features (content-based) of the document. Format-based methods, for example, typically alter letter-spacing [4] and line-spacing [5], change the font attributes [6], and utilize invisible characters [7]. These methods, however, are sensitive to formats, and a slight change of format could cause new errors when extracting secret information. Common content-based methods, on the other hand, may change existing semantics using, e.g., synonym substitution [8,9], and adjust syntactic structures of certain sentences [10]. These traditional methods embed secret information by making some changes to the text, thus they are vulnerable to some steganalysis algorithms [11,12], which lead to poor security.
In recent years, researchers have started to investigate how to generate text, instead of modifying existing one, to hide information. For example, Yu et al. [13] proposed to use a special style of poetry called "Song Ci", originated in the Song Dynasty in ancient China, to form text steganography. This was the first text steganography algorithm to make use of a Chinese art form. However, their method only selects suitable words from an existing Song-Ci poem to recombines a new Ci-poem. It does not really generate new Ci-poems from scratch, and so may limit its usage. In addition, their method randomly chooses words during the generation process and ignores word collocations and the relationships between lines. Because of these, Ci-poems generated by their algorithms often lack a central theme, which might arouse suspicion and thus reduce security.
Recently, deep-learning technologies has achieved great success in the field of image generation [14]. Benefiting from this, more attempts of using such technologies have been made to generate a certain type of text form. For example, Zhang and Lapata [15] studied poem generations as a machine- translation problem using the standard encoder-decoder model. Their method compresses all previously generated lines for a poem to be generated into a vector to help generate the next line. Wang et al. [16,17] and Yi et al. [18] presented a method to generate a poem around a central theme using a bidirectional recurrent neural network (RNN) with attention mechanism, which allow them to focus on the most critical components and deep dependencies of lines in a poem.
Using CNN modeling, researchers have applied text generations to text steganography. For example, Luo et al. [19] presented a method based on Ci-poem generations using a Markov chain model. While their method does produce a better Ci-poem, it has a low embedding capacity for hiding information. They [20] also showed how to use a LSTM model to generate Chinese classic poems and embed secret information into a generated poem during the generation process.
We note that ancient styles of poetry, although once played an important role in the literature, often have a unique style of expressions that makes it difficult for general readers to comprehend. In particular, secret information embedded in a poem may look odd and thus arouse suspicion, leading to weaker security.
To overcome this obstacle, we devise a novel text steganography method using a RNN model to generate Chinese pop music lyrics. Compared to the poems written in a stringent style, lyrics are easier to understand and allowed to have a much longer length, yielding better security and a higher embedding capacity. However, if applying neural networks to lyrics generation directly, especially when combining text steganography, the resulting text may not look like lyrics at all. The reason is that lyrics must also follow a certain structure and properly rhyme. Moreover, lyrics should express emotions consistently. To tackle these issues, we analyze a large number of Chinese pop lyrics, summarize three common types, and use them as structure templates to guide lyric generation. We then present thirteen rhymes, similar to the oblique tones of poems, for generating lyrics with pleasant tones.
Our contributions are the following: First, we devise a RNN-based lyric generator with steganography to offer a much higher embedding capacity than previous steganography methods. Second, we present three structure templates for Chinese pop music and thirteen rhymes to mitigate the lyric-quality decrease incurred during the process of hiding information.
The rest of the paper is organized as follows: In Section 2 we describe preliminary results. In Section 3 we present a detailed description of our RNN-based lyric-generation model suitable for text steganography. In Section 4 we carry out the construction of dataset, show the generated results, evaluate the proposed method and make comparisons with previous methods. Finally, we conclude the paper in Section 5.
2.
Preliminary results
In this section, we describe our preliminary results on Char-RNN, lyric formats, and rhymes.
2.1. Char-RNN
The sequence-to-sequence (S2S) model has been widely used in machine translation, automatic response, text generation, and other fields. S2S may be carried out under the framework of Encoder-Decoder and implemented as a RNN, CNN or GRU. Recurrent Neural Network (RNN) is the most widely used, which has been proved to be the most suitable network model for dealing with sequential tasks. However, a basic RNN model consists of only one hidden state, and the information at the beginning of the sequence is seldom retained in a later stage, there is a severe problem of gradient disappearance [17]. Therefore, basic RNNs are not suitable for generating the long lyrics. To solve these problems, researchers have proposed a number of variants of RNN, including LSTM and GRU.
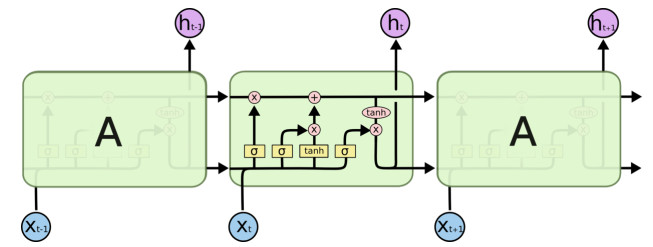
As a special kind of RNN network, LSTM [21] adopts four processing methods that interact with each other in a special way to realize the processing of long-term dependence. The LSTM network model is shown in Figure 1. All recurrent neural networks have the form of a chain of repeating modules of neural network. In standard RNNs, this duplicate module has only one very simple structure, such as a single layer. However, LSTM avoids long-term dependency problems through special design. It usually uses a structure called a 'gate' to remove or increase the transmission of information.
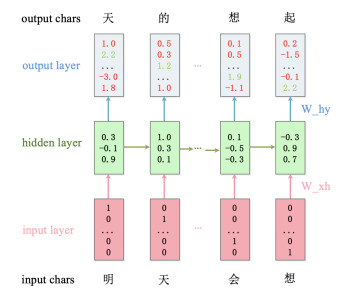
In 2014, Karpathy [22] proposed a Char-RNN model, allowing machines to generate text from the dimension of characters. In other words, the model computes the probability of the next character based on the observed ones. In this paper, we devise a Char-RNN model based on LSTM to deal with long-distance dependency problems, Figure 2 shows the execution process of the model.
2.2. Lyric structure
The Chinese pop music lyrics follow certain formats. After analyzing a large number of them, we found that most of them follow the following three structures: (1) A1 + B, A2 + B, (2) A1 + A2 + A3, (3) A1 + A2 + B1 + B2, where each letter with or without a number represents a lyric component consisting of 3 to 5 lines. Figure 3 shows an example of a classic 4-segment lyric.
2.3. Thirteen rhymes
A good Chinese pop lyric expresses strong emotions that are properly rhymed. To make Chinese pop lyrics rhyme, lyric writers would need to make sure that the pronunciations of the end words of each line rhyme. From the perspective of vocal music, Chinese syllables are divided into thirteen categories, which are called Thirteen-Rhymes [23]. The thirteen rhymes are classified according to the basic principles of the same or similar vowels. Table 1 shows the thirteen rhymes and the common Chinese characters for each rhyme. Figure 4 shows the content of the entire lyric "Deskmate of You", which is popular in mainland China. We can see that the rhyme of this lyric is Yi-Qi (pronunciations). In addition, a lyric may have more than one rhyme, and it is common to have three to five rhymes in a lyric.
3.
Hiding information in a generated lyric
Information hiding starts when the lyric generator produces a vector Y on the input vector X. We denote the output vector by $Y = y_{1}, y_{2}, \ldots, y_{3}$, where N is the length of input and output sequences. Moreover, $y_{i(i = 1, 2, \ldots, N-1)}$ is equal to ${{x}_{i}}_{(i = 2, 3, \ldots, N)}$; in other words, $Y _{N} $ is obtained from $ y_{i(i = 1, 2, ..., N-1)} $ with the highest probability and the model generates next y based on $y _{i(i = 2, 3, ..., N)} $. Here $Y _{N} $ could be a character or word. Thus, to hide secret information, we will filter out candidate characters or words on selected positions, code them, and select one of the most suitable candidates in accord with the secret information.
3.1. Steps of lyrics steganography
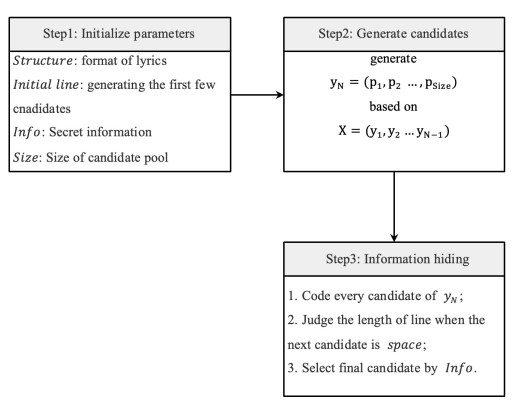
There are three steps: (1) Set parameters. (2) Generate candidates for the next character (or word). (3) Select the most suitable candidate. The whole process of information hiding is shown in Figure 5. In Step 1, we set the following four parameters:
● Structure. This was the underlying structure for the lyric to be generated, which was described in Section 2.2.
● Initialline. It preheats the generator and helps to generate the first few characters, but it is not part of the final lyrics.
● Information. This is a binary stream converted from the secret information, which is hidden, transformed and extracted.
● Size. It is the size of a candidate pool, from which we choose the most probable candidates. It is obvious that is an important factor of the embedding capacity. The larger Size is, the more secret information can be embedded.
In Step 2, the lyric generator produces $Y _{N} $ = ($p _{1} $, $p _{2} $, ..., $p _{Size} $) based on ($y _{1} $, $y _{2} $, ..., $y _{N-1} $), where $p _{i = 1, 2, ..., Size} $ are the probability of Size candidates.
Step 3 is the most critical part of our lyric-steganography method. For each $Y _{N} $, we first predict all the possibilities of the next characters based on the previous information. We then select m most likely characters as candidates, where m = Size. We encode these m characters (such as Huffman code). Finally, we choose the most suitable character to hide the secret information. In addition, it should be pointed out that if $Y _{N} $ is space, we need to judge whether the length of the sentence has reached the minimum requirement. If it is, then the sentence is finished. Otherwise, we need to change the order of the candidates so that lines do not end too early.
3.2. Generating lyrics of high quality
In order to improve the quality of generated lyrics, we applied lyrics structures and rhythm table to experiments, which mentioned above, and propose the Word-RNN model. Then, two results are showed, which are generated by two different models respectively. Finally, we illustrate the extraction method of secret information.
3.2.1. Structure-constrained generation and rhymes
As described in Section 2.2, most Chinese pop lyrics follow three common structures. Thus, we introduce three structure templates to regulate the lyric generations. Taking Structure 3 as an example, we may generate four-verse lyrics with four sentences in each verse. It is common for a line in a verse to contain about 8 to 15 characters. To standardize the structure, it is crucial to control the number of characters per line. Therefore, in the process of creating lyrics, we will make a judgment on the number of characters in each line. If the number of characters has not reached the limit, no space will be generated. If the number of words exceeds the maximum, start a new line.
In addition, as mentioned in the Section 2.3, the ending character in each line should have proper rhyme. Therefore, during the generation process, we first determine whether the character to be generated is the ending character of the line. If it is, then we need to select the m characters with the highest probability from all the results, and these m characters rhyme properly. We then use the same method in Section 3.1 to choose the most suitable character for $Y _{N} $. If it were not the ending character, then we will choose m highest probable characters directly from all probability as the candidates.
3.2.2. Word-RNN
Directly choosing the most suitable character may incur a severe problem, that is, the chosen character may not have a reasonable meaning with adjacent characters. Thus, the quality of lyric will decrease sharply. To overcome this problem, we improve the Char-RNN model to design a Word-RNN model, which have the same structure as Char-RNN. The only difference is that the smallest unit in the training and generation stage is a word instead of a character. Figure 6 shows the principle of Word-RNN.
3.2.3. A steganography example
We present an example to show how to hide the secret information in the process of lyric generations. First, we set the parameters as follows:
● Initial Line:我们手牵手(Your hands in my hands).
● Size: 4 (the size of candidate pool).
● Structure: Classical-16 (that is, four verses with four lines in each verse).
● Information: 100111111100001101.... (converted from '信息隐藏').
At the beginning, we choose a model from Char-RNN and Word-RNN (here we use Char-RNN as example). Then, the initial line will be fed to preheat the model and converted into $x _{i} $.
For the first y, we select the most probable top-4 characters as candidates. We then encode the characters using Huffman code (shown in Table 2, Col. 1). When the beginning of the information is 10, then '你' is chosen as the first character.
To make the ending characters of lines rhyme, we note that the bits of '01' represent character '歇' (shown in Table 2). However, this character does not sound well with the You-Qiu rhyme of the existing lines. Thus, we replace it with another character that rhyme better. Also, it should be noted that the space character in Table 2 is used as the separator between two lines, which can also be used to hide information.
3.2.4. Information extraction
After a lyric embedded with secret information is generated, the sender may send the lyric to the receiver. Meanwhile, the file about candidate pool should be sent together. When the receivers obtain the lyric, they can extract the binary stream converted from secret information according to the candidate pool. In other words, it is impossible to extract secret information without the file of candidate pool. Thus, the file of candidate pool plays an important role in the process of information extraction, because only the legitimate recipients can get the file and extract the secret information.
4.
Experiments and evaluations
In this section, we first illustrate the construction of dataset and how to set the value for each initial parameter. Then, we present two results, which are generated by Char-RNN and Word-RNN respectively. Finally, the performance evaluations are given.
4.1. Dataset and experiments setup
We need a large number of high-quality lyrics to train a satisfactory model. Unfortunately, no Chinese pop lyrics data has been published by any authoritative organization. To obtain training data, we use the Scrapy crawler framework to collect a total of 15,000 Chinese pop lyrics from music websites, including 100 Chinese male singers, 100 Chinese female singers, 100 Chinese bands, and 50 popular songs of each singer. Removing all-English songs and duplicates, we finally obtained a dataset of about 13,500 Chinese pop lyrics.
In the training process, we count all the Chinese characters in the lyric data, and construct a dictionary, to be shared by both inputs and outputs. At the same time, we count the number of Chinese characters as the length of One-Hot Encoding. Finally, we train our model using tensorflow.
For the Word-RNN model, we use the same methods, parameters, and optimization algorithm as the Char-RNN model. The only difference is that we first carry out word segmentation of the lyric data, expressing each song in terms of phrases. Namely, in the One-Hot Encoding, each position now represents a word, instead of a character.
4.2. Examples of results
Figure 7 depicts two Chinese pop lyrics generated by the proposed method with steganography, where (a) is a lyric generated by Char-RNN and the (b) is a lyric generated by Word-RNN.
According to their literal meanings, we can consider that Lyric (a) praises the beauty of love, and Lyric (b) describes sorrow of love. Through the analysis of lyrics, we can find that the lyrics generated by Char-RNN model contain repetitive characters (in red) and broken lines, while the lyrics generated by the Word-RNN model do not have these problems.
4.3. Performance evaluations
We evaluate the proposed steganography method from two important aspects: embedding capacity and security.
4.3.1. Embedding capacity
Embedding capacity is a significant measure to evaluate a steganogaphy methods, which represents how much information can hide in a stego-text. Previous steganography methods based on text generations either have low embedding capacities or do not look natural. For example, the poetry-based methods not only generate a poor naturalness genre, but also have lower embedding capacity than the proposed method. The high embedding capacity of the proposed method stems from longer length of lyrics, and we can hide information at each char-position or word-position. Similarly, we can conclude that char-based methods have higher embedding capacities than word-based methods when the generated lyrics length are the same. The embedding capacity calculation formula of two methods are as follows:
Where $EC _{1} $ represents the embedding capacity of a lyric generated by Char-RNN, num is the number of lines, $C _{i} $ is the number of characters in each line, and Size is the number of candidates. Likewise, $EC _{2} $ represents the embedding capacity of a lyric generated by Word-RNN method, where $W _{i} $ is the number of words in each line.
Figure 8 depicts the comparison results of embedding capacities among different methods, where the value of the embedding capacity is the number of characters embedded in the text carriers. It is easy to see that the proposed methods in this paper have higher embedding capacities than Poem-based steganography method and Ci-based steganography method, and with increase of Size, the capacity will be much higher than these two methods.
4.3.2. Security analysis
Security refers to the invisibility and imperceptibility of secret information, and it is one of the important measurements to evaluate a steganography method.
In modern society, people usually communicate with vernacular. Although poetry is an important achievement in the development of ancient Chinese literature, it is not practical in daily communication in modern society. Therefore, steganography based on poetry generation maybe easily arouses suspicion in the process of text carrier dissemination. Modern popular lyrics have higher naturalness, which means that the lyric text embedded with secret information will not arouses suspicion in the transmission process, thus the security is higher than steganography method based on poetry.
As shown in the Table 3, the results are generated by previous methods, which are embedded with secret information. Obviously, compared with the two results, the lyrics generated by the proposed method are easier to understand and has higher naturalness. Moreover, the proposed method is based on lyrics generation, which does not modify the text carrier like traditional text steganography methods, so it can effectively resist the detection of traditional steganalysis algorithms. Besides, our method is not based on text format, so it could resist the format-based attacks and steganalysis.
5.
Conclusion
We presented a novel method that uses recurrent neural networks to generate the Chinese pop lyrics, and in the process of generation, we successfully embedded the secret information into the lyrics. We first used Char-RNN to predict the probabilities of the possible next characters based on the observed data. We then selected the most suitable character according to the secret information and added the character to the observed sequence, in order to continue to predict and generate. Directly generating lyrics based on secret information, it is likely that the generated characters can not be combined into words. We improved the Char-RNN model and developed the Word-RNN model, using words as units to train the model. Through experimental comparisons, we found that the proposed method offers higher hiding capacity and can generate more natural text, compared with the previous methods. In the future, we will improve our method to generate lyrics of better quality and clearer theme, with higher embedding capacity and better security and robustness.
Acknowledgments
This work was partially supported by National Natural Science Foundation of China (No. 61872134, 61502242), Natural Science Foundation of Hunan Province (No. 2018JJ2062, 2018JJ2301), and National Key Research and Development Program (2017YFC1703306), and Hunan Provincial 2011 Collaborative Innovation Center for Development and Utilization of Finance and Economics Big Data Property (2017TP1025).
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad: