Using nonlinear model predictive control to find optimal therapeutic strategies to modulate inflammation

1.   Introduction

Monogenic disorders are usually caused by the single gene lesion predominantly, though the manifestation of phenotype might depend on several extents on the extra genetic variants in same or other genes, changes in epigenetic and environmental conditions. Though most of the individual monogenic diseases are rate, altogether they signify a high disease load among the population ^[1]. The DNA arrays dependent tests are presently available for diagnosing the human genetic disease which includes tests that were designed for searching the disease that cause mutations in any one of gene numbers that were known to be mutated at desired disease kinds for example the disease that are associated with ataxia ^[2,3]. Also, a technique of sequencing generation might facilitate the entire exome analysis or the genome at some individual. By data collection from huge group of healthy individuals of population followed by data archiving in publications, bioinformatic resources which were established for the assessment of likelihood that a specific genomic variant or sequence variant present in specified patient is of pathologic importance.

Typically, Sickle Cell Disease (SCD) is regarded as a hereditary form of anaemia which outcome from single mutation at 6^th codon of β-globin chain (from the glutamic acid to the values) of adult tetramer (α₂β₂), haemoglobin (Hb) which is more prone to the polymerization of lower levels of oxygen. This is one such sever and prevalent monogenic disorder and several million around the world and over 100,000 individuals in United States were much affected by these both chronic and acute SCD manifestations like crises of frequent pain, infarct of silent cerebral, early death, and end organ damage ^[4]. Also, previous studies shows that about 7000–10,000 children having Major Thalassemia are born in India every year. The treatments that reduce the complications and symptoms of SCD like transfusions of blood, preventive therapies that include penicillin prophylaxis and pneumococcal vaccination, and therapy of hydroxyurea were leverages in clinics. However, blood transfusion might not correct the phenotype and outcome in overload of iron once not accompanied by the therapy of aggressive chelation. The treatment of Hydroxyurea offers clinical significance over the fetal globin induction (α₂γ₂, HbF) that competes sickle globin, thereby decreasing the symptoms of SCD, however the response to the hydroxyurea is not a uniform one among the patients that concerns for the long-term use remain contempt abundant indication for safety ^[5].

For the monogenic disorders, various non-invasive prenatal diagnosis (NIPD) approaches were presented. As the cell free fetal DNA cffDNA occurs in a maternal cfDNA background, previous researchers, like the autosomal diagnosis disorders, genetic disorders that are inherited paternally like rhesus and a compound heterozygotes exclusion of the autosomal recessive disorders such as Maternal plasma, β-thalassemia comprise of cffDNA mixture and the maternal cfDNA though fetal alleles half were maternally inherited. Consequently, a quantitative technique for counting the precise number of various alleles is thus needed for deducing the given locus genotype. For this reason, various techniques were presented in the series study that includes relative mutation dosage (RMD) and a relative haplotype dosage (RHDO) analysis. The approach of RMD thus counts the number of DNA molecules directly for sorting the mutant ratio and wild-type alleles with the use of digital polymerase chain reaction (PCR). The RHDO approach principle is to infer the inheritance of maternally transmitted fetal mutations on quantifying the relative haplotypes dosages along with a single nucleotide polymorphism (SNP) that allies in and around the specified or targeted genes. The data regarding the parental haplotypes must initially be attained by the sequencing techniques whereas the prior knowledge of proband was anymore not needed. Typically, on the whole both RHDO and RMD techniques were found to be helpful at-risk couples of monogenic disorders who might request for NIPD for their first child ^[6]. The existing techniques for diagnosing the conditions of monogenic disorder may include short-read sequencing of exomes or the genomes ^[7].

Though the yield of diagnosis from these techniques is a promising one that ranges from 26% to 40% which might leave cases that are unresolved. The yield is thus augmented by the reanalysis in contradiction of newly discovered disease allied genes and variants, or on employing the analysis that are family based for identifying the variants of de novo, however the enhancements are modest ^[8,9].

The motivation behind this work is that, the direct recognition or the read out of the DNA bases by means of DNA-binding protein includes the amino acids which directly interacts with the specific features to each base. The experimental validation also indicates that in several cases the protein attains the partial sequence through indirect recognition that is by recognizing the structural properties of DNA. Though there were several optimization techniques employed along with classifier like GA, Short Term Load Forecasting (STLF), with fuzzy logic approach. But the computational time is high in these traditional approaches ^[10,11,12]. Also, there were several optimization techniques like arithmetic optimization approach ^[13], Dwarf Mongoose optimization ^[14], Reptile Search Algorithm (RSA) ^[15], and Ebola Optimization Search Algorithm ^[16]. In this paper, Aquila Optimization ^[17] is presented. The main intention of the proposed work is to present a mathematical model using Quantum graph theory to extract elastic properties and to distinguish them as normal cells and sickle cell anemia (SCA) in red blood cells.

The residual part of the paper is arranged as given below. Section Ⅱ provides the related works. The proposed work is described in Section Ⅲ. The analysis of performance and evaluation with the other techniques is given in Section Ⅳ. Finally, Section Ⅴ offers the conclusions.

2.   Related works

Reference ^[18] projected on the statistical analysis of genetic data to identify the neuro developmental disorder and also monogenic disorders. One of the neurodevelopmental disorders is because of sporadic de novo variants that occurs rarely but affects severely. As the genomic screens of large-scale are absent, epidemiological disease recognition is impossible for the variety of de novo monogenic variants. It is important for the researchers and clinicians to know about the incident of disease occurrence for planning the treatment process. So, the estimates of calculated validity are proceeded with two corroboration analyses.

Reference ^[19] proposed about the technique of analyzing DNA of parents and also the complex mutation assessments were illustrated. By this technique the multiplexing capabilities of finding mutations and number of genes would be calculated simultaneously. The detection of fetal monogenic diseases is agreeable and can be done by analysis of maternal plasma DNA. The monogenic disease analysis in prenatal fetus is highly scalable by the scheme.

Reference ^[20] focused on the field of monogenic disorders that is interrelated with NIHF (nonimmune hydrops fetalis). The gathering of fluids in the fetal compartments is dangerous to the life of fetus and this is said to be hydrops fetalis. Many molecular tests are performed in pregnancies of hydrops fetalis and analyzed. Many monogenic disorders have impact because of nonimmune hydrops fetalis.

Reference ^[21] demonstrated about neurodevelopment disorders are the effects of genetic variations that risks more in society. Several human disorders occur by solitary protein coding genetic variant. In general, it is predicted that phenotypic characters of a person having monogenic disorder is impacted by the similar variants, in associating with intracranial volume, autism and birth weight and height.

Reference ^[22] estimated the monogenic variants role over the dystonic disorders range on offering guidance for the exploitation of personalized strategies care and fostering follow-ups for pathophysiological explorations. From the blood genomic DNA is extracted and sequenced the entire exome. Among the categories, 104 out of 160 were the noticed variants influenced genes that are related to neuro development disorders.

Reference ^[23] performed whole exome sequencing in a multi-center cohort consisting of 114 families involving 138 affected with CKD, in order to regulate the similarity of detection of monogenic reasons of CKD in adults. Nearly 500 monogenic disorders of chronic kidney disease CKD have been found in pediatrics. Affected people were employed from 16 families containing extra renal characteristics, positive family past history of 78 families and without family past history and extra renal characteristics of 20 families. Here it is found that a pathogenic mutation is in a CKD gene among 42 families out of 114. Among the identified 42 families with monogenic, the clinical diagnosis in 17 is confirmed by WES, recognized a diagnosis in 16 families with CKD and corrected the 9 clinical diagnoses.

Reference ^[24] analysed sequencing exome and 36 children and adults' data variants were analysed using Common variable immunodeficiency with strong relationships to evaluate the monogenic amount. Recently CVID of 20 percent cases have a defined genetic reason. Diagnosis is on the basis of immunological norms and clinical, after eliminating the other diseases that cause same phenotypes.

Reference ^[25] studied that monogenic lupus is a kind of systemic lupus erythematosus SLE that presents in single gene defect patients. An important gene numbers have been considered in monogenic lupus offering insights into a process of complex disease. Here the genes related to monogenic lupus will be explained and the work of pathogenic influenced by the mutations included by stimulating the autoimmunity. Although the monogenic lupus considers only a small group of lupus patients, it offers important insight into the lupus mechanism and approaches of treatment.

Reference ^[26] focused to recognize clinically related variants within the 68 monogenic inflammatory bowel disease IBD genes in an unchosen cohort of IBD. Monogenic inflammatory bowel disease (IBD) consists of rare cause of mendelian gut infection usually occurs in infants with severe disease. Here, whole exome sequencing was conducted on pediatric onset disease patients.

Reference ^[27] recognized formerly described homozygous mutation in Complement C1q C Chain gene, that describes the patient with SLE phenotype and immunodeficiency. They also found heterozygous variants in DNASE1L3, C1S, DNASE1, RNASEH2A and IFIH1 and 7 rare genes that are included in monogenic Systemic lupus erythematosus. Their experimental findings denote a complex involvement to the entire gene risk of SLE by the occasional gene variants related with the SLE monogenic forms.

Reference ^[28] attempted to find the monogenic disorders which distribute the characteristics of Rett syndrome RTT. RTT is an early occurring neuro developmental disorder which is caused by MECP2 gene mutations. But other gene CDKL5 and FOXG1 defects can cause performances that are similar to classic RTT though they are not entirely similar. 437 patients were researched with RTT like and in 24,217 genes associated to RTT phenotype was performed through a system of HaloPlexTarget-Enrichment.

Reference ^[29] revealed three mutations in COL1A2, LRP5 and COL1A1 in genetic analysis. The results in the data showed that formerly unidentified monogenic bone disorders play a significant role in Pregnancy-associated osteoporosis. Pregnancy is regarded as a skeletal risk factor to promote the starting onset of skeletal monogenic disorders thereby describing the cases with osteoporosis related to pregnancy.

Reference ^[30] reviewed the abnormalities of methylation that is relevant to monogenic diseases, their association with phenotype and genotype and the usage limitation and output interpretation. The modification of Normal methylation is done at multiple or single loci as a result of gene variants acting in trans or cis or through communication with environmental factors. Particular patterns of methylation or signs can be found in DNA for several developmental disorders.

Though, there were several techniques employed for the detection of sickle cell anemia, there were some limitations like low detection accuracy, computational complexity, and fails to analyze the elasticity properties. To overcome this, the proposed model is suggested.

3.   Proposed work

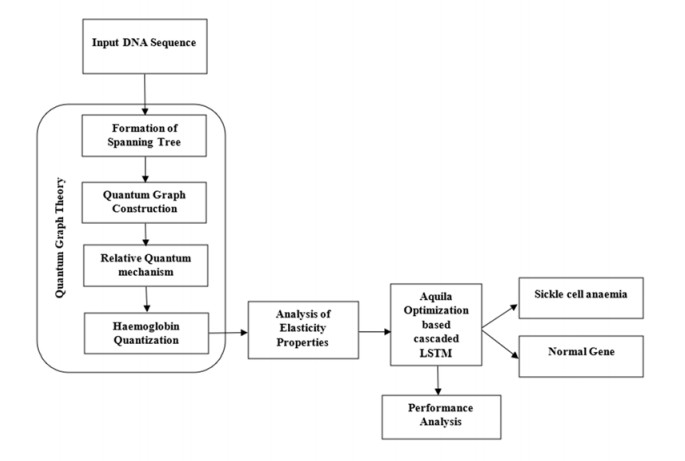
A detailed elucidation of the proposed work is provided in this section. The entire flow of the proposed work is given below in Figure 1. At first, input DNA sequence is considered and the features of elastic property are thus extracted with the use of Quantum graph theory model at which the spanning tree formation is made followed by construction of graph and Hemoglobin quantization. Then, the extracted properties are optimized using Aquila optimization and classified using cascaded LSTM to attain the classified outcome of normal cells and sickle cell.

3.1.   Input DNA sequence

The input DNA sequence from the input dataset is taken and the elastic property features are extracted by using Quantum graph theory model. After which, the extracted properties are optimized and classified to attain the classified outcome of sickle cell and normal cells in the input DNA sequence.

3.2.   Quantum graph theory to extract elastic property features

The input DNA sequence is considered as input and Quantum graph theory is employed for the extraction of elastic property features at which the spanning tree is formed by the construction of Quantum graph. The relative quantum mechanism is computed followed by the quantization of Hemoglobin. To form a metric, graph a quantum one, a differential Hamiltonian operator on δ, which is sometimes required to be self-adjoint.

The negative second derivative,

The more general Schrodinger operator,

It can rewrite as follows,

At a later stage, the possibility of more general scalar or matrix differential or pseudo-differential operators will be discussed. We will focus on the most frequent scalar second order differential operators here, and for the sake of clarity in Eq (1), the Eq (2) is formed.

Vertex circumstances: According to the standard Sobolev trace theorems, a function $f∊H{n}^{2}\left(e\right)$ and its first derivative have correctly defined values at the edge e's endpoints. The vertices of the second order derivatives of $H{n}^{2}$ functions are already devoid of traces. As a result, only the values of $f$ and $\frac{df}{dy}$ at a vertex $v$ may be included in the vertex criteria.

The criteria can, in theory, combine the values at various vertices. It will, however, focus on local vertex conditions exclusively for the time being, that is, those that involve the values of functions and their derivatives at a single vertex at a time.

We'll stick to finite graphs here to avoid certain technical details. We assume, in other words, that the number of edges |E| (and thus the number of vertices |V|) is finite. The length of the edges can still be unlimited.

A typical Kirchhoff's vertex condition,

Sum of overall edges $e$ incident to the vertex $v$ and the derivatives are taken in the orders gone from vertex.

It's also natural since the condition of Neumann boundary for the Laplacian operation. As we'll see in future, the quadratic form domain of the corresponding operator does not enforce any restrictions on a role other than that it be in $H{n}^{1}\left(\delta \right)$(and thus continuous). Another point worth mentioning is that under the boundary requirements, all vertices of degree 2 can be eliminated, resulting in two smooth edges.

This is adequate for handling the challenge of describing the criteria for a junction of single d at a vertex v edges (a "star graph") given local vertex conditions. Because our operator functions as a second order operator along each edge, one would expect to begin two circumstances for each edge, and so the number of conditions at each vertex must correspond to the vertex's degree d.

As previously stated, the conditions for functions in H2 on each edge may only include the function's border values and derivative. The most generic (homogeneous) form of such a condition is plainly,

Here, ${X}_{v}$ and ${Y}_{v}$ are $r*r$ matrices, $F\left(v\right)$ is a column vector of the values at the mentioned vertex $v$, that function is follows,

The derivatives considered along with these edges at the outgoing direction. The rank of the $r\times 2r$ matrix $({X}_{v}, {Y}_{v})$ must be equal to $r$ so as to safeguard the conditions that are independent.

Given two vertexes T and U, sequence UT is considered, with their history. By description, a components number essential for building T once appended to U is represented as $o\left(UT\right) -o\left(U\right)$. This is less than or equal to $o\left(T\right)$ since at any specified step of the making procedure T (on building the UT sequence) for this a huge search space is exploited because of the U existence. Hence, the process of copying is longer which could decrease the exhaustive components number. It could be observed from sub-additivity of complexity of Lempel-Ziv $o\left(UT\right) \le o\left(U\right) +o\left(T\right)$. In what way $o\left(UT\right) -o\left(U\right)$ will be less than o(T) might depends on similarity degree among U and T. For Instance, assume $U = GGA\ CTT\ CTT, R = GCA\ GTT\ CTT\ and\ T = GGA\ TTT\ CCT$. The comprehensive antiquities of these arrangements might be signified as:

On yielding $o\left(U\right) = o\left(R\right) = o\left(T\right) = 5$. The comprehensive sequences histories UT, and RT might be:

Correspondingly, we observe that it might take about three steps for building T at the process of UT production. Instead, five steps are employed for generating T at the process of production of the RT. The reason is that it could take some steps in next case as T is nearer to 'S' on comparing 'R'. for instance, it was observed that on looking the CTT and GGA patterns which S and T shares. The number of steps is formulated as it takes some steps for generating a T sequence S by $c\left(UT\right)-c\left(U\right)$. Therefore, if S is nearer to T on comparing R, then it would be expected that $c\left(UT\right)-c\left(U\right)$ to be lesser than $c\left(RT\right) -c\left(R\right)$ since it is the case in above instances. Depending on the closeness idea, four distance measures were computed.

Distance metrics 1: Two sequences U and T are given, describe the $d(U, T)$ function as:

So as to eradicate the length effect on distance measure, a more substantial role might be the standardized form of $dist(·, ·):$

Distance metrics 2: Two sequences S and Q are given, and the function is defined as:

One more distance measure which might obviously follow from the building sequence T idea using U is signified as the 'sum distance'. This term is employed at this sense which accounts for total amount of steps it would take build T from U and vice versa.

Distance metrics 3: Two sequences U and T are given that defines the $d1(U, T)$ function as:

Likewise, dist1(·, ·) normalized version could be expressed as shown:

Distance metrics 4: Two sequences S and Q are given, which describe the function of $d*1 (S, Q)$ as*

A distance metric, $dist(·, ·),$ might gratify the subsequent circumstances:

● $D(U, T)$ ≥ 0 at which the equality is satisfied if $U = T(identity)$.

● $D(U, T) = D(T, U) (symmetry)$.

● $D(U, T)$ ≤ $D(U, T) + D(R, T)$ (Triangle inequality). Appropriate for a metric to be an effective evolutionary change measure it might also satisfy these conditions:

● $D(T, R) + D(U, R)$ ≤ $max\{D(T, U) + D(R, T), D(T, R) + D(U, R)$ (additivity).

Consequently, effective distance metrics fourth condition are tested on comparing the matrix of distance created by presented metrics with the reconstructed branch lengths of resultant tree.

Theorem (Elastic co-efficient estimator): Let δ be a metric graph with finite edges, Consider the operator $Hn$ working as $-\frac{{d}^{2}}{d{y}^{2}}$ on each edge $e$, with the domain including functions belonging to $H{n}^{2}$ and specific local vertex conditions involving function vertex values and derivatives. If and only if the vertex conditions can be stated in one (and hence any) of the three forms below, the operator is self-adjoint.

● Equation (14) at each vertex, where $\{ {X_v},{Y_v}|v \in V\}$ for the collection of matrices of size ${r}_{v}\ x\ {r}_{v}$ such that,

The maximal rank of (${X}_{v}, {Y}_{v})$ with ${r}_{v}\ x\ 2{r}_{v}$ matrix size.

The matrix (${X}_{v}, {Y}_{v}^{*})$ is self-adjoint.

● There exists a unitary ${r}_{v}\ x\ {r}_{v}$ matrix ${U}_{v}$ for every vertex $v$ of degree ${r}_{v}$ such that the vertex criteria at $v$ are,

where $\beta$ is the ${r}_{v}\ x\ {r}_{v}$ identity matrix.

The ${\alpha }_{2}$ value associated with protein-induced DNA alterations from ${Y}_{v}$ to the ${X}_{v}$ method. The elastic coefficients estimated have the following assets. The tilt modulus ratio ${F}_{11}^{XY}$ to the roll modulus ${F}_{22}^{XY}$ is at range, and twist modulus ratio ${F}_{33}^{XY}$ for the harmonic mean,

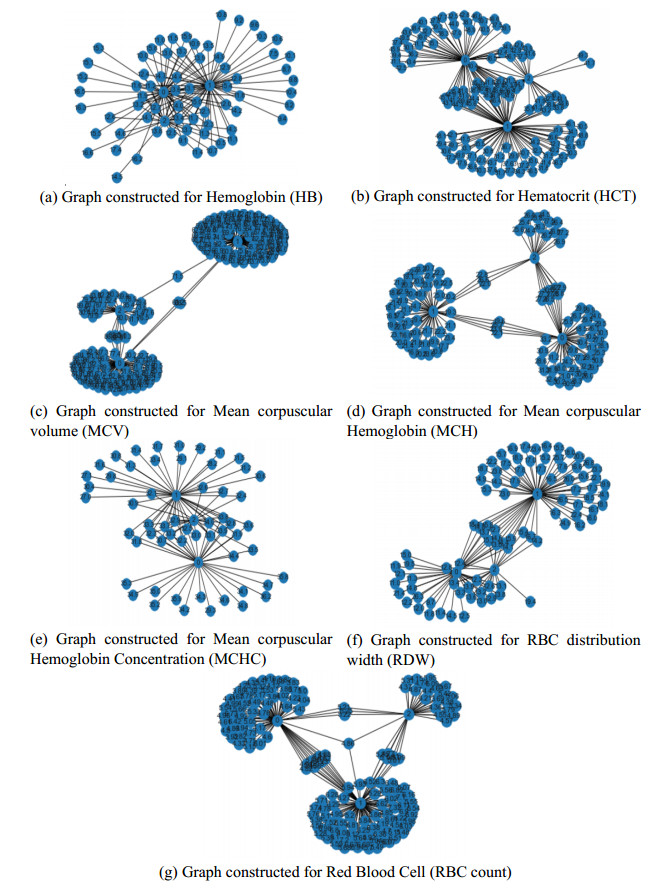
The formation of spanning tree and the outcomes of graph constructed by spanning tree model for each attribute is represented below.

The attributes like HB, HCT, MCV, MCH, MCHC, RDW, and RBC count are considered for the construction of graph using quantum graph theory model. The graph construction takes place based on the variable range values of each attribute and is shown in Figure 2. The attributes values should be within the normal range, if there occurs some variation, then there will be some disorder. Hemoglobin is a protein that carried oxygen in red blood cells. If the hemoglobin becomes defective it causes the red blood cells to change its shape causing sickle cell anemia. The healthy range of hemoglobin (for men are 13.2–16.6 grams per deciliter, for women it is 11.6–15 grams per deciliter (dL)). The normal range for HCT is (38.3–48.6 percent for men and 35.5–44.9 percent for women). The normal MCV value should be between 80 and 100 fL. In case of MCH, the normal value is 29 ± 2 picogram per cell. MCHC denotes the amount of hemoglobin per unit volume and the normal range lies between 33.4 and 35.5 grams per dL. If low MCHC is found then it is considered as anemia due to deficiency of iron and it indicates the thalassemia. The healthy range of RDW is 12.2–16.1 percent in female and it is 11.8–14.5 percent in males. If the score value out of this range occurs, then there is a nutrient deficiency, infections or the other disorder. Usually, women have lower RBC count than men, and the RBC level tends to decline with respect to age. The normal range lies between 4.7 and 6.1 million cells per microliter (cells/mcL) for men and for women it is 4.2–5.4 million cells/mcL.

3.3.   Aquila optimization based cascaded LSTM

Once the quantization is attained by means of Quantum graph theory, the elasticity properties are analyzed and are optimized so as to enhance the performance of classifier ^[17,2]. The Aquila optimization based cascaded LSTM approach is employed so as to classify the monogenic disorder sickle cell anemia and normal cell. The algorithm for this Aquila Optimization based cascaded LSTM is shown below:

Algorithm 1: Aquila optimized cascaded LSTM classification

Input: Train features $Train$, Test Feature $Test$, train Label $Label$

Output: Predicted Class $Outpu{t}_{cl}$

Step 1: The encoder has four convolutional layers, each of which estimates feature maps with different kernel sizes (3, 3, 5, 5).

${I}_{conv} = \left[\frac{Train+\left(2*{p}_{c}\right)+{k}_{c}}{{s}_{c}}\right]$

${I}_{conv}$—Output convolutional features

${p}_{c}$—Convolution padding size

${k}_{c}$—Convolution kernel size

${s}_{c}$—Convolution stride size

Step 2: Three max pooling stages are applied; the signal sizes are divided into two equal parts based on the max pooling process.

${F}_{max} = \mathrm{max}\left({I}_{conv}\left(j\right), {G}_{F}\right)$

where ${G}_{F} = \frac{\delta l}{\delta {k}_{i}}*{I}_{conv}\left(i\right)$

$\delta l$ is the length of the estimated convolutional features

$\delta {k}_{i}$ is the derivative parameter computed by using multi stage probability sampling

$\delta {k}_{i} = \frac{{N}_{I}{\sigma }_{I}^{2}}{{(N}_{I}-1)*\frac{{\mu }_{I}^{2}}{{N}_{I}}+{\sigma }_{I}^{2}}$

${N}_{I}$—number of convolutional features

${\sigma }_{I}$—standard deviation of convolutional features

Step 3: During decodification, the four-layer convolution inverse technique is used, and the size of the features is augmented using an up-sampling procedure that adds duplicates to the number of samples with convolutional features.

Step 4: Two layers related to dense and flatten the results are involved to attain the final reconstructed signal.

${L}_{dense} = {Wt}^{F}*\frac{\partial {L}_{max}^{l}}{\partial t}$

where

${Wt}^{F}$ weight estimated with respect to index features

$\frac{\partial {L}_{max}^{l}}{\partial t}$ derivative for the maximum polling features

Estimated flatten layers with respect to whole dimension

${L}_{flatten} = {L}_{dense}(:)$

Step 5: The optimization algorithm performed using Aquila optimization, with the addition to the stochastic gradient descent along with learning rate 0.001.

$\Delta Op{t}_{L} = -\rho \frac{{v}_{l}}{\sqrt{{s}_{l}+\tau }}$

${v}_{l}$—exponential average of gradients of the features

${s}_{l}$—xponential average of square of gradients of the features

$\rho$—Initial learning rate 0.001

$\tau$—constant value

Step 6: After probability distribution, binary cross entropy is performed as loss function to estimate difference between actual samples

$loss = \sum _{i = 1}^{k}B\left(Labe{l}^{i}\right)*\mathrm{l}\mathrm{o}\mathrm{g}(\Delta Op{t}_{L}^{i})$

// $B\left(.\right)$ is the binary cross entropy operation

Step 7: The final classified output is,

$Outpu{t}_{cl} = Labe{l}^{i}(loss\le 1)$

4.   Performance analysis

The performance assessment of the proposed system is projected in this section. As a part of a collaborative research project done by Jawaharlal Nehru Technological University Institute, Hyderabad TEQIP-Ⅲ, a memorandum of Understanding (MoU dated 15 Oct 2019) was executed among the Institute named Vallurupalli Nageswara Rao Vignana Jyothi Institute of Engineering & Technology, Bachupally, Hyderabad, Telangana. The MoU aims at the objectives like data sharing and technology transfer. A dataset of 1387 patient's records were received who approached Thalassemia and Sickle cell Society (TSCS) for the purpose of diagnosis. Those records were shared as a MoU part and are pre-processed for maintaining the anonymity and confidentiality which satisfies patient's data privacy. Once it is pre-processed, few attributes were recognized with the class label at the blood sample diagnosis.

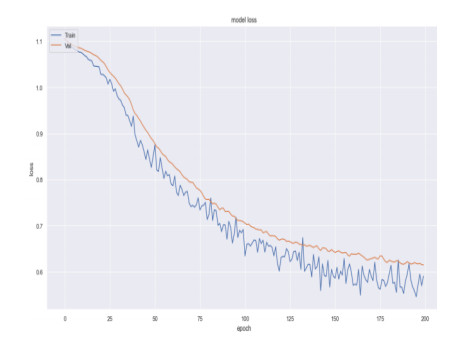
Figure 3 signifies the assessment of model loss in terms of number of epochs for both testing and training data. As the number of epochs increased, the model loss decreases.

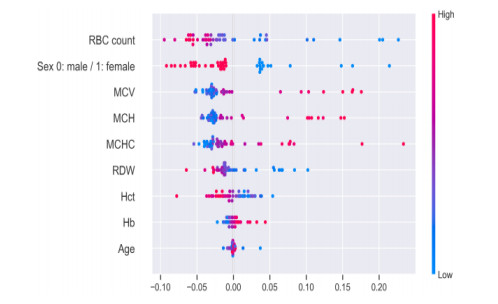
The attributes like Red Blood Cell (RBC) count, sex of the patient, Mean Corpuscular Volume (MCV), Mean Corpuscular Hemoglobin (MCH), RBC Distribution Width (RDW), Hematocrit (HCT), Mean Corpuscular Hemoglobin Concentration (MCHC), Hemoglobin (HB), and age and their corresponding range values low or high is represented for entire attributes. The rose color signifies higher value and blue denotes lower range. Based on the parameters range values variation, the disorder occurrence and cause are predicted.

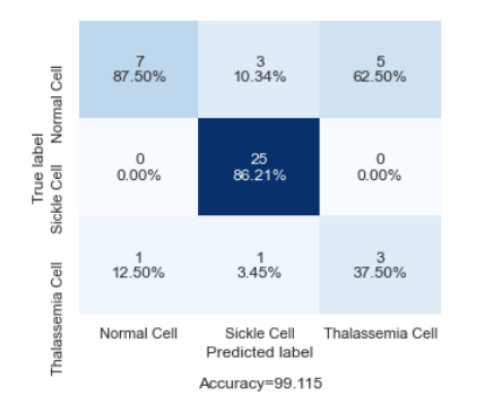
Figure 5 is the representation of confusion matrix formation and the accuracy assessment for the true label and predicted label values indicating normal cells, sickle cell, and Thalassemia cell. The confusion matrix is predicted for true label and predicted label. The accuracy assessment based on the constructed confusion matrix is about 99.115%. The confusion matrix signifies the count from the predicted and the actual values. The output TN denotes true negative values which signifies the number of negative samples that are classified accurately. Likewise, TP signifies the true positive values which signifies the number of positive samples that are classified accurately. FP indicates the values of false positive that is the actual number of negative samples that are classified as positive and FN indicates the value at which the actual positive samples are classified as negative.

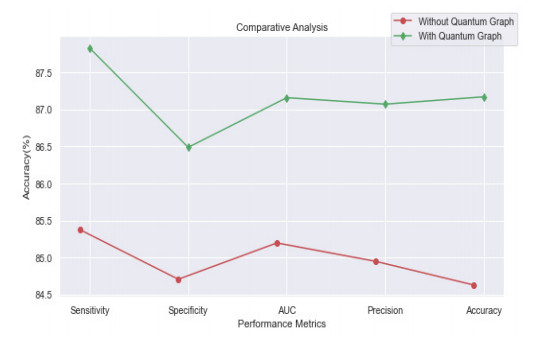
Figure 6 is the comparative analysis made for the performance metrics like sensitivity, specificity, AUC, precision, and accuracy in terms of both (without quantum graph and with Quantum graph). The results indicate that the outcome attained with Quantum graph theory is having higher outcome values on comparing the ones without Quantum graph utilization. The application of Quantum graph model offers better result this is due to the advantage that Quantum algorithms for graph analysis is more effective on comparing their classical counterparts. In the condition of quantization that Eigen function on the graph cloud be defined over the associated plane-wave co-efficient. Since the Eigen function is stationary at Quantum evolution. For these benefits, the outcomes are better on employing Quantum graph theory model.

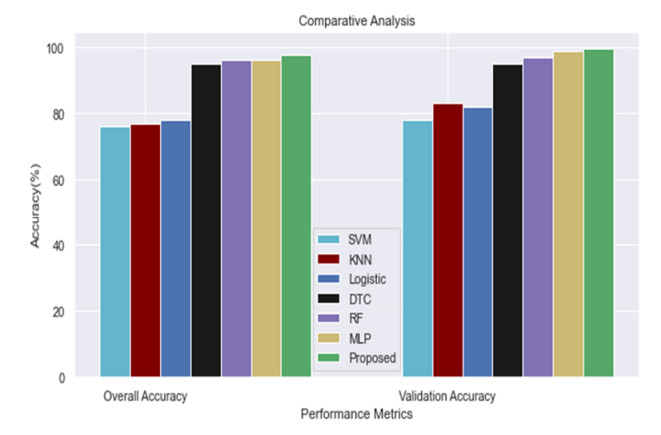
The comparative estimation is made in Figure 7 for overall accuracy and validation accuracy for proposed classifier and existing classifiers like SVM, KNN, Logistic, DTC, RF, and MLP. From the outcome it was evident that proposed system is having higher accuracy rate than the traditional methods. Also, the suggested Quantum graph theory model with the Aquila optimization based cascaded LSTM is offering enhanced output than existing ones. This is due to the reason that Aquila optimization-based technique has advantages like simplicity, flexibility, and ability for avoiding local optima and meta-heuristic optimization approach. Also, this is capable of solving several complex and tricky optimization issues.

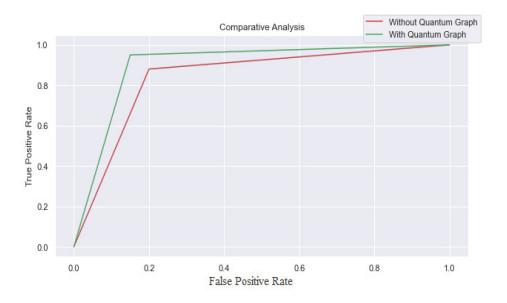
Figure 8 is the comparative analysis made for the False and True Positive Rates in terms of both (without Quantum graph and with Quantum graph). The results indicate that the outcome attained with Quantum graph theory is having higher outcome values on comparing the ones without Quantum graph utilization.

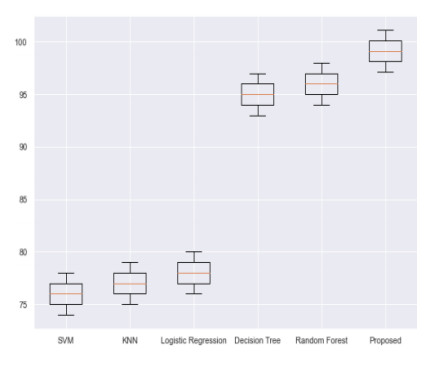
The comparative estimation is made in Table 1 in terms of accuracy for proposed classifier and existing classifiers like SVM, KNN, Logistic, DTC, and RF. From the outcome it was evident that proposed system is having higher accuracy rate than the traditional methods.

Figure 9 is the graphical representation of comparative estimation made in terms of accuracy for proposed classifier and existing classifiers like SVM, KNN, Logistic, DTC, and RF. From the outcome it was evident that proposed system classifier is having higher accuracy rate than the existing approaches. This is because the cascaded LSTM proposed is a generative approach which leverages LSTM approach for the prediction of topological infrastructures over the time of information cascade tree. It is competent of predicting the information cascades of various spatio-temporal growth patterns. For this reason, the presented cascaded LSTM is said to be effective.

5.   Conclusions

The proposed work bids on presenting a mathematical modelling to identify monogenic disorder termed sickle cell anaemia with the use of classifier. This predictive model is effective in offering high accuracy rate of prediction process. Firstly, input DNA sequence is taken and the elastic property features were extracted using Quantum Graph theory model. Then, the extracted properties were optimized using Aquila optimization and classified using cascaded LSTM for attaining classified outcome of sickle cell and normal cells. In conclusion, the performance assessment was carried and the outcomes attained shows improvement in terms of sensitivity (3%), specificity (2.2%), and AUC (1.9%), precision (2%), and accuracy (2.6%) improvement was achieved on applying Quantum graph theory on comparing without Quantum graph theory application. The accuracy was compared with existing classifier like SVM, KNN, Logistic Regression, DTC, RF and MLP algorithms to validate the proposed system effectiveness. The simulations results illustrates that the presented classification offers 99.12% accuracy for predicting and classifying normal and sickle cell anaemia. As of the outcome attained it was evident that proposed system is having higher accuracy rate on comparing traditional approaches. In future, this work can be extended by predicting various other diseases and the algorithm can be enhanced so as to attain high performance.

Conflict of interest

All authors declare no conflicts of interest in this paper.