1. Introduction
Vanadium is sparsely distributed in the earth's crust. It is found at an average concentration of 150 mg kg–1 in mineral ores and in the range of 3–300 mg kg–1 in soil. Vanadium pentoxide, the highest oxidation state 5+ of vanadium, has been known for more than a century. In December 1867, as a part of his Bakerian lecture to the Royal Society, the British chemist Sir Henry Roscoe outlined the multiple oxidation states of binary oxides of vanadium and set the end-member "vanadic acid" V2O5 [1]. The first V2O5 gel was described by the French chemist Ditte in 1885 [2]. The natural occurrence (50%) of V2O5 is found in flue-gas deposits from oil-fired furnaces and residues from elemental phosphate plants. However, V2O5 mineral is rare; shcherbinaite V2O5 (orthorhombic crystal system) is found on the walls of volcanic fissures [3] and navajoite is a mineral trihydrate V2O5·3H2O (monoclinic structure). The titanoferous magnetite ore in lump form contains approximately 1.5–1.7% vanadium pentoxide.
The structure of crystal isolated from fused V2O5 was first elucidated by Katelaar [4] as a rhombic unit cell containing two molecules of V2O5. Refinements were further done by Byström et al. [5] who established the orthorhombic layered structure of V2O5 with Pmmn space group. In 1961, Bachmann et al. [6] redetermined the crystal structure of V2O5 and reported its lattice parameters a = 11.510 Å, b = 4.369 Å, c = 3.563 Å. Their structural description is as follows: "the structure is built up from distorted trigonal bipyramidal coordination polyhedral of O around V, which share edges to form zigzag double chains along [001] and are cross-linked along [100] through shared corners, thus forming sheets in the zz plane". More recently, Enjalbert and Galy [7] proposed the bonding interactions of van der Waals type between two-dimensional V2O5 slabs and stated the presence of "square pyramid" instead of trigonal bipyramid. Ramana et al. [8] and Julien et al. [9] have described the easy cleavage along the (001) plane due to the weak interaction between V2O5 layers. Three V2O5 polymorphs have been identified as α-, β-V2O5, which crystallize with the orthorhombic and tetragonal structure, respectively, and the rutile-type δ-V2O5, which is a modification of β-V2O5 (space group C12/c1) [10]. Recently, Parija et al. [11] evaluated the metastable polymorphs including γ'-, δ'- and ρ'- phase of V2O5 using density functional theory calculations.
Here, we review the properties of V2O5 thin films employed in energy storage and conversion systems, which were prepared with a variety of deposition options. Numerous works prior 2001 have been devoted to the studies of synthesis, physical characterizations and electrochemical performances of films used as either cathode in all-solid-state batteries [12,13,14,15] or electrode of electrochromic devices [16]. Recently, Mo-doped V2O5 thin film has been studied as an electrode of supercapacitors [17]. This is an illustration of the increasing interest in this material in the recent years for many applications, sustained by numerous works that are reviewed here.
This review paper is organized as follows. In Section 2, we summarize the techniques used for the preparation of films and discuss the structure and morphology of V2O5 related to the synthesis conditions (temperature, partial pressure, substrate, etc.). Section 3 is devoted to the physical properties of V2O5 thin films; structure, morphology, vibrational spectroscopy, elemental analysis, electrical properties and intercalation process are considered. In the following Sections 4 and 5, doped V2O5 thin films and composite films are treated, respectively. Finally, Section 6 is devoted to the applications in the field of energy, for which V2O5 thin films are used as electrode materials in lithium microbatteries, electrochromic devices, sensors and supercapacitors.
2. Thin film synthesis
The structure and morphology of vanadium oxide films are intimately related to the deposition method and the operating conditions. As the direct growth of crystalline V2O5 films is very difficult except in the cases of some sub-stoichiometric VOx oxides, an annealing process of the as-prepared films is required in air and high temperature. In this section we describe the different evaporation methods and provide some typical examples for each technique used. Note that the choice of a deposition method depends of the thin film application. For instance, electrodeposition [18], reactive sputtering [19], sol-gel [20], hydrothermal method [21], doctor-blade route [22] were carried out for electrochromic V2O5 films that requests large surface coatings. The reader will find supplementary data in the review by Beke [23]. During the deposition process in vacuum or in a reducing atmosphere, the removal of oxygen atoms occurs from the film network when V2O5 is heated above its melting point that induces the formation of defects or reduced VOx phases. Consequently, the structural and morphological disorders and phase instability can be controlled using appropriate deposition parameters.
2.1. Thermal deposition
The thermal evaporation technique is the simplest method based in the production of flux of vapor in a high vacuum chamber (pressure 100 mPa) to form thin films without the presence of catalyst. In this method, the substance is evaporated by means of resistive heating. Generally, the raw powder is placed in a molybdenum boat heated at Tboat. The modifications of the structure, stoichiometry and morphology of the deposited films are obtained by varying the substrate temperature Ts, the flow of reactive gases (in cm3 min–1 at standard pressure and temperature, expressed as "sccm" hereafter) and the duration of the target evaporation. For example, thermally evaporated polycrystalline V2O5 films (10–20 nm grain size) were fabricated using Tboat = 650 ℃ for 6 h with gas flow 13 sccm Ar + 50% O2
[24]. The nature of the substrate is an important factor to obtain films with preferential orientation [25]. V2O5 films deposited on silicon (111) wafers by vacuum thermal evaporation were amorphous when deposited at Ts ≤ 200 ℃, while polycrystalline at Ts ≥ 300 ℃. This later temperature is optimum for V2O5 films strongly oriented with (001) planes parallel to the substrate [26]. Nanostructured V2O5 thin films (25 nm grain size) thermally deposited onto Ni substrates at Ts = 300 ℃ show preferential (001) orientation. These films have pseudocapacitance of 730 mF cm–2 at current density of 1 mA cm–2 and charge transfer resistance of 7.5 Ω [27]. The thermally evaporated V2O5 films at Ts = 25 ℃, 100-nm thick, crystallized after annealing process at 500 ℃ with grain size 26 nm and exhibited an electrical conductivity of 5.5 S cm–1 (activation energy of 0.16 eV)
[28] and optical bandgap of 2.8 eV.
2.2. Flash-evaporation
In the flash-evaporation method, the powders are placed in a reservoir and poured drop by drop into the boat heated at Tboat to ensure the vaporization. This process allows the control of the vaporization rate and preserves any decomposition of the starting material before evaporation [29]. It was demonstrated that V2O5 flash-evaporated films are more homogeneous [30]. Flash-evaopration was also used for depositing LixV2O5
[31]. Polycrystalline V2O5 flash-evaporated films have been investigated as a function of the deposition conditions: various substrates, substrate temperature (Ts), oxygen partial pressure (pO2) and post-annealing treatment (Ta) [9]. Figure 1 presents the evolution of the O/V ratio as a function of the temperature of the molybdenum boat [32]. Films with the best stoichiometry O/V = 2.497 were obtained for Tboat in the range 910–980 ℃. However, properties of flash-evaporated films are strongly dependent on the deposition "quenching rate" ΔT, which is the difference in temperature between the melt and the substrate (ΔT = Ta – Ts).
2.3. Chemical vapor deposition (CVD)
Chemical vapor deposition (CVD) is a versatile technique that consists of an evaporator and a deposition system. The precursor solution is vaporized into a reactor which acts as a flash evaporation system. The vapor condenses in a cold-wall reactor in which the substrate placed in the central zone is maintained at constant temperature Ts
[33]. This technique has been successfully carried out to grow V2O5 films using pure or diluted triisopropoxyvanadium oxide VO(OC3H7)3 precursor [34]. Typical V2O5 film 240 nm thick was formed at Ts = 300 ℃ in the total pressure pt = 2400 Pa with a flow of O2 of 100 sccm. V3O7 and V4O7 films are deposited when pt decreases to 1200 Pa, while V6O13 films are formed at Ts = 350 ℃ and O2 flow rate of 120 sccm. Highly crystallized films (94 nm crystallite size) were obtained after post-annealing at 500 ℃ for 2 h in O2 atmosphere with a slow cooling process to insure a good adherence on substrate. Plasma-enhanced chemical vapor deposition (PE-CVD) is a method for large scale film deposition. In this technique, glow discharge creating high-energy electrons ionize gaseous molecules and generate chemically reactive ions. Heat-treated (500 ℃ for 2 h) films deposited by CVD technique onto Pt foil are highly structured with homogeneous and smooth surfaces as shown in Figure 2a. The coherence domains along the a-and c-axis are L200 = 71 nm and L001 = 36 nm, respectively. The cross-section image (Figure 2b) displays the compactness of annealed V2O5 films [35].
Barreca et al. [36] prepared V2O5 thin films by PE-CVD using VO(hfa)2·H2O (Hhfa = 1, 1, 1, 5, 5, 5-hexafluoro-2, 4-pentanedione) as precursor. This precursor was vaporized at 70 ℃ at the rate of 2 × 10–4 mmol m–2 s–1 in a reactor in which argon (constant flow rate ϕ = 40 sccm) and oxygen (flow rate 5 ≤ ϕ ≤ 20 sccm) were plasma sources. V2O5 thin films deposited at Ts = 200 ℃ and 10 sccm of O2 are highly textured (14 nm crystallite size) and grow with the (001) preferential orientation. In the metal organic chemical vapor deposition (MOCVD) the organometallic vapor phase takers place at moderate pressure (10–1000 hPa). Watanabe et al. [37] prepared V2O5 thin films by means of microwave plasma MOCVD on ITO-coated fused silica substrate. Bis-acetylacetonatovanadyl, VO(acac)2, VO(C5H7O2)2 heated at ~600 ℃ was selected as vanadium precursor. Its vapor was injected into the oxygen plasma generated by the microwave discharge. Other experimental conditions were as follows: the substrate was maintained at Ts ≈ 300 ℃, the O2 flow was ϕ = 1.2 dm3 h–1 under pressure of 650 Pa. Typical polycrystalline film, 120 nm thick, was deposited after 15 min. Vanadyl(Ⅳ)
β-diketonate has been also used with water in a low-pressure reactor under different conditions [38]. A novel vanadium(Ⅲ) precursor such as vanadium(Ⅲ) alkoxide [V(OCMe2CH2OMe)3] was also used, which presents an appreciable volatility at 55 ℃ under pressure of 200 Pa [39]. Strongly (00l)-oriented film composites of V2O5–V6O13 were grown at temperatures ≥560 ℃ onto fused quartz substrate using vanadyl acetylacetonate as precursor. Single phase was obtained for substrate maintained at Ts = 580 ℃ due to the reentrant-type growth behavior [40]. V2O5 electrochromic films were grown on flexible polymer substrates using plasma-enhanced chemical vapor deposition (PECVD). Films were deposited at high rate of 50 nm min–1 from the decomposition of vanadium oxytrichloride (VOCl3) and O2 [41]. Nandakumar [42] studied the growth rate rG of CVD V2O5 films as a function of Ts and reported an Arrhenius behavior with 0.14 eV activation energy; rG = 50 nm min–1 at Ts ≈ 230 ℃.
2.4. Magnetron sputtering
Sputtering deposition method is the most popular technique to grow metal-oxide films, since it allows faster deposition rates. Its main advantage comes from the production of good surface uniformity of as-deposited films. It includes radio-frequency (r.f.) magnetron sputtering [43,44,45,46], direct current (dc) magnetron sputtering [47,48,49] and ion beam sputtering [50]. The stoichiometry of V2O5 films can be tuned by this evaporation method [51,52]. Typical r.f.-magnetron sputtered V2O5 films are formed in a plasma sputtering chamber using V2O5 target bombarded by argon ions in a plasma of power Pw = 150–300 W. For specific application, low sputtering power Pw < 100 W can be used [53]. The reactive deposition is realized by injection of pure argon and oxygen gases, at flow rate ϕ < 10 sccm. Silversmit et al. [51] obtained V2O5 films on Si (100) wafers by reactive dc magnetron sputtering and studied the influence of deposition parameters on their stoichiometry. These experiments were carried out in a vacuum of 5 × 10–5 Pa with a magnetron discharge voltage at ~550 V and a plasma constant current of 150 mA. The O2 flow was maintained at ϕ = 3.5 sccm. Fateh et al. [54] deposited V2O5 films onto (100) oriented Mg substrates and established detailed synthesis-structure relationships showing the best crystallinity for the film deposited at 80 ℃. Lourenço et al. [55] investigated the effect of different oxygen flow rates on the structure of VOx films and determined that V2O5 films are obtained at high oxygen flows (ϕ > 9 sccm). Benmoussa et al. [56,57] sputtered V2O5 thin films on Corning glass and ITO-coated glass substrates for electrochromic application. The films deposited on both substrates are c-axis preferred oriented showing that texture is substrate independent.
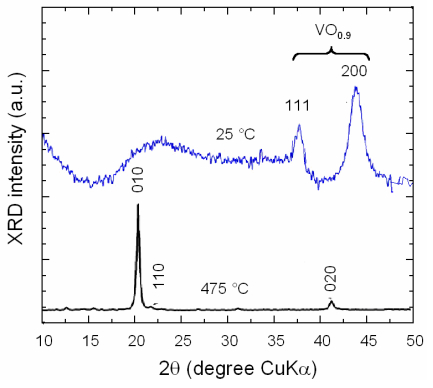
Yoon et al. [58] compared the structure of V2O5 thin films grown on (100) Si wafers by d.c. and r.f. reactive sputtering at room temperature; d.c.-sputtered films are amorphous, while those prepared from reactive r.f.-sputtering crystallized with large grain size that is due to the self-bias effect. Gianneta et al. [46] deposited VOx films using a base pressure 1 mPa, a r.f. plasma power of 200 W and an Ar flow ϕ = 20 sccm. As-deposited films are almost amorphous and exhibit broad XRD reflections matching those of VO0.9, while annealing at 475 ℃ in air for 3 h promotes the well-crystallized V2O5 phase with well-developed orthorhombic shape and grain size > 100 nm (see Figure 3). Ottaviano et al. [59] reported the improved electrochromic properties of rf reactive sputtered films deposited at low O2 flow (2%) showing the highest value of injected charge (49.8 mC cm–2) and the greatest differences in optical density. Lin and Tsai [19,60] prepared V2O5–z films on flexible PET(polyethylene terephthalate)/ITO (indium tin oxide) substrates. Oxygen deficient V2O5–z films (z = 0.13) were formed in a chamber pressure of 6 Pa with Ar and O2 flow rate of 4 sccm that show a transmittance variance od 36.5% after 200 cycles. Kang et al. [61] prepared nanorod-like V2O5 film by electron-beam irradiated amorphous film, which were obtained by r.f. sputtering at power of 200 W at 1 nm min–1 growth rate on alumina substrate.
2.5. Pulsed-laser deposition (PLD)
Extensive works using the PLD technique have been successful for the growth of V2O5 thin films. Advantages include an easily control of the film composition by tuning the deposition parameters and a good reproducible stoichiometry of the target material in the films [62,63,64,65,66,67,68,69,70,71,72,73]. In the PLD technique, a pulsed laser beam (10 ns duration) is focused by a lens to ablate the V2O5 target. The energy of the beam is in the range 100–500 mJ per pulse (laser fluence of 10 J cm–2) with a laser pulse repetition of 10 Hz. Target and substrates are placed inside the deposition chamber evacuated to ~1 mPa. To avoid depletion of deposit at any given spot, the target rotates at 10 rpm. For reactive synthesis, pure oxygen gas is introduced into the chamber with a typical partial pressure (pO2) in the range 0.1–10 Pa to obtain single-phased and stoichiometric V2O5 films. Typical deposition rate is in the range 2–5 Å s–1. Various laser wavelengths are reported in the literature: 532 nm line of a doubled frequency pulsed Nd:YAG laser [63], 248 nm line of a KrF excimer UV laser [62,64] or the 266 nm line of the quadrupled Nd:YAG laser. Zhang et al.
[62] prepared PLD crystalline oriented V2O5 films deposited at 200 ℃ in different partial pressure of O2 + Ar mixed gases. The films grown in oxygen-rich, pO2 = 0.1 Pa, environment at low substrate temperature Ts ≈ 200 ℃ crystallizes in the orthorhombic structure. Iida et al. [65] suggested that films deposited at Ts = 350 ℃ in a chamber under partial pressure pO2 = 13.3 Pa using the 238-nm line of a KrF excimer laser have a surface morphology suitable for electrochromic application. The same process was used to grow doped films, with various elements Nb, Ce, Nd, Dy, Sm, Ag [66]. Fang et al.
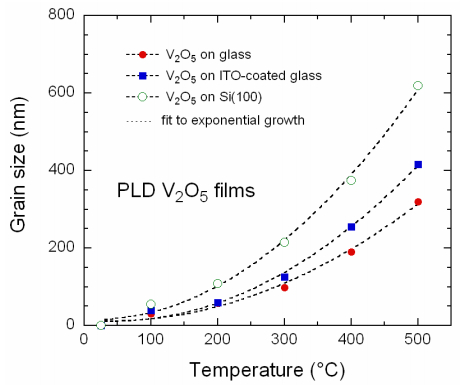
[74] prepared orientated V2O5 electrochromic thin films on glass by pulsed excimer laser ablation. Nanocrystalline films highly oriented along the c-axis were obtained at lower temperature Ts (200 ℃) that that of thermal vacuum deposition (300–500 ℃). McGraw et al. [67] found that the crystallographic texture of PLD V2O5 films depends mainly on temperature and oxygen pressure rather than on the choice of substrate. Films deposited on SnO2/glass substrate are dense and phase pure orthorhombic V2O5. For Ts = 200 ℃ and pO2 = 2.7 Pa, the films are well (200)-textured, while they are (001) and (101) dual-oriented for Ts = 500 ℃ and pO2 > 12 Pa. Ramana et al. [75] investigated the structural patterns of PLD V2O5 films which revealed that stoichiometric specimens are well-crystallized with the layered orthorhombic structure even onto amorphous substrates at Ts = 200 ℃ under partial oxygen atmosphere pO2 = 10 Pa. Atomic force microscopy (AFM) analysis gave a consistent picture of the surface morphology and microstructure: grains of small size, spherical in shape. Figure 4 shows the variation of the grain size as a function of the growth temperature for various substrate materials. The evolution of the grain size follows an exponential law (dashed lines) as [76]:
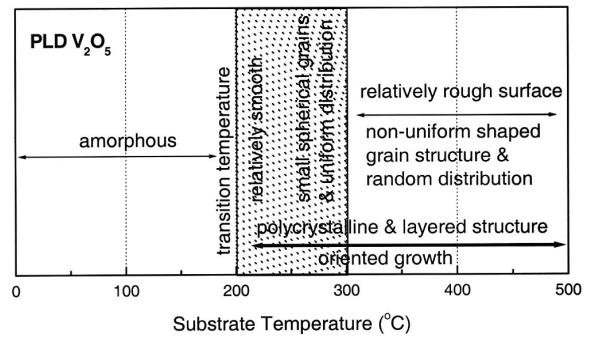
where Qd is the activation energy, kB is the Boltzmann constant, T is the absolute temperature, and Lo is a preexponential factor that depends on the physical properties of the substrate-deposit. The grain size appears to be 50–300 nm for films deposited onto glass, 50–400 nm for films on ITO-coated glass and 60–600 nm for films evaporated on Si wafer. Qd of the PLD V2O5 film in the range 0.43–0.55 eV reflects the nucleation rate [64]. AFM images show that films deposited onto Si (8 nm) and ITO-coated glass (10 nm) exhibited lower surface roughness. The dependence of the substrate temperature on the gross microstructure of PLD V2O5 films is presented in Figure 5. The domain of optimum controlled morphology is illustrated by the shaded region of substrate temperature range 200 ≤ Ts ≤ 300 ℃.
2.6. Electron-beam (e-beam) evaporation
The e-beam evaporation method implies a high vacuum coating unit with vacuum better that 0.1 mPa, in which an electron beam accelerated by a voltage of several kV (typically 6 kV) and power density of ~1.5 kW cm–2 is scanned on the surface of the target. It is a low-cost technique, which allows high deposition rate (30–50 Å s–1) with good control of the structure and morphology, and allows for sequential and co-deposition with minimum contamination [8,77,78,79,80,81,82,83,84].
In their early work, Ramana et al. [81] reported the growth of non-stoichiometric V2O5 films deposited on Corning 7059 glass substrates maintained at Ts = 280 ℃ in a vacuum of 0.05 mPa, while the injection of pure oxygen (partial pressure of 0.1 mPa) produced near-stoichiometric films with pale orange yellow color. The XPS experiments revealed that films formed at room temperature are nearly stoichiometric, while the films formed at elevated temperatures are oxygen deficient. These results are supported by the shift of the vanadyl mode in the FTIR and Raman spectra. However, the films deposited at Ts ≈ 420 ℃ in oxygen partial pressure of 10–4 mbar led to vanadium ions in their highest oxidation state [8,79]. Alumina-doped V2O5 thin films, (V2O5)100–x(Al2O3)x with x = 5, 10, 15, 20 wt.%, were fabricated by e-beam evaporation method [85]. Thiagarajan et al. [84] studied the physical properties of highly oriented V2O5 films (0.8–1.2 µm thick, 31–45 grain size) grown by electron beam evaporation at 200 ℃ throughout all depositions. It was shown that the microstrain decreases with the decrease of the film thickness, due to the reduced dislocation density.
2.7. Spray pyrolysis
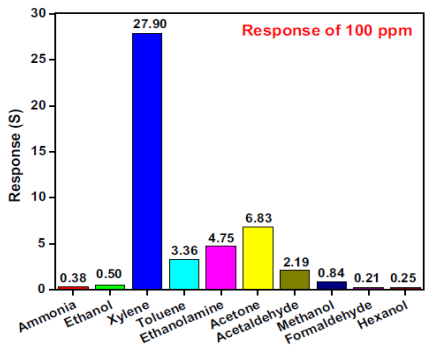
Spray pyrolysis is considered as a cost-efficient technique and has been widely employed to fabricate V2O5 thin films. Currently, the pyrolysis process is performed at relatively low temperature > 500 ℃ [86,87,88,89,90]. The V2O5 films are deposited through thermal decomposition of vanadium precursor such as VCl3 in deionized water [91]. By increasing the spray deposition rates, the crystallite size increases, while the microstrain decreases. Nanostructured flower-like V2O5 (crystallite size of ~25 nm) were prepared by spray pyrolysis from 0.1 mol L–1 ammonium vanadate in aqueous solution. Polycrystalline films deposited at Ts = 300 ℃ exhibit the largest carrier density 3.6 × 1018 cm–3 and the lowest electrical resistivity 5.56 Ω cm–1, which allow to use them as xylene sensors [92]. 10% Mo-doped films (~28 nm crystallite size) prepared by spraying VCl3 and MoCl5 in aqueous solution on substrate maintained at 380 ℃ crystallize with a tetragonal structure [93]. Wei et al. [90] prepared V2O5 films using ultrasonic spray method that revealed a small amount of V4+ species. These films heat-treated at 350 ℃ show good charge storage stability over 10000 electrochromic cycles. A d.c. plasma torch was used to atomize the solution VOCl3 precursor, which is injected externally into the plasma flame and deposited on the substrate [88]. Nanostructural V2O5 thin films deposited by spray pyrolysis technique exhibit the highest transmittance when deposited at 550 ℃. A shift of the absorption edge from 2.5 to 2.8 eV is observed for Ts > 450 ℃ due to modified chemical bonds at the film/substrate interface [89]. The influence of the molarity of the spray pyrolysis precursor on the structure and morphology of V2O5 films shows that vanadium nitrate V(NO3)5·5H2O with concentration ≥0.1 mol L–1 provides orthorhombic structured films with (001) preferred orientation [94].
2.8. Sol-gel
Sol-gel method is a low-temperature wet-chemistry method in which the raw materials are mixed at the molecular level. Wang et al. [95] investigated the structural modifications of spray deposited V2O5·nH2O xerogel films as a function of post-annealing temperatures. Films sprayed at 150 ℃ showed broad peaks in their 51V NMR spectra for heat-treatment at Ta ≈ 120 ℃, which gives evidence of a distortion of the square pyramids. The structural feature of V2O5·nH2O (with structural water) favors the lithium intercalation between the slabs with respect to contracted dried films at Ta > 250 ℃. The effect of deposition conditions and post-annealing treatment of xerogel V2O5 films was studied by several groups. Najdoski et al. [96] examined the electrochromic properties of (NH4)0.3V2O5·1.25H2O nanostructured films deposited onto SnO2:F (FTO) as a function of the temperature of preparation. Elongated aggregates 250–500 nm length were obtained at 50 ℃, while shorter particles (50–300 nm) were obtained at 85 ℃. Chen et al. [97] prepared thin films by spin coating of the sol-gel composed by the mixture of V2O5 powders benzyl alcohol (BA) and isobutanol (IB) (molar ratio 1:40:4) heated at 110 ℃ for 5 h. Wang et al. [98] fabricated V2O5·nH2O xerogel films by reacting V2O5 and H2O2 under ambient conditions. V2O5·⅓H2O film exhibited the best Li+ intercalation properties with a stabilized specific capacity of 185 mAh g–1 at 0.1 mA cm–2 current density after 50 cycles. Cazzanelli et al. [99] analyzed the Raman spectra of xerogel films intercalated with lithium. V2O5·nH2O xerogel films (1.8 ≤ n ≤ 0) were spin-coated at angular velocity of 1500 rpm. Spectral features of Li-intercalated samples show significant effect of the water content in the interlayer space inducing new Raman bands at 800 and 950 cm–1. V2O5 films deposited by the doctor-blade route using polyol dispersed in waterand acetyl acetone crystallized with the C2/c structure, which transformed to orthorhombic Pmmn (86 nm crystallite size) after calcination at 170 ℃ for 3 h [22]. Dip-coating method was used to produce V2O5 xerogel films from organic (vanadium tri-isopropoxide into isopropyl alcohol) and inorganic (V2O5 powers in 15 wt.% H2O2) precursors [100,101]
2.9. Electrodeposition
A typical electrodeposition experiment takes place in an aqueous solution of vanadium precursor such as vanadyl sulfate hydrate (VOSO4·nH2O) or V2O5 powers dissolved in hydrogen peroxide as electrolyte using a constant potential (1.7 V vs. Ag/AgCl)
[18,102,103]. Liu et al. [104] prepared nanostructured V2O5 films by means of cathodic deposition from V2O5 and H2O2 aqueous solution. As-deposited samples contained 14% V4+, while annealing at 500 ℃ in air oxidized all vanadium cations. Electrochromic V2O5 films were synthesized by electrophoretic deposition of a sol formed by the dissolution of V2O5 powers in H2O2 solution with the H2O2/V2O5 ratio of 8:1. The deposition occurred in a Teflon vessel at the voltage of 5 V using a Pt rod as counter electrode [102]. The electrodeposition experiments carried out by Vernardou et al. [18] consisted in the coating of V2O5 powders dissolved in a solution of methanol and water as electrolyte to form an orange suspension. Pt rod was the counter electrode. Experiments were performed using deposition current density of 0.25 mA cm–2.
2.10. Atomic layer deposition (ALD)
The atomic layer chemical vapor deposition (ALCVD) was successfully applied to grow V2O5 films [105,106,107,108,109,110,111,112]. This method provides uniform and compact films with a high control of phase formation and the film thickness that include atomic layer epitaxy (ALE) and atomic layer deposition (ALD). ALD process consists in alternative exposition of a substrate to the precursor fluxes, which are timely separated in space. In principle this process is self-limiting as the monomolecular layers are absorbed with molecular excess flushed away by evacuation of the system. The vapor pressure of the precursor must agree with the deposition temperature chosen. Groult et al. [105,106] prepared nanometric V2O5 thin films deposited onto Si wafers (100) by means of ALCVD.
The atomic layer deposition (ALD) technique is proven suitable for the growth of uniform and pin-hole free V2O5 thin films. ALD is becoming an attractive process to prepare thin films for energy storage, because it allows the control of deposit films of thickness in the range 1–100 nm with remarkable uniformity and control of the thickness. V2O5 has been synthesized by this process by several authors [113,114,115,116,117,118,119]. This scalable method, which allows to do bath processes, is based on self-limited reactions between gas phase precursors and active sites on surfaces. This technique leads to monolayer thickness control. The growth of V2O5 thin films consists of the successive cycles of deposition of atomic layers from the reaction of a vanadium precursor with oxygen. Various vanadium precursors have been proposed such as vanadyl tri-isopropoxide VO(OC3H7)3 (VO(OPri)3, VTIP), vanadyl triethoxide (VO(OEt)3), vanadyl triisobutoxide (VO(OBui)3), vanadyl acetylacetonate (VO(acac)2) and vanadium acetylacetonate (V(acac)3 (acac = C5H7O2–)), VTIP being the most popular due to its high vapor pressure (38 Pa at 45 ℃) and its rapid reaction with water [107,108,109]. Examination of the literature shows that the choice of ALD precursors has a significant impact on the crystallinity and morphology of V2O5 films. One ALD cycle is composed of four pulses in the sequence t1/t2/t3/t4, where ti is the duration (in s) of injection of V precursor, purge, reactive gas, purge, respectively. For instance, the global ALD reaction of VTIP precursor with water is:
|
VO(OC3H7)3+3H2O→V2O5+6HOC3H7
|
(2)
|
The pressure of (VTIP) in the reactor is adjusted to 5 mPa and the water pressure to 0.3 Pa. Typical cycle to grow V2O5 films lasts 17 s (2 s VTIP, 5 s pumping, 5 s reactive gas and 5 second pumping) that makes a growth rate of 0.7 Å per cycle. Several authors demonstrated that the rate-determining step is the oxidant in O3-based or H2O-based ALD reaction [109,110]. Keränen et al. [107] prepared ALD V2O5 films deposited onto various metal oxides for catalytic applications using VO(acac)2 as V precursor with a N2 flow of 3 dm3 h–1. Chen et al. [111] used a water-free system to prepare crystalline as-deposited V2O5 films from VTIP and ozone, using an Al2O3 template at low temperature (170–180 ℃). With this process, a deposition rate of 0.27 Å per cycle onto Si wafer was achieved. Badot et al. [110] reported a growth rate of ~20 ng cm–2 per cycle at 170 ℃ using VTIP + water sequence. With these growth conditions and annealing at 400 ℃, the ALD V2O5 films were well-crystallized and preferentially oriented with the (a, b) planes parallel to the SnO2-coated glass substrate. ALD V2O5 films deposited onto Ti foil using the VTIP-water vapor route in the pulsing sequence—VTIP/N2 purge/H2O vapor/N2 purge of 200/400/2400/1000 ms and annealed at 500 ℃ for 2 h showed a small-polaron drift mobility of 1.84 × 10–2 cm2 V–1 s–1 at room temperature (activation energy of 0.14 eV) [112]. Ostreng et al. [113] prepared nano-structured ALD V2O5 films from vanadyl 2, 2, 6, 6-tetramethylhepta-3, 5-dione (VO(thd)2) and ozone at 215 ℃ with N2 as carrier gas (500 sccm flow) applied as cathode films for lithium microbatteries. 86-nm thick films oriented along a (001)/(010) orientation were thus obtained after 2000 cycles. Chen et al. [114] employed VTIP precursor with both O3 and H2O as oxidant. For ALD cycles operating in the 170–185 ℃ window, the water-VTIP route (growth rate 0.4 Å per cycle) produces amorphous films, while crystalline films are formed with the ozone-VTIP reaction (growth rate 0.20 Å). The transition from amorphous to crystalline structure was characterized by rectangular V2O5 nanograins (20 nm size) with a monomodal distribution starting at 400 ℃.
A comparison of thermal and plasma-enhanced ALD/CVD has been carried out by Musschoot et al. [109]. Chen et al. [114] determined that areal energy and power density is optimized with V2O5 thickness round 60 nm. Larger thickness results in a decrease of the rate capability due to the small intrinsic diffusion coefficient of lithium, while thinner films suffer from a decrease of material loading. The authors estimated that the device would outperform the gravimetric power density of the current Li-ion batteries by one order of magnitude. Song et al. [114] adopted to deposit V2O5 thin films by ALD using vanadyl tri-isopropoxide and water and showed remarkable electrochemical response and voltage-induced insulator-to-metal transition. Ultrathin V2O5 films (10–90 nm thick) were prepared by ALD using vanadyl acetylacetonate as the vanadium precursor [119]. Crystalline films were obtained below 200 ℃ yielding a growth rate of 4.5 pm per cycle. Heterojunction diodes based on TiO2(p)-(n)V2O5 were fabricated as humidity sensor.
3. Characterizations of V2O5 films
3.1. Structure and morphology
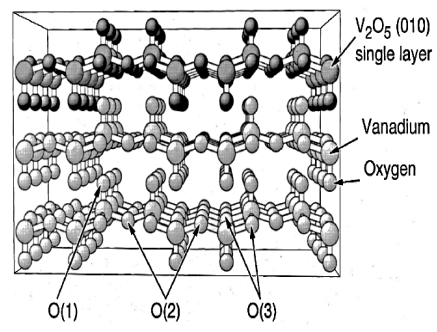
V2O5 is the highest oxidation compound of the vanadium oxide system which crystallizes with a lamellar orthorhombic structure in space group Pmmn (D2h13, No. 59) with lattice parameters a = 11.512 Å, b = 3.564 Å, c = 4.368 Å and V = 179.17 Å3 (see Table 1). It has a layered structure with atomic layers in the [100] × [010] plane and van der Waals-type interlayer coupling. The structure is formed of three types of oxygen atoms: apical-vanadyl (Ovan), bridge (Obri) and chain (Och) (see Figure 6). Oxygen vacancies in V2O5–δ are predominantly of the Ovan type, forming the vanadyl bonds. Atomic positions in V2O5 are summarized in Table 1. Pure V2O5 is a diamagnetic semiconductor with an energy gap (Eg) of 2.2–2.3 eV [120], while oxygen-deficient material is ferromagnetic with spin moment ~2 µB per vacancy [121]. A density functional calcualtion of the electronic structure is given in Refs. [122,123]. The role of octahedral deformations has been explored in [124].
Table 1. Atomic positions in orthorhombic V2O5 (space group Pmmn) (from Ref. [124]).
| Atom |
Wyckoff position |
Parameters |
| x |
y |
z |
| V |
4f |
0.10118 |
0.25 |
–0.1083 |
| Ovan |
4f |
0.10430 |
0.25 |
–0.469 |
| Obr |
2a |
0.25 |
0.25 |
0.001 |
| Och |
4f |
–0.0689 |
0.25 |
0.003 |
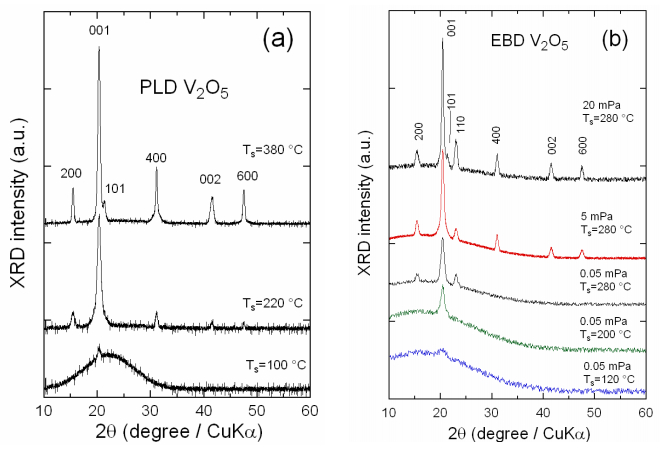
Figure 7 shows the typical XRD patterns of V2O5 films deposited by PLD (a) and (b) by electron beam (EBD) techniques. The spectra of samples deposited at low Ts are rather amorphous, while they can be obtained crystallized by raising the substrate temperature and/or increasing p(O2). The significant feature is the growth of XRD reflections at ca. 2θ = 20.26° and around 2θ = 41.4° that correspond to the (001) and (002) lattice planes of the orthorhombic structure, respectively. The (001) reflection is the dominant line for well-crystallized films showing the preferential c-axis orientation lying perpendicular to the substrate with stacking ab planes [125]. Gradual increase in intensity of the (101) reflection at high Ts is attributed to a re-organization process of the in-plane V–O–V chains in flash-evaporated film. This crystallographic behavior seems to be the general trend for the growth of V2O5 films; it has been found for various deposition techniques: as-prepared r.f. sputtered films under a gas mixture of Ar and O2 [56,126], sol-gel spin-coated films annealed at 400 ℃ [127], pulsed-laser deposited V2O5 films [63], plasma-enhanced CVD method [128] and vapor deposition in high vacuum [26,129] on heated substrates. The c-axis preferred growth was also found for films prepared by ALD [110,113] and EBD [79] processes. Well-ordered V2O5-(001) films were obtained by the oxidation of vacuum deposited vanadium layers with oxygen partial pressure of 50 hPa [130]. Due to the imperfect stacking of ab planes built up of Ovan, the (001) orientation for crystalline V2O5 films deposited by PECVD from a vanadyl(IV) β-diketonate compound appears at Ts as low as 150 ℃ [38], while higher temperature Ts = 240 ℃ for films prepared by CVD of VOCl3 with water [131]. Note that films prepared from sol-gel precursor display complex behavior due to the large fraction of water content. For instance, the XRD spectrum of spin-coated films obtained from V2O5 + H2O2 sol-gel (crystallized at Ta = 150 ℃) displayed the dominant (110) Bragg line, which disappeared and was replaced at Ta = 300 ℃ by the (00l) reflections showing the nucleation parallel to the substrate [121]. Other workers found that spin-coated films crystallize above 350 ℃ [132]. The texture of V2O5 films grown by ALD technique varies with the number of deposition cycles (nc). For nc < 1000, the predominant orientation is along the (001) plane, which is modified for nc ≈ 2000 with the appearance of sharp (0k0) Bragg reflections. Finally (021) and (061) reflections are observed for nc ≈ 5000. This is attributed to the overgrowth of nuclei on the surface of platelets with their edges orientated normal to the substrate [113]. Similar thickness (df) effect was observed on e-beam deposited films [84]. Moreover, the increase of the peak broadening of the (001) lattice place with df is attributed to microstrains inversely proportional to the crystallite size that linearly decreases with the increase in df.
Rajendra-Kumar et al. [133] deposited V2O5 films at various substrate temperatures (25 ≤ Ts ≤ 400 ℃) using vacuum evaporation technique. The orthorhombic lattice parameters "a" and "c" of polycrystalline films determined by Nelson-Rieley function were found to decrease when the deposition temperature increases (Figure 7a). According to the model proposed by Gilles and Boesman [134] from EPR spectroscopy, these structural changes are assigned to the increase of non-stoichiometry (oxygen vacancies) leading to a contraction of the (001) interplanar spacing.
The crystallite size Lc of composites is calculated using the Scherrer's formula by considering the (002) reflection line:
where K is the shape factor, which varies with the crystallite shape (0.89 for spherical crystallites), λ is the wavelength of X-ray radiation (0.15406 nm), B is the full-width at half maximum (FWHM) expressed in radians and θ is the Bragg angle. Generally, the peak intensity and the full-width at half-maximum (FWHM) vary with the deposition conditions, which indicates differences in crystallinity, particle sizes and ordering of local structure between samples. The analysis is obtained by the combination of the Scherrer and Bragg formulæ:
|
B2cos2θ=16e2sin2θ+K2λ2L2c
|
(4)
|
where < e2 > denotes local strain (defined as ∆d/d with d the interplanar spacing). From the slope 16 < e2 > and intercept K2λ2/Lc2 of the plot of B2cos2θ as a function of sin2θ, one can estimate the strain < e2 > and coherence length Lc. The variation of the local strain as a function of the substrate temperature for V2O5 films deposited by PLD method is reported in Figure 7b.
The surface morphology and surface topography are currently investigated by scanning electron microscopy (SEM) and atomic force microscopy (AFM) as a function of at various Ts. The AFM images recorded at the scan area of 2 × 2 μm2 for thermally evaporated V2O5 films are displayed in Figure 8
[82]. These patterns show that both the surface roughness and the grain size increase with the increase in Ts. Surface roughness of 27 nm and grain size of 130 nm are found for films deposited at 300 ℃. It was demonstrated that the morphology, structure and optical and electrical properties of dip-coated V2O5 films are affected by the sol aging [135,136,137,138]. Senapati and Panda [131] investigated nanoscale films prepared by spin coating of V2O5·nH2O sol at different stages of aging. Microstrains of films 92–137 nm thick were found to decrease from 4.93 × 10–3 for fresh sol to 2.62 × 10–3 for 192 h for aged sol in relation to the water loss, while the optical bandgaps decrease from 2.66 to 2.36 eV suggesting a decrease in the localized states with aging.
3.2. Optical properties
Optical properties of V2O5 thin films were investigated by means of absorption measurements for the determination of the optical bandgap, dispersion parameters and spectral window of electrochromic films. Optical absorption coefficient α is calculated by the relation:
|
T=(1−R)2exp(−αd)1−R2exp(−αd)
|
(5)
|
where T and R are the spectral transmittance and reflectance and d the film thickness. The interference effect due to internal reflection at normal incidence is negligible for higher optical density (αd > 1) that reduce Eq 1 to:
and the optical absorption coefficient becomes:
The optical bandgap Egopt of a semiconductor is calculated using the interband absorption theory:
where νi is the incident photon energy, A is a probability parameter and n is the transition coefficient with n = 2 for indirect transition and n = 3/2 for direct bandgap that is the case of V2O5.
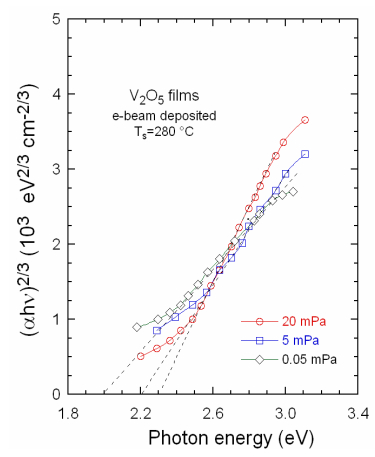
Overall, optical absorption spectra, electrical conductivity and electron paramagnetic resonance (EPR) spectra of V2O5 show a polaronic character. The polaron originates from the oxygen vacancies that result in an excess of electrons localized in the empty 3d orbitals of vanadium atoms. Consequently, V5+/V4+ pairs are closed to oxygen vacancies and result in an absorption in the infrared spectrum. The optical transmittance Topt of V2O5 prepared by e-beam deposition at different oxygen partial pressure revealed a sharp increase of Topt in the spectral range 550–600 nm. This is due to the fundamental absorption edge that shifts towards the higher energy with the increase in oxygen partial pressure. Figure 9 shows the plots of (αhνi)2/3 vs. photon energy for V2O5 deposited at Ts = 280 ℃ under various oxygen partial pressure. The high value of the optical bandgap Eg = 2.32 eV determined by extrapolation of the linear part of the graph to zero (α = 0) indicates that the films are stoichiometric for p(O2) = 20 mPa, while oxygen vacancies are created at lower pressure.
The partial filling of oxygen vacancies results in a decrease of the concentration of electronic localized states and an increase of Eg. The overall process of oxygen loss can be expression by the Kroger notation:
|
Oxo↔Vxo+12O2Vxo↔V∙o+e′↔V∙∙o+2e′
|
(9)
|
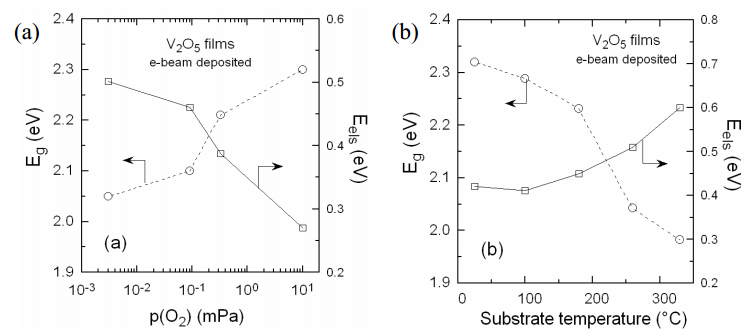
Lourenço et al. [55] studied the effect of oxygen flow rate ϕ on the optical properties of r.f. sputtered V2O5 films. The highest Eg = 2.56 eV was obtained at low ϕ = 1 sccm while higher f produced films with an optical bandgap in the range 2.41–2.45 eV. Optical bandgap data of the literature for r.f. sputtered films are in the range 2.15–2.40 eV [56,139,140]. The evolutions of both the width of electronic localized states Eels and the bandgap Eg as a function of Ts and as a function of p(O2) for e-beam evaporated V2O5 films are shown in Figure 10a, b respectively. These results show that stoichiometric films were obtained at p(O2) > 5 mPa and Ts < 100 ℃ [79].
Song et al. [141] determined the work function of the annealed V2O5 films synthesized by VTOP-based ALD method at 135 ℃ using valence-band ultraviolet photoelectron spectroscopy (UPS). The results showed that the valence band maximum (Ev) is located at ∼2.45 eV below the Fermi level (EF) and gave evidence of an indirect bandgap (Eg) of ~2.63 eV for V2O5 film annealed at 500 ℃ for 1 h in air. Irani et al. [89] investigated the structural and optical properties of nanostructured V2O5 thin films deposited by spray pyrolysis technique. The substrate temperature Ts appears to be the key growth along the (001) direction with an orthorhombic structure. It was pointed out that crystallites increased with elevating Ts, reached a maximum at Ts = 450 ℃ and decreased for Ts > 450 ℃. Optical characterizations showed that the highest transmittance occurs for Ts = 550 ℃ and the absorption edge shifts from 2.5 to 2.8 eV due to the formation of chemical bonds at the interface between V2O5 film and substrate.
Beke et al. [73] determined a bandgap of 2.52 eV for PLD V2O5 films prepared onto amorphous glass substrate with p(O2) = 13.3 Pa and Ts = 220 ℃ but did not distinguish between indirect allowed (n = 1/2) and direct forbidden (n = 3/2) transitions. Luo et al. [142] reported the indirect allowed transition (n = 2) that leads a decrease of Eg from 2.29 to 2.02 eV with increasing Ts from 275 to 320 ℃ for d.c. magnetron sputtered films. Similar trends were obtained on PVD films [143]. Ramana et al. [72] investigated the effect of the grain size on the optical properties of PLD films. The increase of grain size from 0 to 300 nm produces a red shift of the absorption edge (decrease of Eg) from 2.47 to 2.12 eV following a parabolic behavior that is attributed to the imperfections at grain-boundary regions. The optical absorption was explored on e-beam deposited V2O5 films grown at 200 ℃ on glass substrate with various thicknesses (~0.8–1.2 µm) [84]. The authors elucidated the role of film thickness; the indirect optical bandgap Eg = 2.36 eV is found for thicker films. Optical constants of V2O5 films, i.e., refractive index nopt, extinction coefficient k, and plasma frequency ωp have been investigated by Akl [144]. Determination of the optical bandgap of 2.25 eV was obtained after roughness correction for d.c. magnetron reactive-sputtered α-V2O5 films after heating at 500 ℃ for 1 h in oxygen atmosphere [145]. Ellipsometry measurements were performed as a function of incident angles on (001) oriented sputtered films yield the values of the refractive index n = 2.67, optical absorption coefficient k = 0.0011 and thickness d = 165 nm [146].
3.3. X-ray photoelectron spectroscopy
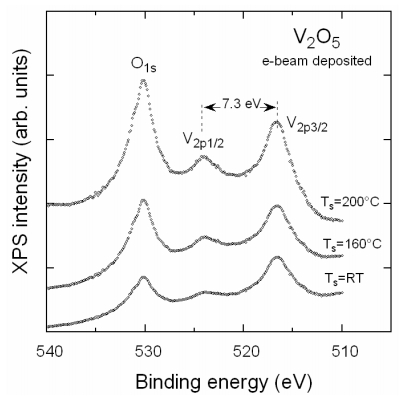
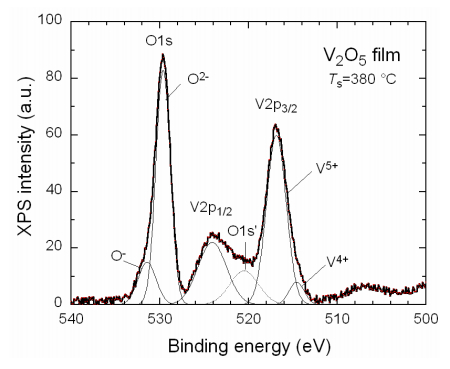
X-ray photoelectron spectroscopy (XPS) is the common technique to investigate the composition of the V2O5 surface and the oxidation states of elements [79,97,147,148,149,150]. The typical V 2p and O 1s XPS spectra recorded in the energy range of 510–540 eV for V2O5 thin films deposited by EBD technique at various Ts are displayed in Figure 11. The clear evolution of the spectral response corresponds to the V/O ratio in VOx lattices. Analysis of the XPS spectrum of a V2O5 film deposited at Ts = 400 ℃ under oxidizing atmosphere p(O2) = 0.01 mPa is presented in Figure 12. The binding energies of the V 2p levels are 516.9 and 524.5 eV for V 2p3/2 and V 2p1/2, respectively, with a splitting of 7.6 eV, whereas the binding energy of the O 1s level is 529.6 eV. For more detailed information, the background corrected spectrum was fitted by Gaussian profiles. Different V 2p and O 1s components are detected upon deconvolution by the fit by six Gaussian functions at binding energies of 514.8, 516.9, 520.8, 524.2, 529.7 and 532.5 eV that correspond to V4+ 2p3/2, V5+ 2p3/2, O 1s' satellite of O2–, V5+ 2p1/2, O 1s of O2–, and O–, respectively, as shown in Figure 12. From these results, the relative amounts of ions in different chemical states could be calculated by taking into account the atomic sensitivity factors: 1.41 for V 2p3/2 and 0.63 for O 1s. Note that the energy splitting between V 2p3/2 and V 2p1/2 levels is Δ = 7.3 eV for stoichiometric VO2.5 film.
The chemical composition and topography of V2O5 thin films at different steps of Li insertion/de-insertion have been investigated by quantitative XPS and AFM analyses [151,152,153,154]. From the first cycle, a solid electrolyte interface (SEI) layer has grown on the whole electrode surface, which consists of Li2CO3 aggregates. XPS analysis shows that various chemistries appeared during the cycle of charge/discharge such as partial dissolution of the initial Li2CO3 layer, residual deposit of ROLi (R = radical), PEO and oxalates. The overall dissolution/residue deposit process explains the capacity loss noticed at the end of the first cycle. Time flight secondary ion mass spectroscopy (ToF-SIMS) was carried out to analysize the ion distribution in V2O5 thin films [150,155].
3.4. Vibrational spectroscopy
Among the local probes, Raman scattering (RS) and Fourier transform infrared (FTIR) spectroscopy are techniques sensitive to the short-range environment of oxygen coordination around the cations [156]. As a first approximation, the spectra consist of a superposition of the components of all local entities present in the same material in contrast to diffraction data, which give a weighted average. As a rule, the frequency and relative intensity of the bands are sensitive to coordination geometry and oxidation states [157]. Both FTIR and RS spectroscopies are also probing the stoichiometry of films (Figure 13). The vibrational spectra of V2O5, which crystallizes in the orthorhombic system (Pmmn space group) with D2h13 spectroscopic symmetry, are composed of internal modes of the V2O5 layer in the ab crystal plane and the external mode in the low-frequency region (~144 cm–1) [158]. V2O5 has the spectroscopic D132h symmetry with the Wyckoff 4f position for the vanadium, vanadyl and chain oxygen atoms whereas the bridge oxygen occupies the Wyckoff 2a position [124]. The vibration modes associated to the D2h factor group decomposed as: Γopt = 7Ag + 7B1g
+ 3B2g + 4A3g
+ 3Au + 3B1u
+ 6B2u + 6B3u. According this decomposition, 21 modes of vibration are Raman active (7Ag + 7B1g
+ 3B2g + 4A3g) and 18 modes are infrared active (3Au + 3B1u + 6B2u
+ 6B3u) [158,159].
Ex situ and in situ FTIR spectra of V2O5 crystalline films prepared by dip-coating from V-oxoisopropoxide sols have been investigated as a function of the degree of Li+ intercalation and analyzed in terms of dispersion analysis (LO and TO phonons)
[160]. A diagnostic test to differentiate the safe region upon intercalation has been established by the red-shift of the V–OA stretching frequency at 1016 cm–1 and the disappearance of the bridging V–OB–V stretching mode at 795 cm–1.
Numerous studies of the Raman spectroscopy of V2O5 films have been performed on as-deposited, heat-treated, and Li-intercalated samples [9,99,161]. The typical Raman spectrum exhibits more or less well-defined internal and external modes, indicative of the film purity and crystallization (Figure 13b). The internal modes (in the high-frequency region) are the V = O bending vibration at 283 and 405 cm–1 and the bending vibration of the bridging V–O–V bonds at 485 cm–1, the V–O stretching mode at 525 cm–1 that results from the corner-shared oxygen atoms, and the vanadyl terminal oxygen stretching mode at 993 cm–1. The external modes are generated by the motions of two V2O5 layers of the elementary unit cell; these translational vibrations occur at 144 and 196 cm–1 (skeleton vibrational modes) [71,76]. The RS spectra of V2O5 films deposited by flash-evaporation onto silicon substrate show frequency shift of the vanadyl mode at 995 cm–1 (due to the shortest (1.58 Å) V = O double chemical bond stoichiometry) in relation with the stoichiometry of the film [9,161]. Ramana et al. [71] reported a frequency shift of the vanadyl vibration at 993 cm–1 with the substrate temperature for V2O5 films prepared by PLD technique at 200 ≤ Ts ≤ 500 ℃, which is attributed to the stress developed in the film. As XRD patterns indicate that the films deposited at Ts > 200 ℃ are polycrystalline with a preferred orientation along the c-axis, the shift of the vanadyl mode suggests a structural organization that introduces a stress associated to a compression in the layered structure. Raman spectroscopy was utilized to characterize the microstructure of V2O5 films prepared by d.c. magnetron sputtering on Si (111) wafer. Optimized films with a mere desirable layer-like lattice were obtained for a gas flow ratio O2/Ar of 3/2 [162]. Several works investigated the microstructure of amorphous V2O5 thin films by means of Raman [30,163,164] and FTIR [75] spectroscopy. Lee et al. [163] reported the spectral fingerprint of as-deposited amorphous V2O5 films, which exhibit two broad bands at ca. 520 and 650 cm–1 assigned to the stretching modes in a disordered V–O–V lattice. The absence of the skeleton mode at 144 cm–1 is due to the lack of long-range order. Flash-evaporated V2O5 thin films at 25 ≤ Ts ≤ 200 ℃ display a poor crystallization observed by the Raman features, which result in the appearance of the intense external mode at 144 cm–1 and ill-resolved internal Raman modes in the high-frequency region [30].
3.5. Electrical properties
V2O5 is a n-type semiconductor. Its semiconducting properties are mainly due to the oxygen non-stoichiometry, which are the consequence oxygen vacancies V2O5–δ. The electrical conductivity of V2O5 thin films have been investigated by means of d.c. four-point probe method and a.c. impedance spectroscopy as a function of the deposition parameters and post-annealing treatment [165]. The temperature dependence of the conductivity follows an Arrhenius law in a large range of temperatures. The general condition for semiconducting behavior is that the transition-metal ion could exhibit several valence states such as V4+ to V5+ in V2O5, so that electron hopping takes place between these two levels. If C = V4+/(V4+ + V5+) is the ratio of the concentration of low valence ions with the total concentration of transition metal ions and A is the average hopping distance, one can estimate the number of charge carriers N = CA–3. Using C ~ 0.02 and A = 0.384 nm, the carrier mobility is quite low lying between 10–7 and 10–2 cm2 V–1 s–1 [166]. Murawski et al. showed that the electrical transport arises from thermally activated hopping that takes place between the electronic states for V2O5 films made by PVD at 840 ℃ [167] and for amorphous V2O5 films obtained by flash evaporation [31]. In V2O5, the V4+/V5+ ionic pair is bound to positively charged defects, i.e., oxygen vacancies. The removal of an electron from the vacancy and produce a free carrier requests an energy e2/κd. The electrical conductivity is usually described in terms of Mott's theory for electronic transport in transition-metal glasses [168]:
|
σ(T)=C(1−C)ν0e2AkBTexp(−2αA)exp(−WkBT)
|
(10)
|
where νo is a phonon frequency, and α is the rate of the wave function decay. The thermal activation energy can be expressed as
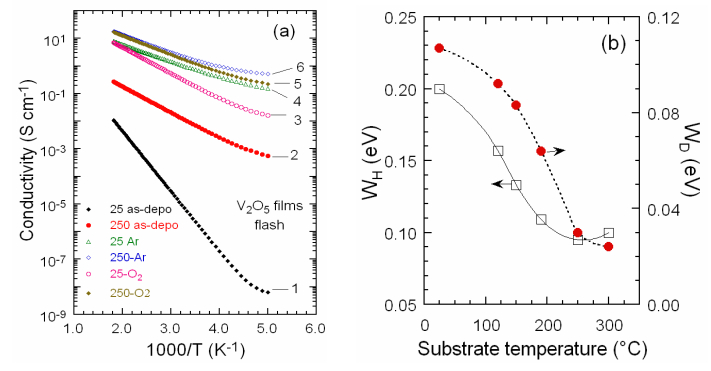
where Wh corresponds to the small polaron formation and Wd to the disorder energy arising from the energy difference of neighboring sites. The separation of W into a polaron and a disorder term is a rather difficult task, which can be partly solved using data taken at low temperatures. Julien et al. [166] reported that oxygen-deficient V2O5 films grown at high substrate temperature (Ts ≈ 250 ℃) are highly conductive with σe = 10–2 S cm–1 due to the quenching rate ΔT of the films.
Figure 14a, b present the Arrhenius plots of the electrical conductivity σ and the activation energies of flash-evaporated films as a function of the substrate temperature and annealing conditions. These results show that (ⅰ) the σ of films deposited at Ts = 25 ℃ is always lower than that of films deposited at higher temperature even after a heat treatment, and (ⅱ) there is a hierarchy in the conductivity such as σad < σarg < σox, where σad, σarg and σox are the conductivities of films as-deposited, annealed in Ar, and annealed in O2, respectively. The resistivity of an as-grown film at Ts = 25 ℃ is ρ = 5 × 104
Ω cm with an activation energy Ea = 0.43 eV, whereas that of a film heat-treated in O2 atmosphere is ρ = 0.62 Ω cm with Ea = 0.15 eV. We expect that C is a function of Ts and Ta due to the preferable desorption of oxygen during the growth. The increase in σ is attributed to the primary consequence of the structural modification from amorphous to polycrystalline state, and from oxygen deficiency of films grown with smaller O/V ratio at high substrate temperature. Similar effect was observed on the activation energy of the electrical conductivity which decreases with the increase of Ts. Sanchez et al. [167] reported a conductivity of 1.4 × 10–5 S cm–1 at 25 ℃ with an activation energy of W = 0.41 eV and a disordered activation energy Wd = 0.16 eV for flash-evaporated films. Kumar et al. [82] reported that thermally deposited films at Ts = 300 ℃ exhibit an electrical resistivity of 3.6 Ω cm. Luo et al. [142] studied the impact of the substrate temperature on the electrical properties of sputtered nanostructured films having semiconducting character. Four-point probe measurements show that the square resistance of film decreases exponentially from 46 to 33 kΩ/□ with the increase of Ts from 230 to 320 ℃.
Rosaiah et al. [83] reported the effect of Ts on the electrical conductivity of e-beam deposited V2O5 films onto ITO-coated flexible Kapton substrate. They showed that σ increases from 2 × 10–6 to 3 × 10–2 S cm–1 by the increase of Ts from 30 to 300 ℃. Crystalline V2O5 thin films (26 nm grain size) deposited by thermal evaporation and annealed at 500 ℃ exhibited thermoelectric properties with a maximum Seebeck coefficient of –218 µV K–1 and electrical conductivity of 0.055 S cm–1
[28]. The electrical conductivity was ~10–7 S cm–1 with a high activation energy Ea = 0.9 eV for sputtered V2O5 films (85 nm thick) obtained in O2/Ar ratio of 20% [169]. Wang et al. [170] demonstrated that a rather thick (200 nm) crystalline V2O5 films can work properly as hole-extraction slab for organic photovoltaic devices. V2O5 thin films grown via r.f. reactive sputtering on fused silica substrates showed good electrical response for use as sensors methane and propane (50–3000 ppm) with an activation energy of 0.153 eV and a CPE exponent of n = 1.046, which approximates a CPE due to Debye-like capacitor [171].
3.6. Intercalation of V2O5 films
The Li+ intercalation into V2O5 films has been widely studied on specimens grown on various substrates using all deposition techniques described above. The insertion/de-insertion process occurs in a large potential window 3.5–1.5 V vs. Li+/Li according the reaction:
|
V2O5(orange)+xLi++xe−↔LixV2O5(green)
|
(12)
|
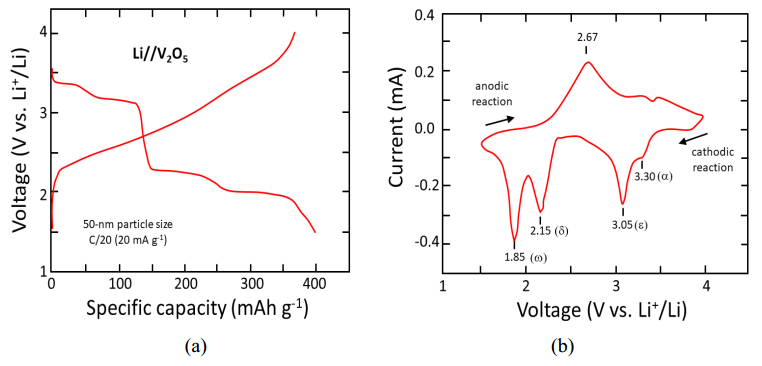
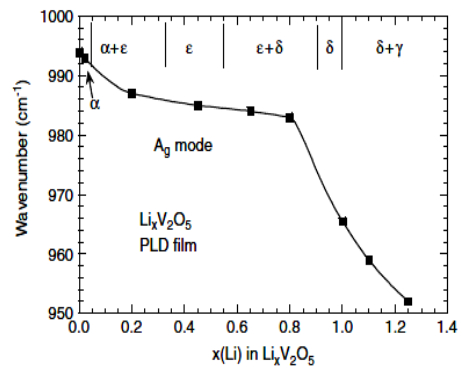
where x is the molar fraction of ions and electrons inserted in the host lattice. About 3e– per mole of V2O5 could be reached at the end of the discharge (1.5 V), providing a theoretical specific capacity of 442 mAh g–1. The insertion of 3Li+ implies the formation of several lithiated phases during discharge with the transitions α→ε (0 < x < 0.5),
ε→δ (0 < x < 0.5),
δ→γ (0 < x < 0.5) that are characterized by voltage plateaus at 3.4, 3.2 and 2.3 V vs. Li+/Li, respectively. This is illustrated in Figure 15a for film formed by 50-nm grain size cycled at C/20 rate (20 mA g–1 current density). The corresponding cyclic voltammogram is shown in Figure 15b. The irreversible ω-Li3V2O5 is formed at the end of the discharge (1.85 V). Subsequent charge appears as a smooth S-shaped voltage profile with a mid-voltage at 2.67 V. As displayed in Figure 15b, four distinctive peaks are observed at 3.30, 3.05, 2.15 and 1.85 V vs. Li+/Li during a cathodic scan, which is a multi-step Li+-ion intercalation process. The corresponding phase transforms from α-V2O5 to ε-Li0.5V2O5 (3.30 V), δ-Li1V2O5 (3.05 V), γ-Li2V2O5 (2.15 V) and ω-Li3V2O5 (1.85 V) represented by the relations:
|
V2O5+0.5Li+0.5e−→Li0.5V2O5
|
(13)
|
|
Li0.5V2O5+0.5Li++0.5e−→LiV2O5
|
(14)
|
|
LiV2O5+1Li++1e−→Li2V2O5
|
(15)
|
|
Li2V2O5+1Li++1e−→Li3V2O5
|
(16)
|
In the following anodic scan, one peak is recorded at 2.67 V vs. Li+/Li corresponding to the delithiation of the ω-Li3V2O5 phase.
The early work of Park et al. [172] showed that spin-coated V2O5 xerogel films can accommodate up to 3.3 moles Li/mole V2O5 in the potential range 3.8–1.9 V vs. Li+/Li. The films are highly reversible hosts and deliver a specific energy density 1137 Wh kg–1 and specific capacity 1682 C g–1. The Li+ insertion into V2O5 films deposited by CVD, rf-sputtered and ALD techniques onto various substrates such as Pt, Ti, stainless steel, glass and F-doped SnO2 was studied by Groult et al. [34,35,126,106,108]. Films grown on stainless steel and heat treated at 350 ℃ show a discharge capacity of 115 mAh g–1 at C/23 rate in the potential range 3.8–2.8 V vs. Li+/Li. The best performances (200 mAh g–1 at C/23 rate) were obtained in the electrochemical window 3.8–2.2 V for V2O5 deposited onto Ti foil. Jourdani et al. [173] reported an increase of the optical absorption edge from 2.3 to 2.8 eV and the (110) Bragg reflection shift from 2θ = 24.8° to 25.2° for spin coated V2O5 intercalated at –0.4 V vs. SCE.
The structural evolution of Li-intercalated V2O5 films has been investigated by in situ and ex situ XRD, FTIR and Raman spectroscopy [174,175,176]. Meulenkamp et al. [177] investigated the different phases of lithiated sol-gel V2O5 films in the range 0 ≤ x ≤ 1.4 using in situ X-ray diffraction measurements and compared the structural changes with those of V2O5 films prepared by other techniques. Spectroscopic studies of Li-intercalated V2O5 polycrystalline films have been reported by several groups [71,174,178,179,180]. Cazzanelli et al. [99] analyzed the Raman spectra of xerogel films intercalated with lithium that showed a significant effect of the water content in the interlayer space inducing new Raman bands at 800 and 950 cm–1. Julien et al.
[174] investigated the vibrational modifications of Li intercalated V2O5 films deposited by flash evaporation. They proposed that the tensile stress in the LixV2O5 film affects the Raman skeleton mode which shifts from 145 to 154 cm–1 due to an increase in the restoring force (Figure 16). Jung et al. [175] confirmed this hypothesis by the correlation of the spectral shift of the Raman mode at 145 cm–1 with the stress change as a function of the degree of intercalation in the LixV2O5 lattice.
Micro-Raman spectroscopy was used to study of electrochemically intercalation LixV2O5
(0 ≤ x ≤ 1.8) samples obtained from V2O5 films deposited by various techniques, i.e., ALD and r.f. sputtering. Results showed the phase transformation from α-LixV2O5 to γ-LixV2O5 via ε and δ phases. A linear correlation exists between the V–O1 stretching (vanadyl) mode frequency and the V–O1 bond length in V2O5 ALD film [179,180]. Careful examination of the high-frequency region of RS spectra of LixV2O5 shows that, for the Li-rich phase (0 ≤ x ≤ 0.5), the vanadyl stretching mode at 984 cm–1 splits into two components, the first one at 975 cm–1, the second at 957 cm–1 for x ≥ 0.7. This is due to the evolution of the local environment of oxygen atoms, i.e., the continuous increase of the interlayer distance with x and it reflects the existence of two different lithium sites [159]. Ramana et al. [71] analyzed the Raman features of the LixV2O5 films prepared by PLD technique in the range 0.00 ≤ x ≤ 1.25. Crystalline V2O5 thin films synthesized by means of r.f. sputtering without post-heating treatment were obtained with different crystallographic preferential orientations by changing the growth parameters (Ts and deposition rate) as follows: (ⅰ) h00-oriented films (ab planes perpendicular to the substrate) were prepared at Ts = 300 ℃ for short time td, (ⅱ) longer deposition time at low Ts leads to 110-oriented films and (ⅲ) the 001-oriented films were obtained at high Ts irrespective on td [45]. Electrochemical tests of the h00-oriented films in Li/EC-DEC–LiPF6/V2O5 cells showed specific discharge capacities > 300 mAh g–1 in the potential range 3.8–1.5 V, with a capacity fading of 3% at C rate over 70 cycles.
Numerous studies of the electrochemical insertion reactions of Li+ ions in the V2O5 film lattice were tested in Li cells with aprotic electrolyte such as 1 mol L-1 LiClO4 in propylene carbonate (PC) solution or 1 mol L–1 LiPF6 in ethylene carbonate (EC):dimethyl carbonate (DMC) (1:1) solution [58,181,182,183,184,185,186]. Park et al. [187] investigated the discharge capacity of V2O5 film cathode as a function of the thickness. Films (230 nm thick) obtained by sputter deposition at power of 100 W in working pressure of 1.3 Pa delivered a specific capacity of ~105 µAh cm–2 s–1 at current density 500 µA cm–2 s–1. Lithium microcells with optimized V2O5 films sputtered in O2/Ar (50/50) atmosphere were investigated by Yoon et al. [58]. When cycled in the range 1.5–3.7 V vs. Li+/Li, the cell delivered a specific capacity of 125 µAh cm–2
µm–1 after a first cycle of formation. Nano-porous crystallized V2O5 films (~35 nm crystallite size) fabricated by gel electrodeposition with the addition of block copolymer Pluoronic P123 delivered a specific discharge capacity of 240 mAh g–1 at 300 mA g–1 current density after 40 cycles [188]. Electrochemical studies of V2O5 films deposited by spin coating of vanadium-tri(isopropoxide)oxide gel show that the specific capacity and Li+ diffusion coefficient increased from 4.2 × 10–12 to 6.8 × 10–10 cm2 s–1 in the non-stoichiometric films [189]. Nanostructured V2O5 thin films made by anodic deposition from V2O5/H2O2 solution displayed a large discharge capacity of 596 mAh g–1 at a current density of 1.08 A g–1 and a fading rate of 1% per cycle in a cell using 1 mol L–1 LiClO4 in PC as the electrolyte and a Pt plate as the counter electrode [190]. The V2O5 thin film cathode with thickness of ~30 nm fabricated using biological templates delivered specific capacities of ~12 µAh cm–2 which is 7–8 times higher than that of planar V2O5 cathodes [191]. The effects of ageing on Li intercalation in V2O5 films, i.e., the evolution of the SEI, were investigated by a combination of techniques such as cyclic voltammetry, XPS, RBS and AFM for more than 3000 cycles [192].
Kinetics of Li+ ions in the lattice of V2O5 films has been widely studied. Li-ion transport, i.e., ionic conduction (σion) and diffusion coefficient (DLi) have been investigated using cyclic voltammetry, galvanostatic titration and electrochemical impedance spectroscopy (EIS)
[106,193,194]. DLi varies in the range 6 × 10–10–2 × 10–11 cm2 s–1 in sol-gel crystalline V2O5 thin films (1–3 µm thick) obtained by impedance spectroscopy [195]. Miyazaki et al. [196] investigated DLi of sputtered films oriented along the a-and b-axis using the chronoamperometry method. Kinetics along the a-axis DLi ≈ 10–11 cm2 s–1 was larger than along the b-axis 10–13
≤
DLi ≤ 10–14 cm2 s–1. McGraw et al. [197] obtained DLi vs. x(Li) in amorphous V2O5 films by PITT measurements on an h00 and 110 oriented films made by PLD method. DLi was initially 5 × 10–13 cm2 s–1 and decreased steadily from 1.2 × 10–13 cm2 s–1 at x = 0.4 to 5.52 × 10–14 cm2 s–1 at x = 1.5 in LixV2O5. Lantelme et al.
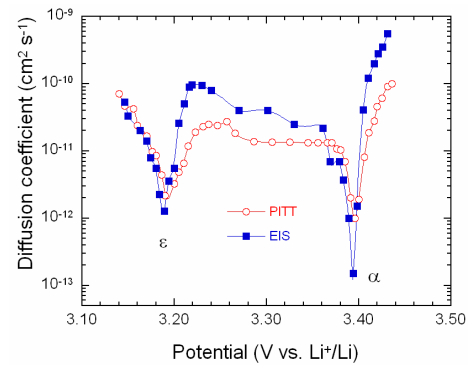
[106] analyzed the phase transition process controlled by diffusion in V2O5 films deposited by CVD method. The component diffusion was estimated as a function of the film thickness: DLi = 0.48 × 10–12 cm2 s–1 for a semi-infinite configuration. DLi was also estimated from both PITT and EIS measurements using a semi-infinite diffusion model [198]. Evolution of the diffusion coefficient DLi in V2O5 film (160 nm thick) as a function of the electrode potential is shown in Figure 17. This figure indicates a good agreement between the two techniques.
Pyun and Bae reported a decrease of the diffusion coefficient of xerogel films from 10–10 to 10–12 cm2 s–1 as the electrode potential fell from 3.0 to 2.2 V vs. Li+/Li [193]. The transport mechanism was described as a transition from the diffusion-controlled insertion to an interfacial-controlled reaction due to a change of the lattice versus water in V2O5·nH2O xerogel. Ultrathin (17 nm) V2O5 thin were fabricated by spin coating and annealed at at 250 ℃ for 3 h in a muffle furnace. In the potential range, these films deliver a specific capacity of 262 mAh g–1 corresponding to Li1.78V2O5 when discharge in the potential range from +1 V to –1 V vs. SCE. The capacity loss is 0.03% per cycle over 600 cycles [199]. The effect of porosity on anomalous behavior of the Li intercalation into V2O5 film prepared by the polymer (Tergitol from Sigma-Aldrich Co.) surfactant templating method has been studied by AFM and EIS [200]. The diffusion impedance Zd, which displays a constant phase element (CPE) response can be expressed by:
|
Zd=LnFAD1/2(∂E∂c)(jω)−α
|
(17)
|
where L is the film thickness, n the valence of inserted ion, A the active surface, F the Faraday constant, ∂E/∂C the slope of the coulometric titration and αd the CPE exponent. Analysis showed that αd is constant in the frequency range 0.63–0.10 Hz is significantly affected by the surface roughness and the formation of pores with a large size. The chemical diffusion coefficient of 1 × 10–11 cm2 s–1 was suggested. Thin films fabricated by electrostatic spray deposition (ESD) followed by heat treatment at 350 ℃ in air demonstrated a high energy efficiency. Ultra-high rate capability is obtained at 56C rate with a specific capacity of 86.7 mAh g–1 in the potential range 2.5–4.0 V vs. Li+/Li corresponding to the transitions of three phases: α ↔ ε ↔ δ. When cycled below 2.5 V, these ESD films have poor electrochemical performance due to irreversible structure degradation of the γ-phase [201,202]. Mui et al. [203] established a relationship between microstructure and kinetics in as-deposited and heat-treated sputtered V2O5 thin-film cathodes.
DLi was determined by the GITT method for two submicrometric films: finer-grained 80 nm size and coarsed-grained 250 nm size. Both samples display similar values of DLi of 1 × 10–11 for the α-Li0.03V2O5 phase and 5 × 10–12 cm2 s–1 for the ε-Li0.35V2O5 and δ-Li0.9V2O5 phases, whereas DLi in finer-grain film decreases to 1 × 10–13 and 1 × 10–15 cm2 s–1 for the α–ε and ε–δ two-phase systems, respectively. Li+ diffusion coefficients of electrochemically inserted V2O5 films (0.6–3.6 µm thick) deposited by r.f. sputtering with h00 or 110 preferred orientation was studied using EIS measurements [194,204]. The easy diffusivity of Li+ ions (2 × 10–11≤ DLi ≤ 3 × 10–10 cm2 s–1) along the b-direction is due to the lattice expansion along the c-axis. The plot DLi vs. x(Li) displays two minima at x = 0.14 and 0.6 that confirm the results of Lu et al. [198]. An energy barrier of 0.98 eV along the b-direction was found from the Arrhenius plot of DLi vs.1/T.
4. Doped V2O5 films
The poor electrochemical performance of V2O5 films during long term cycling attributed to low electronic conductivity can be improved by replacing a dopant for one of the V atoms forming V4+ cations [205,206]. Grégoire et al. [207] showed that octahedral chains are formed with metal dopant atoms making stable the structure during electrochemical process. The EXAFS analysis of Cu-and Zn-doped V2O5 showed that the environment of vanadium atoms is not altered by the doping atoms (M), while new V–O–M interactions are triplets [208]. The enhanced stability of M-doped vanadium pentoxide films used as electrode for lithium microbatteries and electrochromic devices comes from the distorted V2O5 layered structure. For example, the introduction of Ti dopant in spin-coated V2O5 films results in a disturbance of the diffraction peaks of (001) and (002) planes. The formation of V–O–Ti bond opens the interlayer space, distorts the lamellar structure and reduces the oxidation state of V [209]. Numerous metallic ions have been investigated as dopants, including Ag, Fe, Mo, Ta, Mg, Mn, Ti [17,66,93,202,209,210,211,212,213,214].
Dip-coated Ag-doped V2O5 xerogel films with a molar ratio Ag/V in the range 0.005–0.5 showed an increase of the electronic conductivity by 2–3 orders of magnitude that allowed an insertion capacity of 4 Li per mole of AgxV2O5 with an excellent reversibility [215]. AgyV2O5 thin films were prepared by rf magnetron co-sputtering in 14% partial oxygen pressure pO2 = 14% from metallic Ag and V2O5 targets. Ag0.26V2O5 films were amorphous and showed improved intercalation properties due to the porosity and the additional influence of Ag+ ions to the redox reaction [205]. Nam et al. [216] investigated the electrochemical properties of copper-doped V2O5 thin film prepared by d.c. reactive magnetron co-sputtering within atmosphere O2:Ar ratio of 10:90. These films were tested as cathode materials in CuxV2O5/Lipon/Li cell and showed stable cycleability beyond 500 cycles with average capacity of 50 µAh cm–2 µm–1. Mo-doped V2O5 films were grown by thermal evaporation technique onto Ni substrates maintained at Ts = 250 ℃ and applied as electrode in supercapacitor with 1 mol L–1 KCl solution electrolyte. A maximum specific capacity of 175 mF cm–2 was obtained for 4 at.% Mo-doped V2O5 films [17]. The effect of the annealing temperature on the structure of Mo-doped V2O5 films electrochemically deposited resulted in the increase of the interlayer distance from 1.16 nm for as-deposited to 1.38 nm for film annealed at 250 ℃ that enhanced the Li+ ion motion in the electrochromic matrix [217].
Tantalum-doped V2O5 thin films were deposited by sol-gel dip-coating method using anhydrous isopropyl alcohol as solvent [211]. 5 mol% Ta doped films as counter-electrode for electrochromic device exhibited a charge density of 70 mC cm–2 with high stability up to 1500 cycles. Mg-doped V2O5 films deposited by RF magnetron reactive sputtering onto SnO2-coated glass substrates were studied for various amount of dopant. Low Mg content (2 at.%) enhanced the specific discharge capacity and the diffusion coefficient of Li+ inserted ions, while high Mg content (15 at.%) favored the electrochromic window and the switching response time [212].
Molybdenum acts as a n-type dopant in V2O5 that results in an increase of the carrier concentration and a shift of the absorption edge towards shorter wavelengths [93]. Several techniques were used to prepare V2O5 doped with Mn such as electrodeposition [218], e-beam evaporation [219], and dip-coating [213].
Mn-doped V2O5 films were fabricated by dip-coating route with post-annealing at 250 ℃ in air for 3 h using ~1.67% of Mn(Ac)2·4H2O as Mn2+ source. Structural and elemental analyses showed that: (ⅰ) Mn doping suppresses the orthorhombic symmetry, (ⅱ) V4+ and V5+ coexist, (ⅲ) the formation of oxygen vacancies is due to the increase in the Mn2+ cation size. The suggested formula was (Mn, V)2O4.74(VÖ)0.26. The intercalation/deintercalation process is enhanced by the oxygen vacancies that eliminate the phase transition and reduce the irreversible capacity [182,213].
Sn-doped V2O5 films were obtained by drop-casting and further heat treatment at 450 ℃ in air for 2 h. As measured by XPS experiments, the 10% Sn4+ ions accommodation is compensated by the reduction of V+5 to V4+ ions. The introduction of Sn atoms causes a slight expansion of the unit volume due to the small lattice expansion along a-and c-direction, which indicates the presence of Sn4+ ions between the VO5 layers, forming SnO6 octahedra [220]. Ce-doped V2O5 films prepared by sol-gel route and annealed at 400 ℃ showed a phase transition from α-V2O5 orthorhombic to β-V2O5 tetragonal structure. Film doped with 1 mol.% Ce exhibited the best ion storage capacity of ~207 mC cm–2 [221]. Titanium doped V2O5 films have been widely investigated as intercalation hosts for electrochromic devices [209,214,222,223,224,225]. Sol-gel dip-coated (100 – x)V2O5·xTiO2 films as electrochromic electrodes were formed with Ti content up to 20 mol.% by reacting vanadium and titanium tetra-isopropoxide as precursors [214]. The best results were obtained for the proper amount of Ti dopant (5 mol.%) showing that 550 nm-thick films switched with a coloration from pale yellow to a greenish state when reduced with 5.4 mC cm–2 of lithium. Wei et al.
[209] reported a remarkable improved stability of the WO3-based electrochromic devices using Ti-doped V2O5 films. The device utilizing the optimized V2O5:Ti electrode (V:Ti = 2:1) lasted 200,000 cycles in the transmittance range 2–62% without degradation. An increase of the Li intercalation capacity from 14 to 27 mC cm–2 for 5% Ti-doped V2O5 films prepared by spin coating of inorganic sol-gel precursors was attributed to the non-stoichiometry and the smaller grain size [222]. Lee and Cao [223] demonstrated an Li+ intercalation performance improved by 100% in 20 mol.% Ti-doped V2O5 polycrystalline films that results from interaction force between adjacent V2O5 slabs. Highly stable V2O5–TiO2 films fabricated by sol-gel electrodeposition [224,225] were proposed as electrochromic windows using PProDOT-Me2 that is poly (3, 3-dimethyl-3, 4-dihydro-2H thieno[3, 4b][1,4]-di-oxepine). Tungsten-doped V2O5 films were deposited by rf magnetron sputtering on non-alkali glass substrate. Due to their good thermal insulation function, these films were applied as self-cleaning windows or anti-fogging glasses. The optimal thermal insulation temperature is 19.3 ℃ for 3 wt.% W-doped V2O5 thin films [226].
5. Nanocomposite films
V2O5-based nanocomposite films have been fabricated for several applications, such as electrochromic devices and gas sensors. Such a nanocomposite was obtained with V2O5 obtained from an aqueous solutions of equimolar vanadium chloride and ammonium tungstate and F-doped SnO2-coated glass substrates maintained at Ts = 400 ℃. Coloration efficiency (CE) of ~49 cm2 C–1 was obtained for a film mixed with 15% WO3 which is stable up to 1000 cycles [227]. Thin (240 nm) and thick (485 nm) V2O5–MoO3 films were deposited on conducting (SnO2:F) glass by e-beam (3 kV) and thermal vacuum deposition (EBD and TVD, respectively) for opto-electronic applications [228]. A specific capacity of 80 µAh cm–2 s–1 after 70 cycles in the potential range 1.5–3.9 V vs. Li+/Li was delivered by MoO3–V2O5 nanocomposite thin film electrodes deposited by r.f. sputtering from dual targets [229]. Mixed V2O5–WO3 thin films were deposited by pulsed spray pyrolysis technique onto glass [227]. Sol-gel deposited (1 – x)WO3·xV2O5 films at x = 0.035 showed the best electrochromic performance with a brownish blue [230]. Thin films of (V2O5)1–x·(MoO3)x (0 ≤ x ≤ 1) were fabricated by e-beam evaporation in p(O2) = 2 × 10–2 mPa and Ts = 150 ℃. The optical bandgap increases and the electrical conductivity decreased with the increase of composition x [231]. V2O5–28 at.% MoO3 TVD thick films deposited onto borosilicate glass were amorphous, while thin films were crystalline (crystallite size 38 nm) with strong reflections along (131), (160) and (270) direction. The bandgap varies linearly with the atomic wt.% of MoO3 in V2O5–MoO3 EBD thin films, i.e., from 2.35 eV for 10 wt.% to 2.70 eV for 90 wt.%. Composite V2O5 xerogel films assembled with polypyrrole (PPy) showed high electrical conductivity and fast electrochemical response that makes them candidates for redox sensor in flow injection analysis [232]. Graphene/V2O5/MoO3 nanocomposite film was synthesized by dip-coating via sol-gel preparation of the precursors. This composite shows fast switching electrochromic performances with bleaching time of 1.25 s and the coloration time of 1.40 s [20]. V2O5/graphene nanocomposite films prepared by direct intercalation method using V2O5 sol and graphene were developed for their use in fast switching electrochromic devices. The intercalation of graphene improves the stability and the optical reversibility of the films, i.e., 1.5 times larger than that of V2O5 xerogel, due to the fast electron mobility of 1.5 × 104 cm2 V–1 s–1 in graphene [233]. Thin film electrodes for supercapacitors were made of V2O5/carbon nanotubes composites. A symmetric capacitor formed by identical V2O5/CNT electrodes operates in a wide potential range of 1.6 V in aqueous electrolyte delivering a volumetric energy density of 41 Wh dm–3 [234]. V2O5 xerogel films were modified by poly(ethylene-oxide) (PEO). The inserted structure is modified the interaction of hydrogens with oxygens of the V–O bonds that shields the interaction between Li+ ions and V2O5 slabs resulting in an improved anodic electrochromic property [235].
6. Applications
The early potential applications of nanostructured V2O5 were found in the field of lithium-ion batteries [236,237], thin-film microbatteries [12,108,238], actuators [239], catalysis [240], humidity sensors [241], electrochromic display devices [139,242], optical switching memories [243], antirelection coating [81].
6.1. Li microbatteries
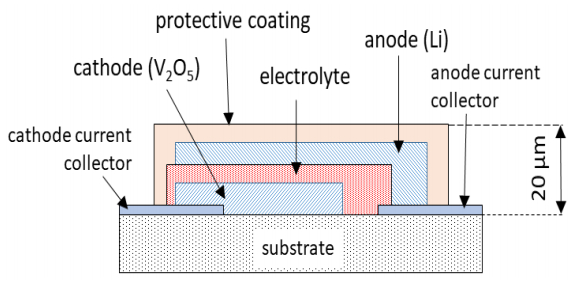
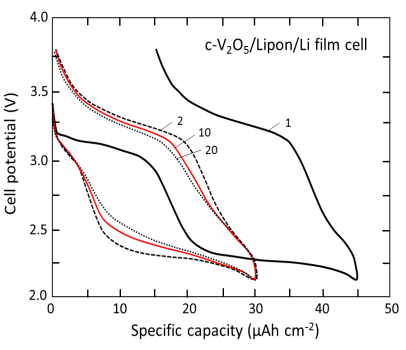
Since the work of Bates et al. [12], V2O5 thin films have been extensively investigated as positive electrodes (so-called cathodes) in rechargeable lithium microbatteries constituted by a lithium metal anode, an amorphous inorganic electrolyte and amorphous or crystalline V2O5
[244]. The most popular solid-electrolyte thin film Li2.9PO3.3N0.46 (named Lipon) was deposited by r.f. magnetron sputtering of Li3PO4 in N2 ambient. Its ionic conductivity is 2 × 10–6 S cm–1 at 25 ℃ [245,246]. A typical solid-state battery (SSB) is built by 1 µm thick amorphous V2O5 film deposited at 25 ℃, a 1 µm thick solid electrolyte and 5 µm thick lithium film (5 times in excess)
[247,248]. Currently, thin-film cells are evaluated at different current densities and their delivered capacity is expressed by surface and thickness in mC cm–2
µm–1 or µAh cm–2 µm–1. Considering the theoretical specific capacity of 440 mAh g–1 for LixV2O5 with uptake of 3 Li per formula and the density d = 3.36 g cm–3 of V2O5, the theoretical specific capacity is Qth = 147.8 µAh cm–2 µm–1 for a film as dense as the crystalline material. The schematic cross-section of a thin-film lithium microbattery is presented in Figure 18.
Prior Li//V2O5 cell cycled in the potential window 3.6–1.5 V delivered a capacity ~100 µAh cm–2 µm–1 at 10 µA cm–2 [12]. Vanadium oxide films (VOx) prepared by several techniques such as PECVD, PLD, rf-sputtering at the National Renewable Energy Lab. (USA) exhibit high discharge capacity and are highly stable during electrochemical cycling. Both crystalline and amorphous PLD V2O5 films (Ts = 200 ℃) deliver a discharge specific capacity of 380 mAh g–1, while for the most stable films prepared by PECVD and exhibiting an O/V ratio close to that of V6O13 (0.5 μm thick) the discharge capacity exceeds 408 mAh g–1 over 4400 cycles. These results indicate that the PECVD technology is very attractive for manufacturing rechargeable lithium microbatteries [62,67]. Typical experimental conditions for the deposition of a thin-film battery made by r.f. sputtering are summarized in Table 2 [249,250]. A solid-state film cell including a crystalline V2O5 cathode (2.4 µm thick), a Lipon electrolyte film (1.4 µm thick) and a lithium metal film (3.5 µm thick) operated in the potential 3.8–2.15 V vs. Li+/Li. Figure 19 displays the discharge-charge profiles of the SSB at 10 µA cm–2 current density. After the first cycle of formation (SEI formation), a stable specific capacity of 30 µAh cm–2 was obtained with a cathode film 2.4 µm thick [250].
Table 2. Experimental conditions for the deposition of thin-film battery active materials [250].
| Component |
Target |
Power density (W cm–2) |
Gas (sccm) |
Deposition pressure (Pa) |
| V2O5 |
Vanadium |
4.5 |
Ar:O2 (50:5) |
0.55 |
| Lipon |
Li3PO4 |
2.2 |
N2 (80) |
2 |
| Lithium |
Li |
Thermal evaporation |
Optimized conditions for rf-sputtering deposition (Ts = 250 ℃, Pw = 50 W) provide discharge capacity of 30.2 µAh cm–2 µm–1 with two potential plateaus at 3.5–3.6 V that corresponds to the Li uptake 0 < x < 1 in LixV2O5. Assuming a gravimetric density of 2.5 g cm–3 for rf-sputtered films, the discharge capacity is 121 mAh g–1. A capacity loss of 0.0076% per cycle was reported over 2000 cycles [251]. V2O5 thin films obtained by electrostatic spray-deposition (ESD) onto Pt substrates from triisopropoxy-vanadium oxide in 0.05 mol L–1 ethyl alcohol solution were tested in Li cells with 1 mol L–1 LiClO4/propylene carbonate (PC) as electrolyte. The crystallized films annealed at 275 ℃ exhibit a good cycleability and high capacity of 270 mAh g–1 at a current rate of 0.2C. After 25 cyles at 1C rate the capacity remains stable at 260 mAh g–1 [252]. Navone et al. [253] reported the fabrication of all-solid-state lithium microbatteries using crystalline sputtered V2O5 thin film (1.2 µm thick) as cathode and lithium phosphorus oxynitride (Lipon) (1 µm thick) as solid electrolyte. The electrochemical performances are strongly affected by the cathode morphology; its porosity depends on the oxygen flow during the film deposition; thus, a 0.6 µm thick porous film was optimized using an oxygen flow of 12.5 sccm (p(O2) = 0.05 Pa). Such a microcell film showed a stable discharge capacity of 35 µAh cm–2 at a current density of 10 µA cm–2 between 3.8 and 2.15 V vs. Li+/Li. Electrochemical performance of 50 µAh cm–2 was obtained with the use of a 1 µm thick dense film. All-solid-state thin-film lithium cells with the configuration Li/Lipon/LixV2O5/Cu were fabricated on stainless steel (SS) substrate using sequential deposition techniques. The amorphous V2O5 cathode film was lithiated by vacuum evaporation of pure Li metal to form the Li1.3V2O5 cathode film (500 nm thick). The microbattery was formed during the first charging cycle, where lithium anode was electroplated in between the Lipon electrolyte layer and the stainless-steel substrate. These "Li-free" cells (1 cm2 active area) delivered a specific capacity of 43 mAh cm–2 µm–1 at a current density of 0.1 mA cm–2 in the potential range 3.8–1.8 V vs. Li+/Li and showed a good stable cycleability up to 770 cycles at 0.1 mA cm–2 current density [254]. All-solid-state microbatteries Li1.5V2O5/Lipon/Li were fabricated by the successive deposition of active elements on Si/Ti substrate as follows: (ⅰ) the substrate was first coated with 0.2 m thick gold film to form a current collector; (ⅱ) crystalline LixV2O5 films with x = 0.8 and 1.5 (1 µm thick) were prepared by thermal evaporation of metallic lithium (0.2 µm thick) deposited on a magnetron sputtered pristine material. This cathode element was keep at rest for 5 days to ensure the diffusion of Li ions into the V2O5 matrix; (ⅲ) the in situ solid electrolyte film was obtained by reactive sputtering of Li3PO4 in N2 atmosphere (p(N2) = 2 Pa) at a power of 350 W to ensure a deposition rate of 034 µm h–1; (iv) the Li anode (3.5 µm thick) was obtained by thermal evaporation at growth rate of 150 nm min–1. The all-solid-state microbattery delivered a typical specific capacity of 50 µAh cm–2 in the potential range 2.15–3.80 V vs. Li+/Li [255].
V2O5 thin films prepared by means of cathodic deposition from V2O5 and H2O2 in aqueous show excellent electrochemical properties as cathodes. The films had a specific discharge capacity of 240 mA h g–1 retained after 200 cycles with a 1.3C rate (200 mA g–1) that corresponds to an energy density of 723 Wh kg–1. Even at high 70C rate, V2O5 film electrodes retained a good discharge capacity of 120 mAh g–1
[104]. Ostreng et al. [113] reported remarkable electrochemical properties of strongly structured ALD V2O5 films as cathodes in Li microbatteries. The best performance was obtained a discharge rate of 120C for more than 1500 cycles for 10-nm nanostructured film. McGraw et al. [197] investigated the intercalation mechanism in LixV2O5 thin films deposited by by pulsed laser deposition and estimated the chemical diffusion coefficients D̃ of Li+ ions from potentiostatic intermittent titration technique (PITT) measurements. D̃ varies in the range from 1.7 × 10–12 cm2 s–1 to 5.8 × 10–15 cm2 s–1 in crystalline PLD films, while D̃ = 5 × 10–13 cm2 s–1 in amorphous V2O5 films. The general trend is a decrease of D̃ upon Li intercalation in the host lattice reaching the final value of 5.5 × 10–14 cm2 s–1 at Li1.5V2O5 (δ phase). The specific discharge capacity 334 mAh g–1 of 10% Sn-doped V2O5 film is twice that of pure V2O5 film [220]. This superior electrochemical performance is attributed the stabilization of VO5 slabs by Sn4+ ions that produces higher diffusion coefficient of Li+ ions. High-rate V2O5-based Li-ion thin film polymer cells show outstanding long-term cyclability. Cathode thin film growth was performed by r.f. sputtering (power 100 W) in high vacuum (1 mPa) at the 1.3 Pa partial pressure of the Ar/O2 gas mixture (ratio 2:1) [256]. The V2O5/solid polymer/Li cells were electrochemically tested in the potential range 2.5–3.8 V at current regimes ranging from 1.5C to 10C. Stable specific capacity of 100 mAh g–1 was maintained up to 5C after 300 cycles.
Recent developments of V2O5 thin films as cathode elements of rechargeable microbatteries shows the general trends of amorphous films. Zeng et al. [257] reported that films prepared via sol-gel and liquid deposition method show a gradual activation upon cycling that yields higher capacity (~200 mAh g–1 after 200 cycles) and faster kinetics. This good performance was attributed to the novel nanostructure obtained from mild synthesis conditions. Mattelaer et al. [258,259] prepared amorphous films by ALD technique based on tetrakis[ethylmethylamino]vanadium in combination with water and ozone. Galvanostatic charging and discharging performed at 1C in the potential range 3.5–2.9 V (LiV2O5) and 4.0–1.5 V (Li3V2O5), the thin films cells deliver volumetric capacities of 488 and 810 mAh cm–3, respectively. Chae et al. [260] compared the electrochemical features of amorphous (a-V2O5) and crystalline (c-V2O5) films. The high performance of a-V2O5 with a reversible specific capacity > 600 mAh g–1 at 13C rate was attributed to the absence of irreversible phase transitions and lithium ions trapping. This remarkable rate property for a-V2O5 films is due to the vacant sites that open the Li+ diffusion pathways [261]. Zhang et al. [238] made a all-solid-state battery V2O5/Lipon/LiCoO2 prepared by r.f. magnetron sputtering in which the V2O5 (200 nm thick) acts as anode film. This microbattery (1.03 µm thick) delivered a volumetric capacity of 9.5 µAh cm–2 µm–1 after 40 cycles.
6.2. Supercapacitors
Electrochemical capacitors (ECs) known as "supercapacitors" employ the electrical double-layer phenomenon to store energy. There are two subclasses of ECs: the electrochemical double-layer capacitors (EDLCs) having a non-faradaic charge character and the pseudocapacitors based on faradaic electrochemical redox reaction. Among transition-metal oxides used as ECs electrode, V2O5 has attracted attention because of its pseudocapacitive features, broad oxidation states and high specific capacitance 294 F g–1. Reports on the properties of V2O5 thin films as electrodes for supercapacitors are rather sparse [17,234,262,263]. Films deposited onto Ni substrates by dc-magnetron sputtering in O2:Ar (1:8) atmosphere and grown with predominant (001) orientation are composed of 32-nm grain size and surface roughness of 14 nm. These films exhibit high specific capacitance of 238 F g–1 at current density of 1 mA cm–2
[263]. 4 at.% MoO3-doped V2O5 films obtained by thermal evaporation on Ni substrates, in which Mo atoms substitute for V, exhibit a specific capacitance of 175 F g–1 [17]. Wu et al. [234] fabricated V2O5/CNT films in three steps: (ⅰ) mixture of carbon nanotubes (CNTs) and V2O5 with ethyl cellulose in ethanol and terpilenol as uniform and viscous slurry, (ⅱ) evaporation of ethanol and "doctor blade" coating onto alumina substrate and (ⅲ) annealing at 350 ℃. Reversible redox reaction was evidenced by cyclic voltammetry providing a specific capacitance of 216 F g–1 at 5 mV s–1 that is 5.2 times of that of CNTs (41 F g–1) and a volumetric capacitance of ≈460 F cm–3. This electrode maintains a power density of 22.2 kW L–1.
6.3. Electrochromic devices
A typical electrochromic device (ECD) includes an electrochromic layer, an electrolyte layer and an ion storage layer. Both electrochromic and storage layers are deposited on transparent substrates coated by transparent conductive film. ECDs operate by a change in optical properties between different colors. V2O5 is utilized as a counter electrode material in ECDs [22,65,96,264,265,266,267,268,269]. During the optical switching, it provides electrochemical redox reactions that balance charge transfer at the electrochromic working electrode. The typical electrochromic reaction of V2O5 can be expressed by the double injection of ions and electrons (Eq 12). The transmittance variance (ΔT) is defined by [270]:
where Tb and Tc are the transmittances (in %) of bleached and colored states, respectively. The coloration efficiency (CE) is defined as the change in the optical density (ΔOD) per unit of electrode area (A) at a given wavelength, as follows:
|
CE=ΔOD/(q/A)=log(Tb/Tc)/(q/A)
|
(19)
|
where q is the inserted charge capacity and the color efficiency (η) is defined by:
Following the work of Sarminio et al. [271] there is a close correlation between the stress change in the crystalline film and the electrochromic properties. Tensile stress varies with the x(Li) composition, the largest obtains with the δ-LiV2O5 phase. V2O5 thin film electrochemically deposited onto ITO glass from a poly-vanadic acid sol were used in ECD cell [272]. The cell was tested more than 8 × 104 times and its response time was 2–20 s, depending upon the cell voltage. Shimizu et al. [273] developed an electrochromic display device using V2O5 thin film deposited by spin coating of V2O5 powder dissolved into a mixed solution of benzyl alcohol and iso-butanol. The films coated onto ITO glass followed by annealing at Ta > 300 ℃ are crystalline and exhibit excellent reversibility of the electrochromism. Mesoporous V2O5 films prepared by hydrolysis of vanadium tri-isopropoxide in the presence of polyethylene glycol (PEG) have shown that the surfactant promotes the formation of micrometric crystallites highly suitable for the development of advanced ECDs [274]. V2O5 thin films deposited by means of microwave plasma MOCVD have a transmittance of 70% at 400 nm absorption edge. The reversible Li intercalation reaction occurs with a change in the film color from yellow (V2O5) to blue (LiV2O5) [37]. The addition of the organic–inorganic template 3-isocyanatopropyltriethoxysilane (ICS) and poly(propylene glycol) bis-2(ammino-propyl-ether) (2-APPG) in sol-gel deposited V2O5 electrochromic thin film implements the storage capacity and increases the diffusivity of Li+ ions by modification of the surface structure of the film [275]. Magnetron sputtered V2O5–z thin films onto flexible polyethylene terephthalate/indium tin oxide (PET/ITO) substrates at oxygen flow rate of 2 sccm were oxygen deficient with z = 0.169 and offered a light modulation of 43.3%. After 200 cycles, at wavelength of 400 nm, an optical density change and color efficiency of 0.38 and 102.5 cm2 C–1 were obtained, respectively [276]. Similar ECD devices were fabricated at 23 ℃ by Lin and Tsai [19], showing an oxygen deficiency z = 0.13 and a transmittance modulation of 36.5% at wavelength of 400 nm.
Recent studies show that high switching speed and coloration efficiency are obtained for titanium-doped V2O5 thin film electrochromic devices [277] and spray-deposited lithium-doped V2O5 [278]. The ammonium intercalated V2O5 xerogel thin film prepared at 50 and 85 ℃ show two-step color changes: yellow/green and green/blue related to the redox process of V4+/V5+ states [96].
6.4. Gas sensors
Because of their excellent catalytic properties, V2O5 thin films have attracted great interest as gas sensors. The adsorbtion of gaseous molecules and catalytic reactions are due to the active sites formed by V5+ ions with d0 electronic configuration [279,280]. Especially in thin film form, V2O5 is used in sensor of volatile organic compounds (VOCs) emitted by industries such as benzene, toluene, acetone, methanol, xylene, etc. that are hazardous substances to human health [70,281,282,283,284,285,286,287]. For a short review of V2O5-based resistive gas sensors, see Ref. [171]. Nanocrystalline V2O5 thin films deposited by a spray pyrolysis technique at Ts = 300 ℃ had a preferential orientation along the (001) direction and revealed the highest sensing response in the presence of ethanol vapor [280]. Nanocrystalline V2O5 thin films synthesized by the ethanol suspension were developed as solid-state sensors. A reversible reaction occurs with ammonia with the formation of ammonium metavanadate (bleaching), which is turn back to the starting state after annealing in air at 350 ℃ [279]. The polycrystalline V2O5 films prepared by spray pyrolysis were found to be highly sensitive towards VOCs. The selective nature of the films deposited at Ts = 300 ℃ are shown in Figure 20
[92].
V2O5 films fabricated by PLD technique were characterized as ammonia sensors even in the presence of NO used in diesel engine exhaust [70]. V2O5 thin films 200–600 nm thick were fabricated at 290 ℃ on fused silica and alumina by means of rf reactive sputtering from a metallic vanadium target for use as gas sensor. Thin films exhibit good response towards hydrogen (5–300 ppm), methane and propane (50–3000 ppm) [171]. Ultrathin crystalline epitaxial V2O5 films (10–90 nm thick) were deposited onto c-Al2O3 by ALD method with oxygen plasma. The films exhibiting a (001) preferred orientation are used as humidity sensors [119]. Nanostructured V2O5 films deposited by dc reactive magnetron sputtering have also been proposed as 2-propanol vapor sensors with an excellent response towards 5–200 ppm under ambient atmosphere [287].
6.5. Healthy and safety issues
A very detailed review (210 pages) on the toxicity of V2O5 can be found on the web site [287]. In short, V2O5 is toxic, and it is specified on the U.S. National Library of Medecine [288] that probable oral lethal dose for humans is between 5 and 50 mg/kg or between 7 drops and 1 teaspoonful for a 70 kg (150 lb.) person. In practice, however, there is little occasion to eat such an amount of vanadium pentoxide and absorption can occur in humans following inhalation exposure. In this case, V2O5 is readily absorbed through the lungs. The effects from exposure may include burns to the skin and eyes, tracheitis, bronchitis, emphysema, pulmonary edema, or bronchial pneumonia. The American Conference of Governmental Industrial Hygienists (ACGIH) has established a threshold limit value time-weighted average (TLV TWA) of 0.05 mg/cu m for respirable dust. When absorbed, V2O5 is eliminated, mainly by urine. In practice, the protection against this product thus concerns people who have to manipulate or prepare it in factories since they are placed in situation where over-exposure may occur. The hygiene and safety policy of laboratories and institutions that are concerned is given in [288].
While hygiene and safety policy practice when handling or dealing with V2O5, this material plays an increasing role to make progress in environmental pollution and industrial safety issue, owing to its use for gas sensing application, reviewed in [289]. The list of targeted gas is constantly increasing [286].
7. Concluding remarks
V2O5 is one of the most important material for many applications, including optical switching devices, gas and humidity sensors, smart widows, window for solar cell, photocatalysis, for electrochromic devices [82], color filters [146], reflectance mirrors, gas sensors, surfaces with tunable emittance for temperature control of space vehicles [81,147], thermochromic thin films for optoelectronic applications [93]. Nanocrystal V2O5 thin film used as hole-extraction layer in normal architecture organic solar cells demonstrated the potential of this material for photovoltaic applications [170], and W-doped V2O5 film can be used for thermal insulation [226].
So many applications explain the huge amount of works devoted to the preparation of V2O5 thin films. The difficulty is that their properties are strongly dependent of the mode of preparation, the film thickness, the orientation of the film, the crystallinity, the purity, the substrate [84], the nature and amount of dopants, the packing density of the film [85], temperature of the substrate [142], deposition rate, in short, deposition conditions [96], post-annealing treatment [217], the choice of precursors [100], porosity [188,201,262], doping.
As electrochromic device, Ti-doped V2O5 electrode has lasted 200,000 cyclic switching times between the lowest (2%) and highest (62%) transmittance with no significant degradation of performance [209]. Nevertheless, V2O5 alone cannot be commercialized as an electrochromic device, because of its low electrical conductivity, poor coloration efficiency and narrow color variation. However, these drawbacks can be overcome by combining V2O5 with other compounds. A recent example is the graphene/V2O5/MoO3 film, which combines the richer colors of MoO3, the high conductivity of graphene and the remarkable electrochromic properties of V2O5. Such films present multi-electrochromic behavior (yellow → green → blue → gray-brown), excellent electrochromic performance, with tranmittence variation of 25.35%, bleaching time of 1.25 seconds, coloration time 1.40 seconds. In addition, it demonstrates good cycling [20]. Such films are thus very good fast switching electrochromic materials. Recently, the growth of large-scale electrodes by atmospheric pressure chemical vapor deposition has been made possible, with good performance for electrochromic devices with a change in optical density per unit inserted charge density reaches 336 cm2 C–1 at 630 nm, with a diffusion coefficient for the lithium as large as 9.19 × 10–11 cm2 s–1 [33].
For use as a supercapacitors, nano-structured V2O5 is needed to increase the surface area. In particular, a grain size of 148 nm of the deposited film exhibited a high rate pseudo capacitance of 730 mF cm–2 at 1 mA cm–2 of current density [27]. Note the result was also obtained under such synthesis conditions that led to a c-axis oriented structure, giving better results than a (201) orientation. A film electrode composed of intertwined V2O5 nanowires and carbon nanotubes (CNTs) demonstrated a volumetric capacitance of ≈460 F cm–3 [234]. A capacity of 397 F g–1 was obtained after ultrasonic weltering [262]. V2O5 thin films with 4 at.% of Mo doping exhibited a maximum specific capacitance of 175 mF/cm2 at current density of 1 mA/cm2 [17].
Regarding the electrochemical properties, high energy density (900 W h kg–1 at 200 mA g–1), power density (28 kW kg–1 at 10.5 A g–1), good cyclic stability over 200 cycles have been obtained with nanostructured V2O5 thin-film electrodes prepared by cathodic deposition [104,190]. These results, as well as results obtained by atomic layer deposition [111,113,114] show so that V2O5 nano-electrodes can now be used with high power and energy densities for thin film Li-ion batteries.
V2O5 is also increasingly used as sensor. Fit has been tested for longer time periods up to 100 h as ammonia sensors. Very stable behavior was found with detection limit of 80 ppb for NH3 both in dry and humid air. The detection limits for NO and CO were 20 ppm and 50 ppm, respectively. The results suggest that the vanadium oxide thin-film sensing layers are good candidates for a Selective Catalytic Reduction (SCR) process control application [70]. The room temperature gas sensing response of V2O5 films was found to be highly selective towards xylene [92]. They also exhibited good response towards hydrogen (5–300 ppm), methane and propane (50–3000 ppm) [171]. Recently, intrinsic thermochromism of V2O5 films was reported as a perceptible thermally induced color change from bright yellow to deep orange [290].
All these recent results show the continuous improvement in the synthesis of the films and the performance for tehes applications. In most of the works that have been published, however, the optimization of the film is made within one deposition technique, for one application. Therefore, further works should address two questions. The first one is to determine which deposition technique and synthesis parameters are best suited for each application. For instance, electrochemical properties of vanadium oxide are reported to be optimized for highly crystallized V2O5 [21], but better kinetics and higher volumetric capacities were observed for the amorphous vanadium oxides compared to their crystalline counterparts in Ref. [259]. Therefore, further works are needed to clarify the conditions that optimize the films for electrochemical applications. The second question is which kind of film should be used to optimize the film as a function of the application that is targeted. For instance, low Mg-doping (2%) is preferred for lithium ion battery applications, but 15% Mg-doping is preferred for electrochromic applications [212]. Only very few such reports have been made to relate the synthesis to applications, and further works along these lines would be very useful in the near future.
Conflict of interest
The authors declare that there is no conflict of interest regarding the publication of this manuscript.









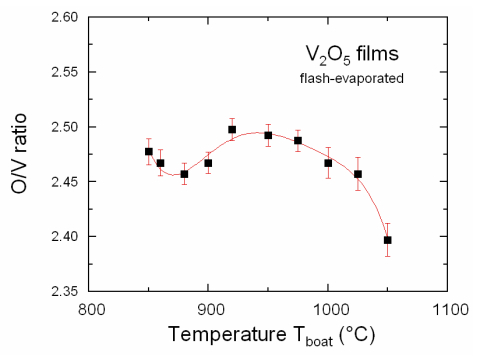
 DownLoad:
DownLoad: