Novel stability criteria on a patch structure Nicholson's blowflies model with multiple pairs of time-varying delays

1.   Introduction

As we all know, dynamic model analysis has developed in many disciplines such as biology, economic sciences, and engineer, etc ^{[1,2,3,4,5,6,7,8,9,10]}. Especially, using mathematical biological model to study the population dynamic behaviors plays an important role in maintaining the function of ecosystem ^[11,12,13], guiding production practice ^[14,15,16], designing artificial ecosystem ^[17,18] and promoting the development of information technology ^[19,20]. In order to better describe the influence of delays in mathematical biological model, the Functional Differential Equations (FDEs) have been applied extensively to the study of population dynamics ^[21], which can be traced back to the 1920s, when Volttera ^[22] studied the predator-prey model. In the past 100 years, the theory of population dynamics has made remarkable progress with main results scattered in numerous research papers ^{[23,24,25,26,27,28,29,30,31,32,33,34,35,36]}. In particular, there have been plenty of papers written about the dynamical characteristic analysis of FDEs, which include global stability ^{[37,38,39,40]}, periodicity ^{[19,20,27,32]}, almost periodicity ^[41,42,43], Hopf bifurcation ^[14], boundedness ^[16] and synchronization ^[17]. Just as pointed out by Berezansky and Braverman ^[18], the following delayed differential equation

can be used to characterise the dynamics of many population models. Here $m$ and $l$ are positive integers, $G$ represents the instantaneous mortality rate, and each $F_{j}$ describes the feedback control depending on the values of the stable variable with respective delays $\tau _{1}(t), \tau _{2}(t), \cdots, \tau _{l}(t)$. Obviously, (1.1) includes the modified Nicholson's blowflies equation ^[23,24]

which in the case $g_{j}(t) \equiv h_{j} (t)$ coincides with the classical models ^{[25,26,27,28,29,30,31,32,33]}. In (1.2), $\alpha(t), \; \beta _{j}(t),$ $\; g _{j}(t), \; h _{j}(t)$ and $\gamma _{j}(t)$ are all continuous and nonnegative functions, $\alpha(t)$ is the death rate of the population which depends on time $t$ and the current population level $x (t)$, $\beta_{j}(t) x(t-g_{j} (t))e^{-\gamma_{j}(t) x(t-h_{j}(t))}$ is the time-dependent birth function which involves maturation delay $g_{ j}(t)$ and incubation delay $h_{ j}(t)$, and gets the reproduce at its maximum rate $\frac{1}{\gamma_{ j}(t)}$, and $j\in I: = \{1, 2, \cdots, m\}$.

It should be noted that, in most of the aforementioned works ^{[23,24,25,26,27,28,29,30,31,32,33]}, the per capita daily adult mortality term $\alpha(t)$ is uniformly positive (that means, there is a positive constant $\alpha^{-}$ such that $\alpha(t)\geq \alpha^{-}$ for all $\ t\geq t_{0}$). However, throughout the time of some seasons, the death or harvest rate may be less or greater than the birth rate in nature ^[33,34,35], it is more reasonable to study Nicholson's blowflies models without restriction on uniform positiveness of the per capita death rate. On the other hand, it is of great practical significance to investigate the dynamic behaviors of the patch structure Nicholson's blowflies model ^[36,37,38]. In recent years, the dynamic behaviors of the following modified Nicholson's blowflies model with patch structure

have aroused the current research interest, and some useful results have been obtained in the existing papers ^{[38,39,40,41,42]}. In particular, without restriction on uniform positiveness of $\alpha_{ii}(t) (i\in Q)$, Xu, Cao and Guo ^[39] established some new criteria for the global attractivity of model (1.3) with the following admissible initial conditions:

where $\ r_{i} = \max\limits_{j\in I}\{\sup\limits_{t\in[t_{0}, +\infty)}\ g_{ij}(t), \sup\limits_{t\in[t_{0}, +\infty)}h_{ij}(t)\}, \ \ C_{+} = \prod\limits_{i = 1}^{n}C([-r_{i}, 0], [0, +\infty))$. Moreover, the authors in ^[39] obtained the main result as follows.

Theorem 1.1. Suppose that

$(W_{1})$ $\lim\limits_{t\rightarrow +\infty}\int_{0}^{t} \alpha(s)ds = +\infty,$ where $\alpha(t) = \min\limits_{i \in Q}\{\alpha_{ii}(t)\}$,

and

$(W_{2})$ $1 > \limsup\limits_{t\rightarrow +\infty}[\sum\limits_{j = 1, j\neq i}^{n} \frac{\alpha_{ij}(t)}{\alpha_{ii}(t)}+\sum\limits_{j = 1}^{m} \frac{\beta_{ij}(t)}{\alpha_{ii}(t)}], \ i\in Q,$

are satisfied. Then the zero equilibrium point in system (1.3) is globally generalized exponentially stable, i.e., there exist two constants $T^{*} > \max\{t_{0}, 0\}$ and $M(\varphi) > 0$ such that every solution $x(t) = x (t; t_{0}, \varphi)$ of (1.3) and (1.4) agrees with that

Unfortunately, there exist two mistakes in the proof of the main results in ^[39]. The first mistake is on lines 1-2 of page 3. More precisely, let $x_{i} (t) = x_{i}(t; t_{0}, \varphi), \ \ y_{i}(t) = \max\limits_{t_{0}-r_{i} \leq s\leq t} x_{i}(s) \ \mbox{ and} \ y(t) = \max\limits_{i\in Q}y_{i}(t)$, the inequality

can not lead to

where $t \in [t_{0}-r_{i}, \ \eta(\varphi))$, $i \in Q$ and $\parallel \varphi \parallel = \max\limits_{i\in Q}\{\max\limits_{t\in [-r_{i}, 0]} |\varphi_{i}(t)|\}$. The same mistake also appeared in ^[40] [see, p. 4], ^[41] [see, p. 5] and ^[43] [see, p. 4]. The logical error for the above mistake is that the left side of (1.6) is the whole maximum value for all $i$, but the right side of (1.6) is only for a fixed $i$. Fortunately, this error will be corrected in the Lemma 2.1 of this present paper. The second mistake in literature ^[39] is on line 26 of page 3 that the inequality

which is absurd. Actually, by taking $\parallel \varphi \parallel = 100$ and letting $t \rightarrow +\infty$, one can find that

is a contradiction.

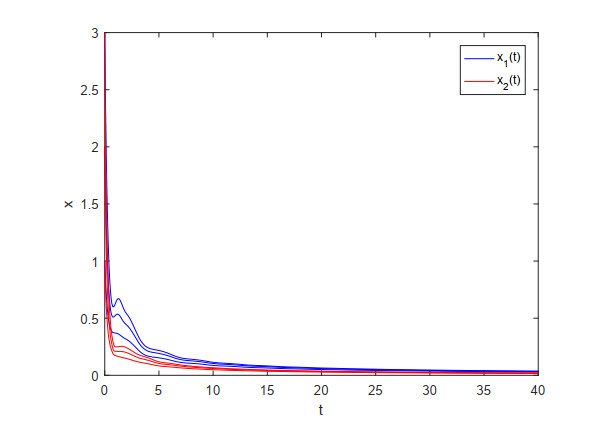
Furthermore, we consider the following concrete example

and its numerical simulations in Figure 1 to illustrate the above mistakes. Obviously, the assumptions $(W_{1})$ and $(W_{2})$ are satisfied in (1.7). Therefore, from Theorem 1.1, we have that the zero equilibrium point of system (1.7) is globally generalized exponentially stable. However, the numerical solutions with three different initial values shown in Figure 1 reveal that three numerical trajectories of (1.7) are convergent to $\bf{0}$ as $t\rightarrow+\infty$, but they are not generalized exponential convergence to $\bf{0}$. This makes us doubt whether the conclusions of Theorem 1.1 are correct.

Based on the above theoretical analysis and numerical simulations, two problems naturally arise. One is whether the assumptions $(W_{1})$ and $(W_{2})$ can guarantee that every solution of (1.3) and (1.4) is convergent to $\bf{0}$ as $t\rightarrow+\infty$. The other is what kind of conditions can ensure the global generalized exponential convergence of the zero equilibrium point of (1.3).

Regarding the above discussions, in this manuscript, we first establish the global convergence of model (1.3) under the original conditions $(W_{1})$ and $(W_{2})$. It is worth noting that, two or more delays appearing in the same time-dependent birth function will cause complex dynamic behaviors, even chaotic oscillations. It is impossible to establish the global exponential convergence of (1.1) without appropriate restrictions on the distinctive delays and some corresponding examples are also given in ^[18]. Therefore, we add a new delay-dependent assumption to obtain some new criteria for the generalized exponential convergence and global exponential asymptotic stability on the zero equilibrium point of (1.3). In a nutshell, our results not only correct the errors in the existing literature ^{[39,40,41,43]}, but also improve and complement the existing conclusions in the recent publications ^{[23,24,26,32,39]}, and the effectiveness is demonstrated by a numerical example.

2.   Materials and method

Hereafter, for $i\in Q, j\in I$, we assume that $\alpha_{ii}, \gamma _{ij}\in C([t_{0}, \ +\infty), (0, +\infty))$ and $\alpha _{ij}(i\neq j), \beta_{ij}, g_{ij}, h_{ij}\in C([t_{0}, +\infty), [0, +\infty))$. Label $x(t; t_{0}, \varphi)$ for a solution of (1.3) associating to (1.4), and $[t_{0}, \ \eta(\varphi))$ be the maximal existence right-interval.

Lemma 2.1. Every solution $x (t) = x (t; t_{0}, \varphi)$ is positive on $[t_{0}, +\infty)$.

Proof. According to (1.3), (1.4) and Theorem 5.2.1 in ^[44] [see p. 81], one can find that $x_{i}(t) \geq 0$ for all $t \in [t_{0}, \eta(\varphi))$ and $i\in Q$. Now, we reveal that $\eta(\varphi) = +\infty$. For all $t \in [t_{0}, \eta(\varphi))$ and $i \in Q$, define $y_{i}(t) = \max\limits_{t_{0}-r_{i} \leq s\leq t} x_{i}(s)$ and $y(t) = \max\limits_{i\in Q} y_{i}(t)$, we gain

and

where $s\in [t_0, \ t]$ and $i\in Q.$ On combining this with the fact that

we deduce that

Hence, by the Gronwall-Bellman inequality, we obtain

This and ^[45] [see Theorem 2.3.1] suggest that $\eta(\varphi) = +\infty$, and $x_{i}(t) \geq 0$ for all $t \in [t_{0}, +\infty)$ and $i\in Q$. Note that $x_{i}(t_{0}) = \varphi_{i} (0) > 0$, we get

which evidences Lemma 2.1.

3.   Results

Theorem 3.1. Under $(W_{1})$ and $(W_{2})$, every solution $x (t) = x (t; t_{0}, \varphi)$ is convergent to $\bf{0}$ as $t\rightarrow+\infty$.

Proof. First, we prove that every solution $x (t) = x (t; t_{0}, \varphi)$ is bounded on $[t_{0}, +\infty)$. By (W2), we have

and hence, $\frac {1-\sigma}{2} > 0$. Therefore, there exists $T_{*} > t_{0}-r_{i}$ such that

Clearly,

Furthermore, we state that

Otherwise, there exist $i^{*}\in Q$ and $T^{**} > T_{*}$ such that

Then

which is a contradiction and proves that $x (t)$ is bounded on $[t_{0}, +\infty)$.

Now, it is sufficient to show that $u = \max\limits_{i\in Q}\limsup\limits_{t\rightarrow +\infty } x _{i}(t) = 0$.

For any $\varepsilon > 0$, one can choose $\Lambda > T^{* }$ such that

Thus,

By taking the upper limits, $(W_{1})$ leads to

which, together with the arbitrariness of $\varepsilon$, implies that $u = 0.$ This finishes the proof of Theorem 3.1.

We now make the following assumptions:

$(W_{2}^{*})$ $1 > \sup\limits_{t\geq t_{0}}[\sum\limits_{j = 1, j\neq i}^{n}\frac{\alpha_{ij}(t)} {\alpha_{ii}(t)}+\sum\limits_{j = 1}^{m}\frac{\beta_{ij}(t)}{\alpha_{ii}(t)}] \ {\rm{for}}\;\;{\rm{all}} \ i\in Q.$

$(W_{3})$ There exists a positive constant $m[\alpha] > 0$ such that

Theorem 3.2. Under assumptions $(W_{1})$, $(W_{2})$ and $(W_{3})$, all positive solutions of system (1.3) are generalized exponentially convergent to the zero equilibrium point. More precisely, there exist positive constants $\kappa, \lambda, M(\varphi)$ such that every solution $x (t) = x (t; t_{0}, \varphi)$ of (1.3) and (1.4) agrees with that

Proof. From (3.1) and $(W_{3})$, one can see that

and there exists $\lambda > 0$ such that

$\mbox{where } \ t\in[T_{*}, +\infty) \ \mbox{and } \ i \in Q.$

Let us consider the following function:

where $\ t\geq t_{0}-r_{i}, \ \kappa = e^{\lambda\int_{t_{0}}^{ T_{*}} \alpha(s) ds}$, and $M(\varphi)$ is defined in (3.2). In view of (3.4) and the fact that

we obtain

$\mbox{where } \ t\in[T_{*}, +\infty) \ \mbox{and } \ i \in Q.$

Hereafter, we show that

It is easy to see that

Next, we prove that

Suppose, for the sake of contradiction, there exist $\widetilde{t} > T_{*}$ and $i_{0}\in Q$ satisfying that

Then, $x_{i_{0}}(t) \leq v(t)$ for all $t \in[t_{0}-r_{i}, \widetilde{t}]$. From (3.5), we have

which together with (1.3) and (3.3), we gain

which yields a contradiction and shows (3.7) holds. Consequently, (3.6) holds, and the proof of Theorem 3.2 is now completed.

Theorem 3.3. Let $(W_{1})$, $(W_{2}^{*})$ and $(W_{3})$ be satisfied, the zero equilibrium point in (1.3) is globally asymptotically stable.

Proof. According to Theorem 3.2, it follows from $(W_{1})$, $(W_{2}^{*})$ and $(W_{3})$ that the zero equilibrium point in system (1.3) is globally attractive. Now, we only need to show the local stability on the zero equilibrium point in system (1.3). By $(W_{2}^{*})$, we gain

For $\varepsilon > 0$, we choose $\delta\in (0, \ \varepsilon)$. Next, we claim that, for $\|\varphi\| < \delta$,

In the contrary case, there exist $t_*\in (t_{0}, +\infty)$ and $i_{*}\in Q$ such that

Consequently, (1.3), (3.8) and (3.10) involve that

which is absurd and proves (3.9). Therefore, the zero equilibrium point is globally asymptotically stable.

Remark 3.1. One can easily see that all convergence results in references ^{[23,24,26,32]} are special ones of Theorems 3.1, 3.2 and 3.3 with $n = 1$ and $g_{ij} (t) \equiv h_{ij}(t)$. In addition, the errors in the existing literatures ^{[39,40,41,43]} have been corrected in the proof of Lemma 2.1 and Theorem 3.2. Specially, we add a new delay-dependent condition $W_{3}$ to ensure the correctness of the main conclusions Theorems 3.1 and 3.2 in ^[39]. Therefore, the obtained results of this present paper improve and complement the above mentioned references ^{[23,24,26,39,40,41,43]}.

4.   A numerical example

In this section, we present an example to check the validity of the main results obtained in Section 3.

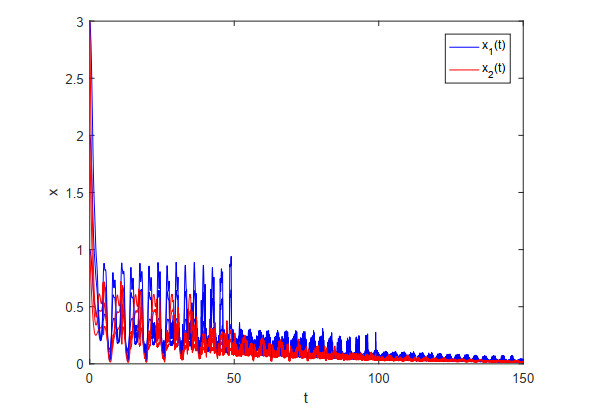
Example 4.1. Consider the following patch structure Nicholson's blowflies model with multiple pairs of time-varying delays:

One can see that (4.1) satisfies all the conditions in Theorem 3.3. It follows that the zero equilibrium point of system (4.1) is globally asymptotically stable on $C_+ = \{\varphi\in C([-1, \ 0], [0, \ +\infty)) \times C([-1, \ 0], [0, \ +\infty))\}$. The numerical trajectories with different initial values are shown in Figure 2, which reveal the above conclusions.

Remark 4.1. It should be pointed out that the per capita daily adult mortality terms of (4.1) are not uniformly positive mortality terms since

In addition, the global stability of the patch structure Nicholson's blowflies model with multiple pairs of time-varying delays has not been touched in ^{[46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66]}. This implies that all the results in ^{[23,24,25,26,27,28,29,30,31,32,33]} and ^{[46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66]} cannot be used to show the global convergence and stability on system (3.1) where $\tau_{ij} (t) \not\equiv h_{ij}(t)(i\in Q, j\in I)$. Moreover, the proposed techniques could be taken into consideration in the dynamics research on other patch structure population models involving two or more delays in the same time-dependent birth function.

5.   Conclusions

In the present manuscript, we investigate the asymptotic behavior for a patch structure Nicholson's blowflies model involving multiple pairs of different time-varying delays. Here, we obtain some novel results about the asymptotic behavior on the zero equilibrium point of the addressed model without assuming the uniform positiveness of the death rate and the boundedness of coefficients, which complement some earlier publications to some extent. In addition, the method used in this paper provides a possible method for studying the global asymptotic stability of other patch structure population dynamic models with multiple pairs of different time-varying delays.

Acknowledgments

I would like to thank the anonymous referees and the editor for very helpful suggestions and comments which led to improvements of my original paper. This work was supported by the Postgraduate Scientific Research Innovation Project of Hunan Province (No. CX20200892) and "Double first class" construction project of CSUST in 2020 ESI construction discipline Grant No. 23/03.

Conflict of interest

We confirm that we have no conflict of interest.