This paper is devoted to the stochastic damped Ostrovsky equation driven by pure jump noise. The uniformly bounded of solutions in H1(R) and L2(R) space are established respectively, which are the key tools to obtain the existence of invariant measure. By applying the convergence in measure in Hilbert space, we prove that the invariant measure is unique if the initial value is non-random. Some numerical simulation are provided to support the theoretical results.
1.
Introduction and main results
In this paper, we concentrate on the following stochastic damped Ostrovsky equation driven by pure jump noise
where λ>0, β and γ are real numbers such that β⋅γ≠0 and ∂−1xf=((iξ)−1ˆf(ξ))∨, and η(dt,dz) denotes the Poisson counting measure. The Ostrovsky equation was introduced by [17] to describe the weakly nonlinear long waves in a rotating liquid, where the parameter γ measures the effect of rotation which is supposed to be small. β represents the capillary waves on the surface of a liquid or for oblique magneto-acoustic waves in plasma. And λ>0 means the positive dispersion.
For the stochastic Ostrvosky equation driven by white noise, Isaza [11,12,13] proved the well-posedness in Hs(R) with s>−34. Yan et al. [21,22] obtained the local well-posedness for the Cauchy problem for (1.1) the initial data u0(⋅,ω)∈Hs(R)(ω∈Ωa.e.) with s>−34, and the global well-posedness in L2(R)(a.e.ω∈Ω). Chen [4] established the existence of random attractor in ˜L2(R). Wu et al. [19] established the ergodicity of stochastic damped Ostrovsky equation with Gaussian noise, but they do not discuss the ergodicity of the equation with Lévy noise.
The dispersive partial differential equation such as Schrödinger equation, KdV equation and Ostrovsky equation are integrable systems with infinite conservation laws. If λ=0, then (1.1) become a stochastic KdV equation. Bouard et al. [2,3] established the local well-posedness for stochastic KdV equation with additive noise and multiplicative noise respectively. The dissipative effect of damped dispersive systems are too weak to apply the theory for dissipative dynamical systems. There are two typical difficulties to establish the ergodicity for stochastic dispersive equation on R need to overtake, one is the non-compactness of the whole real line R, and the other one is the non-compactness of operator semigroup for stochastic linear dispersive equation. Recently, Ekren, Kukavica and Ziane [9,10] applied the stopping time technique to establish the boundedness of the uniform estimate, which can deduce the tightness of the measure sequences in local square integrable space L2loc(R), they also used the convergence in measure in Hilbert space in terms of the idea in [16] to obtain the existence of invariant measure, but they could not provide with the uniqueness and ergodicity, we refer it to [9] for details.
Recently, Bouard et al. [1] studied the nonlinear Schrödinger eqution driven by jump process, and proved the existence of a martingale solution of the nonlinear Schrödinger equation with jump processes with infinite activity, but they could not study the ergodicity of invariant measure for stochastic Schrödinger equation with jump noise. In fact, there are a lot of paper on ergodicity for stochastic dissipative partial differential equation driven by jump process, Dong and Xie [7] studied ergodicity of stochastic 2D Navier-stokes equations with Lévy noise, Dong et.al.[6] study the existence of martingale solutions of stochastic 3D Navier-Stokes equations with jump noise. To the best of our knowledge, there is little paper on the ergodicity of stochastic damped dispersive PDE with Lévy noise due to the above mentioned difficulty.
The goal of this paper is to study the invariant measure of stochastic damped Ostrovsky equation with pure jump noise. The novelty of the current paper to obtain the uniformly bounded of solutions in H1(R) and L2(R) space respectively, which are the key tools to prove the tightness of the measure sequences in local square integrable space L2loc(R). By using the convergence in measure in Hilbert space in terms of the idea in [16], we can obtain the existence of invariant measure. Moreover, by applying the idea of Proposition 3.2.7 in [5], we prove that the invariant measure is unique if the initial value is non-random. The another novelty of the current paper is that the numerical simulation in the sense of E‖u(t,⋅)‖L2x reveals that stochastic damped Ostrovsky equation driven by pure jump may posses an unique ergodic invariant measure.
We state our main result followed as:
Theorem 1.1. Assume that u0∈X1, and the Hypothesis (H1)–(H3) are satisfied. Then stochastic damped Ostrovsky equation (1.1) admits an invariant measures. Moreover, it posses an ergodic invariant measure for the non-random initial data.
The rest of paper is organized as follows. In Section 2, some function setting and useful lemmas or technique theorem are provided. In Section 3, the uniformly bounded of solutions in H1(R) and L2(R) space are established respectively, which are the key tools to obtain the ergodicity. By using the methods of [1,Appendix A], we prove the existence of invariant measure for stochastic damped Ostrovsky equation in Section 4. Moreover, by applying the idea of Proposition 3.2.7 in [5], we prove that the invariant measure is unique if the initial value is restricted to be non-random. In Section 5, some numerical simulation are provide to support the theoretical results.
2.
Preliminary
In this section, we introduce some basic concepts and some inequalities, which are from [1] and [18].
Let (Ω,F,Ft,P) be a complete probability space, (Z,B(Z)) be a measurable space and ν(dz) be a σ−finite measure on it. Let P=(p(t),t∈Dp) be a stationary Ft−Poisson point process on Z with characteristic measure ν(dz), where Dp is a countable subset of [0,+∞) depending on random parameter ω∈Ω. Denote by η(dt,dz) the Poisson counting measure associated with p, that is η(dt,dz)=Σs∈Dp,s⩽t1A(p(s)), where 1A(⋅) is the indicator function with respect to A. Let ˜η(dt,dz)=η(dt,dz)−dtν(dz) be the compensated Poisson measure. If ν(z)<∞, ˜η is a martingale with ⟨˜η(Z)⟩t=tν(z), and ν is the intensity measure of η.
We impose the hypothesis (H1)–(H3) on the Poisson processes just as [8]
(H1) For any u∈X1, there exists a constant C<∞ such that
(H2) ν(0)=0, ∫Z‖z‖2Zν(dz)<∞ and ν(Z)=ρ<∞,
(H3) Z is continuously embedded in H1(R).
The measure ν describes the expected number of jumps of a certain height in a time interval of length 1. The hypothesis means there is an finite number of small jumps is expected.
Let Y be a separable and complete metric space and T>0. The space X(T)=D([0,T];Y) denotes the space of all right continuous functions x:[0,T]→Y with left limits, P(D([0,T];Y)) the space of Borel probability measures on D([0,T];Y). We equip D([0,T];Y) with the Skorohod topology such that D([0,T];Y) is both separable and complete.
Let H be a Hilbert space, Hs(R) is the Sobolev space with norm
where ⟨ξ⟩s=(1+ξ2)s2 for any ξ∈R,Fxu and F−1xu denotes the Fourier transformation and the Fourier inverse transformation of u with respect to its space variable respectively. ˙Hs1,s2(R) is the Sobolev space with norm
and ˙Hs=˙H0,s. With this choice of the antiderivative we have, ∂−1xf=(ˆf(ξ)iξ)∨, so it is natural to define the function space Xs as one in [15]
Space S(R) is the Schwartz space and S′(R) is its dual space. Fu and F−1u denotes the Fourier transformation and the Fourier inverse transformation of u with respect to its all variables respectively.
The following Theorem is the key tool to prove the ergodicity for stochastic equation (1.1), which is from [1],
Lemma 2.1 (Appendix A.1, [1]). Let {xn:n∈N} be a sequence of cˊadlˊag processes, each of the process defined on a probability space (Ωn,Fn,Pn). Then the sequence of laws of {xn:n∈N}is tight on D([0,T];Y) if
(a) there exists a space Y1, with Y1→Y compactly and some r>0, such that
(b) there exist constants c>0, γ>0 and r>0 such that for all θ∈[0,T],t∈[0,T−θ], and n≥0, we have
Denote
Then the mild solution of equation (1.1) can be written as:
Definition 2.1. Assume that (X,T) is a polish space, Σ is a σ-algebra on X, M is a set of measures on Σ. M is said to be tight if for any ε>0, there exists a compact set Kϵ⊂X such that
The following Lemma is the key tool to prove the ergodicity for stochastic equation (1.1), which is from [5].
Lemma 2.2 ([5], Proposition 3.2.7). An invariant probability measure for the semigroup Pt, t≥0, is ergodicity if and only if it is an extremal point of the set of all the invariant probability measures for the semigroup Pt,t≥0.
3.
Uniform bounded and global well-posedness
In this section, we establish the uniform estimates of the solution in L2 norm and H1 norm respectively, which is the key tool to obtain the ergodicity for stochastic Ostrovsky equation (1.1).
Lemma 3.1 ([22]). There exists some monotonely increasingly continous function ~C1(t) and a constant α>0, ∀h,g∈X(T), such that
Here ‖u‖X(T)=sups∈[0,T]‖u(s)‖H1.
Lemma 3.2 ([22]). There exists some monotonely increasingly continuous function ~C2(t), such that
Lemma 3.3. If u(t)∈X1 solves the equation (2.1), and the Hypothesis (H1)–(H3) are satisfied. There exists a constant C>0 such that
Proof. The proof of (3.1) can get by slightly modifying the proof of Lemma 5.1 in [22], we just prove (3.2). Let
Applying the Itô formula to I(u) yields
Direct computation shows that
Taking the expectation and using (H1)–(H3) gives
We can deduce that for I1(t∧τN),
Similarly,
and
For M3, by Agmon's inequality, ‖u‖L∞≤‖u‖1/2L2‖∂xu‖1/2L2, we have
and by (3.1)
Combining the above arguments, we can obtain
Applying Gronwall's inequality leads to
Since τN∧T→T as N→∞,P.a.s.. It follows from Young's inequality that
which implies that
Then, we can prove that
Thus, the proof of Lemma is completed.
Next, we will prove the global well-posdness of (1.1) in D([0,T],H1) by the method developed in [1].
Theorem 3.1. Assume the conditions (H1)–(H3) are satisfied. Then, the equation (1.1) admits a unique global mild solution in X1, which is caˊdlag.
Proof. Let \{\tau_{n}:n\in \mathbb{N}\} be a family of independent exponential distributed random variables with parameter \rho , and set
Define \{N(t):t\geqslant 0\} as the counting process
Then for any fixed t > 0 , N(t) is a Poisson distributed random variable with parameter \rho t . Let \{Y_{n}:n\in \mathbb{N}\} be a family of independent, \nu/\rho distributed random variables. Then
Notice that N(t) = 0 on the interval [0, T_{1}) , then the equation (1.1) can be rewritten as the following equations
Thus, the mild solution of equation (3.5) can be represented as follows
Define the operator F by
Then
for \|u\|_{X_1(T_{1})} < \infty . Lemma 3.1 and 3.2 implies that there exists some constant C > 0 such that
Thus, F maps X_1(T_{1}) into itself. Next, we will verify that the operator F is contractive. In fact, for any u_{1}, u_{2}\in X_1(T_{1}) , we have
Hence, there exists a sufficient small T_{1} > 0 such that equation (3.5) posses an unique local solution on [0, T_1] . In the sequel, we extend the local solution to the global one by Lemma 3.3. To the end, denote this local solution on [0, T_{1}) by u_{1} . We will consider the solution on [T_{1}, T_{2}) . Notice that a jump with size g(u(T_{1}-), Y_{n}) happens at time T_{1} , let u_{1}^{0} = u_{1}(T_{1}-)+g(u_{1}(T_{1}-), Y_{n}) , and we consider a second process on [T_{1}, T_{2}) as following
Similarly, we can deduce that equation (3.6) posses a unique mild solution u_{2} on [T_{1}, T_{2}) . Repeating the above arguments, we can obtain that the equation (1.1) has a unque global mild solution in X(T) .
Since P(N(t) < \infty) = 1 , the solution u(t) is almost surely defined on [0, T] . It is clearly that the jumps take place at each T_{j} , and \lim\limits_{t\downarrow T_{j}}u(t) = u_{j}^{0} , and \lim\limits_{t\uparrow T_{j}}u(t) exists. Then u is c\acute{a}dlag . Thus the proof of Theorem 3.1 is complete.
4.
Ergodicity of stochastic equation (1.1)
In this section, we first prove the tightness of semigroup P(t), t\geq 0 according to Lemma 2.1, then prove the ergodicity of stochastic equation (1.1).
Theorem 4.1. Assume that u_{0}\in H^{1}({\mathbb{R}}) , and the conditions (H1)–(H3) are satisfied. Then for any sequence of deterministic initial conditions \{u_0^{n}\} with R = \sup\limits_{n\in\mathbb{N}}\{\| u_{0}^{n}\|_{H^{1}}\} < \infty , \{P_{t_{n}}(u_{0}^{n}, \cdot):n\in\mathbb{N}\} is tight on H^{1} for any t_{n} > 0 with t_n\to\infty as n\to\infty .
Proof. Without loss of generality, we assume that t_{n} is an increasing sequence. Denote by u_{n}(t) the solution with the initial condition u_{n}(0) . We claim that \{u_{n}(t)\}_{n = 1}^{\infty} converges in H^{1} ({\mathbb{R}}) . In fact, since
then we have
Due to Lemma 2.2, it suffices to prove there exist two constants c > 0 and \gamma > 0 and a real number r > 0 such that for all \theta > 0, t\in [0, T-\theta] , and n\geq 0
By the Definition 2.1, we get
It follows from Lemma 3.1 and assumptions (H1)–(H3) that there exist \gamma > 0 such that
which implies that the tightness of \{P_{t_{n}}(u_{0}^{n}, \cdot):n\in\mathbb{N}\} holds, and the proof of Theorem 4.1 is complete.
Theorem 4.2. Assume that u_{0}\in H^{1}({\mathbb{R}}) and the conditions (H1)–(H3) are satisfied. If K is a compact set of \{H^{1}\} , then the sequence of measures \{P_{s}(v, \cdot):s\in[0, 1], v\in K\} is tight on H^1 .
Proof. We need to prove that \{P_{s}(v, \cdot):s\in[0, 1], v\in K\} posses a convergent subsequence. Without loss of generality, we assume that (s_{n}, v_{n})\in[0, 1]\times K converges to (s, v)\in[0, 1]\times K , because K is a compact set. Let u_{n}(t) be the solution with the initial value v_n(0) , and u(t) the solution with the initial value v . For u\in D([0, 1];H^{1}) , then we can derive that
Next, we will prove that there exists a subsequence (s_{n_{k}}, v_{n_{k}}) of sequence (s_{n}, v_{n}) such that
Finally, set R_{0} = \sup\limits_{v\in K}\|v\|_{H^{1}}+1 , and choose R > 0 such that \frac{C(R_{0})}{R}\leq\frac{\varepsilon}{2} , then we have
Define \tau = \inf\{s\geq 0:4\tilde{C}(t)s^{\alpha}(\tilde{C}(t)R+\|\bar{u}\|_{X(s)}+\|\int_{0}^{s}U(s-r)\partial_x u^2dr\|_{X(s)}) > 1\}. is a stopping time. Let \tau_{0} = \tau , and
and choose N such that P(\tau_{N}\leq 1)\leq \frac{\varepsilon}{2} , we obtain
on the interval A_{n}\bigcap\{\tau_{N}\geq1\} .
Choosing n be large enough such that (2\tilde{C}(t))^{N+1}\|v-v_{n}\|_{H^{1}} < \delta , we have
which implies that
Therefore, there exists a sequence n_{k} such that
We can deduce that
for any real valued uniformly continuous function \xi\in H^{1}({\mathbb{R}}) . Therefore, \{\mathbb{P}_{s}(v, \cdot):s\in[0, 1], v\in K\} has a convergent subsequence. The proof of Theorem 4.2 is complete.
Theorem 4.3. Assume that u_{0}\in H^{1}({\mathbb{R}}) and the conditions (H1)–(H3) are satisfied. Then \mu_{n}(\cdot) = \frac{1}{n}\int_{0}^{n}P_{t}(0, \cdot)dt, n = 1, 2, ... is tight on H^{1}({\mathbb{R}}) .
Proof. Since for any \varepsilon > 0 , \{P_{n}(0, \cdot):n\geq 0\} is tight, we can choose a compact set K_{\varepsilon}\subset H^{1}({\mathbb{R}}) such that \sup\limits_{n}\{P_{n}(0, K_{\varepsilon}^{c})\leq\frac{\varepsilon}{2} , and \{P_{s}(v, \cdot):s\in[0, 1], v\in K\} is tight on H^{1} . We can also choose a compact set A_{\varepsilon}\subset H^{m}({\mathbb{R}}) such that \sup\limits_{s\in[0, 1], v\in K_{\varepsilon}}\{P_{n}(0, A_{\varepsilon}^{c})\leq\frac{\varepsilon}{2} . Therefore, we have
Then we get that \mu_{n}(\cdot) = \frac{1}{n}\int_{0}^{n}P_{t}(0, \cdot)dt , n = 1, 2, ... is tight on H^{1}({\mathbb{R}})\cap \dot{H}^{-1}({\mathbb{R}}) . The proof of Theorem 4.3 is complete.
Theorem 4.4. Assume that u_{0}\in H^{1}({\mathbb{R}}) and the conditions (H1)–(H3) are satisfied. Then equation (1.1) admits an invariant measures. Moreover, equation (1.1) with the deterministic initial condition posses an ergodic invariant measure.
Proof. Using Krylov-Bogoliubov proposition, Theorem 4.1 and Theorem 4.3, we can prove there exist at least an invariant measures for equation (1.1). Denote K be the set of all the invariant measure, then it is easy to check that K is convex. Let \{\mu_{n}\}_{n\in \mathbb{N}^{+}} be a sequence of invariant measures in K . Then there exists some constant C such that
For any deterministic initial condition, \{(\mu_{n}P_{t_{n}})(\cdot):n\in \mathbb{N}^{+}\} = \{\mu_{n}(\cdot):n\in \mathbb{N}^{+}\} is tight. Since K is a self sequentially compact set, then K is compact. It follows from Krein-Milman theorem, a convex compact set posses extremal point. Theorem 2.2 yields that this extremal point is ergodic. Therefore, stochastic equation (1.1) admits an ergodic invariant measure. Thus, the proof of Theorem 4.4 is complete.
5.
Numerical simulation
In this section, we will take the numerical simulation of the invariant measure. To the end, we give the distribution of the solution \frac{1}{T_M} \sum_{m = 0}^{T_M} \mathbb{E}\left[\Phi\left(u(t_m)\right)\right] by using the so-called the Monte Carl method as following. One can prove theoretically that it does have a unique invariant measure, which derive to the ergodicity[5].
We do the numerical simulation to find what happen if the Ostrovsky equation perturbed by pure jump noise. We firstly use the the norm conservative finite difference scheme introduced by [20,scheme 1] to simulate the equation (1.1) as
where
and \sum_{s \leq t} 1_{A}\left(\Delta L_{s}(\omega)\right) is a possion process with the parameter P \Delta t .
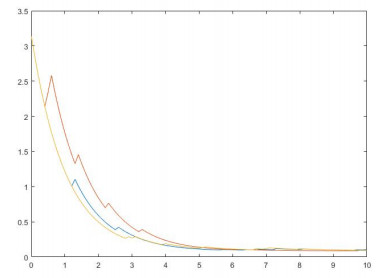
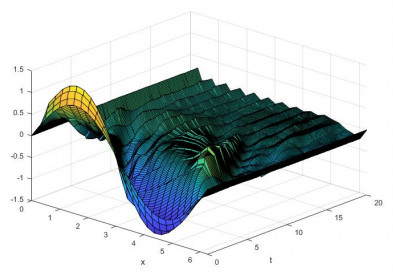
Now we set \beta = 0.01, \gamma = 1 , \lambda = 0.5 , and u_0(x) = sin(x) . The simulation of (1.1) driven by Poisson noise with g(u(t-), z) = 0.2u(t-)z is given in Figure 1. Figure 2 gives time changes of \|u(t, \cdot)\|_{L^2_x} using different sample trajectories.
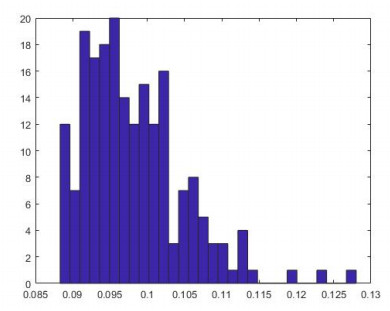
It can be clearly seen from the Figure 2 that the decay rate of the equation is slowed down under the influence of noise. At the same time, as shown in Figure 3, it can be seen that for \Phi(y) = exp(-|y|^2) , the distribution of the solution \frac{1}{N+1} \sum_{n = 0}^{N} \mathbb{E}\left[\Phi\left(U^{(n)}\right)\right] tends to a measure \mu as T \to \infty .
The above numerical simulation of stochastic damped Ostrovsky equation (Figure 3) in the sense of \mathbb{E} \|u(t, \cdot)\|_{L^2_x} reveals that stochastic damped Ostrovsky equation driven by pure jump posses an unique ergodic invariant measure.
6.
Conclusions
In this paper, the global well-posedness of stochastic damped Ostrovsky equation driven by pure jump noise is given at first. Then we use the tightness criterion to investigate the existence of invariant measures, and give the ergodicity under determined initial condition. A numerical experiment is also given to support our results.
Acknowledgments
The paper is Supported by the National Natural Science Foundation of China (No.11771449) and China Postdoctoral Science Foundation(No. 2019T120966).









 DownLoad:
DownLoad: