This paper investigates the asymptotic behavior for a class of n-dimensional population dynamics systems described by delay differential equations. With the help of technique of differential inequality, we show that each solution of the addressed systems tends to a constant vector as t → ∞, which includes many generalizations of Bernfeld-Haddock conjecture. By the way, our results extend some existing literatures.
1.
Introduction
Recently, many differential equations models arising from population dynamics, biological mathematics and engineer have attracted more and more attention [1,2,3,4,5,6], and the hot topics include asymptotical stability [7,8,9,10,11,12], limit cycles [13,14], bifurcation [15,16,17], and periodic solutions [18,19,20]. At the international conference on nonlinear systems and their applications in 1976, the following conjecture:
Conjecture. Each solution of the scalar differential equation
tends to a constant as t→∞.
was proposed by Bernfeld and Haddock [21]. Model (1.1) arises from population dynamics of a single species, where x13(t) and x13(t−r) always describe the instantaneous mortality rate and the feedback controls depending on the values of the stable variable with respective delay r, respectively.
Since the seminal works obtained by Jehu [22] and Ding [23] on the above conjecture, variants of the conjecture have been extensively investigated (see, [24,25,26,27,28,29,30,31,32,33,34]). A simple generalization of the conjecture is described by the following autonomous population dynamics model
where F,G∈C(R1,R1) describe the instantaneous mortality rate and the feedback controls depending on the values of the stable variable with respective delays r, respectively. The higher dimensional generalizations for compartmental systems were also presented in [24,25,26,27,28,29,30]. Yet the time-varying delays are more realistic than constant delays in population and ecology models, so Liu [35,36] generalized the conjecture as the following non-autonomous population dynamics models with time-varying delays:
and Xiao [37] established the following generalized version
Here, Fi,Gi∈C(R,R), Fi is increasing on R, p,γ1,γ2∈C(R,(0, +∞)),i=1,2.
In addition, the results in above references indicate that the solution of the systems which is bounded tends to a constant solution as t→+∞. There are two main methods to prove them, one is the analysis method of the monotone dynamical system [24,25,29,33,34], the other is the differential inequality analysis technique [23,27,32,35,36,37]. In particular, assume that,
where F is strictly increasing on R, and continuous differentiable on R∖{0}, the author in [37] established the convergence of system (1.1) and generalized the Bernfeld-Haddock conjecture to two-dimensional system. Unfortunately, if Fi≢Gi(i=1,2), there is a simple but serious error in proving Theorem 3.1 in [37]. For the convenience of reading, we'll point out the details of this error in Remark 3.1. Furthermore, in order to correct the above error, we take the following n-dimensional non-autonomous population dynamics model with time-varying delays into consideration:
and Fi∈Ω,γi,τi∈C(R,R+),i∈J={1,2,⋯,n}. Evidently, for Fi≡Gi(i∈J), Eqs 1.1, 1.3, 1.4 and the systems in [35] are special models of system (1.5).
Since the non-autonomous delay systems usually do not produce a semiflow, the approach in [23,24,25,27,29,32,33] can not be used to prove the asymptotic behavior of (1.5). In particular, as far as we know, there are no references about the asymptotic behavior of solutions to the n-dimensional system (1.5) involving time-varying delays. On the basis of the above discussions, we expect to propose a novel proof to show a similar conclusion to Bernfeld-Haddock conjecture that every solution of (1.5) tends to a constant vector as t→+∞.
The paper is organized in following way. We present the initial condition and some preliminary results in Section 2. The boundness and asymptotic behavior of solutions are investigated in Section 3, which are our main results. In the next section, some examples with numerical simulations are carried out to illustrate the validity of the obtained results.
2.
Materials and method
In this section, we give the initial condition and present the relevant results which will be used in Section 3.
Denote
where f is and continuous bounded function on R. We suppose that
Define C=∏ni=1C([−τ+i,0],R) as the Banach space equipped with the supremum norm. Moreover, we assume the initial condition
Let x(t;t0,φ)=(x1(t;t0,φ),x2(t;t0,φ),⋯,xn(t;t0,φ)) be the solution of (1.5) with the initial value condition (2.1). And [t0,η(φ)) is the maximal right-interval of existence of x(t;t0,φ).
Now, it is assumed that G∈Ω, and we recall the following Lemmas and Propositions.
Lemma 2.1. (see [34]) For any constant c≠0,t0 and x0, the system
has a unique left-hand solution x(t;t0,x0).
According to Proposition 4∗ and Proposition 5∗ in [35], the following results can be achieved:
Proposition 2.1. Consider the initial value problem
where a≠0 and 0≤ε≤|a|2. Then, we suppose that u=u(t;t0,u0) is the solution of (2.3), and the constant β>0. There must exist σ>0 independent of t0 and ε such that
Proposition 2.2. Consider the initial value problem
where a≠0 and 0≤ε≤|a|2. Then, we suppose that u=u(t;t0,u0) is the solution of (2.3), and the constant β>0. There must exist γ>0 independent of t0 and ε such that
Lemma 2.2. (see [37]) Let t0,x0∈R, α>0, H(t,x)∈C([t0,t0+α]×R, R), and H(t,x) is non-increasing with respect to the x. Then the following differential equation
has a unique solution x=x(t) on [t0,t0+α].
Lemma 2.3. Consider the system (1.5), assume that φ∈C, there is a unique solution x(t;t0,φ) on [t0,+∞).
Proof. Let x(t)=x(t;t0,φ), then, for all i∈J, we shall prove that there is a unique solution x(t) on [t0,t0+τmin]. Let
where
for any t∈[t0,t0+τmin]. Consider the following differential equation
According to Lemma 2.2, there is a unique solution xi(t) on [t0,t0+τmin] for all i∈J, and x(t) exists and is unique on [t0,t0+τmin]. Hence, it is obvious that there is a unique solution x(t) on [t0+τmin,t0+2τmin],[t0+2τmin,t0+3τmin],⋯. We now complete the proof of Lemma 2.3.
3.
Results
Theorem 3.1. x(t)=x(t;t0,φ) is bounded and tends to a constant vector as t→+∞.
Proof. For convenience, we label
and
Then, in order to get the boundness of x(t), we first prove D+v(t)≤0 for all t≥t0+τmax. The proof of this part is divided into the following two cases:
Case 1. If t∈[t0+τmax,+∞)∖M, then there exist i0∈J and t∗∈[t−τmax,t) satisfing that
Since xi(t) are continuous, we choose a constant 0<δ<τmax to satisfy that
which follows that
and hence, for all h∈(0,δ),
Then, the following results can be obtained:
Case 2. If t∈M, one can pick i0∈J such that
Then, (1.5) and (2.7) give us
Let ρ=12 τmin. When v(s)=xi0(s) for all s∈(t,t+ρ], we have
where 0<h<ρ.
On the other hand, if there exists s1∈(t,t+ρ] such that v(s1)>xi0(s1), it suffices to deal with the following two categories (ⅰ) and (ⅱ).
(ⅰ) If v(s1)=vi0(s1)=maxs1−τmax≤s≤s1xi0(s), then, we can choose a constant ˜t∈[s1−τmax,s1) such that
Noting that t−τmax<s1−τmax≤t+ρ−τmax<t<s1, we gain
We claim
Otherwise, xi0(˜t)>xi0(t). Then it is not hard to obtain that t<˜t<s1 and
which follows
In combination with t−τmax≤t−τˉi0(˜t)<˜t−τˉi0(˜t)<˜t−ρ<t<s1, we obtain
which leads to a contradiction and suggests that the above claim is true. Then
which together with t−τmax<s1−τmax≤t+ρ−τmax<t<s1, and
hereafter, we obtain
and hence
(ⅱ) If there exists ˜i∈J,˜i≠i0 such that
then, we can find a constant t1∈[s1−τmax,s1] such that
If s1−τmax≤t1≤t, and from (3.1), we have
which contradicts with (3.3). Therefore, t<t1≤s1 as well as
yields
From (3.1) and the fact that t−τmax<t1−τ˜i+1≤t1−τmin≤t+ρ−τmin<t, one can see that
which contradicts with (3.4). Therefore, category (ⅱ) does not hold, and we can draw that D+v(t)≤0 for all t≥t0+τmax from the proof of the above two cases.
Accordingly, from the definitions of u(t) and T, by using a similar argument as that adopted above, one can evidence that D+u(t)≥0,∀t≥t0+τmax. Overall, we know that u is non-decreasing and v is non-increasing on [t0+τmax,+∞). Now, the boundness of the x(t;t0,φ) is proved.
Next, we prove the convergence of x(t). Let li=lim inft→+∞xi(t;t0,φ),Li=lim supt→+∞xi(t;t0,φ),i∈J.
From the boundedness of x, we can obtain
Clearly, it is need to show Li=li for all i∈J. Combined with the above discussions, we just need to prove that Li>li for all i∈J does not hold. We just consider the case L1>l1, and the remainder of the argument is analogous for i∈J∖{1}. Suppose that, on the contrary, L1>l1. It follows that D<P, one of P and D is not equal to 0. Thus, we suppose that P≠0 and another case is similar. For ˉH∈(l1,L1)⊂(D,P), we can choose t∗0>t0+τmax and {σm}+∞m=1⊂[t∗0+τmax,+∞) such that
From the fact that v(t) is a monotone function and εm=v(σm)−P→0 ( as m→+∞), we can presume that, for any positive integer m,
Since
and
one can find that, for all t∈[σm,σm+(n+1)τmax],
Let z(t)=z(t;σm,εm) be the solution of following system
Note that ˉH<P, on the basis of Proposition 2.1, we get
where μ is unconcerned with σm and εm. With the help of (3.6) and (3.7), we can take a constant α∈(0,μ) such that
and
For s∈[σm+2τmax,σm+(n+1)τmax], according to the fact that
it follows that there exists tn∈[s−τmax,s]⊆[σm+τmax,σm+(n+1)τmax] such that
and
therefore
and
For s∈[σm+3τmax,σm+(n+1)τmax], in view of the fact that
one can choose tn−1∈[s−τmax,s]⊆[σm+2τmax,σm+(n+1)τmax] satisfying
and
which implies that
and
Similarly,
Consequently,
However, we know that limm→+∞v(σm+τmax)=limt→+∞v(t)=P, which leads to a contradiction. Therefore L1=l1.
Finally, based on the above analysis, we obtain Li=li,i∈J and complete the proof of Theorem 3.1.
Remark 3.1. As mentioned before, there are some mistakes in the proof of Theorem 3.1 in [37]. The author briefly explained the proof of D+u(t)≥0, but under the premise of Gi≤Fi, it is impossible to get the conclusion of D+u(t)≥0 in the same way as proving D+v(t)≤0. And for system (1.5), proving D+v(t)≤0 is similar to D+u(t)≥0.
In fact, if γi(t)=1, τi=τ, for different values of n, many generalizations of Bernfeld-Haddock conjecture are special cases of (1.5). Thus, this paper is a more extensive generalization.
Remark 3.2. To some extent, for different dimensions and delays, many systems mentioned above are special cases of n-dimensional non-autonomous differential equations with time-varying delays, which means that this article not only points out the errors in previous results, but also generalizes it.
4.
Numerical simulations
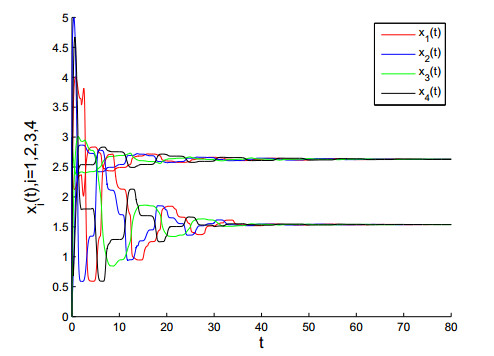
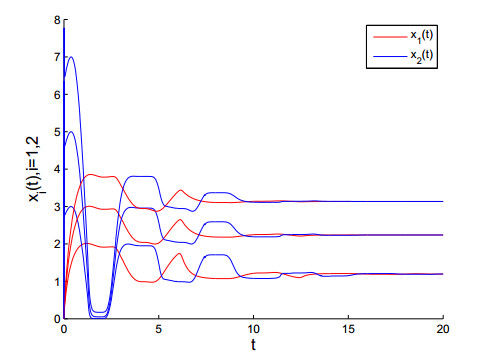
In this section, we give two examples of satisfying population dynamics system (1.5), for different n, we have
and
As Theorem 3.1 and Remark 3.1 mentioned, one can obtain that every solution of the Eqs 4.1 and 4.2 tends to a constant vector as t→∞. The curves in Figures 1 and 2 make it easy to see that our conclusion is correct.
5.
Conclusions
This paper investigates the asymptotic behavior for a class of n-dimensional population dynamics systems described by delay differential equations. With the help of technique of differential inequality, we show that each solution of the addressed systems tends to a constant vector as t→∞, which includes many generalizations of Bernfeld-Haddock conjecture. Our results extend some existing literatures. However, if we generalize the conjecture to a differential equation with impulses, can we have a similar conclusion? It is an interesting and meaningful work, we leave it as an open problem.
Acknowledgments
The authors would like to thank the anonymous referees and the editor for very helpful suggestions and comments which led to improvements of our original paper. This work was supported by the National Natural Science Foundation of China (Nos. 11971076, 51839002)
Conflict of interests
We confirm that we have no conflict of interest.









 DownLoad:
DownLoad: