Dynamical analysis of Kaldor business cycle model with variable depreciation rate of capital stock

1.   Introduction

In economics, business cycle model is a very important research direction. The endogenous economic cycle theory believes that the emergence of business cycle may be derived from the nonlinear properties of the economic system and the existence of time delay in the investment process.

British economist Kaldor proposed a nonlinear business cycle model ^[1] in 1940, which was the first model to investigate business cycle using nonlinear dynamics. In the literature ^[1], Kaldor assumed that investment and saving are nonlinear functions of the gross product and the capital stock. After analysis, the economic system can produce long-term cyclical fluctuations without any external shocks. According to Kaldor's model, Chang and Smith ^[2] proposed the following system in 1971:

where $Y$ is the gross product, $K$ is the capital stock, $\alpha$ is the adjustment coefficient in the goods market, $I(Y, K)$ is investment function, and $S(Y, K)$ is saving function.

In 1994, Grasman and Wentzel further improved (1.1) in the literature ^[3]. They assumed that the saving function is a linear function of the gross product and assumed that the current change in the stock of capital equals the investment minus the depreciation of the capital stock. Then they proposed the following business cycle model:

where $\delta$ is the depreciation rate of the capital stock and $\gamma$ is a constant satisfying $0 < \gamma < 1$. In ^[4], authors proposed a delayed business cycle model with general investment function.

In particular, Krawiec and Szydlowski ^[5] assume that the investment function is $I(Y, K) = I(Y)-\beta K$, and the system (1.2) becomes:

where $\beta > 0$. In 2011, X. P. Wu ^[6] investigated Codimension-2 bifurcations of the system (1.3).

In economics, economists believe that people get experience while they are working, which leads to improved work efficiency. Therefore, in terms of the capital stock, the depreciation rate of the capital stock is not a constant, but will decrease as people's experience increases.

In this paper we aim to analyze the dynamics of system (1.2) with the variable depreciation rate of the capital stock $\delta(K)$ as follows:

where $\alpha, \gamma$ are constants and $0 < \alpha, 0 < \gamma < 1$. Based on reality, we assume $I(Y, K)\geqslant0$ and according to the reference ^[5], the investment function satisfies $I(Y, K) = I(Y)-\beta K$, where $\beta$ is a positive constant. In this paper, we assume $I(Y, K)$ is continuously differentiable in $R^2$ with $\frac{\partial I}{\partial Y} > 0$ and $\frac{\partial I}{\partial K} < 0$.

In terms of the depreciation rate of the capital stock, S. Chatterjee ^[7] assumes that the rate of depreciation of capital is an increasing function of the rate of its utilization. In ^[8], they assume $\delta = \delta\left(\frac{M_{t}}{K_{t-1}}\right)$, where $M_{t}$ is maintenance expenditures and $\delta^{'}\left(\frac{M_{t}}{K_{t-1}}\right) < 0, \delta^{''}\left(\frac{M_{t}}{K_{t-1}}\right) > 0, \lim \limits_{M \to 0} \delta\left(\frac{M_{t}}{K_{t-1}}\right) = \bar{\delta}, \lim \limits_{M \to \infty} \delta\left(\frac{M_{t}}{K_{t-1}}\right) = 0$. Furthermore, M. Ishaq Nadiri and I. R. Prucha ^[9] specify a model of factor demand that allows they to estimate the depreciation rates of both physical and R & D capital. Based on their research results, we consider the depreciation rate of the capital stock from another perspective. When the capital stock is small and management ability is weak, the depreciation rate of the capital stock is the largest. However, with the accumulation of the capital stock and experience, the depreciation rate of the capital stock decrease gradually and approach a limit due to limited management ability. Notice that the decay of the depreciation rate also decreases. Thus we suppose that $\delta^{'} (K) < 0, \delta^{''} (K) > 0, 0 < \delta(0) = \delta_{0} < 1, 0 < \lim \limits_{K \to +\infty} \delta(K) = \delta_{1} < \delta_{0}$ for some constant $K\geqslant 0$ in (1.4). For the convenience of analysis, we assume that the depreciation rate of the capital stock satisfies the following relationship:

Then the system (1.4) can be transformed into the following form:

where $0 < \alpha, 0 < \beta, 0 < \gamma < 1, 0 < \delta_{1} < \delta_{0} < 1$. In general, the investment function $I(Y)$ in model (1.5) satisfies the Lipschitz continuity, and thus there exist unique solutions of (1.5).

The rest of this paper is organized as follows. In section 2, we will present the existence and stability of the unique positive equilibrium point of system (1.5). In addition, the existence of the periodic solution and Hopf bifurcation of system (1.5) are investigated. In Section 3, we will analyze the dynamics of a more specific system (3.2). Further, numerical simulations on system (3.2) are performed in Section 4.

2.   Dynamics analysis

In this section, we investigated the existence of the unique positive equilibrium point of the system (1.5) and analyzed the stability of the positive equilibrium point. We obtained a sufficient condition that the periodic solution does not exist in the first quadrant. In addition, we analyzed Hopf bifurcation of the system (1.5).

2.1.   Existence of the unique positive equilibrium point

For an economic system, we would like to know what is the equilibrium state of the system? We can analyze the existence of the unique positive equilibrium point of system (1.5) in the following theorem.

Theorem 1. System (1.5) has a unique positive equilibrium point $E(Y^*, K^*)$, where $Y^{*} = \frac{\delta_{1}{K^{*}}^{2}+\delta_{0}K^{*}}{\gamma(1+K^{*})}$, if the conditions:

(1) $I(0) > 0$ for all $Y\geqslant 0;$

(2) $\frac{\delta_{1}\gamma K^{2}+2\gamma\delta_{1}K+\delta_{0}\gamma}{\gamma^{2}(1+K)^{2}}I^{'}(Y)-\frac{\delta_{1}\gamma K^{2}+2\gamma\delta_{1}K+\delta_{0}\gamma}{\gamma(1+K)^{2}}-\beta < 0$ for all $Y\geqslant 0, K\geqslant 0;$

(3) There exists a constant $L > 0$ such that $|I(Y)| \leq L$ for all $Y \geqslant 0;$

hold.

Proof. Let the right end of the Eq. (1.5) be 0:

Then we can obtain the relationship between $K$ and $Y$:

Substituting (2.2) into the first equation of (2.1), (2.1) is converted to

Let $U(K) = I(\frac{\delta_{1}K^{2}+\delta_{0}K}{\gamma+\gamma K})-\beta K-\frac{\delta_{1}K^{2}+\delta_{0}K}{1+K}$, then we can get $U^{'}(K) = \frac{\delta_{1}\gamma K^{2}+2\gamma\delta_{1}K+\delta_{0}\gamma}{\gamma^{2}(1+K)^{2}}I^{'}(Y)-\frac{\delta_{1}\gamma K^{2}+2\gamma\delta_{1}K+\delta_{0}\gamma}{\gamma(1+K)^{2}}-\beta$. According to the conditions (1) and (2), we can know $U(0) > 0$ and $U^{'}(K) < 0$ for all $K\geqslant 0$. Based on the condition (3), we can obtain $\lim\limits_{K\to +\infty}U(K) = -\infty$. Then we can know system (1.5) has a unique positive equilibrium point $E(Y^*, K^*)$, where $Y^{*} = \frac{\delta_{1}{K^{*}}^{2}+\delta_{0}K^{*}}{\gamma(1+K^{*})}$.

2.2.   Existence of the periodic solution

For business cycle model, the periodic solution represents the economic cycle phenomenon, so the study of the periodic solution is very important. We can analyze existence of the periodic solution of system (1.5) in the following theorem.

Theorem 2. If $\alpha[I^{'}(Y)-\gamma]-\beta-\delta_{1}+\frac{(\delta_{1}-\delta_{0})K}{(1+K)^{2}} < 0$ or $\alpha[I^{'}(Y)-\gamma]-\beta-\delta_{1}+\frac{(\delta_{1}-\delta_{0})K}{(1+K)^{2}} > 0$ for all $Y\geqslant 0, K\geqslant 0$, the system (1.5) has no periodic solution in the first quadrant.

Proof. Let $P(Y, K) = \alpha [I(Y)- \beta K - \gamma Y], Q(Y, K) = I(Y)-\beta K- (\delta_1+\frac{\delta_{0}-\delta_{1}}{1+K}) K$, we can get $\frac{\partial P}{Y}+\frac{\partial Q}{K} = \alpha[I^{'}(Y)-\gamma]-\beta-\delta_{1}+\frac{\delta_{1}-\delta_{0}}{(1+K)^{2}}$. If $\alpha[I^{'}(Y)-\gamma]-\beta-\delta_{1}+\frac{\delta_{1}-\delta_{0}}{(1+K)^{2}} < 0$ or $\alpha[I^{'}(Y)-\gamma]-\beta-\delta_{1}+\frac{\delta_{1}-\delta_{0}}{(1+K)^{2}} > 0$ always hold for all $Y\geqslant 0, K\geqslant 0$, according to the Bendixson criterion ^[10], the system (1.5) has no periodic solution in the first quadrant.

2.3.   Stability analysis

In this section, we investigated stability of the positive equilibrium point.

For the convenience of research, we make a transformation: $u = Y-Y^*, v = K-K^*$, then the system (1.5) is transformed into the following form:

The Jacobian matrix of system (2.4) at equilibriun $O(0, 0)$ is given by

At the equilibrium point $O(0, 0)$, the linearized system of the system (2.4) is

Then we can know the characteristic equation of ${\bf J}(0, 0)$ is

$\lambda ^{2}+\lambda[\alpha\gamma-\alpha I^{'}(Y^{*})+ \beta +\delta_{1}+\frac{\delta_{0}-\delta_{1}}{(1+K^{*})^2}]+\alpha\beta\gamma+\alpha\gamma\delta_{1}+\alpha\gamma\frac{\delta_{0}-\delta_{1}}{(1+K^{*})^2}-\alpha\delta_{1}I^{'}(Y^{*})-\alpha I^{'}(Y^{*})\frac{\delta_{0}-\delta_{1}}{(1+K^{*})^2} = 0.$

Therefore the eigenvalues of ${\bf J}(0, 0)$ are

$\lambda_{1} = \frac{1}{2}\langle-[\alpha\gamma-\alpha I^{'}(Y^{*})+\beta+ \delta_{1}+\frac{\delta_{0}-\delta_{1}}{(1+K^{*})^2}]+\{[\alpha\gamma-\alpha I^{'}(Y^*)+\beta+\delta_{1}+\frac{\delta_{0}-\delta_{1}}{(1+K^{*})^2}]^2-4\alpha[\beta\gamma+\gamma\delta_{1}+\\\gamma\frac{\delta_{0}-\delta_{1}}{(1+K^{*})^2}-\delta_{1}I^{'}(Y^*)- I^{'}(Y^*)\frac{\delta_{0}-\delta_{1}}{(1+K^{*})^2}]\}^{\frac{1}{2}}\rangle ,$

$\lambda_{2} = \frac{1}{2}\langle-[\alpha\gamma-\alpha I^{'}(Y^{*})+\beta+ \delta_{1}+\frac{\delta_{0}-\delta_{1}}{(1+K^{*})^2}]-\{[\alpha\gamma-\alpha I^{'}(Y^*)+\beta+\delta_{1}+\frac{\delta_{0}-\delta_{1}}{(1+K^{*})^2}]^2-4\alpha[\beta\gamma+\gamma\delta_{1}+\\\gamma\frac{\delta_{0}-\delta_{1}}{(1+K^{*})^2}-\delta_{1}I^{'}(Y^*)- I^{'}(Y^*)\frac{\delta_{0}-\delta_{1}}{(1+K^{*})^2}]\}^{\frac{1}{2}}\rangle .$

Let $\phi(u, v) = \alpha[I(u+Y^{*})-\beta (v+K^*)-\gamma(u+Y^*)], \psi(u, v) = I(u+Y^{*})-\beta(v+K^*)-(\delta_{1}+\frac{\delta_{0}-\delta_{1}}{1+v+K^*})(v+K^*)$, and based on the above calculation, we can get the local stability of the equilibrium point of the system (1.5) and system (2.4).

Theorem 3. If $4\alpha[\beta\gamma+\gamma\delta_{1}+\gamma\frac{\delta_{0}-\delta_{1}}{(1+K^{*})^2}-\delta_{1}I^{'}(Y^*)- I^{'}(Y^*)\frac{\delta_{0}-\delta_{1}}{(1+K^{*})^2}] > 0$, $\phi(u, v)$, $\psi(u, v)$ are analytic functions, then the following (1) and (2) are hold:

(1) when $\alpha\gamma-\alpha I^{'}(Y^{*})+\beta+ \delta_{1}+\frac{\delta_{0}-\delta_{1}}{(1+K^{*})^2} < 0$, the equilibrium point $O(0, 0)$ of (2.4) and the equilibrium point $E(Y^*, K^*)$ of (1.5) are unstable.

(2) when $\alpha\gamma-\alpha I^{'}(Y^{*})+\beta+ \delta_{1}+\frac{\delta_{0}-\delta_{1}}{(1+K^{*})^2} > 0$, the equilibrium point $O(0, 0)$ of (2.4) and the equilibrium point $E(Y^*, K^*)$ of (1.5) are locally asymptotically stable.

Proof. If $\alpha\gamma-\alpha I^{'}(Y^{*})+\beta+ \delta_{1}+\frac{\delta_{0}-\delta_{1}}{(1+K^{*})^2} < 0$, we can know that the real part of the eigenvalues $\lambda_{1, 2}$ are less than 0. We can get the equilibrium point $O(0, 0)$ of (2.4) and the equilibrium point $E(Y^*, K^*)$ of (1.5) are unstable. For (2), the proof are similar to (1). Now, the proof of Theorem (2.3) is finished.

2.4.   Hopf bifurcation

In this section, we use $\alpha$ as a parameter of bifurcation and investigate Hopf bifurcation of the system (2.4).

For the system (2.4), we can know: $\phi(0, 0, \alpha) = 0$, $\psi(0, 0, \alpha) = 0$. At the equilibriun $O(0, 0)$, the Jacobian matrix of the system (2.4) is

When $[\alpha\gamma-\alpha I^{'}(Y^*)+\beta+\delta_{1}+\frac{\delta_{0}-\delta_{1}}{(1+K^{*})^2}]^2 < 4\alpha[\beta\gamma+\gamma\delta_{1}+\gamma\frac{\delta_{0}-\delta_{1}}{(1+K^{*})^2}-\delta_{1}I^{'}(Y^*)- I^{'}(Y^*)\frac{\delta_{0}-\delta_{1}}{(1+K^{*})^2}]$, the eigenvalues of (2.7) is a pair of conjugate complex numbers:

where:

$m(\alpha) = -\frac{1}{2}[\alpha\gamma-\alpha I^{'}(Y^{*})+\beta+ \delta_{1}+\frac{\delta_{0}-\delta_{1}}{(1+K^{*})^2}]$,

$n(\alpha) = \frac{1}{2}\{4\alpha[\beta\gamma+\gamma\delta_{1}+\gamma\frac{\delta_{0}-\delta_{1}}{(1+K^{*})^2}-\delta_{1}I^{'}(Y^*)- I^{'}(Y^*)\frac{\delta_{0}-\delta_{1}}{(1+K^{*})^2}]-[\alpha\gamma-\alpha I^{'}(Y^*)+\beta+\delta_{1}+\frac{\delta_{0}-\delta_{1}}{(1+K^{*})^2}]^2\}^\frac{1}{2}$.

When $\alpha = \alpha^{*} = \frac{-(\beta+\delta_{1})(1+K^{*})^{2}+\delta_{1}-\delta_{0}}{[\gamma-I^{'}(Y^{*})](1+K^{*})^{2}} = \frac{-\beta(1+K^{*})^{2}+\delta_{1}[1-(1+K^{*})^{2}]-\delta_{0}}{[\gamma-I^{'}(Y^{*})](1+K^{*})^{2}}$, we can get:

$m(\alpha^{*}) = 0$,

$n(\alpha^{*}) = \sqrt{\frac{-(\beta+\delta_{1})(1+K^{*})^{2}+\delta_{1}-\delta_{0}}{[\gamma-I^{'}(Y^{*})](1+K^{*})^{2}}[\beta\gamma+\gamma\delta_{1}+\gamma\frac{\delta_{0}-\delta_{1}}{(1+K^{*})^2}-\delta_{1}I^{'}(Y^*)- I^{'}(Y^*)\frac{\delta_{0}-\delta_{1}}{(1+K^{*})^2}]}$,

$\lambda_{1, 2} = \pm in(\alpha^{*})$.

Lemma 1 (J. Zhang and B. Feng ^[11]). Consider the following system:

where $P$ and $Q$ are analytic functions. When parameter $\lambda = 0$, $(0, 0)$ is the center-type stable(unstable) focus. When parameter $\lambda > 0$, $(0, 0)$ is the unstable(stable) focus. The system (2.8) has at least one stable(unstable) limit cycle near point $(0, 0)$ for a sufficiently small $\lambda > 0$.

Theorem 4. If $m(\alpha) > 0$ for all $\alpha > \alpha^{*}$ and $u\alpha^{*}[I(u+Y^{*})-\beta (v+K^*)-\gamma(u+Y^*)]+v[I(u+Y^{*})-\beta(v+K^*)-(\delta_{1}+\frac{\delta_{0}-\delta_{1}}{1+v+K^*})(v+K^*)] < 0$ for all $(u, v)\neq(0, 0)$, then for a sufficiently small $\alpha > \alpha^{*}$, the system (1.5) has at least one stable limit cycle near point $E(Y^*, K^*)$.

Proof. For the system (2.4), we consider the Liapunov function $V(u, v) = u^{2}+v^{2}$. If $2u\alpha^{*}[I(u+Y^{*})-\beta (v+K^*)-\gamma(u+Y^*)]+2v[I(u+Y^{*})-\beta(v+K^*)-(\delta_{1}+\frac{\delta_{0}-\delta_{1}}{1+v+K^*})(v+K^*)] < 0$ for all $(u, v)\neq(0, 0)$, we can easily get $\dot{V}(u, v) < 0$ for all $(u, v)\neq(0, 0)$. The equilibriun $O(0, 0)$ is a stable focus, when $\alpha = \alpha^{*}$. On the other hand, when $\alpha > \alpha^{*}$, we can get $m(\alpha) > 0$. The equilibriun $O(0, 0)$ is an unstable focus. According to the Lemma (1), we can know the system (2.4) has at least one stable limit cycle near point $O(0, 0)$ for a sufficiently small $\alpha > \alpha^{*}$. Correspondingly, the system (1.5) has at least one stable limit cycle near point $E(Y^*, K^*)$ for a sufficiently small $\alpha > \alpha^{*}$.

3.   Application

Particularly, we consider the following Kaldor-type investment function:

We introduce (3.1) into the system (1.5), the system (1.5) can be transformed into the following form:

3.1.   Existence of the unique positive equilibrium point

For the system (3.2), we can combine Theorem (2.1) to study the existence and uniqueness of the positive equilibrium point of the system (3.2).

Theorem 5. If $\frac{e^{Y}}{(1+e^{Y})^{2}}-\frac{\beta+\delta_{1}}{\delta_{1}}\gamma < 0$ for all $Y\geqslant 0$, the system (3.2) has a unique positive equilibrium point $E^{\circ}(Y^{\circ}, K^{\circ})$, where $Y^{\circ} = \frac{\delta_{1}{K^{\circ}}^{2}+\delta_{0}K^{\circ}}{\gamma(1+K^{\circ})}$.

Proof. For system (3.2), $I(Y) = \frac{e^{Y}}{1+e^{Y}}$, we can know $I(0) = \frac{1}{2} > 0$. Obviously, $I^{'}(Y) = \frac{e^{Y}}{(1+e^{Y})^{2}} > 0, \lim\limits_{Y\to +\infty}I(Y) = 1$, so we can get $|I(Y)| < 1$ for $Y\geqslant 0.$ If $\frac{(\delta_{1}\gamma K^{2}+2\gamma\delta_{1}K+\delta_{0}\gamma)e^{Y}}{\gamma^{2}(1+K)^{2}(1+e^{Y})^{2}}-\frac{\delta_{1}\gamma K^{2}+2\gamma\delta_{1}K+\delta_{0}\gamma}{\gamma(1+K)^{2}}-\beta < 0$, for all $Y\geqslant 0, K\geqslant 0$, then the system (3.2) satisfies the Theorem (2.1). Therefore the system (3.2) has a unique positive equilibrium point $E^{\circ}(Y^{\circ}, K^{\circ})$, where $Y^{\circ} = \frac{\delta_{1}{K^{\circ}}^{2}+\delta_{0}K^{\circ}}{\gamma(1+K^{\circ})}$.

3.2.   Existence of the periodic solution

For the system (3.2), we can get the sufficient condition that the system (3.2) has no periodic solution in the first quadrant according to the Theorem (2.2).

Theorem 6. If $\alpha[\frac{e^{Y}}{(1+e^{Y})^{2}}-\gamma]-\beta-\delta_{1}+\frac{(\delta_{1}-\delta_{0})K}{(1+K)^{2}} < 0$ or $\alpha[\frac{e^{Y}}{(1+e^{Y})^{2}}-\gamma]-\beta-\delta_{1}+\frac{(\delta_{1}-\delta_{0})K}{(1+K)^{2}} > 0$ hold for all $Y\geqslant 0, K\geqslant 0$, then the system (3.2) has no periodic solution in the first quadrant.

3.3.   Stability analysis

We can make a transformation: $y = Y-Y^{\circ}$, $k = K-K^{\circ}$, then the system (3.2) is transformed into the following form:

The Jacobian matrix of the system (3.3) at equilibriun $O(0, 0)$ is given by

At the equilibrium point $O(0, 0)$, the linearized system of the system (3.3) is

The characteristic equation of ${\bf J}^{\circ}(0, 0)$ is

$\lambda ^{2}+\lambda[\alpha\gamma-\alpha \frac{e^{Y^{\circ}}}{(1+e^{Y^{\circ}})^{2}}+ \beta +\delta_{1}+\frac{\delta_{0}-\delta_{1}}{(1+K^{\circ})^2}]+\alpha\beta\gamma+\alpha\gamma\delta_{1}+\alpha\gamma\frac{\delta_{0}-\delta_{1}}{(1+K^{\circ})^2}-\alpha\delta_{1}\frac{e^{Y^{\circ}}}{(1+e^{Y^{\circ}})^{2}}-\alpha \frac{(\delta_{0}-\delta_{1})e^{Y^{\circ}}}{(1+e^{Y^{\circ}})^{2}(1+K^{\circ})^2} = 0$.

Therefore the eigenvalues of ${\bf J}^{\circ}(0, 0)$ are

$\lambda_{1} = \frac{1}{2}\langle-[\alpha\gamma-\alpha \frac{e^{Y^{\circ}}}{(1+e^{Y^{\circ}})^{2}}+\beta+ \delta_{1}+\frac{\delta_{0}-\delta_{1}}{(1+K^{\circ})^2}]+\{[\alpha\gamma-\alpha \frac{e^{Y^{\circ}}}{(1+e^{Y^{\circ}})^{2}}+\beta+\delta_{1}+\frac{\delta_{0}-\delta_{1}}{(1+K^{\circ})^2}]^2-4\alpha[\beta\gamma+\gamma\delta_{1}+\\\gamma\frac{\delta_{0}-\delta_{1}}{(1+K^{\circ})^2}-\delta_{1}\frac{e^{Y^{\circ}}}{(1+e^{Y^{\circ}})^{2}}- \frac{(\delta_{0}-\delta_{1})e^{Y^{\circ}}}{(1+e^{Y^{\circ}})^{2}(1+K^{\circ})^2}]\}^{\frac{1}{2}}\rangle ,$

$\lambda_{2} = \frac{1}{2}\langle-[\alpha\gamma-\alpha \frac{e^{Y^{\circ}}}{(1+e^{Y^{\circ}})^{2}}+\beta+ \delta_{1}+\frac{\delta_{0}-\delta_{1}}{(1+K^{\circ})^2}]-\{[\alpha\gamma-\alpha \frac{e^{Y^{\circ}}}{(1+e^{Y^{\circ}})^{2}}+\beta+\delta_{1}+\frac{\delta_{0}-\delta_{1}}{(1+K^{\circ})^2}]^2-4\alpha[\beta\gamma+\gamma\delta_{1}+\\\gamma\frac{\delta_{0}-\delta_{1}}{(1+K^{\circ})^2}-\delta_{1}\frac{e^{Y^{\circ}}}{(1+e^{Y^{\circ}})^{2}}- \frac{(\delta_{0}-\delta_{1})e^{Y^{\circ}}}{(1+e^{Y^{\circ}})^{2}(1+K^{\circ})^2}]\}^{\frac{1}{2}}\rangle .$

Let $\varphi(y, k) = \alpha[\frac{e^{y+Y^{\circ}}}{1+e^{y+Y^{\circ}}}-\beta (k+K^{\circ})-\gamma(y+Y^{\circ})], \varPsi(y, k) = \frac{e^{y+Y^{\circ}}}{1+e^{y+Y^{\circ}}}-\beta(k+K^{\circ})-(\delta_{1}+\frac{\delta_{0}-\delta_{1}}{1+k+K^{\circ}})(k+K^{\circ})$. Since $I^{'}(Y^{\circ}) = \frac{e^{Y^{\circ}}}{(1+e^{Y^{\circ}})^{2}}$, we can substitute $I^{'}(Y^{\circ})$ into the theorem (2.3) to get the local stability of the equilibrium point of the system (3.2) and system (3.3) in the following theorem.

Theorem 7. If $4\alpha[\beta\gamma+\gamma\delta_{1}+\gamma\frac{\delta_{0}-\delta_{1}}{(1+K^{\circ})^2}-\delta_{1}\frac{e^{Y^{\circ}}}{(1+e^{Y^{\circ}})^{2}}- \frac{(\delta_{0}-\delta_{1})e^{Y^{\circ}}}{(1+e^{Y^{\circ}})^{2}(1+K^{\circ})^2}] > 0$, $\varphi(y, k), \varPsi(y, k)$ are analytic functions, then the following (1) and (2) are hold:

(1) when $\alpha\gamma-\alpha \frac{e^{Y^{\circ}}}{(1+e^{Y^{\circ}})^{2}}+\beta+ \delta_{1}+\frac{\delta_{0}-\delta_{1}}{(1+K^{\circ})^2} < 0$, the equilibrium point $O(0, 0)$ of the system (3.3) and the equilibrium point $E^{\circ}(Y^{\circ}, K^{\circ})$ of the system (3.2) are unstable.

(2) when $\alpha\gamma-\alpha \frac{e^{Y^{\circ}}}{(1+e^{Y^{\circ}})^{2}}+\beta+ \delta_{1}+\frac{\delta_{0}-\delta_{1}}{(1+K^{\circ})^2} > 0$, the equilibrium point $O(0, 0)$ of the system (3.3) and the equilibrium point $E^{\circ}(Y^{\circ}, K^{\circ})$ of the system (3.2) are locally asymptotically stable.

3.4.   Hopf bifurcation

For the system (3.3), we can get: $\varphi(0, 0, \alpha) = 0, \varPsi(0, 0, \alpha) = 0$.

At the equilibrium point $O(0, 0)$, we can get the Jacobian matrix of system (3.3):

When $[\alpha\gamma-\alpha \frac{e^{Y^{\circ}}}{(1+e^{Y^{\circ}})^{2}}+\beta+\delta_{1}+\frac{\delta_{0}-\delta_{1}}{(1+K^{\circ})^2}]^2 < 4\alpha[\beta\gamma+\gamma\delta_{1}+\gamma\frac{\delta_{0}-\delta_{1}}{(1+K^{\circ})^2}-\delta_{1}\frac{e^{Y^{\circ}}}{(1+e^{Y^{\circ}})^{2}}- \frac{(\delta_{0}-\delta_{1})e^{Y^{\circ}}}{(1+e^{Y^{\circ}})^{2}(1+K^{\circ})^2}]$, the eigenvalues of (3.6) is a pair of conjugate complex numbers:

where:

$w(\alpha) = -\frac{1}{2}[\alpha\gamma-\alpha \frac{e^{Y^{\circ}}}{(1+e^{Y^{\circ}})^{2}}+\beta+ \delta_{1}+\frac{\delta_{0}-\delta_{1}}{(1+K^{\circ})^2}]$,

$d(\alpha) = \frac{1}{2}\{4\alpha[\beta\gamma+\gamma\delta_{1}+\gamma\frac{\delta_{0}-\delta_{1}}{(1+K^{\circ})^2}-\delta_{1}\frac{e^{Y^{\circ}}}{(1+e^{Y^{\circ}})^{2}}- \frac{(\delta_{0}-\delta_{1})e^{Y^{\circ}}}{(1+e^{Y^{\circ}})^{2}(1+K^{\circ})^2}]-[\alpha\gamma-\alpha \frac{e^{Y^{\circ}}}{(1+e^{Y^{\circ}})^{2}}+\beta+\delta_{1}+\frac{\delta_{0}-\delta_{1}}{(1+K^{\circ})^2}]^2\}^\frac{1}{2}$.

When $\alpha = \alpha^{\circ} = \frac{(-\beta-\delta_{1})(1+K^{\circ})^{2}(1+e^{Y^{\circ}})^{2}+(\delta_{1}-\delta_{0})(1+e^{Y^{\circ}})^{2}}{\gamma(1+K^{\circ})^{2}(1+e^{Y^{\circ}})^{2}-e^{Y^{\circ}}(1+K^{\circ})^{2}}$, we can know:

$w(\alpha^{\circ}) = 0$,

$d(\alpha^{\circ}) = \{\frac{(-\beta-\delta_{1})(1+K^{\circ})^{2}(1+e^{Y^{\circ}})^{2}+(\delta_{1}-\delta_{0})(1+e^{Y^{\circ}})^{2}}{\gamma(1+K^{\circ})^{2}(1+e^{Y^{\circ}})^{2}-e^{Y^{\circ}}(1+K^{\circ})^{2}}[\beta\gamma+\gamma\delta_{1}+\gamma\frac{\delta_{0}-\delta_{1}}{(1+K^{\circ})^2}-\delta_{1}\frac{e^{Y^{\circ}}}{(1+e^{Y^{\circ}})^{2}}- \frac{(\delta_{0}-\delta_{1})e^{Y^{\circ}}}{(1+e^{Y^{\circ}})^{2}(1+K^{\circ})^2}]\}^\frac{1}{2}$,

$\lambda_{1, 2} = \pm id(\alpha^{\circ})$.

Theorem 8. If $w(\alpha) > 0$ for all $\alpha > \alpha^{\circ}$ and $y\alpha^{\circ}[\frac{e^{y+Y^{\circ}}}{1+e^{y+Y^{\circ}}}-\beta (k+K^{\circ})-\gamma(y+Y^{\circ})]+k[\frac{e^{y+Y^{\circ}}}{1+e^{y+Y^{\circ}}}-\beta(k+K^{\circ})-(\delta_{1}+\frac{\delta_{0}-\delta_{1}}{1+k+K^{\circ}})(k+K^{\circ})] < 0$ for all $(y, k)\neq(0, 0)$, then for a sufficiently small $\alpha > \alpha^{\circ}$, the system (3.2) has at least one stable limit cycle near point $E^{\circ}(Y^{\circ}, K^{\circ})$.

Proof. When $\alpha = \alpha^{\circ}$, we consider the Liapunov function $V(y, k) = y^{2}+k^{2}$. If $y\alpha^{\circ}[\frac{e^{y+Y^{\circ}}}{1+e^{y+Y^{\circ}}}-\beta (k+K^{\circ})-\gamma(y+Y^{\circ})]+k[\frac{e^{y+Y^{\circ}}}{1+e^{y+Y^{\circ}}}-\beta(k+K^{\circ})-(\delta_{1}+\frac{\delta_{0}-\delta_{1}}{1+k+K^{\circ}})(k+K^{\circ})] < 0$ for all $(y, k)\neq(0, 0)$, we can easily get $\dot{V}(y, k) < 0$ for all $(y, k)\neq(0, 0)$. The equilibrium $O(0, 0)$ is a stable focus. When $\alpha > \alpha^{\circ}$, we can get $w(\alpha) > 0$. The equilibrium $O(0, 0)$ is an unstable focus. According to the Lemma (1), we can know the system (3.3) has at least one stable limit cycle near point $O(0, 0)$ for a sufficiently small $\alpha > \alpha^{\circ}$. Correspondingly, the system (3.2) has at least one stable limit cycle near point $E^{\circ}(Y^{\circ}, K^{\circ})$ for a sufficiently small $\alpha > \alpha^{\circ}$.

3.5.   Numerical simulations

Let $\gamma = 0.3, \beta = 0.5, \delta_{1} = 0.2, \delta_{0} = 0.8$, then the system (3.2) can be converted to:

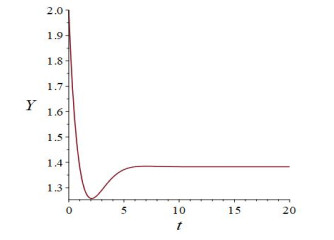
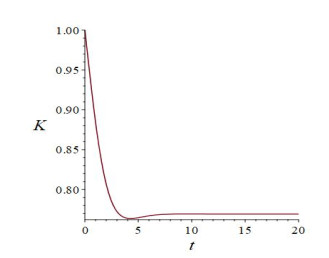
Let $f(Y) = \frac{e^{Y}}{(1+e^{Y})^{2}}-\frac{21}{20}$. When $Y\geqslant0$, we can know $f(Y) < 0$. Based on Theorem (2.4), the system (3.7) has a unique positive equilibrium point $E^{\circ}(1.382467594, 0.7692934721)$. When $\gamma = 0.3, \beta = 0.5, \delta_{1} = 0.2, \delta_{0} = 0.8$, we can get $\alpha[\frac{e^{Y}}{(1+e^{Y})^{2}}-\gamma]-\beta-\delta_{1}+\frac{(\delta_{1}-\delta_{0})K}{(1+K)^{2}} < 0$ for all $\alpha > 0, Y\geqslant 0, K\geqslant 0$. According to the Theorem (3.1) to get the system (3.7) has no periodic solution in the first quadrant. We take $\alpha = 5$ and numerically simulate the system (3.7). When $\alpha = 5$, we can get $4\alpha[\beta\gamma+\gamma\delta_{1}+\gamma\frac{\delta_{0}-\delta_{1}}{(1+ K^{\circ})^2}-\delta_{1}\frac{e^{Y^{\circ}}}{(1+e^{Y^{\circ}})^{2}} - \frac{(\delta_{0}-\delta_{1})e^{Y^{\circ}}}{(1+e^{Y^{\circ}})^{2}(1+ K^{\circ})^2}] = 4.093794628 > 0$ and $\alpha\gamma-\alpha \frac{e^{Y^{\circ}}}{(1+e^{Y^{\circ}})^{2}}+\beta+ \delta_{1}+\frac{\delta_{0}-\delta_{1}}{(1+K^{\circ})^2} = 1.589831756 > 0$. According to the Theorem (3.2), we know $E^{\circ}(1.382467594, 0.7692934721)$ is locally asymptotically stable. The above dynamics analysis can be verified in Figure 1, Figure 2 and Figure 3. In this special case, we can know that Kaldor business cycle model with variable depreciation rate of capital stock does not have a limit cycle and the economic system is stable in the long run.

4.   Conclusions

Due to the complexity of economic phenomena, the depreciation rate of the capital stock is variable. This paper investigated the dynamic behaviors of Kaldor business cycle model with variable depreciation rate of capital stock. First, we investigated the general system's existence of the unique positive equilibrium point and the periodic solution. Second, we analyzed the stability of the equilibrium point and investigated Hopf bifurcation. In addition, we introduced the Kaldor-type investment function to the general system. We analyzed the dynamic behaviors of the specific system and performed numerical simulations. From the results of the study, we can see that the economic system is complex and sensitive. Under different actual conditions, economic systems can evolve into different states. Sometimes the economic system will tend to a stable state, sometimes it will be unstable, and sometimes it will even be in a cyclical state.

Acknowledgments

We thank the unknown referees for their helpful comments that led us to improve this paper. This research was partially supported by NSF of China (11601251, 11771257).

Conflict of interest

The authors declare no conflict of interest.