AIMS Mathematics, 2020, 5(4): 3138-3155. doi: 10.3934/math.2020202

Research article

Export file:

Format

  • RIS(for EndNote,Reference Manager,ProCite)
  • BibTex
  • Text

Content

  • Citation Only
  • Citation and Abstract

On the construction, properties and Hausdorff dimension of random Cantor one pth set

Sudesh Kumari, Renu Chugh, Jinde Cao, Chuangxia Huang

1 Department of Mathematics, Government College for Girls Sector 14, Gurugram 122001, India
2 Department of Mathematics, Maharshi Dayanand University, Rohtak 124001, India
3 Research Center for Complex Systems and Network Sciences, School of Mathematics, Southeast University, Nanjing 210096, China
4 School of Mathematics and Statistics, Changsha University of Science and Technology, Hunan Provincial Key Laboratory of Mathematical Modeling and Analysis in Engineering, Changsha 410114, China

Received: , Accepted: , Published:

Abstract    Full Text(HTML)    Figure/Table    Related pages

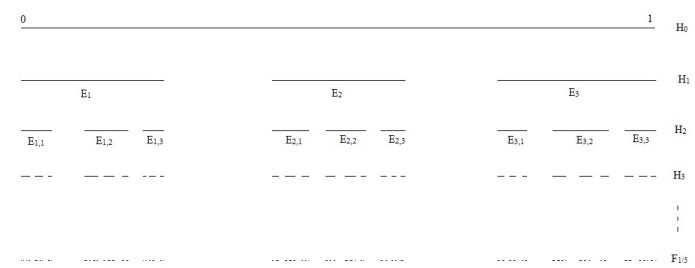
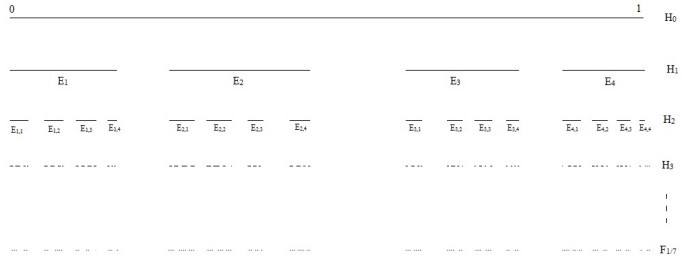
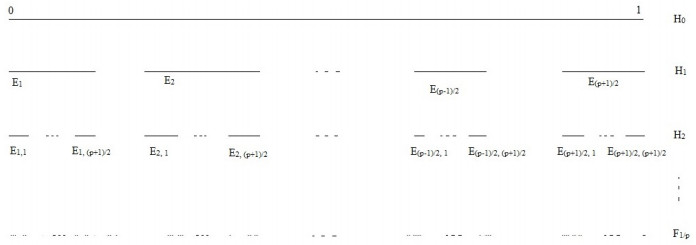
In 1883, German Mathematician George Cantor introduced Cantor ternary set which is a self-similar fractal. K. J. Falconer (1990) defined random Cantor set with statistical self-similarity. The purpose of this paper is to introduce generalized random Cantor sets (one 5th, one 7th and in general one pth). Some properties and results of random Cantor one pth set have also been obtained. We compute Hausdorff dimension of random Cantor one pth sets and show that Hausdorff dimension of these random Cantor sets is less than that of Hausdorff dimension of Cantor one pth sets, calculated by Ashish et al. (2013).
  Figure/Table
  Supplementary
  Article Metrics
Download full text in PDF

Export Citation

Article outline

Copyright © AIMS Press All Rights Reserved