1. Introduction
Composite laminates and sandwich plates constitute a commonly used structural component with many applications in several areas of engineering. Whether considering one or the other type of plate, we have a multilayer configuration, where it is possible to tailor their constitution in order to achieve a better performance, fitted to specific operating requirements and to ensure a satisfactory service life. A typical sandwich structure consists of one or more layers of high-strength and high-stiffness face sheets, or skins, bonded to a core which may have significantly different elastic properties. In this layered configuration we may also consider the stacking of differently oriented fiber reinforced materials, as well as a combination of different composite materials. In any case it may be important to achieve a more realistic characterization of these structures response, namely concerning the description of the plate deformation kinematics, and therefore on the corresponding states of strain and stress distributions. The study of layered composite structures continues to attract the attention of many researchers, although the extent of the work developed so far. This may be due to continuous advances in the constitution of new materials and on their physical characterization, to the advances in technological processes, and probably also because the availability of more powerful computational resources, enables the use of more expensive algorithmic procedures and the manipulation of greater data volumes.
In the context of equivalent single-layer approaches focused on the study of sandwich or laminated composite structures, we may find many published works. Within this broad branch, we may find works based on different basis theories ranging from the classical one to the higher order shear deformation theories. Just to name a few of them, we may refer the work carried out by Reissner [1] who studied the effect of the transverse shear deformations in plates consisting of anisotropic laminations symmetrical about their midplane. Closely related to this work, Whitney [2] has developed a bending theory for simply supported laminated plates, which included transverse shear deformations. He obtained closed form solutions for bending deflections, flexural vibration frequencies, and buckling loads. Later, Lo et al. [3] presented a higher order theory devoted to the study of the of laminated plates deformation, comparing the results obtained with elasticity solutions. Pandya and Kant [4] developed a higher order shear deformation model for the analysis of the bending analysis of symmetric sandwich plates. Their model assumed a non-linear variation of the in-plane displacements and a constant transverse one. Also in the context of the equivalent single-layer (ESL) approaches, Bernardo et al. [4,5] presented a study on the linear static and free vibrations behavior of functionally graded plates. To this purpose they have used plate models based on the first order shear deformation theory and implemented via traditional Lagrangean elements, kriging-based elements and via a meshless approach with radial basis functions. Loja et al. [6] analysed the transient dynamic behavior of sandwich structures, having a metallic core and functionally graded outer layers. The properties of the particulate composite metal-ceramic outer layers, were estimated using Mori-Tanaka scheme and the dynamic analyses considered first order and higher order shear deformation theories implemented though kriging finite element method. The transient dynamic response of these structures is carried out through Bossak-Newmark method. A framework for the formulation and the dynamic analysis computations of moderately thick laminated doubly-curved shells and panels was proposed by Viola et al. [7]. To that purpose a higher-order shear deformation theory was considered and the differential geometry was used to define the arbitrary shape of the middle surface of shells and panels with different curvatures. Following this single-layer approach, but in the context of non-linear theories, we can refer the work presented by Reddy [8] which proposed a higher-order shear deformation theory of plates accounting for the von Karman strains. Ferreira and Barbosa [9] presented a finite element model for the geometric non-linear analysis of composite shell structures. The non-linear incremental equilibrium equations were established using a total Lagrangian displacement formulation and the solution was obtained via the incremental/iterative Newton-Raphson method as well as a spherical formulation of the arc-length methods. Recently, Dehkordi et al. [10] proceeded to a nonlinear dynamic analysis of sandwich plate with flexible core and laminated composite face sheets embedded with shape memory alloy wires. This study was based on the mixed layerwise and equivalent single layer (LW/ESL) models in the framework of Carrera’s Unified Formulation. It is also relevant to mention the work developed by Thai and his colleagues [11,12,13,14,15] in the context of the isogeometric analysis of laminated structures. This research field is expanding due to its versatility and integrative character; which goes from the computer aided design to the computer aided engineering wherein one may consider included the analysis of structures.
The importance and adequacy of layerwise approaches to multilayer structural elements, as more efficient alternative methodologies when compared to the equivalent single layer ones, has been an object of study and discussion, and some comprehensive studies and reviews were published upon this subject, namely the ones due to Carrera [16,17]. In the first mentioned work of Carrera, he carried out an historical review on the zig-zag theories developed for the analysis of multilayered structures, wherein they describe a piecewise continuous displacement field in the plate thickness direction and fulfill interlaminar continuity of transverse stresses at each layer interface. In the second one referred in the present study, he made a review on the derivation of governing equations and finite element matrices for some of the most relevant plate/shell theories. He also addressed extensive numerical evaluations of available results, along with assessment and benchmarking. In a comprehensive study, Demasi et al. [18] assessed the accuracy of the variational asymptotic plate and shell analysis, when compared to different higher-order, zig-zag and layerwise theories generated through the invariant axiomatic framework denoted as generalized unified formulation. The axiomatic models were also compared to the elasticity solution developed for the case of sandwich structures with high face to core stiffness ratio. Among other works that have already been carried out within the layerwise theories, in the broad sense, we refer some. Filippi et al. [19] proposed one-dimensional layerwise theories using higher-order zig-zag functions defined over fictitious/mathematical layers of the cross-sectional area of laminated beams. Variable kinematics theories have been obtained using piecewise continuous power series expansions of an arbitrary order. Ferreira [20] combined a layerwise theory with the multiquadrics discretization to analyse laminated composite and sandwich plates. To this aim, he used radial basis functions to approximate the differential governing equations and the boundary conditions. Vuksanović and Ćetković [21] proposed Navier-type closed-form solution for static analysis of simply supported composite plate, based on generalized laminate plate theory. The mathematical model assumed a piecewise linear variation of the in-plane displacement components and a constant transverse displacement through the thickness. Nosier et al. [22] considered Reddy’s layer-wise theory to carry out free-vibration analysis of laminated plates, which results were further compared with those obtained from a full-fledged three-dimensional elasticity analysis and various ESL theories. The use of LW approaches to study the dynamic behavior of damped structures has also been used by some researchers, namely by Sainsbury and Zhang [23], Daya and Potier-Ferry [24], Barkanov et al. [25] and Araújo et al. [26]. Sainsbury and Zhang [23] proposed a finite element for damped sandwich beam structures combining polynomial shape functions of conventional finite element analysis with Galerkin orthogonal functions. They accounted for displacement consistency over the interfaces between the damping layer and the elastic layers to guarantee good accuracy. Daya and Pottier-Ferry [24] proposed a numerical method for the exact solution of nonlinear eigenvalue problems. This method associates homotopy and asymptotic numerical techniques and it was applied to the calculation of the natural frequencies and the loss factors of viscoelastically damped sandwich structures. An inverse technique to characterize the nonlinear mechanical properties of viscoelastic core layers in sandwich panels was developed by Barkanov et al. [25]. This technique was based in vibration tests, allowing preserving the frequency and temperature dependences of the storage and loss moduli of viscoelastic materials. The use of an optimization approach based on the planning of the experiments and the response surface technique to minimize the error functional, enabled additionally the reduction of the computational cost. More recently, Araújo et al. [26] carried out optimization and parameter estimation studies of frequency dependent passive damping of sandwich structures with viscoelastic core. To this purpose he used a mixed-layerwise finite element model and the complex modulus approach to model the viscoelastic material behavior.
In the present work, the authors consider a layerwise theory based on the assumptions of the first order shear deformation theory, layer by layer. The global kinematic through the thickness is therefore approximated in a piecewise manner, being potentially advantageous when compared to other equivalent single-layer higher order theories. A study both on the linear static and free vibrations behavior of three-layered configuration composite plates is presented. The viscoelastic behavior of softer cores is not considered in the present work. A parametric assessment on the influence of different geometrical and material factors is carried out.
2. Materials and Methods
2.1. Composite Materials and Constitutive Relations
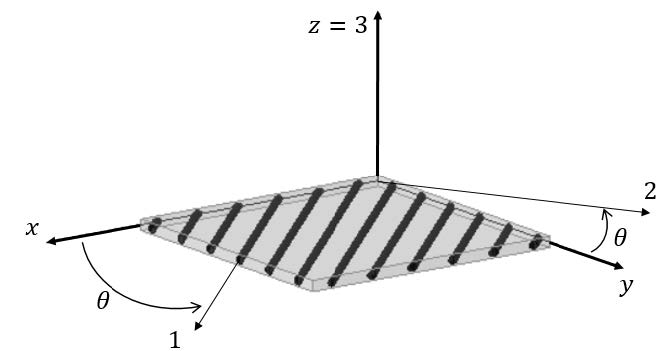
A laminated composite can be constructed by superposing layers of materials, which can be for example, orthotropic fibrous composite materials or isotropic materials, among other possibilities. Underlying these layers superposition, it is considered that a set of assumptions is verified, namely, that there exist a perfect adhesion among constituent phases and between adjacent layers, the inexistence of voids, the continuity of displacements and the validity of a linear elastic regime, in the structure operating conditions. In Figure 1, we can observe a typical stacking sequence of laminae, each possessing a different fiber orientation.
In the present study, one considers a layerwise formulation which assumes negligible the transverse normal deformations, within each layer, thus leading to a constant transverse displacement [27,28]. Neglecting as well the transverse normal stress one has for an orthotropic k-th layer, the stress-strain relations in the material coordinate system (1, 2, 3):
|
{σ(k)1σ(k)2τ(k)12τ(k)23τ(k)31}=[Q11Q12000Q12Q2200000Q6600000Q4400000Q55](k){ε(k)1ε(k)2γ(k)12γ(k)23γ(k)31}
|
(1)
|
where the subscripts 1 and 2 denote respectively the directions of the fiber and the in-plane normal to fiber, and the subscript 3 is associated to the ply transverse normal direction. Q(k)ij, represent the reduced elastic stiffness coefficients of the k-th layer. As each layer may have a different fiber orientation, as we can observe in Figures 1 and 2, it is thus necessary to carry out a transformation procedure so that the necessary analyses involving the whole laminate can be performed.
The angle that characterizes the fiber orientation angle is measured between the positive senses of directions 1 and x. By performing the adequate coordinate transformation the constitutive relations in the laminate coordinate system is finally given as in [29], where represents the transformed reduced elastic stiffness coefficients, associated to each k-th layer.
|
{σ(k)xxσ(k)yyτ(k)xyτ(k)yzτ(k)zx}=[ˉQ(k)11ˉQ(k)12ˉQ(k)1600ˉQ(k)12ˉQ(k)22ˉQ(k)2600ˉQ(k)16ˉQ(k)26ˉQ(k)6600000ˉQ(k)44ˉQ(k)45000ˉQ(k)45ˉQ(k)55](k){ε(k)xxε(k)yyγ(k)xyγ(k)yzγ(k)zx}
|
(2)
|
The mentioned transformation is carried out layer by layer, being not needed if for example, a specific layer has coinciding axes 1 − x (positive senses) or if one uses a material that can be considered to be isotropic. Usually, when considering an ESL approach and using a first order shear deformation theory, one uses shear correction factors to overcome the through-thickness constant prediction of the transverse shear stresses and thus to approximate the model response to the 3D elasticity distributions. The present LW model considers the FSDT assumptions within each layer, yielding to a kinematics description wherein the rotations at each layer, are independent. Under these conditions, and according to some research works [25,26,27,28], the use of the shear correction factors is not considered. However to enable a comparative study, in the present study one has considered in some cases both approaches, i.e., the use of a shear correction factor equal to 1 and equal to a commonly used value, 5/6.
2.2. Layerwise Theory and Equilibrium Equations
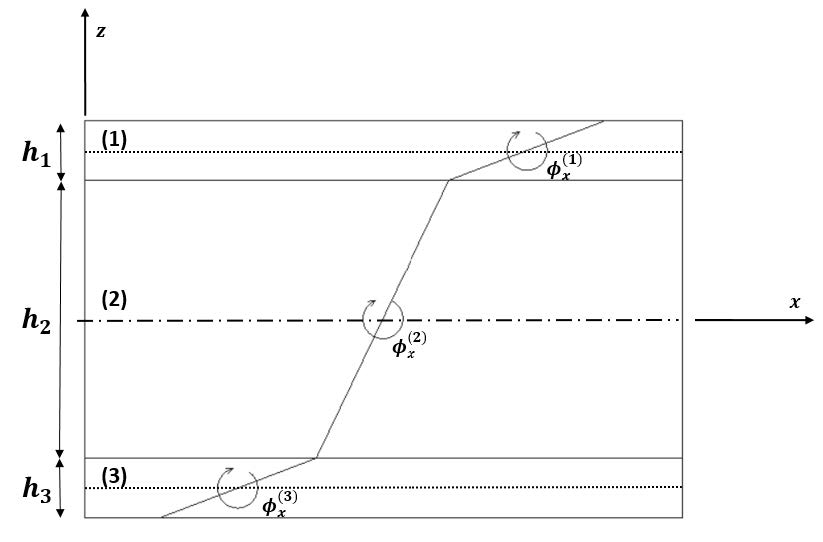
In the present study we have considered that the deformation kinematics of the layered plate would be described through a layerwise approach wherein each of the layers response is based on the first-order shear deformation theory assumptions and by imposing the continuity of displacements at the layer’s interfaces. It is relevant to note that the stresses that result from the constitutive relation (Eqn. 2) may not satisfy the continuity of tractions across these interfaces. However the deviations introduced by this approximation is considered acceptable, as reported by other researchers [27,28]. Similar approaches have been used in the context of the dynamic analysis of viscoelastic sandwich beams and plates, by Barkanov et al. [25] and Araújo et al. [26]. The prediction of the transverse shear stresses within each layer yields a constant value, according to the constitutive relation, thus leading to a stepwise distribution profile. However, a continuous distribution may be obtained if one uses the elasticity equilibrium equations in a post-processing phase. To illustrate the specific case of a three-layered configuration, independently of the nature of the constituent materials, we present in Figure 3, a schematic representation of the kinematics of the present approach.
The major reason for the use of the first order shear deformation theory is related to its minor computational cost when compared to other approaches. If one considers higher order displacement fields in layerwise or equivalent single layer theories, the dimension of the problem can become significantly higher. If one would aim to proceed with a failure analysis, for instances, it would be at any time possible, in a post-processing stage, to calculate the transverse normal and shear stresses via the equilibrium equations. Considering this three-layered configuration, and according to the referred kinematics assumptions, the middle layer (core) displacement components, u(2), v(2), w(2), respectively along the x,y,z, directions, are described as:
|
u(2)(x,y,z,t)=u0(x,y,t)+z(2)θ(2)x(x,y,t)v(2)(x,y,z,t)=v0(x,y,t)+z(2)θ(2)y(x,y,t)w(2)(x,y,z,t)=w0(x,y,t)
|
(3)
|
where u and v are the in-plane displacements at any point characterized by the coordinates (x, y, z, t) at a generic time instant t; u0 and v0 denote the in-plane displacements of a point in the plate mid-plane (x, y, 0, t); is the transverse deflection; and θ(2)x and θ(2)y are the rotations of the normals to the core layer mid-plane about the y and x axes, respectively. After the imposition of displacements’ continuity at the layers’ interfaces, the displacement fields for the upper (1) and lower (3) layers, are respectively given as:
|
u(1)(x,y,z,t)=u0(x,y,t)+h22θ(2)x(x,y,t)+h12θ(1)x(x,y,t)+z(1)θ(1)x(x,y,t)v(1)(x,y,z,t)=v0(x,y,t)+h22θ(2)y(x,y,t)+h12θ(1)y(x,y,t)+z(1)θ(1)y(x,y,t)w(1)(x,y,z,t)=w0(x,y,t)
|
(4)
|
|
u(3)(x,y,z,t)=u0(x,y,t)−h22θ(2)x(x,y,t)−h32θ(3)x(x,y,t)+z(3)θ(3)x(x,y,t)v(3)(x,y,z,t)=v0(x,y,t)−h22θ(2)y(x,y,t)−h32θ(3)y(x,y,t)+z(3)θ(3)y(x,y,t)w(3)(x,y,z,t)=w0(x,y,t)
|
(5)
|
where hk is the th-layer thickness and z(k)∈[−hk/2,hk/2] are the kth-layer z coordinates. Considering the kinematical relations from the elasticity for small deformations, we obtain for a generic kth layer (omitting time and spatial coordinates’ dependency):
|
{ε(k)xxε(k)yyγ(k)xy}={∂u(k)∂x∂v(k)∂y∂u(k)∂y+∂v(k)∂x}={εm(k)xxεm(k)yyγm(k)xy}+z(k){εb(k)xxεb(k)yyγb(k)xy}+{εmb(k)xxεmb(k)yyγmb(k)xy}{γ(k)xzγ(k)yz}={∂u(k)∂z+∂w(k)∂x∂v(k)∂z+∂w(k)∂y}={∂w0∂x+θ(k)x∂w0∂y+θ(k)x}
|
(6)
|
The bending (superscript b) and the membrane (superscript m) components are expressed as:
|
{εb(k)xxεb(k)yyγb(k)xy}={∂θ(k)x∂x∂θ(k)y∂y∂θ(k)x∂y+∂θ(k)y∂x};{εm(k)xxεm(k)yyγm(k)xy}={∂u0∂x∂v0∂y∂u0∂y+∂v0∂x}
|
(7)
|
and the membrane-bending (superscript mb) components for outer layers are respectively given by:
|
{εmb(3)xxεmb(3)yyγmb(3)xy}={−h22∂θ(2)x∂x−h32∂θ(3)x∂x−h22∂θ(2)y∂y−h32∂θ(3)y∂y−h22(∂θ(2)x∂y+∂θ(2)y∂x)−h32(∂θ(3)x∂y+∂θ(3)y∂x)}
|
(8)
|
|
{εmb(1)xxεmb(1)yyγmb(1)xy}={h22∂θ(2)x∂x+h12∂θ(1)x∂xh22∂θ(2)y∂y+h32∂θ(1)y∂yh22(∂θ(2)x∂y+∂θ(2)y∂x)+h12(∂θ(1)x∂y+∂θ(1)y∂x)}
|
(9)
|
The equilibrium equations that will enable to perform the static and free vibrations of the laminated or sandwich composite plate, can be obtained through Hamilton principle [29] which can be written as:
where U, V, W represent respectively the elastic strain energy, the kinetic energy and the work done by external forces applied to the system. Each of these parameters is generically given by:
|
δU=∫Ω(δεTσ)dΩ;δV=∫Ω(ρδ˙qT˙q)dΩ;δW=∫A(pδq)dA
|
(11)
|
with Ω,A being the volume of the plate and the loading application area; ε,σ are the generalized strains and stresses’ vectors. The density and the pressure loading are respectively represented by ρ and p. After the constitution of the element matrices and vectors, and their subsequent assembly considering the discretized domain, we can write the equilibrium equation:
where K, M, F represent respectively the global elastic stiffness and mass matrices and the global load vector, and q,¨q stand for the generalized displacements and accelerations vectors. The vector of the generalized degrees of freedom is then given as:
|
qT=[u0,v0,w0,θx1,θy1,θx2,θy2,θx3,θy3]
|
(13)
|
Assuming free harmonic vibrations we’ll have:
with ωi representing the ith natural frequency associated to the ith vibration mode qi. For a linear static problem, the equilibrium equation becomes reduced to:
In any case, these equilibrium equations are solved only after the imposition of the boundary conditions associated to the problem under study.
3. Results and Discussion
The laminated plates considered in the studies carried out possess a three-layered configuration and comprise two main types of plates: a first one where the outer layers are made of orthotropic composite layers and the core is an isotropic foam. In the second group of plates, all the layers are from orthotropic composite materials. The composite layers consider a 60% volume fraction of long reinforcement fibers (carbon or glass) embedded in an epoxy resin. Tables 1 and 2, present the properties used in the present study.
Table 1. Material properties of composites.
| Vf = 60% | E1 (GPa) | E2 (GPa) | G12 (GPa) | υ12 | (ρ kg/m3) |
| Glass-Epoxy | 45.0 | 12.0 | 4.5 | 0.3 | 2080 |
| Carbon-Epoxy | 134.0 | 7.0 | 4.2 | 0.25 | 1530 |
Table 2. Material properties of foams.
| H35 | H45 | H60 | H80 | H100 | H130 | H160 | H200 | H250 |
| Young’s modulus (MPa) | 49 | 55 | 75 | 95 | 130 | 175 | 205 | 250 | 320 |
| Poisson’s ratio | 0.4 | 0.4 | 0.4 | 0.4 | 0.4 | 0.4 | 0.4 | 0.4 | 0.4 |
| Density (kg/m3) | 38 | 48 | 60 | 80 | 100 | 130 | 160 | 200 | 250 |
Concerning to the materials presented in Table 2, which properties were consulted in the manufacturer site [30] and more specifically to the softness of the core, it is important to say that to obtain a more effective prediction of the response of a soft core sandwich it would be advisable to adopt a more adequate approach that takes into account its viscoelastic behavior. The study of soft core sandwich structures constitutes an investigation field where others researchers have been carrying out different studies. Among others we may refer Daya and Pottier-Ferry [24], Barkanov et al. [24] and Araújo et al. [26]. Considering however just the elastic behavior, a higher order methodology may be an approach to consider in particular if the aspect ratio of the plates is not high. The transverse displacement and the stress components determined in the different case studies, as well as the natural frequencies, are presented in a non-dimensional form using the following multipliers:
|
ˉw=w(l2,l2,0)q,ˉσ1x=σ(1)x(l2,l2,h2)q,ˉσ2x=σ(1)x(l2,l2,hcore2)q,ˉσ3x=σ(2)x(l2,l2,hcore2)qˉσ1y=σ(1)y(l2,l2,h2)q,ˉσ2y=σ(1)y(l2,l2,hcore2)q,ˉσ3y=σ(1)y(l2,l2,hcore2)qˉτ1xz=τ(2)xz(0,l2,0)q,ˉτ2xz=τ(2)xz(0,l2,hcore2)q,ˉω=ωh√ρE2
|
(16)
|
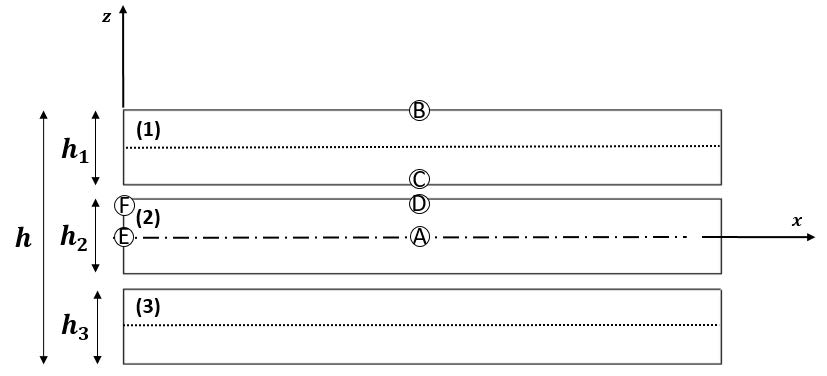
The points where these quantities are assessed, as well as its plate spatial correspondence can be respectively exemplified in Figure 4. In Table 3, the presented coordinates are exemplified for a situation where all the layers have equal thickness.
Table 3. Points of deflection and stresses evaluation (illustrated xz plane).
| A | B | C | D | E | F |
| w(l2,l2,0) | σ(1)x(l2,l2,h2)
σ(1)y(l2,l2,h2) | σ(1)x(l2,l2,hcore2)
σ(1)y(l2,l2,hcore2) | σ(2)x(l2,l2,hcore2)
σ(1)y(l2,l2,hcore2) | τ(2)xz(0,l2,0) | τ(2)xz(0,l2,hcore2) |
The present layerwise model was implemented using a Lagrange quadrilateral plate finite element model with nine nodes, each having nine degrees of freedom, according to equation 13. The discretization used comprised a plate elements mesh, unless otherwise stated. In this work, one considers aspect ratios ranging from five to twenty. As it would be possible to observe, the results obtained, allow to conclude that thicker composites can still be analyzed using this theory. If one considers thinner laminates, a simpler theory may be more adequate.
3.1. Validation Studies
Two first case studies were considered in the present work, to validate the results obtained using the layerwise model taking as reference the results obtained by other authors. The first case is devoted to the static analysis of a sandwich plate, and the second case is focused on the characterization of the eight first natural frequencies of a laminated composite. The discretization considered for the studies carried out was a mesh.
3.1.1. Sandwich Plate Under Uniform Load
In this first case, one considered the static analysis of a simply supported square sandwich plate having skin thicknesses of each, and a core thickness equal to, being (h) the total thickness. The plate is submitted to a uniformly distributed transverse load. The elastic stiffness coefficients of the sandwich core are expressed in the matrix, ˉQcore as [31]:
|
ˉQcore=[0.9997810.2311920000.2311920.524886000000.62931000000.266810000000.159914]
|
The skins’ elastic stiffness coefficients are related to the core coefficients by a factor as follows:
The results obtained, namely the transverse displacements and the stresses are presented in a non-dimensional form using the multipliers,
|
ˉw=w(l2,l2,0)0.999781hq,ˉσ1x=σ(1)x(l2,l2,h2)q,ˉσ2x=σ(1)x(l2,l2,4h10)q,ˉσ3x=σ(2)x(l2,l2,4h10)q,ˉσ1y=σ(1)y(l2,l2,h2)q,ˉσ2y=σ(1)y(l2,l2,4h10)q,ˉσ3y=σ(1)y(l2,l2,4h10)q,ˉτ1xz=τ(2)xz(0,l2,0)q,ˉτ2xz=τ(2)xz(0,l2,4h10)q
|
In Tables 4-6 one summarizes the transverse displacements and the stresses in non-dimensional form, for different ratios (R) between the elastic stiffness coefficients of the skins and the ones of the core. The present results are denoted in Tables 4-7 by Q4 and Q9 to denote the two quadrilateral bilinear and biquadratic finite elements used.
Table 4. Non-dimensional deflection and stress components (R = 5).
| Models | ˉw | ˉσ1x | ˉσ2x | ˉσ3x | ˉσ1y | ˉσ2y | ˉσ3y | ˉτ1xz | ˉτ2xz |
| HSDT [4] | 256.13 | 62.38 | 46.91 | 9.382 | 38.93 | 30.33 | 6.065 | 3.089 | 2.566 |
| Exact [31] | 258.97 | 60.353 | 46.623 | 9.34 | 38.491 | 30.097 | 6.161 | 4.3641 | 3.2675 |
| Ferreira [32] | 258.834 | 60.088 | 46.372 | 9.274 | - | - | - | 3.880 | 1.731 |
| Ferreira [27] | 258.180 | 60.0262 | 46.3926 | 9.2785 | 38.3644 | 30.0294 | 6.0059 | 4.095 | 2.0418 |
| Q4,(4 × 4) | 259.5352 | 55.923 | 42.7778 | 8.5556 | 36.8245 | 28.6415 | 5.7283 | 2.9135 | 1.2510 |
| Q4,(10 × 10) | 258.8336 | 59.5704 | 45.9692 | 9.1938 | 38.2179 | 29.8914 | 5.9783 | 3.6289 | 1.5831 |
| Q4,(12 × 12) | 258.8424 | 59.8026 | 46.1183 | 9.2237 | 38.3128 | 29.9483 | 5.9897 | 3.7122 | 1.6286 |
| Q4,(20 × 20) | 258.8342 | 60.0881 | 46.3718 | 9.2744 | 38.4267 | 30.0523 | 6.0105 | 3.8804 | 1.7314 |
| Q9,(4 × 4) | 258.5895 | 60.3915 | 46.942 | 9.3884 | 38.6598 | 30.4271 | 6.0854 | 4.0522 | 1.8705 |
| Q9,(10 × 10) | 258.8281 | 60.2736 | 46.556 | 9.3112 | 38.4985 | 30.127 | 6.0254 | 4.0669 | 1.9366 |
| Q9,(12 × 12) | 258.8314 | 60.2689 | 46.5404 | 9.3081 | 38.4972 | 30.1202 | 6.024 | 4.0719 | 1.952 |
| Q9,(20 × 20) | 258.8342 | 60.2607 | 46.5197 | 9.3039 | 38.4959 | 30.1124 | 6.0225 | 4.0841 | 1.9826 |
Table 5. Non-dimensional deflection and stress components (R = 10).
| Models | ˉw | ˉσ1x | ˉσ2x | ˉσ3x | ˉσ1y | ˉσ2y | ˉσ3y | ˉτ1xz | ˉτ2xz |
| HSDT [4] | 152.33 | 64.65 | 51.31 | 5.131 | 42.83 | 33.97 | 3.397 | 3.147 | 2.587 |
| Exact [31] | 159.38 | 65.332 | 48.857 | 4.903 | 43.566 | 33.413 | 3.5 | 4.0959 | 3.5154 |
| Ferreira [32] | 159.476 | 65.047 | 48.576 | 4.858 | - | - | - | 3.792 | 1.928 |
| Ferreira [27] | 158.9117 | 64.9927 | 48.6009 | 4.8601 | 43.4907 | 33.4089 | 3.3409 | 3.9803 | 2.3325 |
| Q4,(4 × 4) | 162.0181 | 60.543 | 44.4486 | 4.4449 | 41.9587 | 31.8772 | 3.1877 | 2.8323 | 1.3629 |
| Q4,(10 × 10) | 159.6822 | 64.4631 | 48.1314 | 4.8131 | 43.3636 | 33.2797 | 3.328 | 3.5483 | 1.747 |
| Q4,(12 × 12) | 159.6097 | 64.7366 | 48.2823 | 4.8282 | 43.4708 | 33.3274 | 3.3327 | 3.6295 | 1.8016 |
| Q4,(20 × 20) | 159.4757 | 65.0473 | 48.5758 | 4.8576 | 43.5805 | 33.4408 | 3.3441 | 3.7918 | 1.9279 |
| Q9,(4 × 4) | 159.3758 | 65.4971 | 49.2619 | 4.9262 | 43.932 | 33.9226 | 3.3923 | 3.8726 | 2.007 |
| Q9,(10 × 10) | 159.4047 | 65.2546 | 48.782 | 4.8782 | 43.6564 | 33.5212 | 3.3521 | 3.9533 | 2.1755 |
| Q9,(12 × 12) | 159.4053 | 65.2476 | 48.7654 | 4.8765 | 43.6535 | 33.5134 | 3.3513 | 3.9621 | 2.2073 |
| Q9,(20 × 20) | 159.4058 | 65.2373 | 48.7433 | 4.8743 | 43.6505 | 33.5042 | 3.3504 | 3.9779 | 2.2689 |
Table 6. Non-dimensional deflection and stress components (R = 15).
| Models | ˉw | ˉσ1x | ˉσ2x | ˉσ3x | ˉσ1y | ˉσ2y | ˉσ3y | ˉτ1xz | ˉτ2xz |
| HSDT [4] | 110.43 | 66.62 | 51.97 | 3.465 | 44.92 | 35.41 | 2.361 | 3.035 | 2.691 |
| Exact [31] | 121.72 | 66.787 | 48.299 | 3.238 | 46.424 | 34.955 | 2.494 | 3.9638 | 3.5768 |
| Ferreira [32] | 121.871 | 66.490 | 48.000 | 3.200 | - | - | - | 3.730 | 2.019 |
| Ferreira [27] | 121.3474 | 66.4362 | 48.0104 | 3.2007 | 46.3849 | 34.9650 | 2.331 | 3.9024 | 2.4811 |
| Q4,(4 × 4) | 125.0593 | 61.9463 | 43.5915 | 2.9061 | 44.8984 | 33.3497 | 2.2233 | 2.7739 | 1.4016 |
| Q4,(10 × 10) | 122.1499 | 65.8759 | 47.5395 | 3.1693 | 46.2623 | 34.8631 | 2.3242 | 3.4912 | 1.8158 |
| Q4,(12 × 12) | 122.0484 | 66.1709 | 47.6863 | 3.1791 | 46.3774 | 34.9007 | 2.3267 | 3.5712 | 1.8766 |
| Q4,(20 × 20) | 121.8709 | 66.4903 | 48.0001 | 3.2 | 46.4797 | 35.0191 | 2.3346 | 3.7297 | 2.0192 |
| Q9,(4 × 4) | 121.8099 | 67.0141 | 48.6933 | 3.2462 | 46.8978 | 35.5358 | 2.3691 | 3.7749 | 2.0626 |
| Q9,(10 × 10) | 121.7767 | 66.7069 | 48.2131 | 3.2142 | 46.5567 | 35.1012 | 2.3401 | 3.8804 | 2.3078 |
| Q9,(12 × 12) | 121.7766 | 66.6983 | 48.1976 | 3.2132 | 46.5525 | 35.0931 | 2.3395 | 3.8899 | 2.3516 |
| Q9,(20 × 20) | 121.7765 | 66.6866 | 48.1768 | 3.2118 | 46.5478 | 35.0835 | 2.3389 | 3.9054 | 2.433 |
Table 7. Non-dimensional deflection and stress components (k = 5/6).
| Models | ˉw | ˉσ1x | ˉσ2x | ˉσ3x | ˉσ1y | ˉσ2y | ˉσ3y | ˉτ1xz | ˉτ2xz |
| R = 5 | | | | | | | | | |
| Exact [31] | 258.97 | 60.353 | 46.623 | 9.34 | 38.491 | 30.097 | 6.161 | 4.3641 | 3.2675 |
| Ferreira [32] | 258.834 | 60.088 | 46.372 | 9.274 | - | - | - | 3.880 | 1.731 |
| Ferreira [27] | 258.180 | 60.0262 | 46.3926 | 9.2785 | 38.3644 | 30.0294 | 6.0059 | 4.095 | 2.0418 |
| Q4 | 258.8342 | 60.0881 | 46.3718 | 9.2744 | 38.4267 | 30.0523 | 6.0105 | 3.8804 | 1.7314 |
| Q9 | 258.8342 | 60.2607 | 46.5197 | 9.3039 | 38.4959 | 30.1124 | 6.0225 | 4.0841 | 1.9826 |
| Q4,k = 5/6 | 267.1507 | 59.9246 | 45.9070 | 9.1814 | 38.7909 | 30.2055 | 6.0411 | 3.8675 | 1.7430 |
| Q9,k = 5/6 | 267.1177 | 60.0977 | 46.0558 | 9.2112 | 38.8587 | 30.2646 | 6.0529 | 4.0667 | 1.9980 |
| R = 10 | | | | | | | | | |
| Exact [31] | 159.38 | 65.332 | 48.857 | 4.903 | 43.566 | 33.413 | 3.5 | 4.0959 | 3.5154 |
| Ferreira [32] | 159.476 | 65.047 | 48.576 | 4.858 | - | - | - | 3.792 | 1.928 |
| Ferreira [27] | 158.9117 | 64.9927 | 48.6009 | 4.8601 | 43.4907 | 33.4089 | 3.3409 | 3.9803 | 2.3325 |
| Q4 | 159.4757 | 65.0473 | 48.5758 | 4.8576 | 43.5805 | 33.4408 | 3.3441 | 3.7918 | 1.9279 |
| Q9 | 159.4058 | 65.2373 | 48.7433 | 4.8743 | 43.6505 | 33.5042 | 3.3504 | 3.9779 | 2.2689 |
| Q4,k = 5/6 | 167.4872 | 64.7566 | 47.6721 | 4.7672 | 44.2484 | 33.6886 | 3.3689 | 3.7697 | 1.9447 |
| Q9,k = 5/6 | 167.3863 | 64.9468 | 47.8409 | 4.7841 | 44.3164 | 33.7511 | 3.3751 | 3.9513 | 2.2977 |
| R = 15 | | | | | | | | | |
| Exact [31] | 121.72 | 66.787 | 48.299 | 3.238 | 46.424 | 34.955 | 2.494 | 3.9638 | 3.5768 |
| Ferreira [32] | 121.871 | 66.490 | 48.000 | 3.200 | - | - | - | 3.730 | 2.019 |
| Ferreira [27] | 121.3474 | 66.4362 | 48.0104 | 3.2007 | 46.3849 | 34.9650 | 2.331 | 3.9024 | 2.4811 |
| Q4 | 121.8709 | 66.4903 | 48.0001 | 3.2 | 46.4797 | 35.0191 | 2.3346 | 3.7297 | 2.0192 |
| Q9 | 121.7765 | 66.6866 | 48.1768 | 3.2118 | 46.5478 | 35.0835 | 2.3389 | 3.9054 | 2.433 |
| Q4,k=5/6 | 129.7105 | 66.1127 | 46.7050 | 3.1137 | 47.4140 | 35.3295 | 2.3553 | 3.6995 | 2.0400 |
| Q9,k=5/6 | 129.5865 | 66.3085 | 46.8830 | 3.1255 | 47.4803 | 35.3936 | 2.3596 | 3.8704 | 2.4703 |
As it is possible to conclude, the present results show a general good agreement with the reference solutions. The results obtained with the LW-Q9 model are in good agreement with the ones obtained by Ferreira et al. [27] which used a LW theory and radial basis functions discretization. Although in the present work, one only presents results obtained with nine-node elements, the results obtained with the four-node element implement can be observed also in these tables. A good agreement is found with Ferreira [32] solution which used a bilinear quadrilateral finite element based on a simplified formulation where the membrane degrees of freedom were neglected. Considering a shear correction factor of 5/6, the results will be the ones presented in Table 7.
As it is possible to conclude, and as expected, the use of a shear correction equal to 5/6, produces alterations in the different quantities presented. In the present cases, the agreement with the reference solutions is better when k = 1.
3.1.2. Fundamental Frequencies of Laminated Plates with Different Stiffness Ratios
This second validation study, considers a cross-ply simply supported laminated plate with the following stacking sequence [0º/90º/90º/0º]. The thickness-to-span ratio h/a is 0.2 and the thickness of all the plies is equal. The material properties of the composite are E1/E2 = 10, 20, 30, 40; G12 = G13 = 0.6 E2;G23 = 0.5 E2; v12 = 0.25. Table 8 presents the fundamental frequency in a non-dimensional form using the multiplier ˉω=ωa2h√ρE2.
Table 8. Non-dimensional fundamental frequency. Different stiffness ratios.
| k | Method | 10 | 20 | 30 | 40 |
| 1 | Liew et al. [33] | 8.2924 | 9.5613 | 10.320 | 10.849 |
| Khdeir et al. [34] | 8.2982 | 9.5671 | 10.326 | 10.854 |
| Ferreira et al. [28] | 8.5846 | 9.8384 | 10.5695 | 10.0649 |
| 1 | Present (11 × 11) | 8.4255 | 9.5735 | 10.2072 | 10.62 |
| Present (15 × 15) | 8.4244 | 9.5724 | 10.2063 | 10.6192 |
| Present (19 × 19) | 8.4241 | 9.5722 | 10.2061 | 10.619 |
| 5/6 | Present (11 × 11) | 8.14 | 9.1314 | 9.6646 | 10.0078 |
| Present (15 × 15) | 8.1389 | 9.1305 | 9.6638 | 10.0071 |
| Present (19 × 19) | 8.1387 | 9.1303 | 9.6636 | 10.0069 |
From Table 8 it is possible to conclude on the good agreement with the reference results for the different stiffness ratios considered. As we may conclude, in these cases the use of a unit shear correction factor yields a better agreement when compared to the use of a 5/6 shear correction factor.
3.1.3. Natural Frequencies of a Composite Laminated Plate
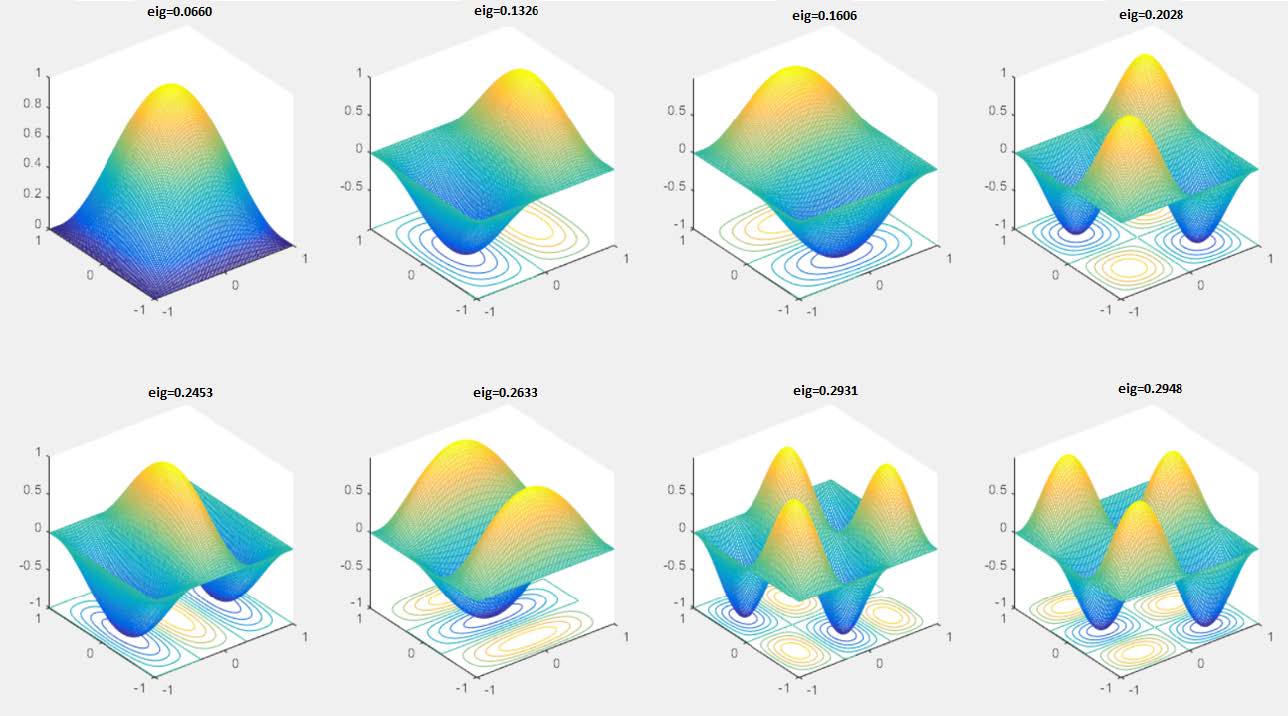
In this second validation study, one has considered a simply supported square laminated plate with the following stacking sequence [0º/90º/90º/0º]. The side-to-thickness ratio a/h is set to 10 and the thickness of each ply is h/3. The material properties of the composite are: E1 = 173 MPa; E2 = 33.1 MPa; G12 = 9.38 MPa; G13 = 8.27 MPa; G23 = 3.24 MPa; v12 = 0.036; v13 = 0.25; v23 = 0.171. For illustrative purposes, we present in Figure 5 the corresponding first eight vibration modes.
The results obtained in the free vibrations analyses carried out, are presented in Table 9.
Table 9. Non-dimensional natural frequencies for the laminate plate.
| Method | (1,1) | (1,2) | (2,1) | (2,2) | (1,3) | (2,3) | (3,1) | (3,2) |
| Exact [35] | 0.0672 | 0.1281 | 0.1722 | 0.2080 | - | - | - | - |
| Nosier et al. [22] | 0.0672 | 0.1282 | 0.1723 | 0.2081 | - | - | - | - |
| Ferreira et al. [27] | 0.0681 | 0.1322 | 0.1762 | 0.2150 | 0.2376 | 0.2954 | 0.3009 | 0.3288 |
| Present,(4 × 4) | 0.0687 | 0.1277 | 0.1829 | 0.2166 | 0.2263 | 0.2882 | 0.3175 | 0.3397 |
| Present,(10 × 10) | 0.0687 | 0.127 | 0.1817 | 0.2155 | 0.2195 | 0.2836 | 0.3099 | 0.3286 |
| Present,(12 × 12) | 0.0687 | 0.1269 | 0.1817 | 0.2155 | 0.2194 | 0.2836 | 0.3098 | 0.3281 |
| Present,(20 × 20) | 0.0687 | 0.1269 | 0.1817 | 0.2155 | 0.2193 | 0.2835 | 0.3097 | 0.3277 |
The frequencies in Table 9 are non-dimensionalized using the corresponding multiplier in Eqn. 16. We can also observe a general good agreement with the reference results.
3.2. Case Studies
3.2.1. Influence of Core on the Static and Free Vibrations of a Sandwich Plate with Composite Skins
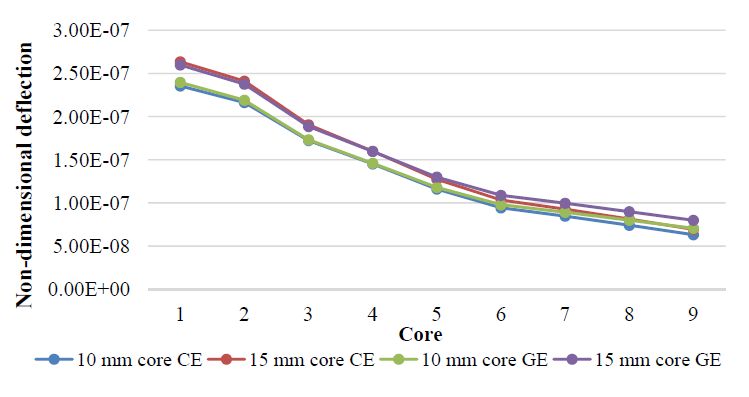
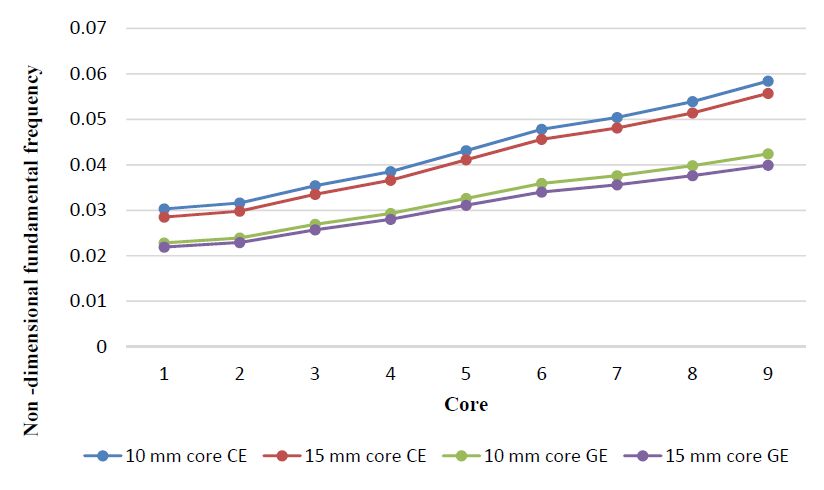
Following the previous validation studies, we considered a case study where the inner layer, the core, was made from different density polyvinyl chloride (PVC) foams [30]. This configuration is able to present a favorable lightweight solution, namely when the structure weight can be a constraint. To this purpose one has studied the effect of considering different foams with different thicknesses. The outer layers, were assumed to be made of unidirectional carbon-epoxy or glass-epoxy composite. The material properties are presented in Tables 1 and 2, and an aspect ratio a/h = 10 was considered. The plates were subjected to a uniformly distributed transverse load (1 Pa). The maximum deflection and the first five natural frequencies for a sandwich configuration with carbon-epoxy skins and a core with 10 mm and 15 mm thickness are respectively presented in Tables 10 and 11, in a non-dimensional form. The thickness of each skin is 2 mm, in both cases.
Table 10. Non-dimensional deflection and frequencies. Carbon-epoxy skins, 10 mm core.
| Core Id. | Material Id. | Deflection | Vibration modes |
| (1, 1) | (2, 1) | (1, 2) | (2, 2) | (3, 1) |
| 1 | H35 | 2.35E−07 | 0.0303 | 0.0489 | 0.0619 | 0.0723 | 0.0736 |
| 2 | H45 | 2.16E−07 | 0.0316 | 0.0511 | 0.064 | 0.0758 | 0.0765 |
| 3 | H60 | 1.72E−07 | 0.0354 | 0.0576 | 0.0707 | 0.085 | 0.0859 |
| 4 | H80 | 1.45E−07 | 0.0385 | 0.0629 | 0.0767 | 0.0924 | 0.0944 |
| 5 | H100 | 1.16E−07 | 0.0431 | 0.0703 | 0.0858 | 0.1034 | 0.1067 |
| 6 | H130 | 9.43E−08 | 0.0478 | 0.0777 | 0.0959 | 0.1153 | 0.1193 |
| 7 | H160 | 8.47E−08 | 0.0504 | 0.0817 | 0.1019 | 0.1222 | 0.1263 |
| 8 | H200 | 7.41E−08 | 0.0539 | 0.0869 | 0.1101 | 0.1314 | 0.1354 |
| 9 | H250 | 6.32E−08 | 0.0584 | 0.0934 | 0.1213 | 0.1438 | 0.1469 |
Table 11. Non-dimensional deflection and frequencies. Carbon-epoxy skins, 15 mm core.
| Core Id. | Material Id. | Deflection | Vibration modes |
| 1 | H35 | 2.64E−07 | 0.0285 | 0.0465 | 0.0541 | 0.0659 | 0.0688 |
| 2 | H45 | 2.41E−07 | 0.0298 | 0.0487 | 0.0565 | 0.0689 | 0.0722 |
| 3 | H60 | 1.91E−07 | 0.0335 | 0.0550 | 0.0639 | 0.0779 | 0.0822 |
| 4 | H80 | 1.60E−07 | 0.0366 | 0.0600 | 0.0702 | 0.0856 | 0.0906 |
| 5 | H100 | 1.27E−07 | 0.0411 | 0.0671 | 0.0799 | 0.0969 | 0.1024 |
| 6 | H130 | 1.03E−07 | 0.0456 | 0.0740 | 0.0903 | 0.1089 | 0.1144 |
| 7 | H160 | 9.28E−08 | 0.0481 | 0.0778 | 0.0965 | 0.1158 | 0.1210 |
| 8 | H200 | 8.13E−08 | 0.0514 | 0.0826 | 0.1048 | 0.1250 | 0.1295 |
| 9 | H250 | 6.94E−08 | 0.0557 | 0.0887 | 0.1161 | 0.1373 | 0.1403 |
From Table 10, we see that as we go from the H35 to the H250 foam core, the maximum deflection decreases, which is expected as the foams provide an increasing stiffness to the plate. Concerning to the frequencies we observe an opposite trend as expected. Table 11 presents now a similar set of studies, considering a thicker core.
Again we observe that the maximum deflection decreases for the higher density cores configurations, and the frequencies increase. We see additionally that in this last situation, where the core is thicker but the skins have the same thickness, we achieve a less stiff solution, which would be expectable.
The identification of the core material in the horizontal axis of the graphics, correspond to the core identification in Tables 10 and 11, CE and GE denotes the carbon-epoxy and glass-epoxy skins.
Similar trends are observed if one considers glass-epoxy skins, as depicted in Figures 6 and 7. In addition to the stiffening effect provided by the two types of skins at different distances from the middle-plane, it is also worth of mention the evolution of the Young’s modulus and the density for the different cores configurations considered. We may conclude from the material data (Table 2) that we have a greater gradient in the case of the Young’s modulus, although for the second core, the evolution rate of the Young’s modulus is lower. Considering these aspects, the static and dynamic response of the sandwich plate in the neighborhood of this second configuration becomes clearer.
Also concerning to the remaining response evolution, the evolution rate of the Young’s modulus slows down again in the case of the seventh core, but not the density one. This is again visible in the responses (Figures 6 and 7). Globally, we can conclude that despite the proximity perception of the curves which may be affected by the magnitude of the different scales’ axes; the thicker these cores are, the greater the deflection and the minor the fundamental frequency of the sandwich plate. Moreover, when we consider a growing density core, regardless its thickness, the fundamental frequency increases and the deflection decreases.
3.2.2. Influence of Geometric Ratios on the Static and Free Vibrations of Three-Layered Composite Plate
In order to characterize the influence of plate aspect ratio (a/h) in its mechanical response, we considered a unit edge length, simply supported square laminated plate [0º/90º/0º], subjected to a uniformly distributed transverse load (1 Pa) and three side-to-thickness ratios (a/h = 5, 10 and 20). The material properties of the carbon-epoxy composite used in the plate are listed in Table 1, and the transverse displacement and the stress components are presented in non-dimensional form.
In Table 12 we can observe the non-dimensional transverse displacement and stresses for the three aspect ratios. Additionally we can also see how the plate behaves if for each a/h we consider the variation of the skins thicknesses in an equal manner. We can conclude that as the aspect ratio (a/h) increases, the plate goes thinner and the non-dimensional transverse displacement also increases.
Table 12. Non-dimensional transverse deflection and stresses vs. ratio a/h.
| a/h | hk | ˉw | ˉσ1x | ˉσ2x | ˉσ3x | ˉσ1y | ˉσ2y | ˉσ3y | ˉτ1xz | ˉτ2xz |
| 5 | h/6 | 1.48E−09 | 19.5679 | 13.0317 | 0.8189 | 1.3064 | 0.7513 | 11.3281 | 2.4376 | 1.2329 |
| h/5 | 1.50E−09 | 18.5382 | 11.2410 | 0.7236 | 1.3899 | 0.7205 | 11.1640 | 2.6190 | 1.3573 |
| h/4 | 1.57E−09 | 17.5487 | 9.1203 | 0.6083 | 1.5917 | 0.6740 | 10.7743 | 2.8794 | 1.5397 |
| h/3 | 1.72E−09 | 16.7142 | 6.2640 | 0.4399 | 1.9373 | 0.5558 | 9.1840 | 3.2748 | 1.8389 |
| 10 | h/6 | 1.50E−08 | 78.2689 | 52.1422 | 3.3108 | 4.8995 | 3.1501 | 48.0947 | 4.8990 | 2.4775 |
| h/5 | 1.51E−08 | 76.6934 | 46.1283 | 2.9489 | 4.9249 | 2.8708 | 44.1609 | 5.3622 | 2.7893 |
| h/4 | 1.53E−08 | 75.1630 | 37.9595 | 2.4446 | 4.9481 | 2.4378 | 37.7885 | 5.9820 | 3.2284 |
| h/3 | 1.59E−08 | 73.8013 | 25.3755 | 1.6389 | 5.4659 | 1.6997 | 27.4375 | 6.8049 | 3.8884 |
| 20 | h/6 | 2.05E−07 | 313.4683 | 208.9234 | 13.3188 | 19.4379 | 12.8451 | 196.9901 | 9.8338 | 4.9746 |
| h/5 | 2.05E−07 | 311.7869 | 187.1772 | 11.9098 | 19.1397 | 11.4128 | 174.6566 | 10.8530 | 5.6574 |
| h/4 | 2.05E−07 | 309.2712 | 155.0268 | 9.8104 | 18.4756 | 9.2265 | 141.4401 | 12.1659 | 6.5958 |
| h/3 | 2.06E−07 | 304.6326 | 102.3482 | 6.3685 | 19.2816 | 6.2762 | 102.4880 | 13.7655 | 7.9295 |
A similar response pattern is visible in the case of the stresses. For a specific a/h when we consider the thickening of the skins (hk) we can conclude that the increasing trend also occurs for the transverse displacement. In the case of the evolution of stresses, it shows a similar consistent trend.
In Table 13 it is also possible to see the first four non-dimensional natural frequencies, for the same aspect ratios and skins’ thicknesses.
Table 13. Non-dimensional natural frequencies vs. aspect ratio a/h.
| a/h | hk | (1, 1) | (2, 1) | (1, 2) | (2, 2) |
| 5 | h/6 | 0.3811 | 0.6345 | 0.8080 | 0.9135 |
| h/5 | 0.3774 | 0.6037 | 0.8158 | 0.8883 |
| h/4 | 0.3694 | 0.5804 | 0.7996 | 0.8661 |
| h/3 | 0.3535 | 0.5501 | 0.7645 | 0.8537 |
| 10 | h/6 | 0.1216 | 0.2339 | 0.3189 | 0.3812 |
| h/5 | 0.1211 | 0.2222 | 0.3223 | 0.3631 |
| h/4 | 0.1199 | 0.2054 | 0.3228 | 0.3365 |
| h/3 | 0.1172 | 0.1828 | 0.3005 | 0.3164 |
| 20 | h/6 | 0.0331 | 0.0725 | 0.0993 | 0.1216 |
| h/5 | 0.0331 | 0.0671 | 0.1024 | 0.1211 |
| h/4 | 0.0330 | 0.0600 | 0.1052 | 0.1090 |
| h/3 | 0.0328 | 0.0513 | 0.0888 | 0.1067 |
Regarding the natural frequencies, it is possible to see that as the aspect ratio increases, the natural frequencies decrease. This pattern trend is also visible when the thickness of the middle layer decreases.
3.2.3. Influence of Fiber Orientation on the Static and Free Vibrations of Three-Layered Composite Plate
To characterize the effect of the fibers’ orientations on the static and free vibration behavior of the previous plates, we carried out another study. To this purpose we have considered three types of laminates, which stacking sequences may be summarized as [θº/0º/θº], [−θº/0º/θº] and [−θº/90º/θº]. The material properties of the composite and the aspect ratios considered were the same of the previous case study and the transverse displacement and the stress components are again presented in a non-dimensional form. The results obtained are presented in Tables 14 to 15.
Table 14. Non-dimensional deflection and stress components for the [θº/0º/θº] laminates.
| a/h | Stacking sequence | ˉw | ˉσ1x | ˉσ2x | ˉσ3x | ˉσ1y | ˉσ2y | ˉσ3y | ˉτ1xz | ˉτ2xz |
| 5 | [0°/0°/0°] | 2.14E−09 | 18.8606 | 2.2167 | 2.2167 | 2.5442 | 0.7787 | 0.7787 | 3.0414 | 1.9686 |
| [30°/0°/30°] | 1.70E−09 | 12.0237 | 3.3023 | 4.3633 | 5.5495 | 1.3426 | 0.5884 | 2.5117 | 1.6649 |
| [45°/0°/45°] | 1.53E−09 | 8.1046 | 2.3263 | 3.4907 | 8.3541 | 2.5853 | 0.5242 | 2.2195 | 1.4765 |
| [60°/0°/60°] | 1.56E−09 | 5.1650 | 1.1668 | 5.3923 | 12.4994 | 3.1178 | 0.4897 | 1.9449 | 1.1327 |
| [90°/0°/90°] | 1.72E−09 | 1.9373 | 0.5558 | 9.1840 | 16.7142 | 6.2640 | 0.4399 | 1.3839 | 0.6264 |
| 10 | [0°/0°/0°] | 1.78E−08 | 76.2657 | 20.5571 | 20.5571 | 6.5166 | 2.0940 | 2.0940 | 6.8372 | 3.9905 |
| [30°/0°/30°] | 1.60E−08 | 47.4375 | 12.7804 | 27.0856 | 19.6930 | 5.5572 | 2.1496 | 5.7971 | 3.3289 |
| [45°/0°/45°] | 1.50E−08 | 30.1627 | 8.2030 | 24.8592 | 30.6463 | 8.8301 | 2.3782 | 5.0787 | 2.9633 |
| [60°/0°/60°] | 1.53E−08 | 19.5482 | 5.9614 | 25.8571 | 48.5890 | 15.2072 | 2.3090 | 4.5459 | 2.2036 |
| [90°/0°/90°] | 1.59E−08 | 5.4659 | 1.6997 | 27.4375 | 73.8013 | 25.3755 | 1.6389 | 2.6868 | 0.9767 |
| 20 | [0°/0°/0°] | 2.11E−07 | 303.6790 | 96.2366 | 96.2366 | 21.9219 | 7.2265 | 7.2265 | 14.1760 | 7.8875 |
| [30°/0°/30°] | 2.06E−07 | 188.8223 | 59.9691 | 129.9897 | 75.9990 | 24.3419 | 8.2395 | 12.4625 | 6.7458 |
| [45°/0°/45°] | 1.98E−07 | 118.8191 | 37.7501 | 121.8943 | 119.3034 | 38.1318 | 9.3731 | 11.1544 | 6.2335 |
| [60°/0°/60°] | 2.03E−07 | 76.3067 | 24.8855 | 110.2294 | 189.6396 | 62.3118 | 8.8632 | 10.8669 | 4.5299 |
| [90°/0°/90°] | 2.06E−07 | 19.2816 | 6.2762 | 102.4880 | 304.6326 | 102.3482 | 6.3685 | 5.4941 | 1.7139 |
Table 15. Non-dimensional natural frequencies for the [θº/0º/θº] laminates.
| a/h | Stacking sequence | (1, 1) | (2, 1) | (1, 2) | (2, 2) |
| 5 | [0°/0°/0°] | 0.3184 | 0.5296 | 0.6699 | 0.8151 |
| [30°/0°/30°] | 0.3568 | 0.5996 | 0.7204 | 0.8591 |
| [45°/0°/45°] | 0.3759 | 0.6251 | 0.7582 | 0.8795 |
| [60°/0°/60°] | 0.3727 | 0.6052 | 0.7736 | 0.8715 |
| [90°/0°/90°] | 0.3535 | 0.5501 | 0.7645 | 0.8537 |
| 10 | [0°/0°/0°] | 0.1104 | 0.1660 | 0.2795 | 0.2838 |
| [30°/0°/30°] | 0.1174 | 0.1997 | 0.2832 | 0.3055 |
| [45°/0°/45°] | 0.1212 | 0.2137 | 0.2866 | 0.3167 |
| [60°/0°/60°] | 0.1203 | 0.2082 | 0.2999 | 0.3166 |
| [90°/0°/90°] | 0.1172 | 0.1828 | 0.3005 | 0.3164 |
| 20 | [0°/0°/0°] | 0.0321 | 0.0464 | 0.0768 | 0.1016 |
| [30°/0°/30°] | 0.0329 | 0.0569 | 0.0900 | 0.0933 |
| [45°/0°/45°] | 0.0336 | 0.0615 | 0.0900 | 0.0949 |
| [60°/0°/60°] | 0.0332 | 0.0601 | 0.0949 | 0.0957 |
| [90°/0°/90°] | 0.0328 | 0.0513 | 0.0888 | 0.1067 |
From Table 14 it is possible to conclude that angle-ply and cross-ply three-layered laminates perform more conservatively specially for thick and moderately thick laminates. The results obtained for the stresses’ components are in accordance with this.
The natural frequencies in Table 15 present a consistent trend with the Table 14 results.
When the outer plies do not follow the same unidirectional angle of the core, the fundamental frequency, as well as the other higher order frequencies, becomes higher, being higher in the case of the 45º outer plies’ laminate. Again this effect is more significant for thicker plates. From these results, one may conclude that the better stacking sequence concerning the minimum transverse deformation and the maximum fundamental frequency is presented the [45º/0º/45º] laminate. In Table 16, we can now observe the static response of the plates that possess a symmetric orientation angle in the outer layers.
Table 16. Non-dimensional deflection and stress components for the [−θº/0º/θº] laminates.
| a/h | Stacking sequence | ˉw | ˉσ1x | ˉσ2x | ˉσ3x | ˉσ1y | ˉσ2y | ˉσ3y | ˉτ1xz | ˉτ2xz |
| 5 | [−30°/0°/30°] | 1.36E−09 | 10.6046 | 2.2560 | 6.1698 | 4.5360 | 0.9185 | 1.0381 | 2.2967 | 1.6094 |
| [−45°/0°/45°] | 1.20E−09 | 7.2749 | 1.7780 | 3.3350 | 7.2567 | 1.8070 | 1.4519 | 1.9979 | 1.4215 |
| [−60°/0°/60°] | 1.31E−09 | 4.3180 | 1.2189 | 2.7765 | 10.6534 | 3.4639 | 1.3589 | 1.6848 | 1.1015 |
| 10 | [−30°/0°/30°] | 1.18E−08 | 39.0379 | 12.3092 | 21.9477 | 15.7575 | 4.7019 | 3.4992 | 5.0932 | 3.5805 |
| [−45°/0°/45°] | 1.05E−08 | 26.9461 | 10.9467 | 14.2479 | 27.2759 | 11.0915 | 5.0608 | 4.4088 | 3.0320 |
| [−60°/0°/60°] | 1.17E−08 | 15.6310 | 6.4519 | 14.7755 | 40.0437 | 18.3180 | 4.6169 | 3.7081 | 2.2366 |
| 20 | [−30°/0°/30°] | 1.43E−07 | 154.4374 | 52.6199 | 80.4305 | 59.8252 | 19.7365 | 11.5330 | 10.6298 | 9.9229 |
| [−45°/0°/45°] | 1.29E−07 | 107.6135 | 45.2929 | 59.0214 | 108.8538 | 45.8082 | 16.5644 | 9.1362 | 8.0365 |
| [−60°/0°/60°] | 1.44E−07 | 60.4675 | 25.1479 | 61.1296 | 158.0092 | 71.2223 | 15.0004 | 7.7873 | 5.3613 |
From Table 16 we see that when the angles of the outer layers are symmetrical, the laminate presents a stiffer behavior, when compared to the configuration in Table 14. One may also conclude that the better stacking sequence concerning the minimum transverse deflection is given by the [−45º/0º/45º] configuration. In Table 17, for the same laminates, we may conclude on a similar pattern in the opposite sense (maximum frequencies values) concerning the natural frequencies.
Table 17. Non-dimensional natural frequencies for the [−θº/0º/θº] laminates.
| a/h | Stacking sequence | (1, 1) | (2, 1) | (1, 2) | (2, 2) |
| 5 | [−30°/0°/30°] | 0.3976 | 0.6774 | 0.7444 | 0.9865 |
| [−45°/0°/45°] | 0.4220 | 0.7353 | 0.7778 | 1.0323 |
| [−60°/0°/60°] | 0.4050 | 0.6630 | 0.8061 | 0.9850 |
| 10 | [−30°/0°/30°] | 0.1361 | 0.2424 | 0.2994 | 0.3875 |
| [−45°/0°/45°] | 0.1441 | 0.2859 | 0.2915 | 0.4243 |
| [−60°/0°/60°] | 0.1368 | 0.2458 | 0.3171 | 0.3849 |
| 20 | [−30°/0°/30°] | 0.0393 | 0.0737 | 0.0999 | 0.1216 |
| [−45°/0°/45°] | 0.0415 | 0.0906 | 0.0914 | 0.1458 |
| [−60°/0°/60°] | 0.0392 | 0.0757 | 0.1013 | 0.1267 |
Next, in Table 18, we present, the non-dimensional maximum deflection and stress components for the [−θº/90º/θº] lamination, where the lamination [−45º/90º/45º] shows to be more favorable, similarly with the results in Table 16, due to the equal thicknesses configuration considered.
Table 18. Non-dimensional deflection and stress components for the [−θº/90º/θº] laminates.
| a/h | Stacking sequence | ˉw | ˉσ1x | ˉσ2x | ˉσ3x | ˉσ1y | ˉσ2y | ˉσ3y | ˉτ1xz | ˉτ2xz |
| 5 | [0°/90°/0°] | 1.72E−09 | 16.7142 | 6.2640 | 0.4399 | 1.9373 | 0.5558 | 9.1840 | 3.2748 | 1.8389 |
| [−30°/90°/30°] | 1.31E−09 | 10.6534 | 3.4639 | 1.3589 | 4.3180 | 1.2189 | 2.7765 | 2.6221 | 1.8097 |
| [−45°/90°/45°] | 1.20E−09 | 7.2567 | 1.8070 | 1.4519 | 7.2749 | 1.7780 | 3.3350 | 2.1744 | 1.6364 |
| [−60°/90°/60°] | 1.36E−09 | 4.5360 | 0.9185 | 1.0381 | 10.6046 | 2.2560 | 6.1698 | 1.7903 | 1.2796 |
| 10 | [0°/90°/0°] | 1.59E−08 | 73.8013 | 25.3755 | 1.6389 | 5.4659 | 1.6997 | 27.4375 | 6.8049 | 3.8884 |
| [−30°/90°/30°] | 1.17E−08 | 40.0437 | 18.3180 | 4.6169 | 15.6310 | 6.4519 | 14.7755 | 5.3656 | 4.9047 |
| [−45°/90°/45°] | 1.05E−08 | 27.2759 | 11.0915 | 5.0608 | 26.9461 | 10.9467 | 14.2479 | 4.4455 | 4.3578 |
| [−60°/90°/60°] | 1.18E−08 | 15.7575 | 4.7019 | 3.4992 | 39.0379 | 12.3092 | 21.9477 | 3.4952 | 2.9696 |
| 20 | [0°/90°/0°] | 2.06E−07 | 304.6326 | 102.3482 | 6.3685 | 19.2816 | 6.2762 | 102.4880 | 13.7655 | 7.9295 |
| [−30°/90°/30°] | 1.44E−07 | 158.0092 | 71.2223 | 15.0004 | 60.4675 | 25.1479 | 61.1296 | 10.8575 | 14.2759 |
| [−45°/90°/45°] | 1.29E−07 | 108.8538 | 45.8082 | 16.5644 | 107.6135 | 45.2929 | 59.0214 | 9.0321 | 12.3551 |
| [−60°/90°/60°] | 1.43E−07 | 59.8252 | 19.7365 | 11.5330 | 154.4374 | 52.6199 | 80.4305 | 7.0534 | 7.9900 |
A similar conclusion concerning the more favorable stacking configuration, may be drawn for the fundamental frequency and higher ones, in Table 19.
Table 19. Non-dimensional natural frequencies for the [−θº/90º/θº] laminates.
| a/h | Stacking sequence | (1, 1) | (2, 1) | (1, 2) | (2, 2) |
| 5 | [0°/90°/0°] | 0.3535 | 0.5501 | 0.7645 | 0.8537 |
| [−30°/90°/30°] | 0.4050 | 0.6630 | 0.8061 | 0.9850 |
| [−45°/90°/45°] | 0.4220 | 0.7353 | 0.7778 | 1.0323 |
| [−60°/90°/60°] | 0.3976 | 0.6774 | 0.7444 | 0.9865 |
| 10 | [0°/90°/0°] | 0.1172 | 0.1828 | 0.3005 | 0.3164 |
| [−30°/90°/30°] | 0.1368 | 0.2458 | 0.3171 | 0.3849 |
| [−45°/90°/45°] | 0.1441 | 0.2859 | 0.2915 | 0.4243 |
| [−60°/90°/60°] | 0.1361 | 0.2424 | 0.2994 | 0.3875 |
| 20 | [0°/90°/0°] | 0.0328 | 0.0513 | 0.0888 | 0.1067 |
| [−30°/90°/30°] | 0.0392 | 0.0757 | 0.1013 | 0.1267 |
| [−45°/90°/45°] | 0.0415 | 0.0906 | 0.0914 | 0.1458 |
| [−60°/90°/60°] | 0.0393 | 0.0737 | 0.0999 | 0.1216 |
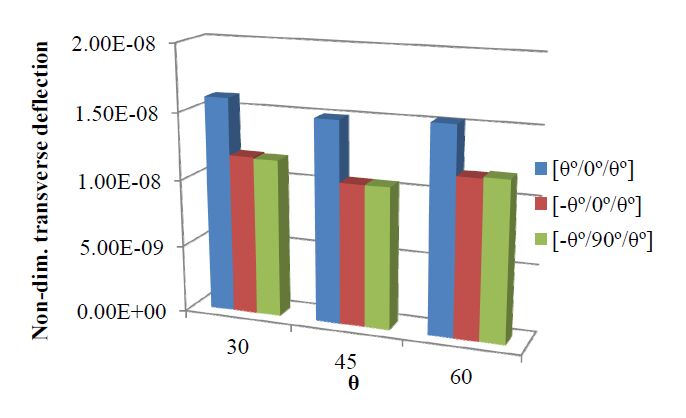
In Figure 8, by comparing the three sets of the previous deflection results for an aspect ratio a/h = 10, we conclude that for the studied laminations, the solution [−45º/0º/45º] provide a stiffer plate.
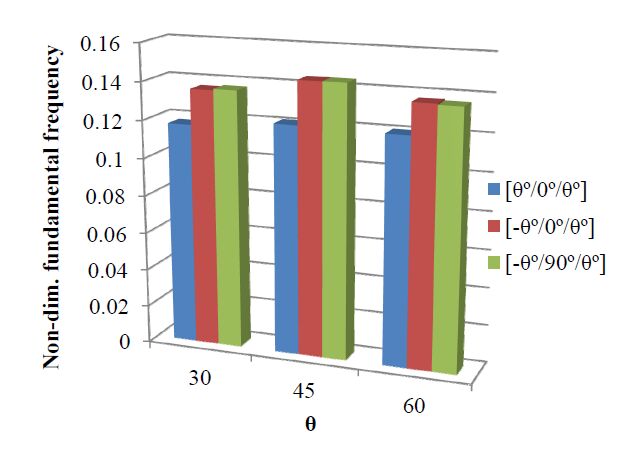
Similarly for the non-dimensional fundamental frequency, presented in Figure 9, we arrive at a similar conclusion, concerning the maximization of that frequency.
From the different configurations considered, it is possible to conclude that stacking sequences [−45º/90º/45º] and [−45º/0º/45º] would perform better.
3.2.4. Influence of Fiber Material on the Static and Free Vibrations of Three-Layered Composite Plate
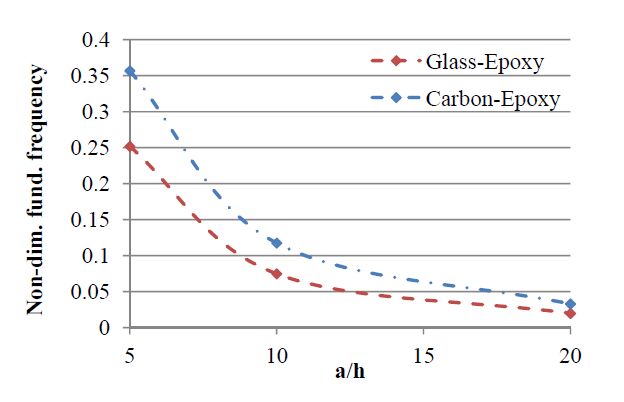
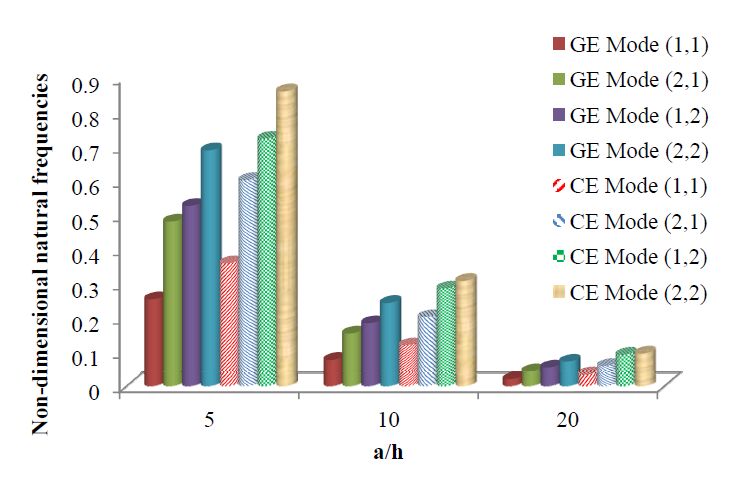
In this case study, one intends to assess the static and free vibration behavior of three-layered plates, having the same matrix phase and different reinforcement fibers. To the purpose of this study we have considered a fixed stacking sequence, namely [30º/0º/30º] maintaining the same equal thickness in all layers. The boundary conditions, loading and the discretization used are identical to the ones in the previous case studies. The material properties used in the present case, are shown in Table 1. Again the results are presented in a non-dimensional form. The results obtained can be observed in Table 20 and in Figure 10 and 11, respectively for the static and free vibrations analyses. In Table 20, GE and CE represent respectively the glass-epoxy and the carbon-epoxy composite.
Table 20. Non-dimensional deflection and stress components.
| Vf = 0.6 | a/h | ˉw | ˉσ1x | ˉσ2x | ˉσ3x | ˉσ1y | ˉσ2y | ˉσ3y | ˉτ1xz | ˉτ2xz |
| GE | 5 | 2.01E−09 | 8.8353 | 2.0988 | 2.7273 | 6.0754 | 1.6864 | 1.3079 | 2.3512 | 1.4542 |
| 10 | 2.33E−08 | 35.5669 | 11.0048 | 14.5513 | 22.3650 | 7.1129 | 5.0361 | 5.0489 | 2.9002 |
| 20 | 3.36E−07 | 142.3576 | 46.6049 | 61.7848 | 87.3974 | 28.7909 | 19.9212 | 10.4751 | 5.8138 |
| CE | 5 | 1.70E−09 | 12.0237 | 3.3023 | 4.3633 | 5.5495 | 1.3426 | 0.5884 | 2.5117 | 1.6649 |
| 10 | 1.60E−08 | 47.4375 | 12.7804 | 27.0856 | 19.6930 | 5.5572 | 2.1496 | 5.7971 | 3.3289 |
| 20 | 2.06E−07 | 188.8223 | 59.9691 | 129.9897 | 75.9990 | 24.3419 | 8.2395 | 12.4625 | 6.7458 |
From Table 20 we conclude that, as expected the carbon-epoxy composite provides a stiffer plate when compared to the glass-epoxy composite laminated plate. As previously, as the aspect ratio increases, the deflection follows the same increasing trend. The stress components accompany an identical behavior to that one already observed.
Concerning to Figure 10, it is important to note that the results are presented in a non-dimensional form (Eqn. 16). So, assuming that the linear elastic operating conditions of the structure would be not compromised, if we considered further increases in the aspect ratio, this doesn’t means that the frequencies would be the same, irrespective to the material nature. As expected, also in Figure 11 we may conclude on the stiffening effect of the carbon in the composite, yielding higher fundamental frequencies regardless the aspect ratio value.
In the legend of Figure 11, GE and CE stand respectively for glass-epoxy and carbon-epoxy. From this figure we may see extended to the higher vibration modes, the conclusion that the carbon-epoxy plates present higher frequencies’ values when compared to the glass-epoxy ones. It is also possible to globally observe that the natural frequencies present a decreasing trend for higher aspect ratios.
4. Conclusions
This work presents a study on the static and free vibrations response of sandwich and laminated composite plates, carried out through a first order shear deformation layerwise theory. The parametric analyses carried out allowed characterizing the influence of material and geometrical properties of these plates. Summarizing the results obtained in the different parametric studies carried out, it is possible to conclude on the importance of the sandwich core stiffness as well as on the nature of the reinforcement fiber and on the stacking sequence in the case of the three-layered fiber reinforced composite. The influence of the geometrical parameters considered namely the plate’s aspect ratio and the layers thicknesses was also verified in both cases. Globally, one considers that the results obtained in this parametric study, contributes to the understanding of the static and free vibrations behavior of sandwich and three-layered composite plates. It is also relevant to add that this layerwise theory, besides the achievement of a detailed kinematics description, may be computationally less expensive when compared to other equivalent single-layer higher order theories.
Acknowledgments
The authors acknowledge the support of FCT/MEC through the Project LAETA UID/EMS/50022/2013.
Conflict of Interest
All authors declare no conflict of interest.









 DownLoad:
DownLoad: