1. Introduction
Since their introduction by O’Regan and Gratzel [1], dye-sensitized solar cells (DSCs) have continuously improved their performance. The champion DSC now boasts an efficiency exceeding 13% [2]. In addition, DSCs have inspired an entire class of perovskite-based devices that have demonstrated unprecedented leaps in power conversion efficiency given the short time they have been studied, improving to 15% efficiency in 2013 and to over 20% more recently [3,4,5,6]. DSCs are an attractive solar technology due to their low production cost, ease of manufacture, and also potential for low light applications. Of the semiconductor materials that are used in DSCs, TiO2 and ZnO are reported most often [7,8]. TiO2 and ZnO are similar in that they both have large band gaps (EB, TiO2, anatase = 3.2 eV vs. EB, ZnO = 3.3-3.4 eV), [1,9,10] with the difference that ZnO has a much higher electron mobility, m, than TiO2 (mZnO = 102 cm2/V-s vs. mTiO2 = 10−5 cm2/V-s) [11,12].
Despite the higher electron mobility, studies of DSCs composed of ZnO nanoparticles have shown that their power conversion efficiencies are lower than those of DSCs composed of TiO2 [13,14,15]. The standard architecture of a DSC calls for a working electrode composed of semiconductor nanoparticles to maximize the surface area available for sensitizer adsorption [1]. For these types of nanoparticle networks, a trap-limited model has been proposed whereby excited photoelectrons must hop from particle to particle in order to exit from the semiconductor network into the collector [16,17,18,19]. In this model, electron transport through the nanoparticle network and recombination of the electrons with holes (specifically with oxidized electrolyte molecules) are both governed by trap-limited electron diffusion and are considered to be linked. As a result, the characteristic time constants for electron transport and electron lifetime (before recombination), τd and τn, respectively, are interdependent [20]. This dependence has been confirmed for ZnO nanoparticle-based DSCs by showing that the τn/τd ratio is constant over a range of illumination intensities [21] providing one explanation for why the higher electron mobility of ZnO does not lead to improved efficiencies. Interestingly, however, there is evidence that the τd/τn interdependence can be decoupled when ZnO nanoparticles are replaced by ZnO nanowire arrays [21].
When ZnO is grown into one-dimensional nanostructures, i.e., ZnO nanowire arrays, and incorporated into DSCs, enhanced electron dynamics have been observed, indicating that the high electron mobility of ZnO is being utilized [22,23,24]. For example, a ZnO nanowire array used as a DSC working electrode shows an enhanced electron transport time compared to a ZnO nanoparticle DSC (τd, array = 30 µs vs. τd, NP = 10 ms) [23]. Further, the electron diffusion coefficient, Dn, for ZnO nanowires has been estimated to be orders of magnitudes larger (Dn, NW = 0.05-0.5 cm2/s) than that of ZnO nanoparticle films (Dn, NP = 1.7 × 10−4 cm2/s [25]) based on resistivity, carrier concentration and mobility measurements performed on single, dry ZnO nanowires [24]. Comparison of ZnO nanowire array DSCs and ZnO nanoparticle DSCs by Martinson et al. [21] revealed that in the case of the nanoparticle DSC, the τn/τd ratio remained constant, whereas in the ZnO nanowire array DSC, the τn/τd ratio decreased dramatically as the photon flux increased. These observations indicate that both the shape of the ZnO material and its interconnectivity strongly affect the way electrons are transported through the DSC electrode. Although ZnO nanowire array DSCs represent a promising route, they suffer from a smaller available surface area for dye loading. Attempts to correct for the reduction in surface area have included packing nanoparticles into the voids between the nanowires or by growing dendritic 1-D structures onto underlying 1-D or 2-D structures [26,27,28,29].
In the present work, we investigate a different strategy by utilizing unarrayed solution-grown ZnO nanorods to maintain a large surface area while simultaneously leveraging the high electron mobility of ZnO. The few reports available in the literature regarding DSCs composed of unarrayed 1-D ZnO nanostructures [30,31,32] focus primarily on synthetic techniques with only one study investigating their electron dynamics using impedance spectroscopy [32]. We seek to understand whether the τd/τn interdependence can be disentangled in such devices by investigating the electron dynamics of a ZnO nanorod-based DSC over a range of illumination intensities using intensity modulated photocurrent spectroscopy (IMPS) and intensity modulated photovoltage spectroscopy (IMVS), i.e., photoelectrical techniques that measure electron transport time and electron lifetime values, respectively. Electron diffusion lengths and effective diffusion coefficients of ZnO nanomaterials are also calculated and the results are presented as a function of particle shape. Finally, we compare the performance of DSCs made from ZnO nanoparticles and nanorods under low light and standard solar testing conditions and qualitatively discuss observed differences and similarities in the context of ZnO nanomaterial shape.
2. Materials and Method
2.1. ZnO nanoparticle and nanorod synthesis and characterization
2 mmol of zinc acetate dihydrate (Fisher Scientific, Pittsburgh, PA) are dissolved per 100 ml of ethanol. Upon addition of 2 g of sodium hydroxide, a white precipitate is observed. Subsequently, the solution is continuously stirred at room temperature for 1.5 hours. The aspect ratio of the ZnO product is controlled by varying the growth time. The product is cleaned twice by centrifuging, removing the supernatant and replacing it with fresh ethanol. Next, ethanol is replaced with deionized water and the ZnO product is dispersed, frozen and freeze-dried in a lyophilizer yielding a white ZnO powder that shows the characteristic photoluminescence peak at 380 nm (see Supporting Information, Figure S1). Further characterization of the ZnO nanomaterials is performed using high-resolution transmission electron microscopy (JEOL 2100), X-ray powder diffraction (PANalytical X’Pert Pro with Cu Kα radiation 1.541Å), and high-resolution scanning electron microscopy (FEI Nova NanoSEM). Solution grown nanoparticles (grown for 1 day) and nanorods (grown for 3 weeks) are designated SG-NP and SG-NR3, respectively. Commercial ZnO nanoparticles (Strem-NP) purchased from Strem Chemicals (Newburyport, MA) are used as control.
2.2. DSC assembly and testing
Glass slides (1 cm × 2.5 cm) coated on one side with fluorine tin oxide (TEC-7) purchased from Hartford Glass Company (Hartford City, IN) are cleaned by sonication in isopropanol, followed by acetone and then deionized water. The slides are used as substrates for both the working and counter electrodes.
To construct working electrodes, 20 mg of zinc oxide powder is mixed with 10 µL of Triton-X (Acros) and 5.5 µL of acetic acid (5% solution in water) to form a paste. The paste is applied to FTO coated glass slides via doctor blading to give zinc oxide working electrodes with a thickness of 30 mm and an area of 0.25 cm2 (0.5 cm × 0.5 cm). Subsequently, the zinc oxide film is calcined at 400 °C for 30 minutes forming the working electrode of the DSC. Electrodes are then dyed by immersion in an ethanolic 0.5 mM N719 dye (Sigma Aldrich, St. Louis, MO) solution for 30 minutes. The excess dye solution is rinsed off with ethanol and the electrodes are air dried.
Counter electrodes are prepared by first drilling a pair of filling holes into the slides using a drill press. Then, a 10 nm layer of platinum is evaporated onto the conductive side of the slide. Physical vapor deposition (PVD) of platinum wire (Ted Pella) is performed using a Cressington Desktop HV Pump Station 308R-EM and Cressington Evaporation Supply LT750. A Cressington Thickness Monitor MTM-10 is used to monitor the thickness of the platinum film.
A gasket is fabricated using Surlyn tape (300 mm) and sandwiched between the working and counter electrodes. Heat is applied to seal the DSC cell together. Next, the cell is filled with 15.5 ml of redox electrolyte solution consisting of 0.5M lithium iodide and 0.05M iodine in acetonitrile. The fill holes are sealed with Surlyn tape completing the DSC assembly.
Intensity modulated photocurrent spectroscopy (IMPS) and intensity modulated photovoltage spectroscopy (IMVS) data are obtained by synchronizing two Gamry Reference 600 potentiostats. One potentiostat is used to power an LED (blue light at 470 nm) under current control, with 10% AC current superimposed on a DC current at intensities of 9, 190, and 500 mA. The second potentiostat is used to record the DSC response as the frequency of the input is modulated continuously from 10−1 to 104 Hz. Linear sweep voltammetry performed with a Gamry Reference 600 potentiostat is used to evaluate cell performance. Low light testing is performed using a compact fluorescent lamp (CFL) bulb at 20,000 lux. DSCs are also tested under standard solar testing condition of AM 1.5 using a Newport 67005 Xenon arc lamp (Oriel Instruments, USA) at a light intensity of 100 mW/cm2.
3. Results
In the following section, the ZnO synthesis products (SG-NR3 and SG-NP) and the ZnO control (Strem-NP) are characterized using electron microscopy and X-ray diffraction to confirm the identity and crystallinity of the nanomaterials and to determine particle size and shape. ImageJ software is used to measure d-spacings from TEM micrographs and to evaluate the porosity of the fabricated working electrodes from SEM micrographs. Subsequently, the working electrodes fabricated from each of the three nanomaterials are incorporated into DSCs and tested to determine the effect of particle shape and porosity on electron dynamics using intensity modulated photocurrent spectroscopy (IMPS) and intensity-modulated photovoltage spectroscopy (IMVS).
3.1. Characterization of ZnO nanomaterials
ZnO nanorods with a controllable aspect ratio are grown using a solution phase process [33]. High resolution (HR) TEM allows characterization of the particle size, particle shape, and crystallinity of the ZnO samples as shown in Figure 1. The top row (Figure 1A-C) shows the size and shape of the particles: Strem-NPs are irregularly shaped and show an average diameter of davg, Strem-NP = 13.8 ± 3.7 nm, SG-NR3s have an average diameter of davg, SG-NR3 = 11.5 ± 1.3 nm and an average length of lavg, SG-NR3 = 29.9 ± 6.9 nm and SG-NPs have an average diameter of davg, SG-NP = 6.1 ± 1.1 nm. Lattice fringes evident in Figure 1D-F indicate the single crystalline nature of the commercially available Strem-NP powder as well as of the solution-grown SG-NR3 and SG-NP powders. The d-spacings are measured using ImageJ and are indicated in Figure 1D-F. The d-spacing values of 0.28, 0.26, and 0.25 nm found in the HR-TEM images are in good agreement with the corresponding (100), (002) and (101) facets of crystalline ZnO in the wurtzite configuration.
X-ray powder diffraction is employed to further analyze the crystalline nature of the three ZnO powders used in the study. The diffraction patterns (see Supporting Information) from before calcination (Figure S2) and after calcination (Figure S3) confirm the crystalline nature of the ZnO material by exhibiting typical diffraction peaks that correspond to the (100), (002), (101), (102), (110), (103), and (112) planes of ZnO in the hexagonal wurtzite configuration (JPCDS 00-36-1451) [34]. The Strem-NP sample shows additional peaks indicating the presence of the corrosion product zinc hydrocarbonate (Zn4CO3(OH)6, JCPDS 00-11-0287), which disappears upon calcination (compare Figures S2 and S3). XRD spectra of calcined samples are taken on the FTO glass substrate resulting in typical FTO peaks at 2q = 26.8, 33.8, 37.9, 51.8, 61.7, and 65.8° (JPCDS 04-008-8135) [35]. Upon inspection, spectra of the calcined samples exhibit identical peak positions as the uncalcined samples, but decreased peak widths indicating that the ZnO crystal size increases during heat treatment. For example, for the SG-NP sample, the mean crystallite size of the powder increases from 13.2 ±2.7 nm to 30.4 ±3.1 nm. Potential origins for the increase of the crystallite size during the sintering of individual nanoparticles into a network are neck formation between crystallites and thermally induced Ostwald ripening [36].
HR-SEM analysis of the ZnO powders after they have been sintered for use as electrodes reveals that each nanomaterial produces a working electrode with a distinct surface porosity (Figure 2). ImageJ analysis shows that the Strem-NP and SG-NR3 have porosities of 21.6 ± 2.0% and 18.9 ± 4.1% respectively, while the SG-NP has the highest porosity at 34.6 ± 3.7%. Enhanced capillary coalescence due to surface tension effects [37] is a likely cause for the tighter nanorod packing observed compared to the nanoparticles. Further, it is known that the different facets of ZnO, particularly the (100) and (010) facets parallel to the long c-axis and the (001) facet perpendicular to it, possess dissimilar free energies [33]. Since the parallel facets are much more prevalent in the nanorods than in the nanoparticles, the differing free energies might also contribute to the observed divergence in packing behavior. In addition, the presence of the corrosion layer in the Strem-NP sample may lead to enhanced sintering of the Strem-NPs at elevated temperatures. The effect of the varying packing behavior on electron dynamics is highlighted in more detail in the Discussion.
3.2. IMPS and IMVS characterization of electron dynamics
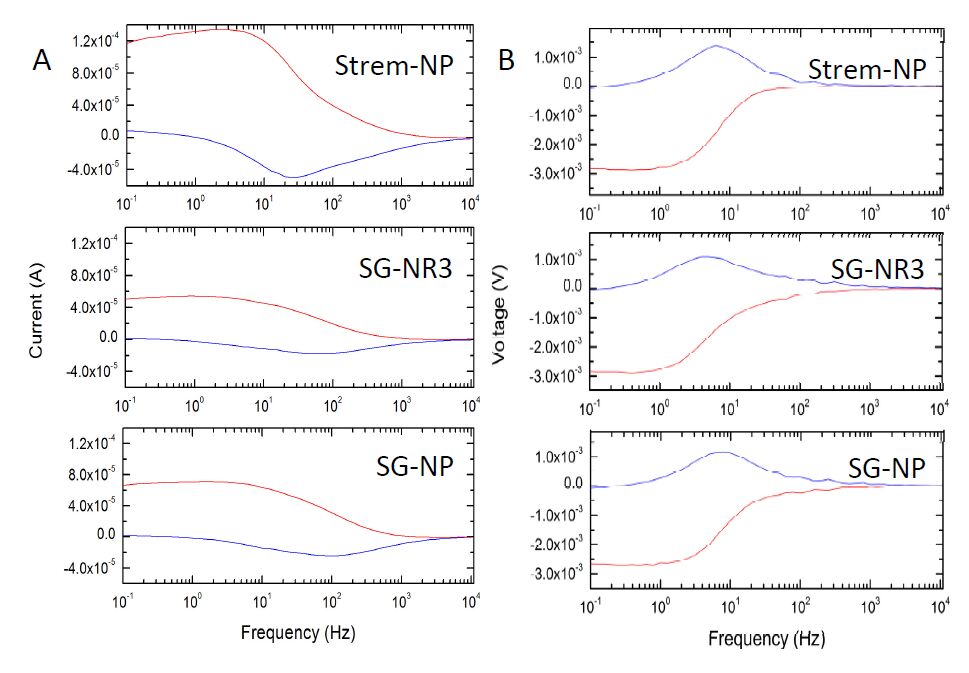
Intensity modulated photocurrent spectroscopy (IMPS) and intensity modulated photovoltage spectroscopy (IMVS) are used to investigate the impact of nanoparticle shape on electron dynamics in the DSCs. These two techniques provide information on electron dynamics within the working electrode of the DSC, giving values for the electron transport time (τd), the electron lifetime (τn), as well as parameters that can be derived from these values. IMPS testing performed at an LED intensity of 500 mA on the SG-NR3 DSCs versus the Strem-NP DSCs shows a clear shift in the imaginary component (blue curve) of the photocurrent response (Table 1 and Figure 3A top and middle). According to the IMPS theory, the frequency at which the minimum in the imaginary component occurs can be used to determine the electron transport time, τd, using the expression:
Table 1. Intensity modulated photocurrentspectroscopy (IMPS) and Intensity modulated photovoltage spectroscopy (IMVS) parameters at 500 mA: minimum frequency (fmin ), electron transport time (td), maximum frequency (fmax), electron lifetime (tn), effective diffusion coefficient (Dn), electron diffusion length (Ln), and ratio of tn/td.
| IMPS | IMVS | | | |
| DSC Type | fmin (Hz) | τd (s) | fmax (Hz) | τn (s) | Dn (cm2/s) | Ln (cm) | τn/ τd |
| Strem NP | 25.12 | 0.0063 | 6.31 | 0.0252 | 0.0014286 | 0.0060 | 4.0 |
| SG NR3 | 63.10 | 0.0025 | 3.98 | 0.0400 | 0.0036000 | 0.0120 | 15.9 |
| SG NP | 100.00 | 0.0016 | 7.94 | 0.0200 | 0.0056250 | 0.0106 | 12.5 |
The fmin peak occurs at 25.12 Hz for the Strem-NP DSC, whereas it is observed at 63.10 Hz for the SG-NR3 DSC. The values correspond to electron transport times of 6.3 ms and 2.5 ms respectively. The fmin peak is shifted even higher to 100 Hz for the SG-NP DSC (Figure 3A, bottom), resulting in a τd of 1.6 ms.
IMVS is analogous to IMPS except that in this case, the photovoltage response to a frequency modulated light source is recorded (rather than the photocurrent response) and the peak in the imaginary component is a maximum rather than a minimum. The maximum in the imaginary component of the response provides the electron lifetime, τn, using the following expression:
The IMVS results show that the SG-NR3 DSC has an fmax peak at 3.98 Hz corresponding to a τn of 40.0 ms (Table 1,Figure 3B middle). In contrast, higher fmax peak values are measured for both the Strem-NP and SG-NP DSCs resulting in shorter electron lifetimes of τn = 25.2 and 20.0 ms, respectively, (Figure 3B top and bottom).
In addition to the IMPS and IMVS results, Table 1 presents values for the effective diffusion coefficient (Dn) and the electron diffusion length (Ln), which are obtained from τd and τn values using the following relations:
where L is the thickness of the working electrode and is constant. Values for the ratio of τ
n/τ
d are also given in
Table 1 for the three DSC types at an LED intensity of 500 mA.
4. Discussion
Using results of IMPS and IMVS measurements as those shown in the previous section, it is possible to address the intriguing question of whether unarrayed ZnO nanorods allow for the decoupling of τn and τd. Additionally, the results reveal differences in electron lifetime, electron transport time, electron diffusivity and electron diffusion length owing to changes in the ZnO nanomaterial shape and working electrode porosity.
In the Introduction, the question is posed whether an elongated nanomaterial shape reduces particle hopping events that limit electron transport through a NP-based DSC working electrode. Other groups have observed markedly enhanced electron transport in ZnO nanowire arrays [21,22,23,24]. One group, Martinson et al., even reports a decoupling of τn and τd in these arrays due to τd values that are unaffected by increased illumination [21], indicating that τd can be improved such that the constant τn/τd ratio that characterizes NP-based DSCs breaks down [20]. In these ZnO nanowire arrays, it appears that the elongated shape allows for the high electron mobility of ZnO to be taken advantage of and also significantly reduces the contact points between particles.
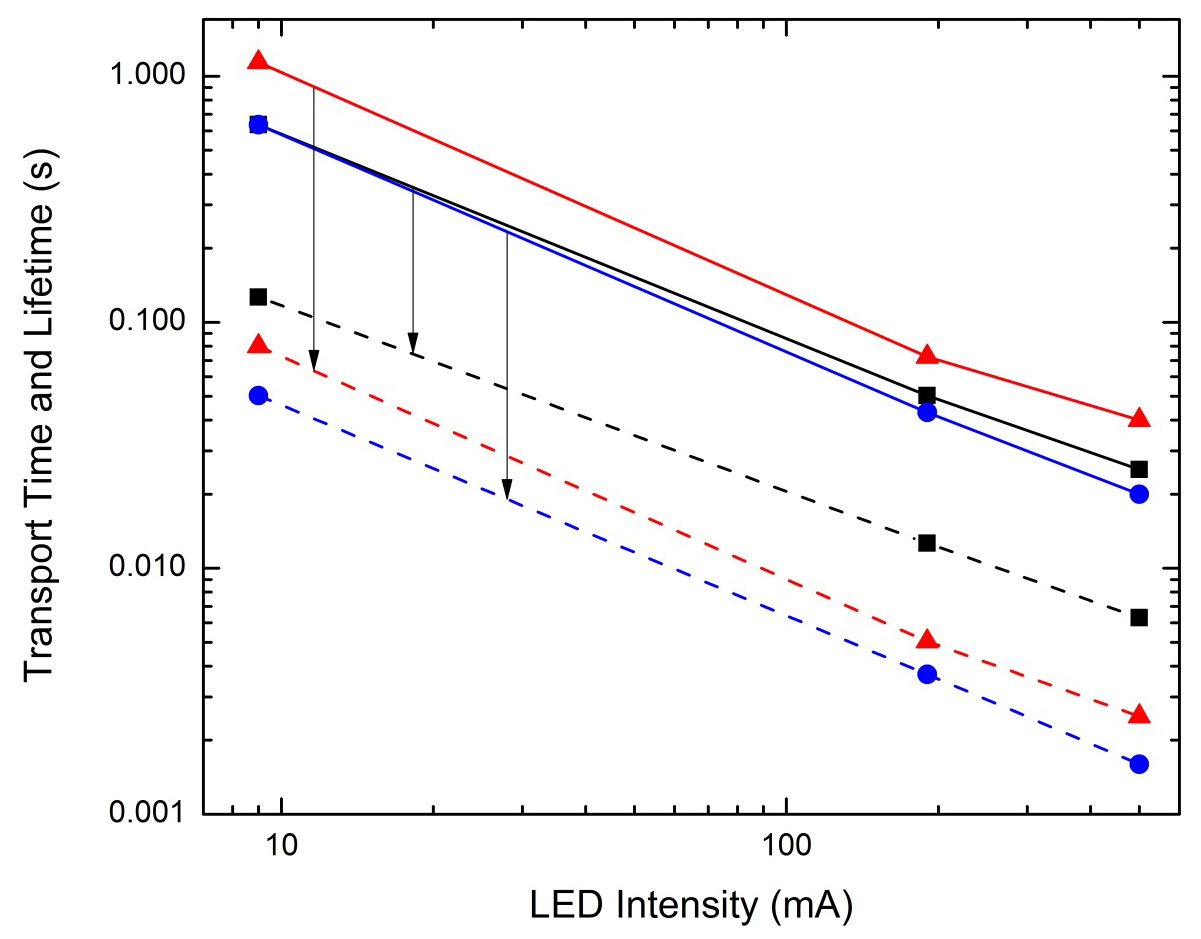
In order to determine whether the use of unarrayed ZnO nanorods leads to a similar breakdown of the τn and τd interdependence, IMPS measurements are performed at three illumination intensities (9, 190, and 500 mA) to establish whether τd remains constant as LED intensity increases in the case of the SG-NR3 DSC. In the case of the Strem-NP and SG-NP DSCs, i.e., nanoparticle DSC, τd is expected to decrease as LED intensity increases because as more photoelectrons are generated, deep electron traps present in the ZnO nanoparticles are filled, leaving only shallower traps and thus allowing for faster electron transport. While the same filling of traps is expected to occur in the SG-NR3 DSC, the reduced number of contact points, i.e., potential trap sites, in a nanorod network compared to a nanoparticle network, is expected to result in shorter τd values in the SG-NR3 DSC even at lower LED intensity and subsequently, reduced dependence at higher LED intensities. IMVS measurements are also carried out at the three illumination intensities for all three types of DSCs. As the LED intensity increases, the number of photoelectrons and holes generated simultaneously in the working electrode increases. The increased carrier density is expected to lead to accelerated recombination and a shortened τn in all three DSC types.
In Figure 4, the two NP-based DSCs (black squares and blue circles) show constant τn/τd ratios, in good agreement with the understanding of trap-limited electron transport in NP-based DSCs as τn and τd both decrease with increasing LED intensity [20,21]. Unexpectedly, the τn/τd ratio for the SG-NR3 DSC (red triangles) is also found to be constant indicating that τn and τd in the SG-NR3 DSC are not decoupled. τn decreases with increasing LED intensity as expected, but τd also shows the same inverse dependence. A rationale for the unexpected τd behavior could be that the ZnO nanorods are not long enough to allow electrons to overcome trap-limited transport in the electrodes. With the given increase in aspect ratio (from 1:1 to ~ 3:1), the SG-NR3 DSC exhibits a reduction in the number of point contacts resulting in the longer τn and shorter τd compared to the Strem-NP DSC (Figure 4). However, unlike in a nanowire array, there are still numerous contact points between the nanorods in the SG-NR3 DSC. Further investigation of ZnO nanorods with aspect ratios between the ~ 3:1 investigated here and ~30:1 aspect ratio of the nanowire array synthesized by Martinson et al. [21] is required, as well as investigation into how to reduce the frequency of contacts. Nevertheless, the measurements summarized in Figure 4 are instructive because they demonstrate that a change in ZnO nanomaterial shape improves DSC electron dynamics.
Interestingly, the ZnO nanorod DSC exhibits the highest electron lifetimes over the range of intensity values studied when compared to both types of nanoparticle DSCs (see solid lines in Figure 4). Since the SG-NR3 DSC has a longer electron lifetime than either the densely packed Strem-NP DSC or the loosely packed SG-NP DSC, the IMVS results indicate a clear influence of particle shape uncomplicated by packing behavior. τn is a measure of how long an electron can survive in the working electrode before it recombines with a hole. In the Strem-NP and SG-NP DSCs, each time an electron crosses from one nanoparticle to another, it can potentially recombine with a hole, for example, an oxidized electrolyte molecule. The same holes are present in the SG-NR3 DSC, however, because of the increased length along one axis of the nanorod, electrons can reach the anode while crossing fewer junctions and therefore experience fewer potential recombination events. The longer electron lifetime measured for the SG-NR3 DSC may be a reflection of this lower probability of recombination.
With regard to the electron transport time, τd, the IMPS results show that electrons exit the working electrode of the SG-NR3 DSC more rapidly than that of the Strem-NP DSC. This behavior is observed for a range of intensities as shown in Figure 4 (dashed lines) and indicates that the difference in particle shape (nanorod versus spherical nanoparticle) affects τd. In particular, the high electron mobility of ZnO contributes to the faster τd in the SG-NR3 DSC compared to Strem-NP DSC because electrons can take advantage of this material property when moving through the 1-D structure of the nanorods, but cannot do so in a nanoparticle-based electrode. Additionally, the IMPS result for the SG-NP DSC suggests that particle packing has an important influence on τd as well. The SG-NR3 DSC and Strem-NP DSC have similar porosities (Figure 2) and therefore the difference in their electron transport times is attributed to the effect of shape. This argument is further supported by the similar working electrode surface areas available for dye loading calculated for the Strem-NP DSC and the SG-NR3 DSC of AS, Strem-NP DSC = 6.42 × 1016 nm2 and AS, SG-NR3 DSC = 6.14 × 1016 nm2, respectively (see Supporting Information). Meanwhile, the SG-NP DSC has the shortest τd of all three DSC types, is also the least densely packed, and has the highest working electrode surface area of AS, SG-NP DSC = 1.72 × 1017 nm2 (see Supporting Information). Since the SG-NP DSC has more than twice the working electrode surface area for dye loading compared to the Strem-NP and SG-NR3 DSCs, a shorter τd is expected due to a higher electron density and the increased filling of shallower traps in the SG-NP DSC. The result for the SG-NP DSC is also in agreement with a trap-limited model of electron transport. Electron transport through a porous nanoparticle network as described by this model proceeds by an electron hopping mechanism that is quite slow due to the vast number of particles an electron must visit in order to reach the anode. If the number of particles is reduced (i.e., lower density particle packing), the electrons will encounter fewer nanoparticles and electron transport times decrease as is observed for the SG-NP DSC. This observation also suggests that a method for decreasing the τd of the SG-NR3 DSC further is to increase the porosity of the working electrode. One idea is to fabricate ZnO nanorods with magnetically addressable capped ends that can be assembled into an ordered porous structure, thereby limiting the number of junctions and decreasing τd. The open structure would also be more compatible with solid polymeric electrolytes and viscous electrolytes such as ionic liquids.
An additional conclusion from Figure 4 is that the magnitude of the τn/τd ratio is greatest for the ZnO nanorod DSC compared to the ZnO nanoparticle DSCs. This can be discerned from the length of the arrows connecting the τn and τd values for each type of DSC and the calculated τn/τd ratios are also given in Table 1. The result indicates that the SG-NR3 DSC gives photoelectrons a better chance of percolating through the working electrode before they recombine since the electron lifetime is proportionally longer than the transport time in the nanoparticle DSCs.
As for the calculated electron diffusion coefficients, as expected, Dn is higher for the SG-NR3 DSC than for the Strem-NP DSC, because the effective diffusion coefficient and the measured electron transport time are inversely proportional. Regarding values for Ln, the electron diffusion length is greatest for the SG-NR3 DSC. It is twice as long as that for the Strem-NP DSC and slightly longer than that for the SG-NP DSC. Because Ln depends on τd, the differences in particle packing that affect τd should also have an effect on Ln. However, any decrease in τd due to looser particle packing would be at least partially offset by a decrease in τn as well. This can be seen in the case of the SG-NP DSC (see Table 1). It exhibits the lowest τd (1.6 ms) as well as the lowest τn (20.0 ms), both of which can be explained by its less dense working electrode packing. Due to such packing, an individual nanoparticle has fewer neighboring particles, i.e., fewer contact points. This shortens τd while also exposing the particles in the SG-NP DSC to greater interfacial contact with hole-conducting species in the liquid electrolyte, making recombination more likely and reducing the electron lifetime. Referring to Equations (4) and (5), it can be seen that the effect of low density packing is to increase Dn (since τd and Dn are inversely proportional) but to lower τn. In calculating Ln, the two values offset each other and the effect of particle packing on Ln is diminished. Therefore the fact that Ln is measured to be highest for the SG-NR3 DSC is significant because it suggests the nanorod shape gives the longest electron diffusion length, regardless of differences in particle packing among the three DSC types. In general, Ln > L is a requirement for a well-functioning DSC. The lowest Ln value obtained, 60 µm for the Strem-NP DSC, is twice the working electrode thickness of L = 30 µm. While Ln > L is routinely achieved for a functional DSC, a longer Ln could be of benefit in some types of highly porous DSCs that attempt to accommodate solid state or ionic liquid electrolytes. Nanorod DSCs could be useful for this purpose. They might also be useful in attempts to replace the iodide/triiodide couple in the electrolyte. If the kinetically slow recombination of photoelectrons with triiodide is replaced by a different, faster recombination reaction, τn will likely drop. However, if as seen with the ZnO nanorods, the DSC already exhibits a higher τn, perhaps such a system will tolerate faster one-electron redox systems.
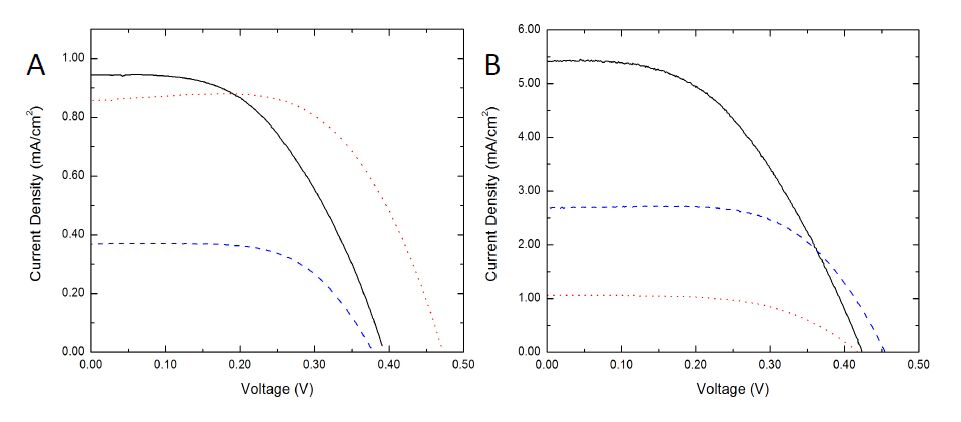
Finally, the J-V characteristics of ZnO DSCs with the three nanomaterials at low light and standard solar testing conditions are provided for completeness in Figure 5A and B, respectively. Under low light testing conditions (Pin = 2.9 mW/cm2), the short circuit density, JSC, for the SG-NR3 DSC is 874 ± 143 µA/cm2 and 933 ± 116 µA/cm2 for the Strem-NP DSC. For the SG-NP DSC, the JSC is 394 ± 51 µA/cm2. Meanwhile, under low light, the open circuit voltage, VOC, for the SG-NR3 DSC is 467 ± 8 mV compared to 387± 10 mV for the Strem-NP DSC and 381 ± 9 mV for the SG-NP DSC. The DSCs are also tested under standard solar testing conditions (Pin = 100 mW/cm2) and exhibit a JSC of 0.92 ± 0.18 mA/cm2 for the SG-NR3 DSC, 5.69 ± 0.22 mA/cm2 for the Strem-NP DSC, and 2.85 ± 0.16 mA/cm2 for the SG-NP DSC. The VOC values are 416 ± 11 mV for the SG-NR3 DSC, 435 ± 11 mV for the Strem-NP DSC, and 457 ± 9 mV for the SG-NP DSC.
A direct quantitative comparison between the J-V curves for the three types of DSC electrodes is difficult, because of variations in actual surface area and light harvesting efficiency [21]. However, several qualitative observations can be made regarding trends in JSC taking into account the estimated surface area available for dye loading and the inter-particle pore size (see Supporting Information). The working electrode surface area for the Strem-NP DSC (AS, Strem-NP DSC = 6.42 × 1016 nm2) is slightly larger than that for the SG-NR3 DSC (AS, SG-NR3 DSC = 6.14 × 1016 nm2). The electrode surface areas are in good agreement with the measured JSC values because increased dye loading correlates with a larger JSC (see Figure 5A). In contrast, the SG-NP DSC has the largest calculated surface area (AS, SG-NP DSC = 1.72 × 1017 nm2) and also the shortest τd as measured by IMPS (see Figure 4), but the lowest JSC. A rationale for the inverted trend might be the 5x smaller inter-particle pore size in the SG-NP DCS electrode, which might hinder diffusion of both the N719 dye during impregnation and the electrolyte components (acetonitrile, iodide ions, and triiodide ions) during operation. The molecular/hydrodynamic radii of these species range from 0.1 to 1 nm [38,39,40]. The hindered mass transport of ions might also explain why the shorter τd of the SG-NP DSC (see Figure 4) does not translate into a higher JSC when the SG-NP DSC is under operation. Further, the observed 80 mV upward shift in VOC for the SG-NR3 DSC can be explained by the longer electron lifetime in the SG-NR3 DSC compared to Strem-NP and SG-NP DSCs (see Table 1). Similar shifts in VOC have been reported by other groups for TiO2-based DSCs [41,42]. An increased VOC is an indication of an upward shift in the Fermi level of the DSC semiconductor due to an increase in electron density [43]. In the SG-NR3 DSC the increase in electron density results from the longer electron lifetime. Further, an increase of illumination from low-light to standard AM 1.5 solar testing conditions results in increased current densities as expected (Figure 5B). However, the magnitude of increase shows some variation among the three DSC types. More studies are underway to identify the origin of these variations.
5. Conclusion
Overall, the results demonstrate that nanoparticle shape is a parameter that affects electron dynamics in ZnO DSC electrodes. We observe that nanorod-based DSCs exhibit shorter electron transport times, longer electron lifetimes and a high τn/τd ratio compared to nanoparticle DSCs. When the τn/τd ratio is measured as a function of increasing illumination intensity, we find that nanorods of ~3:1 aspect ratio do not yet allow electron transport to be decoupled from electron recombination. It is proposed that if the aspect ratio is increased, and porosity is increased so as to reduce the number of point contacts, electrons can overcome trap-limited transport and take advantage of the higher electron mobility associated with ZnO.
Acknowledgments
This work was supported by the Center for Exploitation of Nanostructures in Sensors and Energy Systems (CENSES) at the City College of New York. The authors would like to acknowledge the CUNY Advanced Science Research Center for use of their FEI Nova NanoSEM. Additionally, we would like to thank Nicholas Proscia, Steven Vallone and Professor Luat Vuong at Queens College for their help with solar testing and IMPS/IMVS measurements.
Conflict of Interest
The authors declare no conflicts of interest regarding this paper.










 DownLoad:
DownLoad: