Phosphate deposits in south-western Iran are part of the South Tethyan Phosphogenic Province, a huge carbonate-dominated strata that extends to the Middle East. The Tethyan phosphorites of Iran are dated Eocene-Oligocene (Pabdeh Formation) and categorized as low-grade ore deposits on a global scale. Depositional conditions of the facies indicate that the Pabdeh Formation was deposited on a carbonate ramp setting as a distally steepened ramp. Under such an environment, turbidity currents transported phosphate particles from the back-shoal setting to the deeper middle and outer ramp of the ocean where they were suspended and deposited as shell-lag and phosphate lamination. Microfacies studies demonstrate that all the phosphatic ooids and phosphatized foraminifera, fish scales, bones and phosphatic intraclasts reworked from shallow parts of the Tethyan Ocean to deeper parts with the help of turbidity currents. Analysis and interpretation of the data reveal positive correlation between. REE+Y and P2O5 in all studied sections which attests to their strong coherence as a geochemical group. The shale normalized REE patterns of Mondun phosphorites are characterized by negative Ce anomalies. This anomaly indicate that the depositional environment was oxic and highly reworked, bioturbated with higher energy realm during phosphate deposition, conversely Nill section with Ce enrichment reflect conditions of relatively deeper water sedimentation. These geochemical findings are in accordance with microfacies studies which indicate shallow and high energy condition for Mondun section with negative cerium anomalies and a deep ramp setting for Nill and Siah sections which denote a positive cerium anomalies in REE patterns.
1.
Introduction
The Zagros fold and thrust belt extends from south Turkey through Iraq to southwest Iran and is about 1800 km long and 150 km wide. The belt is associated with a foreland basin and represents the oldest and richest hydrocarbon zone in the area [1]. The late Palaeocene to early Oligocene Pabdeh Formation and the underlying Gurpi Formation are known for their potential oil reserves. The Pabdeh Formation, with a thin (1–3 m), purple, sandy to silty shale at the base, overlies a highly weathered, glauconitic-rich layer (the top of the Gurpi Formation) which indicates a significant unconformity [2]. Palaeontological data suggests a missing period of about 10 my for this unconformity [3].
The Pabdeh Formation in the study area consists of thin- to thick-bedded limestones alternating with dark to light grey shales and green to grey marls, rich in planktonic microfauna. In most parts of the Zagros, especially in the Dezful embayment, this formation is described as a fine-grained, matrix-rich, carbonate-dominated succession with some hydrocarbon source potential [4,5,6]. Although many studies have been carried out on its potential oil reserves, the Pabdeh Formation has rarely been investigated for its phosphate bearing horizons.
This study investigates the facies characteristics, precise potential and depositional conditions of the phosphate-bearing horizons of the Pabdeh formation in the best outcrops of the Zagros region. We reconstruct the depositional environment of the Pabdeh Formation with emphasis on the phosphate and non-phosphate horizons using microfacies studies and sedimentary, geochemical and fossil evidence. This study focuses on the phosphate-bearing horizons of the Pabdeh formation and presents the first fully integrated geochemical study of the Pabdeh Formation, highlighting the key similarities and differences between the phosphate-bearing horizons. This work addresses the abundances of major, trace, and rare-earth elements, their distribution patterns and inter-element relationships.
2.
Geological setting and stratigraphy
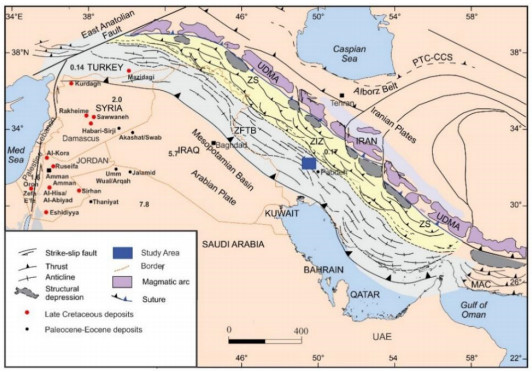
The NW–SE trending Mountains of west and southwest Iran are parts of the Alpine–Himalayan orogenic belt, known as the Zagros belt [7]. The Zagros belt represents the NE margin of the Arabian plate, in which discontinuous deposition occurred from the very late Precambrian to the Late Miocene [2,8]. This fold and thrust belt is a result of the structural deformation of the Zagros (peripheral) proforeland system, whose present-day expression is the marine Persian Gulf and continental Mesopotamia basins [9,10,11,12], and the underlying preproforeland, mostly platformal and continental shelf deposits. The closure is related to the Arabian Plate subduction beneath the Central Iran block that was formed in the Late Cretaceous [2,8,13,14]. Subsequently, the collisional mountain-building that began in the Middle Maastrichtian (about 68 Ma) has continued with variable intensity until recently [2]. This collision led to the closure of the Neo-Tethys basin and the formation of the Zagros foreland basin with a sedimentary record from the Late Cretaceous until recently [15]. The deep-marine Pabdeh Formation with hemipelagic-pelagic calcareous shale, marl, and lime mudstone with subordinate argillaceous limestone was deposited in the Zagros proforeland basin during the Early Eocene to Oligocene. Most studies relate the depositional environment of the formation to a ramp setting [16,17,18,19]. Evidence of a deep marine environment [20] and pelagic conditions with common gravity flows [21] can be observed in places (Figure 1).
Mohseni and Al-Aasm [17] and Mohseni et al. [18] found evidence of marine currents and storm deposition during the late depositional stages of the Pabdeh Formation. Moreover, some carbonate tempestites were reported in the stratigraphic record of the formation [17,22,23,24,25,26,27,28,29,30].
In Iran, the Tethyan phosphorites are restricted to the Eocene-Oligocene Pabdeh Formation. The phosphatic layers of the Pabdeh Formation are categorized as a low-grade ore deposits in the world. The average grade of phosphate in Pabdeh is 8–12% P2O5 whereas the average grade of Tethyan phosphorite deposits is 25–30%.
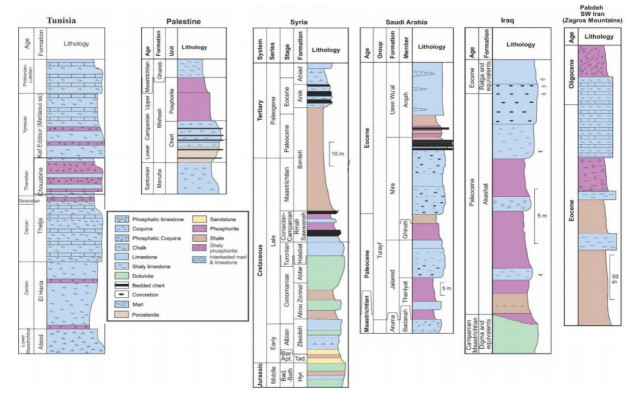
The eastern Mediterranean region and North Africa hold more than half the world’s phosphorite resources, amounting to about 80 billion tonnes of high-grade commercial phosphorites [32,33,34]. These deposits form part of the Late Cretaceous to Eocene Tethyan Phosphorite Regime that extends through North and northwest Africa, and into parts of the Caribbean and Columbia and Venezuela in northern South America [31,35,36,37,38,39]. These tectonic activities were responsible for setting the scene for the formation of the major phosphorite deposits in the eastern Mediterranean region and throughout the Tethys realm [31]. The Pabdeh Formation is related to Mediterranean phosphatic belt formations such as the Akashat in Iraq [40], Jalamid, Mira and Umm Wu’al and Dammam in Saudi Arabia, Sawwaneh, Rmah and Bardeh in Syria, Mishash (Palestine), Thelja (Tunisia), Vilga, Abu tarbur, Al-Hisa (Jordan) and Usfan (Saudi Arabia) (Figure 1).
The Akashat Formation is predominantly exposed in the western parts of the Iraq. This Formation, consists of alternation of grey phosphorites and limestones [41] with phosphatic conglomerate or breccia. Depositional environment indicates inner to outer shelf, under subtidal and warm conditions.
The type locality of the Dammam Formation is on the Dammam dome in Saudi Arabia [40]. This Formation which was revealed by Bramkamp [42] consist of sequence of shallow water shelf carbonates interbedded with marls.
Economic phosphorites of Palestine are concentrated in the upper part of the Mishash Formation. The Mishash Formation is of late Campanian in age and forms the uppermost part of a shallow marine epicontinental sediments in Negev region of Palestine phosphorites [43,44].
Tunisia is one of the largest producers of rock phosphate in the world. In Tunisia, significant deposits of phosphorites are found in the Gafsa basin dated Paleocene to early Eocene [45]. The sedimentary rocks are of the Metlaoui group [46], specifically the Thelja Formation [47] which is overlain by the Chouabine Formation and overlies the El Haria Formation [46] (Figure 2). The Ypresian Chouabine Formation contains massive phosphorite layers which alternate with marly limestone, marls and silica-rich layers [48,49,50,51,52,53]. Sedimentation in the Gafsa-Metlaoui Basin occurred in a relatively restricted setting, which fluctuated between littoral and lagoonal conditions, resulting in rhythmic or episodic sedimentation [52,53]. The Thelja Formation is made up of shallowing-upwards, evaporitic cycles. The Thelja Formation series forms a pattern of nine principal facies that show a gradual transition from offshore marine facies to Sebkha facies with no slope deposits along a gentle inclined platform [54] (Figure 2).
Phosphate deposits in south-western Iran are part of the South Tethyan Phosphogenic Province (STPP), a huge carbonate-dominated Upper Cretaceous to Eocene phosphorite strata that extends from Colombia, through Venezuela, north and northwest Africa to the Middle East [37].
High-grade phosphorites in Syria are limited to the southeastern parts. Rmah Formation is composed of fossiliferous interbedded marl, limestone, dolomite and some chert nodules, overlain by alternations of bedded chert, limestone and thin phosphorite units. Sawwaneh Formation contains the major Syrian phosphorite deposits. The formation consists of marly limestone interbedded with phosphorites.The upper part of the formation is dominated by marl and marly limestone overlain by a glauconitic-phosphatic marl.
Phosphate deposits in northern Saudi Arabia occur in Hazm El-Jalamid, Mira, and Umm Wu’al Formations of the Turayf Group (Paleocene and middle Eocene) (Figure 2). The total thicknesses of the phosphorite beds range between 3 m and 5 m, with up to seven discrete beds [55]. Sedimentary facies analysis of the Hazm Al-Jalamid phosphorites suggests that these phosphorites represent transgressive lag deposits that accumulated in an oxic, bioturbated, and wave dominated shelf environment that developed as a result of the Campanian transgressions of Tethys [56].
The above information suggests that in contrast to the eastern Mediterranean region and north and northwest Africa, where phosphate deposits formed in shallow marine depositional environments and evaporitic cycles, the phosphate horizons of the Pabdeh Formation were formed in a deep marine environment. The condition is in accordance with palaeogeographic map of Tethyan Phosphorite Regime which extends through the eastern Mediterranean region to north and northwest Africa (Figure 3).
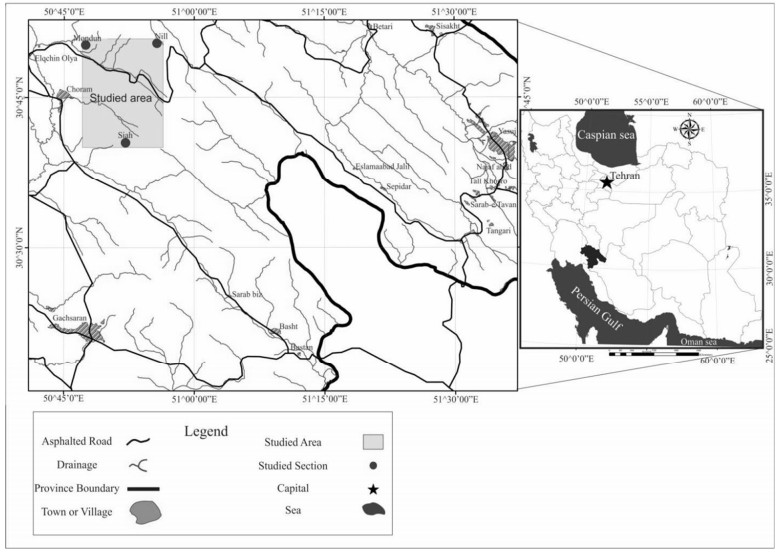
The study area is located in the Zagros fold and contains the best outcrops of the Pabdeh Formation. Three sections (Nil, Siah and Moundun) of the formation with a total thickness of 1122 m were investigated in this study (Figure 4). In the Nil anticline (115 km north of the city of Gachsaran), the formation consists mainly of interbedded thin to medium limestone, marl and dark grey shale with a total thickness of 512 m. In the Siah Anticline (60 km north of Gachsaran) the formation consists of thin to medium bedded limestone interbedded with shale and marl with a total thickness of 255 m. The Pabdeh Formation at the Mondun Section (85 km north of Gachsaran) is 355 m thick and consists of interbedded limestone and marl at the base and interbedded shale, marl and thin bedded limestone at the middle to top of the formation. The formation is Early Eocene to Oligocene in age and is overlain by the Oligo-Miocene Asmari Formation and lies above the late Cretaceous Gurpi Formation in the studied sections.
2.1. The Nill section
The Nill Mountain is a well-developed anticline in which the Gurpi, Pabdeh and Asmari formations are exposed. The bottom of the section contains the upper part of the Gurpi Formation (6 m thick) that consists of thin to medium bedded grey marl interbedded with thin layers of argillaceous limestone. Results from petrographic studies of this formation show a dominance of pelagic facies with Globotruncana sp. (see Supplementary) The purple shale unit has not been exposed and alternating layers of dark grey shale and thin bedded limestone of the Pabdeh Formation unconformably overly the Gurpi Formation. Field evidences demonstrate that the Asmari Formation conformably overlies the Pabdeh Formation in this section. The base of the Asmari Formation shows alternating medium to thick bedded limestone and marl which gradually change to thick bedded limestone (Figure 5).
The Pabdeh Formation in Nill section composed of alternating bioturbated argillaceous limestone and black shales at the bottom. Rhythmic alternations between limestone, green marls and dark gray marls. The top of the Formation represents alternating marls and limestone horizons of varying thicknesses with abundant benthic foraminifera. Three phosphatic units developed within the Formation, separated by alternating dark grey shale and thin bedded limestones. The average total thickness of the phosphatic beds is 12 m. The first phosphatic horizon is dominated by phosphatized limestone with an average thickness of 6 m. The second phosphatic horizon consist of thin bedded limestone intercalated with phosphatized shale and marl with a total thickness of 2 m (Figure 6). The third phosphatic horizon is 4 m thick. The average grade of the phosphatic layers is 2.94% P2O5. Biostratigraphic studies of planktonic foraminifera and the presence of Orbulinoides beckmani (Supplimentary) indicate a Lutetian and Bartonian age for the second and third units respectively.
2.2. The Mondun section
The Mondun Anticline with a NW–SE trend is located 85 km north of Gachsaran. In this anticline the Pabdeh Formation (355 m) occurs on top of the Gurpi limestones with a distinct unconformity. The formation is divided into four stratigraphic units based on their sedimentological characteristics and fossil content (Figure 6). The purple shale unit at the base of the Pabdeh Formation has not been exposed in this outcrop, hence the lower part of the formation is greenish grey marl associated with thin interlayers of argillaceous cream limestone (25 m thick). Foraminiferal fauna indicates Hantkenina nuttalli, Pseudohastigerina wilcoxensis, Dentoglobigerina yequaensis and Globigerinatheka index (Supplimentary). The second stratigraphic unit (120 m) is marked by thin to medium bedded limestone. The presence of planktonic foraminifera such as Acarinina wilcoxensis, Acarinina collactea, Acarinina bullbrooki and Pesudohastigerina wilcoxensis (Supplimentary) demonstrates that this horizon is of Early Eocene (Ypresian) age. The third stratigraphic unit (50 m thick) is characterized by alternating layers of dark grey shale, grey marls and thin bedded limestones. The forth part of the formation (135 m) is dominated by greenish grey shale with intercalation of thin to medium bedded beige to yellow pelagic limestone. This part is the uppermost part of the formation. Microfacies studies show well-rounded, well-sorted bioclastic, phosphatic, foraminiferal/oolitic grainstone (See section 4.3.1). All four horizons contain laminated and phosphatized-bedded bioclastic packstone.
The phosphatic horizons are present in five stratigraphic levels (from bottom to the top: layers I-V, Figure 6) separated by thin bedded planktonic foraminiferal-bearing limestones. All phosphatic horizons composed of phosphatized limestone. Their P concentration is commonly high (III and IV ~23% P2O5), and their carbonate content (mostly calcite) is generally high as well. The first and the second horizons (I and II) composed of alternations of phosphate-rich and carbonate-rich laminae.The P2O5 grade of these horizons are 5.51% and 5.08% respectively. The third phosphorite horizon consists of grainstone (1 m thick) facies with small phosphatized pellets, ooids, intraclasts and planktonic foraminiferal tests, fish scales and bones with the average grade of 25.12% P2O5. This is a well-sorted facies, in which the main allochems are dominantly superficial ooids and pellets (See section 4.3.1). Minor allochems are foraminiferal tests, fish scales and bones (Figure 7). The most distinctive feature of the third phosphatic layer (III) is the existence of ooid and pelletal phosphatized grains. The phosphate fraction of this horizon typically consists of medium-sized (>200 µm) phosphate grains, various amounts of phosphatized intraclasts, fish scales and bones. The common features of the fourth and fifth (V) phosphorite horizons is Shell-lag bedsand and the average grade are 22.32% and 4.12% respectively. The average total thickness of the phosphatic beds is 5 m.The Mondun phosphorite units are more lithologically and facially diverse than the others in the study area (See section 4.3.1). They are light brown, lithified, phosphatized pellet and oolite-rich and locally phosphatized granular beds, and exhibit distinctive high-grade mineralization in some levels. The average grade of the phosphatized layers in all horizons is 12.43% P2O5.
2.3. The Siah section
The Pabdeh Formation on the north flank of the Siah anticline (60 km north of Gachsaran) is 255 m thick. The formation is divided into four stratigraphic units based on the sedimentological characteristics and fossil content (Figure 6).
The lower lithostratigraphical unit above the Gurpi Formation contains thin bedded purple shale (~2 m thick) which considered as a key layer of Pabdeh Formation in zagros region. The second stratigraphic unit (95 m thick) is marked by thin to medium bedded limestone. The third stratigraphic unit (98 m thick) is characterized by alternating layers of dark grey shale, grey marls and thin bedded limestone. The fourth unit of the formation (57 m thick) is dominated by greenish grey marl with intercalation of thin to medium bedded beige to yellow pelagic limestone. This is the uppermost part of the formation. The upper lithostratigraphic boundary with the Asmari Formation is transitional.
The phosphatic horizon (5 m thick), which is located 127 m from the bottom of the section (In the third stratigraphic unit), consists of phosphatized limestone. Field observations found sedimentological structures on these phosphatic horizons such as shell-lags, hummocky cross stratification and ripple marks on the top of the beds. The average grade of the phosphatic horizon is 5% P2O5.
3.
Materials and method
Systematic sampling to examine the lithological variation was carried out in the sections. A total of 487 thin sections from the samples were prepared for petrographic studies (191 from the Nill, 170 from the Mondun and 126 from the Siah sections). The facies analysis was based on the petrographic studies (microfacies description) and field observations (lithofacies description). The geometry of the sedimentary structures, the depositional textures, grain size, macrofaunal and trace fossil content, stratal surfaces and the stacking pattern of the facies were studied in the field. The microfossil content, lithology, depositional texture, and diagenesis were investigated in petrographic studies. We collected 37 samples from the phosphate horizons. Major and Trace element of whole rock analyses were analyzed at Kansaran Binaloud Co (Tehran, Iran). Major-elements [SiO2, TiO2, Al2O3, Fe2O3 (T), MnO, MgO, CaO, Na2O, K2O, P2O5] and selected trace elements (TEs: Ba, Sr, V, Y, Zr) determinations were obtained by Inductively Coupled Plasma - Atomic Emission Spectrometry (ICP-AES) analysis. Other TEs (Hf, Mo, Nb, Rb, Th, U) along with rare-earth elements (REEs): La, Ce, Pr, Nd, Sm, Eu, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu), were obtained by ICP-mass spectrometry (ICP-MS) analysis of the fusion solutions. Detection limits were 0.01% for all the major elements except MnO and TiO2, for which the limits were 0.001%. The detection limits (ppm) for the TEs were: Sc, Th, U, 0.1; Hf, Sb, 0.2; As, Br, Cd, 0.5; Cu, Nb, Ni, Zn, 1; Mo, Rb, Sr, Y, 2; Ba, 3; Zr, 4; Cr, V, 5. The detection limits (ppm) for the REEs were: La, Ce, Nd, Sm, Gd, Tb, Dy, Ho, Er, Yb, 0.1; Pr, Eu, Tm, 0.05; Lu, 0.04. The XRD analysis was implemented at Kansaran Binaloud Co (Tehran, Iran).
Detailed palaeontological studies and biostratigraphic analysis of the samples were carried out using the biozonation model proposed by Wade et al. [58]. The microfacies classification of the carbonates was based on Dunham [59], Wilson [22] and Flugel [60].
4.
Results
4.1. Petrography and mineralogy
Petrographical studies were performed using a Zeiss Axioplan 2 Polarized Light Microscope (Islamic Azad University, Science and Research branch, Tehran, Iran) and denote that calcite, quartz, pyrite and orthoclase are the gangue minerals. The Pabdeh Formation consist of a large variety of skeletal and non-skeletal grains, calcite cements and micrite. Differences in the abundance of allochems exist between the 3 study sections.
Non-skeletal grains are abundant in the Mondun anticline and consist mainly of ooids, intraclasts and peloids (Figure 8). The nuclei of ooids are commonly peloids, and in some cases the nuclei consist of the foraminiferal test. Intraclasts are present in all samples of the Nill, Mondun and Siah anticlines. Most intraclasts are consist of phosphate, while others contain bioclasts and peloids. Peloids are recognized in all sections, but are more abundant in Mondun anticline than in the Nill and Siah anticlines. In Phosphatized horizons of Mondun section, most pellets are uniform in size and have the small, similar-sized, well-sorted, uniform-shaped and orange colored. Skeletal grains are mostly, crinoids, bryozoas, ostracoda and plentiful planktonic and benthic foraminifera. Benthic Foraminifera such as Heterolepa sp, Haplophragmium sp., Elphidium sp., Reusella sp., Nephrolepidina sp., Pseudolituonella reichelli and Pyrgo sp and planktonic foraminifera such as Acarinina sp., Morozovela sp, Globigerinatheka sp, Turborotalia sp, Hantkenina sp., and Globigerina sp. (see Supplementary).
Intergranular space within the phosphatic and non-phosphatic grains display variable cementation by calcite (as a micrite, microsparite and rarely sparite). In phosphatized horizons these may also replace by the phosphatic grains. Petrographic studies shows similarities in the phosphatic constituents (pellets, phosphatized intraclasts, ooids, bioclasts including bone and teeth) of Pabdeh Formation in comparison with the different deposits, but distinct variation in the non-phosphatic constituents (quartz, glauconite, lithoclasts, calcitic bioclasts and microcrystalline agammaegates of carbonate minerals) was observed. Nonphosphatic constituents in the Pabdeh Formation phosphorites are dominated by calcite. Accessory minerals include glauconite and sulphides (pyrite) are present in some beds.
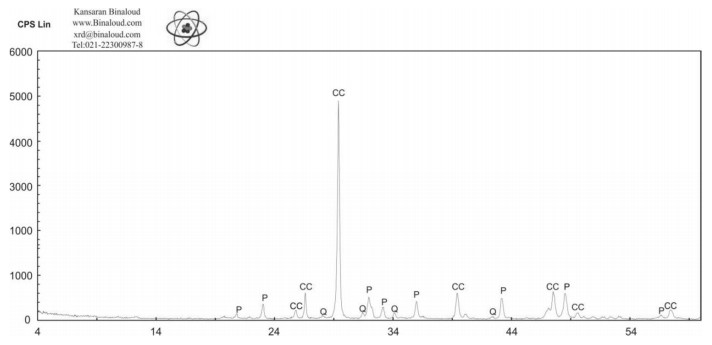
The results of the XRD analysis (Figure 9) demonstrate that the phosphatic ore minerals in the Pabdeh Formation are composed predominantly of fluorapatite while the associated gangue minerals include calcite, quartz, clay minerals (kaolinite, illite), pyrite and feldspars (orthoclase and albite).
The results of XRD analysis are presented in Table 1 and the results of major-element XRF analysis are presented in Table 2. Based on the tabulated results, it is evident that the phosphate deposits, with an initial P2O5 grade of 8–10%, are of a very low grade, and given the high CaO concentration, can be considered as sedimentary phosphate ore with carbonate gangue.
4.2. Geochemistry
Phosphorites and its constituent apatite studied throughout the world for their economic importance [62] and especially the geochemistry of phosphorites is used to the estimation of paleo-marine geochemistry [63].
Phosphorites are generally contains considerable amount of trace elements and of REE and yttrium (Y) in respect to the average shale and other sedimentary rocks because of the substitution of REE3+ and Y3+ for Ca2+ in apatite [62,64,65,66,67]. The results of the major element, trace elements, and REY analyses for shales and phosphatic layers (Grey columns) obtained in the present study are presented in Table 3.
4.2.1. Major elements
The major oxides in the phosphate-bearing horizons are dominated by CaO, SiO2 and P2O5, while Al2O3, Fe2O3 (T) are the next most abundant elements. The concentrations of all the other oxides [MgO, Na2O, SO3, MnO, K2O, TiO2] is generally low (<1%). The highest P2O5 values (20–25%) were recorded in samples from the Mondun section (Table 3). Taking an average P2O5 content of 23% for fluorapatite yields an average fluorapatite content of 81% for the Mondun Basin sediments and 38% for the Siah and Nill Basins.
Samples from all three sections are characterized by the high CaO (32.45–48.65%) and very low MgO (0.4–1.09%) contents, reflecting high proportions of calcite and indicates that Mg might not have been incorporated in the apatite structure. The average concentration of CaO is about 40.43%. Weak correlation observed between CaO and P2O5 (R2 = 0.014). The SiO2 contents range from 6.37% to 31.35%, showing significant variation that reflects the changing proportion of quartz (detrital and from biogenic sources) [68]. The TiO2 values vary between 0.004% and 0.19%, and are considered to represent mainly clay minerals as this element shows a relatively strong positive correlation with Al2O3 (R2 = 0.47). The Al2O3 concentrations show significant variation (0.69–5.52%) that reflects the presence of clay mineral assemblages in the deposits. The alkali components Na2O and K2O show some variability (0.01% to 0.27% and 0.27% to 1.05%, respectively). Very weak correlation observed between Na2O and P2O5 (R2 = 0.019) and negative relationship between K2O and P2O5 (R2 = 053) may reflect Na and K substitution in the feldspar contents. The K2O content is primarily determined by the type and amount of illite, glauconite and K-feldspar in the assemblage. The Fe2O3 contents range from 0.86% to 3.75%. The low values of Fe2O3 are due to the carbonate nature of mineralized and non-mineralized layers. The SO3 content ranges from 0.002% to 0.41% which can be attributed to the occurrence of sulphate as a constituent element [67,69], and the presence of sulphides (pyrite) [70].
4.2.2. Trace elements
It is broadly recognized that an enriched trace elements group consisting Sc, Mo, Zn, Cd, Ag, U, Y, and REEs characterize the phosphorite facies [67,71,72,73].
The average concentrations of Trace Elements (ppm) in phosphatized samples in descending order is: Sr (1222.9 ppm), Cr (142.4 ppm), Ba (138.6 ppm), Zn (71.1 ppm), V (66.8 ppm), Ni (59.8 ppm), Cu (22.9 ppm), Mo (11.4 ppm), Zr (10.5 ppm), U (7 ppm), Th (6.8 ppm), As (6.6 ppm), Sc (4.5 ppm) and Sb (1 ppm). According to the elements concentrations, the distribution of trace elements in phosphorite horizons can be categorized into three groups: The first group composed of Cr and Ba, with relatively high concentrations (~140 ppm). The second group is made up TEs in moderate concentrations (10 to 70 ppm): Mo, Ni, Zn, V, Zr and CuThe third group consists of TEs in relatively low concentrations (<10 ppm): U, Th, Sc, As, and Sb.
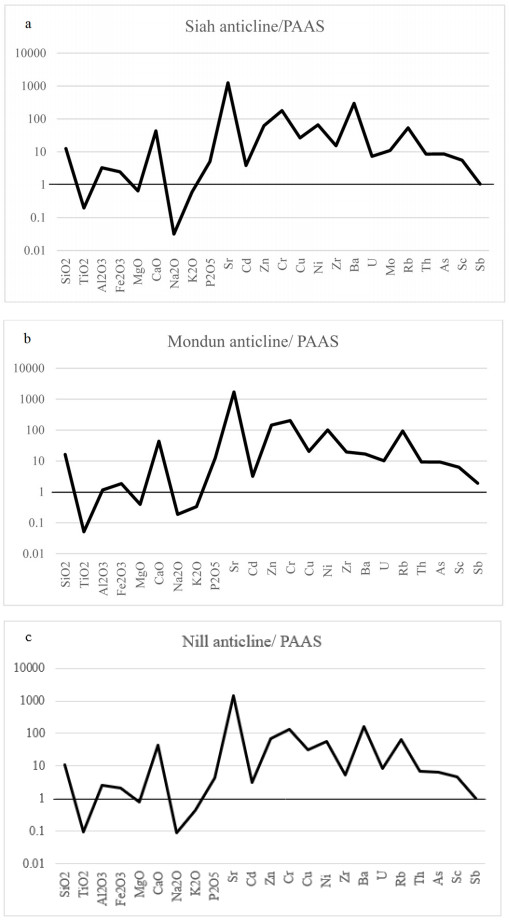
Trace-element patterns
Compared with the Post Archean AustralianShale normalized (PAAS), there is major and traces elements fractionation (Figure 10a–c). For values > 1, the concentrations of SiO2, Al2O3, CaO, P2O5, Sr, Cd, Zn, Cr, Cu, Ni, Zr, Ba, Rb, Th, As and Sc are in excess relative to PAAS. If values are < 1, the deficit is in relation to the composition of PAAS (Na2O, TiO2 and Fe2O3). MgO and Sb have values close to PAAS.
Strontium concentration in phosphorites of the study area varies from 486 to 2075 ppm. The good correlation between Sr and P2O5 (R2 = 0.79) stated that Sr is situated in the fluorapatite structure. The relatively high concentration of Sr in these phosphorites may be due to the result of substitutes for Ca in fluorapatite [67]. Chromium content in these phosphorites ranges from 23 to 370 ppm with an average concentration of about 138.6 ppm. Positive correlation between Cr and P2O5 (R2 = 0.81) reveals that Cr could be attributed in apatite structure.
Prevot and Lucas [74] reported that Cr is principally carried away by the apatite and is secure in clays so it can be stated that chromium concentration was secured in the clay and ironiferous minerals during the precipitation of phosphatic ores, thereby the relatively high concentration of Cr observed in phosphorites. Zn content in these phosphorites ranges from 23 to 253 ppm with an average concentration of 71.1 ppm. High concentration of Zn in Mondun phosphorites may be due to the availability of pyrite and plenty of organic matter. In these phosphorites, the Uranium occurs in small quantity which ranges from 2.97 to 13.2 ppm with an average concentration of 5.43 ppm (Table 3). This element is commonly believed to be easily incorporated into the apatite lattice [71,75,76]. Positive correlation between U and P2O5 (R2 = 0.77) in this study, indicates that most of the uranium content held by the apatite phase in the phosphorites [71,77,78,79,80,81,82]. Zirconium expresses a weakpositive correlation with P2O5 (R2 = 0.086) which indicates that Zr does not occur in apatite structure. Ni content in these phosphorites range from 22 to 140 ppm with an average 51.57 ppm. Positive correlation between Ni and P2O5 (R2 = 0.73) suggest that a high amount of Ni may be located to the apatite lattice [83,84]. Individual phosphatic horizons from Mondun demonstrated the highest contents of Sr, Zn, Y, Ni and U, whereas phosphatic horizons from the Nill and Siah contained the highest Ba contents.
In the present investigation, Ba concentration ranges from 2 to 707. It can be mentioned that negative correlation of P2O5 with Ba suggest the limited substitution of Ca by Ba. Regardless of the fact that Ba and Sr have the same geochemical behavior because of the higher ionic radii, Ba cannot replace Ca in fluorapatite lattice as Sr [52]. An important possibility of higher concentration of Ba in Siah section may be due to the availability of barite occurrences in the depositional area [52].
Similar trends are not seen in the bulk non-phosphatic horizons (Table 3), although in this case individual Mondun non-phosphatic sediment samples exhibit very slight changes of TE concentrations.
The highest As and Sb concentrations occur in phosphorites from Mondun, attributable to the high glauconite content of the sediments [85,86]. Thorium contents range from 4.95 to 13.2 ppm. High Th values characterize the samples from the phosphorite beds of the Mondun section. This element can replace Ca in fluorapatite lattice because of their same ionic radii.
The cadmium concentrations in the Pabdeh phosphatic horizons are variable, particularly in some of the Siah section samples the cadmium content is 7.1 ppm (>1.1 average shale).
4.2.3. Rare-earth elements and yttrium
Rare earth elements used as a tools for identification of the depositional environmental system such as extensive marine anoxia [87,88,89], lithology and diagenesis [90,91,92,93], oceanic palaeo-redox conditions [94,95], and paleogeography and depositional models [96,97]. REEs are not easily fractionated at the time of sedimentation, and their patterns may provide a key to average provenance compositions [98]. Distribution pattern and concentration of REEs in phosphorites may be affected by weathering, burial diagenesis and metamorphic processes [99]. Recent studies of marine phosphorite deposits reveal that phosphorites can incorporate plenty of rare earth elements during their growth in oceanic sediments leading to very early diagenesis [100]. The enrichment of REEs in phosphorite layers have long been recognized for more than a century compared with other sedimentary rocks [101,102,103] because REE+Y are readily incorporated into the apatite structure directly from seawater during early diagenesis [67,99,104]. For example, fish debris apatite in slowly accumulating modern deep-sea muds may contain in excess of 3% ∑REE+Y [105].
Post-Archean Australian Shale normalized (PAAS) of Taylor & McLennan [106] selected to normalize the phosphorite REE in this study.
The REE+Y concentrations (ppm) and elemental ratios are presented in Table 3. The total REE (∑REE) and Y contents ranges from 27.1 to 103 and 7 to 52.2 ppm, respectively in average shale versus phosphorite horizons.
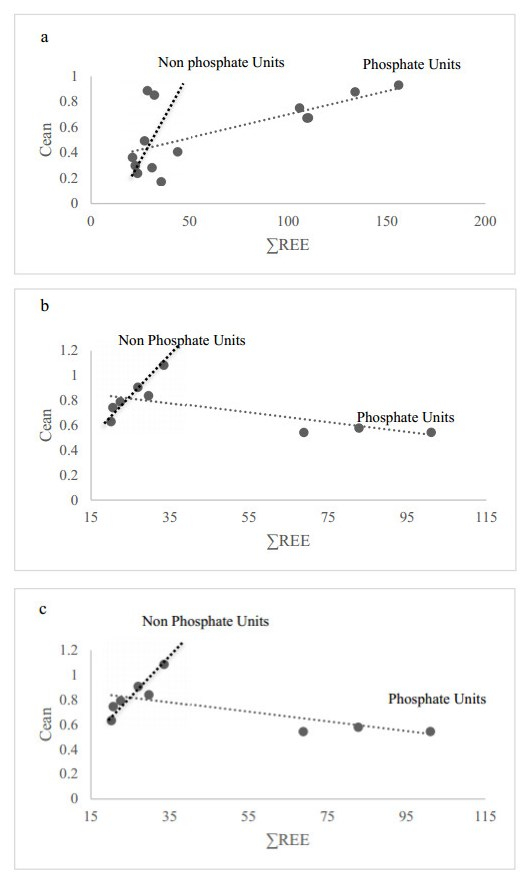
Samples from Mondun section (∑REE range 105.8 to 156.4 ppm, average 123.1 ppm) have higher REE contents than those from the Siah (84.8 to 133 ppm, average 101.9 ppm) and Nill (68.8 to 101 ppm, average 84.2 ppm) sections. These concentrations are comparable to the P2O5 contents in the Mondun samples. The Siah phosphate deposits (With the average of 84.2 ppm) is characterized by the lowest REE contents (Figure 11).
It seems therefore that there is a competition between the REE into the apatite lattice. The shale normalized (PAAS) REE patterns (Figure 12c, d) of Mondun phosphorites are characterized by negative LREE (La, Ce, Pr, Nd) and enrichment in the middle REE (MREE) and Heavy REE (HREE). The lowest ∑REE concentrations, recorded at the Nill section, occur in low grade phosphate levels (P2O5 < 4.5%). Most phosphorite values in Nill and Siah sections are close to, or in some cases less than the PAAS (Figure 12a, b, e, f).
Shale normalized REE patterns characteristically denote a progressive enrichment towards the heavier REE (HREE) and a relative depletion of cerium with respect to its REE neighbours lanthanum (La) and praesodymium (Pr) or neodymium (Nd). This negative Ce anomaly (Ce/Ce*) is considered to relate to the decrease in solubility that accompanies the oxidation of Ce (III) to Ce (IV) and subsequent removal together with other multivalent metals [107].
The Ce anomaly (Ce/Ce*) was applied by many authors [52,108,109,110]. The Ce anomaly calculated from:
where N refers to the Shale normalization of concentrations [88]. When Ce anomaly is equal to 1, indicate that there is no anomaly. For values lower than 1, it’s described as negative and when it is higher than 1, described as positive [52].
Samples with negative Ce anomalies indicate that these phosphates have been formed in suboxic environments deficient in this element [107].
The REE pattern includes most of the phosphorite samples from all three sections, which have a strongly negative to positive Ce anomalies (values varying between 0.24 and 1.08). All the samples analysed present Shale normalized negative Ce anomalies of varying magnitudes. This anomaly, in addition to a HREE enrichment, is typical of ocean water REE composition [111].
Also there are strong positive correlations between ∑REE+Y and Ce anomaly in Mondun Section but conversely there are negative correlations between ∑REE+Y and Ce anomaly in Nill and Siah sections (Figure 13a–c) [67,99].
4.3. Facies analysis
4.3.1. Carbonate facies
Based on field descriptions and petrographic studies, four sedimentary facies in addition to the basal purple shale and thin beds of marl with planktonic forams, such as Acarininidae, Globigerinidae, Morozovelidae, Turburotalidae Families and benthic forams, were identified in the Pabdeh Formation. Although previous studies identified pelagic shales of deep marine setting [3,112] we found shallow water carbonates and marls in the Pabdeh Formation samples. The carbonate facies are: (i) bioclastic mudstone/wackestone; (ii) burrowed bioclastic wackestone/packstone with diverse fossils; (iii) graded, laminated and phosphatized-bedded bioclastic packstone; and (iv) bioclastic foraminiferal/algal/peloidal packstone.
● Bioclastic mudstone/wackestone
This is a planktonic and benthic foraminiferal lime mudstone with intercalations of argillaceous limestone and marl. The constituent allochems of the facies are sparse planktonic foraminifera such as Morozovellids, Hantkeninids, Pseudohastigerinids, Subbotinids, Turborotalids, Globigerinathekids,
Orbulinids and Globigerinids and benthic foraminifera such as Elphidium sp., Heterolepa sp. and scattered Echinoderms (Figure 14a, b).
Bioclastic mudstone/wackestonefacies occurs as limestone, dark grey shale and grey marls in the field. Low planktonic foraminiferal content and pyritization suggest that the bioclastic mudstone/wackestone microfacies were deposited below the Fair Weather Wave Base (FWWB), in a deep outer-ramp setting close to the basin edge.
● Burrowed Bioclastic wacke/packstone with diverse fossils
This is a bioclastic wacke/packstone with diverse fossils. The allochems consist of sparse fragments of planktonic and benthic foraminifera, echinoderm and echinoid spines and fragments. Horizontal and vertical burrows are common on the bedding planes (Figure 15a, b).
Burrowed Bioclastic wacke/packstone with diverse fossils were deposited below the FWWB in a deep outer-ramp setting close to the basin edge.
● Graded, laminated and phosphatized-bedded bioclastic packstone
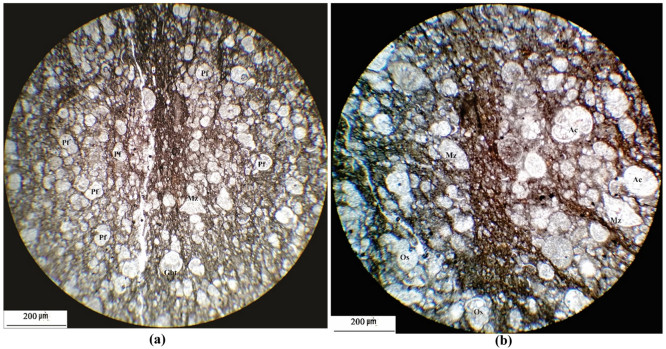
The microfacies are characterized by interlayered dark mudstones and bioclastic packstone which has erosional basal contact, fining-upward succession and ripple marks on the top of the beds similar to Hips study [30]. Another characteristic feature of the microfacies is the occurrence of shell-lag beds which indicate deposition under episodic strong storm currents and various signs of reworking and transport of sediment from the inner ramp to this setting (Figure 16a). The bioclastic packstone consists of phosphatic ooids and phosphatized foraminifera, fossilized fish scales and bones and phosphatic intraclasts (Figure 16b, c).
These microfacies occur in an outer ramp setting or near the middle–outer ramp boundary and are interpreted to have been deposited as carbonate tempestite, indicating storm influences on the ramp [17]. This microfacies is equivalent to the standard microfacies (SMF 14) of Wilson [22] and RMF 9 and RMF 29 of ramp carbonates [60]. Episodic strong storm currents transported sediment from the inner ramp to this setting. Well-rounded, well sorted bioclastic, phosphatic, foraminiferal oolitic grainstone (Figure 16d) is another characteristic feature of these microfacies, demonstrating deposition in a shallow-water setting which is equivalent to the RMF 29 of ramp carbonates [60].
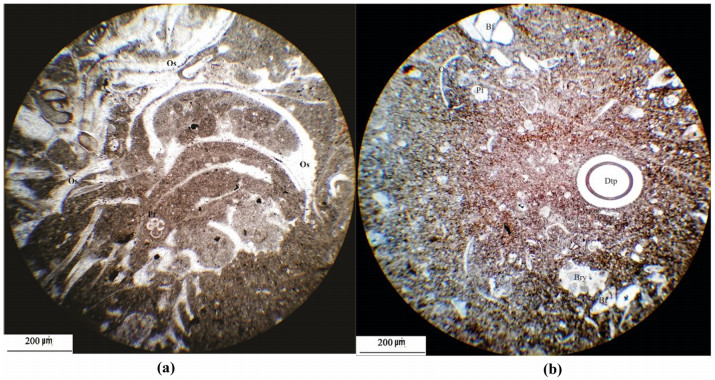
The evidence for the origin of the storm in phosphatic Pabdeh Formation is the occurrences of packstone interbedded with bioturbated mudstones, commonly in upward fine grade form, ripple marks, and also hummocky cross stratification (HCS), which are also identified in field studies (Figure 17a, b). These features are good indicators of storm wave base (SWB) around 100 m, which is influenced by storm [113].
● Bioclastic foraminiferal/algal packstone with large benthic foraminifera and crinoids
This microfacies comprise the upper parts of the Pabdeh Formation with an overall thickness of about 164 m. They contain algae, benthic foraminifera (e.g. Ditropa sp., Operculina sp. (Supplementary), crinoids and bryozoans (e.g. Tubucellaria sp.). The planktonic foraminifera occur with low fossil content (Figure 18a, b). The main components of this microfacies are algae accompanied by benthic foraminifera. The upper boundary of these microfacies is graded and can be recognized by the first appearance of Paragloburotalia kugleri [114]. From a lithological point of view the contact with the overlying Asmari Formation is marked by a gradual change from the medium-bedded packstone of the Pabdeh Formation which contains thin particles of marls and limestone, to the massive bedded, cliff-forming limestone of the Asmari Formation, which contains large benthic foraminifera [17]. The first appearance of thick to massive bedded limestone identifies the boundary between the Pabdeh and Asmari formations.
5.
Discussion
Faunal association of Pabdeh Formation (including echinoderms, Benthic and Planktonic foraminifera, Bryozoan and Radiolaria) represents a foraminiferal-bryozoan association. These communities live in temperate and cold water and also at deeper settings in comparison to the tropical chlorozoan association [60,115].
The presence of sedimentological structures include of ripple marks, hummocky cross stratification (HCS), grainstone microfacies, the occurrence of bioclastic carbonates containing shallow water faunas in hemipelagic environments, burrows structures, shell lags, alternation of packstone and mudstone laminae which are also identified in field studies, indicate episodes of intense storm-generated currents activities. These storm currents carried carbonate sediments into the deeper parts of the basin, where they were deposited on top of mudstone with an erosional contact [17]. The findings of the depositional conditions of the facies indicate that the Pabdeh Formation was deposited on a carbonate ramp setting infuenced by repetition of storm conditions. The presence of algae and the abundance of benthic foraminifera (Nummulitidae family) in upper parts of Pabdeh Formation with no evidence of evaporative precipitation or restricted hypersaline microfauna suggest that this microfacies was deposited in the outer part of the Middle ramp setting or near the middle–outer ramp boundary and are interpreted to have been deposited as carbonate tempestite, indicating storm influences on the ramp [17].
Storm events significantly affected the phosphate deposition in the deep areas of the Pabdeh Formation while oceanic circulation, upwelling processes and cold nutrient-rich currents rising to the ocean surface were not involved in the formation of the phosphate horizons.
The lack of facies attributable to a rimmed shelf environment such as a shallow protected rimmed shelf with a shoal suggests that the depositional environment of the Pabdeh Formation was a distally steepened ramp. Storm currents in shallow areas provided well-rounded, well sorted foraminiferal oolitic grainstone from the back-shoal setting to the middle of the ramp. Other evidence for the ramp setting for the Pabdeh Formation includes the absence of either a slope break or abrupt facies changes from the platform to the deep basin [17].The lack of any marginal reef development, and the presence of pelagic microfauna and low-energy mudstone facies are evidence that the Pabdeh Formation was deposited on a carbonate ramp setting in this area.
Bioclastic mudstone/wackestone microfacies of Pabdeh Formation are comparable to the standard microfacies (SMF 3) of Wilson [22] and RMF 5 of ramp carbonates [60]. Burrowed Bioclastic wacke/packstone with diverse fossils of this formation are comparable to the standard microfacies (SMF 8) of Wilson [22] and RMF 3 of ramp carbonates [60].
Most of the sediments in the Pabdeh Formation were deposited in the middle and outer parts of the ramp. The distribution of these sediments in this setting was carried out by storm currents and turbidity systems.
The middle and outer ramp sediments comprise recurring facies which show alteration of mudstone and wacke to packstone laminations. Episodic storm currents transported sediments to these parts of the ramp forming a cyclic pattern of facies in the middle and outer ramp setting. Stratigraphically open marine outer-ramp pelagic facies gradually changed into middle-ramp facies influenced by marine currents. In the final stage of ramp development, a shallow carbonate shelf (the Asmari Formation) was deposited over the Pabdeh Formation as an overlying blanket [116,117]. Although strong agreement exists on the general character of the Pabdeh Formation, the palaeobathymetry of the pelagic deposits is still under debate. In this anticline, well-rounded, well sorted bioclastic, oolitic and phosphatic foraminiferal grainstone indicate shallow-water deposits from what were previously thought to be deep pelagic facies in the Pabdeh Formation. Shallowing-upward cycles, including some with prograding oolitic shoals at the top, appear again in these pelagic settings. Phosphatic grainstone formed through successive winnowing, transport and redeposition of phosphatic grains and intraclasts derived from shallow environments via storm-generated currents.
Trace element pattern indicate that Mondun section have the highest contents of Mo, Zn and Sb whereas phosphatic particles from the Nill section contained the highest amount of Ba, As, Cd, Cr, Cu, Ni, Sc, Sr, Th, V and Zr. Enriched concentration of Cu, Ni and Zn in the Nill phosphatic horizons has been considered to be typical of organic matter derived from marine plankton [118,119]. Copper and Ni provide the best proxies for organic carbon flux, itself a measure of surface-water productivity [120] andthe highest enrichment of Ba, As, Cd, Cr, Cu, Ni, Sc, Sr, Th, V and Zr in Nill and Siah sections is likely associated with low-grade P2O5 content.
Low iron contents in the Mondun phosphorites can be considered as a result of the presence of minor glauconite, ferromagnesian and pyrite minerals in the sediments. It’s close to 2% Fe2O3 for all the sections. Although the highest P2O5 content occurs in the Mondun section, it also contains high amounts of Mo, Zn and Sb.
In contrast to the eastern Mediterranean and north and northwest Africa, where phosphate deposits formed in shallow marine depositional environments and evaporitic cycles, the phosphate horizons of Pabdeh Formation were formed in middle and outer ramp setting conditions. Several recent studies show evidence for depth control on the extent of Ce anomalies in marine authigenic minerals [94,121,122] where shallowing is associated with Ce depletion, Thus the Mondun section, with a reduced negative cerium anomaly (0.56), represents highly reworked, bioturbated with higher energy realm conversely Nill section with Ce enrichment considered to represent deeper water sedimentation. REE data from the phosphatic horizons of Pabdeh Formation also supports the depositional conditions of the deep water environment for this nominated Formation. The Shale normalized REE patterns of Mondun phosphorites are characterized by negative Ce anomalies. This anomaly indicate that the depositional environment was oxic during phosphate deposition.
These geochemical findings are in accordance with microfacies studies which indicate shallow and high energy condition for Mondun section with negative cerium anomalies and a deep ramp setting for Nill and Siah sections which denote a positive cerium anomalies in REE patterns.
6.
Conclusion
Major Eocene-Oligocene phosphate-bearing deposits occur in a ramp settings in south-western Iran: the Nill, Mondun and Siah basins.
The principal conclusions drawn from the study of these three sites are as follows.
Four lithofacies were identified at the three studied outcrop sections: (ⅰ) bioclastic mudstone/wackestone; (ⅱ) burrowed bioclastic wacke/packstone with diverse fossils; (ⅲ) graded, laminated and phosphatized-bedded bioclastic packstone; and (ⅳ) bioclastic foraminiferal/algal/peloidal packstone.
Most of the carbonate sequences from the Pabdeh Formation were deposited in Middle to outer ramp environments in the Nill, Mondun and Siah anticlines.
Biostratigraphic studies of planktonic foraminifera and the presence of Orbulinoides beckmani (Supplementary) demonstrate that the first phosphatic horizon in all the sections is of middle Eocene age (Lutetian stage); the second and third horizons are Bartonian.
The Pabdeh Formation can be categorized in global terms as a low-grade ore deposit. The average grade of the Pabdeh Formation phosphate is 8–12% P2O5 but the average grade of phosphorites in Tethyan phosphate deposits is 25–30%.
Microfacies studies demonstrate that all the phosphatic ooids and phosphatized foraminifera, fish scales, bones and phosphatic intraclasts reworked from shallow parts of the Tethyan Ocean (in the eastern Mediterranean, north and northwest Africa e.g., Tunisia, Iraq, Saudi Arabia, Morocco and Algeria) to deeper parts with the help of turbidity currents. Storm-generated surges transported phosphate particles to the deeper inner ramp of the ocean where they were suspended and deposited alternately as shell-lag and phosphate laminations. This is the first report of phosphate-bearing horizons, previously thought to be formed in nutrient-rich currents, deposited in a deep-water environment. Major-element, TE and REE+Y data from the phosphorites demonstrate distinctive geochemical signatures in the three sections of the Pabdeh Formation. There are strong positive inter-elemental correlations between all the REE+Y and P2O5 which attest to their strong coherence as a geochemical group. The Mondun section, with a reduced negative cerium anomaly (0.56), represents highly reworked, bioturbated with higher energy realm conversely Nill section with Ce enrichment considered to represent deeper water sedimentation.
Acknowledgments
We thank Dalia Lahav-Jones, from Liwen Bianji, Edanz Group China (www.liwenbianji.cn/ac), for editing the English text of a draft of this manuscript and express appreciation to R & D department of Zarrin Industry and Mining Holding for their contribution to the quality of the scientific results by proving us with pertinent invaluable data. We would also like to express our deepest gratitude to the Earth sciences Faculty of Islamic Azad University Science & Research branch for giving us access to their laboratory equipment.
Conflict of interest
The authors declare no conflict of interest in publishing this article.









 DownLoad:
DownLoad: