1. Introduction
The ever increasing number of sequenced genomes for eukaryotic organisms has made it clear that differences in organism complexity are not correlated with the number of protein coding genes but is more likely attributable to differences in how the genes are regulated. The recent ENCODE project, which thoroughly catalogued regulatory factors, has highlighted the complexity of gene regulation for the human genome [1]. These factors involve a number of dynamically changing regulatory layers. It has also become clear that phenotypic differences in the absence of genetic differences may be the result of changes in these regulatory layers. Waddington [2] coined the term epigenetics to explain phenotypic differences observed in the absence of genetic changes. Epigenetics is now a rapidly expanding field as it is now more widely appreciated that changes to the epigenetic regulation of gene expression mediate the interaction between environment and phenotype.
Epigenetic mechanisms regulate gene expression by changing the accessibility of DNA to the transcription machinery. Much of what we currently understand about epigenetics has been learnt from studies on humans and mice, particularly in regards to the mechanisms involved in the epigenetic phenomena of X chromosome inactivation involving the silencing of one X chromosome in female somatic cells of most mammals [3], and genomic imprinting where genes are expressed in a parent-of-origin fashion [4], but also from investigating the epigenetic changes occurring in tumours [5]. The epigenetic modifications required for the development of immune cells and to induce expression of immune genes in response to a pathogen have also been studied for many years [6]. More recently, there has been a burst of studies examining the role epigenetics plays in adapting to other environmental cues, such as the effect of nutrition or stressors on the epigenetic landscape, and the effect this has on human health and subsequent generations [7].
It is becoming increasingly evident that changes in epigenetic profiles could allow for rapid, heritable adaptation to environmental cues without the need for the more slowly evolving changes in DNA sequence [8]. In fact, it appears that epigenetic diversity in the absence of genetic diversity enables invasive species to successfully adapt to new environments [9,10,11]. Nonetheless, we have a limited understanding of epigenetic mechanisms in an evolutionary context. How conserved are the epigenetic mechanisms which have been observed in humans and mice? Just as comparative genomics has provided important insight into gene and genome evolution, the emerging field of comparative epigenetics will afford valuable insight into the evolution of epigenetic mechanisms involved in gene regulation.
Comparative epigenetics involves the comparative analysis of epigenetic marks between species to understand the evolutionary conservation of epigenetic regulation for a given biological function. Studies using other model organisms such as yeast (Schizisaccharomyces pombe), nematode worms (Caenorhabditis elegans), fruit flies (Drosophila melanogaster), frogs (Xenopus laevis) and plants (Arabidopsis thaliana) have provided some comparative epigenetic information but for understanding the evolution of epigenetic mechanisms involved in particular biological systems, comparisons over smaller evolutionary time frames will be more informative. This will require epigenetic data from non-model species to be obtained. In the past, this is something that was difficult to do but the technical advances in the field are now making it possible to study non-model species.
Here, we describe what is known regarding the conservation of epigenetic mechanisms from studies predominantly of model species, provide an example of an evolutionary epigenetic study including non-model species and highlight two biological systems in vertebrates showing considerable adaptation between species; the immune system and sex determination. An evolutionary epigenomics approach to the study of these systems will reveal the conserved epigenetic mechanisms that are essential to each.
2. Epigenetic mechanisms
DNA in eukaryotic cells is packaged into a structure known as chromatin. The first stage of the packaging process is winding of the DNA fibre around a nucleosome, which is composed of 146 base pairs of DNA wrapped around a histone core consisting of two each of four different core histone proteins (H2A, H2B, H3 and H4) or other histone variants [12]. It has become clear that dynamic changes in chromatin structure play a key role in regulating genome functions, including transcription [13,14]. Highly compacted chromatin structures are enriched in nucleosomes and are generally transcriptionally silent as the DNA template is inaccessible to the transcriptional apparatus. In contrast, a net loss of nucleosomes from gene-specifi c regulatory regions increases chromatin accessibility, enabling the binding of transcriptional regulators. Some of the key mechanisms involved in the regulation of gene expression that have been studied in evolutionary diverse organisms include post translational histone modifications and histone variants, histone modifying complexes, chromatin remodeling complexes, DNA methylation and non-coding RNAs. It is yet to be confirmed if all of these mechanisms are truly epigenetic (i. e. mitotically or meiotically inherited), nevertheless all have been included here.
2.1. Histone modifications and variants
Core histones are among the most highly conserved proteins in eukaryotes as they are critical to the structure and function of chromatin. Each of these conserved histones interacts with other histones and DNA within the nucleosome via a structured globular domain. Flexible tails of the histones extend from the nucleosome. The tails of histones H3 and H4 show a particularly high level of evolutionary conservation, being conserved from yeast to human [15] (Table 1). Histone tails act as substrates for numerous enzymes to mediate post-translational modifications, including acetylation, methylation, ubiquitination, sumoylation, biotinylation and crotonylation of lysines (K), and phosphorylation of serines (S) and threonines (T) [16,17,18]. The coordinated and dynamic changes in chromatin structure and histone modifi cations are considered a key underlying mechanism that directs temporal and cell lineage-specifi c gene transcription. The possible functions of these modifi cations can be divided into three main groups: (i) alteration of the biophysical properties of chromatin; (ii) establishment of a histone code that provides a platform to modulate binding of transcriptional regulators; or (iii) segregation of the genome into distinct domains such as euchromatin (where chromatin is maintained as accessible for transcription) or heterochromatin (chromatin regions that are less accessible for transcription) [16,17]. While particular functions have been ascribed to various histone modifi cations, it is becoming increasingly evident that it is the combination of histone modifi cations at a particular locus that is critical for transcription regulation [16].
Table 1. A comparison of the enrichment of modified histones between human, fruit fly and nematode worm [19]
| Highly enriched: +++, moderately enriched: ++, lowly enriched: +, absent: − |
| | Human | Fruit fly | Nematode worm | |
| Promoters | | | | |
| H3K4me3 | +++ | +++ | +++ | Active marks |
| H3K4me1 | + | + | + |
| H3K27ac | ++ | ++ | ++ |
| H3K79me2 | + | + | + |
| H3K36me3 | − | − | + |
| Heterochromatin | | | | |
| H3K27me3 | − | − | + | Repressive marks |
| H3K9me3 | ++ | +++ | +++ |
Many modifications have a conserved function among eukaryotes and yet others do not. For instance, the methylation of H3K4, a modification associated with transcriptional activity, is a conserved mark of euchromatin in eukaryotes (Table 1). However, methylation of H3K9 and H3K27 typically mark heterochromatin but show more variability across species in their subnuclear distributions [19,20]. One striking example of the functional differences between species is the cell-cycle dependent phosphorylation of H3S10, H3S28 and H3T11. In eutherian mammals, H3T11ph is restricted to the centromeric regions during cell division and appears to be involved in centromere cohesion whereas H3S10ph and H3S28ph spread along the chromosome and are presumed to be involved in chromosome condensation [21,22]. The opposite situation is observed in plants, where H3T11ph is involved in chromosome condensation and H3S10ph and H3S28ph are restricted to the pericentric regions and are associated with centromere cohesion [20].
Histone variants are also known to contribute to chromatin structure. Variants are non-allelic isoforms of canonical histones that flank nucleosome free regions of active promoters/regulatory elements [23,24]. There are several well-characterized histone variants that add to the chromatin structure by creating specialized nucleosomes [25]. The most commonly researched variants from the H2A family are H2A. Z and H2A. X, which are found in most eukaryotic organisms (Table 2). Some variants have a more restricted phylogenetic distribution, like H2A. W which has only been described to date in plants [26], macroH2A only found in animals [27], and H2A. B (also known as H2A. Bbd) [27] and H2A. L restricted to the mammalian lineage [28].
2.2. Chromatin-remodeling complexes
Histones and histone variants are not the only proteins that interact with DNA amongst the epigenetic landscape. Cellular tools, such as chromatin remodeling complexes and the recruitment of specialized transcription factors, physically alter chromatin structure and function [29]. Chromatin remodeling affects gene silencing and expression by altering chromatin structure in a number of different ways. This allows restructuring, repositioning and/or removal of nucleosomes, thereby affecting accessibility to DNA for the binding of the transcription factors, co-activators and transcriptional machinery, such as Pol II [30].
The large, multi-protein chromatin-remodeling complexes can be divided into five families, each conferring different functions; SWI/SNF, ISWI, NuRD/Mi-2/CHD, INO80 and SWR1. They all possess a conserved ATPase domain which uses the energy of ATP hydrolysis to mobilize and restructure nucleosomes by changing or disrupting the histone composition [31]. The best-described remodeling proteins come from the SWI/SNF family. They contain bromodomains, which recognize acetylated histones [32]. They are able to act alone and can be found in yeast, flies, plants and humans [33]. They have the ability to slide nucleosomes across DNA, remove histones from the DNA template, and displace H2A-H2B dimers [33,34]. The ISWI family proteins are another well-characterized family of chromatin remodelers. They are only found in mammals and also possess the ability to slide nucleosomes.
2.3. DNA methylation
DNA methylation is a heritable post-synthetic modification of DNA which converts cytosine nucleotides to 5-methylcytosine (5-mC) by DNA methyltransferases (DNMTs) [35]. This is the most well studied epigenetic mechanism in evolutionary terms. In humans and mice, nearly all DNA methylation occurs at CpG islands, resulting in the modified base 5-methylcytosine [36] and methylation of these islands correlates with transcriptional repression [37]. Methylation is not a universal epigenetic mark among invertebrates, or even yeast, with methylation and its associated enzymes absent from the model species D. melanogaster, C. elegans and S. pombe [38]. Comparisons between methylation of honeybee (Apis mellifera) and human genomes reveal differences in the level of involvement of this epigenetic mark. Only a small portion of the honey bee genome containing critical, ubiquitously expressed genes is methylated compared to the heavily methylated human genome [39]. These differences highlight the importance of performing comparative epigenomic studies.
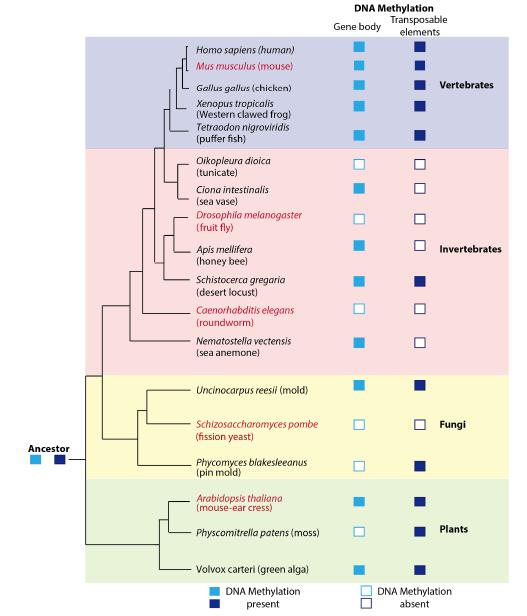
Advances in sequencing technology capable of determining the genome-wide methylation status has enabled methylomes of over 20 species spanning across the eukaryote phylogeny, including non-model species, to be determined. These comparisons have highlighted that methylation is a commonly utilized epigenetic mechanism, despite having been lost in some species [40,41]. One category of methylation observed in at least some species from each of these four major eukaryote lineages is methylation of gene bodies. The biological function of gene body methylation is yet to be elucidated but there is an interesting relationship between gene body methylation and gene expression, with moderately expressed genes more likely to be methylated than those that have very low or high levels of expression [40,41,42]. Transposable elements are methylated in at least one species studied from each major group of eukaryotes [40,41,43], including invertebrates, which until recently were thought to lack methylation of these repetitive sequences [43,44]. Methylation of transposable elements is most likely a defense mechanism used to silence invading foreign DNA. It has been possible to predict the methylation pattern of the common ancestor of plants, fungi, invertebrates and vertebrates by comparing methylomes of representative species from each of these groups, which most likely had methylation in gene bodies and within transposable elements (Figure 1) [41].
5-hydroxymethyl-cytosine (5-hmC), which is produced by the oxidation of 5-mC, has recently received considerable attention [45]. Most research to date on 5-hmC has focused on humans and mice, demonstrating that it is enriched in embryonic stems cells and brain tissue and may function as an independent epigenetic mark [46]. The limited number of studies so far carried out on other vertebrates suggests some level of conservation but also potentially some major differences in the role of 5-hmC between different vertebrate lineages. For instances, neural cells are enriched for 5-hmC both in the amphibian X. laevis as well as humans and mice [47]. In contrast, 5-hmC is undetectable by immunochemical methods in zebrafish and chicken embryos compared to the enrichment observed in mice [48]. Beyond vertebrates, 5-hmC has been detected in the honeybee, with the highest levels observed in drone testes and queen ovaries as well as relatively high levels detected in brain compared to most other tissues [49]. No doubt future studies across diverse taxa will help to elucidate the role and evolution of this epigenetic modification.
2.4. RNA-associated silencing
The most exciting new addition to the epigenetic landscape is non-coding RNAs. Multiple mechanisms are controlled by non-coding RNAs, with evidence from flies to humans demonstrating that they play a significant role in the control of epigenetic regulation and chromosomal dynamics [50,51,52,53]. Furthermore, studies in fission yeast and plants reveal a role for noncoding RNAs in the establishment of heterochromatin formation [54,55,56]. Large non-coding RNAs function in a molecular trafficking system, modulating chromatin-remodeling complexes to establish specific epigenetic landscapes [51]. On the other hand, small RNAs (short interfering RNAs, siRNAs; micro-RNAs, miRNAs; PIWI interacting RNAs, piRNAs) can lead to transcriptional gene silencing (TGS) through chromatin changes involving histone methylation and/or DNA methylation. Such studies have been extended into mammalian systems suggesting these mechanisms are evolutionary conserved [53]. There are other components of the epigenome that work with noncoding RNAs to achieve stable silencing among diverse species. There is emerging evidence that TGS-evoking RNAs (e. g. , repeat-associated siRNAs, Xist long non-coding RNA in eutherian mammals, and small RNAs in S. pombe) are capable of directing epigenetic changes, as they can induce long-term silencing effects that can be inherited through cell division [57,58,59,60].
miRNAs are worthy of particular note as they have received considerable attention in the past decade, including in non-model species. These RNAs are generally produced by the generation of small double stranded RNAs by RNA III Dicer-like enzymes. The small RNA duplexes then bind to the RNA-induced silencing complex (RISC), which contains Argonaute-related proteins. The RISC is activated by the removal of one strand of the RNA duplex. The remaining RNA strand guides the RISC to targets sites, resulting in TGS. In animals, miRNA biogenesis is initiated in the nucleus by the RNA III endonuclease Drosha that cleaves the long primary miRNA transcript (≈ 1 kb) into shorter (≈ 65 nucleotides) stem loop structures. The stem loop structure is then further processed in the cytoplasm by the Dicer pathway. Plants do not have a Drosha homologue but use Dicer-like 1 (DCL1) to process primary miRNA transcripts.
Many miRNAs are highly conserved in sequence and function across divergent species. For example, miR-124 shows sequence conservation across 28 vertebrate species [61] with conserved expression in neural tissue in worms [62], flies [63] and vertebrates [64,65]. However, miRNAs are also a source of lineage-specific gene regulation [66]. Next generation, deep sequencing approaches used to catalogue miRNAs in non-model species are leading to the discovery of many novel and potentially species-specific miRNAs. Recent examples include the discovery of 20 novel white shrimp miRNAs [67], 178 novel miRNAs in chickpeas [68] and 96 novel mRNAs in the black flyingfox [69]. This has led to a database containing more than 24, 000 miRNA loci from over 200 species [70]. Future comparative studies will ultimately provide important glimpses to what extent microRNAs target the same transcription regulators across different species.
3. An example of a comparative epigenetic study
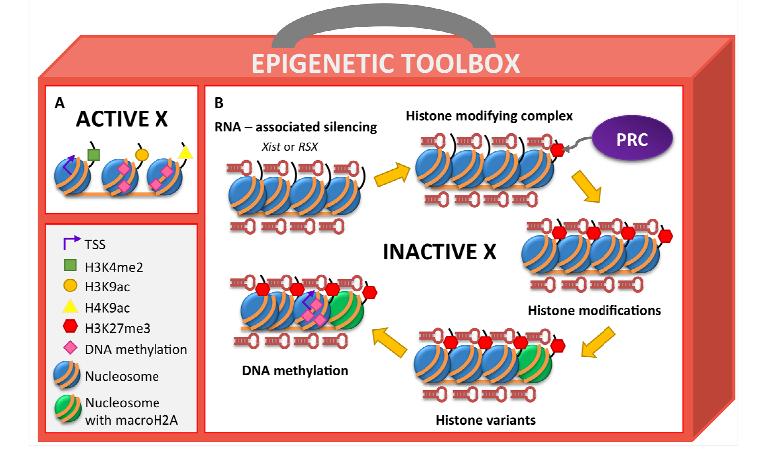
As highlighted above, comparisons of epigenetic mechanisms were performed on a very broad scale between model organisms such as yeast, plants, flies, mice and humans. These comparisons have provided important insight into the conserved components of the universal epigenetic “toolbox” that can be employed to regulate gene expression (Figure 2). However, the evolutionary gap between these model species is much too large to dissect out the evolution of epigenetic mechanisms relevant to particular biological systems. With the technical advancements that have been made for analyzing epigenetic mechanisms in non-model species, we are now in a position to rapidly gain information on the role these mechanisms play in different biological systems.
Dosage compensation mechanisms exist in diverse species to balance expression of X-borne genes between females with two X chromosomes and males with just one. Such mechanisms have been studied in the model nematode, fruit fly and mouse but the gene content of their X chromosomes is completely different and, not surprisingly, so are their dosage compensation mechanisms [71]. This means that in order to determine the steps in the evolution of the mammalian dosage compensation mechanism, we need to compare species which share homology between their X chromosomes. Comparisons of the mechanisms involved in X chromosomes inactivation, which is thought to be part of the mammalian dosage compensation mechanism, between humans, mice and marsupials is one of the few examples of comparative epigenetic analysis where model species have been compared to non-model species over a shorter evolutionary scale. This comparison has enabled some of the steps in the evolution of X chromosome inactivation to be elucidated.
3.1. X chromosome inactivation
Therian mammals (marsupials and placentals) silence one X chromosome in female somatic cells in what is assumed to be a dosage compensation mechanism for the imbalance of X chromosome genes between XY males and XX females. Since its discovery by Mary Lyon [72], the mechanisms involved in achieving this transcriptional silencing have been extensively studied in humans and mice and to a lesser extent in marsupials, although the recent availability of marsupial genome sequences has facilitated research and promoted rapid progress in this area [73].
Marsupials diverged from eutherian mammals around 145 million years ago. Their X chromosomes are homologous to two-thirds of the human X chromosome, with an addition to the X having occurred in the eutherian lineage [74,75]. With a large degree of conservation of gene content, it might be expected that the silencing mechanism employed in both mammalian lineages might be conserved. Indeed, some features are conserved between these two mammalian lineages but there are also some striking differences. It is this comparison that is making it possible to determine how X chromosome inactivation has evolved.
In humans and mice, X chromosome inactivation is initiated by the non-coding RNA XIST (X inactive specific transcript). This gene is absent in marsupials but its function appears to be performed by a marsupial-specific XIST -like gene called RSX (RNA on the silent X) [76]. XIST and RSX coat the X to be inactivated, initiating the silencing process [76,77].
In eutherians, chromatin remodelling of the inactive X occurs via histone modifications and DNA methylation (reviewed in [78]). Some of the epigenetic marks responsible for this remodelling are shared between eutherians and marsupials. Histone modifications associated with active chromatin, such as H3K4me2, H3K9ac and H4Kac are depleted on the marsupial inactive X as they are in eutherians [79,80,81]. The repressive mark H3K27me3 associated with the inactive X in eutherians has been observed on the inactive X in marsupials to varying degrees [80,82,83]. Interestingly, enrichment of H3K27me3 on the inactive X in eutherians is due to the recruitment of Polycomb Repressive Complexes (PRC) by the non-coding RNA XIST [84,85]. Unlike eutherians, where it is present throughout the cell cycle, H3K27me3 is transient in marsupials, beginning to appear on the inactive X in early S phase and accumulating more in late S phase and early G2 phase [82]. Likewise, RSX appears to be associated with H3K27me3 enrichment and monoallelic expression of an X-linked gene [76]. Additional repressive marks (H3K9me3, HP1α and H4K20me3) not found on the inactive X of eutherians, are enriched on the inactive X in marsupials [80,82].
In eutherians, silencing of the inactive X chromosome is stabilized by the enrichment of the histone variant macroH2A [86]. Inactivation in marsupials appears to be less stable than that of their eutherian counterparts, which may be explained by the lack of hypermethylation of 5’ CpG islands of genes on the inactive X [87,88,89,90]. However, there is a difference in the global methylation status of the active and inactive X chromosomes in marsupials, with the inactive X being hypomethylated compared to the active X and autosomes [80,91]. This is most likely due to gene-body methylation differences, similar to those reported for human cells [92].
Monotremes, the most basal mammalian lineage, diverged from marsupials and eutherians approximately 166 million years ago. Their multiple sex chromosomes share no homology with the X chromosome of therian mammals but some level of inactivation of genes on four of the five platypus X chromosomes has been observed [93,94]. It is unclear at this stage what epigenetic marks may be involved as immunofluorescence on metaphase chromosomes observed identical distributions of various active and repressive histone modifications, and global DNA methylation on platypus sex chromosomes [80]. In contrast, preliminary ChIP-seq results indicate that the repressive mark H3K27me3 is enriched on platypus X5 [95]. A more comprehensive investigation of epigenetic modifications is required for this mammalian lineage but it does appear that X chromosome inactivation has independently evolved in each mammalian lineage, yet in each case have utilised tools in the epigenetic toolbox to achieve silencing of X chromosome genes (Figure 2).
The above discussions clearly highlight, not only the novelty of the outcomes derived from a comparative epigenomics study, but also emphasize the need for comparative studies in understanding evolution of epigenetic regulation beyond mammals and flies. Therefore, comparative studies using non-model species from divergent taxa, such as fish, reptiles and marsupials, are likely to provide further novel outcomes.
4. The role of epigenetics in rapidly evolving systems
We are currently exploring comparative epigenetic studies into two other interesting biological systems in non-model vertebrate species. The first is the immune system, which is essential to the survival of an organism since it provides a defense mechanism against pathogens. The interaction between pathogen and a host’s immune system is one of the most dynamic interactions in nature and we know from studies on humans and mice that the expression of many immune genes in response to a pathogen is modulated by epigenetic mechanisms. The second is the sex determination system, which determines whether an individual will develop as a male or female, has evolved many times during the course of vertebrate evolution. Sex determination can be either genetic or dependent on environmental factors. The role epigenetic regulation plays in either of these sex determining modes is largely unexplored but the few studies that have been conducted in this area have produced exciting results and highlight the need for more comparative studies.
4.1. The immune system
The immune system is a well-established model used to investigate epigenetic regulation of gene expression. This is mainly because immune cells develop in a precisely coordinated fashion [96]. From studies of mice and humans, we know that immune cells arise from a common progenitor called the hematopoietic stem cell (HSC). Differentiation of HSCs occurs in a step-by-step manner, resulting in multiple cell lineages and in due course, different cell types [97]. At each step, remodeling of the epigenome occurs to restrict gene expression from other lineages. This involves a coordinated series of events including inducible transcription factors, chromatin-remodeling complexes, histone modifying enzymes and chromatin-associated signaling kinases. The outcome of these events is the expression of genes appropriate to the cell lineage. Being able to isolate each step using specific cell surface markers allows epigenetic analysis at given time points during differentiation, hence, unraveling the mechanisms involved in the regulation of the epigenome [96]. Furthermore, we know that epigenetic regulation in the immune system is important for the immunological response to pathogens and immune memory in humans and mice [98] but how does this compare to more distantly related non-model species? The diversity in immune gene sequence and number between species raises the question of whether the epigenetic mechanisms observed in humans and mice would be conserved in other amniote species, such as marsupials, monotremes and reptiles, or are the epigenetic signatures different to create even more diversity in response to the arms race between pathogen and host.
The epigenetic signatures of the human immune system have been extensively characterized, particularly for T cells, as a result of genome wide studies using next generation sequencing [99,100,101,102,103,104,105,106]. In general, promoters of active genes have permissive histone modifications such as H3K4me and H3 acetylation while inactive gene promoters are marked by repressive histone methylations such as H3K9me and H3K27me3. There has also been studies describing the presence of bivalent promoters (having both the permissive H3K4me3 and repressive H3K27me3) in T cells, poising immune genes for activation but repressing its expression until activation signals are received [99,101,107]. Similarly, promoters of poised genes also have permissive modifications like H3K9ac and H3K4me3 but lack the repressive histone modification H3K27me3 at the promoter [99,101,105,108]. Interestingly, the epigenetic signature of the poised immune genes prior to activation remains unchanged upon gene activation, a phenomenon that is seen in both human and mouse models [108,109,110]. This suggests that immune genes are possibly primed for activation through epigenetic mechanisms, thus enabling the genes to be activated rapidly for its immune function. Whether a similar form of epigenetic priming is present in marsupials is yet to be seen.
It has only been in the last decade that the presence of many of the immune genes found in eutherian species has been confirmed in marsupials, their closest relatives. For many years, the immune response of marsupials was thought to be inferior to that of their eutherian counterparts but it became clear when the immune genes present in opossum (Monodelphis domestica), the first marsupial to be sequenced, were catalogued that the immune gene repertoire of marsupials was just as complex as eutherians [111]. The difficulties in characterizing the immune response of marsupials using reagents developed for eutherian species became evident when the low sequence identity observed for many immune genes was observed. However, there is one striking difference of the marsupial immune response that has remained when marsupial-specific reagents were used; marsupials have a prolonged primary response, lasting at least nine [112] to as long as 26 weeks [113]. It is unclear if they have a true secondary response as most often immunization trials ceased before an observed drop in the primary response or alternatively, typical eutherian immunsation regimes were employed, where boosters were administered well before a drop in the primary response [112]. It will therefore be very interesting to see if there are conserved epigenetic signatures involved in the immune system of marsupials.
Studies of marsupial immune cells were hampered in the past by the lack of cross-reactivity of eutherian cell population markers with marsupials largely due to the limited amino acid sequence identity between eutherians and marsupials. For example, opossum and tammar wallaby CD8 proteins share 36-45% sequence identity with eutherians [114]. We now have a database of marsupial immune genes [115] and the ability to generate marsupial-specific reagents for the analysis of specific immune cell subsets [116,117] that will make it possible to conduct comparative epigenetic studies.
Various vertebrate species display seasonal variation of the immune response. Reptiles provide an interesting model for studying the role of epigenetics in this seasonal variation as observations from several species of lizards and snakes indicate that the structure of the lymphoid tissues [118,119,120] and their antibody responses are season-dependent [121,122]. An increasing number of reptilian genomes have been sequenced in recent years [123,124,125,126,127], providing the basis on which to build epigenetic studies and determine the extent to which these seasonal variations are controlled by epigenetic changes.
4.2. Epigenetics in sex determination
We know that for the survival and evolution of most species, the development of two sexes is crucial [128]. We also know that developmental gene expression is precisely coordinated across levels of epigenetic, transcriptional, and post-transcriptional regulation. This highlights the process of sex determination as a good model to study environmental influences of epigenetic regulation and maintenance.
The role that epigenetics plays in genetic sex determination (GSD) is an emerging area of interest. A recent study of Sry, the sex determining gene in most mammals, showed that mice lacking the enzyme Jmjd1a, an enzyme responsible for the demethylation of H3K9, experienced male-to-female sex reversal [129]. Apart from eutherian mammals, master sex determining genes have been identified in only few vertebrates and remain to be conclusively identified in most of those species, making it more challenging to conduct similar studies in non-model species. There is perhaps more scope for studying the role epigenetics plays in environmental sex determination (ESD).
The enigma about how environment temperature influences sex determination in species with temperature dependent sex determination (TSD) has been debated since its discovery in a dragon lizard Agama agama [130]. Temperature influencing the hormonal pathway has been in the limelight as the driver in the TSD mechanism, rather than temperature influencing gene(s). In recent years, more and more studies provide evidence that temperature influence is primarily maintained via the epigenome rather than the genome. This occurs mainly via changes in the methylation pattern, through histone modifications or through chromatin remodeling [131]. These advancements of our understanding in epigenetic regulation shifted our focus towards how epigenetics may play a role in sex determination in those species with ESD. ESD and TSD are particularly common in reptiles with all crocodiles and marine turtles, many lizards having TSD, while only a few fish species display TSD [131]. Often closely related species display TSD and GSD, which are almost identical in genome sequences.
In the early 2000s, Gorelick [132] proposed that changes in methylation induced by changes in temperatures during egg incubation are likely mechanisms that determine offspring sex in TSD species. Later Eggert [133] suggested that epigenetics may play a role in natural sex reversal among amphibians (no TSD has been discovered in amphibians). Recently, several studies provide evidence that epigenetic mechanisms regulate enzymatic, transcription and nuclear reception activities involved in the steroidogenic pathway and biosynthesis [134,135]. Therefore, epigenetic mechanisms are perfectly placed to influence/induce gonad differentiation through maintenance and regulation of gonadal steroid biosynthesis, overriding genetic influence. This makes epigenetic regulation a perfect and legitimate contender as a master switch triggered by environment temperature in TSD species.
A study by Navarro-Martin and colleagues [136] has provided the first evidence of such regulation in a fish species. They showed that exposing developing embryos to high temperature during TSD increased the methylation level of the aromatase gene (cyp19a) promoter in females. The proposed aromatase gene expression is methylation dependent and as such is one of the regulatory mechanisms that determine sex in TSD species [136]. In the red-eared slider turtle (Trachemys scripta), aromatase gene expression during gonad development is dependent on ambient temperature. High expression is observed at what is known as female producing temperature (FPT, 31 ℃), and low expression at male producing temperature (MPT, 26 ℃) [137]. Temperature-dependent DNA methylation signatures during gonad development in this species have begun to be identified. A change from MPT to FPT, but not from FPT to MPT changed the level of DNA methylation during gonad development. Demethylation of specific CpG sites at aromatase gene promoter regions at FPT resulted in the temperature-specific expression of aromatase [138]. Epigenetic landscapes that are being generated using temperature induced modeling systems like this will enhance our understanding of the mechanisms required in the process of TSD.
More recently, methylome analysis of gonadal DNA in the half-smooth tongue sole (Cynoglossus semilaevis), uncovered a potentially important role of methylation in tongue sole sex determination [139]. This species has a ZZ male/ZW female GSD system, which can be overridden with exposure to a high temperature (28 ℃) to result in fertile sex reversed ZW “pseudomales” [140]. By comparing the methylation status between females, males and ZW males for key genes in sex determination, Shao et al. [140] observed methylation differences in 16 of 58 genes. Among these genes was dmrt1, a Z-linked gene in this species expressed specifically in the testes during the critical period of gonadal differentiation. This gene has a region in the promoter hypermethylated in ovaries compared to normal males and pseudomale testes, making it a prime candidate for being the critical gene required in the tongue sole to respond to environmental change and for triggering of the sex reversal cascade [140].
A recent review by Piferrer [131] highlighted the overarching role of the epigenome in sex determination, not only in fish or reptiles with TSD but across divergent taxa. With the continuous development of molecular and sequencing technology, it is likely we will be able to further enhance our understanding of the evolution and maintenance of epigenetic regulatory mechanisms. A comparative approach involving non-model species such as fish, amphibians and reptiles will play a central role.
5. Conclusion
Much of our current understanding of epigenetic regulatory mechanisms is derived from observations using yeast, mice and human models. Although there is an increasing volume of novel mechanisms being identified, the evolutionary conserved perspective is still in its infancy. This is poised to change with epigenomic studies now possible on non-model species. Future research should therefore conduct evolutionary comparative analysis using non-model species to further investigate the epigenetic landscapes and regulation of the epigenome across various divergent taxa. Such research is now more achievable due to advancement of techniques in epigenetics and the affordability of next generation sequencing. The systems that may be of most interest from an evolutionary perspective may be those that undergo rapid adaptation between species, such as the immune and sex determination systems.
Acknowledgements
JED and TE are supported by ARC Future Fellowships (FT100100426, FT110100733). Our work on comparative epigenomics of the immune system and sex determination is supported by a University of Canberra postdoctoral fellowship (awarded to TE, SR, JED, Arthur Georges, Stephen Sarre and Kristine Hardy).
Conflict of Interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: