Panic disorder is characterized by symptoms with abrupt surges of fear with palpitations, sweating, trembling, heat sensations. Considering its disease burden on each individual and on society, understanding its etiology is important. Though no one specific etiology has been known, like other psychiatric disorders, multiple factors such as genetic, environmental, neurobiological, psychopathological factors have been suggested. In this article, we reviewed currently known etiologies and related study results, regarding especially genetic and epigenetic aspects of the panic disorder. Early studies, including twin studies, family studies, adoption studies suggested highly familial trait of panic disorder. Linkage studies, either, found panic disorder is not a single gene disorder but confirmed existence of multiple related genes. Chromosome and candidate gene studies found few related genes, NPY, ADORA2A, COMT, IKBKE. Newer method, genome-wide association studies (GWAS) have been searching for newer genes. No genome-wide significant genes, however, were detected, confirming previously known candidate genes, NPY5R on 4q31.3-32, BDKRB2 on 14q32, instead. Epigenetic modification has also been studied on many different psychiatric disorders. Monoamine oxidase A (MAOA) hypomethylation, taken together with negative life events, showed relation with panic disorder. Glutamate decarbodylases 1 (GAD1) hypomethylation was also specific on panic disorder patients. Relation with noradrenaline transporter (NET) gene SLC6a2 promoter methylation has also been studied. In conclusion, no specific gene or epigenetic pattern can fully explain etiology of panic disorder. Few genes and epigenetic patterns, however, showed strong association with panic disorder compared to healthy controls. Considering its multivariable background, further studies with larger populations can confirm current results and clarify etiologies of panic disorder.
1.
Introduction
The randomness of interest rates deeply influences the accuracy of actuarial values of life insurances and life annuities, especially for long-term policies. Hence it is important to consider stochastic interest models in actuarial science. So far, there are numerous papers which have investigated stochastic interest models and their applications in actuarial science. Bellhouse and Panjer Bellhouse and Panjer(1980, 1981) computed the moments of insurance and annuity functions based on AR(1) stochastic interest models. Li et al. (2017) also used AR(1) interest models in the survivorship life insurance portfolios. Dhaene (1989) modeled the force of interest as an ARIMA(p, d, q) process in the analysis of the moments of present value functions. Cai and Dickson (2004) used a Markov process to model the interest rates in the research of ruin probability. Beekman and Fuelling(1990, 1991) modeled the accumulated force of interest as an Ornstein-Uhlenbeck process and a Wiener process respectively in the study of continuous-time life annuity. Later, Hoedemakrs et al. (2005) and Dufresne (2007) discussed the distribution of life annuity under Beekman and Fuelling's methods. Zhao et al. (2007) and Zhao and Zhang (2012) expressed the accumulated force of interest by a Wiener Process and a Poisson Process in the research of optimal dividend and pricing perpetual options respectively.
Generally, stochastic interest models based on time series methods require the assumption that the interest rate in one year is fixed, which does not always fit in with market interest rates. The methods by modeling the accumulated force of interest bring convenience to both theoretical analysis and calculation, but the behavior of the force of interest can't be indicated distinctly. So Parker(1994a, 1994b) studied the first three moments of homogeneous portfolios of life insurance and endowment policies by modeling the force of interest directly based on a Wiener process or an Ornstein-Uhlenbeck process. Especially, the modeling method based on Ornstein-Uhlenbeck process is also called as Vasicek model in finance, and has been applied extensively (such as Boulier et al., 2001; Liang et al., 2017, etc.). Parker (1994c) further compared the randomness of annuity of the models describing the accumulated force of interest with that of the ones describing the force of interest directly. Considering stochastic jumps of the force of interest in financial markets, Li et al. (2017) modeled the force of interest directly by a compound Poisson process.
Considering the change of yield rate in insurance company, the following two aspects are involved: stochastic continuous fluctuation from risk-free investments of insurance companies and stochastic jumps from adjustments of market interest rate (epically official rate of interest). So we might combine these two parts together to aim to introduce a class of interest models, in which the force of interest is expressed by a compound Poisson process and a Brownian motion. Our model is a generalization of Parker(1994a, 1994b, 1994c) and Li et al. (2017). It not only considers discrete and continuous changes simultaneously, but also assumes random adjustment range in each jump about the force of interest. These characters can interpret random changes of interest on financial market. In literature, stochastic interest models with jumps have been studied by stochastic differential equation, for example, Brigo and Mercurio (2006), Deng (2015), Li et al. (2016) and Hu and Chen (2016) etc. But the modeling thinking-way and research method are different from the one presented in this paper.
The paper is organized as follows. In Section 2, we introduce the stochastic interest model driven by a compound Poisson process and a Brownian motion. In Section 3, we give an explicit formula of the expected discounted functions of the proposed model under general circumstances, discuss the validity of this model and investigate their properties under different parameter and distribution settings through analytical and numerical analysis. In Section 4, we give actuarial present values of life annuities in discrete and continuous conditions. Lastly, we end this paper with a conclusion.
2.
Stochastic interest models driven by compound Poisson process and Brownian motion
Assume that all random variables and stochastic processes under consideration are defined on an appropriate probability space $(\Omega, P, \mathscr{F})$ and are integrable. In this section, we construct a class of stochastic interest models including a discrete part and a continuous part.
For the discrete part, we follow and generalize the idea of Li et al. (2017), and the following three assumptions are satisfied:
(1) The jumping number of the force of interest can be expressed by a Poisson process;
(2) The adjustment direction (rise or fall) of interest rates in every jump of the force of interest is independent of each other; and
(3) The adjustment ranges of interest rates in all jumps are independent and identically distributed.
For the continuous part, Brownian motion is usually used to describe stochastic tiny fluctuations of all kinds of financial assets. Due to the excellent mathematical properties of Brownian motion and the consistency between the change rules of finance assets and stochastic fluctuations of Brownian motion, we choose Brownian motion to describe continuous tiny fluctuations of the force of interest.
So the force of interest $\delta_t, t\geq 0$ is expressed by
where $\{N(t), t\geq0\}$ is a Poisson process with parameter $\lambda$ and denotes the jumping number of the force of interest on interval $[0, t]$. $\{Y_i\}_{i = 1}^{+\infty}$ are independent and identically distributed random variables and each $Y_i$ expresses the jumping range of the $i$-th jump of the force of interest. So $\sum_{i = 1}^{N(t)}Y_i$, $t>0$, is a compound Poisson process. The stochastic process $\{B(t), t\geq 0\}$ is a standard Brownian motion which describes the stochastic fluctuations of the force of interest and the constant $\sigma$ represents the fluctuation intensity.
The jumping range of the force of interest $Y_i$ can be further written as
where $I_i(i = 1, 2, 3, ...)$ is the direction of the $i$-th jump of the force of interest with $\{I_i = 1\}$ for a rise and $\{I_i = -1\}$ for a fall. The random variable $I_i(i = 1, 2, 3, ...)$ obeys $P(I_i = 1) = 1-P(I_i = -1) = p (0\leq p \leq 1)$, in which $p$ is called the up-jumping probability of the force of interest. The random variable $Z_i(i = 1, 2, 3...)$ is non-negative and can be interpreted as the adjustment range of the $i$-th jump of the force of interest with identical distribution $F(z) = P(Z_i\leq z)$. Both of $\{I_i(i = 1, 2, 3, ...)\}$ and $\{Z_i(i = 1, 2, 3, ...)\}$ are independent and identically distributed sequences of random variables. Furthermore, the random sequences $\{I_i(i = 1, 2, 3, ...)\}$, $\{Z_i(i = 1, 2, 3, ...)\}$, $\{N(t), t\geq0\}$ and $\{B(t), t\geq 0\}$ are independent of each other.
Remark 1. If $P(Z_i = 0) = 1$, or $P(Z_i = \alpha) = 1$ and $\sigma = 0$, our interest model will be reduced to one in Parker (1994c) and Li et al. (2017) respectively.
Here, we give an important property (refer to Ross (1996)) on Poisson process which will be used in the following analysis.
Lemma 1. For a Poisson process, if the occur times of all the events are considered as unordered random variables under the condition $N(t) = n$, these random variables are distributed independently and uniformly on the time interval $[0, t]$.
3.
Expected discounted function under stochastic interest model
In this section, we will study the accumulated interest force function and the expected discounted function of the stochastic interest model (1).
3.1. Expected discounted function
The accumulated interest force on the time interval $[0, t]$ can be expressed as
(a) In formula (2), by changing the integral direction (refer to Section 2.2 in Li et al. (2017)), we obtain
where $T_i~~(i = 1, 2, 3, ...)$ denotes the $i$-th jumping time of the force of interest.
(b) Through stochastic calculus (see Klebaner (2005)), we know
So from formulas (2), (3) and (4), we have
The discounted function, which is the random present value of one-unit payment at time $t$, can be expressed as
From formula (4) and Section 2 in Parker (1994c), we have,
Moreover, it can be obtained from the law of total expectation that
By Lemma 1 and the independent assumptions in Section 2, we have
where the random variables, $U_1, U_2, ..., U_{N(t)}$ are independent and identically distributed on the time interval $[0, t]$ and
Based on the foregoing analysis, we obtain the following theorem.
Theorem 1. Under the stochastic interest model (1), the expected discounted function can be expressed as
Proof. See the Appendix.
Remark 2. From equation (10) and $\beta_t$ in formula (9), we can prove that the expected discounted function is an increasing function of $\sigma$ and a decreasing function of $p$. We will further demonstrate this property in Section 3.2 through numerical analysis.
In practice, the jump sizes of interest rate are relatively fixed, for examples, the Federal reserve rate and the Chinas central bank benchmark interest rate etc. In addition, the jump sizes of interest rate are not too big. Hence, we give three special distributions about the jump size as special cases in the following corollary.
Corollary 1. The expected discounted function $E[\exp(-J_0^t)]$ is influenced by the distribution function $F(z)$ and the up-jumping probability $p$. There are some special cases of $F(z)$ and $p$ as follows,
(1) If $P(Z_i = \alpha) = 1~(i = 1, 2, 3, ...)$ for a positive constant $\alpha$, the result of $\beta_t$ is consistent with that in Li et al. (2017) which is generalized further in this paper, we obtain that
(2) If $P(Z_i = \alpha_1) = q = 1-P(Z_i = \alpha_2)~~(i = 1, 2, 3, ...)$ for two positive constants $\alpha_1$ and $\alpha_2$, that is, $Z_i(i = 1, 2, 3, ...)$ obeys a two-point distribution, we have that
(3) If $F(z) = z/\theta$ for $z\in [0, \theta]$, that is, the random variable $Z_i(i = 1, 2, 3, ...)$ is uniformly distributed on the time interval $[0, \theta]$, we have that
(4) If $p = 0$, the market interest will always jump down at the moments when interest rates jump. Because $\exp(zt)-1>zt$, we have that
In this case, the interest rate might be negative if the jumping number of the interest rates on the time interval $[0, t]$ is sufficiently large.
(5) If $p = 1$, the market interest will always jump up at the moments when the interest rates jump. Because $1-\exp(-zt) < zt$, we have that
In this case, the larger the jumping number of interest rates is, the smaller the expected discounted function is.
3.2. Analysis of validity of Stochastic Interest Model
As a general rule, the accumulated interest force function should be increasing with respect to time $t$ which means that the expected discounted function in formula (10) is decreasing. This property is called the validity of stochastic interest model which will be analyzed in this section. Now, we will discuss how to restrict the value of the future time $t$ in order to ensure this validity.
Let $f(t) = (\delta_0+\lambda)t-\sigma^2t^3/6+\lambda\beta_tt$, and we should ensure this function is increasing. Obviously, the derivative function of $f(t)$ exists if the function $f(t)$ is finite. In fact, we can find that $\lim_{t\rightarrow 0^+}\beta_t = 1$ and $\beta_t\leq \int_0^{+\infty}\frac{\exp{zt}-1}{zt}dF(z)~~t\in(0, +\infty).$ Hence, if $F(\cdot)$ is a light-tailed distribution, $\beta_t$ is finite for any $t\in [0, +\infty)$, and so is the function $f(t)$.
Under the condition of light-tailed distribution, the derivative function can be expressed as
We can find that $f'(0) = \lambda_0>0$ and $\lim_{t\rightarrow +\infty}f'(t) < 0$, then there is at least one critical value in interval $(0, +\infty)$ which satisfies $f'(t) = 0$ and the first one is denoted as $t^{\ast}$. Hence, this model is valid if time $t\in[0, t^{\ast}]$. Now, we will try to find the values of $t^{\ast}$ under various cases of the probability distribution of $Z_i$, $F(\cdot)$ given in Corollary 1 respectively.
(1) In case that $P(Z_i = \alpha) = 1~(i = 1, 2, 3, ...)$ for a positive constant $\alpha$, we have
(2) In case that $P(Z_i = \alpha_1) = q = 1-P(Z_i = \alpha_2)~~(i = 1, 2, 3, ...)$ for two positive constants $\alpha_1$ and $\alpha_2$, we have
(3) In case that $F(z) = z/\theta$ for $z\in [0, \theta]$, we have that
For each case above, since there are exponential functions part and power function part in equation $f'(t) = 0$, it is very difficult to solve this equation directly. However, we can obtain the value of $t^{\ast}$ by numerical approach and then can use the interest model in formula (1) when $t\in(0, t^{\ast})$. For instance, if $\delta_0 = 0.04, \lambda = 2, \sigma = 0.01, \alpha = 0.0025$ and $p = 0.6$ under case (1), we can obtain $t^{\ast} = 37.01$; and if $\delta_0 = 0.04, \lambda = 2, \sigma = 0.01, \theta = 0.004$ and $p = 0.6$ under case (3), we can obtain $t^{\ast} = 35.08$.
3.3. Numerical analysis
In this subsection, we analyze the changes of the expected discounted function under different assumptions in Corollary 1. We consider three types of distribution function $F(z)$, including one-point distributions, two-point distributions and uniform distributions. The parameter $\delta_0$ is assumed to be $0.04$. Firstly, we suppose $\lambda = 2$ and $t = 10$ to calculate the values of the expected discounted functions, shown in Tables 1–3. In addition, the range of the parameters of $F(z)$ is chosen based on the condition of jump amplitudes of major market interest rates (such as the Federal reserve rate and the China's central bank benchmark interest rate).
It can be observed from Table 1, Table 2 and Table 3 that the values of the expected discounted functions become larger with increasing $\sigma$ or decreasing $p$ under three distribution assumptions. This result verifies Remark 2. Furthermore, we can obtain that the values of the expected discounted functions become larger with increasing $\alpha$ under the assumption $P(Z_i = \alpha) = 1$, or with increasing $q$, decreasing both $\alpha_1$ and $\alpha_2$ under the two-point distribution assumption for $Z_i$, or with decreasing $\theta$ under the uniform distribution assumption for $Z_i$ if $p\leq0.5$. The values change in the opposite direction if $p\geq0.6$.
Remark 3. In the above tables, we only display partial results due to limited space. We also find that there is an equilibrium up-jumping probability $p^{\ast}$ under any one of these three assumptions when the time $t = 10$, which satisfies $0.5 < p^{\ast} < 0.6$. The change regulation for $p < p^{\ast}$ and $p>p^{\ast}$ is similar to that when $p = 0.5$ and $p = 0.6$ respectively. In fact, $p^{\ast}$ is the solution of equation $\beta_t = 1$ which is related to $F(z)$ and $t$. So it can be expressed as $p^{\ast}(F(z), t)$.
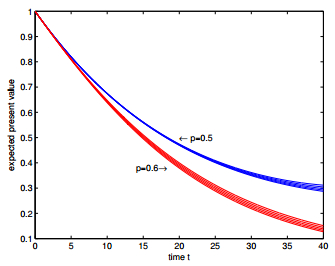
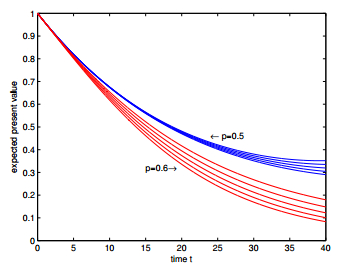
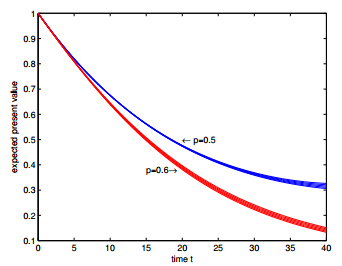
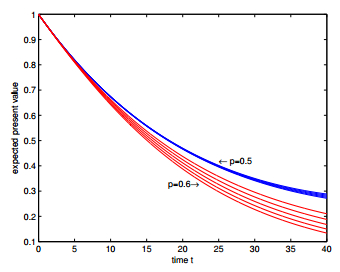
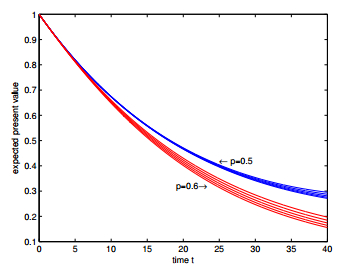
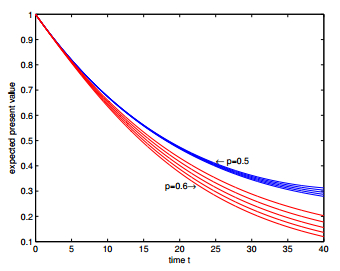
In Figures 1–6, we present the expected discounted functions as functions of time under different settings. In Figure 1, the upper five curves show the expected discounted functions for $\alpha = 0.0028$, $0.0026$, $0.0024$, $0.0022$ and $0.0020$ from top to bottom under the one-point distribution assumption when $p = 0.5$, while the lower five curves show those functions from bottom to top when $p = 0.6$; in Figure 3, the upper five curves show the expected discounted functions for $q = 0.40$, $0.45$, $0.50$, $0.55$ and $0.60$ from top to bottom under the two-point distribution assumption when $p = 0.5$, while the lower five curves show those functions from bottom to top when $p = 0.6$; in Figure 5, the upper five curves show the expected discounted functions for $\theta = 0.0040, 0.0035, $ $0.0030, 0.0025$ and $0.0020$ from top to bottom under the uniform distribution assumption when $p = 0.5$, while the lower five curves show those functions from bottom to top when $p = 0.6$; and in Figure 2, Figure 4 and Figure 6, every upper five curves show the expected discounted functions from bottom to top for $\lambda = 0.5$, $1$, $1.5$, $2$ and $2.5$ with other parameters keep constant respectively when $p = 0.5$ under three distribution assumptions respectively and the lower five curves show the corresponding expected discounted functions from bottom to top respectively when $p = 0.6$.
From Figures 1–6, we further observe that the differences between the values of expected discounted functions under different settings become significantly large as the parameter $p$ or the time $t$ increases. This implies that the expected discounted functions is sensitive to $F(z)$ and $\lambda$ for large $p$ and $t$. Hence, more emphasis is required on the selection of parameters in the up-cycle of interest rate.
4.
Application in life contingencies
In this section, we will apply the proposed stochastic interest model (1) to discrete life annuity and continuous life annuity, life insurance payable at the end of the year of death and life insurance payable at the moment of death. The actuarial present values (APVs) for these life annuities and life insuriance will be shown under different stochastic interest assumptions.
Following Bowers et al. (1997), the symbol $(x)$ denotes a life-age-$x$. The future lifetime and the curate-future-lifetime of $(x)$ are indicated by $T(x)$ and $K(x)$ respectively.
4.1. APVs of life annuities
In insurance science, there are two types of discrete life annuities which are discrete life annuity-due and discrete life annuity-immediate. Without loss of generality, we only consider the former. In the nomenclature, an $n$-year temporary life annuity-due of one per year is the one that pays one unit amount at the beginning of each year while the annuitant $(x)$ survives during the next $n$ years and the actuarial present value of this life annuity is denoted by $\ddot{a}_{x:\overline{n|}}$.
Referring to Chapter 5 in Bowers et al. (1997), the actuarial present value of this life annuity $\ddot{a}_{x:\overline{n|}}$ can be expressed as
where $_kp_x$ is the probability that the annuitant $(x)$ will attain age $x+k$. Combining (11) with (10), we obtain
Next, we consider the $n$-year temporary continuous life annuity for the annuitant $(x)$, and the corresponding actuarial present value is denoted by $\overline{a}_{x:\overline{n|}}$. From Chapter 5 in Bowers et al. (1997), we have that
and
So, we obtain the expression of $\overline{a}_{x:\overline{n|}}$ though Fubini's theorem as follows,
4.2. APVs of continuous life insurances
In this section, we analyse the APVs of life insurances by taking two whole life insurances for example which are the whole life insurance paying one unit at the end of the year of death and the one paying one unit at the moment of death for some insured $(x)$. Following standard symbols in Bowers et al. (1997), $A_x$ denotes the actuarial present value of the whole life insurance payable at the end of the year of death and $\overline{A}_x$ denotes the one of payable at the moment of death.
Firstly, we discuss the expression of $A_x$.
Secondly, we show the expression of $\overline{A}_x$ under our stochastic interest model.
4.3. Numerical analysis
In this section, under different parameter and distribution settings, we calculate the APVs of the $20$-year temporary discrete life annuity-due under the one-point distribution and the two-point distribution assumption and the APVs of the $20$-year temporary continuous life annuity for the annuitant $(30)$ under the uniform distribution of death assumption (refer to Section 3.7 in Bowers et al. (1997)). Note that the numerical analysis on life insurances will not be given because of the similarity. The mortality rate is from China Life Insurance Mortality Table (2010-2013) (CL5, Pension life table for male). The results are shown in Tables 4–6. Comparing Tables 4–6 with Tables 1–3, we find that the APVs of life annuity change about parameters following the same law of the values of expected discounted functions in Section 3.3. This is an inevitable conclusion from the relation between the APVs of life annuities and the values of expected discounted functions.
5.
Conclusions
In this paper, we introduce a new stochastic interest model in which the force of interest is expressed by a compound Poisson process and a Brownian motion. The advantage of this model is that the random jumping behavior and the continuous tiny random fluctuations are described simultaneously and the adjustment ranges of the force of interest in the random jump part of the proposed model are governed by a random variable sequence, which generalizes the modeling methods in Parker(1994a, 1994b, 1994c) and Li et al. (2017). In addition, we derive the expected discounted functions of the proposed model in general circumstances and further discuss the cases under the one point distribution, the two-point distribution and the uniform distribution assumption on random jumping amplitudes $Z_i$ respectively. We also use the proposed model to study two types of common life annuities. Our numerical analysis shows that both the values of expected discounted functions and the APVs of life annuities are influenced distinctly by the change of the interest model parameters under different distribution assumptions of $Z_i$. Especially when the up-jumping probability $p$ is sufficiently large, the influence of parameters in discrete part of interest model is totally opposite to that when the up-jumping probability $p$ is sufficiently small.
Acknowledgments
The work was partially supported by NSFC (Grant No. 71671104 and No. 11571198), the key project of NSSFC (Grant No. 16AZD019), the Ministry of education of Humanities and Social Science project (Grant No. 16YJA910003), Project of Shandong Province Higher Educational Science and Technology Program (Grant No. J15LI01 and No. J17KA162), Special Funds of Taishan Scholars Project of Shandong Province and Incubation Group Project of Financial Statistics and Risk Management of SDUFE.
Conflict of Interest
All authors declare no conflict of interest.









 DownLoad:
DownLoad: