1. Introduction

Pinal County, Arizona—an arid, desert and agricultural region located south of the Phoenix metropolitan area—routinely exceeds the PM₁₀ National Ambient Air Quality Standards (NAAQS). Fine particle mass concentrations are also approaching the NAAQS for PM_2.5 [1]. Because PM₁₀ concentrations exceed the federal standard, government agencies, in conjunction with local stakeholders, have the responsibility for developing and enacting policies to reduce ambient PM concentrations to meet the PM₁₀ NAAQS [2].

A short-term source apportionment study was conducted in October 2003 to identify emission sources that contributed to elevated particulate matter (PM) concentrations in the region [3]. This source apportionment study, employing chemical mass balance (CMB) modeling, indicated that crustal material was the main contributor to elevated PM₁₀ concentrations within the region. Re-suspended crustal related material from feedlot operations was also an important contributor to PM₁₀, even at monitoring locations well removed from these sources.

Since 2003, Pinal County, as well as other parts of the desert southwest, have continued to struggle with elevated PM concentrations and continue to be out of compliance with the PM₁₀ NAAQS [4]. Urban growth, spilling over from the nearby Phoenix and Tucson metropolitan regions, has altered the demographics and emissions in Pinal County. While extreme weather conditions including late summer monsoons are believed to occasionally contribute to elevated PM levels [5], NAAQS exceedances occur at all times of the year [6]. A more in-depth look at the PM sources in this region, and their relative contribution of each, can provide policy makers with critical information needed to reduce levels of PM in the area.

The Desert Southwest Coarse Particulate Matter Study was undertaken in Pinal County, Arizona to better understand the sources and their relative impacts to ambient fine (PM_2.5; particles less than 2.5 µm aerodynamic diameter (AD)) and coarse (PMc; particles in the range between 2.5 and 10 µm AD) particle concentrations. Clements et al. [7] reported results of this year-long, 1-in-6 day study, which examined the spatial and temporal chemical characteristics of fine and coarse PM mass. Results presented here include detailed 6-week time-averaged data on organic species, as well as CMB modeling using the inorganic and organic speciated dataset to identify and quantify source impacts observed at the three receptor sites. New source profiles for four local soil types, plant detritus, and fungal spore sources in the area also are presented and used in the CMB modeling.

2. Methods

2.1. Ambient sampling and chemical characterization

Filter-based PM samples were collected on a 1-in-6 day schedule between February 2009 and February 2010 at three monitoring locations in Pinal County, AZ resulting in an average of 64 filter samples per monitoring site in each particle size range (PM_2.5 and PMc). Detailed information about the sampling program, sampling locations, and chemical analysis of the collected samples were reported in Clements et al. [7]. Briefly, samples were collected at Casa Grande (CG), an urban location located in a small urban business district more distantly surrounded by residential neighborhoods; Cowtown (COW), a rural site located 27 km to the northwest of Casa Grande and in the immediate vicinity of a cattle feedlot, a grain processing operation, and railroad and vehicle traffic; and Pinal County Housing (PCH), a rural site 18 km east of Casa Grande, surrounded by native desert and active agricultural fields. Samples were kept cold during transport and stored below −4 ºC to stabilize semi-volatile components.

Four Sierra-Anderson Model 241 dichotomous samplers were operated at each site, each collecting one fine and one coarse particle sample over 24 hr from midnight to midnight in accordance with the locally-established air quality monitoring schedule. Two of the samplers were used Teflon filters, which were subsequently analyzed for PM mass, ion, and elemental concentrations. One sampler used quartz-fiber filters, which were analyzed for bulk elemental carbon (EC) and organic carbon (OC) concentrations. Remaining portions of the quartz-fiber filters were aggregated into 6-week periods (resulting in 8 aggregated samples for each site and in each particle size range) and analyzed for a series of individual organic marker species (see below). The fourth sampler was used for duplicates and precision estimates.

2.2. Source sampling

During the ambient sampling campaign, a series of local soil samples were collected to characterize the chemical composition of potential sources of re-suspended crustal material [8]. Samples were collected from 15 different sites within the sampling area, representing material from various types of land use including agricultural cropping, native desert (unaltered desert in close proximity to the site), paved and unpaved roads, and material representing a local cattle feedlot. All samples were obtained from the top 15 mm of the surface using a trowel, or by broom on paved surfaces, and placed into pre-baked glass jars for storage and transport. Samples were shipped and stored similarly to the ambient samples.

These samples were re-suspended in the laboratory to provide PM_2.5 and PM₁₀ size fractions from each soil type. More information about the soil re-suspension procedure can be found in Upadhyay et al. [8]. Re-suspended source samples were collected on one Teflon and two quartz-fiber filters for each sample and each PM size fraction. At least 5 mg of re-suspended soil was collected on each filter. The Teflon filter sample was analyzed for mass and elements, one quartz-fiber filter was analyzed for bulk organic and elemental carbon as well as water soluble ions, and the second quartz-fiber filter was extracted and the extract analyzed by gas chromatography-mass spectroscopy (GCMS) for organic species in a manner analogous to that used for the ambient filters. For CMB modeling purposes, the chemical species data from similar source types were aggregated into four source categories representing agricultural soils, native desert dust, paved-road dust, and feedlot material.

2.3. Chemical analysis

Ambient PM and re-suspended soil samples were analyzed for a variety of chemical components as detailed elsewhere [7,8]. Mass measurements were determined gravimetrically from all Teflon filters. After gravimetric analysis, one set of the Teflon filters (from both ambient and source samples) was microwave digested in a nitric, hydrochloric, and hydrofluoric acid mixture and analyzed for 63 trace elements by high-resolution inductively coupled plasma mass spectrometry (ICPMS, Thermo Finnigan ELEMENT 2) [8]. The second set of Teflon filters (ambient samples) was wetted with ethanol ([9]; Fisher HPLC grade) and then extracted with ultrapure water. For re-suspended source samples, a 3 cm² punch from one quartz-fiber filter was removed and extracted with ultrapure water. The extracts from both ambient and re-suspended source samples were analyzed for five anions (chloride, nitrite, nitrate, phosphate, and sulfate) and five cations (sodium, ammonium, potassium, magnesium, and calcium) by ion chromatography (Dionex IC20 system with CG12A and AS12A analytical columns). Ambient bulk OC and EC concentrations were determined by thermal-optical transmission (TOT) (Sunset Laboratories, Tigard, OR) using a 1 cm × 1.5 cm punch from the quartz-fiber filters from both ambient and source samples [10].

This study expands on previously reported results [7] by quantifying key organic molecular markers. Due to the relatively low mass of sample collected by the ambient samplers, filters from eight 24-hr sampling periods were combined to produce sufficient organic material for GCMS analysis. The result was eight 6-week composited samples for each sampling site and in each particle size range. To obtain a uniform database for all chemical species for CMB modeling, the other 1-in-6 day chemical composition data were averaged into corresponding 6-week aggregates.

For GCMS analysis, composited filters were placed in a clean glass extraction vessel and spiked with 40 µL of two different internal calibration standards to monitor the extraction efficiency and compound loss during concentration. The non-polar standard included n-tetracosane-D50, n-triacontane-D62, n-hexatriacontane-D74, chrysene-D12, dibenz[a, h]anthracene-D14, decanoic acid-D19, and tetradecanoic acid-D27 at a concentration of 200 mg/L each. The polar standard included 100 mg/L of β-D-glucose-1, 2, 3, 4, 5, 6, 6-D7. Once dry, filters were extracted by adding 20 mL of dichloromethane and 10 mL of methanol to the glass extraction vessel, which fully covered the filters. The sealed vessels were then placed in an ultrasonic bath for 10 minutes. After sonication, the liquid was decanted from the extraction vessel into a clean 250 mL round bottom flask. Two more sequential, equivalent extractions were performed and the supernatant from each was poured into the flask.

The extract was concentrated using a Buchi rotary evaporator to reduce the total volume from 90 to 10 mL. The system was operated at ambient pressure with a water bath at 70 °C. The sample was removed from the rotary evaporator, filtered through a pre-baked glass-fiber filter, and transferred to a clean 15 mL round bottom flask. The sample was then evaporated to a volume of 200 µL under ultrapure nitrogen. The exact sample volume was measured using a glass syringe and the sample was transferred to a new GC vial with a glass insert. An aliquot from this total extract was analyzed by GCMS to measure non-polar compounds.

A 50 µL aliquot from each extract was silylated to generate the trimethylsilyl derivatives of carboxylic acids, alcohols, and sugars, which improves the GCMS instrument response to these polar compounds [11]. The aliquot for derivatization was placed in a new GC vial with a glass insert and reduced to dryness under ultrapure nitrogen. Once dry, the sample was reconstituted with 150 µL of N, O-bis(trimethylsilyl)trifluoroacetamide (BSTFA) containing 1% trimethylchlorosilane (TMCS) and 50 µL pyridine. The vial was capped, inverted to mix, and heated to 70 °C for 3 hours. An aliquot from this sample was analyzed by GCMS to identify and quantify polar compounds.

For each GCMS analysis, 2 µL aliquots of the original and derivatized extracts were manually injected separately into the GC, along with a co-injection of a 1 µL aliquot of 30 mg/L 1-phenyldodecane (1-PD), in splitless mode at 250 °C. The GC oven was programmed to hold a temperature of 65 °C for 10 minutes followed by a ramp to 310 °C at a rate of 5 °C per minute to a final isothermal hold of 2 minutes. The mass selective detector was operated in electron impact mode at 70 eV at 230 °C in ion scan mode, which scanned mass to charge ratios of 50 to 500 Dalton at 2.94 scans/s.

The 1-PD co-injection was used to monitor the proper injection of the sample, while internal deuterated standards were used to monitor extraction efficiency. Authentic calibration standards, which were derivatized and analyzed with equivalent techniques, were used to determine instrument response and to confirm elution time. Compounds were identified by retention time and mass fragmentation patterns, and were quantified using the selected ion peak area and converted to compound mass using the relative response factor method.

2.4. Chemical mass balance analysis

CMB source apportionment uses known source profiles to determine the optimal contribution of different sources that best fit the ambient data measured at receptor sites. This requires detailed chemical characterization information for a number of possible sources. Some source profiles were created during the course of this work but others were obtained from results previously reported in the literature. The latter detailed source profiles included chemical characterization of PM_2.5 and sometimes PM₁₀. If a speciated source profile was available for PM_2.5 but not for PM₁₀, the size distribution of particles emitted from these sources was considered. PM₁₀ can operationally be considered equal to PM_2.5 + PMc for sources known to emit primarily fine particles since the PMc contribution is considered negligible. The chemical components are also considered equivalent. Chemical speciation of PMc source samples is seldom obtained since PMc is rarely collected and because PMc concentrations are small for most combustion sources. Determining a PMc source profile from the known PM_2.5 and PM₁₀ literature profiles can therefore result in large errors, making the derived source profiles unusable. Thus, PM_2.5 and PMc measurements made as part of this study were combined to form a PM₁₀ dataset and CMB modeling was done only on the resulting PM₁₀ and PM_2.5 chemically speciated datasets.

All sources modeled in the 2003 study [3] were initially included in the CMB modeling in the present study. These included mobile sources (characterized by organic/elemental carbon ratios, alkanes, and hopanes), vegetative burning (unique potassium marker), coal-fired power plants (unique selenium marker), and secondary aerosol formation [3]. Secondary aerosol formation only included ammonium nitrate and ammonium sulfate, while secondary formation of other ionic or organic aerosol mass was not considered. Source profiles for three additional factors, including meat cooking (characterized by cholesterol and organic acid markers), and separate consideration of gasoline powered motor vehicles (characterized by alkane markers) and diesel engines (characterized by hopane markers) for mobile sources were developed based on the inorganic compositional analysis from Chow et al. [12] and organic speciation data from Schauer et al. [13,14,15]. Previously developed plant detritus and fungal spore source profiles (characterized by sugar markers) obtained from Central Arizona also were included [16] along with the four source profiles for crustal material generated in this study. The latter included agricultural/native soil, road dust, paved-road dust (all characterized primarily by inorganic species common in crustal species), and cattle feedlot material (characterized by crustal minerals plus high sulfate and organic carbon concentrations). The chemical composition for the six source profiles not previously reported in the literature is included in Table 1.

Table 1. Source Profiles (in mg/g) for Plants, Spores, and Newly Developed Crustal Sources Sampled within the Study Area.

PM10

PM2.5

Bio-Plant

Bio-Spore

Ag/Natural

Dirt Road

Paved Road

Feedlot

Bio-Plant

Bio-Spore

Ag/Natural

Dirt Road

Paved Road

Feedlot

aluminum

–

–

60 ± 7

67 ± 7

67 ± 7

52 ± 6

–

–

61 ± 7

62 ± 7

74 ± 8

60 ± 7

silica

–

–

210 ± 26

230 ± 28

230 ± 28

180 ± 22

–

–

210 ± 26

220 ± 28

260 ± 32

210 ± 26

calcium

–

–

42 ± 5

40 ± 5

87 ± 11

41 ± 5

–

–

42 ± 5

40 ± 5

83 ± 11

43 ± 5

iron

–

–

33 ± 4

32 ± 4

34 ± 4

24 ± 3

–

–

34 ± 4

32 ± 4

39 ± 5

26 ± 3

potassium

–

–

32 ± 4

41 ± 5

19 ± 2

28 ± 3

–

–

34 ± 4

39 ± 5

23 ± 3

31 ± 4

selenium

–

–

nd

nd

nd

nd

–

–

nd

nd

nd

nd

arsenic

–

–

0.01 ± 0.01

0.01 ± 0.01

0.01 ± 0.01

0.01 ± 0.01

–

–

0.01 ± 0.01

0.01 ± 0.01

0.02 ± 0.02

0.01 ± 0.01

copper

–

–

0.07 ± 0.05

0.07 ± 0.05

0.07 ± 0.05

0.08 ± 0.05

–

–

0.08 ± 0.05

0.07 ± 0.05

0.08 ± 0.05

0.09 ± 0.05

zinc

–

–

0.2 ± 0.05

0.4 ± 0.05

0.2 ± 0.05

0.5 ± 0.06

–

–

0.2 ± 0.05

0.4 ± 0.05

0.2 ± 0.05

0.6 ± 0.06

magnesium

–

–

16 ± 2

20 ± 3

14 ± 2

15 ± 2

–

–

17 ± 2

18 ± 3

21 ± 3

17 ± 2

ammonium

–

–

0.9 ± 0.1

4.7 ± 0.5

0.3 +/ -0.03

3.5 ± 0.4

–

–

0.9 ± 0.1

4.9 ± 0.5

0.2 +/ -0.03

3.0 ± 0.3

nitrate

–

–

0.5 ± 0.06

2.0 ± 0.2

0.4 ± 0.04

0.4 ± 0.04

–

–

0.4 ± 0.05

1.8 ± 0.2

0.6 ± 0.06

0.5 ± 0.05

sulfate

–

–

0.8 ± 0.08

7.5 ± 0.8

2.0 ± 0.2

28 ± 3

–

–

0.9 ± 0.09

6.4 ± 0.7

2.0 ± 0.2

22 ± 2

organic carbon

1020 ± 50

606 ± 30

18 ± 0.9

20 ± 1.0

76 ± 3.8

240 ± 12

1020 ± 50

606 ± 30

19 ± 1.0

17 ± 0.9

71 ± 3.6

220 ± 11

elemental carbon

nd

nd

nd

nd

2.4 ± 0.4

0.7 ±0.4

nd

nd

nd

nd

2.0 ± 0.4

0.8 ± 0.4

n-heptacosane

–

–

0.01 ± 0.01

0.01 ± 0.01

0.01 ± 0.01

0.02 ± 0.02

–

–

0.01 ± 0.01

nd

0.02 ± 0.02

0.02 ± 0.02

n-octacosane

–

–

0.01 ± 0.01

0.01 ± 0.01

0.01 ± 0.01

0.02 ± 0.02

–

–

0.01 ± 0.01

0.01 ± 0.01

0.02 ± 0.02

0.02 ± 0.02

n-nonacosane

–

–

0.01 ± 0.01

0.01 ± 0.01

0.01 ± 0.01

0.02 ± 0.02

–

–

0.01 ± 0.01

0.01 ± 0.01

0.03 ± 0.03

0.02 ± 0.02

n-triacontane

–

–

0.01 ± 0.01

0.01 ± 0.01

0.02 ± 0.02

0.01 ± 0.01

–

–

0.01 ± 0.01

0.01 ± 0.01

0.02 ± 0.02

0.01 ± 0.01

n-hentriacontane

–

–

0.01 ± 0.01

nd

0.02 ± 0.02

0.02 ± 0.02

–

–

0.01 ± 0.01

nd

0.03 ± 0.03

0.02 ± 0.02

17a-trisnorhopane

–

–

0.01 ± 0.01

0.01 ± 0.01

0.01 ± 0.01

0.03 ± 0.03

–

–

0.01 ± 0.01

0.01 ± 0.01

0.02 ± 0.02

0.03 ± 0.03

17a, 21b-29-hopane

–

–

0.01 ± 0.01

nd

0.05 ± 0.05

nd

–

–

0.01 ± 0.01

0.01 ± 0.01

0.06 ± 0.05

0.01 ± 0.01

17a, 21b-hopane

–

–

nd

nd

0.02 ± 0.02

nd

–

–

nd

nd

0.02 ± 0.02

0.01 ± 0.01

22(R+S)-17a, 21b-30-homohopane

–

–

0.01 ± 0.01

nd

0.03 ± 0.03

0.03 ± 0.03

–

–

nd

0.01 ± 0.01

0.02 ± 0.02

0.01 ± 0.01

22(R+S)-17a, 21b-30-bishomohopane

–

–

nd

nd

0.01 ± 0.01

nd

–

–

nd

nd

0.01 ± 0.01

nd

levoglucosan

–

–

nd

nd

nd

nd

–

–

nd

nd

nd

nd

glucose

1.8 ± 0.4

0.89 ± 0.18

nd

nd

0.01 ± 0.01

0.03 ± 0.03

1.8 ± 0.4

0.89 ± 0.18

nd

nd

0.01 ± 0.01

0.01 ± 0.01

sucrose

69 ± 14

0.09 ± 0.04

0.01 ± 0.01

nd

0.01 ± 0.01

0.01 ± 0.01

69 ± 14

0.09 ± 0.04

0.01 ± 0.01

nd

0.07 ± 0.05

0.01 ± 0.01

trehalose

0.24 ± 0.05

87 ± 17

0.02 ± 0.02

nd

0.02 ± 0.02

1.7 ± 0.2

0.24 ± 0.05

87 ± 17

0.02 ± 0.02

nd

0.09 ± 0.05

0.4 ± 0.1

arabitol

0.02 ± 0.02

0.03 ± 0.02

nd

nd

nd

0.01 ± 0.01

0.02 ± 0.02

0.03 ± 0.02

nd

nd

nd

0.01 ± 0.01

manitol

0.08 ± 0.02

nd

nd

nd

nd

nd

0.08 ± 0.02

nd

nd

nd

nd

nd

fluoranthene

–

–

nd

nd

nd

nd

–

–

0.01 ± 0.01

nd

0.01 ± 0.01

0.01 ± 0.01

pyrene

–

–

nd

nd

nd

nd

–

–

nd

nd

0.01 ± 0.01

0.01 ± 0.01

chrysene

–

–

nd

nd

nd

nd

–

–

nd

nd

nd

nd

benzo(a)anthracene

–

–

nd

nd

nd

nd

–

–

0.01 ± 0.01

nd

0.02 ± 0.02

0.02 ± 0.02

hexadecanoic acid

–

–

0.8 ± 0.1

0.3 ± 0.1

0.9 ± 0.2

4.8 ± 0.6

–

–

0.8 ± 0.1

0.3 ± 0.1

1.6 ± 0.2

3.4 ± 0.5

octadecanoic

–

–

1.1 ± 0.1

0.4 ± 0.1

1.1 ± 0.2

21 ± 5

–

–

0.9 ± 0.1

0.43 ± 0.1

1.7 ± 0.3

8 ± 2

oleic acid isomers

–

–

0.1 ± 0.08

0.05 ± 0.05

0.1 ± 0.08

2 ± 0.3

–

–

0.04 ± 0.04

0.04 ± 0.04

0.2 ± 0.08

2 ± 0.3

chlosterol

–

–

nd

nd

nd

0.02 ± 0.02

–

–

nd

nd

nd

0.02 ± 0.02

nd = non detect; - indicates a non-measured species

 | Show Table

DownLoad: CSV

The inclusion of this many source profiles from a number of different sources creates a level of uncertainty that can influence CMB modeling results. Additionally, the choice of analytical and extraction methods can influence the results because of the recovery efficiency of the methods. For instance, elements measured in this study were analyzed by ICPMS, which requires filter extraction, whereas some source profiles obtained from the literature and used in the modeling were analyzed by XRF, which does not require an extraction step. The bias created by these differences is expected to be smaller than the uncertainty in the modeling.

Chemical speciation resulted in a 6-week averaged dataset including 8 samples for each sampling site and each size fraction. The inclusion of too many species or too many species in a given subset can lead to excessive co-linearity or inappropriate weighting of one or more sources, so the dataset was reduced in size to include 10 elements, 3 ions, 5 alkanes, 5 hopanes, 5 sugars, 4 PAHs, 3 organic acids, levoglucosan, cholesterol, and 2 bulk carbon fractions (Table 1).

This reduced dataset was modeled using CMB v8.2 [18]. Data from the three ambient sampling locations were modeled independently as were the two size fractions. Initial model runs used all source profiles with sources eliminated sequentially when excessive co-variation prevented sources with similar chemical composition from converging. Using trial-and-error, sources providing the best improvement in the model metrics (R² and percent mass apportioned) were retained. Once co-linear source profiles were eliminated, sources were investigated one-by-one to determine if inclusion or exclusion improved model performance. Once model performance was optimized by removal of sources, the list of chemical species used for the apportionment was reviewed. Species that were not well modeled were investigated to determine if model performance was greatly enhanced by the exclusion of one or more species. In this work, removal of a couple of the alkane and hopane species resulted in an improvement in the modeled-to-measured PM₁₀ mass agreement. Once optimized, excluded sources were tested one more time to determine if the elimination of a chemical species affected the model performance enough to warrant re-inclusion of one of the previously excluded sources. Crustal material, motor vehicles, paved road dust, coal-fired power plants, plants and spores, and secondary particles were the important sources in both particle size ranges. Biomass burning and meat cooking were also important sources in PM_2.5 and PM₁₀, respectively. Tables 2 and 3 detail the mass apportioned to each source for both size ranges.

Table 2. Average of 8 samples modeled by CMB for source apportionment of PM₁₀ mass. Concentration and confidence given in µg/m³.

	Casa Grande	Cowtown	Pinal County Housing
Measured Mass	38 ± 8	77 ± 15	55 ± 11
Modeled Mass	41 ± 3	64 ± 5	52 ± 4
Crustal Material	24 ± 4	51 ± 8	42 ± 6
Motor Vehicles	11 ± 2	9 ± 2	1.0 ± 0.5
Paved Road Dust	5 ± 2	4 ± 4	0 ± 3
Meat Cooking	1.0 ± 1.2	1 ± 2	6 ± 2
Ammonium Sulfate	1.0 ± 0.3	1.2 ± 0.4	0.9 ± 0.3
Ammonium Nitrate	1.1 ± 0.3	2.0 ± 0.5	1.2 ± 0.4
Coal-Fired Power Plant	1.12 ± 0.04	0.13 ± 0.05	0.15 ± 0.06
Plants and Spores	0.08 ± 0.03	0.14 ± 0.09	0.08 ± 0.03
Unapportioned	3 ± 8	13 ± 16	3 ± 12

 | Show Table

DownLoad: CSV

Table 3. Average of 8 samples modeled by CMB for source apportionment of PM_2.5 mass. Concentration and confidence given in µg/m³.

	Casa Grande	Cowtown	Pinal County Housing
Measured Mass	8 ± 2	11 ± 2	9 ± 2
Modeled Mass	9.0 ± 0.7	12 ± 1	10.0 ± 0.8
Motor Vehicles	4.6 ± 0.7	4.5 ± 0.7	3.4 ± 0.5
Crustal Material	1.1 ± 0.2	3.7 ± 0.6	5.4 ± 0.9
Ammonium Sulfate	1.1 ± 0.3	1.1 ± 0.3	0.9 ± 0.2
Ammonium Nitrate	0.5 ± 0.1	1.4 ± 0.4	0.6 ± 0.2
Biomass Burning	0.8 ± 0.3	1.1 ± 0.5	0.01 ± 0.01
Road Dust	0.9 ± 0.3	0.01 ± 0.01	0.01 ± 0.01
Coal-Fired Power Plant	0.14 ± 0.05	0.17 ± 0.06	0.11 ± 0.03
Plants and Spores	0.02 ± 0.01	0.02 ± 0.01	0.02 ± 0.01
Unapportioned	1 ± 2	1 ± 2	1 ± 2

 | Show Table

DownLoad: CSV

3. Results and Discussion

3.1. PM₁₀ and PM_2.5 composition

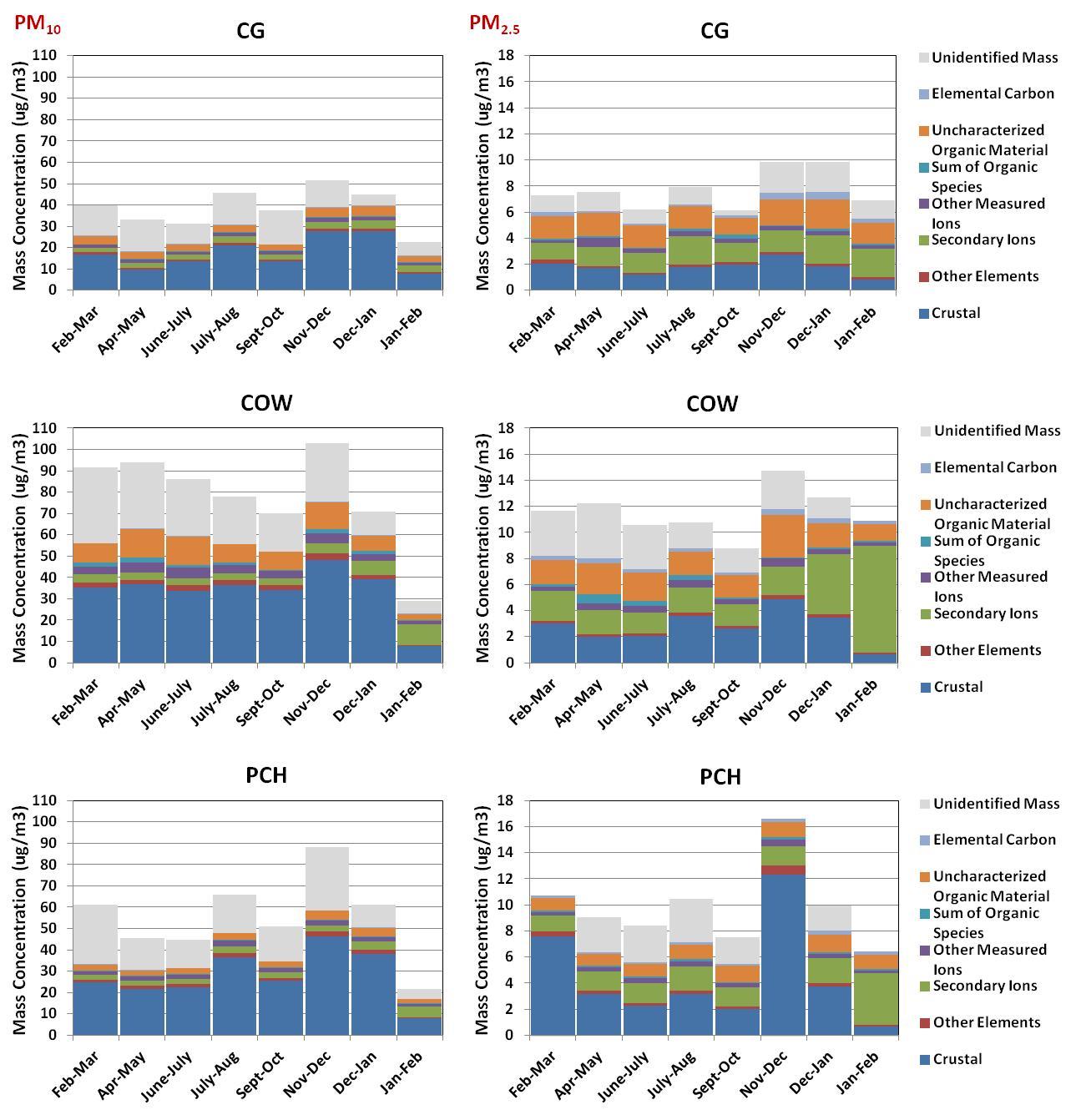
Figure 1 details the average PM₁₀ and PM_2.5 chemical mass balance for the six-week averaged data collected during the study. Information about coarse particles (PM_10-2.5) and more time-resolved chemical composition results can be found elsewhere [7].

Figure 1. Averaged measured PM₁₀ and PM_2.5 compositions.

DownLoad: Full-Size ImgPowerPoint

Figure 1 provides results for eight components, including crustal material, other elements, secondary ions, other measured ions, sum of organic species, uncharacterized organic carbon, EC, and unidentified mass. The crustal material component was calculated by assuming that the major trace elements in crustal material were present in their most common oxide forms using the equation:

Silicon was not determined by ICPMS and was estimated using an average Si to Al ratio of 3.5 based on ratios reported for upper continental crust [19] and road dust samples from California and Texas [12,20]. The other elements component included the sum of the other elements determined by ICPMS. The secondary ions component included the sum of sulfate, nitrate, and ammonium whereas the other ions (chloride, nitrite, phosphate, sodium, potassium, magnesium, and calcium), as measured by IC, were included as the other measured ions component. The concentrations of all organic chemical species identified and quantified by GCMS were summed and included in the sum of organic species component. Uncharacterized organic material was determined by the difference between twice the measured OC concentration, the latter by TOT [21] and the sum of the organic species measured by GCMS. The elemental carbon component, determined by TOT, was measured directly and the unidentified mass component equaled the difference between the measured mass and the sum of the other components.

Average PM₁₀ and PM_2.5 mass concentrations were roughly 57 and 9 µg/m³, respectively. Overall, the highest mass concentrations for both size fractions were at COW, which was consistent with compliance monitoring data within the county where average PM₁₀ and PM_2.5 concentrations in 2011 were 85 and 13 µg/m³, respectively [6]. Mass measurements showed several periods of elevated PM mass in February-March, July-August, and November-December. The higher levels in July-August were consistent with the monsoon season and were likely associated with wind-blown dust events [7]. PM₁₀ and PM_2.5 concentrations also appeared elevated during tilling and harvesting (March and late October/early November, respectively) when these activities entrain dust into the atmosphere [5].

On average, crustal material was the largest component of PM₁₀, comprising approximately 50% of the PM₁₀ mass. COW had an elevated organic carbon component not observed at other monitoring sites, representing approximately 10% of the PM₁₀ mass. COW PM₁₀ data also showed higher relative concentrations of sulfate and measureable amounts of soluble potassium that were not observed at the other sites. These observations were consistent with the chemical composition of feedlot material (Table 1 and [8]) and represented a departure from the 2003 study where PM was apportioned to the feedlot source at all monitoring locations [3].

The chemical composition of PM_2.5 across the region was more varied than PM₁₀; however, crustal material was still a major component comprising 14-51% of the aerosol mass. Elevated fine particle mass concentrations at PCH were accompanied by higher levels of metals common to crustal minerals indicating that dust entrainment can drive PM_2.5 mass concentrations. While the crustal component in the fine particle fraction in this study most likely represented local emissions activities, since these species are in the fine fraction, this component may also include transported regional crustal material or the impact of industrial emissions including perhaps from neighboring Phoenix. The organic material (sum of organic species and uncharacterized organic matter) and secondary ion components each comprised approximately 20% of the fine particle mass at all sites. The organic matter and secondary ion components showed a fairly consistent contribution month-to-month at each site. There were occasional exceptions to this general observation but these variations did not correlate with the fine crustal material (assuming local origin), suggesting different emission sources, possibly regional in nature for organic material and precursors to secondary ion formation. An increase in secondary ions during the spring planting season at the rural sampling locations may have originated from the application of fertilizers; however, this cannot be verified based on the data in this study.

3.2. Measured source profiles

Table 1 details the chemical composition of the novel source types characterized as part of this study, and lists the chemical compounds used for CMB modeling. Uncertainties were based on the analytical precision of the measurement approach used to quantify each component. The source profiles given in Table 1 were developed with two goals: to differentiate among the various crustal source types based on their detailed chemical composition and to provide locally-generated source profiles to reduce uncertainty in the CMB modeling as related work showed differences between local soils and generic upper continental crust profiles [8].

Plant detritus and fungal spore source profiles were derived from abraded samples of plant leaves and branches and spores collected from fungi common to the local desert ecosystem [16]. While these samples were only analyzed for OC and organic saccharide species, they remain the most representative source profiles available in this area. As seen in Table 1, mannitol and sucrose were candidate marker species for the desert plant detritus given their strong enrichment relative to other sources. Fungal spores were enriched in trehalose compared to all other source profiles used in this study. These observations were consistent with other studies that found mannitol, sucrose, and trehalose associated with primary biological particles [22].

Most variations in the chemical composition of the characterized soil types were minor and insufficient to differentiate ambient concentrations of entrained soils. Elemental carbon was greater than the minimum detection limit (MDL) of 0.4 mg/g in road and feedlot samples only. The feedlot profile was also distinguished as the only profile with cholesterol above the MDL of 0.008 mg/g as well as a much higher contribution from sulfate when compared to the other soil types.

3.3. CMB model performance evaluation

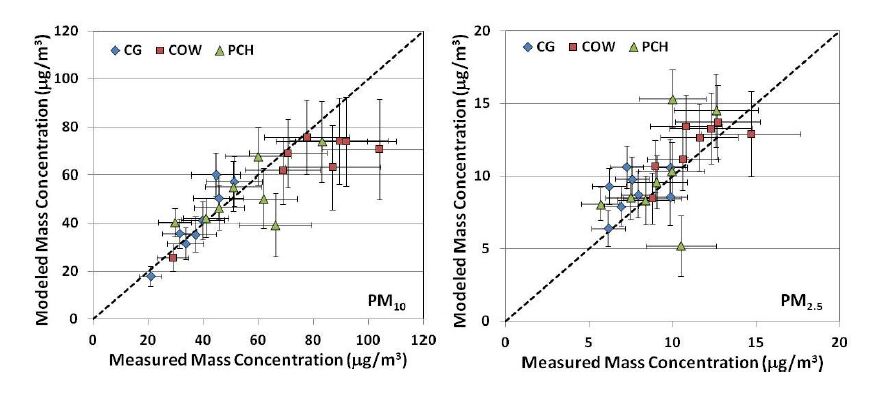
Agreement between measured (horizontal axis) and CMB modeled (vertical axis) PM₁₀ and PM_2.5 mass is one metric used to determine model performance; these comparisons are shown in Figure 2. Error bars in the measured mass concentration represented an estimated 20% uncertainty based on propagation of error from the mass measurements and sample collection. Error bars in the modeled mass concentration represented the uncertainty estimated by the CMB model. Based on regression analysis, the modeled-to-measured mass for PM₁₀ was within 6% at PCH and CG and within 16% at COW. For PM_2.5 mass, the COW site was within 10% and PCH and CG were within 19%. PM₁₀ mass concentrations at COW were among the highest measured and the model generally under predicted higher PM₁₀ mass values by up to 25%. One possible explanation for this observation is that an important source impacting this site was missing from the source profiles used in the CMB analysis. The model-predicted PM_2.5 mass concentrations at the COW site were in better agreement with the measured mass concentrations, however, the model-predicted PM_2.5 mass concentrations at PCH and CG were almost always over predicted. This may again suggest a missing source impacting the COW site and thus a missing PM2.5 source profile as well as a scaling issue all of which may lead to the over prediction of the modeled PM_2.5 mass.

Figure 2. Model performance evaluation—model vs. gravimetrically measured mass.

DownLoad: Full-Size ImgPowerPoint

3.4. Average source apportionment results

Table 2 presents the modeled source apportionment results for PM₁₀ for the three monitoring locations. CMB results confirmed previous measurements [5,7] that coarse particles were largely crustal in nature. Estimated contributions of crustal material range from 52 to 90% of the PM₁₀. The influence of crustal material was highest at the two rural sites (COW and PCH) with the largest impact observed at PCH, which was surrounded by active agricultural fields. These results were also consistent with the 2003 study [3]. CMB modeling was unable to reliably separate contributions to PM₁₀ from agricultural/native dust, road dust, and feedlot material. This inability to distinguish soil types was likely due to profile co-linearity since source profiles had similar chemical characteristics and temporal variations. Thus, the attribution of the measured PM₁₀ mass to each of the three source profiles was combined into one source type called crustal material.

Motor vehicles (4-28%; modeled using the source profile for gasoline engines with catalytic converters) and road dust (2-15%) were also important sources of PM₁₀ (Table 2). Motor vehicles exhibited the greatest impact (15%) at CG, the more urban site with the greatest density of mobile sources. The impact of motor vehicles was lowest at rural PCH, which was more removed from the roadway and had a lower traffic density compared to the COW site. COW was adjacent to a regional 2-lane highway between Casa Grande and Maricopa, while PCH was near a small rural paved road. GC and COW had at least twice the traffic volume than that measured near PCH.

Meat cooking contributed 13% to the CMB modeled PM₁₀ mass at PCH and only a few percent at the other sites. Although this seems high, this site was located adjacent to the Pinal County Housing Complex where such sources might be important. Surprisingly, a similar observation was not made at GC where the population density was greater suggesting that this source may be inappropriately labeled. The meat cooking source signature included high concentrations of organic carbon paired with a signature from organic acids with a minor contribution from cholesterol. Although these organic acids are most abundant in animal fats, they are also found in plants, vegetables, and even microorganisms suggesting agricultural or waste management practices near PCH might be producing a similar chemical signature.

Estimated contributions from ammonium sulfate and ammonium nitrate to PM₁₀ were small (2-4%) at each site. Although small, their contribution to PM₁₀ might, in part, be due to emissions of these species from the application of fertilizer based on the results in Tables 2 and 3, where the ammonium nitrate contribution to PM₁₀ was between 1.3 and 2.2 times that of PM_2.5. A coarse particle source of this component is likely and may be due to the release of these species during the application of the fertilizer or more likely associated with the re-entrainment of soil particles and some plant materials with which the fertilizer has incorporated. The remaining sources, including coal fired power plants and biological material from plants and spores were less than 1% of the apportioned mass.

Table 3 shows the modeled source apportionment results for PM_2.5 at each site. Results indicated that motor vehicles and crustal material were the dominant sources but as many as 6 different sources contributed greater than 5% to the apportioned PM_2.5 mass. CMB modeling was unable to reliably isolate the individual impacts of agricultural/native dust, road dust, and feedlot material, so these sources were again aggregated into the crustal material source type. Paved-road dust was only important at CG.

Results indicated that motor vehicles (modeled as gasoline engines with catalytic converters) were an important source of PM_2.5 similar to PM₁₀ as noted above. The lowest contribution from motor vehicles was at the more rural PCH site (30%) with higher contributions at the rural COW (37%) site adjacent and closer to the 2-lane highway whereas the contribution from motor vehicles was highest at CG (50%) located in the center of Casa Grande.

The contribution from road dust to PM_2.5 (9%) was only observed at CG and equal to approximately 20% of the motor vehicles contribution. However, road dust was only weakly correlated (R²—0.54 at CG) to the motor vehicles contribution, likely due to differences in the source profiles. The road dust source contained higher concentrations of heavy metals consistent with lower end of the crustal material size distribution created by mechanical abrasion, while the motor vehicle profile contained a higher concentration of organic carbon consistent with direct and secondary tail-pipe emissions from motor vehicles [23]. One possible explanation for the differing contribution from road dust and motor vehicle factors relates to particle size. Mechanically derived road dust particles are generally larger (>PM₁) than particles associated with direct motor vehicle exhaust emissions. This difference in size may lead to variations in atmospheric transport and residence times including travel distance in both horizontal and vertical distances from roadways.

Approximately 14, 31, and 52% of the PM_2.5 mass was apportioned to crustal material at CG, COW, and PCH, respectively. The relative contribution of crustal material to PM_2.5 was similar to that observed for PM₁₀ with crustal material contributing more at the rural sites than the urban site. On a mass concentration basis, the amount of crustal material in PM_2.5 was much smaller than in PM₁₀ (Tables 2 and 3), indicating that most of the crustal material was in the coarse particle mode.

A similar amount of ammonium sulfate was apportioned to each size fraction on a mass concentration basis. This indicated that almost all of the ammonium sulfate was in fine fraction. The apportioned ammonium nitrate was split between both size fractions ranging from 45 to 70% in the fine fraction or about evenly split between PM_2.5 and PM₁₀. Coarse particle concentrations of ammonium nitrate may be due to primary fertilizer emissions and/or absorption of those emissions onto soil particles or directly mixed into the soils.

Approximately 10% of the apportioned PM_2.5 mass at CG and COW was attributed to biomass burning. The remaining sources, including coal fired power plants and biological material from plants and spores contributed less than 1% each to the apportioned PM_2.5 mass at each of the three sites.

3.5. Seasonal averaged source apportionment results

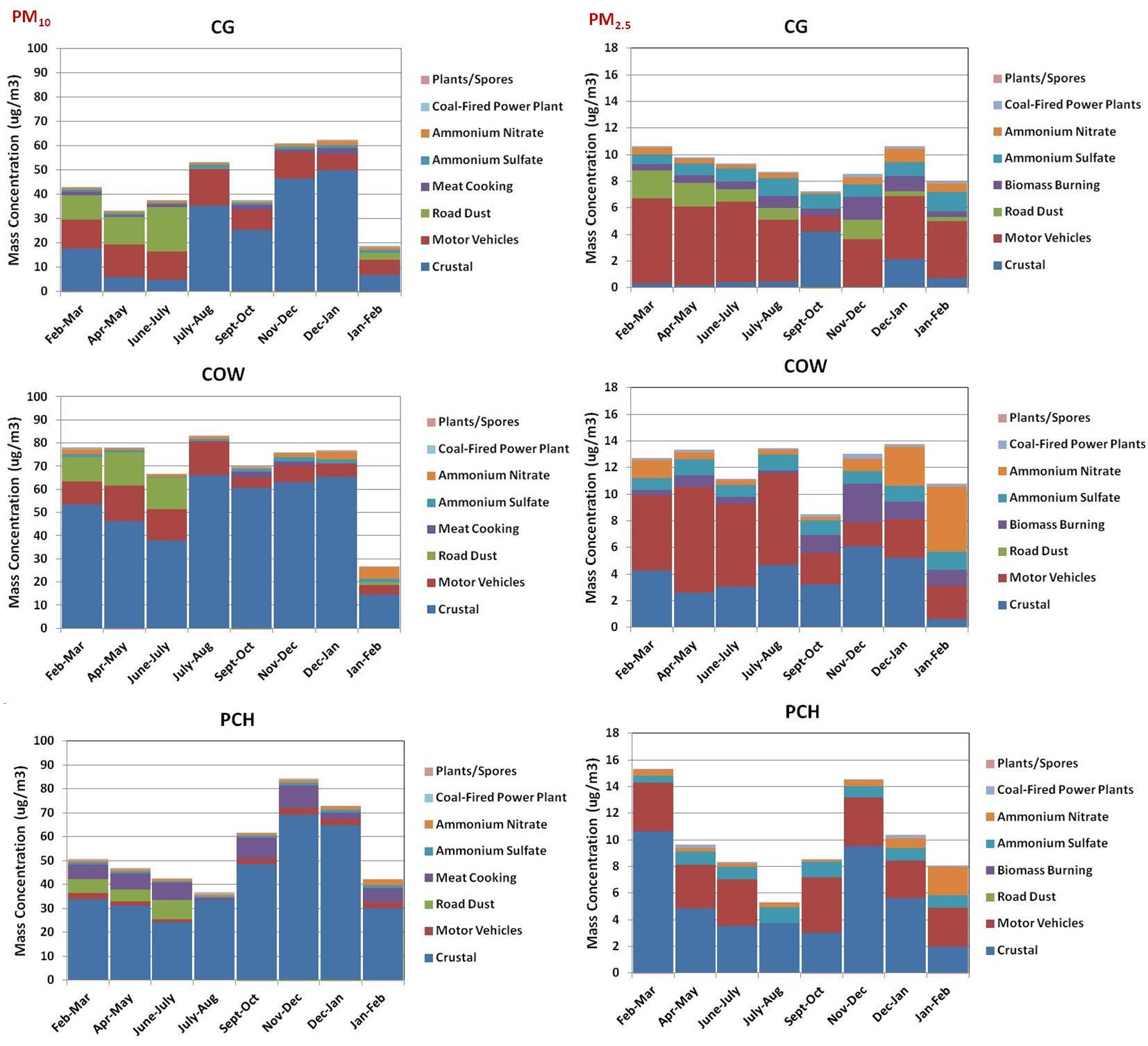
The averaged PM₁₀ and PM_2.5 seasonal source apportionment results for each 6-week period are presented in Figure 3. Crustal material was a major contributor to apportioned PM₁₀ mass at COW and PCH all year, and at CG during the late-summer through early-winter. At CG, periods with low contributions from crustal material simultaneously had high contributions from road dust. One possible explanation was a lack of differentiation between the source profiles for road dust and crustal material, which would cause problems isolating these similar sources. A comparison of the mass concentration apportioned to road dust in PM_2.5 and PM₁₀ revealed that a larger fraction of the mass concentration was apportioned to PM₁₀ indicating a majority of this component was in the coarse mode.

Figure 3. Averaged Seasonal source apportionment of PM₁₀ and PM_2.5.

DownLoad: Full-Size ImgPowerPoint

The motor vehicle component in PM_2.5 was fairly uniform throughout the year at PCH, except for the July-August period, where no mass was apportioned to this source. At CG, the mass concentration apportioned to motor vehicles for the September-October period was significantly smaller than the mass concentrations apportioned to this source throughout the rest of the year. CMB results for COW showed a marked decrease in the contribution attributed to motor vehicles beginning in September-October through the end of the year with larger contributions from crustal material, ammonium nitrate, and/or biomass burning. The cause for the decrease in the motor vehicles contribution was unknown and site observations did not suggest a change in vehicle traffic over these sampling periods. A comparison of the mass concentration apportioned to motor vehicles in PM_2.5 and PM₁₀ showed that at CG and COW, approximately twice as much of this component was apportioned to this source in PM₁₀. This indicated that approximately equal amounts were in the fine and coarse (PM_10-2.5) particle size fractions. The comparison is remarkably different at PCH where almost equal amounts were in PM₁₀ and PM_2.5 indicating no coarse particle emissions from motor vehicles.

Biomass burning was isolated as a significant source for fine particles only at CG and COW. The largest impact was modeled during November-December, which was consistent with the end of the harvesting season and could coincide with burning residual material on agricultural fields as well as residential burning for home heating. However, there was no direct evidence of these activities recorded by site operators in the site logs, but sites were only visited for a short period of time once every six days.

The larger attribution of mass to ammonium nitrate near the end of the study at the rural COW and PCH sites may be due to the application of fertilizers to agricultural soils and subsequent re-entrainment as noted earlier. Lower temperatures may also have allowed for greater partitioning to the particle phase, especially in the fine particle fraction where the about half of the mass concentration was observed. The impact of ammonium sulfate to PM_2.5 was uniform throughout the year and relatively consistent among all three locations. This suggested the regional nature of this component as seen elsewhere [24].

4. Summary and Conclusions

The Desert Southwest Coarse Particulate Matter Study was undertaken in Pinal County, AZ to better understand sources contributing to fine and coarse PM concentrations in rural, arid regions of the desert southwest. This study expands on information available from the one-month 2003 source apportionment study [3] that examined the impact of local and regional PM sources by 1) investigating seasonal variations through a full-year sampling period, 2) expanding the chemical species identified to include speciated organic compounds and a wider range of trace elements, and 3) developing more specific chemical signatures for several soil types in the area. This additional information enabled more detailed source apportionment modeling to estimate source impacts contributing to fine and PM₁₀.

Detailed chemical profiles for two groups of biological particles (plant detritus and fungal spores) and four types of crustal material were used in the CMB modeling including agricultural/native dust, road dust, road dust, and feedlot material. Unique marker species for the biological material were observed in ambient data; however, unique markers for the different sources of crustal material were not observed in the ambient data. Significant co-variation within these soil types results in an inconsistent apportionment to the targeted crustal source types using CMB. While distinct marker species for the plants and fungal spores evaluated were observed, their contribution to either PM₁₀ or PM_2.5 mass as determined by CMB was small (~1%). Still, these unique chemical signatures may be of future use in understanding the relative contribution of different sources to aerosols in the desert southwest or other agricultural areas.

Crustal material, motor vehicles, road dust, meat cooking, ammonium sulfate, and ammonium nitrate were the largest contributors to PM₁₀ mass. Crustal material was the single largest source contributing to PM₁₀ mass, ranging between 50 and 79% and with highest contributions during seasons that coincided with local agricultural tilling and harvesting as well as the summer monsoon storm season. The motor vehicle and road dust source contributions were highest at the urban CG site, together contributing to about 42% of the PM₁₀ mass.

In general, the same six sources contributed to the apportioned PM_2.5 mass with the addition of biomass burning, which was estimated at ~10% of the PM_2.5 mass at GC and COW. The contribution to PM_2.5 from coal fired power plants was small (<1%) at the three sites. In this size fraction, crustal material contributed between 14 and 50% of the PM mass while the motor vehicles source contributed between 30 and 50%. Source contributions to ambient fine particles varied by site as well as season.

Results from this study indicated that the largest reductions in PM₁₀ concentrations would be achieved by reducing emissions from crustal related sources, such as agricultural cropping and dairy feedlots. Other relatively large sources, the contribution of which varies by the time of year and by site, include motor vehicles, paved-road dust, and ammonium nitrate (likely from fertilizer and gas-particle phase partitioning). Reductions in crustal material, road dust, and ammonium nitrate should also result in lower levels of PM_2.5, important since fine particle concentrations are close the value of the PM_2.5 NAAQS.

Acknowledgments

The authors wish to acknowledge and thank the Pinal County Air Quality Control District for their assistance with collection of the ambient air quality samples as well as for power and access to their field sampling sites. We also acknowledge the State of Arizona Department of Environmental Quality for the loan of the dichotomous samplers that made this work possible. We thank Dr. Yuling Jia and Patrick Montgomery who assisted with the gravimetric measurements of filter media and Dr. Nabin Upadhyay for assistance with data compilation. Funding for this work was provided through EPA’s Region 9 Regional Applied Research Effort (RARE), EPA’s Office of Research and Development, and the Pinal County Air Quality Control District. The United States Environmental Protection Agency through its Office of Research and Development partially funded and collaborated in the research described here under assistance agreement 83404901 to Arizona State University. It has been subjected to Agency review and approved for publication.

Conflict of interest

The authors have no conflicts of interest to report.