The interplay between lipids and embedded proteins in plasma membrane is complex. Membrane proteins affect the stretching or disorder of lipid chains, transbilayer movement and lateral organization of lipids, thus influencing biological processes such as fusion or fission. Membrane lipids can regulate some protein functions by modulating their structure and organization. Cholesterol is a lipid of cell membranes that has been intensively investigated and found to be associated with some membrane proteins and to play an important role in diseases. Human calcitonin (hCt), an amyloid-forming peptide, is a small peptide hormone. The oligomerization and fibrillation processes of hCt can be modulated by different factors such as pH, solvent, peptide concentration, and chaperones. In this work, we investigated the role of cholesterol in hCt incorporation and channel formation in planar lipid membranes made up of palmitoyl-oleoyl-phosphatidylcholine in which no channel activity had been found. The results obtained in this study indicate that cholesterol promotes hCt incorporation and channel formation in planar lipid membranes, suggesting a possible role of sterol as a lipid target for hCt.
1.
Introduction
Many biological processes that involve membranes are based on interactions between membrane lipids and proteins. On binding to lipid bilayers, many proteins or peptides perform roles such as signal transduction [1], vesicle trafficking [2],[3], modulating the functions of membrane channels [4] or permeabilizing bilayers in bacteria [5]. The basic principles of lipid-protein interactions have still not been completely elucidated, as lipids and proteins can affect each other. The effects of membrane proteins on surrounding lipids can include stretch or disorder of lipid chains, transbilayer movement and lateral organization of lipids, as well as biological processes such as fusion and fission. On the other hand, membrane lipids can influence both protein structures (e.g., backbone conformation or rotation angle of the transmembrane segments) as well as the organization of proteins into membranes (i.e., self-association).
Cholesterol (Chol) is a lipid of eukaryotic cell membranes. It is an amphipathic molecule formed by a rigid planar polycyclic ring with an isooctyl chain attached to C17 and a β-hydroxyl group attached to C3. Membrane Chol partitions between the raft and no raft phases. Lipid rafts are small platforms composed of sphingolipids and Chol in the outer exoplasmic leaflet, connected to phospholipids and Chol in the inner cytoplasmic leaflet of the lipid bilayer [6]. Chol is thought to serve as a spacer between the hydrocarbon chains of sphingolipids and to function as a dynamic glue that keeps the raft assembly together. Many studies show that Chol affects membrane protein structure, function and dynamics by means indirect or direct interactions with proteins [7],[8].
Human Calcitonin (hCt) is a small peptide hormone, present in all vertebrates, that exerts its physiological effect on calcium metabolism through a membrane-bound receptor. The hCt receptor belongs to a superfamily of 7 transmembrane-spanning helices G-protein-coupled receptors that act via a second messenger [9]. However, the study carried out by Rymer and Good [10] show that the bovine calcitonin and Aβ peptides, which are amyloid-forming peptides, alter G-protein activity by increasing GTPase activity.
The hCt structure presents an N-terminal portion, specific for receptor activation, and a central helical segment. In aqueous solution, hCt shows a high tendency to form fibrils, thus limiting its clinical use and biological activity. The mechanism of fibril formation consists in two steps: in the first, the fibril nucleus forms by a homogeneous process; in the second, the fibril matures by a heterogeneous autocatalytic process. The fibrils formed at neutral or weakly basic pH are composed of antiparallel β-sheets [11]. Several studies show that the central segment of hCt structure (15–19) is involved in the oligomerization and subsequently in the fibrillation processes [11],[12]. The oligomerization and fibrillation processes of hCt, as for other fibrillating peptides, can be modulated by various factors, such as pH, solvent, peptide concentration, chaperones etc. The role of membrane Chol and ganglioside is a subject of debate among researchers. Some have shown that Chol and ganglioside increase the toxicity of some peptides, e.g., bovine calcitonin and Aβ peptide, promoting a conformational variation of the β-sheet structure [13]. Other researchers have shown that Chol increases the α-helix content of Aβ peptide, decreasing its β-sheet content, in DMPC vesicles [14]. Electrophysiological studies have shown that calcitonins (Cts) (including human calcitonin) form ion channels in planar lipid membranes (PLMs) [14]–[18] while transmission electron microscopy studies have confirmed channel formation by salmon calcitonin [19].
In this work, we evaluated the role of Chol on hCt incorporation and channel formation in palmitoyl-oleoyl-phosphatidylcholine (POPC) PLMs. We carried out experiments in which we monitored the formation and incorporation of hCt ion channels into PLMs made up of POPC:Chol, at different Chol concentrations. Preliminarily, we evaluated the secondary structure of hCt in an aqueous environment by means of Circular Dichroism (CD). Finally, we compared the electrophysiological characteristics of hCt channels obtained from POPC:Chol PLMs with those from palmitoyl-oleoyl- phosphatidylcholine:dioleoyl-phosphatidylglycerol (POPC:DOPG = 85:15, w/w) and DOPG PLMs.
2.
Materials and methods
2.1. Circular dichroism measurement
Circular Dichroism (CD) measurements were performed at 24 °C under a constant flow of nitrogen on a Jasco J-810 spectropolarimeter at an hCt concentration of 1.25 × 10−5 M, using a quartz cuvette with a 1 cm optical path, a wavelength interval of 200–250 nm and 0.1 nm data pitch. All spectra, corresponding to an average of 5 scans, were baseline-corrected.
Salts, buffers, and ACS reagent-grade H2O were obtained from Sigma-Aldrich (Germany). hCt was purchased from Calbiochem. The hCt stock solution concentration was 5.83 × 10−3 M.
In order to evaluate the hCt secondary structure, two different experimental procedures were performed:
in the first series of experiments, the effect of different incubation times was studied. A peptide solution was prepared by diluting 3.22 µL of hCt stock solution with bidistilled H2O (pH 7), while CD spectra were recorded 10 min (T0), 24 (T24) and 48 (T48) hours after preparing the samples. During the incubation period, all peptide samples were kept in quartz cuvettes, at 24 °C and monitored at different time intervals by CD;
in the second series of experiments, the effect of different aqueous buffers was studied. Two different peptide solutions were prepared. In the first, 3.22 µL of hCt stock solution was diluted with bidistilled H2O (pH 7); in the second, 3.22 µL of hCt stock solution was diluted with a mixture of bidistilled H2O (pH 7) and trifluoroethanol (TFE) at a volume ratio of TFE 30%. CD spectra were recorded 10 min after preparing the samples.
Molar ellipticity was calculated using CD experimental data (reported as ellipticity) and taking into account cell pathlength (1 cm), hCt concentration (1.25 × 10−5 M) and number of amino acids in the hCt peptide (32 amino acids).
2.2. Single-channel measurement
PLMs at different Chol concentrations were used to monitor hCt channel activity. To test the effect of Chol, the channel activity was monitored in PLMs made up of POPC, in which the Chol amount (mol %) increases from 10% to 30%, in 1% n-decane prepared as previously described [20].
We used a Teflon chamber with two aqueous compartments (volume 4000 µL) connected by a small circular hole with a diameter of 300 µm. The aqueous solutions were composed of KCl 1M, pH 7, temperature 22 ± 2 °C and were used unbuffered. The salts used in the experiments were of analytical grade. Bilayers were formed across the hole in the Teflon partition by the Müller-Rudin or painting technique, using lipids solubilised in n-decane. Briefly, a small volume of 0.5–1 µL of lipid solution is applied through a micropipette directly onto the hole of the Teflon set; a PLM forms in about 10 min after draining the excess solvent into the aqueous bathing solution. In all hCt experiments performed and before peptide addition, the conductance and capacitance of each membrane was tested by applying a voltage of ±150 mV for 15–20 minutes under stirring to ensure that the membrane was stable.
A stock solution of hCt was prepared by dissolving hCt powder (1 mg) in 50 µL of bidistilled sterile water under stirring for 3 min to obtain a concentration of 5.83 × 10−3 M. From this solution, different solutions at scalar concentrations were prepared, stocked and stored at −20 °C until use and 8.58 µL of the solution at concentration of 5.83 × 10−5 M was added to the cis side of the membrane, to obtain the final concentration of 1.25 × 10−7 M.
In single-channel experiments, the membrane current was monitored with an oscilloscope and recorded on a chart recorder for further analysis by hand. The cis and trans chambers were connected to the amplifier head stage by Ag/AgCl electrodes in series with a voltage source and a highly sensitive current amplifier (OPA 129). The single-channel instrumentation had a time resolution of 1–10 ms depending on the magnitude of the single-channel conductance. The polarity of the voltage was defined according to the side where hCt was added (the cis side). A trans-negative potential (indicated by a minus sign) means that a negative potential was applied to the trans side, the compartment opposite the one where hCt was added.
2.3. Data analysis
Membrane capacitance was calculated using a calibration curve obtained by simulating the membrane capacitance with a discrete set of capacitances of known values, Cn, and measuring the corresponding output voltage, Vlh. The data obtained were fitted by the formula:
in which A and B are free parameters to be estimated by the fitting procedures. The values of parameters A and B were used to transform the V
lh value into capacitance data, as described by Micelli et al.
[21]. hCt incorporation into PLMs and channel formation manifested as non-random discrete current fluctuations, compatible with channel-type openings and closures with different conductance levels, lifetimes and frequencies.
The single-channel data, filtered at 300 Hz were obtained from at least three experiments (more than 150 single channels per experiment) performed on different days. Data were analysed by hand. All single channels were used to calculate the biophysical and statistic parameters of the hCt channel.
The permeability ratio was calculated by means of the equation [22]:
where a
c /a
t is the activity ratio of the ion species in the
cis and
trans compartments, respectively; where P
Cl− and P
K+ are the permeabilities of the Cl
− and K
+, respectively; where R, T and F are respectively molar gas constant, thermodynamic temperature and Faraday constant.
3.
Results
3.1. Analysis of hCt secondary structure by CD
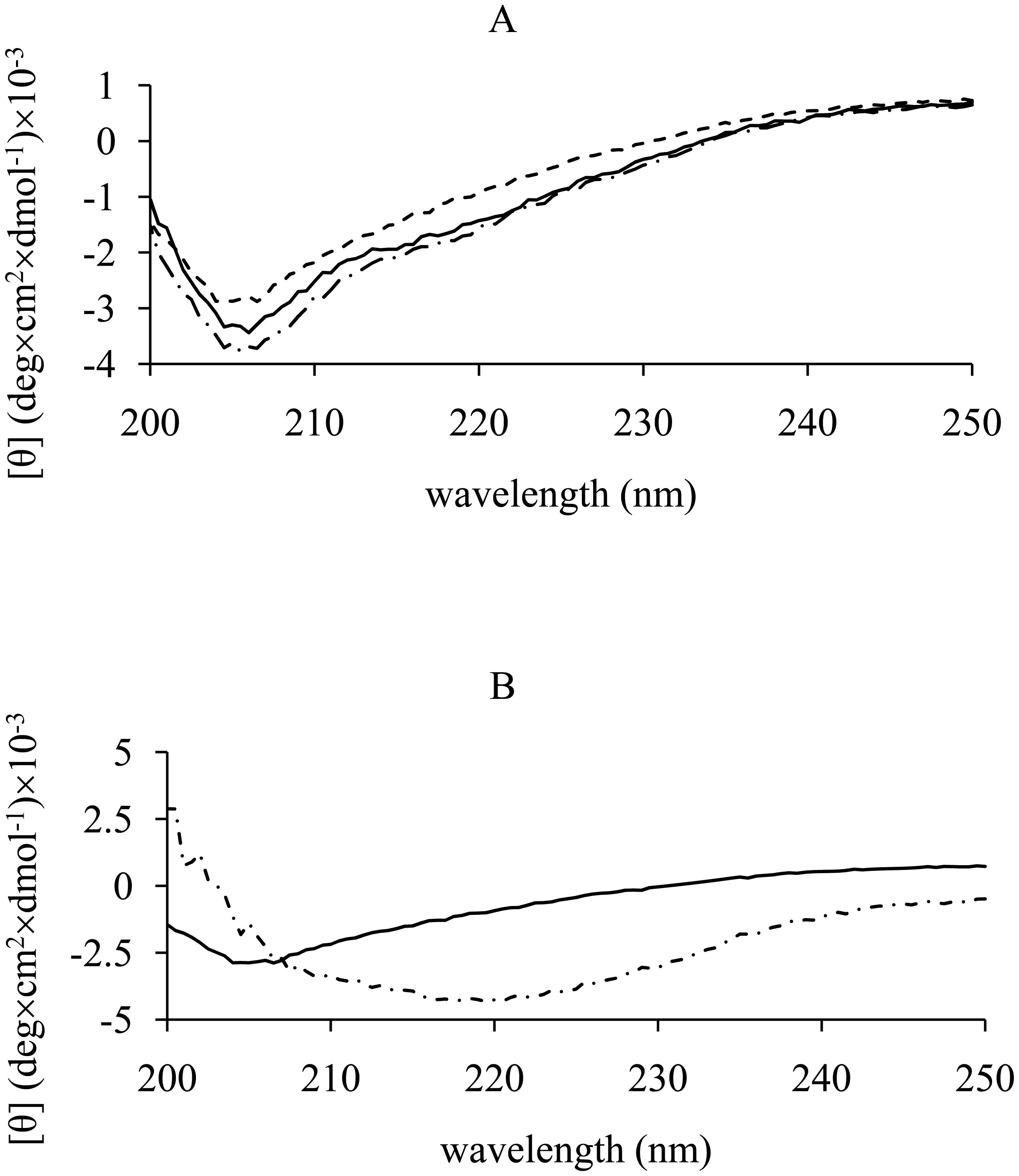
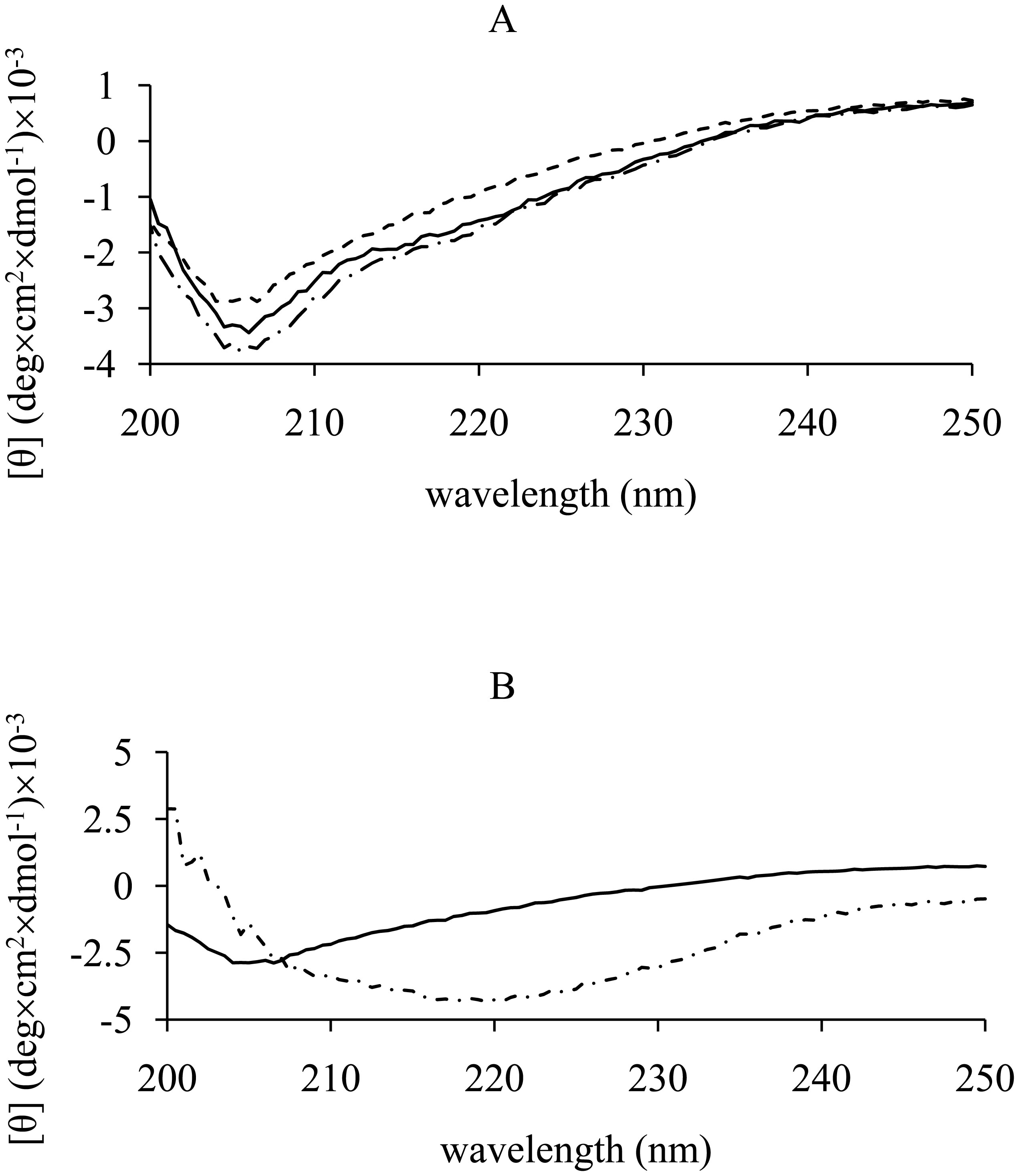
We checked the secondary structure of hCt used in this study by CD. To test whether the secondary structure of hCt changed over time, we performed CD experiments following the first experimental procedure described in Materials and Methods. Figure 1A shows the CD spectra of hCt at the three different measurement times. At T0, hCt exhibited a CD profile that qualitatively indicates the presence in solution of the peptide in disordered conformation, as found by other authors. After 24 and 48 h of incubation in the above conditions, no significant change in the CD profile and a slight increase in signal intensity were observed. Our results could indicate that the presence of an unstructured and disordered structure is correlated with metastable secondary structure and formation of amorphous agammaegates and fiber.
To exclude any non-specific effects of solvent (bidistilled H2O (pH 7)) on hCt secondary structure, we performed CD experiments following the second experimental procedure described in Materials and Methods. The CD spectra of hCt in the two different aqueous buffers are shown in Figure 1B, where changes in the CD profile were revealed for the peptide in the mixture of bidistilled H2O (pH 7) and TFE (volume ratio 30%). The features of the spectra show a conformational transition in accord with a higher α-helix content than the spectra where the aqueous buffer is bidistilled H2O alone. Our results seem to be in line with those obtained by other authors, who show that hCt adopts an α-helical structure comprising up to 40–48% amino acids in methanol/water and trifluoroethanol/water mixtures, whereas it easily associates and precipitates as insoluble fibrils when stored in aqueous solution.
3.2. Effect of different cholesterol concentration on hCt ion channel activity
In this study, we monitored hCt incorporation and channel formation in PLMs made up of POPC:Chol at different mole percentages of Chol 10, 20 and 30 mol %.
Preliminarily, to test the membrane stability and to exclude the non-specific effects on the PLM, we performed control experiments with the lipid mixtures only. No variation in parameters of conductance and capacitance was observed for a long period of time (over 24 hours) at applied voltages of ±100 and ±150 mV or when the bilayer was broken and withdrawn by the operator.
In the series of experiments in the presence of hCt and before its addition to the cis side of the medium, PLM stability was tested by applying a voltage of ±150 mV for 10–15 min under stirring and monitoring constant values for PLM conductance and capacitance. Neither conductance nor capacitance ever exceeded 12.5 pS and 0.30 μF/cm2, respectively, and neither showed channel-like activity. In many different experiments on POPC:Chol (10, 20 mol %) PLMs, the addition of 1.25 × 10−7 M of hCt to the cis side of the medium facing the membrane did not lead to any conductance variation for a long period of time (> 24 h), upon application of voltages as high as 150 mV. hCt channel activity did not appear even after operator PLM breakage and withdrawal, indicating that the hCt peptide did not incorporate into the membrane.
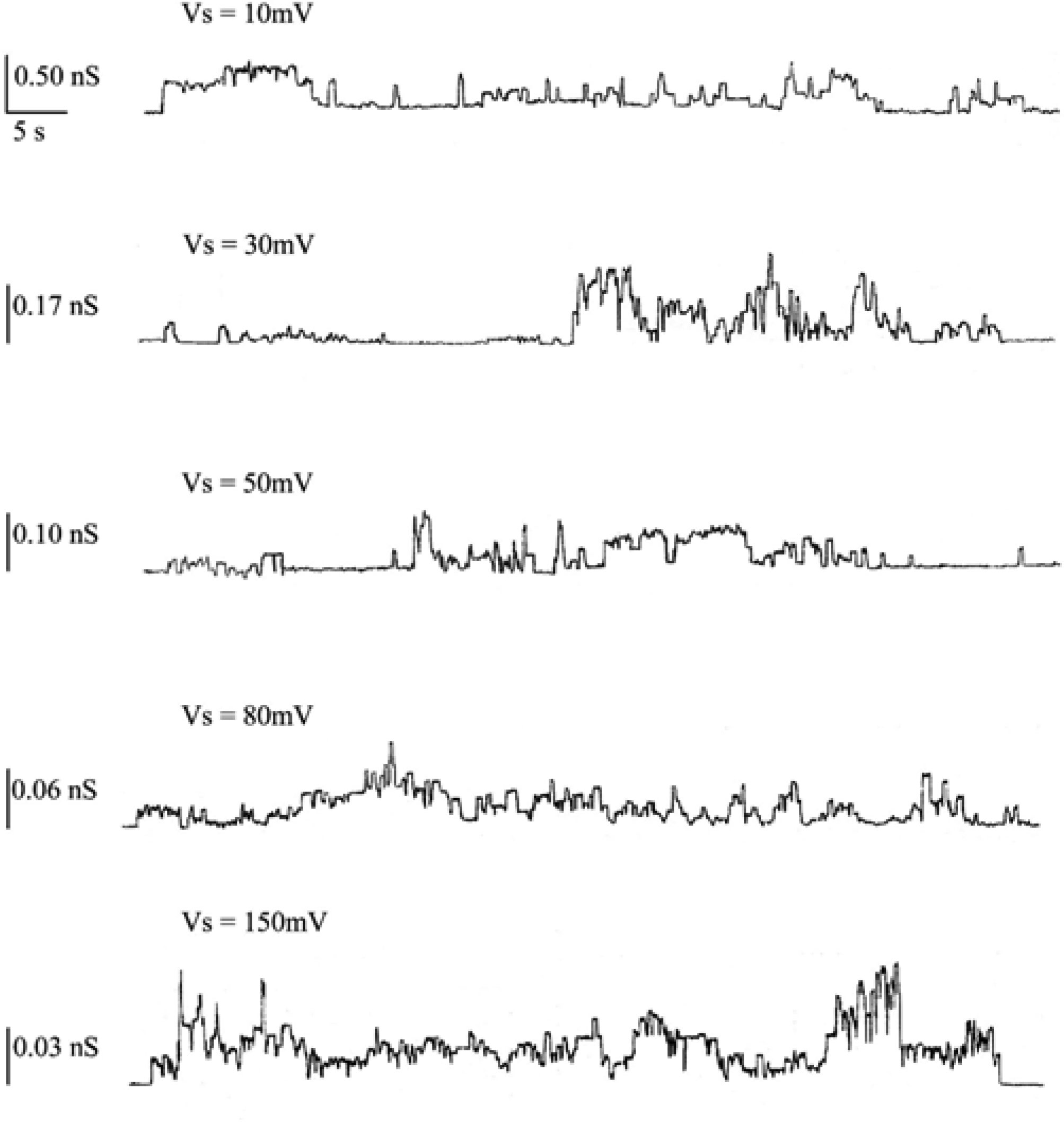
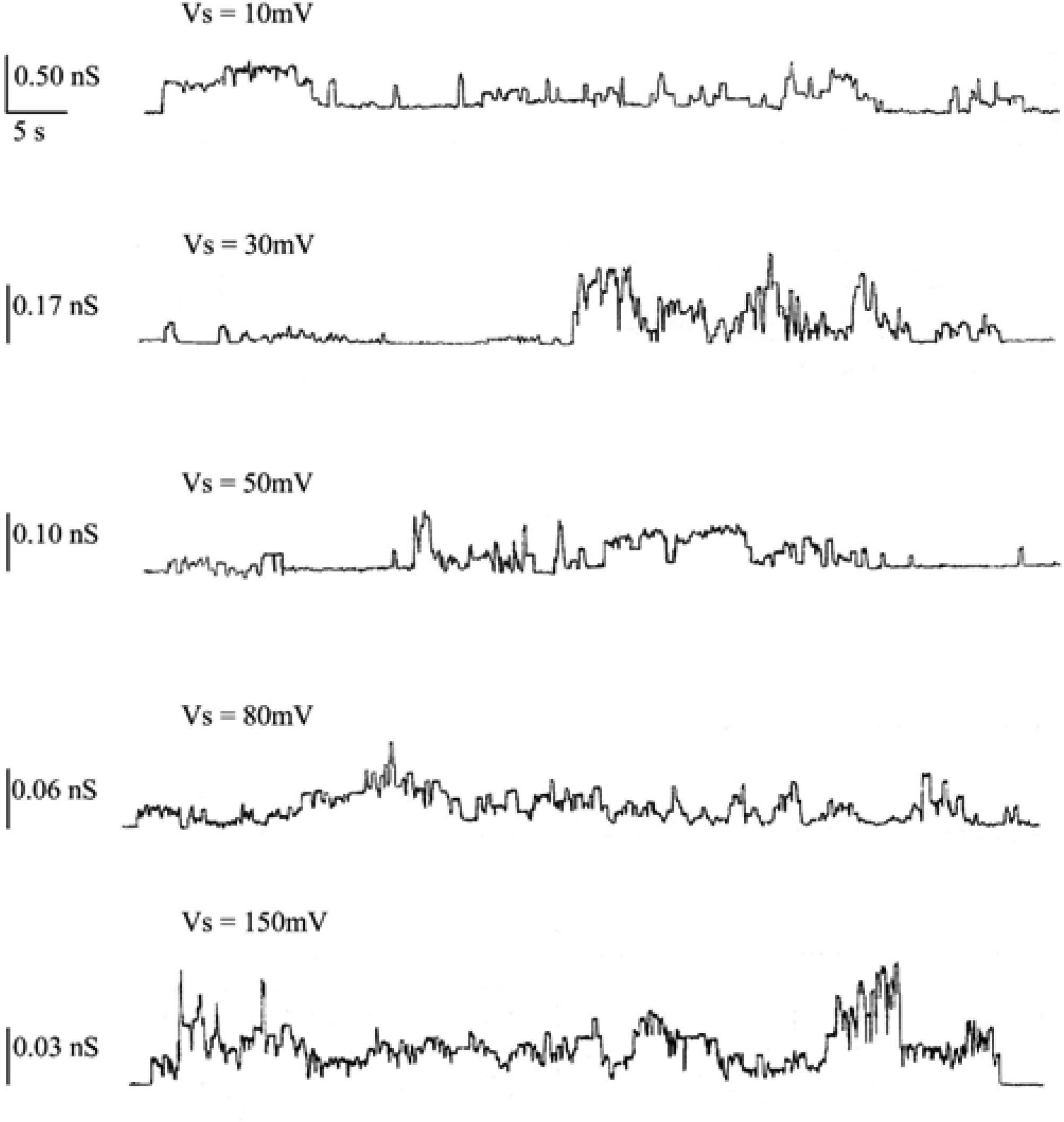
A Chol concentration increase to 30 mol % in POPC PLMs enables the hCt peptide to incorporate into the membrane and to form non-random discrete current fluctuations, compatible with channel-type opening and closure, with different conductance levels, frequencies and lifetimes. hCt channel activity manifested after a lag time of 90 minutes when a constant voltage of 150 mV was applied across the membrane. After the first channel formation, the applied voltage can be lowered to 10 mV and channel amplitude can be monitored. Each voltage was applied for 90 minutes starting from 150 mV (activation voltage), i.e., 90 minutes at 150 mV, followed by 90 minutes at 80 mV and so on. It is worth noting that at higher applied voltages (150 and 80 mV) channel activity showed alternating periods of paroxystic activity, during which it is impossible to make a rigorous analysis of the number of channels, followed by quiescent periods, open times interrupted by closures and conductance steps, some several times higher than central conductance. Figure 2 reports an example of chart recordings of hCt channel activity when incorporated into the POPC:Chol (30 mol %) PLM at applied voltages of 10, 30, 50, 80 and 150 mV.
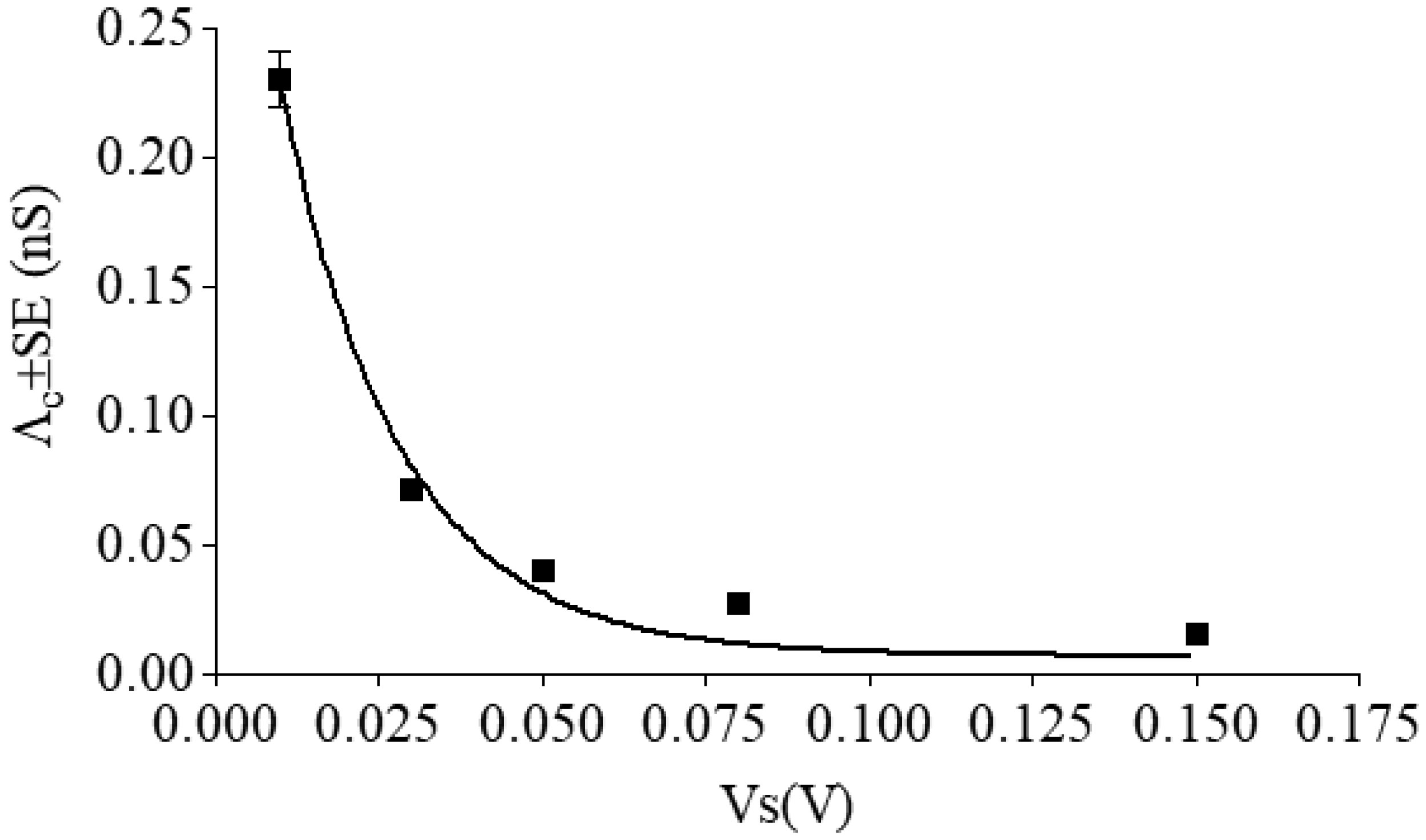
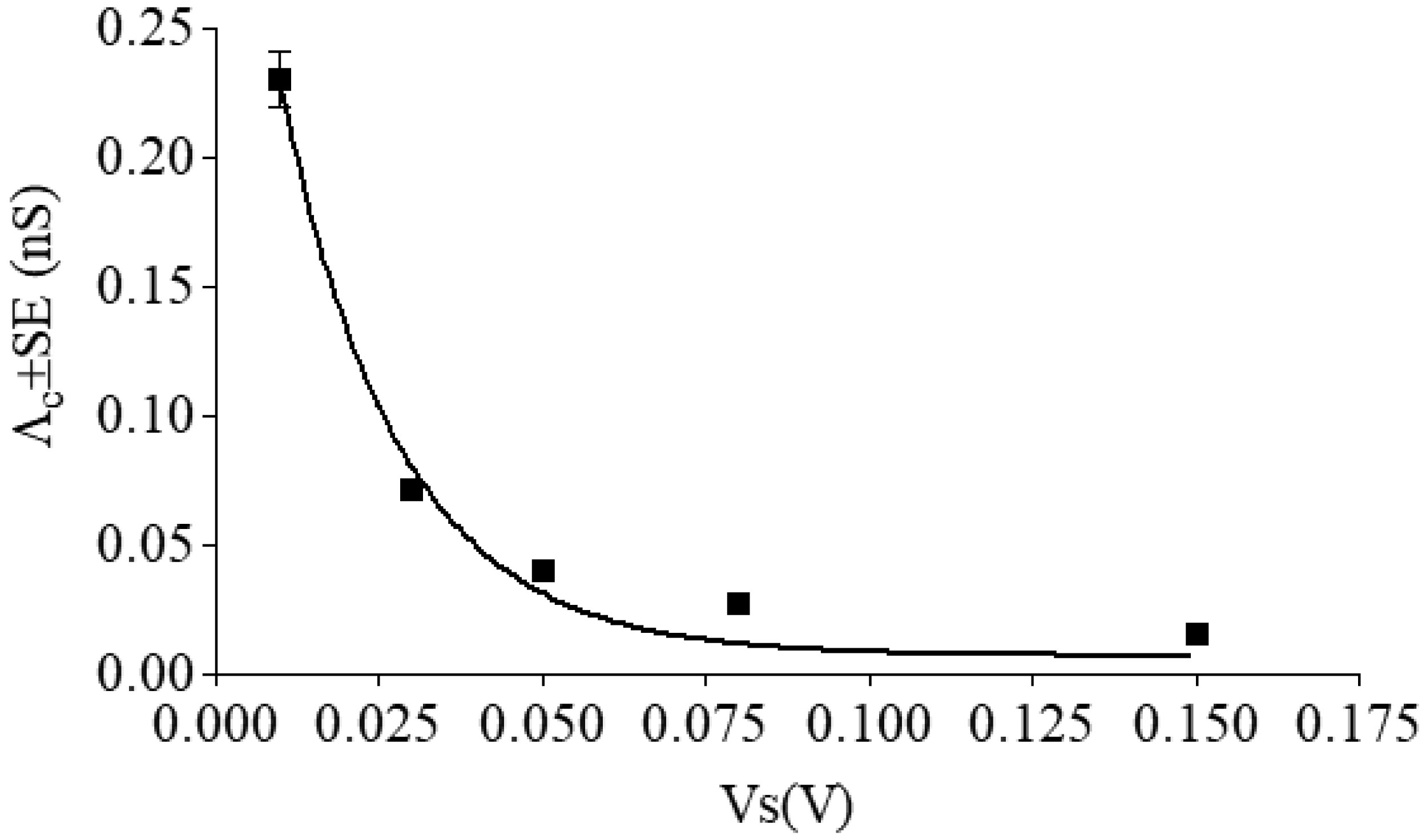
All single channels were used to calculate the channel amplitudes that revealed the existence of one main conductance level at different applied voltages. A histogram of amplitude distribution was constructed and fitted by a Gaussian distribution function and gave the central value of the single-channel conductance. Table 1 reports the values of central conductance (Λc ± SE) of the hCt channel obtained by the Gaussian best-fit at the different applied voltages. The central conductance seems to be dependent on applied voltages decreasing as the voltage increases.
The frequency values, reported in Table 1, seem to have the same behaviour as the central conductance at the different applied voltages, being higher at applied voltages of 10 and 30 mV. It is worth noting that the lower frequency values at higher applied voltages may depend on the presence of paroxystic activity that makes it impossible to carry out a rigorous analysis of the number of channels.
The single-channel lifetime (τ), obtained by analysis with equation 2 of cumulative open-state distributions, is the other parameter that characterizes the hCt channel incorporated into POPC:Chol (30 mol %) PLMs. The results indicate that the distribution of the open states follows a two-exponential function (P < 0.05), except for the applied voltage of 10 mV in which statistical testing does not distinguish between a one- or two-exponential function (P = 0.3732). These results are reported in Table 1. The prevalence of dual-channel populations at the different applied voltages indicates stability of the hCt channel.
One aspect that characterizes the hCt channel is that its conductance remains inversely correlated with membrane potential (Figure 3). The hypothesis that the hCt channel switches from the open to closed state was tested by parameterizing the conductance by means of Eq 3. The A, K and n values, obtained by a fitting procedure for the hCt channel incorporated into POPC:Chol (30 mol %), are: A = 0.38 ± 0.04 nS, K = 55.01 ± 7.40 V−1, n = 1.40, R2 = 0.98. The value of n indicates the gating charge and dipole moment of the hCt channel.
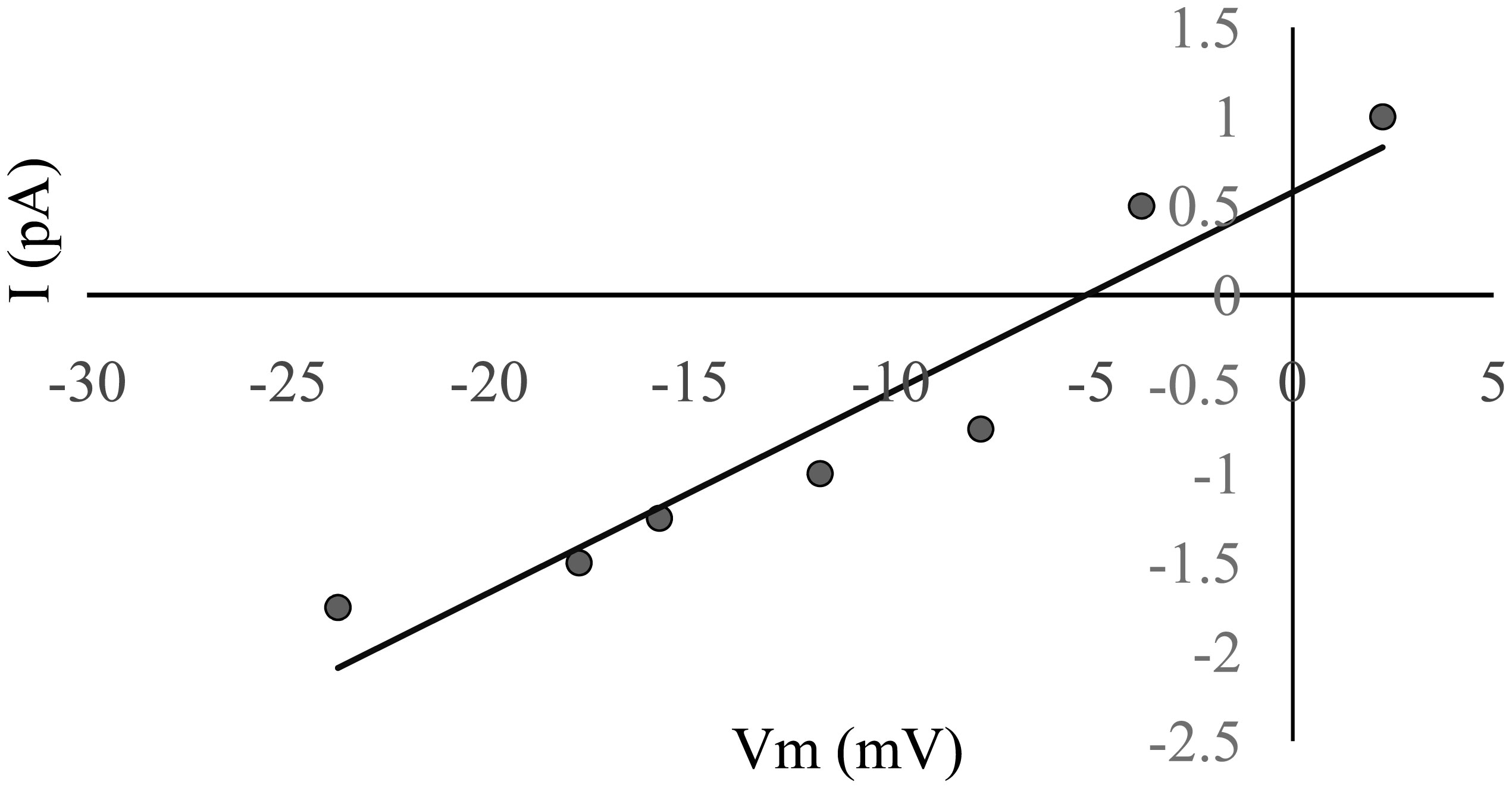
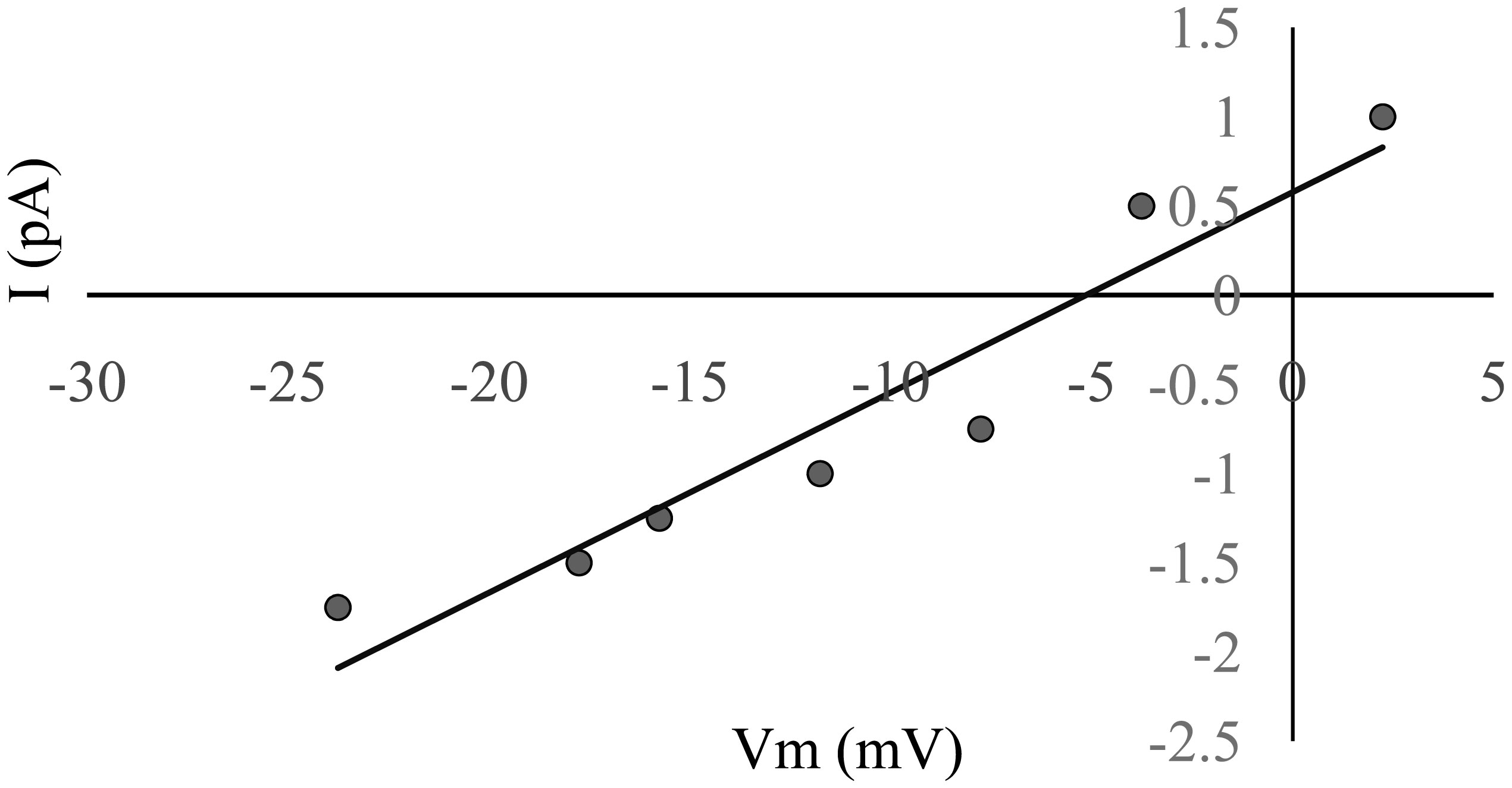
To identify the charge on the ion carrying the current, the shift in the reversal potential, induced by a change from a symmetrical to an asymmetrical KCl solution system, was measured. A concentration gradient was set with 1 M on the cis side and 0.5 M on the trans side. The reversal potential was determined by an I-V curve when the measured amplitude of the channel events at each potential was used (Figure 4). The reversal potential was −5.1 mV. The permeability ratio (PK+/PCl−), calculated using Eq 4, was 1.8, indicating a poorly cation-selective channel.
The peptide-lipid interaction and peptide accumulation on the membrane surface depend on various factors such as electrostatic interactions, hydrophobic effect and the type of phospholipid headgroups. Table 2 shows frequency and lifetime values of the hCt ion channel obtained in negatively-charged DOPG and zwitterionic POPC containing 15% negatively-charged DOPG PLMs. One interesting aspect that emerges is that the frequency values obtained in charged PLMs are significantly higher than those obtained in POPC:Chol PLMs except for POPC:DOPG PLM at an applied voltage of 150 mV. These results seem to indicate that the negative charge of the membrane increases the turnover of hCt channels.
Table 2 reports the lifetimes of the hCt ion channel when incorporated into POPC:DOPG or DOPG PLMs. The hCt channel manifests one lifetime at nearly all voltages studied, but two in POPC:Chol PLMs, indicating that membrane sterol stabilizes the hCt channel.
4.
Discussion
In membranes, lipids and proteins can affect each other. Numerous studies have shown that membrane proteins' effects on surrounding lipids and membrane lipids can influence both the protein structures (i.e., backbone conformation or rotation angle of the transmembrane segments) as well as the organization of the proteins in membranes. Therefore, membrane proteins and adjacent lipids can be considered a dynamic complex.
One important aspect emerging from studies of lipid-protein interactions is that specific lipids can participate as molecular chaperones in the insertion, folding and topology of membrane proteins. One extensively studied example is that of lactose permease (LacY). It has been shown that phosphatidylethanolamine (PE) is necessary for the cellular function, assembly and folding of the secondary transporter [23]–[25]. More specifically, PE is not required for insertion into the membrane, but is required for its active transport function because the phospholipid permits correct topological organization. Other examples, in which PE is necessary for correct topological organization and function, are those of phenylalanine permease (PheP) and γ-aminobutyric acid permease (GabP) [26],[27]. In vitro studies show that the folded state of nitro reductase (NfsB) is amply stabilized by the presence of DOPG in bilayers made up of DOPC. The optimal amount of DOPG to stabilize NfsB is in the range 15–50% [28]. The finding of Chaparro Sosa and colleagues provides evidence for the chaperone-like activity of mixed DOPG/DOPC lipid bilayers.
Chol, an integral component of eukaryotic cell membranes, is a versatile molecule able to interact with other membrane lipids and proteins as it can adopt various conformations due to the flexibility of its isooctyl chain linked to the planar tetracyclic ring. These features give Chol regulatory and modulatory functions on other membrane components [8]. Chol can be considered a molecular chaperone for many membrane proteins, including receptors, ion channels and transporters. The results of recent studies indicate that G-protein-coupled receptors (GPCRs) are located in membranes rich in Chol which forms hydrogen bonds with carbonyl groups of the receptor's backbone and residue side chains located deep within the hydrophobic core of bilayers [29]. Similar results have been obtained by Guixà-Gonzales and colleagues who used crystal structures of A2A receptor (A2AR) to confirm the formation of stable bonds between Chol molecules and receptor surface, suggesting an allosteric role of this lipid [30]. Several studies have shown that some ion channels are sensitive to the level of membrane Chol. Indeed, for nicotinic acetylcholine receptor (nAChR) and γ-aminobutyric acid type A receptor (GABAAR), Chol is necessary for ligand-mediated channel activity. On the other hand, it has been demonstrated that the activity of Ca2+- and voltage-gated and inwardly-rectifying K+ channels decreases in response to Chol due to the binding of sterol with the CRAC motifs present in the structure of these channels [7]. Unlike K+ channels, Aquaporin 0 prefers membranes with high levels of Chol for its activity [31].
As is the case for membrane proteins, the insertion, folding and function of some peptides, e.g., Aβ and amylin, are also influenced by the lipid composition of the membrane. Chol and gangliosides play a critical role in functions carried out by these peptides, which are involved in common diseases such as Alzheimer's or diabetes mellitus type 2. The protective or harmful role of membrane Chol in the toxicity of these peptides is controversial – when the adsorption of the peptide at the membrane surface decreases the amount of free peptide (possible mechanism of clearance) it is protective, whereas Chol plays a harmful role when it favours the formation of membrane-spanning pores (possible mechanism of ionic imbalance) or of seed formation in the fibrillation process; however, the common denominator of the two interpretations is that these peptides show high affinity for this membrane sterol, which can modulate the folding and subsequently the toxicity of the peptides.
In this study, we monitored different concentrations of Chol so as to find the minimal concentration of this sterol in POPC PLMs needed to achieve incorporation and channel formation of hCt, and we evaluated the effect of Chol on the biophysical parameters of the hCt channel incorporated into POPC:Chol PLMs. hCt is a peptide forming ion channels whose interaction with lipid bilayers depends on the presence of specific lipids. In our previous studies [16], we have shown that hCt, at pH 7, can form voltage-dependent channels interacting with negatively-charged DOPG bilayers and with zwitterionic POPC containing 15% negatively-charged DOPG, but not with POPC bilayers. Similar results have been found by other authors who highlighted that phosphatidylglycerol promotes insertion into bilayers of salmon calcitonin [32] and eel, porcine, salmon and human calcitonin [33].
On the other hand, hCt shows a high tendency to form fibrils in aqueous solution due to local conformational transitions from α-helix to β-sheet at the C-terminus region as found by other authors. The first result obtained by our study is that there seems to be a minimal concentration of Chol, i.e., a mole percentage of 30 in POPC PLMs, at which it is possible to observe the channel activity of hCt. Due to the fact that Chol molecules are non-randomly distributed in the membrane but organized in ordered microdomains, it is plausible to hypothesize that the amount of 30 mol % Chol is the minimal concentration to achieve organisation into microdomains in PLMs, once the Chol molecules become “visible” to those of hCt. Therefore, Chol seems to promote the insertion and formation of the hCt channel in POPC PLMs, indicating a possible role of sterol as a molecular chaperone. Indeed, our CD results indicate that hCt diluted in bidistilled H2O (pH 7) presents a disordered conformation that remains stable for 48 hours and the solvent-reduced polarity, due to TFE, promotes a conformational transition with a higher α-helix content, therefore it is possible to hypothesize that the Chol promotes hCt transition from β-sheet and random coil to α-helix, a key requisite for insertion and channel formation in the membrane.
Numerous examples demonstrating that Chol and other sterols are a target for peptides with antibiotic and toxin activity, have been reported [34]–[38]. This property of Chol has been described by some authors who have shown that the Aβ structure is drastically altered by the addition of 33% Chol in DMPC vesicles, i.e., the β-sheet structure decreases to zero while the α-helix increases to 58.8% [14]. The study carried out by Ashely and colleagues demonstrates that auto-insertion of Aβ42 oligomers into POPC:Chol membranes is accompanied by relocation of the sterol towards the bilayer surface [39]. A molecular dynamics study has shown that Aβ42 and Aβ40 exhibit insertion into the POPC:Chol bilayers for 100% and 50% of replicates, respectively [40].
The peptide-lipid interaction may depend on the lipid headgroups and the membrane surface. By comparing hCt channel parameters for different PLMs, under the same experimental conditions, the following features can be noted:
-
the same applied potential is necessary for channel activation, i.e., 150 mV, but with different lag times. The lag time from experiments in POPC:Chol PLMs is longer (90 min) than those measured in previous experiments carried out with PLMs made up of POPC:DOPG (85:15) and DOPG (49 and 43 minutes, respectively) [16];
-
the conductance-voltage relationship for hCt channels in each PLM remains inversely correlated with membrane potential. The A, K and n values, obtained by a fitting procedure (Eq 3) for the hCt channel incorporated into POPC:Chol (30 mol %) PLMs, are similar to those obtained for POPC:DOPG (85:15,w/w) and DOPG PLMs [16];
-
the conductance values of hCt channel in POPC:Chol (30% mol) membrane are significantly higher than those in POPC:DOPG or DOPG PLMs at low applied voltages (10 and 30 mV; P < 0.001, P = 0.026, Anova-Tukey test, respectively) [16];
-
channel selectivity was poorly cationic (PK+/PCl− = 1.8) in POPC:Chol (30 mol %) PLMs while it was neutral (PK+/PCl− = 0.75) in POPC:DOPG PLMs [16].
The lag time, i.e., the time between hCt addition to the cis side of the medium facing the membrane and the first channel appearance, seems to depend on both membrane lipids-peptide and on peptide-peptide interactions. Our results seem to indicate that the electrostatic interactions between negatively-charged headgroups of lipids and amino acid residues of hCt are very important for interaction with membrane and subsequently insertion of hCt into PLMs, but not necessary. Considering that the amino acid sequence of hCt contains a CRAC motif and that Lys18 (a component of the CRAC motif) is located in the short fragment (15–19) of hCt that is capable of forming fibrils [11],[12], it is possible to hypothesize that membrane Chol, interacting with the hCt molecules in solution, encourages their accumulation on the lipid surface, folding and subsequent insertion into the membrane.
The second result obtained by this study is that, in POPC:Chol PLMs (30 mol %), the conductance values are significantly higher at applied voltages of 10 and 30 mV than those in POPC:DOPG or DOPG PLMs (Λc ± SE (nS): 0.194 ± 0.009 and 0.190 ± 0.002, respectively). Higher conductance values can indicate a different channel assembly. By means of the conductance value, and assuming a water-filled channel with an ion mobility similar to that of the bulk solution, knowing the thickness of the bilayer and the equivalent conductivity of the ions, the channel diameter can be calculated. In our case, in POPC:Chol, POPC:DOPG and DOPG membranes (with an average thickness of 5 nm) and at an applied voltage of 10 mV, the channel diameter of hCt was 3.85, 3.52 and 3.48 Å, respectively. It is worth underlining, however, that the calculation of pore area by means of conductance, assuming the channel to be a water-filled hole, is not a straightforward rule [41]. This result shows that the size of the pore through the channel is larger in POPC:Chol PLMs than in POPC:DOPG and DOPG PLMs, indicating that a different assembly of hCt molecules may be due to small changes in the flexibility of the peptide in the presence of sterol. Besides, in POPC:Chol PLMs, the hCt channel manifests two lifetimes that are longer-lasting, at all studied voltages except for 10 mV, unlike that found in POPC:DOPG and DOPG PLMs. The hCt channel seems to be more stable in POPC PLMs containing sterol than its counterpart in exclusively phospholipidic PLMs, due to the presence of two channel populations and to a longer opening time. On the other hand, membrane Chol seems not to modify the voltage-dependence characteristics, gating charges and dipole moment of the hCt channel compared with those found in POPC:DOPG and DOPG PLMs. Similar results, using computational [42] and electrophysiological [21],[43],[44] studies, have been found for the mitochondrial voltage-dependent anion channel (VDAC), reconstituted in a lipid membrane made up of DOPC/Chol. The Chol effects on channel size and stability but not the ion diffusion through the pore and the potential for movement of ions therefore channel activity was not modified by sterol.
5.
Conclusion
The results of our study show that: 1) membrane Chol can be regarded as a molecular target for hCt, enabling its insertion and folding in membranes made up of POPC, in which no insertion and channel formation had previously been found. Although it is not possible to distinguish, by the method used in this study, whether modulation of hCt by Chol occurs indirectly through changes to the physiochemical properties of the membrane or directly through sterol binding to the peptides since hCt has a CRAC motif, an important aspect to emerge is the affinity of hCt for Chol; 2) hCt interaction with a lipid membrane containing Chol and subsequent channel formation counteracts the tendency of the peptide to fibrillate. Membrane-induced conformational variations of the peptide could be one of the first steps promoting the α-helical structure, which is considered to be a prerequisite both for incorporation into the membrane and for receptor interaction. Our results raise the concept that the interactions between membrane lipids and proteins/peptides are a complex process in which insertion, folding and functions of some peptides or proteins can be modulated by specific membrane lipids.









 DownLoad:
DownLoad: