Promoter engineering for the recombinant protein production in prokaryotic systems

Ozgun Firat Duzenli; Sezer Okay; Ozgun Firat Duzenli; Sezer Okay

doi:10.3934/bioeng.2020007

AIMS Bioengineering

2020, Volume 7, Issue 2: 62-81. doi: 10.3934/bioeng.2020007

Previous Article Next Article

Review

Promoter engineering for the recombinant protein production in prokaryotic systems

Ozgun Firat Duzenli ¹,
Sezer Okay ^{2
,
,}

1.
Department of Pharmaceutical Biotechnology, Faculty of Pharmacy, Hacettepe University, Ankara, Turkey
2.
Department of Vaccine Technology, Vaccine Institute, Hacettepe University, Ankara, Turkey

Received: 20 February 2020 Accepted: 07 April 2020 Published: 08 April 2020

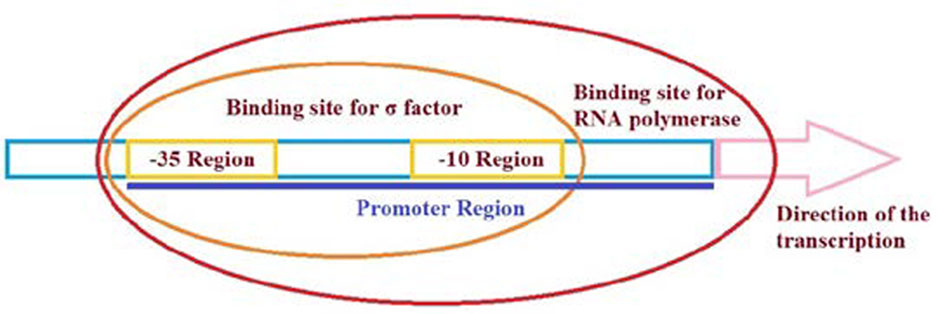
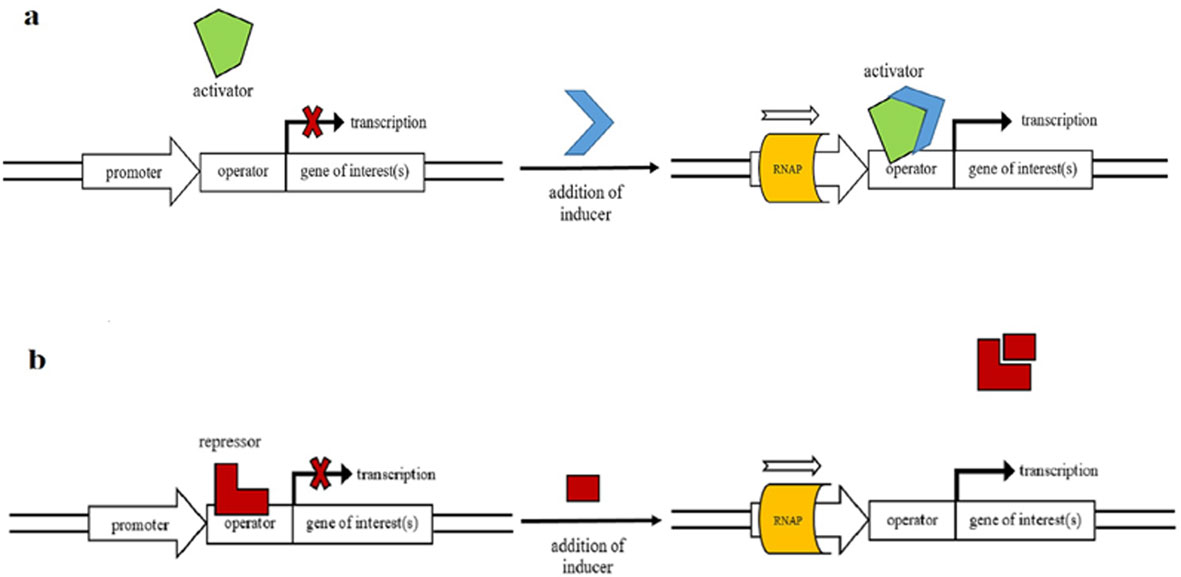
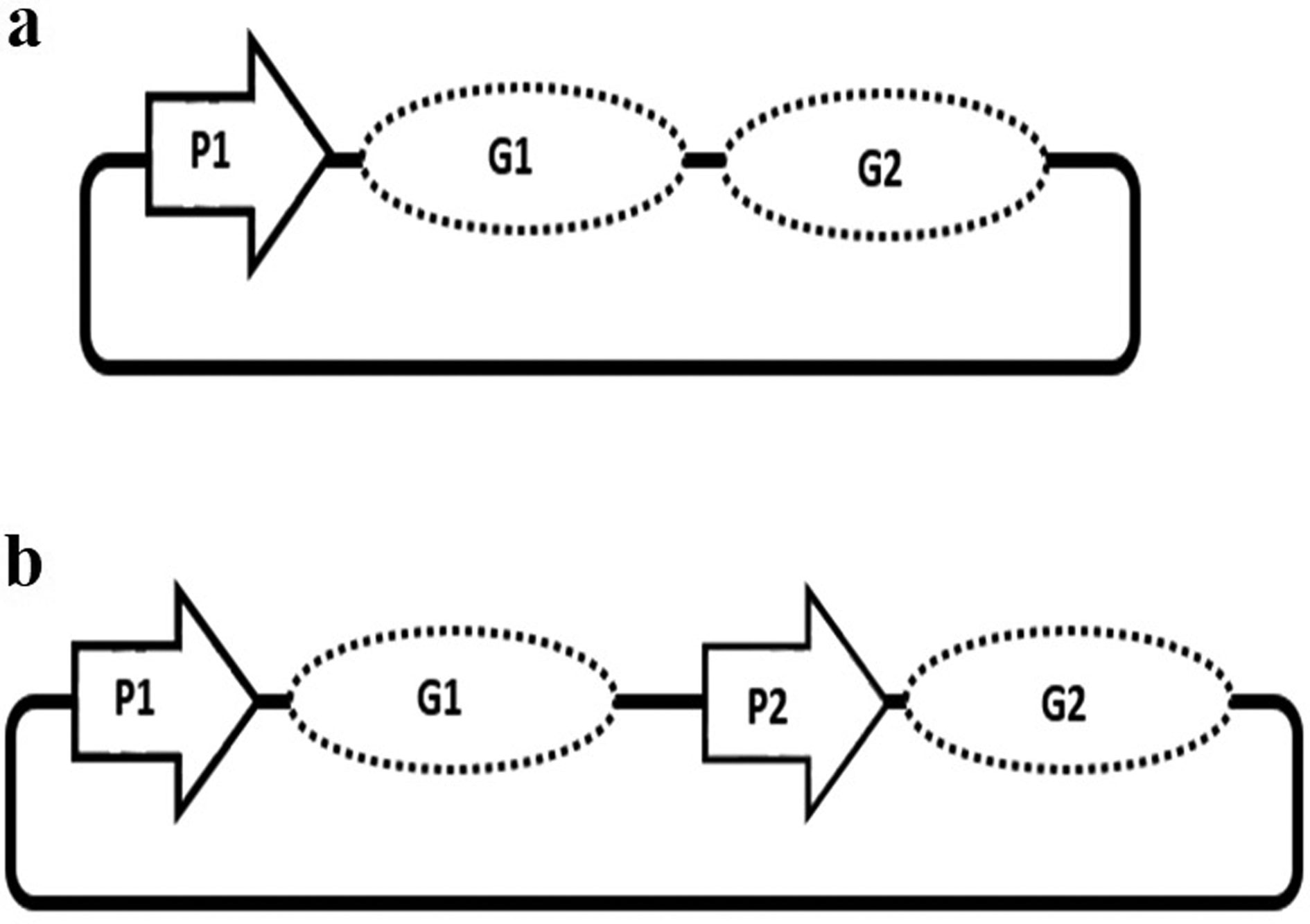
Recombinant proteins have an economical value with their utilization in many areas from food industry to pharmaceutical and chemical industry. Therefore, it is of great importance to establish optimum production systems for the proteins of interest. One of the critical steps in protein production is regulation of the gene expression. Promoters are among the key regulatory elements which can directly control the level of recombinant gene expression in a host cell. Thus, a suitable promoter is required for optimum gene expression. Promoter engineering is an innovative approach to find out the best promoter system for the expression of recombinant genes, which influences the overproduction of proteins of interest. In this review, some of the bacterial hosts highly used in recombinant protein production were discussed. Next, the importance of promoters in recombinant gene expression, and promoter engineering for enhanced protein production were described. Utilization of double promoter systems was highlighted as one of the successful techniques in overproduction of recombinant proteins. Increment in the variety and availability of the novel methodologies especially in the synthetic biology is expected to increase the quality and the quantity of recombinant proteins with an economical value.

Keywords:

Citation: Ozgun Firat Duzenli, Sezer Okay. Promoter engineering for the recombinant protein production in prokaryotic systems[J]. AIMS Bioengineering, 2020, 7(2): 62-81. doi: 10.3934/bioeng.2020007

Related Papers:

[1]	Dojin Kim, Patcharee Wongsason, Jongkyum Kwon . Type 2 degenerate modified poly-Bernoulli polynomials arising from the degenerate poly-exponential functions. AIMS Mathematics, 2022, 7(6): 9716-9730. doi: 10.3934/math.2022541
[2]	Taekyun Kim, Dae San Kim, Dmitry V. Dolgy, Hye Kyung Kim, Hyunseok Lee . A new approach to Bell and poly-Bell numbers and polynomials. AIMS Mathematics, 2022, 7(3): 4004-4016. doi: 10.3934/math.2022221
[3]	Jongkyum Kwon, Patcharee Wongsason, Yunjae Kim, Dojin Kim . Representations of modified type 2 degenerate poly-Bernoulli polynomials. AIMS Mathematics, 2022, 7(6): 11443-11463. doi: 10.3934/math.2022638
[4]	Sang Jo Yun, Jin-Woo Park . On a generation of degenerate Daehee polynomials. AIMS Mathematics, 2025, 10(5): 12286-12298. doi: 10.3934/math.2025556
[5]	Taekyun Kim, Hye Kyung Kim, Dae San Kim . Some identities on degenerate hyperbolic functions arising from $ p $-adic integrals on $ \mathbb{Z}_p $. AIMS Mathematics, 2023, 8(11): 25443-25453. doi: 10.3934/math.20231298
[6]	Taekyun Kim, Dae San Kim, Hye Kyung Kim . Some identities involving degenerate Stirling numbers arising from normal ordering. AIMS Mathematics, 2022, 7(9): 17357-17368. doi: 10.3934/math.2022956
[7]	Taekyun Kim, Dae San Kim, Hyunseok Lee, Lee-Chae Jang . A note on degenerate derangement polynomials and numbers. AIMS Mathematics, 2021, 6(6): 6469-6481. doi: 10.3934/math.2021380
[8]	Hye Kyung Kim, Dmitry V. Dolgy . Degenerate Catalan-Daehee numbers and polynomials of order $ r $ arising from degenerate umbral calculus. AIMS Mathematics, 2022, 7(3): 3845-3865. doi: 10.3934/math.2022213
[9]	Taekyun Kim, Dae San Kim, Jin-Woo Park . Degenerate $ r $-truncated Stirling numbers. AIMS Mathematics, 2023, 8(11): 25957-25965. doi: 10.3934/math.20231322
[10]	Jung Yoog Kang, Cheon Seoung Ryoo . The forms of $ (q, h) $-difference equation and the roots structure of their solutions with degenerate quantum Genocchi polynomials. AIMS Mathematics, 2024, 9(11): 29645-29661. doi: 10.3934/math.20241436

Abstract

1. Introduction

In ^[1,2], Carlitz initiated study of the degenerate Bernoulli and Euler polynomials and obtained some arithmetic and combinatorial results on them. In recent years, many mathematicians have drawn their attention to various degenerate versions of some old and new polynomials and numbers, namely some degenerate versions of Bernoulli numbers and polynomials of the second kind, Changhee numbers of the second kind, Daehee numbers of the second kind, Bernstein polynomials, central Bell numbers and polynomials, central factorial numbers of the second kind, Cauchy numbers, Eulerian numbers and polynomials, Fubini polynomials, Stirling numbers of the first kind, Stirling polynomials of the second kind, central complete Bell polynomials, Bell numbers and polynomials, type 2 Bernoulli numbers and polynomials, type 2 Bernoulli polynomials of the second kind, poly-Bernoulli numbers and polynomials, poly-Cauchy polynomials, and of Frobenius-Euler polynomials, to name a few ^{[3,14,16,17,18]} and the references therein. They have studied those polynomials and numbers with their interest not only in combinatorial and arithmetic properties but also in differential equations and certain symmetric identities ^[4,5] and references therein, and found many interesting results related to them ^{[12,19,20,21,22,23,24,25,26,27,28]}. It is remarkable that studying degenerate versions is not only limited to polynomials but also extended to transcendental functions.

The Bernoulli polynomials of the second are defined by as follows (see ^[9,13])

$\begin{align} \frac{z}{\log(1+z)}(1+z)^x = \sum\limits_{q = 0}^{\infty}b_q(x)\frac{z^q}{q!}. \end{align}$

(1.1)

When $x = 0$ , $b_q(0) = b_q$ are called the Bernoulli numbers of the second kind.

The degenerate exponential function $e_{\lambda}^{x}(z)$ is defined by (see ^{[6,7,8,9,10,11,12,13,14,15,16,17,18,19]})

$\begin{align} e_{\lambda}^{x}(z) = (1+\lambda z)^{\frac{x}{\lambda}}, \; \; e_{\lambda}(z) = (1+\lambda z)^{\frac{1}{\lambda}}, \; \lambda\in \mathbb{C}\backslash \{0\}. \end{align}$

(1.2)

We note that

$\begin{align} e_{\lambda}^{x}(z) = \sum\limits_{q = 0}^{\infty}(x)_{q, \lambda}\frac{z^q}{q!}, {\rm{(see \; [4, 21])}}, \end{align}$

(1.3)

where $(x)_{q, \lambda} = x(x-\lambda)\cdots(x-(q-1)\lambda), (q\geq1)$ , $(x)_{0, \lambda} = 1$ .

Note that

$\lim\limits_{\lambda\rightarrow 0}e_{\lambda}^{x}(z) = \sum\limits_{q = 0}^{\infty}x^q\frac{z^q}{q!} = e^{xz}.$

The degenerate Bernoulli polynomials which are defined by Carlitz's as follows (see ^[1,2])

$\begin{align} \frac{z}{e_{\lambda}(z)-1}e_{\lambda}^{x}(z) = \frac{z}{(1+\lambda z)^{\frac{1}{\lambda}}-1}(1+\lambda z)^{\frac{x}{\lambda}} = \sum\limits_{q = 0}^{\infty}\beta_{q}(x;\lambda)\frac{z^q}{q!}. \end{align}$

(1.4)

At the point $x = 0$ , $\beta_{q}(\lambda) = \beta_{q}(0;\lambda)$ are called the degenerate Bernoulli numbers.

Note that

$\lim\limits_{\lambda \longrightarrow 0}\beta_{q}(x;\lambda) = B_{q}(x).$

The polylogarithm function is defined by

$\begin{align} {\rm Li}_{k}(x) = \sum\limits_{q = 1}^{\infty}\frac{x^q}{q^k}\; \; \; (k\in\mathbb Z, \; \mid x\mid < 1), {\rm{(see \; [7])}}. \end{align}$

(1.5)

Note that

$\begin{align} {\rm Li}_{1}(x) = \sum\limits_{q = 1}^{\infty}\frac{x^q}{q} = -\log(1-x). \end{align}$

(1.6)

The poly-Bernoulli polynomials of the second are defined by (see ^[13])

$\begin{align} \frac{{\rm Li}_{k}(1-e^{-z})}{\log(1+z)}(1+z)^{x} = \sum\limits_{q = 0}^{\infty}b_{q}^{(k)}(x)\frac{z^q}{q!}. \end{align}$

(1.7)

In the case when $x = 0$ , $b_{q}^{(k)} = b_{q}^{(k)}(0)$ are called the poly-Bernoulli numbers of the second kind.

The modified degenerate polyexponential function is defined by (see ^[14])

$\begin{align} {\rm Ei}_{k, \lambda}(x) = \sum\limits_{q = 1}^{\infty}\frac{(1)_{q, \lambda}}{(q-1)!q^k}x^q. \end{align}$

(1.8)

It is noteworthy to mention that

${\rm Ei}_{1, \lambda}(x) = \sum\limits_{q = 1}^{\infty}\frac{(1)_{q, \lambda}}{q!}x^q = e_{\lambda}(x)-1.$

The degenerate poly-Genocchi polynomials which are defined by Kim et al. as follows (see ^[14])

$\begin{align} \frac{2{\rm Ei}_{k, \lambda}\left(\log_{\lambda}(1+z)\right)}{e_{\lambda}(z)+1}e_{\lambda}^{x}(z) = \sum\limits_{q = 0}^{\infty}G_{q, \lambda}^{(k)}(x)\frac{z^q}{q!}\; \; \; (k\in\mathbb Z). \end{align}$

(1.9)

When $x = 0$ , $G_{q, \lambda}^{(k)} = G_{q, \lambda}^{(k)}(0)$ are called the degenerate poly-Genocchi numbers.

For $\lambda\in\mathbb R$ , Kim-Kim defined the degenerate version of the logarithm function, denoted by $\log_{\lambda}(1+t)$ as follows (see ^[11])

$\begin{align} \log_{\lambda}(1+z) = \sum\limits_{q = 1}^{\infty}\lambda^{\lambda-1}(1)_{q, 1/\lambda}\frac{z^q}{q!}, \end{align}$

(1.10)

being the inverse of the degenerate version of the exponential function $e_{\lambda}(z)$ as has been shown below

$e_{\lambda}(\log_{\lambda}(z)) = \log_{\lambda}(e_{\lambda}(z)) = z.$

It is noteworthy to mention that

$\lim\limits_{\lambda\rightarrow 0}\log_{\lambda}(1+z) = \sum\limits_{q = 1}^{\infty}(-1)^{q-1}\frac{z^q}{q!} = \log(1+z).$

The degenerate Daehee polynomials are defined by (see ^[15])

$\begin{align} \frac{\log_{\lambda}(1+z)}{z}(1+z)^{x} = \sum\limits_{q = 0}^{\infty}D_{q, \lambda}(x)\frac{z^q}{q!}. \end{align}$

(1.11)

In the case when $x = 0$ , $D_{q, \lambda} = D_{q, \lambda}(0)$ denotes the degenerate Daehee numbers.

The degenerate Bernoulli polynomials of the second kind which are defined by Kim et al. as follows (see ^[9])

$\begin{align} \frac{z}{\log_{\lambda}(1+z)}(1+z)^{x} = \sum\limits_{q = 0}^{\infty}b_{q, \lambda}(x)\frac{z^q}{q!}. \end{align}$

(1.12)

When $x = 0$ , $b_{q, \lambda} = b_{q, \lambda}(0)$ are called the degenerate Bernoulli numbers of the second kind.

Note here that $\lim_{\lambda \rightarrow 0}b_{q, \lambda}(x) = b_q(x), (q\geq 0)$ .

The degenerate Stirling numbers of the first kind are defined by

$\begin{align} \frac{1}{k!}(\log_{\lambda}(1+z))^k = \sum\limits_{q = k}^{\infty}S_{1, \lambda}(q, k)\frac{z^q}{q!}\; \; (k\geq 0), \rm{(see \; [11, 12])}. \end{align}$

(1.13)

It is noticed that

$\lim\limits_{\lambda\rightarrow 0}S_{1, \lambda}(q, k) = S_1(q, k),$

are the Stirling numbers of the first kind presented by

$\frac{1}{k!}(\log(1+z))^k = \sum\limits_{q = k}^{\infty}S_{1}(q, k)\frac{z^q}{q!}\; \; (k\geq 0), {\rm{(see \; [7, 17])}}.$

The degenerate Stirling numbers of the second kind are defined by (see ^[8])

$\begin{align} \frac{1}{k!}(e_{\lambda}(z)-1)^k = \sum\limits_{q = k}^{\infty}S_{2, \lambda}(q, k)\frac{z^q}{q!}\; \; (k\geq 0). \end{align}$

(1.14)

It is clear that

$\lim\limits_{\lambda\rightarrow 0}S_{2, \lambda}(q, k) = S_2(q, k),$

are the Stirling numbers of the second kind specified by

$\frac{1}{k!}(e^z-1)^k = \sum\limits_{q = k}^{\infty}S_{2}(q, k)\frac{z^q}{q!}\; \; (k\geq 0), {\rm{(see \; [1-28])}}.$

Motivated by the works of Kim et al. ^[11,14], in this paper, we study the type 2 degenerate poly-Bernoulli polynomials of the second kind arising from modified degenerate polyexponential function and obtain some related identities and explicit expressions. Also, we establish the type 2 degenerate unipoly-Bernoulli polynomials of the second kind attached to an arithmetic function by using modified degenerate polyexponential function and discuss some properties of them.

2. Type 2 degenerate poly-Bernoulli polynomials of the second kind

Here, the type 2 degenerate poly-Bernoulli polynomials of the second kind are defined by using the modified degenerate polyexponential function which is called the degenerate poly-Bernoulli polynomials of the second kind as

$\begin{align} \frac{{\rm Ei}_{k, \lambda}\left(\log_{\lambda}(1+z)\right)}{\log_{\lambda}(1+z)}(1+z)^{x} = \sum\limits_{j = 0}^{\infty}Pb_{j, \lambda}^{(k)}(x)\frac{z^j}{j!}, (k\in\mathbb Z). \end{align}$

(2.1)

When $x = 0$ , $Pb_{j, \lambda}^{(k)} = Pb_{j, \lambda}^{(k)}(0)$ are called the type 2 degenerate poly-Bernoulli numbers of the second kind.

Note that

$\lim\limits_{\lambda\rightarrow 0}\frac{{\rm Ei}_{k, \lambda}\left(\log_{\lambda}(1+z)\right)}{\log_{\lambda}(1+z)}(1+z)^{x} = \sum\limits_{j = 0}^{\infty}\lim\limits_{\lambda\rightarrow 0}Pb_{j, \lambda}^{(k)}(x)\frac{z^j}{j!}$

$\begin{align} = \frac{{\rm Ei}_{k}\left(\log(1+z)\right)}{\log(1+z)}(1+z)^{x} = \sum\limits_{j = 0}^{\infty}Pb_{j}^{(k)}(x)\frac{z^j}{j!}, (k\in\mathbb Z), \end{align}$

(2.2)

where $Pb_{j}^{(k)}(x)$ are called the type 2 poly-Bernoulli polynomials of the second kind (see ^[9]).

First, we note that

${\rm Ei}_{k, \lambda}\left(\log_{\lambda}(1+z)\right) = \sum\limits_{q = 1}^{\infty}\frac{(1)_{q, \lambda}(\log_{\lambda}(1+z))^q}{(q-1)!q^k}$

$= \sum\limits_{q = 0}^{\infty}\frac{(1)_{q+1, \lambda}(\log_{\lambda}(1+z))^{q+1}}{(q+1)^kq!}$

$= \sum\limits_{q = 0}^{\infty}\frac{(1)_{q+1, \lambda}}{(q+1)^{k-1}}\frac{1}{(q+1)!}(\log_{\lambda}(1+z))^{q+1}$

$\begin{align} = \sum\limits_{q = 0}^{\infty}\frac{(1)_{q+1, \lambda}}{(q+1)^{k-1}}\sum\limits_{r = q+1}^{\infty}S_{1, \lambda}(r, q+1)\frac{z^r}{r!}. \end{align}$

(2.3)

By making use of (2.1) and (2.3), we see that

$\frac{z}{\log_{\lambda}(1+z)}(1+z)^{x}{\rm Ei}_{k, \lambda}\left(\log_{\lambda}(1+z)\right) \quad$

$= \frac{z}{\log_{\lambda}(1+z)}(1+z)^{x}\sum\limits_{q = 0}^{\infty}\frac{(1)_{q+1, \lambda}}{(q+1)^{k-1}} \sum\limits_{r = q}^{\infty}\frac{S_{1, \lambda}(r+1, q+1)}{r+1}\frac{z^r}{r!}$

$= \sum\limits_{j = 0}^{\infty}b_{j, \lambda}(x)\frac{z^j}{j!}\sum\limits_{q = 0}^{\infty}\frac{(1)_{q+1, \lambda}}{(q+1)^{k-1}}\sum\limits_{r = q}^{\infty} \frac{S_{1, \lambda}(r+1, q+1)}{r+1}\frac{z^r}{r!}$

$\begin{align} = \sum\limits_{j = 0}^{\infty}\left(\sum\limits_{r = 0}^{j}\binom{j}{r}\sum\limits_{q = 0}^{r}\frac{(1)_{q+1, \lambda}}{(q+1)^{k-1}}\frac{S_{1, \lambda}(r+1, q+1)}{r+1}b_{j-r, \lambda}(x)\right)\frac{z^j}{j!}. \end{align}$

(2.4)

Therefore, by (2.3) and (2.4), we obtain the following theorem.

Theorem 2.1. For $k\in\mathbb Z$ and $j\geq 0$ , we have

$Pb_{j, \lambda}^{(k)}(x) = \sum\limits_{r = 0}^{j}\binom{j}{r}\sum\limits_{q = 0}^{r}\frac{(1)_{q+1, \lambda}}{(q+1)^{k-1}}\frac{S_{1, \lambda}(r+1, q+1)}{r+1} b_{j-r, \lambda}(x).$

Corollary 2.1. Putting $k = 1$ in Theorem 2.1 yields

$Pb_{j, \lambda}(x) = \sum\limits_{r = 0}^{j}\binom{j}{r}\sum\limits_{q = 0}^{r}\frac{(1)_{q+1, \lambda}S_{1, \lambda}(r+1, q+1)}{r+1}b_{j-r, \lambda}(x).$

Let $1\leq k\in\mathbb{Z}$ . For $s\in\mathbb C$ , the function $\chi_{k, \lambda}(s)$ is given as

$\begin{align} \chi_{k, \lambda}(s) = \frac{1}{\Gamma (s)}\int_{0}^{\infty}\frac{z^{s-1}}{\log_{\lambda}(1+z)}{\rm Ei}_{k, \lambda}\left(\log_{\lambda}(1+z)\right)dz. \end{align}$

(2.5)

From Eq (2.5), we have

$\chi_{k, \lambda}(s) = \frac{1}{\Gamma (s)}\int_{0}^{\infty}\frac{z^{s-1}}{\log_{\lambda}(1+z)}{\rm Ei}_{k, \lambda}\left(\log_{\lambda}(1+z)\right)dz$

$= \frac{1}{\Gamma (s)}\int_{0}^{1}\frac{z^{s-1}}{\log_{\lambda}(1+z)}{\rm Ei}_{k, \lambda}\left(\log_{\lambda}(1+z)\right)dz$

$\begin{align} +\frac{1}{\Gamma (s)}\int_{1}^{\infty}\frac{z^{s-1}}{\log_{\lambda}(1+z)}{\rm Ei}_{k, \lambda}\left(\log_{\lambda}(1+z)\right)dz. \end{align}$

(2.6)

For any $s\in\mathbb C$ , the second integral is absolutely convergent and thus, the second term on the r.h.s. vanishes at non-positive integers. That is,

$\begin{align} \lim\limits_{s\rightarrow -m}\left|\frac{1}{\Gamma (s)}\int_{1}^{\infty}\frac{z^{s-1}}{\log_{\lambda}(1+z)}{\rm Ei}_{k, \lambda}\left(\log_{\lambda}(1+z)\right)dz\right|\leq\frac{1}{\Gamma(-m)}M = 0. \end{align}$

(2.7)

On the other hand, the first integral in Eq (2.7), for $\Re(s) > 0$ can be written as

$\frac{1}{\Gamma (s)}\sum\limits_{r = 0}^{\infty}\frac{Pb_{r, \lambda}^{(k)}}{r!}\frac{1}{s+r},$

which defines an entire function of $s$ . Thus, we may include that $\chi_{k, \lambda}(s)$ can be continued to an entire function of $s$ .

Further, from (2.6) and (2.7), we obtain

$\chi_{k, \lambda}(-m) = \lim\limits_{s\rightarrow -m}\frac{1}{\Gamma (s)}\int_{0}^{1}\frac{z^{s-1}}{\log_{\lambda}(1+z)}{\rm Ei}_{k, \lambda}\left(\log_{\lambda}(1+z)\right)dz$

$= \lim\limits_{s\rightarrow -m}\frac{1}{\Gamma (s)}\int_{0}^{1}z^{s-1}\sum\limits_{r = 0}^{\infty}\frac{Pb_{r, \lambda}^{(k)}z^r}{r!}dz = \lim\limits_{s\rightarrow -m}\frac{1}{\Gamma (s)}\sum\limits_{r = 0}^{\infty}\frac{Pb_{r, \lambda}^{(k)}}{s+r}\frac{1}{r!}$

$\begin{align} = \cdots+0+\cdots+0+\lim\limits_{s\rightarrow -m}\frac{1}{\Gamma (s)}\frac{1}{s+m}\frac{Pb_{m, \lambda}^{(k)}}{m!}+0+0+\cdots \end{align}$

(2.8)

$= \lim\limits_{s\rightarrow -m}\frac{\left(\frac{\Gamma(1-s)\sin\pi s}{\pi}\right)}{s+m}\frac{Pb_{m, \lambda}^{(k)}}{m!} = \Gamma(1+m)\cos(\pi m)\frac{Pb_{m, \lambda}^{(k)}}{m!}$

$= (-1)^mPb_{m, \lambda}^{(k)}.$

In view of (2.8), we obtain the following theorem.

Theorem 2.2. Let $k\geq 1$ and $m\in\mathbb N\bigcup\{0\}$ , $s\in\mathbb C$ , we have

$\chi_{k, \lambda}(-m) = (-1)^mPb_{m, \lambda}^{(k)}.$

Using (1.8), we observe that

$\frac{\rm{d}}{\rm{dx}}{\rm Ei}_{k, \lambda}\left(\log_{\lambda}(1+x)\right) = \frac{\rm{d}}{\rm{dx}}\sum\limits_{j = 1}^{\infty}\frac{(1)_{j, \lambda}(\log_{\lambda}(1+x))^{j}}{j^{k}(j-1)!}$

$\begin{align} = \frac{(1+x)^{\lambda-1}}{\log_{\lambda}(1+x)}\sum\limits_{j = 1}^{\infty}\frac{(1)_{j, \lambda}(\log_{\lambda}(1+x))^{j}}{j^{k-1}(j-1)!} = \frac{(1+x)^{\lambda-1}}{\log_{\lambda}(1+x)}{\rm Ei}_{k-1, \lambda}(\log_{\lambda}(1+x)). \end{align}$

(2.9)

Thus, by (2.9), for $k\geq 2$ , we get

${\rm Ei}_{k, \lambda}(\log_{\lambda}(1+x)) = \int_{0}^{x}\frac{(1+z)^{\lambda-1}}{\log(1+z)}{\rm Ei}_{k-1, \lambda}(\log_{\lambda}(1+z))dz$

$= \int_{0}^{x}{\underbrace {\frac{(1+z)^{\lambda-1}}{\log_{\lambda}(1+z)}\int_{0}^{z}\cdots\frac{(1+z)^{\lambda-1}}{\log_{\lambda}(1+z)} \int_{0}^{z}\frac{(1+z)^{\lambda-1}}{\log_{\lambda}(1+z)}}_{(k-2)- \mbox{times}}}dz\cdots dz$

$\times {\rm Ei}_{1, \lambda}(\log_{\lambda}(1+z))dz\cdots dz$

$\begin{align} = \int_{0}^{x}{\underbrace {\frac{(1+z)^{\lambda-1}}{\log_{\lambda}(1+z)}\int_{0}^{z}\cdots\frac{(1+z)^{\lambda-1}}{\log_{\lambda}(1+z)}\int_{0}^{z}\frac{(1+z)^{\lambda-1}}{\log_{\lambda}(1+z)}}_{(k-2)- \mbox{times}}}zdz\cdots dz. \end{align}$

(2.10)

From (2.1) and (2.10), we get

$\sum\limits_{j = 0}^{\infty}Pb_{j, \lambda}^{(k)}\frac{x^j}{j!} = \frac{{\rm Ei}_{k, \lambda}\left(\log_{\lambda}(1+x)\right)}{\log_{\lambda}(1+x)} = \frac{1}{\log_{\lambda}(1+x)}$

$\begin{align} \times\int_{0}^{x}{\underbrace {\frac{(1+z)^{\lambda-1}}{\log_{\lambda}(1+z)}\int_{0}^{z}\frac{(1+z)^{\lambda-1}}{\log_{\lambda}(1+z)}\cdots\int_{0}^{z}}_{(k-2)- \mbox{times}}}\frac{(1+z)^{\lambda-1}}{\log_{\lambda}(1+z)}zdz\cdots dz. \end{align}$

(2.11)

$= \frac{x}{\log_{\lambda}(1+x)}\sum\limits_{q = 0}^{\infty}\sum\limits_{q_1+\cdots+q_{k-1} = q}\binom{q}{q_1, \cdots, q_{k-1}}$

$\times \frac{b_{q_1, \lambda}(\lambda-1)}{q_1+1}\frac{b_{q_2, \lambda}(\lambda-1)}{q_1+q_2+1}\cdots\frac{b_{q_{k-1}, \lambda}(\lambda-1)}{q_1+\cdots+q_{k-1}+1}\frac{x^q}{q!}$

$= \sum\limits_{j = 0}^{\infty}\sum\limits_{q = 0}^{j}\binom{j}{q}\sum\limits_{q_1+\cdots+q_{k-1} = q}\binom{q}{q_1, \cdots, q_{k-1}}b_{j-q, \lambda}$

$\begin{align} \times \frac{b_{q_1, \lambda}(\lambda-1)}{q_1+1}\frac{b_{q_2, \lambda}(\lambda-1)}{q_1+q_2+1}\cdots\frac{b_{q_{k-1}, \lambda}(\lambda-1)}{q_1+\cdots+q_{k-1}+1}\frac{x^j}{j!}. \end{align}$

(2.12)

Therefore, by (2.12), we obtain the following theorem.

Theorem 2.3. For $j\in\mathbb N$ and $k\in\mathbb Z$ , we have

$Pb_{j, \lambda}^{(k)} = \sum\limits_{q = 0}^{j}\binom{j}{q}\sum\limits_{q_1+\cdots+q_{k-1} = q}\binom{q}{q_1, \cdots, q_{k-1}}b_{j-q, \lambda}$

$\times \frac{b_{q_1, \lambda}(\lambda-1)}{q_1+1}\frac{b_{q_2, \lambda}(\lambda-1)}{q_1+q_2+1}\cdots\frac{b_{q_{k-1}, \lambda}(\lambda-1)}{q_1+\cdots+q_{k-1}+1}.$

Corollary 2.2. Taking $k = 2$ in Theorem 2.3 yields

$Pb_{j, \lambda}^{(2)} = \sum\limits_{q = 0}^{j}\binom{j}{q}\frac{b_{q, \lambda}(\lambda-1)}{q+1}b_{j-q, \lambda}.$

Replacing $z$ by $e_{\lambda}(z)-1$ in (2.1), we get

$\sum\limits_{q = 0}^{\infty}Pb_{q, \lambda}^{(k)}(x)\frac{(e_{\lambda}(z)-1)^q}{q!} = \frac{{\rm Ei}_{k, \lambda}\left(z\right)}{z}e_{\lambda}^{x}(z)$

$\begin{align} = \sum\limits_{j = 0}^{\infty}\frac{(x)_{j, \lambda}z^j}{j!}\sum\limits_{r = 0}^{\infty}\frac{(1)_{r+1, \lambda}z^r}{(r+1)^kr!} = \sum\limits_{j = 0}^{\infty} \left(\sum\limits_{r = 0}^{j}\binom{j}{r}\frac{(1)_{r+1, \lambda}(x)_{j-r, \lambda}}{(r+1)^k}\right)\frac{z^j}{j!}. \end{align}$

(2.13)

On the other hand,

$\sum\limits_{q = 0}^{\infty}Pb_{q, \lambda}^{(k)}(x)\frac{(e_{\lambda}(z)-1)^q}{q!} = \sum\limits_{q = 0}^{\infty}Pb_{q, \lambda}^{(k)}(x) \sum\limits_{j = q}^{\infty}S_{2, \lambda}(j, q)\frac{z^j}{j!}$

$\begin{align} = \sum\limits_{j = 0}^{\infty}\left(\sum\limits_{q = 0}^{j}Pb_{q, \lambda}^{(k)}(x)S_{2, \lambda}(j, q)\right)\frac{z^j}{j!}. \end{align}$

(2.14)

In view of (2.13) and (2.14), we get the following theorem.

Theorem 2.4. For $k\in\mathbb Z$ and $j\geq 0$ , we have

$\sum\limits_{q = 0}^{j}Pb_{q, \lambda}^{(k)}(x)S_{2, \lambda}(j, q) = \sum\limits_{r = 0}^{j}\binom{j}{r}\frac{(1)_{r+1, \lambda}(x)_{j-r, \lambda}}{(r+1)^k}.$

By using (2.1), we get

$\sum\limits_{j = 1}^{\infty}\left[Pb_{j, \lambda}^{(k)}(x+1)-Pb_{j, \lambda}^{(k)}(x)\right]\frac{z^j}{j!} = \frac{{\rm Ei}_{k, \lambda}\left(\log_{\lambda}(1+z)\right)}{\log_{\lambda}(1+z)}(1+z)^{x+1}-\frac{{\rm Ei}_{k, \lambda}\left(\log_{\lambda}(1+z)\right)}{\log_{\lambda}(1+z)}(1+z)^{x}$

$= \frac{z{\rm Ei}_{k, \lambda}\left(\log_{\lambda}(1+z)\right)}{\log_{\lambda}(1+z)}(1+z)^{x} = \left(\frac{z}{\log_{\lambda}(1+z)}(1+z)^{x}\right) \left({\rm Ei}_{k, \lambda}\left(\log_{\lambda}(1+z)\right)\right)$

$= \left(\sum\limits_{j = 0}^{\infty}b_{j, \lambda}(x)\frac{z^j}{j!}\right)\left(\sum\limits_{q = 1}^{\infty}\frac{(1)_{q, \lambda}(\log_{\lambda}(1+z))^q}{(q-1)!q^k}\right)$

$= \left(\sum\limits_{j = 0}^{\infty}b_{j, \lambda}(x)\frac{z^j}{j!}\right)\left(\sum\limits_{q = 1}^{\infty}\frac{(1)_{q, \lambda}(\log_{\lambda}(1+z))^{q}}{(q-1)!q^k}\right)$

$= \left(\sum\limits_{j = 1}^{\infty}b_{j, \lambda}(x)\frac{z^j}{j!}\right)\left(\sum\limits_{r = 1}^{\infty}\sum\limits_{q = 1}^{r}\frac{(1)_{q, \lambda}}{q^{k-1}}S_{1, \lambda}(r, q)\frac{z^r}{r!}\right)$

$\begin{align} = \sum\limits_{j = 1}^{\infty}\left(\sum\limits_{r = 1}^{j}\binom{j}{r}\sum\limits_{q = 1}^{r}\frac{(1)_{q, \lambda}}{q^{k-1}}S_{1, \lambda}(r, q)b_{j-r, \lambda}(x)\right)\frac{z^j}{j!}. \end{align}$

(2.15)

Therefore, by comparing the coefficients on both sides of (2.15), we obtain the following theorem.

Theorem 2.5. For $j\geq 0$ , we have

$Pb_{j, \lambda}^{(k)}(x+1)-Pb_{j, \lambda}^{(k)}(x) = \sum\limits_{r = 1}^{j}\binom{j}{r}\sum\limits_{q = 1}^{r}\frac{(1)_{q, \lambda}}{q^{k-1}}S_{1, \lambda}(r, q)b_{j-r, \lambda}(x).$

By making use of (1.3) and (2.1), we have

$\sum\limits_{j = 0}^{\infty}Pb_{j, \lambda}^{(k)}(x+\eta)\frac{z^j}{j!} = \frac{{\rm Ei}_{k, \lambda}\left(\log_{\lambda}(1+z)\right)}{\log_{\lambda}(1+z)}(1+z)^{x+\eta}$

$= \frac{{\rm Ei}_{k, \lambda}\left(\log_{\lambda}(1+z)\right)}{\log_{\lambda}(1+z)}(1+z)^{x}(1+z)^{\eta} = \left(\sum\limits_{j = 0}^{\infty}Pb_{j, \lambda}^{(k)}(x)\frac{z^j}{j!}\right) \left(\sum\limits_{q = 0}^{\infty}(\eta)_q\frac{z^q}{q!}\right)$

$\begin{align} = \sum\limits_{j = 0}^{\infty}\left(\sum\limits_{q = 0}^{j}\binom{j}{q}Pb_{j-q, \lambda}^{(k)}(x)(\eta)_q\right)\frac{z^j}{j!}. \end{align}$

(2.16)

Therefore, by Eq (2.16), we obtain the following theorem.

Theorem 2.6. For $j\geq 0$ , we have

$Pb_{j, \lambda}^{(k)}(x+\eta) = \sum\limits_{q = 0}^{j}\binom{j}{q}Pb_{j-q, \lambda}^{(k)}(x)(\eta)_q.$

By using (2.1), we have

$\frac{{\rm Ei}_{k, \lambda}\left(\log_{\lambda}(1+z)\right)}{\log_{\lambda}(1+z)} = \sum\limits_{j = 0}^{\infty}Pb_{j, \lambda}^{(k)}\frac{z^j}{j!}$

${\rm Ei}_{k, \lambda}\left(\log_{\lambda}(1+z)\right) = \log_{\lambda}(1+z)\sum\limits_{j = 0}^{\infty}Pb_{j, \lambda}^{(k)}\frac{z^j}{j!}$

$\frac{{\rm Ei}_{k, \lambda}\left(\log_{\lambda}(1+z)\right)}{z} = \frac{\log_{\lambda}(1+z)}{z}\sum\limits_{j = 0}^{\infty}Pb_{j, \lambda}^{(k)}\frac{z^j}{j!}$

$= \left(\sum\limits_{q = 0}^{\infty}D_{q, \lambda}\frac{t^q}{q!}\right)\left(\sum\limits_{j = 0}^{\infty}Pb_{j, \lambda}^{(k)}\frac{z^j}{j!}\right)$

$\begin{align} = \sum\limits_{j = 0}^{\infty}\left(\sum\limits_{q = 0}^{j}\binom{j}{q}Pb_{j-q, \lambda}^{(k)}D_{q, \lambda}\right)\frac{z^j}{j!}. \end{align}$

(2.17)

On the other hand,

$\frac{{\rm Ei}_{k, \lambda}\left(\log_{\lambda}(1+z)\right)}{z} = \frac{1}{z}\sum\limits_{q = 1}^{\infty}\frac{(1)_{q, \lambda}(\log_{\lambda}(1+z))^q}{(q-1)!q^k}$

$= \frac{1}{z}\sum\limits_{q = 0}^{\infty}\frac{(1)_{q+1, \lambda}(\log_{\lambda}(1+z))^{q+1}}{q^k!(q+1)}$

$= \frac{1}{z}\sum\limits_{q = 0}^{\infty}\frac{(1)_{q+1, \lambda}}{(q+1)^{k-1}}\frac{1}{(q+1)!}(\log_{\lambda}(1+z))^{q+1}$

$\begin{align} = \sum\limits_{j = 0}^{\infty}\left(\sum\limits_{q = 0}^{j}\frac{(1)_{q+1, \lambda}}{(q+1)^{k-1}}\frac{S_{1, \lambda}(j+1, q+1)}{j+1}\right)\frac{z^j}{j!}. \end{align}$

(2.18)

Thus, by equations (2.17) and (2.18), we get the following theorem.

Theorem 2.7. For $j\geq 0$ , we have

$\sum\limits_{q = 0}^{j}\binom{j}{q}Pb_{j-q, \lambda}^{(k)}D_{q, \lambda} = \sum\limits_{q = 0}^{j}\frac{(1)_{q+1, \lambda}}{(q+1)^{k-1}}\frac{S_{1, \lambda}(j+1, q+1)}{j+1}.$

From (2.1), we have

$\sum\limits_{n = 0}^{\infty}Pb_{j, \lambda}^{(k)}(x)\frac{z^j}{j!} = \frac{{\rm Ei}_{k, \lambda}\left(\log_{\lambda}(1+z)\right)} {\log_{\lambda}(1+z)}(1+z)^{x}$

$= \frac{{\rm Ei}_{k, \lambda}\left(\log_{\lambda}(1+z)\right)}{\log_{\lambda}(1+z)}e_{\lambda}^{x}(\log_{\lambda}(1+z))$

$= \sum\limits_{j = 0}^{\infty}Pb_{j, \lambda}^{(k)}(x)\frac{z^j}{j!}\sum\limits_{q = 0}^{\infty}(x)_{q, \lambda}\sum\limits_{r = q}^{\infty}S_{1, \lambda}(r, q)\frac{z^r}{r!}$

$= \sum\limits_{j = 0}^{\infty}Pb_{j, \lambda}^{(k)}(x)\frac{z^j}{j!}\sum\limits_{r = 0}^{\infty}\sum\limits_{q = 0}^{r}(x)_{q, \lambda}S_{1, \lambda}(r, q)\frac{z^r}{r!}$

$\begin{align} = \sum\limits_{j = 0}^{\infty}\left(\sum\limits_{r = 0}^{j}\binom{j}{r}Pb_{j-r, \lambda}^{(k)}(x)_{q, \lambda}S_{1, \lambda}(r, q)\right)\frac{z^j}{j!}. \end{align}$

(2.19)

Therefore, by comparing the coefficients on both sides of (2.19), we obtain the following theorem.

Theorem 2.8. For $j\geq 0$ , we have

$Pb_{j, \lambda}^{(k)}(x) = \sum\limits_{r = 0}^{j}\binom{j}{r}Pb_{j-r, \lambda}^{(k)}(x)_{q, \lambda}S_{1, \lambda}(r, q).$

3. The degenerate unipoly-Bernoulli polynomials of the second kind

Let $p$ be any arithmetic real or complex valued function defined on $\mathbb N$ . Kim-Kim ^[7] presented the unipoly function attached to polynomials $p(x)$ as

$\begin{align} u_k(x|p) = \sum\limits_{j = 1}^{\infty}\frac{p(j)}{j^k}x^n, (k\in\mathbb Z). \end{align}$

(3.1)

Moreover,

$\begin{align} u_k(x|1) = \sum\limits_{j = 1}^{\infty}\frac{x^j}{j^k} = {\rm Li}_{k}(x), \rm{(see \; [10, 14])}, \end{align}$

(3.2)

represent the known ordinary polylogarithm function.

Dolgy and Khan ^[3] introduced the degenerate unipoly function attached to polynomials $p(x)$ are considered as follows

$\begin{align} u_{k, \lambda}(x|p) = \sum\limits_{j = 1}^{\infty}p(j)\frac{(1)_{j, \lambda}x^j}{j^k}. \end{align}$

(3.3)

We see that

$\begin{align} u_{k, \lambda}\left(x|\frac{1}{\Gamma}\right) = {\rm Ei}_{k, \lambda}(x), \rm{{(see[14])}} \end{align}$

(3.4)

is the modified degenerate polyexponential function.

Now, we introduce the degenerate unipoly-Bernoulli polynomials of the second kind attached to polynomials $p(x)$ as

$\begin{align} \frac{u_{k, \lambda}\left(\log_{\lambda}(1+z)|p\right)}{\log_{\lambda}(1+z)}(1+z)^{x} = \sum\limits_{j = 0}^{\infty}Pb_{j, \lambda, p}^{(k)}(x)\frac{z^j}{j!}. \end{align}$

(3.5)

When $x = 0$ , $Pb_{j, \lambda, p}^{(k)} = Pb_{j, \lambda, p}^{(k)}(0)$ are called the degenerate unipoly-Bernoulli numbers of the second kind attached to $p$ .

If we take $p(j) = \frac{1}{\Gamma (j)}$ . Then, we have

$\sum\limits_{j = 0}^{\infty}Pb_{j, \lambda, \frac{1}{\Gamma}}^{(k)}(x)\frac{z^j}{j!} = \frac{1}{\log_{\lambda}(1+z)}(1+z)^{x}u_{k, \lambda}\left(\log_{\lambda}(1+z)|\frac{1}{\Gamma}\right)$

$\begin{align} = \frac{1}{\log_{\lambda}(1+z)}(1+z)^{x}\sum\limits_{q = 1}^{\infty}\frac{(1)_{q, \lambda}(\log_{\lambda}(1+z))^q}{q^k(q-1)!}. \end{align}$

(3.6)

For $k = 1$ , we have

$\begin{align} \sum\limits_{j = 0}^{\infty}Pb_{j, \lambda, \frac{1}{\Gamma}}^{(1)}(x)\frac{z^j}{j!} = \frac{1}{\log_{\lambda}(1+z)}(1+z)^{x}\sum\limits_{q = 1}^{\infty} \frac{(1)_{q, \lambda}(\log_{\lambda}(1+z))^q}{q!} = \frac{z}{\log_{\lambda}(1+z)}(1+z)^{x}. \end{align}$

(3.7)

Thus, we have

$\begin{align} Pb_{j, \lambda, \frac{1}{\Gamma}}^{(1)}(x) = b_{j, \lambda}(x), (j\geq 0). \end{align}$

(3.8)

By making use of (1.12) and (3.3), we note that

$u_{k, \lambda}\left(\log_{\lambda}(1+z)|p\right) = \sum\limits_{q = 1}^{\infty}p(q)\frac{(1)_{q, \lambda}(\log_{\lambda}(1+z))^q}{q^k}$

$= \sum\limits_{q = 1}^{\infty}\frac{p(q)(1)_{q, \lambda}(\log_{\lambda}(1+z))^q}{q^k}\frac{q!}{q!}$

$= \sum\limits_{q = 1}^{\infty}\frac{p(q)(1)_{q, \lambda}q!}{q^k}\frac{(\log_{\lambda}(1+z))^q}{q!}$

$= \sum\limits_{q = 1}^{\infty}\frac{p(q)(1)_{q, \lambda}q!}{q^k}\sum\limits_{r = q}^{\infty}S_{1, \lambda}(r, q)\frac{z^r}{r!}$

$= \sum\limits_{r = 1}^{\infty}\left(\sum\limits_{q = 1}^{r}\frac{p(q)(1)_{q, \lambda}q!}{q^k}S_{1, \lambda}(r, q)\right)\frac{z^r}{r!}.$

Thus, we have the required result.

Lemma 3.1. For $k\in\mathbb Z$ , we have

$u_{k, \lambda}\left(\log_{\lambda}(1+z)|p\right) = \sum\limits_{r = 1}^{\infty}\left(\sum\limits_{q = 1}^{r}\frac{p(q)(1)_{q, \lambda}q!}{q^k}S_{1, \lambda}(r, q)\right)\frac{z^r}{r!}.$

Recalling from (3.5), we have

$\sum\limits_{j = 0}^{\infty}Pb_{j, \lambda, p}^{(k)}(x)\frac{z^j}{j!} = \frac{1}{\log_{\lambda}(1+z)}(1+z)^{x} u_{k, \lambda}\left(\log_{\lambda}(1+z)|p\right)$

$= \frac{1}{\log_{\lambda}(1+z)}(1+z)^{x}\sum\limits_{q = 1}^{\infty}\frac{(1)_{q, \lambda}p(q)}{q^k}(\log_{\lambda}(1+z))^q$

$= \frac{1}{\log_{\lambda}(1+z)}(1+z)^{x}\sum\limits_{q = 0}^{\infty}\frac{(1)_{q+1, \lambda}p(q+1)}{(q+1)^k}(\log_{\lambda}(1+z))^{q+1}$

$= \frac{1}{\log_{\lambda}(1+z)}(1+z)^{x}\sum\limits_{q = 0}^{\infty}\frac{(1)_{q+1, \lambda}p(q+1)(q+1)!}{(q+1)^k}\sum\limits_{r = q+1}^{\infty}S_{r, \lambda}(r, q+1)\frac{z^r}{r!}$

$= \frac{z}{\log_{\lambda}(1+z)}(1+z)^{x}\sum\limits_{q = 0}^{\infty}\frac{(1)_{q+1, \lambda}p(q+1)(q+1)!}{(q+1)^k}\sum\limits_{r = q}^{\infty}\frac{S_{1, \lambda}(r+1, q+1)}{r+1}\frac{z^r}{r!}$

$= \sum\limits_{j = 0}^{\infty}b_{j, \lambda}(x)\frac{z^j}{j!}\sum\limits_{r = 0}^{\infty} \left(\sum\limits_{q = 0}^{r}\frac{(1)_{q+1, \lambda}p(q+1)(q+1)!}{(q+1)^k}\frac{S_{1, \lambda}(r+1, q+1)}{r+1}\right)\frac{z^r}{r!}$

$\begin{align} = \sum\limits_{j = 0}^{\infty}\left(\sum\limits_{r = 0}^{j}\sum\limits_{q = 0}^{r}\binom{j}{r}\frac{(1)_{q+1, \lambda}p(q+1)(q+1)!}{(q+1)^k} \frac{S_{1, \lambda}(r+1, q+1)}{r+1}b_{j-r, \lambda}(x)\right)\frac{z^j}{j!}. \end{align}$

(3.9)

Therefore, by comparing the coefficients on both sides of (3.9), we obtain the following theorem.

Theorem 3.1. For $j\geq 0$ and $k\in\mathbb Z$ . Then

$Pb_{j, \lambda, p}^{(k)}(x) = \sum\limits_{r = 0}^{j}\sum\limits_{q = 0}^{r}\binom{j}{r}\frac{(1)_{q+1, \lambda}p(q+1)(q+1)!}{(q+1)^k} \frac{S_{1, \lambda}(r+1, q+1)}{r+1}b_{j-r, \lambda}(x).$

Moreover,

$Pb_{j, \lambda, \frac{1}{\Gamma}}^{(k)}(x) = \sum\limits_{r = 0}^{j}\sum\limits_{q = 0}^{r}\binom{j}{r}\frac{b_{j-r, \lambda}(x)}{(q+1)^{k-1}} \frac{S_{1, \lambda}(r+1, q+1)}{r+1}.$

Using (3.5), we have

$\sum\limits_{j = 0}^{\infty}Pb_{j, \lambda, p}^{(k)}(x)\frac{z^j}{j!} = \frac{1}{\log_{\lambda}(1+z)}u_{k, \lambda}(\log_{\lambda}(1+z)|p)(1+z)^{x}$

$= \frac{u_{k, \lambda}\left(\log_{\lambda}(1+z)|p\right)}{\log_{\lambda}(1+z)}\sum\limits_{j = 0}^{\infty}(x)_{j}\frac{z^j}{j!}$

$= \sum\limits_{i = 0}^{\infty}Pb_{i, \lambda, p}^{(k)}\frac{z^i}{i!}\sum\limits_{j = 0}^{\infty}(x)_{j}\frac{z^j}{j!}$

$\begin{align} = \sum\limits_{j = 0}^{\infty}\left(\sum\limits_{i = 0}^{j}\binom{j}{i}Pb_{i, \lambda, p}^{(k)}(x)_{j-i}\right)\frac{z^j}{j!}. \end{align}$

(3.10)

Upon comparing the coefficients on both sides of Eq (3.10), we get the following theorem.

Theorem 3.2. For $j\geq 0$ and $k\in\mathbb Z$ . Then

$Pb_{j, \lambda, p}^{(k)}(x) = \sum\limits_{i = 0}^{j}\binom{j}{i}Pb_{i, \lambda, p}^{(k)}(x)_{j-i}.$

By making use of (1.11), (1.12) and (3.5), we have

$\sum\limits_{j = 0}^{\infty}Pb_{j, \lambda, p}^{(k)}\frac{z^j}{j!} = \frac{1}{\log_{\lambda}(1+z)}u_{k}\left(\log_{\lambda}(1+z)|p\right)$

$= \frac{1}{\log_{\lambda}(1+z)}\sum\limits_{q = 1}^{\infty}\frac{(1)_{q, \lambda}p(q)}{q^k}(\log_{\lambda}(1+z))^q$

$= \sum\limits_{q = 0}^{\infty}\frac{(1)_{q, \lambda}p(q+1)}{(q+1)^k}(\log_{\lambda}(1+z))^{q+1}$

$= \frac{z}{\log_{\lambda}(1+z)}\frac{\log_{\lambda}(1+z)}{z}\sum\limits_{q = 0}^{\infty}\frac{(1)_{q+1, \lambda}p(q+1)q!}{(q+1)^k} \frac{(\log_{\lambda}(1+z))^{q}}{q!}$

$= \sum\limits_{j = 0}^{\infty}D_{j, \lambda}\frac{z^j}{j!}\sum\limits_{i = 0}^{\infty}b_{i, \lambda}\frac{z^i}{i!} \sum\limits_{q = 0}^{\infty}\frac{(1)_{q+1, \lambda}p(q+1)q!}{(q+1)^k}\sum\limits_{r = q}^{\infty}S_{1, \lambda}(r, q)\frac{z^r}{r!}$

$= \sum\limits_{j = 0}^{\infty}D_{j, \lambda}\frac{z^j}{j!}\sum\limits_{i = 0}^{\infty}b_{i, \lambda}\frac{z^i}{i!}\sum\limits_{r = 0}^{\infty} \sum\limits_{q = 0}^{r}\frac{(1)_{q+1, \lambda}p(q+1)q!}{(q+1)^k}S_{1, \lambda}(r, q)\frac{z^r}{r!}$

$= \sum\limits_{j = 0}^{\infty}\sum\limits_{i = 0}^{j}\binom{j}{i}D_{j-i, \lambda}b_{i, \lambda}\frac{z^j}{j!}\sum\limits_{r = 0}^{\infty} \sum\limits_{q = 0}^{r}\frac{(1)_{q+1, \lambda}p(q+1)q!}{(q+1)^k}S_{1, \lambda}(r, q)\frac{z^r}{r!}$

$\begin{align} = \sum\limits_{j = 0}^{\infty}\left(\sum\limits_{r = 0}^{j} \sum\limits_{q = 0}^{r}\sum\limits_{i = 0}^{j-r}\binom{j-r}{i}\binom{j}{r}D_{j-i-r, \lambda}b_{i, \lambda}\frac{(1)_{q+1, \lambda}p(q+1)q!}{(q+1)^k} S_{1, \lambda}(r, q)\right)\frac{z^j}{j!}. \end{align}$

(3.11)

Thus, by comparing the coefficients on both sides of (3.11), we obtain the following theorem.

Theorem 3.3. For $j\geq 0$ and $k\in\mathbb Z$ . Then

$Pb_{j, \lambda, p}^{(k)} = \sum\limits_{r = 0}^{j} \sum\limits_{q = 0}^{r}\sum\limits_{i = 0}^{j-r}\binom{j-r}{i}\binom{j}{r}D_{j-i-r, \lambda}b_{i, \lambda}\frac{(1)_{q+1, \lambda}p(q+1)q!}{(q+1)^k}S_{1, \lambda}(r, q).$

4. Numerical computations

In this section, certain numerical computations are done to calculate certain zeros of the degenerate poly-Bernoulli polynomials of the second kind and show some graphical representations. The first five members of $Pb_{j, \lambda}^{(k)}(x)$ are calculated and given as:

$\begin{align*} &Pb_{0, \lambda}^{(k)}(x) = 1, \\&Pb_{1, \lambda}^{(k)}(x) = \frac{1}{2}+x-\frac{1}{8 \log 3}-\frac{\log 81}{8 \log 3}, \\&Pb_{2, \lambda}^{(k)}(x) = \frac{1}{2}+x^2+\frac{10}{81 (\log 3)^2}+\frac{1}{8 \log 3}-\frac{x}{4 \log 3}-\frac{\log 81}{8 \log 3}-\frac{x \log 81}{4 \log 3}, \\&Pb_{3, \lambda}^{(k)}(x) = -\frac{1}{4}+2 x-\frac{3 x^2}{2}+x^3-\frac{5}{16 (\log 3)^3}-\frac{10}{27 (\log 3)^2}+\frac{10 x}{27 (\log 3)^2}\\& \quad -\frac{1}{4 \log 3}+\frac{3 x}{4 \log 3}-\frac{3 x^2}{8 \log 3}+\frac{\log 81}{16 \log 3}-\frac{3 x^2 \log 81}{8 \log 3}, \\&Pb_{4, \lambda}^{(k)}(x) = \frac{1}{2}-6 x+8 x^2-4 x^3+x^4+\frac{176}{125 (\log 3)^4}+\frac{15}{8 (\log 3)^3}-\frac{5 x}{4 (\log 3)^3}\\& \quad +\frac{110}{81 (\log 3)^2}-\frac{20 x}{9 (\log 3)^2}+\frac{20 x^2}{27 (\log 3)^2}+\frac{3}{4 \log 3}-\frac{11 x}{4 \log 3}\\& \quad +\frac{9 x^2}{4 \log 3}-\frac{x^3}{2 \log 3}-\frac{\log 81}{8 \log 3}+\frac{3 x^2 \log 81}{4 \log 3}-\frac{x^3 \log 81}{2 \log 3}. \end{align*}$

To show the behavior of $Pb_{j, \lambda}^{(k)}(x)$ , we display the graph $Pb_{j, \lambda}^{(k)}(x)$ for $k = 4$ and $\lambda = 3$ , this graph is presented in Figure 1.

Figure 1. Graph of

$Pb_{j, \lambda}^{(k)}(x)$ .

DownLoad: Full-Size Img PowerPoint

Next, the approximate solutions of $Pb_{j, \lambda}^{(k)}(x) = 0$ when $k = 4$ and $\lambda = 3$ , are calculated and listed in Table 1.

Table 1. Approximate solutions of

$Pb_{j, \lambda}^{(k)}(x) = 0$ .

$j$	Real zeros	Complex zeros
1	$0.11378$	-
2	$0.212959, \; 1.0146$	-
3	$0.468628, \; 0.788431, \; 2.08428$	-
4	$2.27482, \; 3.00114$	$0.589582 - 0.515659\; i, 0.589582 + 0.515659\; i$
5	$4.09322$	$0.470967 - 0.872952\; i, \; 0.470967 + 0.872952\; i,$
		$2.76687 - 0.464588\; i, \; 2.76687 + 0.464588\; i$
6	$4.47754, \; 4.94352$	$0.270509 - 1.2071\; i, \; 0.270509 + 1.2071\; i$
		$2.8603 - 1.06554\; i, \; 2.8603 + 1.06554\; i$
7	$6.12953$	$-0.00407237 - 1.52417\; i, \; -0.00407237 + 1.52417\; i,$
		$2.8544 - 1.67974\; i, \; 2.8544 +1.67974\; i$
		$4.98314 - 0.749479\; i, \; 4.98314 + 0.749479\; i$
8	-	$-0.344872 - 1.82511 \; i, \; -0.344872 + 1.82511 \; i,$
		$2.7537 - 2.30093\; i, \; 2.7537 + 2.30093\; i,$
		$5.21262 - 1.46596 \; i, \; 5.21262 + 1.46596 \; i,$
		$6.83367 - 0.248836 \; i, \; 6.83367 + 0.248836 \; i$

| Show Table

DownLoad: CSV

The zeros of $Pb_{j, \lambda}^{(k)}(x)$ for $\lambda \in \mathbb{C}, j = 12$ are plotted in Figure 2.

Figure 2. Zeros of

$Pb_{12, \lambda}^{(k)}(x)$ .

DownLoad: Full-Size Img PowerPoint

The stacking structure of approximate zeros of $Pb_{j, \lambda}^{(k)}(x) = 0$ for $\lambda = 4, j = 1, 2, ..., 12$ is given in Figure 3.

Figure 3. Stacking structure of zeros

$Pb_{j, \lambda}^{(k)}(x)$ .

DownLoad: Full-Size Img PowerPoint

5. Conclusions

In this article, we introduced the type 2 degenerate poly-Bernoulli polynomials of the second kind and derived many related interesting properties. Furthermore, we defined the degenerate unipoly Bernoulli polynomials of the second kind and established some considerable results. Finally, certain related beautiful zeros and graphs are shown.

Acknowledgments

The authors would like to express the gratitude to Deanship of Scientific Research at King Khalid University, Saudi Arabia for providing funding research group under the research grant number R G P.1/162/42.

Conflict of interest

The authors declare no conflict of interest.

Conflict of interest

The authors declare no conflict of interest.

References

[1]	Puetz J, Wurm FM (2019) Recombinant proteins for industrial versus pharmaceutical purposes: a review of process and pricing. Processes 7: 476. doi: 10.3390/pr7080476
[2]	Zhang W, Yang Y, Liu X, et al. (2019) Development of a secretory expression system with high compatibility between expression elements and an optimized host for endoxylanase production in Corynebacterium glutamicum. Microb Cell Fact 18: 72. doi: 10.1186/s12934-019-1116-y
[3]	Sadeghian-Rizi T, Ebrahimi A, Moazzen F, et al. (2019) Improvement of solubility and yield of recombinant protein expression in E. coli using a two-step system. Res Pharm Sci 14: 400-407. doi: 10.4103/1735-5362.268200
[4]	Mikiewicz D, Plucienniczak A, Krzysik-Bierczynska A, et al. (2019) Novel expression vectors based on the pIGDM1 plasmid. Mol Biotechnol 61: 763-773. doi: 10.1007/s12033-019-00201-6
[5]	Duggar BM (1948) Aureomycin: a product of the continuing search for new antibiotics. Ann NY Acad Sci 51: 177-181. doi: 10.1111/j.1749-6632.1948.tb27262.x
[6]	Nagarajan R, Boeck LD, Gorman M, et al. (1971) Beta-lactam antibiotics from Streptomyces. J Am Chem Soc 93: 2308-2310. doi: 10.1021/ja00738a035
[7]	Waksman SA, Lechevalier HA (1949) Neomycin, a new antibiotic active against streptomycin-resistant bacteria, including tuberculosis organisms. Science 109: 305-307. doi: 10.1126/science.109.2830.305
[8]	Waksman SA (1953) Streptomycin: background, isolation, properties, and utilization. Science 118: 259-266. doi: 10.1126/science.118.3062.259
[9]	Vining LC, Shapiro S (1984) Chloramphenicol production in carbon-limited media: effect of methyl α-glucoside. J Antibiot 37: 74-76. doi: 10.7164/antibiotics.37.74
[10]	De Lima Procópio RE, Da Silva IR, Martins MK, et al. (2012) Antibiotics produced by Streptomyces. Braz J Infect Dis 16: 466-471. doi: 10.1016/j.bjid.2012.08.014
[11]	Baltz RH (2010) Streptomyces and Saccharopolyspora hosts for heterologous expression of secondary metabolite gene clusters. J Ind Microbiol Biotechnol 37: 759-772. doi: 10.1007/s10295-010-0730-9
[12]	Raja A, Prabakarana P (2011) Actinomycetes and drug-an overview. Am J Drug Discov Dev 1: 75-84. doi: 10.3923/ajdd.2011.75.84
[13]	Gamboa-Suasnavart RA, Marín-Palacio LD, Martínez-Sotelo JA, et al. (2013) Scale-up from shake flasks to bioreactor, based on power input and Streptomyces lividans morphology, for the production of recombinant APA (45/47 kDa protein) from Mycobacterium tuberculosis. World J Microbiol Biotechnol 29: 1421-1429. doi: 10.1007/s11274-013-1305-5
[14]	Muhamadali H, Xu Y, Ellis DI, et al. (2015) Metabolomics investigation of recombinant mTNFα production in Streptomyces lividans. Microb Cell Fact 14: 157-157. doi: 10.1186/s12934-015-0350-1
[15]	Hamed MB, Karamanou S, Olafsdottir S, et al. (2017) Large-scale production of a thermostable Rhodothermus marinus cellulase by heterologous secretion from Streptomyces lividans. Microb Cell Fact 16: 232. doi: 10.1186/s12934-017-0847-x
[16]	Anné J, Maldonado B, Van Impe J, et al. (2012) Recombinant protein production and Streptomycetes. J Biotechnol 158: 159-167. doi: 10.1016/j.jbiotec.2011.06.028
[17]	Daniels W, Bouvin J, Busche T, et al. (2018) Transcriptomic and fluxomic changes in Streptomyces lividans producing heterologous protein. Microb Cell Fact 17: 198. doi: 10.1186/s12934-018-1040-6
[18]	Simonen M, Palva I (1993) Protein secretion in Bacillus species. Microbiol Mol Biol Rev 57: 109-137.
[19]	Wu SC, Ye R, Wu XC, et al. (1998) Enhanced secretory production of a single-chain antibody fragment from Bacillus subtilis by coproduction of molecular chaperones. J Bacteriol 180: 2830-2835. doi: 10.1128/JB.180.11.2830-2835.1998
[20]	Wu SC, Yeung JC, Duan Y, et al. (2002) Functional production and characterization of a fibrin-specific single-chain antibody fragment from Bacillus subtilis: effects of molecular chaperones and a wall-bound protease on antibody fragment production. Appl Environ Microbiol 68: 3261-3269. doi: 10.1128/AEM.68.7.3261-3269.2002
[21]	Lakowitz A, Krull R, Biedendieck R (2017) Recombinant production of the antibody fragment D1.3 scFv with different Bacillus strains. Microb Cell Fact 16: 14. doi: 10.1186/s12934-017-0625-9
[22]	Inoue Y, Ohta T, Tada H, et al. (1997) Efficient production of a functional mouse/human chimeric Fab′ against human urokinase-type plasminogen activator by Bacillus brevis. Appl Microbiol Biotechnol 48: 487-492. doi: 10.1007/s002530051084
[23]	Shiroza T, Shinozaki-Kuwahara N, Hayakawa M, et al. (2003) Production of a single-chain variable fraction capable of inhibiting the Streptococcus mutans glucosyltransferase in Bacillus brevis: construction of a chimeric shuttle plasmid secreting its gene product. Biochim Biophys Acta 1626: 57-64. doi: 10.1016/S0167-4781(03)00038-1
[24]	Jordan E, Hust M, Roth A, et al. (2007) Production of recombinant antibody fragments in Bacillus megaterium. Microb Cell Fact 6: 2. doi: 10.1186/1475-2859-6-2
[25]	Wang H, Zhang X, Qiu J, et al. (2019) Development of Bacillus amyloliquefaciens as a high-level recombinant protein expression system. J Ind Microbiol Biotechnol 46: 113-123. doi: 10.1007/s10295-018-2089-2
[26]	Zhang XZ, Cui ZL, Hong Q, et al. (2005) High-level expression and secretion of methyl parathion hydrolase in Bacillus subtilis WB800. Appl Environ Microbiol 71: 4101-4103. doi: 10.1128/AEM.71.7.4101-4103.2005
[27]	Contesini FJ, De Melo RR, Sato HH (2018) An overview of Bacillus proteases: from production to application. Crit Rev Biotechnol 38: 321-334. doi: 10.1080/07388551.2017.1354354
[28]	Cai D, Rao Y, Zhan Y, et al. (2019) Engineering Bacillus for efficient production of heterologous protein: current progress, challenge and prospect. J Appl Microbiol 126: 1632-1642. doi: 10.1111/jam.14192
[29]	Song AAL, In LLA, Lim SHE, et al. (2017) A review on Lactococcus lactis: from food to factory. Microb Cell Fact 16: 55. doi: 10.1186/s12934-017-0669-x
[30]	Boumaiza M, Colarusso A, Parrilli E, et al. (2018) Getting value from the waste: recombinant production of a sweet protein by Lactococcus lactis grown on cheese whey. Microb Cell Fact 17: 126. doi: 10.1186/s12934-018-0974-z
[31]	Singh SK, Tiendrebeogo RW, Chourasia BK, et al. (2018) Lactococcus lactis provides an efficient platform for production of disulfide-rich recombinant proteins from Plasmodium falciparum. Microb Cell Fact 17: 55. doi: 10.1186/s12934-018-0902-2
[32]	Rezaei M, Rabbani Khorasgani M, Zarkesh Esfahani SH, et al. (2019) Production of Brucella melitensis Omp16 protein fused to the human interleukin 2 in Lactococcus lactis MG1363 toward developing a Lactococcus-based vaccine against brucellosis. Can J Microbiol 66: 39-45. doi: 10.1139/cjm-2019-0261
[33]	Lahiri A, Sharif S, Mallick AI (2019) Intragastric delivery of recombinant Lactococcus lactis displaying ectodomain of influenza matrix protein 2 (M2e) and neuraminidase (NA) induced focused mucosal and systemic immune responses in chickens. Mol Immunol 114: 497-512. doi: 10.1016/j.molimm.2019.08.015
[34]	Song S, Li P, Zhang R, et al. (2019) Oral vaccine of recombinant Lactococcus lactis expressing the VP1 protein of duck hepatitis A virus type 3 induces mucosal and systemic immune responses. Vaccine 37: 4364-4369. doi: 10.1016/j.vaccine.2019.06.026
[35]	Ghasemi Z, Varasteh AR, Moghadam M, et al. (2018) Production of recombinant protein of Salsola kali (Sal k1) pollen allergen in Lactococcus lactis. Iran J Allergy Asthma Immunol 17: 134-143.
[36]	Taghinezhad-S S, Mohseni AH, Keyvani H, et al. (2019) Protection against human papillomavirus type 16-induced tumors in C57BL/6 mice by mucosal vaccination with Lactococcus lactis NZ9000 expressing E6 oncoprotein. Microb Pathog 126: 149-156. doi: 10.1016/j.micpath.2018.10.043
[37]	Loh JMS, Lorenz N, Tsai CJY, et al. (2017) Mucosal vaccination with pili from Group A Streptococcus expressed on Lactococcus lactis generates protective immune responses. Sci Rep 7: 7174. doi: 10.1038/s41598-017-07602-0
[38]	Joseph BC, Pichaimuthu S, Srimeenakshi S, et al. (2015) An overview of the parameters for recombinant protein expression in Escherichia coli. J Cell Sci Ther 6: 1000221. doi: 10.4172/2157-7013.1000221
[39]	Itakura K, Hirose T, Crea R, et al. (1977) Expression in Escherichia coli of a chemically synthesized gene for the hormone somatostatin. Science 198: 1056-1063. doi: 10.1126/science.412251
[40]	Hayat SMG, Farahani N, Golichenati B, et al. (2018) Recombinant protein expression in Escherichia coli (E.coli): what we need to know. Curr Pharm Des 24: 718-725. doi: 10.2174/1381612824666180131121940
[41]	Tripathi NK (2016) Production and purification of recombinant proteins from Escherichia coli. Chem Bio Eng Rev 3: 116-133.
[42]	Liu HL, Yang SJ, Liu Q, et al. (2018) A process for production of trehalose by recombinant trehalose synthase and its purification. Enzyme Microb Technol 113: 83-90. doi: 10.1016/j.enzmictec.2017.11.008
[43]	Celesia D, Salzmann I, Porto EV, et al. (2017) Production of a recombinant catechol 2,3-dioxygenase for the degradation of micropollutants. CHIMIA Int J Chem 71: 734-738. doi: 10.2533/chimia.2017.734
[44]	Tajbakhsh M, Akhavan MM, Fallah F, et al. (2018) A recombinant snake cathelicidin derivative peptide: antibiofilm properties and expression in Escherichia coli. Biomolecules 8: 118. doi: 10.3390/biom8040118
[45]	Jin H, Cantin GT, Maki S, et al. (2011) Soluble periplasmic production of human granulocyte colony-stimulating factor (G-CSF) in Pseudomonas fluorescens. Protein Expres Purif 78: 69-77. doi: 10.1016/j.pep.2011.03.002
[46]	Retallack DM, Schneider JC, Mitchell J, et al. (2007) Transport of heterologous proteins to the periplasmic space of Pseudomonas fluorescens using a variety of native signal sequences. Biotechnol Lett 29: 1483-1491. doi: 10.1007/s10529-007-9415-5
[47]	Chen R (2012) Bacterial expression systems for recombinant protein production: E. coli and beyond. Biotechnol Adv 30: 1102-1107. doi: 10.1016/j.biotechadv.2011.09.013
[48]	Hermann T (2003) Industrial production of amino acids by coryneform bacteria. J Biotechnol 104: 155-172. doi: 10.1016/S0168-1656(03)00149-4
[49]	Kondoh M, Hirasawa T (2019) L-cysteine production by metabolically engineered Corynebacterium glutamicum. Appl Microbiol Biotechnol 103: 2609-2619. doi: 10.1007/s00253-019-09663-9
[50]	Liu X, Zhang W, Zhao Z, et al. (2017) Protein secretion in Corynebacterium glutamicum. Crit Rev Biotechnol 37: 541-551. doi: 10.1080/07388551.2016.1206059
[51]	Date M, Itaya H, Matsui H, et al. (2006) Secretion of human epidermal growth factor by Corynebacterium glutamicum. Lett Appl Microbiol 42: 66-70. doi: 10.1111/j.1472-765X.2005.01802.x
[52]	Lee MJ, Kim P (2018) Recombinant protein expression system in Corynebacterium glutamicum and its application. Front Microbiol 9: 2523. doi: 10.3389/fmicb.2018.02523
[53]	Haas T, Graf M, Nieß A, et al. (2019) Identifying the growth modulon of Corynebacterium glutamicum. Front Microbiol 10: 974. doi: 10.3389/fmicb.2019.00974
[54]	Felpeto-Santero C, Galan B, Luengo JM, et al. (2019) Identification and expression of the 11β-steroid hydroxylase from Cochliobolus lunatus in Corynebacterium glutamicum. Microb Biotechnol 12: 856-868. doi: 10.1111/1751-7915.13428
[55]	Overton TW (2014) Recombinant protein production in bacterial hosts. Drug Discov Today 19: 590-601. doi: 10.1016/j.drudis.2013.11.008
[56]	Jin LQ, Jin WR, Ma ZC, et al. (2019) Promoter engineering strategies for the overproduction of valuable metabolites in microbes. Appl Microbiol Biotechnol 103: 8725-8736. doi: 10.1007/s00253-019-10172-y
[57]	Goldstein MA, Doi RH (1995) Prokaryotic promoters in biotechnology. Biotechnology Annual Review Amsterdam: Elsevier, 105-128. doi: 10.1016/S1387-2656(08)70049-8
[58]	Chaudhary AK, Lee EY (2015) Tightly regulated and high level expression vector construction for Escherichia coli BL21 (DE3). J Ind Eng Chem 31: 367-373. doi: 10.1016/j.jiec.2015.07.011
[59]	Trung NT, Hung NM, Thuan NH, et al. (2019) An auto-inducible phosphate-controlled expression system of Bacillus licheniformis. BMC Biotechnol 19: 3. doi: 10.1186/s12896-018-0490-6
[60]	Meyers A, Furtmann C, Gesing K, et al. (2019) Cell density—dependent auto—inducible promoters for expression of recombinant proteins in Pseudomonas putida. Microb Biotechnol 12: 1003-1013. doi: 10.1111/1751-7915.13455
[61]	Brunner M, Bujard H (1987) Promoter recognition and promoter strength in the Escherichia coli system. EMBO J 6: 3139-3144. doi: 10.1002/j.1460-2075.1987.tb02624.x
[62]	Shimada T, Yamazaki Y, Tanaka K, et al. (2014) The whole set of constitutive promoters recognized by RNA polymerase RpoD holoenzyme of Escherichia coli. PLoS One 9: e90447. doi: 10.1371/journal.pone.0090447
[63]	Pavco PA, Steege DA (1991) Characterization of elongating T7 and SP6 RNA polymerases and their response to a roadblock generated by a site-specific DNA binding protein. Nucleic Acids Res 19: 4639-4646. doi: 10.1093/nar/19.17.4639
[64]	Vavrová Ľ, Muchová K, Barák I (2010) Comparison of different Bacillus subtilis expression systems. Res Microbiol 161: 791-797. doi: 10.1016/j.resmic.2010.09.004
[65]	Retnoningrum DS, Santika IWM, Kesuma S, et al. (2019) Construction and characterization of a medium copy number expression vector carrying auto-inducible dps promoter to overproduce a bacterial superoxide dismutase in Escherichia coli. Mol Biotechnol 61: 231-240. doi: 10.1007/s12033-018-00151-5
[66]	Jaishankar J, Srivastava P (2017) Molecular basis of stationary phase survival and applications. Front Microbiol 8: 2000. doi: 10.3389/fmicb.2017.02000
[67]	Xu J, Liu X, Yu X, et al. (2020) Identification and characterization of sequence signatures in the Bacillus subtilis promoter P_ylb for tuning promoter strength. Biotechnol Lett 42: 115-124. doi: 10.1007/s10529-019-02749-4
[68]	Zhou C, Ye B, Cheng S, et al. (2019) Promoter engineering enables overproduction of foreign proteins from a single copy expression cassette in Bacillus subtilis. Microb Cell Fact 18: 111. doi: 10.1186/s12934-019-1159-0
[69]	Yu X, Xu J, Liu X, et al. (2015) Identification of a highly efficient stationary phase promoter in Bacillus subtilis. Sci Rep 5: 18405. doi: 10.1038/srep18405
[70]	Ma Y, Cui Y, Du L, et al. (2018) Identification and application of a growth-regulated promoter for improving L-valine production in Corynebacterium glutamicum. Microb Cell Fact 17: 185. doi: 10.1186/s12934-018-1031-7
[71]	Brewster RC, Jones DL, Phillips R (2012) Tuning promoter strength through RNA polymerase binding site design in Escherichia coli. PLoS Comput Biol 8: e1002811. doi: 10.1371/journal.pcbi.1002811
[72]	Hannig G, Makrides SC (1998) Strategies for optimizing heterologous protein expression in Escherichia coli. Trends Biotechnol 16: 54-60. doi: 10.1016/S0167-7799(97)01155-4
[73]	Tegel H, Ottosson J, Hober S (2011) Enhancing the protein production levels in Escherichia coli with a strong promoter. FEBS J 278: 729-739. doi: 10.1111/j.1742-4658.2010.07991.x
[74]	Seyfi R, Babaeipour V, Mofid MR, et al. (2019) Expression and production of recombinant scorpine as a potassium channel blocker protein in Escherichia coli. Biotechnol Appl Bioc 66: 119-129. doi: 10.1002/bab.1704
[75]	Qaiser H, Aslam F, Iftikhar S, et al. (2018) Construction and recombinant expression of Pseudomonas aeruginosa truncated exotoxin A in Escherichia coli. Cell Mol Biol 64: 64-69. doi: 10.14715/cmb/2018.64.1.12
[76]	Khushoo A, Pal Y, Mukherjee KJ (2005) Optimization of extracellular production of recombinant asparaginase in Escherichia coli in shake-flask and bioreactor. Appl Microbiol Biotechnol 68: 189-197. doi: 10.1007/s00253-004-1867-0
[77]	Przystałowska H, Zeyland J, Kosmider A, et al. (2015) 1, 3-propanediol production by Escherichia coli using genes from Citrobacter freundii atcc 8090. Acta Biochim Pol 62: 589-597. doi: 10.18388/abp.2015_1061
[78]	Liang Q, Zhang H, Li S, et al. (2011) Construction of stress-induced metabolic pathway from glucose to 1,3-propanediol in Escherichia coli. Appl Microbiol Biotechnol 89: 57-62. doi: 10.1007/s00253-010-2853-3
[79]	Hjelm A, Karyolaimos A, Zhang Z, et al. (2017) Tailoring Escherichia coli for the L-rhamnose P_bad promoter-based production of membrane and secretory proteins. ACS Synth Biol 6: 985-994. doi: 10.1021/acssynbio.6b00321
[80]	Nguyen NH, Kim JR, Park S (2019) Development of biosensor for 3-hydroxypropionic acid. Biotechnol Bioproc E 24: 109-118. doi: 10.1007/s12257-018-0380-8
[81]	Liu Q, Ouyanga S, Kim J, et al. (2007) The impact of PHB accumulation on L-glutamate production by recombinant Corynebacterium glutamicum. J Biotechnol 132: 273-279. doi: 10.1016/j.jbiotec.2007.03.014
[82]	Skerra A (1994) Use of the tetracycline promoter for the tightly regulated production of a murine antibody fragment in Escherichia coli. Gene 151: 131-135. doi: 10.1016/0378-1119(94)90643-2
[83]	Suzuki N, Watanabe K, Okibe N, et al. (2008) Identification of new secreted proteins and secretion of heterologous amylase by C. glutamicum. Appl Microbiol Biotechnol 82: 491-500. doi: 10.1007/s00253-008-1786-6
[84]	Donovan RS, Robinson CW, Glick BR (2000) Optimizing the expression of a monoclonal antibody fragment under the transcriptional control of the Escherichia coli lac promoter. Can J Microbiol 46: 532-541. doi: 10.1139/w00-026
[85]	Jia H, Li H, Zhang L, et al. (2018) Development of a novel gene expression system for secretory production of heterologous proteins via the general secretory (sec) pathway in Corynebacterium glutamicum. Iran J Biotechnol 16: e1746.
[86]	Caspeta L, Flores N, Pérez NO, et al. (2009) The effect of heating rate on Escherichia coli metabolism, physiological stress, transcriptional response, and production of temperature-induced recombinant protein: a scale-down study. Biotechnol Bioeng 102: 468-482. doi: 10.1002/bit.22084
[87]	Wild J, Hradecna Z, Szybalski W (2002) Conditionally amplifiable BACs: switching from single-copy to high-copy vectors and genomic clones. Genome Res 12: 1434-1444. doi: 10.1101/gr.130502
[88]	Paek A, Kim MJ, Park HY, et al. (2020) Functional expression of recombinant hybrid enzymes composed of bacterial and insect's chitinase domains in E. coli. Enzyme Microb Technol 136: 109492. doi: 10.1016/j.enzmictec.2019.109492
[89]	Liu H, Wang S, Song L, et al. (2019) Trehalose production using recombinant trehalose synthase in Bacillus subtilis by integrating fermentation and biocatalysis. J Agric Food Chem 67: 9314-9324. doi: 10.1021/acs.jafc.9b03402
[90]	Phan HTT, Nhi NNY, Tien LT, et al. (2019) Construction of expression plasmid for Bacillus subtilis using P_spac promoter and BgaB as a reporter. Sci Technol Dev J 22: 239-246. doi: 10.32508/stdj.v22i2.1284
[91]	Jørgensen CM, Vrang A, Madsen SM (2014) Recombinant protein expression in Lactococcus lactis using the P170 expression system. FEMS Microbiol Lett 351: 170-178. doi: 10.1111/1574-6968.12351
[92]	Hanif MU, Gul R, Hanif MI, et al. (2017) Heterologous secretory expression and characterization of dimerized bone morphogenetic protein 2 in Bacillus subtilis. Biomed Res Int 2017: 9350537. doi: 10.1155/2017/9350537
[93]	Hallewell RA, Emtage S (1980) Plasmid vectors containing the tryptophan operon promoter suitable for efficient regulated expression of foreign genes. Gene 9: 27-47. doi: 10.1016/0378-1119(80)90165-1
[94]	Han L, Cui W, Suo F, et al. (2019) Development of a novel strategy for robust synthetic bacterial promoters based on a stepwise evolution targeting the spacer region of the core promoter in Bacillus subtilis. Microb Cell Fact 18: 96. doi: 10.1186/s12934-019-1148-3
[95]	Pothoulakis G, Ellis T (2018) Construction of hybrid regulated mother-specific yeast promoters for inducible differential gene expression. PLoS One 13: e0194588. doi: 10.1371/journal.pone.0194588
[96]	Zhang M, Li F, Marquez-Lago TT, et al. (2019) MULTiPly: a novel multi-layer predictor for discovering general and specific types of promoters. Bioinformatics 35: 2957-2965. doi: 10.1093/bioinformatics/btz016
[97]	Liu X, Yang H, Zheng J, et al. (2017) Identification of strong promoters based on the transcriptome of Bacillus licheniformis. Biotechnol Lett 39: 873-881. doi: 10.1007/s10529-017-2304-7
[98]	Yuan F, Li K, Zhou C, et al. (2020) Identification of two novel highly inducible promoters from Bacillus licheniformis by screening transcriptomic data. Genomics 112: 1866-1871. doi: 10.1016/j.ygeno.2019.10.021
[99]	Wang Y, Wang H, Liu L, et al. (2019) Synthetic promoter design in Escherichia coli based on generative adversarial network. BioRxiv 2019: 563775.
[100]	Presnell KV, Flexer-Harrison M, Alper HS (2019) Design and synthesis of synthetic UP elements for modulation of gene expression in Escherichia coli. Synth Syst Biotechnol 4: 99-106. doi: 10.1016/j.synbio.2019.04.002
[101]	Rhodius VA, Mutalik VK (2010) Predicting strength and function for promoters of the Escherichia coli alternative sigma factor, σ^E. PNAS 107: 2854-2859. doi: 10.1073/pnas.0915066107
[102]	Meng F, Zhu X, Nie T, et al. (2018) Enhanced expression of pullulanase in Bacillus subtilis by new strong promoters mined from transcriptome data, both alone and in combination. Front Microbiol 9: 2635. doi: 10.3389/fmicb.2018.02635
[103]	Hou Y, Chen S, Wang J, et al. (2019) Isolating promoters from Corynebacterium ammoniagenes ATCC 6871 and application in CoA synthesis. BMC Biotechnol 19: 76. doi: 10.1186/s12896-019-0568-9
[104]	Wang J, Ai X, Mei H, et al. (2013) High-throughput identification of promoters and screening of highly active promoter-5′-UTR DNA region with different characteristics from Bacillus thuringiensis. PLoS One 8: e62960. doi: 10.1371/journal.pone.0062960
[105]	Yim SS, An SJ, Kang M, et al. (2013) Isolation of fully synthetic promoters for high-level gene expression in Corynebacterium glutamicum. Biotechnol Bioeng 110: 2959-2969. doi: 10.1002/bit.24954
[106]	Nie Z, Luo H, Li J, et al. (2020) High-throughput screening of T7 promoter mutants for soluble expression of cephalosporin C acylase in E. coli. Appl Biochem Biotechnol 190: 293-304. doi: 10.1007/s12010-019-03113-y
[107]	Yang S, Liu Q, Zhang Y, et al. (2018) Construction and characterization of broad-spectrum promoters for synthetic biology. ACS Synth Biol 7: 287-291. doi: 10.1021/acssynbio.7b00258
[108]	Yang J, Ruff AJ, Hamer SN, et al. (2016) Screening through the PLICable promoter toolbox enhances protein production in Escherichia coli. Biotechnol J 11: 1639-1647. doi: 10.1002/biot.201600270
[109]	Aoki S, Kondo T, Ishiura M (2002) A promoter-trap vector for clock-controlled genes in the cyanobacterium Synechocystis sp. PCC 6803. J Microbiol Methods 49: 265-274. doi: 10.1016/S0167-7012(01)00376-1
[110]	Yang M, Zhang W, Ji S, et al. (2013) Generation of an artificial double promoter for protein expression in Bacillus subtilis through a promoter trap system. PLoS one 8: e56321. doi: 10.1371/journal.pone.0056321
[111]	Yim SS, An SJ, Choi JW, et al. (2014) High-level secretory production of recombinant single-chain variable fragment (scFv) in Corynebacterium glutamicum. Appl Microbiol Biotechnol 98: 273-284. doi: 10.1007/s00253-013-5315-x
[112]	Morowvat MH, Babaeipour V, Memari HR, et al. (2015) Optimization of fermentation conditions for recombinant human interferon beta production by Escherichia coli using the response surface methodology. Jundishapur J Microbiol 8: e16236. doi: 10.5812/jjm.8(4)2015.16236
[113]	Sevillano L, Vijgenboom E, van Wezel GP, et al. (2016) New approaches to achieve high level enzyme production in Streptomyces lividans. Microb Cell Fact 15: 28. doi: 10.1186/s12934-016-0425-7
[114]	Shen R, Yin J, Ye JW, et al. (2018) Promoter engineering for enhanced P (3HB-co-4HB) production by Halomonas bluephagenesis. ACS Synth Biol 7: 1897-1906. doi: 10.1021/acssynbio.8b00102
[115]	Gawin A, Peebo K, Hans S, et al. (2019) Construction and characterization of broad-host-range reporter plasmid suitable for on-line analysis of bacterial host responses related to recombinant protein production. Microb Cell Fact 18: 80. doi: 10.1186/s12934-019-1128-7
[116]	Thakur KG, Jaiswal RK, Shukla JK, et al. (2010) Over-expression and purification strategies for recombinant multi-protein oligomers: A case study of Mycobacterium tuberculosis σ/anti-σ factor protein complexes. Protein Express Purif 74: 223-230. doi: 10.1016/j.pep.2010.06.018
[117]	Dzivenu OK, Park HH, Wu H (2004) General co-expression vectors for the overexpression of heterodimeric protein complexes in Escherichia coli. Protein Express Purif 38: 1-8. doi: 10.1016/j.pep.2004.07.016
[118]	Johnston K, Clements A, Venkataramani RN, et al. (2000) Coexpression of proteins in bacteria using T7-based expression plasmids: expression of heteromeric cell-cycle and transcriptional regulatory complexes. Protein Express Purif 20: 435-443. doi: 10.1006/prep.2000.1313
[119]	Rucker P, Torti FM, Torti SV (1997) Recombinant ferritin: modulation of subunit stoichiometry in bacterial expression systems. Protein Eng 10: 967-973. doi: 10.1093/protein/10.8.967
[120]	Kim KJ, Kim HE, Lee KH, et al. (2004) Two-promoter vector is highly efficient for overproduction of protein complexes. Protein Sci 13: 1698-1703. doi: 10.1110/ps.04644504
[121]	McNally EM, Goodwin EB, Spudich JA, et al. (1988) Coexpression and assembly of myosin heavy chain and myosin light chain in Escherichia coli. Proc Natl Acad Sci 85: 7270-7273. doi: 10.1073/pnas.85.19.7270
[122]	Öztürk S, Ergün BG, Çalık P (2017) Double promoter expression systems for recombinant protein production by industrial microorganisms. Appl Microbiol Biotechnol 101: 7459-7475. doi: 10.1007/s00253-017-8487-y
[123]	Ray MVL, Meenan CP, Consalvo AP, et al. (2002) Production of salmon calcitonin by direct expression of a glycine-extended precursor in Escherichia coli. Protein Express Purif 26: 249-259. doi: 10.1016/S1046-5928(02)00523-5
[124]	Tao X, Zhao M, Zhang Y, et al. (2019) Comparison of the expression of phospholipase D from Streptomyces halstedii in different hosts and its over-expression in Streptomyces lividans. FEMS Microbiol Lett 366: fnz051.
[125]	Liu Y, Shi C, Li D, et al. (2019) Engineering a highly efficient expression system to produce BcaPRO protease in Bacillus subtilis by an optimized promoter and signal peptide. Int J Biol Macromol 138: 903-911. doi: 10.1016/j.ijbiomac.2019.07.175
[126]	Guan C, Cui W, Cheng J, et al. (2016) Construction of a highly active secretory expression system via an engineered dual promoter and a highly efficient signal peptide in Bacillus subtilis. New Biotechnol 33: 372-379. doi: 10.1016/j.nbt.2016.01.005
[127]	Zhang K, Su L, Duan X, et al. (2017) High-level extracellular protein production in Bacillus subtilis using an optimized dual-promoter expression system. Microb Cell Fact 16: 32. doi: 10.1186/s12934-017-0649-1
[128]	Liu X, Wang H, Wang B, et al. (2018) Efficient production of extracellular pullulanase in Bacillus subtilis ATCC6051 using the host strain construction and promoter optimization expression system. Microb Cell Fact 17: 163. doi: 10.1186/s12934-018-1011-y
[129]	Bayat H, Hossienzadeh S, Pourmaleki E, et al. (2018) Evaluation of different vector design strategies for the expression of recombinant monoclonal antibody in CHO cells. Prep Biochem Biotechnol 48: 160-164. doi: 10.1080/10826068.2017.1421966
[130]	Lueking A, Holz C, Gotthold C, et al. (2000) A system for dual protein expression in Pichia pastoris and Escherichia coli. Protein Express Purif 20: 372-378. doi: 10.1006/prep.2000.1317
[131]	Sinah N, Williams CA, Piper RC, et al. (2012) A set of dual promoter vectors for high throughput cloning, screening, and protein expression in eukaryotic and prokaryotic systems from a single plasmid. BMC Biotechnol 12: 54. doi: 10.1186/1472-6750-12-54

This article has been cited by:

1.	Ghulam Muhiuddin, Waseem A. Khan, Deena Al-Kadi, Some Identities of the Degenerate Poly-Cauchy and Unipoly Cauchy Polynomials of the Second Kind, 2022, 132, 1526-1506, 763, 10.32604/cmes.2022.017272
2.	Dojin Kim, Patcharee Wongsason, Jongkyum Kwon, Type 2 degenerate modified poly-Bernoulli polynomials arising from the degenerate poly-exponential functions, 2022, 7, 2473-6988, 9716, 10.3934/math.2022541
3.	Ghulam Muhiuddin, Waseem Ahmad Khan, Jihad Younis, Yuan Yi, Construction of Type 2 Poly-Changhee Polynomials and Its Applications, 2021, 2021, 2314-4785, 1, 10.1155/2021/7167633
4.	Maryam Salem Alatawi, Waseem Ahmad Khan, New Type of Degenerate Changhee–Genocchi Polynomials, 2022, 11, 2075-1680, 355, 10.3390/axioms11080355
5.	Waseem A. Khan, Jihad Younis, Mohd Nadeem, Construction of partially degenerate Laguerre–Bernoulli polynomials of the first kind, 2022, 30, 2769-0911, 362, 10.1080/27690911.2022.2079641
6.	Shahid Ahmad Wani, Ibtehal Alazman, Badr Saad T. Alkahtani, Certain Properties and Applications of Convoluted Δh Multi-Variate Hermite and Appell Sequences, 2023, 15, 2073-8994, 828, 10.3390/sym15040828
7.	Ibtehal Alazman, Badr Saad T. Alkahtani, Shahid Ahmad Wani, Certain Properties of Δh Multi-Variate Hermite Polynomials, 2023, 15, 2073-8994, 839, 10.3390/sym15040839
8.	Azhar Iqbal, Waseem A. Khan, Mohd Nadeem, 2023, Chapter 34, 978-981-19-9857-7, 411, 10.1007/978-981-19-9858-4_34
9.	Waseem Ahmad Khan, Ugur Duran, Jihad Younis, Cheon Seoung Ryoo, On some extensions for degenerate Frobenius-Euler-Genocchi polynomials with applications in computer modeling, 2024, 32, 2769-0911, 10.1080/27690911.2023.2297072
10.	Azhar Iqbal, Waseem A. Khan, 2023, Chapter 6, 978-981-19-9857-7, 59, 10.1007/978-981-19-9858-4_6
11.	Mohra Zayed, Shahid Ahmad Wani, A Study on Generalized Degenerate Form of 2D Appell Polynomials via Fractional Operators, 2023, 7, 2504-3110, 723, 10.3390/fractalfract7100723
12.	Mohra Zayed, Shahid Wani, Exploring the versatile properties and applications of multidimensional degenerate Hermite polynomials, 2023, 8, 2473-6988, 30813, 10.3934/math.20231575
13.	Noor Alam, Waseem Ahmad Khan, Serkan Araci, Hasan Nihal Zaidi, Anas Al Taleb, Evaluation of the Poly-Jindalrae and Poly-Gaenari Polynomials in Terms of Degenerate Functions, 2023, 15, 2073-8994, 1587, 10.3390/sym15081587
14.	Musawa Yahya Almusawa, Exploring the Characteristics of Δh Bivariate Appell Polynomials: An In-Depth Investigation and Extension through Fractional Operators, 2024, 8, 2504-3110, 67, 10.3390/fractalfract8010067
15.	Lingling Luo, Yuankui Ma, Taekyun Kim, Hongze Li, Some identities on degenerate poly-Euler polynomials arising from degenerate polylogarithm functions, 2023, 31, 2769-0911, 10.1080/27690911.2023.2257369
16.	Shahid Ahmad Wani, Two-iterated degenerate Appell polynomials: properties and applications, 2024, 31, 2576-5299, 83, 10.1080/25765299.2024.2302502
17.	Waseem A. Khan, Azhar Iqbal, Mohd Nadeem, 2023, Chapter 50, 978-981-19-9857-7, 589, 10.1007/978-981-19-9858-4_50
18.	Waseem Ahmad Khan, 2024, 2900, 0094-243X, 020001, 10.1063/5.0207187
19.	Lingling Luo, Yuankui Ma, Taekyun Kim, Rongrong Xu, Series involving degenerate harmonic numbers and degenerate Stirling numbers, 2024, 32, 2769-0911, 10.1080/27690911.2023.2297045
20.	Awatif Muflih Alqahtani, Saleem Yousuf, Shahid Ahmad Wani, Roberto S. Costas-Santos, Investigating Multidimensional Degenerate Hybrid Special Polynomials and Their Connection to Appell Sequences: Properties and Applications, 2024, 13, 2075-1680, 859, 10.3390/axioms13120859
21.	Shahid Ahmad Wani, Tabinda Nahid, Ramírez William, Mdi Begum Jeelani, On a new family of degenerate-Sheffer polynomials and related hybrid forms via generating function, 2025, 74, 0009-725X, 10.1007/s12215-025-01228-2

Reader Comments

Your name:*

Email:*
© 2020 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

AIMS Bioengineering

1.2

Metrics

Article views(15798) PDF downloads(2143) Cited by(25)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

Figures and Tables

Figures(3) / Tables(2)

AIMS Bioengineering

Promoter engineering for the recombinant protein production in prokaryotic systems

Related Papers:

Abstract

1. Introduction

2. Type 2 degenerate poly-Bernoulli polynomials of the second kind

3. The degenerate unipoly-Bernoulli polynomials of the second kind

4. Numerical computations

5. Conclusions

Acknowledgments

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Catalog

AIMS Bioengineering

Promoter engineering for the recombinant protein production in prokaryotic systems

Related Papers:

Abstract

1. Introduction

2. Type 2 degenerate poly-Bernoulli polynomials of the second kind

3. The degenerate unipoly-Bernoulli polynomials of the second kind

4. Numerical computations

5. Conclusions

Acknowledgments

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog