Recent advances in bioengineering of the oleaginous yeast Yarrowia lipolytica

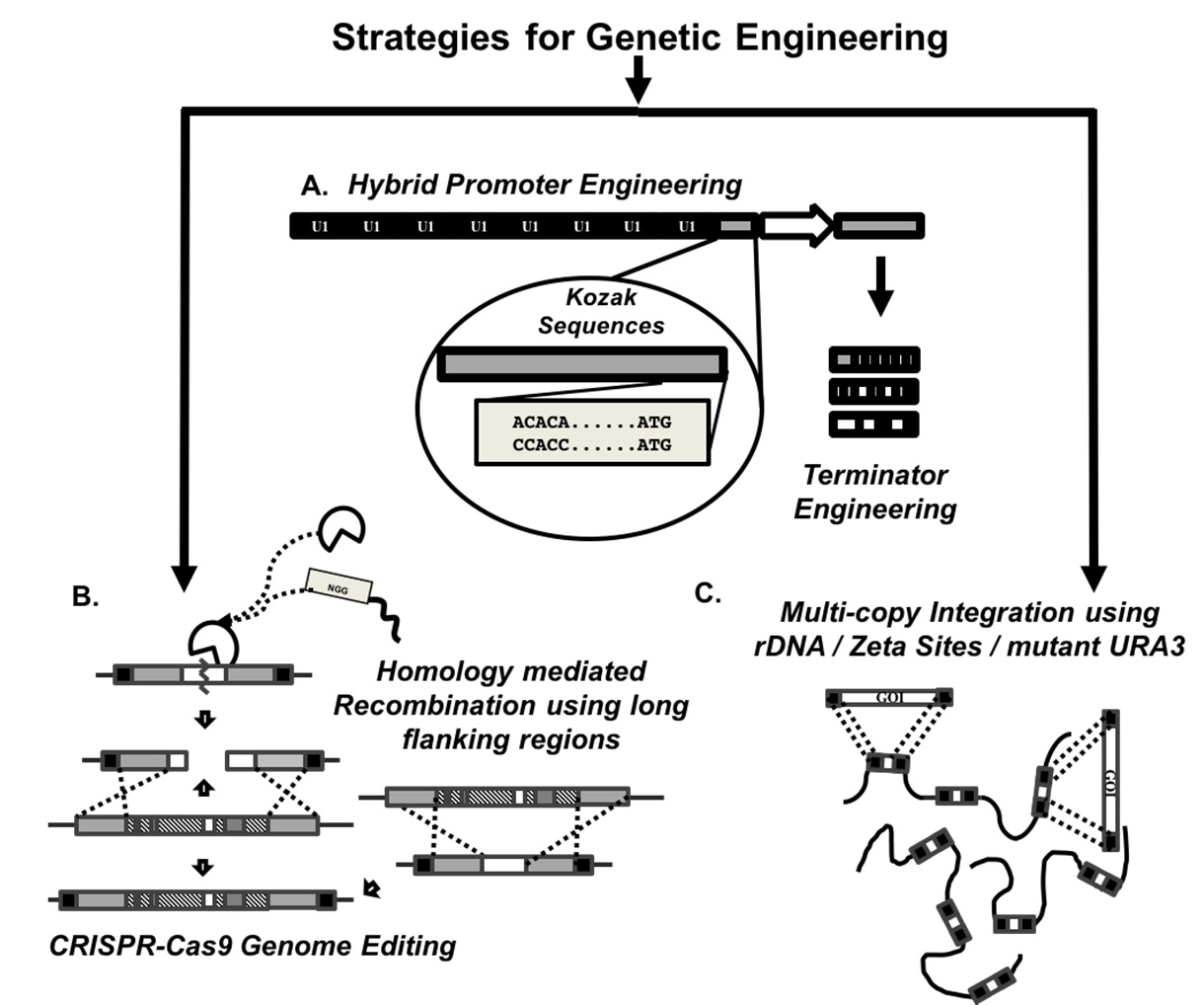
1.   Introduction

Coronavirus disease 2019 (COVID-19) is an infectious disease caused by the severe acute respiratory syndrome coronavirus which can lead to severe sequelae or death due to breathing difficulties, headaches and loss of taste or smell ^[1,2]. Since the outbreak of COVID-19 in 2019, it has seriously affected the development of society and people's lives all over the world. In order to control COVID-19 as soon as possible, mathematical researchers have studied the infectious disease by establishing mathematical models for COVID-19 and analyzed their dynamical behavior^{[3,4,5,6,7,8]}.

The mathematical model of infectious disease was first proposed by Kermack and McKendrick^[9]. They considered a fixed population with only three parts, i.e., $SIR$: the susceptible population $S(t)$, the infected population $I(t)$ and the recovery population $R(t)$. Since then, many improved models, such as $SEIR$ and $SIRS$ models, have been used to describe various properties and laws of disease transmission^{[10,11,12,13,14,15]}. Batabyal^[16] built an $SEIR$ model based on the seasonal transmission nature of the virus, analyzed the stability of the model and obtained the influence of the parameters on the basic regeneration number. Gumel et al.^[17] proposed extended models of the infectious disease in which the stability of the equilibrium point and parameter estimation was studied. The global properties of an SIR model with nonlocal disperse and immigration effects were studied in ^[18]; they evaluated the persistence, extinction of the disease, global stability analysis of the model, existence of the positive equilibrium state and its uniqueness. The above deterministic models have well revealed the mechanism of infectious diseases. In fact, due to the disturbance of uncertain factors such as the environment, temperature, virus variation, prevention and control measures, the COVID-19 model with random factors has gradually attracted more and more attention^{[19,20,21,22,23]}. Sweilam et al.^[24] considered environmental noise and fractional calculus in the COVID-19 model which concluded that random factors have a considerable impact on the demise of infection. In a stochastic $SIQ$ model affected by white noise, the sufficient conditions for stable distribution and disease extinction were proved by Din et al.^[25]. Khan et al.^[26] described a stochastic $SEQIR$ model disturbed by white noise and telegraph noise at the same time; the uniqueness of global positive solutions and random thresholds was obtained. The stochastic coronavirus disease model with jump diffusion has also been researched, and Tesfay et al.^[27] found that random disturbance can inhibit the outbreak of disease better than the deterministic model.

As we all know, vaccination can improve the level of immunity of the population and control the spread of the epidemic^{[28,29,30,31]}. Djilali and Bentout^[32] investigated an $SVIR$ system with distributed delay and drew the conclusion that increasing the number of people vaccinated will reduce the spread of the disease. Zhang et al. ^[33] proposed a stochastic $SVIR$ model based on one vaccination and got the sufficient conditions for the existence of non-trivial periodic solutions. A basic qualitative analysis of the positivity, invariant region and stability of disease-free equilibrium points was performed for a stochastic $SVITR$ model with vaccination^[34]. Wang et al.^[35] constructed a stochastic COVID-19 mathematical model with quarantine, isolation and vaccination; they also studied the influence of vaccination rates, vaccine effectiveness and immune loss rates on COVID-19. Omar et al.^[36] studied a discrete time-delayed influenza model with two strains and two vaccinations, and then concluded that the vaccination of one strain would affect the disease dynamics of the other strain. Alshaikh^[37] generated a fractional order stochastic model based on the secondary vaccination and analyzed various vaccination strategies. With the development of current medical technology and research, more and more of the population has completed a secondary vaccination, even the third vaccination. Based on the above references, although there have been extensive studies and application of COVID-19, it should be pointed out that the complexity modeling of COVID-19 is still not enough, and that the mechanisms of transmission for the complex model are unclear. Based on this, the research on the transmission dynamics characteristics of stochastic COVID-19 epidemics with secondary vaccination is very necessary.

In this paper, a stochastic disease model with secondary vaccination is established in Section 2. In Section 3, we apply random Lyapunov function theory to study the qualitative characteristics. In the last section, numerical simulations are applied to verify the theoretical results.

2.   Model building

In this study, we divided the population into seven time-dependent categories and built a mathematical model of COVID-19 with secondary vaccination (see Figure 1) based on the current situation of the epidemic. That is, it includes the susceptible person $S(t)$, exposed person $E(t)$, first vaccinator $V_{1}(t)$, second vaccinator $V_{2}(t)$, asymptomatic infected person $A(t)$, symptomatic infected person $I(t)$ and recovering person $R(t)$.

In order to obtain the required results, we present the following assumptions:

1) The recovered population has immunity and will not be infected again.

2) Most people who receive the second vaccination will have immunity and will not be infected again.

3) Vaccinated people will transfer to exposure after being infected.

4) Assuming that the interval between two vaccinations is short, the first vaccinated person will not be infected temporarily.

The model is shown in Eq (2.1):

where $\Lambda$ is the constant migration rate of the susceptible population, $\beta_{1}$ is the transmission rate of asymptomatic infected persons, $\beta_{2}$ is the transmission rate of symptomatic infected persons, $\rho_{1}$ is the first vaccination rate, $\rho_{2}$ is the second vaccination rate, $\sigma$ is the infection rate of the exposed to the infected, $\omega$ is the proportion of infections in symptomatic patients, $\alpha$ is the ratio of asymptomatic infected people to symptomatic infected people and $\alpha_{2}$ $(0 < \alpha_{2} < 1)$ is the ratio of secondary vaccinators to symptomatic infected people, so $1-\alpha_{2}$ is the effectiveness of the vaccine. $\gamma_{1}$ and $\gamma_{2}$ respectively represent the recovery rate of asymptomatic and symptomatic infected persons. $\mu_{1}$ and $\mu_{2}$ represent the natural mortality rate and disease-related mortality rate respectively. All parameters are positive.

The disease-free equilibrium point of Eq (2.1) can be obtained ($E, A$ and $I$ are all zero)

where

Using the next generation matrix method^[17], the basic regeneration number of Eq (2.1) is

As we all know, the following theoretical results on equilibrium stability have been established^[1]:

1) when $R_{0} < 1$, the disease-free equilibrium point of the infectious disease model is locally asymptotically stable; otherwise, it is unstable;

2) when $R_{0} = 1$, the infectious model passes through a transcritical bifurcation near the disease-free equilibrium.

In fact, in order to have a more accurate understanding of the real disease development process, we added the influence of random factors into Eq (2.1). The improved stochastic model $SEV_{1}V_{2}AIR$ is as follows:

where $B_{i}(t), i = 1, 2, 3, \cdots, 7$ is the independent standard Brownian motion which represents small disturbance on each variable, and $\sigma_{i}\geq0$ is the intensity of $B_{i}(t), i = 1, 2, 3, \cdots, 7$.

3.   Existence and uniqueness of global positive solutions

In order to study the dynamical behavior of the infectious disease model proposed in this paper, we first need to consider whether the solution is global and non-negative. So in this section, we will prove that there exists a unique global positive solution for Eq (2.2).

Theorem 1. For any given initial value $\left\{S(0), E(0), V_{1}(0), V_{2}(0), A(0), I(0), R(0)\right\} \in R_{+}^{7}$, $Eq$ $(2.2)$ has a unique positive solution $\left\{S(t), E(t), V_{1}(t), V_{2}(t), A(t), I(t), R(t)\right\}$ at $t\geq0$, and this solution will stay in $R_{+}^{7}$ with a probability of 1. So, for all $t\geq0$, the solution $\left\{S(t), E(t), V_{1}(t), V_{2}(t), A(t), I(t), R(t)\right\} \in R_{+}^{7}$ a.s.

Proof: Since the coefficients of the equation are Lipschitz continuous, for any given initial value $\left\{S(0), E(0), V_{1}(0), V_{2}(0), A(0), I(0), R(0)\right\} \in R_{+}^{7}$, there is a unique local solution $\left\{S(t), E(t), V_{1}(t), V_{2}(t), A(t), I(t), R(t)\right\}, t \in\left[0, \tau_{e}\right)$, where $\tau_{e}$ stands for the explosion time, and if $\tau_{e} = \infty$, this local solution is global. To do that, we have to make $k_{0}$ sufficiently large and $S(t)$, $E(t)$, $V_{1}(t)$, $V_{2}(t)$, $A(t)$, $I(t)$, $R(t)$ is in the interval $[\frac{1}{k_{0}}, k_{0}]$. For each integer $k\geq k_{0}$, we define the stopping time as follows:

In this section, we set $inf\emptyset = \infty$ ($\emptyset$ denotes the empty set). It is easy to get $\tau_{k}$ that is increasing as $k\rightarrow \infty$. Set $\tau_{\infty} = lim_{k\rightarrow \infty}\tau_{k}$ which implies $\tau_{\infty} < \tau_{k}$ a.s.. If the hypothesis $\tau_{\infty} < \infty$ is true, then $\tau_{e} = \infty$ a.s. For all $t\geq0$, this means

In other words, we just prove $\tau_{e} = \infty$ a.s. If this statement is wrong, then there are constants $T > 0$ and $\varepsilon\in (0, 1)$ which make $P\left\{\tau_{\infty} < T\right\} > \varepsilon$. Hence there is an integer $k_{1} > k_{0}$ such that

Define a $C^{2}-$function $V: R_{+}^{7}\rightarrow R_{+}$ as follows:

the non-negativity of Eq (3.2) can be obtained from

Using $It\hat{o}s$ formula, we can get

where $LV: R_{+}^{7}\rightarrow R_{+}$ is defined by

where $\beta_{2}\leq max\left\{\frac{\mu_{1}}{1-\alpha_{2}}, \mu_{1}\right\}$ is assumed and $K\; (K\in N^{+})$ is a positive constant, which does not rely on $S$, $E$, $V_{1}$, $V_{2}$, $A$, $I$, $R$ and $t$. So, there is

Let us integrate both sides of Eq (3.4) from $0$ to $\tau_{k}\wedge T = min\left\{\tau_{k}, T\right\}$ and then take the expectation; we can get

Set $\Omega_{k} = \left\{\tau_{k}\leq T\right\}$, and we obtain $P\left\{\Omega_{k}\right\}\geq\varepsilon$ by Eq (3.1). Now, notice that, for every $\omega\in\Omega_{k}$, there is at least one of $S(\tau_{k}, \omega)$, $E(\tau_{k}, \omega)$, $V_{1}(\tau_{k}, \omega)$, $V_{2} (\tau_{k}, \omega)$, $A(\tau_{k}, \omega)$, $I(\tau_{k}, \omega)$ or $R(\tau_{k}, \omega)$ that equals to $k$ or $\frac{1}{k}$.

Therefore

is no less than

thus,

Substitute Eq (3.5) into Eq (3.6), we have

where $1_{\Omega_{k_{\omega}}}$ denotes the indicator function of $\Omega_{k}$. Letting $k\rightarrow \infty$, then

Equation (3.8) is a contradiction. Therefore we have $\tau_{\infty} = \infty$. The proof is completed. Therefore, there exists a unique global positive solution to Eq (2.2).

4.   Extinction of disease

Lemma 1. For any initial value

Eq (2.2) always has a unique positive solution

$\left\{S(t), E(t), V_{1}(t), V_{2}(t), A(t), I(t), R(t)\right\}$ has the following properties:

and

as well as

In order to get the conditions of disease extinction, we set Theorem 2.

Theorem 2. Let $\left\{S(t), E(t), V_{1}(t), V_{2}(t), A(t), I(t), R(t)\right\}\in R_{+}^{7}$ be a positive solution for Eq (2.2), and the initial solution of Eq (2.2) is $\left\{S(0), E(0), V_{1}(0), V_{2}(0), A(0), I(0), R(0)\right\}$.

If $R_{0}^{S} = \frac{(1-\omega)\sigma\Lambda}{\mu_{1}\left(\alpha+\gamma_{1}+\mu_{1}+\mu_{2}+\frac{\sigma_{5}^{2}}{2}\right)} < 1$, then the solution of the system has the following properties:

Proof: First, integrate Eq (2.2) to obtain

Adding the left and right sides of Eq (4.5) respectively, we obtain

At this time, we have

where

We can also obtained

Then, $It\hat{o}s$ formula is used for the fifth formula in Eq (2.2), we can get

Integrate Eq (4.8) from $0$ to $t$:

Substitute Eq (4.7) into Eq (4.9) and divide by $t$, so there is

where $\varphi(t) = \sigma(1-\omega) \phi(t)$. $R_{0}^{s}$ is the called random threshold and it is shown as

According to the strong number theorem, we have $\lim\limits_{t \rightarrow \infty} \frac{B_{5}(t)}{t} = 0$, i.e., $\lim\limits_{t \rightarrow \infty} \frac{\sigma_{5} B_{5}(t)}{t} = 0$. Therefore, take the limit on both sides of Eq (4.10) at the same time; we then get

this means that when $R^{s}_{0} < 1$

Taking the limit on both sides of Eq (4.6) at the same time, we can obtain

Set $M = \left\{\omega = \Omega: \lim _{t \rightarrow \infty} S(t) = \frac{\Lambda}{\mu_{1}}\right\}$, which means that $P(M) = 1$ at this point.

From Eq (4.7), we can get

For $\forall \omega \in M, t > 0$, we can get $\lim\limits_{t \rightarrow \infty} E(\omega, t) = 0, \ \omega \in M$. Considering that $P(M) = 1$, we can obtain

It can be seen from Eq (4.5) that

i.e.

It can be concluded that $\lim _{t \rightarrow \infty}\langle I(t)\rangle = 0$, a.s.

Therefore, this conclusion is proved.

5.   Numerical simulation

In this section, in order to verify the effects of vaccination and random disturbance on controlling the spread of disease, we used the Milstein method^[38,39] to conduct numerical simulations of the stochastic model described by Eq (2.2).

The parameter values of Eq (2.2) are shown in the following table (Table 1).

Eq (2.2) is discretized into the following format:

where $\zeta_{j}(j = 1, 2, \cdots, n)$ are independent Gaussian random variables $N(0, 1)$. Based on the parameters in Table 1, the initial value of the numerical experiment was set as $(S(0), E(0), V_{1}(0), V_{2}(0), A(0), I(0), R(0)) = (0.1, 0.1, 0, 0, 0.1, 0.2, 0)$.

Based on Table 1, let $\rho_{1} = 0.9, \rho_{2} = 0.9, \alpha_{2} = 0.008$, $\sigma_{1} = 0.15$, $\sigma_{2} = 0.063$, $\sigma_{3} = 0.338$, $\sigma_{4} = 0.068$, $\sigma_{5} = 0.25$, $\sigma_{6} = 0.09$ and $\sigma_{7} = 0.023$. The asymptotic behavior of the stochastic model at the disease-free equilibrium point $E_{0} = (0.0303, 0, 0.0275, 0.0229, 0, 0, 0.2526)$ can be shown in Figure 2. At this time, the random threshold is $R^{s}_{0} = 0.0209 < R_{0} = 0.2872 < 1$.

In Figure 2, asymptomatic and symptomatic infections gradually decrease until they disappear, which means that the disease tends to extinction. This is consistent with the previous theoretical results on the extinction of disease. In other words, appropriate noise intensity can promote the extinction of the disease. With the passage of time, the probability of disease extinction becomes 1.

Based on the parameters given in Table 1, $\rho_{1} = 0.9, \alpha_{2} = 0.008$ and we let $\rho_{2}$ equal to $0$, $0.5$ and $0.9$ respectively, the extinction trends of asymptomatic infected person $A$ and symptomatic infected person $I$ are shown in Figure 3(a) and (b). It is clear from Figure 3 that with the increase of the secondary vaccination rate, disease extinction approaches faster. In addition, when $\rho_{1} = 0.9, \rho_{2} = 0.9$, the extinction trends of the two infected populations are shown in Figure 3(c) and (d) as $\alpha_{2}$ is equal to $0.008$, $0.025$ and $0.05$ respectively. We found that the smaller the value of $\alpha_{2}$ and the higher the vaccine efficiency, the faster the disease tends to extinction. So, we can know from Figure 3 that improving the secondary vaccination rate and vaccine efficiency is one of the important measures to effectively control the epidemic.

According to Theorem 2, $\sigma_{5}$ is random intensity acting on asymptomatic infected persons which can directly affect the random threshold $R^{s}_{0}$. This means that $\sigma_{5}$ can directly affect the speed of the extinction of the disease and that other noise intensity types indirectly affects the extinction of the disease. Therefore the influence of $\sigma_{5}$ on the extinction of the disease was mainly investigated. When other noise intensity types are kept constant and $\sigma_{5}$ is set to $0$, $0.05$, $0.15$ and $0.25$ respectively, the influence of different noise intensities on disease extinction is shown in Figure 4. It can be seen in Figure 4 that the noise intensity can promote the extinction of the infected population. Under the constraint of a random threshold, the higher the noise intensity $\sigma_{5}$, the faster the disease-free equilibrium point is reached.

In real life, $\sigma_{5}$ represents the disturbance intensity of infected persons under the policies of isolation measures, the effective diagnosis of asymptomatic infected persons and self-protection. From the above analysis, it can be seen that the more complete the intervention policies for infected people, the better the disease prevention and control.

6.   Conclusions

At present, the mathematical modeling of infectious diseases plays an important role in providing epidemic prevention and control strategies. In order to control the epidemic in real life, quarantine and other epidemic prevention measures have been proposed, which have become a random disturbance factor affecting the spread of the epidemic in the infectious disease model. So far, vaccination is considered to be one of the most popular and effective methods to alleviate and prevent epidemics. Based on this, the $SEV_{1}V_{2}AIR$ model was established by considering random disturbance and secondary vaccination, and then the dynamical analysis of the model was carried out. First, using the stop time theory and Lyapunov analysis method, it was proved that the proposed model has a globally unique positive solution. Then, we obtained the theoretical results about the random threshold $R^{s}_{0}$. When $R_{0}^{S} < 1$, the disease tends to become extinct. Finally, numerical simulations were performed to verify the theoretical results.

In this paper, the theoretical and numerical simulations show that vaccination and random disturbance have a great impact on disease dynamics. The intensity of the random disturbance directly affects the extinction rate of the infected population. In addition, the higher the secondary vaccination rate and vaccine effectiveness, the faster the extinction rate of the disease. In order to control infectious diseases, we can not only reduce the disease transmission rate through isolation, self-protection and other measures, but also encourage susceptible individuals to get vaccinated and improve the effectiveness of the vaccine. These conclusions provide theoretical basis for preventing and controlling the spread of COVID-19.

Furthmore, the impact of some discontinuous factors and vaccine frequency on COVID-19 will be discussed in the future work because of more influential disturbances, such as large-scale human aggregation, the promotion of antiviral drugs and so on.

Acknowledgments

This work was supported by grants from the National Natural Science Foundation of China (No. 11772002), Ningxia higher education first-class discipline construction funding project (NXYLXK2017B09), Major special project of North Minzu University (No. ZDZX201902), Open project of The Key Laboratory of Intelligent Information and Big Data Processing of NingXia Province (No. 2019KLBD008) and Postgraduate innovation project of North Minzu University (YCX22099). The authors would like to thank the editors and reviewers for their valuable suggestions on the logic and preciseness of this article.

Conflict of interest

The authors declare that there is no conflict of interest.