Taking arbitrage opportunities into consideration in an incomplete market, dealers will price bonds based on asymmetric information. The dealer with the best offering price wins the bid. The risk premium in dealer's offering price is primarily determined by the dealer's add-on rate of change to the term structure. To optimize the trading strategy, a new equilibrium trading model is introduced. Optimal sequential estimation scheme for detecting the risk premium due to private inforamtion is proposed based on historical prices, and the best bond pricing formula is given with the according optimal trading strategy. Numerical examples are provided to illustrate the economic insights under the certain stochastic term structure interest rate models.
1.
Introduction
Characterized by the increase in interest rate volatility and the prevalent use of contingent claims, the study of various term structure models becomes a primary concern in financial research. Traditional trading models are based upon the following assumptions:
1. there is no arbitrage profit with zero-setup cost;
2. all information is known to the public;
3. there are no frictions.
Under these assumptions, many mathematical models were developed, for example (Black and Scholes, 1973; Chan et al., 1992; Cox and Ingersoll, 1985; Duffie and Kan, 1996; Heath et al., 1992; Ho and Lee, 1986; Hull and White, 1990; Ji and Yin, 1993) and the references therein. The literature have been devoted to problems under the premise that there is no arbitrage opportunity. In addition, most financial models are pure-exchange models and are not concerned with production economies (Subrahmanyam, 1996). Although the models allow us to carry out analysis in various investigation, they cannot give accurate description for the ever changing market places.
Generally speaking, there are two types of fundamental model setup: arbitrage-free complete market or supply-demand equilibrium. Arbitrage free models assume that the market is complete, and there is no risk-free strategy that yields guaranteed positive returns with zero-setup cost. These models derive the price of contingent claims from the stochastic behavior of the underlying instrument assuming there are no arbitrage opportunities on the market. Contrary to arbitrage free models, equilibrium term structure models begin with the assumption of the investor preferences, typically quantified by utility functions, and the description of the economy. By seeking a balance of supply and demand, equilibrium models attempt to explain the overall economy behavior, derive the term structure of interest rates, and price the risk premium, etc. Examples of equilibrium models are Vasicek (Vasicek, 1977), CIR (Cox and Ingersoll, 1985), and many generalizations afterwards. One of the important issues of equilibrium models is that, in practice, the investor preferences and economy behaviors are usually unavailable or not easy to quantify. This may be one of the reasons that the yield curves generated by equilibrium term structure models are usually inconsistent with current market prices. This paper proposes a new approach that could get around of the aforementioned challenge, and has practical advantage in trading exercise.
To begin with, in the trading practice, more often than not the arbitrage-free condition is violated, and the first assumption is not satisfied. Moreover, the information is not open to the public all the time. Considering that the treasury bond market is very liquid, and acting as market maker the primary dealers buy and sell securities and make a profit by offering prices with added markup, also known as risk premium, to the actual value of the bond. The offering prices take into account the public information on the previous closing prices from the market, the private information from the dealer and the arbitrage effects. On the other hand, the retail investor buys or sells securities by quoting from multiple dealers, and chooses the best offering price. The dealer should maintain a certain level of profit to bear the risk, and provide the best offer that beats other dealers' offers. To determine the bond pricing, the dominating factor to consider is the term structure. Assume the spread over the risk free rate could be expressed by a stochastic differential equation (SDE). Traditionally, the stochastic term structure models attempt to explain the dynamic relationship to various factors like risk-free rate, volatility, etc. (Brennan and Schwartz, 1977; Cox and Ingersoll, 1985; Cox et al., 1980; Cox and Ross, 1976; Dothan, 1978; Litterman and Scheinkman, 1991; Vasicek, 1977). For the effect of asymmetric information to the term structure, Duffie and Lando (2001) studied the conditional distribution of assets with incomplete information filtration. Zhou (2001) argued that the incomplete information could be explained by jumps. Madan and Unal (2000) developed a two-factor hazard rate models for pricing risky debt. In this paper, the arbitrage effects and private information of the dealer are factored into the dealer's rate of change to the spread. Thus the drift term in the SDE of the spread is determined by two stochastic processes: the rate of change by public domain, and the dealer's add-on to the rate of change which is associated to the dealer's risk premium. To the best knowledge of the authors, this is the first term structure model that considers the dealer's asymmetric information and preference as a factor in the drift term of spread. In trading, a natural question is whether a dealer's add-on exists. This can be treated as a hypothesis testing problem. Given the observed bond spread, which is a stochastic process, the problem being considered involves hypothesis testing on the presence or absence of the dealer's add-on process. This problem can be solved by finding the optimal sequential estimation scheme of hypothesis testing characterized by the stopping time and final decision at the end of the observation.
Assume that all dealers' add-on to the rate of change of spread exist, then the dealer's offering price of the bond is a function of the add-on process. Comparing the quote prices from multiple dealers, the final price will be the one having minimum dealer add-on. A dealer needs to find the optimal add-on such that with risk premium added in the offered price is the best among other dealers. In this paper, a novel approach is proposed by considering the bond price as a cost function, and the dealer add-on process as a control term. Then this can be treated as a stochastic optimal control problem. The bond price can be determined by solving the Hamilton-Jacobi-Bellman equation. Using stochastic control approach for finance problems has been studied by many authors (Chang and Sundaresan, 1999; Duffie et al., 1997; Gao, 2008; Taksar and Zhou, 1998; Vecer, 2001).
Karoui and Quenez (1995) studied the contingent claim price range in an incomplete market and determined the maximum and minimum prices.
Korn and Kraft (2002) considered the optimal portfolio investment strategy with stochastic interest rate.
Fleming and Stein (2004) applied dynamic programming to the pricing problem of international finance in open economy. To the best knowledge of the authors, this is the first work that the dealer's add-on to the spread change is considered as a control term in solving bond pricing problem in an incomplete market.
In summary, a new equilibrium trading model that is very different from previous considerations is introduced, and a new optimal trading strategy is developed, which is more realistic from a practical point of view regarding asymmetric information. More specifically, the spread over risk-free rate is expressed by a SDE in which the drift term consists of two factors: the rate of change by public domain, and the dealer's add-on that is associated to the dealer's risk premium. To determine the existence of the dealer's add-on, a hypothesis test with an optimal sequential estimation scheme is proposed by using historical observations. Assuming all dealers' add-on exist, to determine the best bond pricing with optimal trading strategy, a stochastic optimal control problem is formally proposed with the bond price as cost function and the dealer add-on as the control term.
The rest of the paper is organized as follows. A new trading model is introduced and formulated in Section 2. Section 3 considers the risk premium charged by dealers, which is primarily determined by dealer's add-on rate of change to the bond term structure, where the spread is considered as a stochastic differential equation. A crucial issue is to estimate this risk premium and this problem is dealt with in Section 4, where a sequential detection procedure is suggested. Finally, a valuation formula is given for best bond pricing with corresponding optimal trading strategy in Section 5, and some examples are provided for illustration.
2.
A new trading model
We consider the trading practice in treasury bond market which is known to be a very liquid one. The prices are controlled mainly by those prime dealers. Suppose that a company wishes to sell a treasury bond from its portfolio, the representative of this company will contact several dealers to get bid (offer) prices. He or she will then choose the "bid price" by taking the best offer (i.e., the maximum value of all the offers). This can be written as:
where Pb denotes the "bid price" and D represents a dealer. Similarly, if one wants to buy a bond from the market, he or she will selects the "ask price" that is the cheapest one, i.e.,
where Pa denotes the "ask price".
The bid offer and ask offer are calculated by using the term structure, which is an average of all the bonds. The prices which are known to the public are the information on the closing price. In other word, the information of prices is only available to the public at certain time. Due to the availability of the information, the term structures for different dealers are the same after closing the market, but are otherwise different. At any trading instance, the prices are determined by inter-day term structure, which is determined in accordance with
1. the prime dealers' trading screen, which is not available to anyone else,
2. the estimates of the interest trend by individuals, and
3. the dealers' private information.
It is readily seen that the inter-day term structures are different for different dealers.
It is clear that the private information and arbitrage effect are essential in the processing of determining the "bid price" and "ask price". The apparent violation of the classical assumptions indicates that a new trading approach ought to be developed.
3.
The risk premium
In this section, we consider a dominating factor–the spread. Much work has been done regarding to the volatility as a main factor. A typical case is treating the volatility σ as σ(t) a function of t , i.e., assuming that the volatility is time varying. Nevertheless, the change of σ does not make significant contribution to the overall system. In fact, the probability of changing σ is quite small. Hence, we assume that the volatility is constant throughout the bidding process, and is denoted as the σ .
Let the public term structure be r0(t) at time 0 , where t is the term, i.e., time to maturity. Let St be the bond's spread over the risk-free rate. The bond spread is completely observable on the market. The spread St is assumed to be described by the following stochastic differential equation under the risk-neutral measure.
where wt is a standard Brownian motion, σ is the volatility, vt is the rate of change for dealer D , and bt is the drift term determined by the public domain.
As a consequence, the price can be divided in two parts: the static part, which is determined by the public information of last closing and is constant for different dealers, and the risk premium. Suppose that there is a zero-coupon corporate bond with face value F . The fundamental value of the bond can then be expressed by
where E[⋅] is the expectation under risk-neutral measure. Hence, the prices are given by
and
Owing to (5) and (6), dealers' prices are adjusted by the risk premium due to private information. In this model, arbitrage opportunity as well as private information have been taken into account. Then the risk premium due to private information is a function of the dealer's rate of change vt . The dealer adjusts the bid price based on past private information. The rate of adjustment vt can be considered as a control variable. In what follows, we assume that vt is a random process that depends on the past information up to time t . One of the key issues is to determine vt based on known information. This is our main concern in the next section.
4.
A sequential detection procedure
We assume that vt is a stochastic process, that is independent of wt . The problem of finding vt becomes a detection problem or hypothesis testing problem. Consider:
We shall test the two hypotheses on the presence or absence of vt from the observed spread St .
Let τ=τ(x) be a stopping time with respect to the σ -algebra: Gt=σ{xs;s≤t} , where xt ,
t≥0 is continuous and x0=b0 . Let δ=δ(x) be a Gτ measurable decision function such that
Let the first and the second kind of error probabilities be
For notational simplicity, we shall write the probability on the right-hand side of (8) as P1(δ(s)=0) and P0(δ(s)=1) respectively. Similarly, Ei will denote the corresponding expectation. We assume that:
(A) For each t<∞ , E|vt|<∞ ,
Let Δα,β be the class of sequential schemes Δ=Δ(τ,δ) with α(Δ)≤α ,
β(Δ)≤β , α+β<1 , and
Proposition 4.1. Suppose that Condition (A) is satisfied. Then there is an optimal strategy Δ∗=Δ(τ∗,δ∗) , defined by
where
The optimality is in the sense that for any strategy Δ=Δ(τ,δ)∈Δα,β ,
where
Proof. To prove this proposition, we need to use the techniques developed in Theorem 17.8 of [23]. The details are omitted.
Proposition 4.1 deals with a hypothesis testing problem. Given the observed bond spread St , the problem being considered involves a hypothesis testing on the presence or absence of the dealer's add-on process. This problem can be solved by finding the optimal sequential estimation scheme of hypothesis testing characterized by the stopping time and final decision at the end of the observation.
5.
Valuation problems
This section provides an equilibrium trading scheme when vt is detected. In the presence of vt , dealers will adjust the bid prices by adding risk premiums due to the private information. Under our designed trading scheme, the bid price is assumed as a function of the observed spread St and time when optimal rate of change vt is adopted by dealers. Hence, the price of the bond is given by
Using the alternative hypothesis and the above price as a cost function, we can write down the Hamilton-Jacobi-Bellman equation (see [14]) of bid price P as
where P is short notation of P(t,S) .
Remark 5.1. In view of (9), we assume that dealers aim to minimize the cost of buying the bonds. Then a minimal risk premium is added in each bidding process. In this work, our objective is to design a trading scheme taking into account the detected "rate of change" vt due to the private inoframtion. In the equilibrium trading scenario, we adopt the form of HJB equation and assume that the price Pt satisfies (10). Hence, the bid price Pt is an equilibrium price satisfying a HJB equation under our trading scheme.
It can be verified that a solution of the above equation is given by
And vt is adopted as
An important question is if the solution of (10) is unique. This problem remains to be open in a general case. However, according to specific trading strategies, boundary conditions can be imposed to guarantee the uniqueness of the solutions of the Hamilton-Jacobi-Bellman equation.
To proceed, we assume that the dealers are rational to design the trading strategies taking into account all of the market conditions and asset values therein. Then the boundary conditions and terminal condition are adopted as follows.
Boundary conditions. To consider the boundary conditions and terminal conditions of the bid price, we assume that the bidders are rational in finite time horizon of the bidding process. Following the work in Black and Cox (1976), we assume that the bid price at the terminal time equals the minimum of risk-neutral price and the face value of the bond. Further, for rational bidders, the risk neutral price of a zero-coupon bond converges towards the face value at the redemption date. Hence, the bid price of the bond at the time T satisfies P(T,S)=F. The boundary conditions follow
where rs is the short rate and
(13) shows that the bid price is no more than the price of a risk-free bond if the bond is arbitrarily secured. (14) means that the bond is valueless if the spread is arbitrary high.
In following subsections, we will develop trading schemes in two cases when the short rate follows two types of equilibrium short rate models: the Vasicek model and the Cox–Ingersoll–Ross model. The bid prices with corresponding short rate models are obtained accordingly.
5.1. Case 1: vasicek model
We assume that the dynamics of short rate rs follows the Vasicek model for s∈[0,T] . That is,
where k,θ,σ1>0 and zs is a Brownian motion under the risk-neutral measure. Then, ∀t∈[0,T], (13) can be rewritten as
where
and
See Page 58 in Brigo and Mercurio (1999).
In this example, from the reality of risk premium we set St in a reasonable range of [0,100%]. The length of the bidding process and the contract life is set as T=3 . The face value of the bond is set to be 1. Further, for simplicity, we let the drift term of the spread bt be a constant with bt=0.5 . The volatility of the spread is also set as a constant with σ=0.15 . In Vasicek model, the rate of mean-reverting is k=1 , the long-term interest rate expectation is assumed to be θ=0.05 , and the volatility of the interest rate is σ1=0.12 .
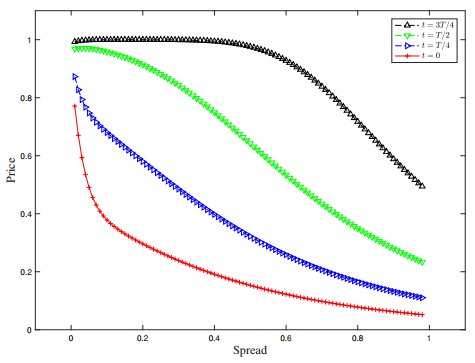
In Figure 1, it is shown that the optimal bid price is a humped shape against the spread during the life time of the bond contract. As the time goes towards the maturity of the contract, the bid price increases towards the face value of the bond. Further at any time t , the optimal bid price achieves its maixmum when the spread is relatively small. As the spread goes higher, the optimal bid price drops significantly, which is shown by the sharply decreasing curves. This means that rational bidders are relatively risk averse when adopting this type of bidding strategies. In addition, we find that the sensitivity of the optimal bid price is higher when the spread is relatively small. The curves are more flat when the spread is much higher. It demonstrates that rational bidders will not change the bid price much even it is a bit less risky when the risk of the bond is sufficiently high.
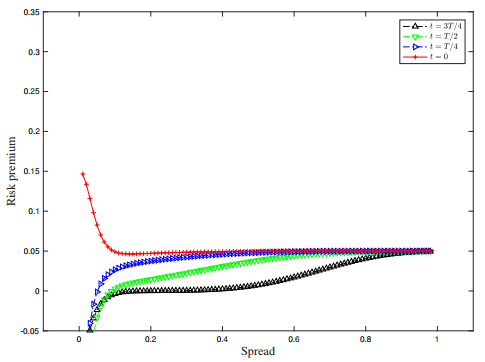
In Figure 2, the optimal risk premium vt are plotted against the spreads at different times. We find that the risk premium is a decreasing function of time in this trading strategies. Further, it is shown that the risk premiums converge as the spread moves higher at all times. That is, the risk premium is much less sensitive to the age of the bond and the spreads when the spread is sufficiently high.
5.2. Case 2: Cox–Ingersoll–Ross model
We assume that the dynamics of short rate rs follows the Cox–Ingersoll–Ross (CIR) model. Here for s∈[0,T], we put
in the risk-neutral measure. Then ∀t∈[0,T] , (13) can be rewritten as
with
and
where
See Page 66 in Brigo and Mercurio (2007).
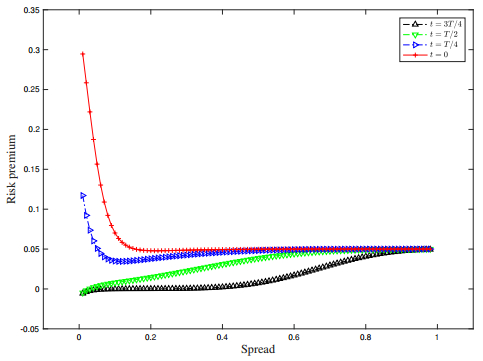
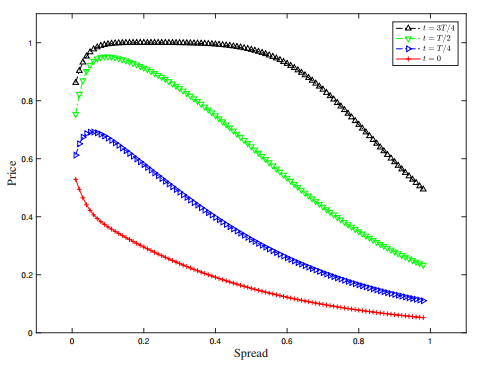
In this example, we set the same values of S , T , F , and bt as in Section 5.1. In CIR model, the rate of mean-reverting is a=1 , the long-term interest rate expectation is assumed to be μ=0.05 , and the volatility of the interest rate is σ2=0.15 . Overall, Figure 3 and Figure 4 have similar shapes with Figure 1 and Figure 2. However, both bid prices and risk premiums in CIR model have different values comparing with the values in Vasicek model, even though the interest rates have the same mean-reverting speed, long-term mean and volatility. Particularly, the optimal bid prices are less humped against the spread as in Figure 1. Moreover, similar to Figure 4, the premium is a decreasing function with respect to spreads when the bond is younger, whereas it is an increasing function when the bond is older. It demonstrates that rational bidders are less willing to pay much risk premiums when the bonds are nearly matured.
6.
Conclusions
In this paper, a new equilibrium trading model with asymmetric information is proposed, in which the dealer's private information is considered as a drift add-on factor of the bond price spread process. An optimal sequential estimation scheme is proposed to detect the existence of the dealer's add-on factor. To determine the best offering price, an optimal trading strategy is proposed by solving a stochastic optimal control problem where the bond price is considered as the cost function and the dealer's add-on is considered as a control term. A few examples are provided to illustrate the method and the economic insights in the model.
For simplicity, this paper considers the case when spread volatility is constant. One future work could be considering stochastic volatility in the model. Future more, the drift term bt determined by public information is in a general form in this paper. Multi-factor term structure models are more versatile and widely used in recent years. Expanding bt to a more complex and realistic form could be another work in the future.
Acknowledgments
We are grateful to the anonymous referees for his/her valuable comments and suggestions. We are also grateful to the late Dr. Dunmu Ji for his insight and valuable contributions. We also thank Prof. George Yin for the comments and suggestions. The research of Lianzhang Bao was supported by China Postdoctoral Science Foundation. The research of Zhuo Jin was supported in part by Research Grants Council of the Hong Kong Special Administrative Region (project No. HKU 17330816).
Conflict of Interest
The views expressed in this publication do not reflect the views of General Electric.









 DownLoad:
DownLoad: