Approximation of solutions of multi-dimensional linear stochastic differential equations defined by weakly dependent random variables

1.   Introduction

The foundation of fixed point theory is the idea of metric spaces and the Banach contraction principle. An enormous number of academics are motivated to the axiomatic interpretation of metric space because of its spaciousness. The metric space has experienced numerous generalizations until

now. This demonstrates the attraction, enchantment, and development of the idea of metric spaces.

After being given the notion of fuzzy sets (FSs) by Zadeh ^[1], researchers provided various generalizations for classical structures ^[2,3,4,5]. In this continuation, Kramosil and Michalek ^[6] originated the approach of fuzzy metric spaces, while George and Veeramani ^[7] introduced the concept of fuzzy metric spaces. Garbiec ^[8] gave the fuzzy interpretation of Banach contraction principle in fuzzy metric spaces.

The idea of fuzzy extended b-metric spaces was first established by Mehmood ^[9]. Metric-like spaces (MLSs), which is generalization of the idea of metric spaces, were introduced by Harandi ^[10]. The notions controlled metric type spaces and controlled metric-like spaces were first introduced by Mlaiki ^[11,12]. Recently, Sezen ^[13] generalized the concept of controlled type metric spaces and introduced the concept of Controlled fuzzy metric spaces (CFMS). Shukla and Abbas ^[14] reformulated the definition of MLSs and introduced the concept of fuzzy metric like spaces (FMLSs). Later, Javed et al. ^[15] obtained fixed point results in the context of fuzzy b-metric-like spaces. The approach of intuitionistic fuzzy metric spaces was tossed by Park ^[16] that deals with membership and non-membership functions.

Smarandache ^[17] established the concept of neutrosophic logic and the concept of neutrosophic set in 1998. The concept of neutrosophic sets have three functions, which are membership function, non-membership function and naturalness respectively. Thus, neutrosophic sets are the more general form of fuzzy sets ^[1] and intuitionistic fuzzy sets ^[18]. Hence, researchers in ^{[19,20,21,22]} have made studies on the concept of neutrosophic sets. Recently, Aslan et al. ^[23] obtained decision making applications for neutrosophic modeling of Talcott Parsons's Action and Kargın et al. ^[24] introduced decision making applications for law based on generalized set valued neutrosophic quadruple numbers. Şahin et al. ^[25] studied adequacy of online education using Hausdorff Measures based on neutrosophic quadruple sets. Also, Researchers in ^[26,27] studied types of metric space based on neutrosophic theory. Recently, Şahin and Kargın ^[28] obtained neutrosophic triplet metric spaces and neutrosophic triplet normed spaces. Kirişci and Simsek ^[29] established the concept of neutrosophic metric spaces (NMSs) that deals with membership, non-membership and naturalness functions. Şahin and Kargın ^[30] studied neutrosophic triplet v-generalized metric spaces and Şahin et al. ^[31] introduced the concept of neutrosophic triplet bipolar metric spaces. Simsek and Kirişci ^[32] derived various fixed point theorems for neutrosophic metric space. Şahin and Kargın ^[33] introduced the concept of neutrosophic triplet b–metric space. Şahin and Kargın ^[32] established neutrosophic triplet b-metric space and Sowndrarajan et al. ^[34] studied contradiction mapping results for neutrosophic metric space. Saleem et al. ^[35,36,37] proved various fixed point results for contraction mappings. Khater ^[38] did nice work on diverse solitary and Jacobian solutions in a continually laminated fluid with respect to shear flows through the Ostrovsky equation and Khater ^[39] worked on numerical simulations of Zakharov's (ZK) non-dimensional equation arising in Langmuir and ion-acoustic waves.

In this manuscript, we introduce the notion of controlled neutrosophic metric-like spaces as a generalization of a NMSs introduced in ^[29]. We replaced the following conditions of NMS

with

Also, we used a controlled function $\phi :{\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}\times {\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}\to \left[1, \infty \right)$ in the triangle inequalities of NMS. These both things generalized the defined notions existing in the literature. We also, derived several fixed-point results for contraction mappings in the context of new introduced space with non-trivial examples and graphical structure. At the end, we established an application to integral equation to show the validity of our main result.

In Section 2, we give basic definitions and basic properties for fuzzy metric spaces and neutrosophic metric spaces from ^{[4,10,12,13,14,15,16,29]}. In Section 3, we define controlled neutrosophic metric-like spaces and definitions of open ball, G-convergent sequence, G-Cauchy sequence, G-complete space and some examples for controlled neutrosophic metric-like spaces. Also, we give some fixed point (FP) results and illustrative examples. In Section 4, we give conclusions.

2.   Preliminaries

The following definitions are useful in the sequel.

Definition 2.1. ^[15] A binary operation ${*}$ : [0, 1]$\times$ [0, 1] $\to$ [0, 1] is called a continuous triangle norm (briefly CTN), if it meets the below assertions:

1) $𝛶*\varrho = \varrho *𝛶, \left(\forall \right)𝛶, \varrho \in \left[0, 1\right];$

2) $*$ is continuous;

3) $𝛶*1 = 𝛶, \left(\forall \right)𝛶\in \left[0, 1\right];$

4) $\left(𝛶*\varrho \right)*\varkappa = 𝛶*\left(\varrho *\varkappa \right), \left(\forall \right)𝛶, \varrho, \varkappa \in \left[0, 1\right];$

5) If $𝛶\le \varkappa$ and $\varrho \le d,$ with $𝛶, \varrho, \varkappa, d\in \left[0, 1\right],$ then $𝛶*\varrho \le \varkappa *d.$

Example 2.1. ^[4,15] Some fundamental examples of t-norms are: $𝛶*\varrho = 𝛶\cdot \varrho, 𝛶*\varrho = \mathrm{m}\mathrm{i}\mathrm{n}\{𝛶, \varrho \}$ and $𝛶*\varrho = \mathrm{max}\left\{𝛶+\varrho -1, 0\right\}.$

Definition 2.2. ^[15] A binary operation $○$ : [0, 1]$\times$ [0, 1] $\to$ [0, 1] is called a continuous triangle conorm (briefly CTCN) if it meets the below assertions:

1) $𝛶○\varrho = \varrho ○𝛶, \ \mathrm{f}\mathrm{o}\mathrm{r}\ \mathrm{a}\mathrm{l}\mathrm{l}\ 𝛶, \varrho \in \left[0, 1\right];$

2) $○$ is continuous;

3) $𝛶○0 = 0, \ \mathrm{f}\mathrm{o}\mathrm{r}\ \mathrm{a}\mathrm{l}\mathrm{l}\ 𝛶\in \left[0, 1\right];$

4) $\left(𝛶○\varrho \right)○\varkappa = 𝛶○\left(\varrho ○\varkappa \right), \ \mathrm{f}\mathrm{o}\mathrm{r}\ \mathrm{a}\mathrm{l}\mathrm{l}\ 𝛶, \varrho, \varkappa \in \left[0, 1\right];$

5) If $𝛶\le \varkappa$ and $\varrho \le d,$ with $𝛶, \varrho, \varkappa, d\in \left[0, 1\right],$ then $𝛶○\varrho \le \varkappa ○d.$

Example 2.2. ^[15] $𝛶○\varrho = \mathrm{max}\left\{𝛶, \varrho \right\}\ \mathrm{a}\mathrm{n}\mathrm{d}\ 𝛶○\varrho = \mathrm{min}\left\{𝛶+\varrho, 1\right\}$ are examples of CTCNs.

Definition 2.3. ^[10] Suppose ${\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}\ne \varnothing$ be a set. A mapping ${\mathit{\Theta}} :{\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}\times {\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}\to \left[1, \infty \right)$ is known as a metric-like, if it satisfying the following conditions:

1) ${\mathit{\Theta}} \left(\varpi, \nu \right) = 0\mathrm{i}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{i}\mathrm{e}\mathrm{s}\varpi = \nu;$

2) ${\mathit{\Theta}} \left(\varpi, \nu \right) = {\mathit{\Theta}} \left(\nu, \varpi \right);$

3) ${\mathit{\Theta}} \left(\varpi, \nu \right)\le {\mathit{\Theta}} \left(\varpi, \mathit{\boldsymbol{\lambda }}\right)+{\mathit{\Theta}} \left(\mathit{\boldsymbol{\lambda }}, \nu \right);$

for all $\varpi, \nu, \mathit{\boldsymbol{\lambda }}\in {\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}.$

Also, $\left({\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}, {\mathit{\Theta}} \right)$ is called a metric-like space.

Definition 2.4. ^[12] Let ${\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}\ne \varnothing,$ $\psi :{\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}\times {\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}\to \left[1, \infty \right)$ be a function and ${\mathit{\Theta}} :{\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}\times {\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}\to {\mathbb{R}}^{+}$. If the following properties are satisfied:

1) ${\mathit{\Theta}} \left(\varpi, \nu \right) = 0\mathrm{i}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{i}\mathrm{e}\mathrm{s}\varpi = \nu;$

2) ${\mathit{\Theta}} \left(\varpi, \nu \right) = {\mathit{\Theta}} \left(\nu, \varpi \right);$

3) ${\mathit{\Theta}} \left(\varpi, \nu \right)\le \psi (\left(\varpi, \mathit{\boldsymbol{\lambda }}\right){\mathit{\Theta}} \left(\varpi, \mathit{\boldsymbol{\lambda }}\right)+\psi \left(\mathit{\boldsymbol{\lambda }}, \varpi \right){\mathit{\Theta}} \left(\mathit{\boldsymbol{\lambda }}, \nu \right);$

for all $\varpi, \nu, \mathit{\boldsymbol{\lambda }}\in {\mathit{\boldsymbol{ \boldsymbol{\varXi} }}},$ then ${\mathit{\Theta}}$ is said to be a controlled metric-like and $\left({\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}, \mathrm{{\mathit{\Theta}} }\right)$ is known as a controlled metric-like space.

Definition 2.5. ^[13] Suppose ${\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}\ne \varnothing$, $h:{\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}\times {\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}\to \left[1, \infty \right)$ be a mapping, ∗ is a CTN and ${{\mathit{\Delta}} }_{h}$ is a FS on ${\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}\times {\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}\times (0, \infty)$. Four-tuple $\left({\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}, {{\mathit{\Delta}} }_{h}, *, h\right)$ is called CFMS if it meets the below assertions for all $\varpi, \nu, \mathit{\boldsymbol{\lambda }}\in {\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}\ \mathrm{a}\mathrm{n}\mathrm{d}\ {\mathit{\boldsymbol{\tau }}}, \mathit{\boldsymbol{ \boldsymbol{\varsigma } }} > 0$:

$h1)\ {{\mathit{\Delta}} }_{h}\left(\varpi, \nu, 0\right) = 0;$

$h2) \ {{\mathit{\Delta}} }_{h}\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right) = 1⟺\varpi = \nu;$

$h3) \ {{\mathit{\Delta}} }_{h}\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right) = {{\mathit{\Delta}} }_{h}\left(\nu, \varpi, {\mathit{\boldsymbol{\tau }}}\right);$

$h4)\ {{\mathit{\Delta}} }_{h}\left(\varpi, \mathit{\boldsymbol{\lambda }}, ({\mathit{\boldsymbol{\tau }}}+\mathit{\boldsymbol{ \boldsymbol{\varsigma } }})\right)\ge {{\mathit{\Delta}} }_{h}\left(\varpi, \nu, \frac{{\mathit{\boldsymbol{\tau }}}}{h\left(\varpi, \nu \right)}\right)*{{\mathit{\Delta}} }_{h}\left(\nu, \mathit{\boldsymbol{\lambda }}, \frac{\mathit{\boldsymbol{ \boldsymbol{\varsigma } }}}{h\left(\nu, \mathit{\boldsymbol{\lambda }}\right)}\right);$

$h5)$ ${{\mathit{\Delta}} }_{h}\left(\varpi, \nu, \cdot \right):\left(0, \infty \right)\to \left[\mathrm{0, 1}\right]$ is continuous.

Definition 2.6. ^[16] Let ${\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}\ne \varnothing$, $\text{*}$ be a CTN, P be a FSs on ${\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}\times {\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}\times \left(0, \infty \right)$. If triplet $({\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}, {\mathit{\Theta}}, \text{*)}$ verifies the following for all $\varpi, \nu, \mathit{\boldsymbol{\lambda }}\in {\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}\ \mathrm{a}\mathrm{n}\mathrm{d}\ \mathit{\boldsymbol{ \boldsymbol{\varsigma } }}, {\mathit{\boldsymbol{\tau }}} > 0:$

1) ${\mathit{\Theta}} \left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right) > 0;$

2) ${\mathit{\Theta}} \left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right) = 1⟺\varpi = \nu;$

3) ${\mathit{\Theta}} \left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right) = {\mathit{\Theta}} \left(\nu, \varpi, {\mathit{\boldsymbol{\tau }}}\right);$

4) ${\mathit{\Theta}} \left(\varpi, \mathit{\boldsymbol{\lambda }}, b\left({\mathit{\boldsymbol{\tau }}}+\mathit{\boldsymbol{ \boldsymbol{\varsigma } }}\right)\right)\ge {\mathit{\Theta}} \left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right)\text{*}{\mathit{\Theta}} \left(\nu, \mathit{\boldsymbol{\lambda }}, {\mathit{\boldsymbol{\tau }}}\right);$

5) ${\mathit{\Theta}} \left(\varpi, \nu, \cdot \right)$: $\left(0, \infty \right)$ $\to$ [0, 1] is a continuous mapping.

then $({\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}, {\mathit{\Theta}}, \text{*)}$ is called an FMLS.

Definition 2.7. ^[14] Let ${\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}$ be a universal set. For $\forall \varpi \in E, {0}^{-}\le {T}_{\mathcal{A}}\left(\varpi \right)+{I}_{\mathcal{A}}\left(\varpi \right)+{F}_{\mathcal{A}}\left(\varpi \right)\le {3}^{+}$, by the help of the functions ${T}_{\mathcal{A}}:E\to$]^– 0, ${1}^{+}$ [, ${I}_{\mathcal{A}}:E\to$]^– 0, ${1}^{+}$ [and ${F}_{\mathcal{A}}:E\to$]^– 0, ${1}^{+}$[a neutrosophic set $\mathcal{A}$ on ${\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}$ is defined by

Here, ${T}_{\mathcal{A}}\left(\varpi \right), {I}_{\mathcal{A}}\left(\varpi \right)$ and ${F}_{\mathcal{A}}\left(\varpi \right)$ are the degrees of trueness, indeterminacy and falsity of $\varpi \in {\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}$ respectively.

Definition 2.8. ^[29] Let $\Xi \ne \varnothing$, $*$ is a CTN, $○$ be a CTCN and

be a neutrosophic set such that $\mathcal{A}$: ${\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}\times {\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}\times \left(0, \infty \right)\to$ [0, 1]. If for all $\varpi, \nu, \mathit{\boldsymbol{\lambda }}\in {\mathit{\boldsymbol{ \boldsymbol{\varXi} }}},$ the below circumstances are satisfying:

1) 0 $\le { P}\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right)$ $\le$ 1, 0 $\le Q\left(\varpi, \nu, \tau \right)$ $\le$ 1 and 0 $\le S\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right)$ $\le$ 1,

2) ${ P}\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right)+Q\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right)+S\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right)\le 3;$

3) ${ P}\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right) > 0;$

4) ${ P}\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right) = 1\ \mathrm{f}\mathrm{o}\mathrm{r}\ \mathrm{a}\mathrm{l}\mathrm{l}\ {\mathit{\boldsymbol{\tau }}} > 0, \ \mathrm{i}\mathrm{f}\ \mathrm{a}\mathrm{n}\mathrm{d}\ \mathrm{o}\mathrm{n}\mathrm{l}\mathrm{y}\ \mathrm{i}\mathrm{f}\ \varpi = \nu;$

5) ${ P}\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right) = { P}\left(\nu, \varpi, {\mathit{\boldsymbol{\tau }}}\right);$

6) ${ P}\left(\varpi, \mathit{\boldsymbol{\lambda }}, {\mathit{\boldsymbol{\tau }}}+\mathit{\boldsymbol{ \boldsymbol{\varsigma } }}\right)\ge { P}\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right)*{ P}\left(\nu, \lambda, \varsigma \right);$

7) ${ P}\left(\varpi, \nu, \cdot \right):\left(0, \infty \right)\to \left[\mathrm{0, 1}\right]$ is continuous and $\underset{{\mathit{\boldsymbol{\tau }}}\to \infty }{\mathrm{lim}}{ P}\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right) = 1$;

8) $Q\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right) < 1;$

9) $Q\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right) = 0\ \mathrm{f}\mathrm{o}\mathrm{r}\ \mathrm{a}\mathrm{l}\mathrm{l}\ {\mathit{\boldsymbol{\tau }}} > 0, \ \mathrm{i}\mathrm{f}\ \mathrm{a}\mathrm{n}\mathrm{d}\ \mathrm{o}\mathrm{n}\mathrm{l}\mathrm{y}\ \mathrm{i}\mathrm{f}\ \varpi = \nu;$

10) $Q\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right) = Q\left(\nu, \varpi, {\mathit{\boldsymbol{\tau }}}\right);$

11) $Q\left(\varpi, \mathit{\boldsymbol{\lambda }}, {\mathit{\boldsymbol{\tau }}}+\mathit{\boldsymbol{ \boldsymbol{\varsigma } }}\right)\le Q\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right)○Q\left(\nu, \mathit{\boldsymbol{\lambda }}, \mathit{\boldsymbol{ \boldsymbol{\varsigma } }}\right);$

12) $Q\left(\varpi, \nu, \cdot \right):\left(0, \infty \right)\to \left[\mathrm{0, 1}\right]$ is continuous and $\underset{{\mathit{\boldsymbol{\tau }}}\to \infty }{\mathrm{lim}}Q\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right) = 0$;

13) $S\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right) < 1;$

14) $S\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right) = 0\ \mathrm{f}\mathrm{o}\mathrm{r}\ \mathrm{a}\mathrm{l}\mathrm{l}\ {\mathit{\boldsymbol{\tau }}} > 0, \ \mathrm{i}\mathrm{f}\ \mathrm{a}\mathrm{n}\mathrm{d}\ \mathrm{o}\mathrm{n}\mathrm{l}\mathrm{y}\ \mathrm{i}\mathrm{f}\ \varpi = \nu;$

15) $S\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right) = S\left(\nu, \varpi, {\mathit{\boldsymbol{\tau }}}\right);$

16) $S\left(\varpi, \mathit{\boldsymbol{\lambda }}, {\mathit{\boldsymbol{\tau }}}+\mathit{\boldsymbol{ \boldsymbol{\varsigma } }}\right)\le S\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right)○S\left(\nu, \mathit{\boldsymbol{\lambda }}, \mathit{\boldsymbol{ \boldsymbol{\varsigma } }}\right);$

17) $S\left(\varpi, \nu, \cdot \right):\left(0, \infty \right)\to \left[\mathrm{0, 1}\right]$ is continuous and $\underset{{\mathit{\boldsymbol{\tau }}}\to \infty }{\mathrm{lim}}S\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right) = 0;$

18) If ${\mathit{\boldsymbol{\tau }}}\le 0,$ then ${ P}\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right) = 0, Q\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right) = 1\ \mathrm{a}\mathrm{n}\mathrm{d}\ S\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right) = 1.$

then four-tuple $\left({\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}, \mathcal{A}, \mathcal{*}, ○\right)$ is called an NMS.

Where; ${ P}\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right)$ is degree of nearness, $Q\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right)$ is degree of neutralness and $S\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right)$ is degree of non-nearness.

3.   Main results

In this section, we introduce the notion of a CNMLS and prove some related FP results.

Definition 3.1. Suppose ${\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}\ne \varnothing$, assume a six tuple $({\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}, {{ P}}_{\phi }{, Q}_{\phi }{, R}_{\phi }\text{, *, ○)}$ where $\text{*}$ is a CTN, $\text{○}$ is a CTCN, $\phi :{\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}\times {\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}\to \left[1, \infty \right)$ be a function and ${{ P}}_{\phi }{, Q}_{\phi }{, R}_{\phi }$ are neutrosophic sets (NSs) on ${\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}\times {\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}\times \left(0, \infty \right)$. If $({\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}, {{ P}}_{\phi }{, Q}_{\phi }, {, R}_{\phi }\text{, *, ○)}$ meet the below circumstances for all $\varpi, \nu, \mathit{\boldsymbol{\lambda }}\in {\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}\ \mathrm{a}\mathrm{n}\mathrm{d}\ \mathit{\boldsymbol{ \boldsymbol{\varsigma } }}, {\mathit{\boldsymbol{\tau }}} > 0:$

1) ${{ P}}_{\phi }\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right)+{Q}_{\phi }\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right)+{R}_{\phi }\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right)\le 3,$

2) ${{ P}}_{\phi }\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right) > 0,$

3) ${{ P}}_{\phi }\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right) = 1\mathrm{i}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{i}\mathrm{e}\mathrm{s}\varpi = \nu,$

4) ${{ P}}_{\phi }\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right) = {{ P}}_{\phi }\left(\nu, \varpi, {\mathit{\boldsymbol{\tau }}}\right),$

5) ${{ P}}_{\phi }\left(\varpi, \mathit{\boldsymbol{\lambda }}, \left({\mathit{\boldsymbol{\tau }}}+\mathit{\boldsymbol{ \boldsymbol{\varsigma } }}\right)\right)\ge {{ P}}_{\phi }\left(\varpi, \nu, \frac{{\mathit{\boldsymbol{\tau }}}}{\phi \left(\varpi, \nu \right)}\right)\text{*}{{ P}}_{\phi }\left(\nu, \mathit{\boldsymbol{\lambda }}, \frac{\mathit{\boldsymbol{ \boldsymbol{\varsigma } }}}{\phi \left(\nu, \mathit{\boldsymbol{\lambda }}\right)}\right),$

6) ${{ P}}_{\phi }\left(\varpi, \nu, \cdot \right)$ is ND function of ${\mathbb{R}}^{+}$ and $\underset{{\mathit{\boldsymbol{\tau }}}\to \infty }{\mathrm{lim}}{{ P}}_{\phi }\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right) = 1,$

7) ${Q}_{\phi }\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right) < 1,$

8) ${Q}_{\phi }\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right) = 0$ $\mathrm{i}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{i}\mathrm{e}\mathrm{s}\varpi = \nu,$

9) ${Q}_{\phi }\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right) = {Q}_{\phi }\left(\nu, \varpi, {\mathit{\boldsymbol{\tau }}}\right),$

10) ${Q}_{\phi }\left(\varpi, \mathit{\boldsymbol{\lambda }}, \left({\mathit{\boldsymbol{\tau }}}+\mathit{\boldsymbol{ \boldsymbol{\varsigma } }}\right)\right)\le {Q}_{\phi }\left(\varpi, \nu, \frac{{\mathit{\boldsymbol{\tau }}}}{\phi \left(\varpi, \nu \right)}\right)○{Q}_{\phi }\left(\nu, \mathit{\boldsymbol{\lambda }}, \frac{\mathit{\boldsymbol{ \boldsymbol{\varsigma } }}}{\phi \left(\nu, \mathit{\boldsymbol{\lambda }}\right)}\right),$

11) ${Q}_{\phi }\left(\varpi, \nu, \cdot \right)$ is NI function of ${\mathbb{R}}^{+}$ and $\underset{{\mathit{\boldsymbol{\tau }}}\to \infty }{\mathrm{lim}}{Q}_{\phi }\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right) = 0,$

12) ${R}_{\phi }\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right) < 1,$

13) ${R}_{\phi }\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right) = 0$ $\mathrm{i}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{i}\mathrm{e}\mathrm{s}\varpi = \nu,$

14) ${R}_{\phi }\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right) = {R}_{\phi }\left(\nu, \varpi, {\mathit{\boldsymbol{\tau }}}\right),$

15) ${R}_{\phi }\left(\varpi, \mathit{\boldsymbol{\lambda }}, \left({\mathit{\boldsymbol{\tau }}}+\mathit{\boldsymbol{ \boldsymbol{\varsigma } }}\right)\right)\le {R}_{\phi }\left(\varpi, \nu, \frac{{\mathit{\boldsymbol{\tau }}}}{\phi \left(\varpi, \nu \right)}\right)○{R}_{\phi }\left(\nu, \mathit{\boldsymbol{\lambda }}, \frac{\mathit{\boldsymbol{ \boldsymbol{\varsigma } }}}{\phi \left(\nu, \mathit{\boldsymbol{\lambda }}\right)}\right),$

16) ${R}_{\phi }\left(\varpi, \nu, \cdot \right)$ is NI function of ${\mathbb{R}}^{+}$ and $\underset{{\mathit{\boldsymbol{\tau }}}\to \infty }{\mathrm{lim}}{R}_{\phi }\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right) = 0,$

17) If ${\mathit{\boldsymbol{\tau }}}\le 0$, then ${{ P}}_{\phi }\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right) = 0, {Q}_{\phi }\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right) = 1$ and ${R}_{\phi }\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right) = 1.$

Then five-tuple $\left({\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}, {\mathcal{A}}_{\phi }, \phi, *, ○\right)$ is called a CNMLS.

Where; ${{ P}}_{\phi }\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right)$ is degree of nearness, ${Q}_{\phi }\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right)$ is degree of neutralness and ${R}_{\phi }\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right)$ is degree of non-nearness.

Example 3.1. Let ${\mathit{\boldsymbol{ \boldsymbol{\varXi} }}} = \left(0, \infty \right), \ \mathrm{d}\mathrm{e}\mathrm{f}\mathrm{i}\mathrm{n}\mathrm{e}\ {{ P}}_{\phi }, {Q}_{\phi }, {R}_{\phi }:{\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}\times {\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}\times \left(0, \infty \right)\to \left[\mathrm{0, 1}\right]$ by

for all $\varpi, \nu \in {\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}\ \mathrm{a}\mathrm{n}\mathrm{d}\ {\mathit{\boldsymbol{\tau }}} > 0,$ define CTN $"\text{*"}$ by $𝛶*\varrho = 𝛶\cdot \varrho$ and CTCN $"\text{○"}$ by $𝛶○\varrho = \mathrm{max}\left\{𝛶, \varrho \right\}$ and define $"\phi "$ by

Then five-tuple $\left({\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}, {\mathcal{A}}_{\phi }, \phi, *, ○\right)$ is a CNMS.

Proof. $\left(\mathrm{i}\right)-\left(\mathrm{i}\mathrm{v}\right), \left(\mathrm{v}\mathrm{i}\right)-\left(\mathrm{i}\mathrm{x}\right), \left(\mathrm{i}\mathrm{x}\right)-\left(\mathrm{x}\mathrm{i}\mathrm{v}\right), \left(\mathrm{x}\mathrm{v}\mathrm{i}\right)\ \mathrm{a}\mathrm{n}\mathrm{d}\ \left(\mathrm{x}\mathrm{v}\mathrm{i}\mathrm{i}\right)$ are trivial, here we examine $\left(\mathrm{v}\right), \left(\mathrm{x}\right)\ \mathrm{a}\mathrm{n}\mathrm{d}\ \left(\mathrm{x}\mathrm{v}\right),$

Therefore,

That is,

Then,

Hence,

$({\rm{v}})$ is satisfied.

Therefore,

Then,

That is,

Hence,

$({\rm{x}})$ is satisfied.

It is easy to see that

That is,

Hence,

$({\rm{xv}})$ is satisfied.

Remark 3.1. If we let, $𝛶*\varrho = \mathrm{min}\left\{𝛶, \varrho \right\}$ and $𝛶○\varrho = \mathrm{max}\left\{𝛶, \varrho \right\},$ then above example is also a CNMLS.

Example 3.2. Suppose $\mathrm{\Xi } = \left(0, \infty \right), \ \mathrm{d}\mathrm{e}\mathrm{f}\mathrm{i}\mathrm{n}\mathrm{e}\ {{ P}}_{\phi }, {Q}_{\phi }, {R}_{\phi }:{\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}\times {\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}\times \left(0, \infty \right)\to \left[\mathrm{0, 1}\right]$ by

and

for all $\varpi, \nu \in {\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}\ \mathrm{a}\mathrm{n}\mathrm{d}\ {\mathit{\boldsymbol{\tau }}} > 0,$ define CTN $"\text{*"}$ by $𝛶*\varrho = 𝛶\cdot \varrho$ and CTCN $"\text{○"}$ by $𝛶○\varrho = \mathrm{max}\left\{𝛶, \varrho \right\}$ and define $"\phi "$ by

Then $\left({\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}, {{ P}}_{\phi }, {Q}_{\phi }, {R}_{\phi }, *, ○\right)$ be a CNMLS.

Remark 3.2. The above Examples 3.1 and 3.2 are not neutrosophic metric spaces.

Definition 3.2. Let $\left({\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}, {{ P}}_{\phi }, {Q}_{\phi }, {R}_{\phi }, *, ○\right)$ is a CNMLS, then we define an open ball $B\left(\varpi, r, {\mathit{\boldsymbol{\tau }}}\right)$ with centre $\varpi,$ radius $r, 0 < r < 1$ and ${\mathit{\boldsymbol{\tau }}} > 0$ as follows:

Definition 3.3. Let $\left({\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}, {{ P}}_{\phi }, {Q}_{\phi }, {R}_{\phi }, *, ○\right)$ be a CNMLS. Then

1) a sequence $\left\{{\varpi }_{n}\right\}$ in ${\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}$ is named to be G-Cauchy sequence (GCS) if and only if for all $q > 0\ \mathrm{a}\mathrm{n}\mathrm{d}\ {\mathit{\boldsymbol{\tau }}} > 0,$

2) a sequence $\left\{{\varpi }_{n}\right\}$ in ${\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}$ is named to be G-convergent (GC) to $\varpi$ in ${\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}$, if and only if for all ${\mathit{\boldsymbol{\tau }}} > 0,$

3) a CNMLS is named to be complete if each GCS is convergent i.e.,

Theorem 3.1. Suppose $\left({\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}, {{ P}}_{\phi }, {Q}_{\phi }, {R}_{\phi }, *, ○\right)$ be a G-complete CNMLS with $\phi :{\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}\times {\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}\to \left[1, \infty \right)$ and assume that

for all $\varpi, \nu \in {\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}$ and ${\mathit{\boldsymbol{\tau }}} > 0$. Suppose $\xi :{\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}\to {\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}$ be a mapping verifying

for all $\varpi, \nu \in {\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}$, $0 < £ < 1$ and ${\mathit{\boldsymbol{\tau }}} > 0.$ Also assume that for every $\varpi \in { Z},$

exists and finite. Then $\zeta$ has a unique fixed point in ${ Z}.$ Then $\xi$ has a unique FP.

Proof. Let ${\varpi }_{0}$ be an arbitrary point of ${\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}$ and define a sequence ${\varpi }_{n}$ by ${\varpi }_{n} = {\xi }^{n}{\varpi }_{0} = \xi {\varpi }_{n-1}$, $n\in \mathbb{N}.$ By utilizing $\left(2\right)$ for all ${\mathit{\boldsymbol{\tau }}} > 0,$ we get

and

We obtain

for any $q\in \mathbb{N}, \mathrm{u}\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{g}\left(\mathrm{v}\right), \left(\mathrm{x}\right)\ \mathrm{a}\mathrm{n}\mathrm{d}\ \left(\mathrm{x}\mathrm{v}\right)$, we deduce

and

Using (4) in the above inequalities, we deduce

and

Using (1), $\ \mathrm{f}\mathrm{o}\mathrm{r}\ n\to \infty,$ we deduce

i.e., $\left\{{\varpi }_{n}\right\}$ is a GCS. Therefore, $\left({\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}, {{ P}}_{\phi }, {Q}_{\phi }, {R}_{\phi }, *, ○\right)$ be a G-complete CNMS, there exists $\varpi \in {\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}.$

Now investigate that $\varpi$ is a FP of $\xi$, using $\left(\mathrm{v}\right), \left(\mathrm{x}\right), \left(\mathrm{x}\mathrm{v}\right)\ \mathrm{a}\mathrm{n}\mathrm{d}\ \left(1\right),$ we obtain

$\mathrm{a}\mathrm{s}\ n\to \infty,$ and

$\mathrm{a}\mathrm{s}\ n\to \infty.$ This implies that $\xi \varpi = \varpi,$ a FP. Now we show the uniqueness, suppose $\xi c = c$ for some $c\in {\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}$, then

and

by using $\left(\mathrm{i}\mathrm{i}\mathrm{i}\right), \left(\mathrm{v}\mathrm{i}\mathrm{i}\mathrm{i}\right)\ \mathrm{a}\mathrm{n}\mathrm{d}\ \left(\mathrm{x}\mathrm{i}\mathrm{i}\right), \varpi = c.$

Definition 3.4. Let $\left({\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}, {{ P}}_{\phi }, {Q}_{\phi }, {R}_{\phi }, *, ○\right)$ be a CNMLS. A map $\xi :{\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}\to {\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}$ is CNL-contraction if there exists $0 < £ < 1$, such that

and

for all $\varpi, \nu \in {\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}\ \mathrm{a}\mathrm{n}\mathrm{d}\ {\mathit{\boldsymbol{\tau }}} > 0.$

Theorem 3.2. Let $\left({\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}, {{ P}}_{\phi }, {Q}_{\phi }, {R}_{\phi }, *, ○\right)$ be a G-complete CNMLS with $\phi :{\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}\times {\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}\to \left[1, \infty \right)$ and suppose that

for all $\varpi, \nu \in {\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}$ and ${\mathit{\boldsymbol{\tau }}} > 0$. Let $\xi :{\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}\to {\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}$ be a CN-contraction. Further, assume that for an arbitrary ${\varpi }_{0}\in {\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}, \ \mathrm{a}\mathrm{n}\mathrm{d}\ n, q\in \mathbb{N},$ where ${\varpi }_{n} = {\xi }^{n}{\varpi }_{0} = \xi {\varpi }_{n-1}$ also $\underset{n\to \infty }{\mathrm{lim}}\phi \left({\varpi }_{n}, \nu \right)$ and $\underset{n\to \infty }{\mathrm{lim}}\phi \left(\nu, {\varpi }_{n}\right)$ exists and finite. Then $\xi$ has a unique FP.

Proof. Suppose ${\varpi }_{0}$ be an arbitrary point of ${\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}$ and define a sequence ${\varpi }_{n}$ by ${\varpi }_{n} = {\xi }^{n}{\varpi }_{0} = \xi {\varpi }_{n-1}$, $n\in \mathbb{N}.$ By utilizing $\left(5\right)$ and $\left(6\right)$ for all ${\mathit{\boldsymbol{\tau }}} > 0,$ $n > q,$ we get

Continuing in this way, we get

We obtain

and

for any $q\in \mathbb{N}, \mathrm{u}\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{g}\left(\mathrm{v}\right), \left(\mathrm{x}\right)\ \mathrm{a}\mathrm{n}\mathrm{d}\ \left(\mathrm{x}\mathrm{v}\right)$, we deduce

and

and

Therefore,

i.e., $\left\{{\varpi }_{n}\right\}$ is a GCS. Therefore, $\left({\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}, {{ P}}_{\phi }, {Q}_{\phi }, {R}_{\phi }, *, ○\right)$ be a G-complete CNMS, there exists $\varpi \in {\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}.$

Now, we show that $\varpi$ is a FP of $\xi$, utilizing $\left(\mathrm{v}\right), \left(\mathrm{x}\right)\ \mathrm{a}\mathrm{n}\mathrm{d}\ \left(\mathrm{x}\mathrm{v}\right),$ we get

Using above inequality, we obtain

$\mathrm{a}\mathrm{s}\ n\to \infty$, and

Hence, $\xi \varpi = \varpi,$ a FP.

Uniqueness: Assume $\xi c = c$ for some $c\in \Xi$, then

a contradiction, and

are contradictions.

Therefore, we must have ${{ P}}_{\phi }\left(\varpi, c, {\mathit{\boldsymbol{\tau }}}\right) = 1, {Q}_{\phi }\left(\varpi, c, {\mathit{\boldsymbol{\tau }}}\right) = 0\ \mathrm{a}\mathrm{n}\mathrm{d}\ {R}_{\phi }\left(\varpi, c, {\mathit{\boldsymbol{\tau }}}\right) = 0$, that is $\varpi = c.$

Example 3.3. Suppose ${\mathit{\boldsymbol{ \boldsymbol{\varXi} }}} = \left[\mathrm{0, 1}\right]$. Define 𝜙 by

Also, define

and

with $𝛶*\varrho = 𝛶.\varrho \ \mathrm{a}\mathrm{n}\mathrm{d}\ 𝛶○\varrho = \mathrm{max}\left\{𝛶, \varrho \right\}.$ Then $\left({\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}, {{ P}}_{\phi }, {Q}_{\phi }, {R}_{\phi }, *, ○\right)$ is a G-complete CNMLS. Observe that $\underset{{\mathit{\boldsymbol{\tau }}}\to \infty }{\mathrm{lim}}{{ P}}_{\phi }\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right) = 1, \underset{{\mathit{\boldsymbol{\tau }}}\to \infty }{\mathrm{lim}}{Q}_{\phi }\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right) = 0\ \mathrm{a}\mathrm{n}\mathrm{d}\ \underset{{\mathit{\boldsymbol{\tau }}}\to \infty }{\mathrm{lim}}{R}_{\phi }\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right) = 0,$ satisfied. Define $\xi :{\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}\to {\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}$ by

Then,

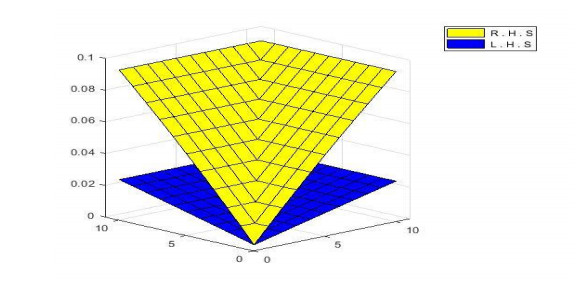
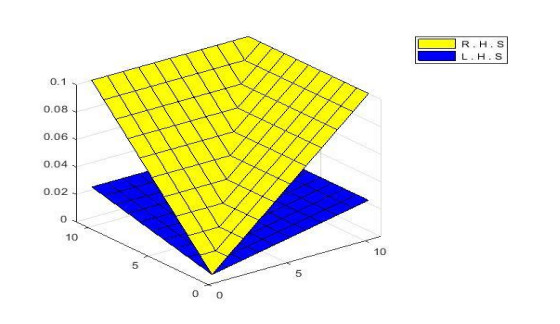
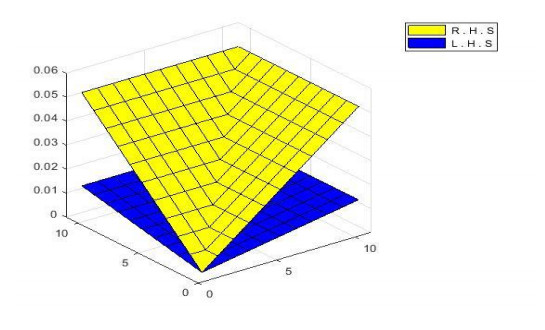
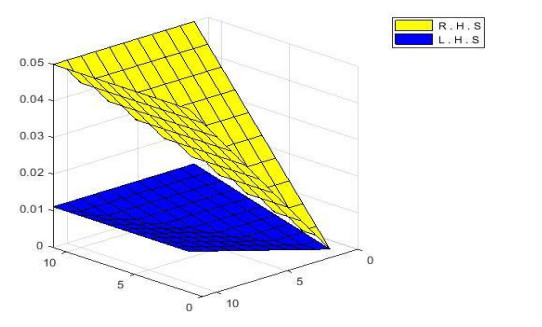
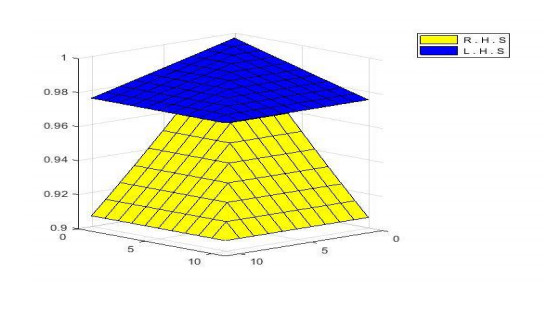
are satisfied for $£ \in \left[\frac{1}{2}, 1\right)$, as we can see that Figure 1 shows that ${{ P}}_{\phi }\left(\xi \varpi, \xi \nu, £ {\mathit{\boldsymbol{\tau }}}\right)\ge {{ P}}_{\phi }\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right),$ Figure 2 shows that ${Q}_{\phi }\left(\xi \varpi, \xi \nu, £ {\mathit{\boldsymbol{\tau }}}\right)\le {Q}_{\phi }\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right)$ and Figure 3 shows that ${R}_{\phi }\left(\xi \varpi, \xi \nu, £ {\mathit{\boldsymbol{\tau }}}\right)\le {R}_{\phi }\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right).$

Also,

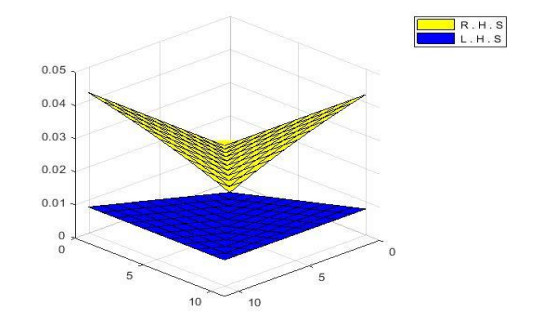
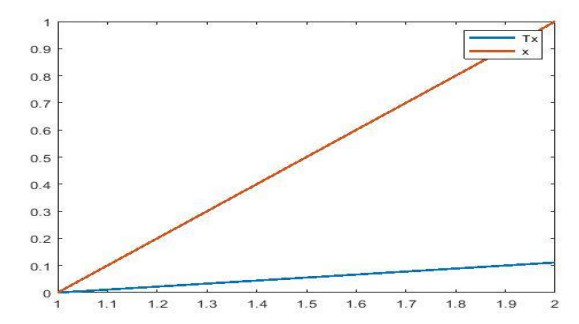
are satisfied for $£ \in \left[\frac{1}{2}, 1\right),$ as we can see that Figure 4 shows that $\frac{1}{{{ P}}_{\phi }\left(\xi \varpi, \xi \nu, {\mathit{\boldsymbol{\tau }}}\right)}-1\le £ \left[\frac{1}{{{ P}}_{\phi }\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right)}-1\right],$ Figure 5 shows that ${Q}_{\phi }\left(\xi \varpi, \xi \nu, {\mathit{\boldsymbol{\tau }}}\right)\le £ {Q}_{\phi }\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right)$ and Figure 6 shows that ${R}_{\phi }\left(\xi \varpi, \xi \nu, {\mathit{\boldsymbol{\tau }}}\right)\le £ {R}_{\phi }\left(\varpi, \nu, {\mathit{\boldsymbol{\tau }}}\right).$

We can easily see that $\underset{n\to \infty }{\mathrm{lim}}\phi \left({\varpi }_{n}, \nu \right)$ and $\underset{n\to \infty }{\mathrm{lim}}\phi \left(\nu, {\varpi }_{n}\right)$ exists and finite. Observe that all circumstances of Theorems 3.1 and 3.2 are fulfilled, and 0 is a unique FP of $\xi$ as we can see in the Figure 7.

4.   Application

Suppose $\Xi = C(\left[{\rm{c}}, а\right], \mathbb{ }\mathbb{ }\mathbb{ }\mathbb{ }\mathbb{R})$ be the set of real valued continuous functions defined on $[\mathbb{{\rm{c}}}, \mathbb{ }\mathbb{а}]$.

Suppose the integral equation:

where $\delta > 0, \Lambda \left(\upsilon \right)$ is a function of $\upsilon :\upsilon \in \left[{\rm{c}}, а\right]$ and $Л:C\left(\left[{\rm{c}}, а\right]\times \mathbb{ }\mathbb{ }\mathbb{ }\mathbb{ }\mathbb{ }\mathbb{ }\mathbb{R}\right)\to {\mathbb{R}}^{+}.$ Define $P\ \mathrm{a}\mathrm{n}\mathrm{d}\ Q$ by

and

with continuous t-norm and continuous t-conorm define by $ȇ*ā = ȇ.ā\ \mathrm{a}\mathrm{n}\mathrm{d}\ ȇ○ā = \mathrm{max}\left\{ȇ, ā\right\}.$ Define $\xi, \mathfrak{Г}:\mathfrak{C}\times \mathfrak{C}\to \left[1, \infty \right)$ as

Then $({\mathit{\boldsymbol{ \boldsymbol{\varXi} }}}, \mathit{\boldsymbol{P}}, \mathit{\boldsymbol{Q}}, \mathit{\boldsymbol{R}}, {*}, ○)$ be a complete controlled neutrosophic metric-like space.

Suppose that

$\left|\mathrm{Л}\left(\tau, \upsilon \right)\varpi \left(\tau \right)-\mathrm{Л}\left(\tau, \upsilon \right)\nu \left(\tau \right)\right|\le \left|\varpi \left(\tau \right)-\nu \left(\tau \right)\right|$ for $\varpi, \nu \in \mathfrak{C}$, $\theta \in (0, \ 1)$ and $\forall \tau, \upsilon \in [\mathrm{{\rm{c}}}, \ \mathrm{а}]$. Also, let ${\mathrm{Л}\left(\tau, \upsilon \right)\left(\delta {\int }_{\mathrm{{\rm{c}}}}^{\mathrm{а}}d\upsilon \right)}^{2}\le \theta < 1.$ Then integral Eq (11) has a unique solution.

Proof. Define $\xi :\mathfrak{C}\to \mathfrak{C}$ by

Now for all $\varpi, \nu \in \mathfrak{C}$, we deduce

and

As a result, all of the conditions of Theorem 3.1 are satisfied and operator $\xi$ has a unique fixed point. This indicates that an integral Eq (11) has a unique solution.

5.   Conclusions

In this manuscript, we introduced the notion of controlled neutrosophic metric-like spaces as a generalization of a neutrosophic metric space and established some new type of fixed point theorems for contraction mappings in this new setting. Moreover, we provided the non-trivial examples with graphical analysis to demonstrate the viability of the proposed methods. Also, our structure is more general than the controlled fuzzy metric space and fuzzy metric like space and neutrosophic metric space. Also, our results and notions expand and generalize a number of previously published results.

Conflict of interest

The authors declare no conflict of interest.