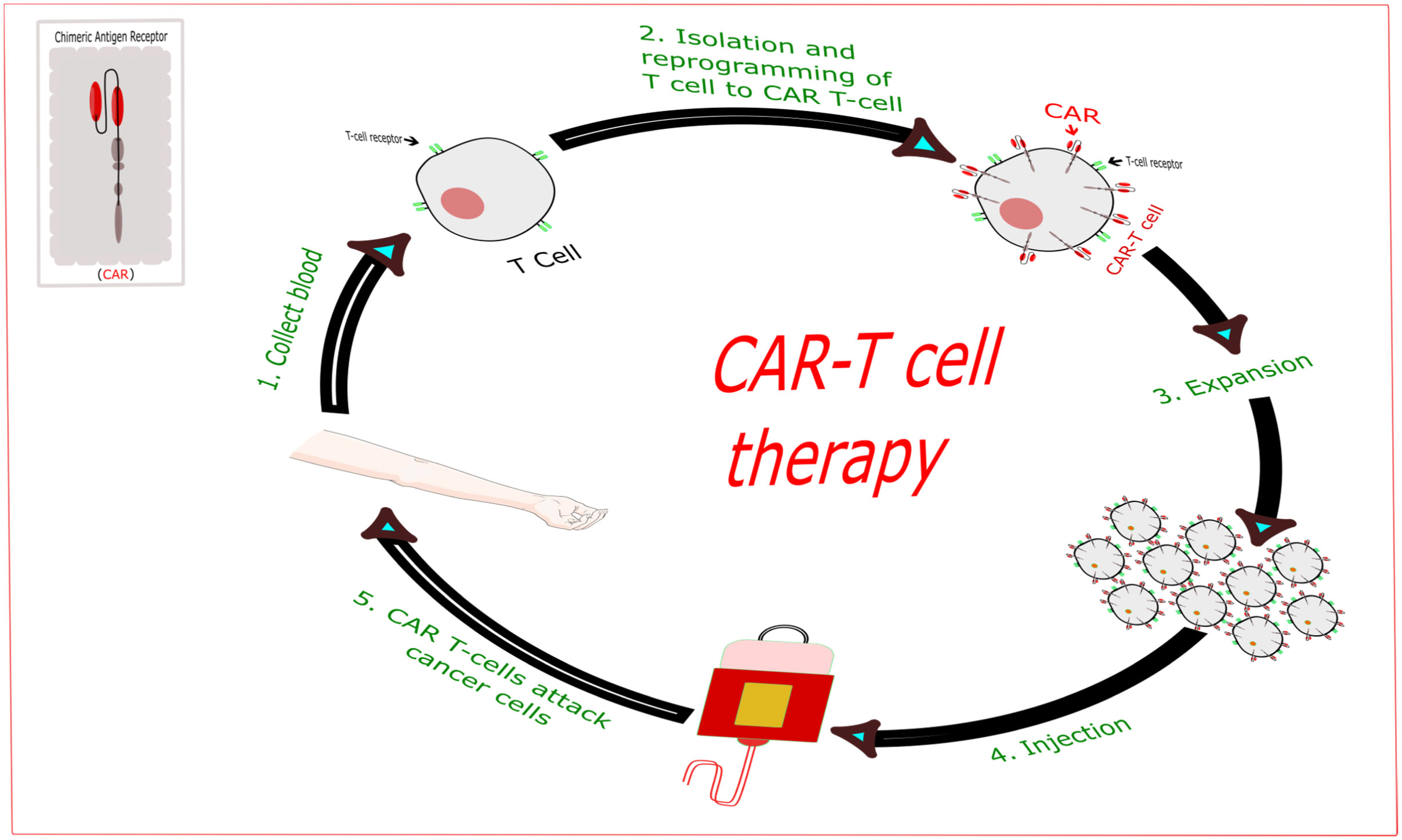
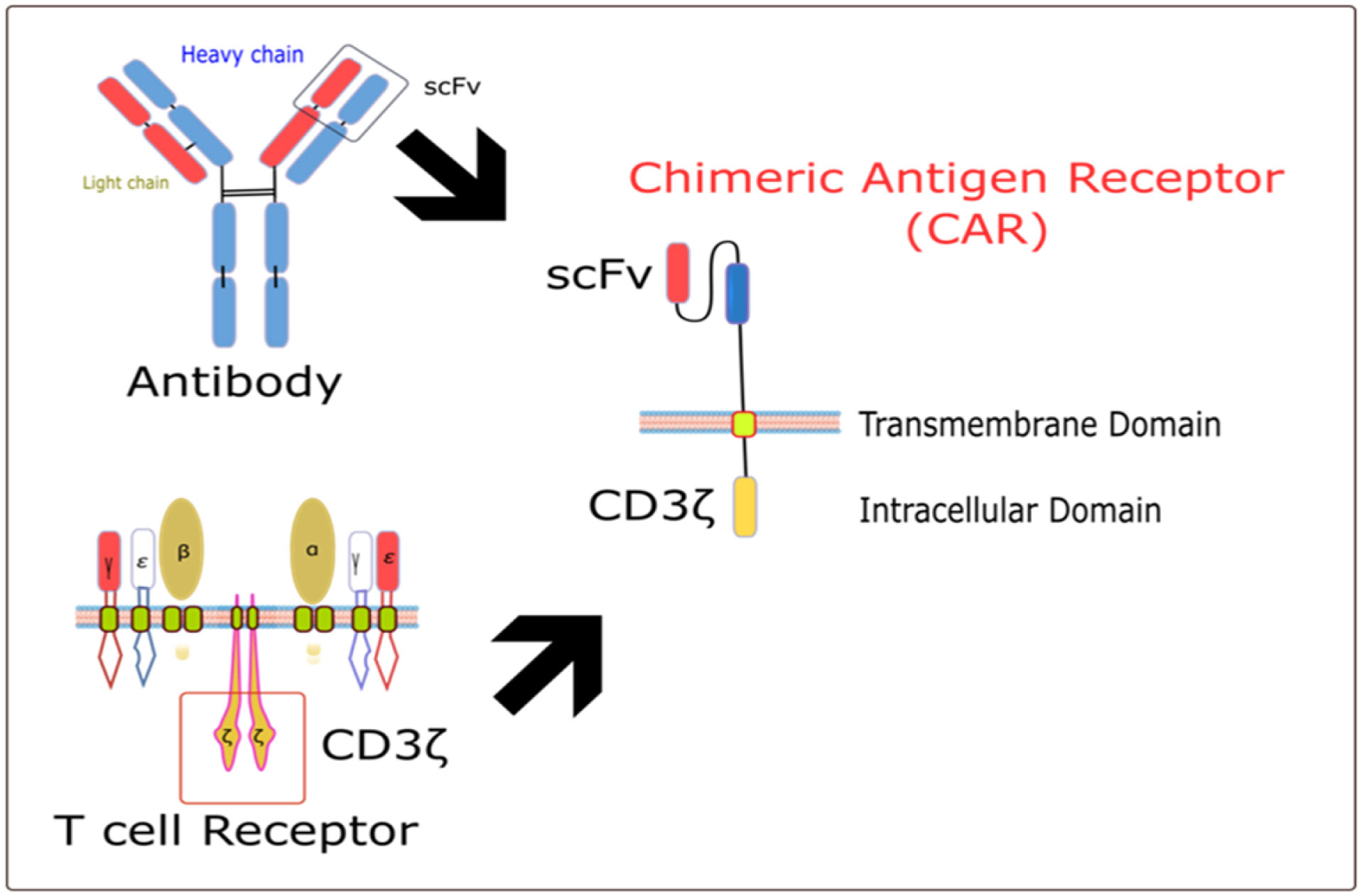
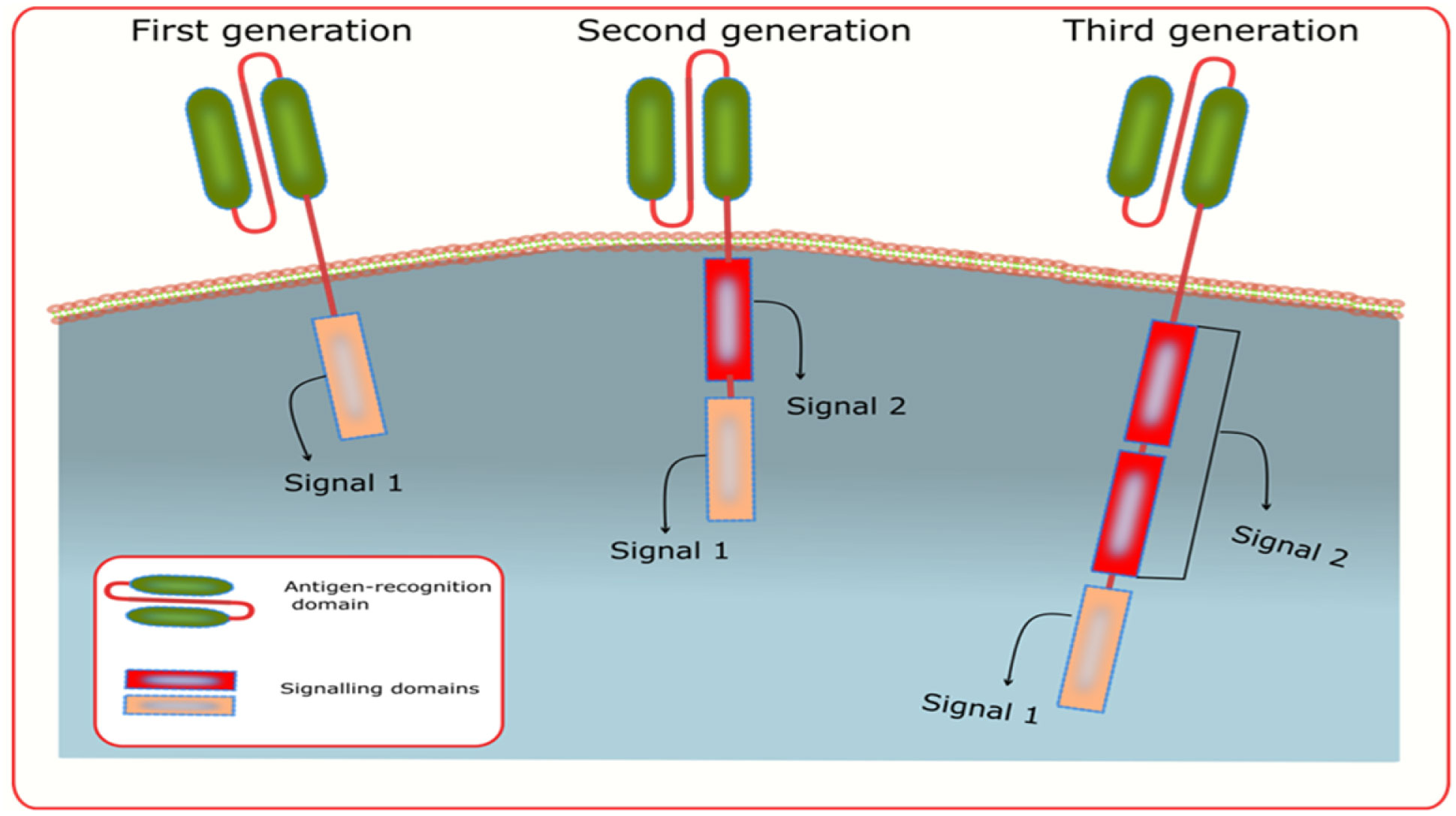
Cancer therapy and diagnosis have long been challenges for humans. Despite accumulated knowledge and information, there are many complications and difficulties with cancer therapy and diagnosis. The challenges of cancer treatment are modified according to the new forms that have been discovered by researchers. Each stage of development has involved new techniques for cancer therapy, culminating in the modern immunotherapy approach using chimeric antigen receptor (CAR) cytotoxic T lymphocytes. This strategy is an example of the latest version of cancer cell therapy. Chimeric antigen receptor T-cell therapy drew interest soon after its implementation by researchers as a new strategy to control various types of cancer cells, and it is considered a living drug in the body that detects and destroys cancer cells in a long-term manner, with CAR T-cells remaining as memory cells. CAR T-cell therapy has shown remarkable effects against both primary acute lymphoblastic leukemia (ALL) and relapsed ALL, with a high remission rate observed in adults and children (approximately 90%). Although the use of CAR T-cell therapy for solid tumors has encountered obstacles associated with the microenvironment and immunosuppression, researchers are poised to improve effective CAR T-cell therapy for solid tumors. In this mini review, we describe some attempts that have applied CAR T-cells from the past and present; in addition, it contains many aspects of new anticancer strategies featuring CAR T-cells, especially CAR T-cell killing mechanisms.
1.
Introduction
Stagnation point flow reveals in practically all flow branches of engineering and science. Free stagnation point or a line exists interior of the fluid domain while in some situations flow is stagnated by a solid wall.
Hiemenz [1] demonstrated that Navier-Stokes equations are able to describe the stagnation point flow. Plane stagnation point flow which is called the Hiemenz flow, firstly discussed by Hiemenz as follows:
with the boundaries:
Gersten et al. [2] generalized these results to the stagnation point flow in three dimensions. Homotopy analysis method is used by Liao [3] to the 2D laminar viscous flow over a semi-infinite plate. Existence and uniqueness consequences for nonlinear third-order ODEs appeared in the stagnation point flow of a hydromagnetic fluid are discussed by Van Gorder et al. [4]. The flow characteristics in an electrically conducting second grade fluid pervaded by a uniform magnetic field over a stretching sheet is discussed by Vajravelu et al. [5]. Steady 2D stagnation-point flow of an incompressible viscous electrically conducting fluid over a flat deformable sheet is studied by Mahapatra et al. [6]. Van Gorder et al. [7] established the existence and uniqueness consequences for fourth-order ODEs over the semi-infinite interval, arising in the hydromagnetic stagnation point flow of a second grade fluid over a stretching sheet.
The concept of Lie groups plays an significant rule in establishing some intense numerical approaches to integrate ODEs, which conserve the geometrical properties. Preserving the geometry construction under discretization, is essential in the improvement of a qualitatively true performance in the minimization of approximation errors. So, along with the geometric structure and invariance of the ODEs, novel approaches may be invented, which are more stable and effective than the common approximation techniques.
A novel geometric method based on GL(6,R) is introduced for the magneto-hemodynamic flow in a semi-porous channel in [8]. Moreover, in [9], a nonlinear heat transfer equation is considered by SL(2,R). Order of differential equations and different initial or boundary conditions conclude different geometric algorithms for solving differential equations. That is, numerical algorithms based on e.g. GL(6,R) and GL(4,R) is completely different. Combination of radial basis functions with GPS are discussed in [10]. Some other recent papers of geometric numerical approach, Lie group analysis, and exact solution can be found in [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33].
This paper is organized as follows. In the further section, we will touch only a few aspects of the Mathematical formulation for the hydromagnetic stagnation point flow. In Section 3, we derive an interesting algorithm to integrate the underlying nonlinear equation. Section 4 deals with the numerical results. Final remarks are provided in the conclusion section.
2.
Mathematical formulation
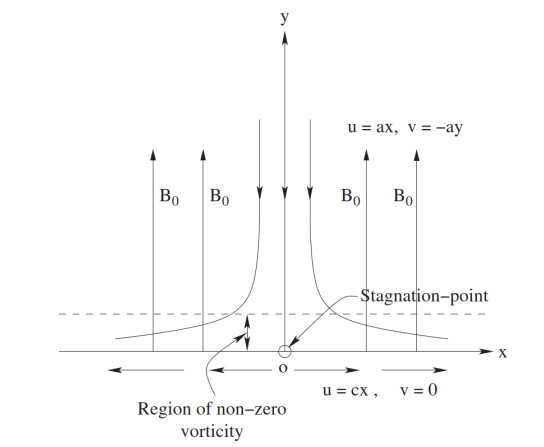
Let us investigate the 2D steady stagnation-point flow of an electrically conducting fluid in the existence of a uniform transverse magnetic field towards a flat surface coinciding with the plane y=0, the flow being enclosed to the region y>0. Two equivalent and converse forces are considered in direction of the x−axis such that the wall is stretched keeping the origin fixed, and a uniform magnetic field B0 is forced along the y−axis (Figure 1).
In the usual notation, the MHD equations for steady 2D stagnation-point flow in the boundary layer along the stretching surface are [6,34]:
where ρ, σ, B0 are density, electrical conductivity and magnetic field respectively. Also, (u,v) are the fluid velocity components toward x and y. U(x) stands for the stagnation-point velocity in the inviscid free stream.
For this problem, the boundaries are
where c,a∈R+. Eqs (2.1) and (2.2) together with the conditions (2.3) and (2.4) have the similarities of the form
Substituting (2.5) into (2.2), concludes
where M=B20(σρc), C=ac and √M is the Hartmann number.
With the use of the transformation (2.5), the boundary conditions (2.3) and (2.4) read f(0)=0, f′(0)=1, f′(∞)=C.
The self-similar solutions will normally be made to meet Eq (2.6) with additional nonlinear terms
in the governing differential equation, where K≥0 is the viscoelastic parameter. By the additional condition f″(∞)=0, we investigate the following fourth order differential equation:
with
where M=σ0B20/ρB≥0 is the magnetic parameter, K=ωB/ν≥0 is the viscoelastic parameter, s≥0, C is the parameter due to the stagnation point flow, and χ is the stretching of the sheet.
3.
An GL(4,R) Lie group method
There is no loss of generality in assuming
This supposition is possible. Because in the other case, we can obtain a constant γ>0 such that
where
and c1-c3 are integration constants which we can assume all of them to be positive. Also, from this assumption we clearly have |F(ξ)|>0. Using these transformations, Eq (2.8) converts into:
subject to
Now, we are willing to erect GL(4,R) Lie group method. Suppose y1(ξ)=f(ξ), y2(ξ)=f′(ξ), y3(ξ)=f″(ξ) and y4(ξ)=f‴(ξ). Then equivalent system of (2.8) leaves
with boundary conditions:
Equivalent system of (3.7) is:
where
which is well-defined because of supposition (3.1). System (3.9), in spite of its nonlinearity, admits a Lie-group of GL(4,R) and we have:
where
Now, we are able to erect a GPS to consider Eq (3.9) as follows:
where Yn=Y|ξ=ξn. Integrating (3.9) by (3.13) along with initial condition Y(0)=Y0, results the demanded value Y(ξ). Suppose the GPS method:
where
and Δξ=1/N is the GPS iteration stepsize. In fact, this approach approximates the solution of
Then
computes Y(ξ)|ξ=η∞, * at ξ=η∞. From the closure property of the Lie groups, G:=GN(Δξ)⋯G1(Δξ)∈GL(4,R). Therefore, we can develop a one-step transformation from Y0 to Yf as:
* By using the truncation rule for the differential equations over the infinite or semi-infinite intervals, we set ξf=η∞ as the final value of interval [0,∞).
From Eqs (3.11) and (3.18) we obtain
Along with (3.8) and generalized mid-point rule, let us assume
where r∈[0,1] has to be determined. Therefore Eq (3.19) may be rewritten as:
where
In this letter, y01=s, y02=χ, yf2=C, yf3=0 are known and yf1, y03, y04, yf4 are unknown values of the current problem, which after determining y03 and y04, the B.V.P. (2.8) converts to an I.V.P.
For the fixed A∈gl(4,R), † we have
† gl(4,R) is the Lie algebra associated with the Lie group GL(4,R).
where
Therefore, each of this Lie group elements may be erected by a single parameter G(r), with r∈[0,1].
From (3.18) and (3.22) we have:
Thus, for a given r, we may get the values yf1, y03, y04 and yf4 by the further explained process.
Imposing the initial guesses of y03, y04, yf1 and yf4, and the given boundary values of y01=s, y02=χ, yf2=C and y03=0, with a specified r∈[0,1], and from
we may produce new values of yf1, y03, y04 and yf4. If these values satisfy the convergence criterion:
then iterations stop.
For a fixed value of r, we are able to compute y03 and y04 from Eq (3.25) and then approximately integrate Eq (3.7) by GPS from 0 to η∞, and compare the end value of yf2 and yf3 with the exact ones y2(η∞)=C and y3(η∞)=0 respectively. That is, we have to find the minimum value of
In the appendix, we give a brief algorithm of our proposed method to find the initial values of problem.
In the non-geometric numerical methods, investigation of the method stability is an important task which guarantees the validity of techniques. Without considering the convergence and error analysis, results may lead to solutions with no physical meaning or high-level of errors. This issue may arise from that, we do not know information about the geometric structure of original problem. However, in this paper we introduce a GL(4,R) method which conserve the geometrical properties of problem. Preserving the geometry construction under discretization, is essential in the improvement of a qualitatively true performance in the minimization of approximation errors.
4.
Numerical results
We emphasize that the stepping approach developed for integrating the IVP needs the initial values f1(0)=f(0), f2(0)=f′(0), f3(0)=f″(0) and f4(0)=f‴(0) for the fourth-order ODEs. Both of the last initial values in Eq (2.8) are unknown. Therefore, approximating f″(0) and f‴(0) converts Eq (2.8) into an IVP. It is worth pointing out that every IVP can be integrated by GPS.
Indeed, our proposed method in this paper is split into two parts. In the first part, initial conditions of the problem are obtain by the GL(4,R) method. Our method is implemented by the convergence criterion of (3.26) with ϵ=10−8. For this value of convergence criterion, only four or five steps of algorithm, mentioned in the Appendix, are needed. So, very fast convergence occur in this part of the proposed method Second part of this technique starts when we obtain the initial values of BVP from the first part. Second part which is nominated as the GPS, is an explicit iteration method which is well-known as the weighted Euler method. Convergence of this part can be guaranteed from the geometric structure of method.
The results of this paper were announced with η∞=7 and Δξ=0.01 for the GPS procedure. There is no loss of generality in assuming y03=y04=yf1=yf4=1 as initial guesses.
Some mis-matching errors with various M, C, s, K and χ are plotted in Figure 2(a)-(d). Desired values of r=0.5314, r=0.4993, r=0.814 and r=0.9546 are noticeable from these figures.
In Figure 3(a)-(d), we plot the profiles of f(ξ), f′(ξ), f″(ξ) and f‴(ξ) for various values of magnetic parameter (the Hartmann number) M (√M), and fixed values of the other parameters. It is observable that the profiles of f(ξ) and f′(ξ) decrease, when the magnetic parameter increases, while the reverse situation occur for f″(ξ) and it decrease more rapidly toward zero as ξ tends to η∞.
Figure 4(a)-(d) show the absorbing dependence of the solutions on the various viscoelastic parameter K. Uniform decrease in the magnitudes of f(ξ) and f′(ξ) are observable for increasing values in K. Inverse results occur for the profiles of f(ξ) and f′(ξ) when χ is greater than the boundary value C; see Figure 5(a)-(d). Notice that the plots are in a good agreement with the boundary conditions f′(η∞)=C and f″(η∞)=0.
It may be seen from Figure 6(a)-(d) that for fixed values of K,s,M and χ, the transverse velocity increases with increase in the stagnation point flow C. Notice the behavior of solutions in the profiles of f(ξ), f′(ξ) and f″(ξ) for different cases χ<C and χ>C which are against to the profile of f‴(ξ).
From the Figure 7(a)-(d), an increase in the stretching sheet parameter χ results in a increase in the profiles of f(ξ), f′(ξ) and f‴(ξ). Also, an increase in χ consequences in a decrease in the magnitude of the shear stress at the wall, f″(0).
The double mesh principle is applied to estimate the error
where N is the number of GPS iterations. Residual errors of the present method applied for Eq (2.8) with N=10000 are plotted in Figure 8 for various parameters of equation. This figure shows that our method is reliable for current types of equations. Besides, obtained solutions and results are in good agreement with the results of [7].
5.
Conclusions
In this paper, a novel iterative technique based on the Lie group of GL(4,R), as the first time, is proposed to solve the hydromagnetic stagnation point flow of a second grade fluid over a stretching sheet. Structures of the Lie group elements in GL(4,R) and corresponding Lie algebra elements in gl(4,R) are completely innovative for the underlying problem in this paper. Against the non-geometric numerical techniques, the proposed method uses the geometric structure of original problem and this guarantees that obtained results are reliable and the proposed method avoid the ghost solutions. Effects of equation parameters are graphically considered. Point-wise errors for various parameters show the power and effectiveness of proposed method.
Conflict of interest
No potential competing interest was reported by the authors.
Appendix
Algorithm of finding initial values of the problem:
(i) Take arbitrary initial guesses for y03, y04, yf1 and yf4.
(ii) Specify an r∈[0,1] and a small ϵ∈R+.
(iii) Calculate G(r) and ω from (3.22) and (3.23), respectively.
(iv) Compute updated values of y03, y04, yf1 and yf4 from (3.25).
(v) If convergence criterion (3.26) is valid for given ϵ, then y03 and y04 are desired initial values of the problem. Otherwise, go to Step (ii).









 DownLoad:
DownLoad: