1. Introduction

Big Data brings many problems to the general attention of physicists, mathematicians, social scientists, biologists, etc. [18,1]. A first attempt to categorize them into major groups runs into the problem of choosing a criterion of classification among many available ones. Differentiation of Big Data operates through their types (complex data structures) and the relationships that can be established between them (complex data patterns). Knowing Big Data distributional laws might simplify the task of understanding the essential characteristics (sufficient statistics) of their complexities through newly designed sampling techniques, fast data mining methods and efficient algorithmic processing.

---

1.1. Data dominium and statistical complexity

Let us consider three features or attributes of data complexity destined to change due to the effect of size or bigness: dimensionality, heterogeneity and uncertainty (Figure 1). Let us also assume that Big Data uncertainty requires almost axiomatic solutions (say, cross-validation), ranging across a myriad of statistical model selection methods suitably adapted. In general, uncertainty can be associated to entropy and considering a fluctuation theorem for networks, changes in entropy reflect positive changes in resilience against perturbations [6]. In particular, bigger average shortest path lengths in resilient networks mitigate node removal effects, inducing slower network disintegration.

Among the challenges, the one coming from imbalanced data classification and incompleteness, is inherently data dependent. In general, given data with a stratified structure, a lack of balance exists when the classes are not equally represented in the data, which might reflect the sparseness of features rather than the class definition itself [5]. Thus, a class of interest could be the one addressing treated patients, and presenting few instances compared to a more largely represented class of control patients. Moving to a larger dataset is the most immediate solution towards the goal of rebalancing the classes. Sampling is also a strategy that can augment the poorer class (over-sampling) or diminish the richer one (under-sampling). The common aspect is ending up in both scenarios with synthetic samples. Importing a penalization strategy into the model is another possible route aimed to discount classification mistakes. By bringing penalties into the model, the latter can rebalance the over- and under-represented classes.

---

1.2.

Interestingly, with Big Data one turns from the usual curse of dimensionality (large $p$, small $n$, with $p$ number of measurements, and $n$ the number of samples) also to a curse of heterogeneity (Figure 1) [28]. Here, a data generation mixture processing could be conceivable as an underlying Big Data mechanism through which the emergence of sub-populations may be observed [9,16]. Simply speaking, the data mixture would mirror a variety of heterogeneous groups, say $k$, and considering $y$ as our response, $X$ as our covariate vector, $\Theta$ as a parameter vector, and $d(.)$ as density functions, a possible Big Data Generating Process might be associated with the mixture probability density function D as follows:

$ D_{\pi}(y, X, \Theta) = \pi_{1} d_{1}(y, X, \Theta_{1}) + \pi_{2}d_{2}(y, X, \Theta_{2}) + \ldots + \pi_{k} d_{k}(y, X, \Theta_{k}) $

(1)

Several interdependent influences need to be considered for model selection purposes in an attempt to improve analyses and inference: additional dimensions or further stratifications in data are expected to weaken the ratio between systematic versus erratic systems characterization. Nevertheless, major problems are most likely coming from:

● Mismatch between dimensions (typically, sample size and characterizing variables), requiring regularized solutions;

● Existence of inherent but latent stratifications, inducing clusters or communities;

● Influence of stochastic components (only in part observable)

Superior precision of estimates and stabilization of variability are expected with Big Data, but the complexity increases too, due to novel classifications and sampling rates, both becoming sub-optimal at aggregate level. With regard to the latter aspect, an important question is: how likely is the chance of operating at under-sampled data conditions with Big Data? Then, how to recover a correct sampling rate in such a context, a problem related to the so-called Nyquist rate? An associated problem is aliasing, which arises when a signal is discretely sampled at a rate that does not allow to capture the changes in the signal. To avoid aliasing, the sampling frequency should be at least twice the highest frequency contained in the signal [12,24,4]. With a plethora of measurements coming from heterogeneous digital instruments and sensors, the sampling rate from corresponding signals is necessarily different at individual source and most likely largely undetermined at the aggregate level. The challenge is that of identifying specific data stratifications and segmentations, at the cost of relatively heavy computations.

With Big Data, not only the likely increase of dimensionality might augment the general complexity (spurious correlations, error propagation etc.) and affect the confidence in models, but in many cases the original data comes unstructured or based on a huge number of primitives, and in both cases either transformations or reductions are pursued. In general, the patterns at individual and population levels may differ substantially, and thus be hardly summarized by some statistics or predicted with some confidence.

It is expected that by integrating information from a variety of sources, the assimilation of the whole data spectrum could not incur in significant loss of information (a good example might be again a subset of patients responding to the same treatment). Therefore, big data in medicine, for instance, would benefit from the ability to recognize disease heterogeneity and to stratify even further in order to be more accurate in the assessment of therapies [2]. In such regards, we might thus consider the blessing of Big Data.

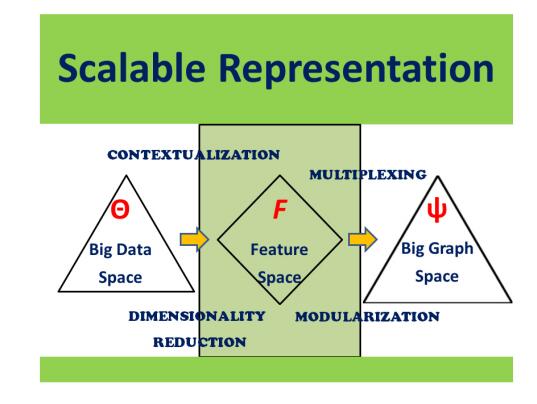
Finally, Figure 1 implies a key role for sufficient statistics, supposed to simplify statistical analysis [20]. A crucial question is: what is a sufficient statistics in Big Data? Can we achieve full information about the data from only a reduced set of it, considering that we only have a partial knowledge of the granularity of the original $\Theta$? In turn, how measurable and reliable can be other statistics (say, necessary statistics) that are computed from the previous one? Moving from data to graphs can elucidate further this matter.

---

2. All-connected systems complexity

Despite data liquidity flows fast and abundantly, Big Data does not represent a self-organized space, say $\Theta$. Observable connections co-exist with many false signals (false positives) and latent connections (false negatives). Linked, and even more linkable data, are destined to become crucial domains, once features are identified (Figure 2). In parallel with Eq. (1), networks too encompass latent structures and stochastic aspects, under the hypothesis of an average network connectivity degree fluctuating according to some probability law.

Therefore, hidden networks can depend on a network generator mechanism subject to some level of unknown uncertainty. Mixture mechanisms enable network approximation by a superposition of random networks (Poisson type, for large N) multiplied by the hidden variable distribution (HVD) [22,19]. Thus, given a Poisson-like $p(k)$, an observed network degree distribution is possibly represented as

$ p(k) = \int \pi(\lambda) p(k|\lambda) d\lambda $

(2)

More in general, there exists an interplay between information and disequilibrium in a system, which can represent complexity $C$ according to: $C = U D$, with $U$ as the uncertainty measure (such as Shannon Information or entropy), and $D$ as the disequilibrium (distance form equilibrium or equipartition of the probability distribution between states) [17]. Complexity grows or attenuates depending on both information and disequilibrium. Notably, while the former factor refers to the probability distribution of accessible states of a system in equilibrium (inference principle of maximum entropy), no methods in disequilibrium can deliver the probability distribution, i.e. we cannot predict the system's behavior.

When we consider the space $\Theta$, its expansion occurs because both $U$ and $D$ may grow. Instead, joint consideration of Big Graph space, say $\Psi$, suggests reduction of complexity by reconciling single node dynamics within entangled entities of a more complex nature but undergoing a common probability law, thus a different behavior and state of equilibrium. The representation property of networks can also take advantage from tensors (multidimensional arrays), in which each dimension is a mode. Let us name $T$ a $n$-node tensor with $n = 1 \ldots, N$, and $N$ big, which is $T \in R^{(I_{1}x I_{2}x \ldots x I_{N})}$. Some tensors would involve modes embedding node features. This way, tensor networks can enable multidimensional intra-an inter-modularization interactive dynamics according to various degrees of features interdependence.

The context built through $F$ possibly mitigates data information gaps, but likely does not compensate for them. Indeed, $F$ needs to be well designed to parallel the role played by a set of sufficient statistics as a coarse representation of data useful to identify good statistical estimation procedures, say. Data gaps that do not convey information about the underlying distribution, would have effects balanced by sufficient statistics replacing the sample information without any loss. Because of missing data, inhomogeneous measurements, different scales, etc., it is likely that Big Data would exacerbate such gaps and the corresponding information loss could be harder to contrast or not even recoverable by sufficient statistics. Without measuring the latter, we cannot determine its distribution either. Mapping data to features becomes almost a necessity, and many projective techniques allow such step. Among the most popular approaches, compressive sensing is the one looking at the signals/data structure to represent them with minimal measurements/features [3,7,8].

In $\Psi$, two main properties are key. One is multiplexing, which addresses the fact that multiple layers of complex interactions interplay among network nodes, such that the latter are interconnected via multiple types of links [14]. The other is modularization, which delivers a community map from the initial network, thus dealing naturally with heterogeneity.

As said earlier with tensor networks, nodes are particularly interesting when their feature contents are considered, say a certain function $\beta (f \in F)$ may be applied to them. This is to say that the connectivity patterns obtained from $\beta (f_{n}, f_{m})$, given two features $f_{n}$ and $f_{m}$, would constrain the adjacency matrix to the form $A_{n, m} = \beta(f_{n}, f_{m})$, thus qualitatively enriching the network [26]. Back to modularization, the more complex appears the structure of the feature patterns and the harder becomes to partition the network into modules or communities. The latter would usually require some kind of algorithmic search (greedy-like) [21], but may also involve further pre-processing steps, for instance the elimination of problematic nodes like hubs. Then, it might be facilitating random walk switching between modules, thus better conductance property and in turn goodness of community structure [15]. It is known that conductance of scale-free networks is a very heterogeneous property that depends on the node degrees [13].

---

3. Entanglement

It is important to note that tensor networks recall a rich architecture of interconnected nodes whose glue is due to entanglement, telling about the underlying information [25]. Many topological measures provide information on network structures, including entropic ones. Mutual information can be for instance computed between two network modules, say $I$ and $J$, so as to measure their correlation by $MI = S(I) + S(J) - S(IJ)$, in which both individual (first two terms) and combined (third term) entropies are considered. However, also entanglement is a quantum measure of correlation that can be put in relationships with topology, thus associating graphs to quantum states [10].

In general, quantum entanglement occurs when for interacting particles their quantum state cannot be described independently but only as a system. When such system interplays with the environment, a loss of information occurs, something generally called decoherence. In isomorphic graphs, defined by having adjacency matrix unique up to permutations of rows and columns, the same entanglement entropy is reflected into equivalent network states. The presence of synchronization [23] (say, nodes pulsing at the same frequency and thus representing a synchronized state) somehow ensures about the existence of entanglement between nodes, and protects the network from decoherence effects.

---

4. Symmetries

Network hubs are good candidate nodes to analyze node and edge dynamics. They have been the first object of network control, for instance. And it turns out they are not categorized as drivers due to the fact that due to their nature, the relatively large interconnected network regions receive similar signals through them, leaving unexplored many other regions which are possible targets. This is an effect of the presence of symmetries induced by the hubs, which reduce the number of nodes to be controlled but at the same time expand the number of edges through which the control signals flow [27].

In general, symmetries in a network induce, through some transformations, the invariance in its elements. This holds for transformations leaving the network s properties unchanged. Network invariant is called any property that is preserved under any of its possible isomorphisms, thus independently of its representation. A symmetry group $S_{g}$ acting on a set of nodes $N$ of a network defines for each node $n \in N$ an orbit, $O_{x} = \{s * x: s \in S_{g}\}$ [11]. The symmetry group partitions the sets of nodes into unique orbits, thus reducing the redundancy. If we consider the stochastic nature of networks, and the relevance of network ensembles, these objects call for further analysis under the lens of symmetries.

---