"We review recent research results on stochastic arrangement increasing risks in financial and actuarial risk management, including allocation of deductibles and coverage limits concerned with multiple dependent risks in an insurance policy, the independence model and the threshold models for a portfolio of defaults risks with dependence, and the optimal capital allocation for a financial institute with multiple line of business."
1.
Introduction
Ordering random risks play a vital role in both financial and actuarial sciences. In traditional theory of stochastic orders, researchers mainly focus on differing magnitude, dispersion and monotonicity etc. of two independent random variables, and hence only the two involved marginal distributions play the role in ordering the random variables. For comprehensive references on traditional stochastic orders and their application, one may refer to standard monographs Müller and Stoyan (2002) and Shaked and Shanthikumar (2007). Due to the mathematical tractability, for a long time in the study of financial and actuarial risk management the independence is always assumed among risks. However, random risks usually share with some mutual risk factors due to the common economic and financial environment, and the ignorance of the dependence among them may incur the underestimate of potential risks.
In the past two decades, the study of statistical dependence has been vigorously developed, among which the copula is one most popular dependence notion in the literature due to the convenient semi-parametric structure. As a characterization of dependence independent of the marginal distributions, the copula theory is widely used in financial and actuarial risk, biomedical science, operations research and reliability etc. Readers may refer to Nelsen (2006) for a comprehensive discussion on copulas and their applications. On the other hand, by means of bivariate characterization of stochastic orders, Shanthikumar and Yao (1991) developed new notions of joint stochastic orders, including joint likelihood ratio order, joint hazard rate order and joint usual stochastic order, which take the joint distribution of the two concerned random variables into account. Later, such a new approach to stochastically compare two dependent random variables was successfully applied in reliability. See for example, Belzunce et al.(2011, 2013), Pellerey and Zalzadeh (2015), Belzunce et al. (2016), Li et al. (2016) and Fang and Li (2016).
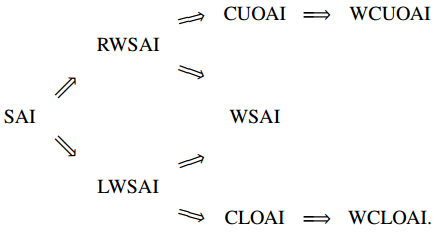
Along this line, Cai and Wei(2014, 2015) afterwards got these new notions generalized to multiple random variables and brought forth the stochastic arrangement increasing (SAI), right tail weakly stochastic arrangement increasing (RWSAI), left tail weakly stochastic arrangement increasing (LWSAI) and weakly stochastic arrangement increasing (WSAI) with the aid of multivariate arrangement increasing (AI) functions and weak version of AI functions. These multivariate dependence notions are the multivariate generalization of the joint stochastic orders in Shanthikumar and Yao (1991). Simultaneously, Li and You (2015) proposed upper/lower tail permutation decreasing (UTPD/LTPD) notion of multivariate absolutely continuous random vectors. For absolutely continuous random vectors, the SAI property is equivalent to the AI property of the joint density, and UTPD/LTPD coincides with RWSAI/LWSAI. Based on the AI property of joint survival function and distribution function, Cai and Wei (2014), Li and Li (2016) and Li and Li (2017a) further introduced some weak versions of RWSAI and LWSAI, for example, conditionally upper orthant arrangement increasing (CUOAI), weak conditionally upper orthant arrangement increasing (WCUOAI), conditionally lower orthant arrangement increasing (CLOAI) and weak conditionally lower orthant arrangement increasing (WCLOAI), where CUOAI is equivalent to the joint weak hazard rate order introduced in Belzunce et al. (2016). For more on joint stochastic orders, one may refer to Shanthikumar and Yao (1991), Righter and Shanthikumar (1992), Pellerey and Zakzadeh (2015), Pellerey and Spizzichino (2016), and Wei (2017).
In this review, we throw a light on the main results about the applications of SAI and weak version of SAI notions in actuarial and financial risk, which provides a platform for the researchers having interest in this topic to understand relevant results. The remaining of this paper is rolled out as follows. For ease of reference Section 2 recalls some concerned notions. We present in Section 3 the main results on allocations of insurance coverage limits and deductibles, including the ordering properties of the optimal allocations and the comparison results of retained losses when the allocation vectors are ordered according to the majorization order. In Section 4 we review related results on allocations to portfolios of assets without the default risks, and results on the independence model and the threshold model in the context of default risks. Also, we review the existing results on capital allocation in Section 5.
Throughout this review paper, all random variables are implicitly assumed to be nonnegative, all expectations are finite whenever utilized, and the terms increasing and decreasing mean nondecreasing and nonincreasing, respectively.
2.
Preliminaries
For real vectors x=(x1,⋯,xn)∈Rn and ω=(ω1,⋯,ωn)∈Rn, denote the inner product ω⋅x=ω1x1+⋯+ωnxn. Let
be the set of all real vectors with decreasing coordinates and that with positive decreasing coordinates, respectively, and let
be the set of all vectors with increasing coordinates and that with positive increasing coordinates, respectively. Denote In={1,⋯,n} and set τ=(τ1,⋯,τn) a permutation of {1,⋯,n}.
2.1. Aging notions
A random variable X with distribution function F and survival function ˉF=1−F is of
● increasing hazard rate (IHR) if
● decreasing reversed hazard rate (DRHR) if
Both IHR and DRHR are quite useful in reliability, survival analysis and management science, and they are found to be characterized through the log-concave survival function and the log-concave distribution function, respectively: A nonnegative random variable is IHR if and only if it has a log-concave survival function, and a nonnegative random variable is DRHR if and only if it has a log-concave distribution function. For more on IHR and DRHR one may refer to Marshall and Olkin (2007) and Block et al. (1998).
2.2. Comonotonicity and exchangeability
A subset A⊂Rn is said to be comonotonic if either xi≤yi for all i or xi≥yi for all i whenever x=(x1,⋯,xn) and y=(y1,⋯,yn) belong to A. A random vector X=(X1,⋯,Xn)∈Rn is said to be comonotonic if P(X∈A)=1 for some comonotonic subset A⊂Rn.
A random vector (X1,⋯,Xn) is said to be exchangeable if, for any permutation τ of (1,⋯,n),
(X1,⋯,Xn) and (Xτ1,⋯,Xτn) have the same probability distribution.
2.3. Distortion risk measure
A distortion function is an increasing mapping h:[0,1]↦[0,1] such that h(0)=0 and h(1)=1. For a random risk X with distribution function F, the distortion risk measure ρh is defined as
According to Denuit et al. (2005), for any random variables X,Y,
2.4. Majorization order
Denote x(1)≤⋯≤x(n) the increasing arrangement of x1,⋯,xn. A real vector x=(x1,⋯,xn) is said to be majorized by the other one y=(y1,⋯,yn) (denoted as xm⪯y) if
For more on the majorization order of real vectors, we refer readers to Marshall et al. (2011).
2.5. Stochastic orders
For two random variables X and Y with distribution functions F and G, survival functions ˉF and ˉG, density functions f and g, respectively, X is said to be smaller than Y in the
(ⅰ) likelihood ratio order (denoted as X≤lrY) if g(x)/f(x) increases in x;
(ⅱ) hazard rate order (denoted as X≤hrY) if ˉG(x)/ˉF(x) is increasing for all x;
(ⅲ) reversed hazard rate order (denoted as X≤rhY) if G(x)/F(x) is increasing for all x;
(ⅳ) usual stochastic order (denoted as X≤stY) if ˉF(x)≤ˉG(x) for all x;
(ⅴ) increasing convex order (denoted as X≤icxY) if ∫+∞xˉF(t)dt≤∫+∞xˉG(t)dt for all x;
(ⅵ) increasing concave order (denoted as X≤icvY) if ∫x−∞F(t)dt≥∫x−∞G(t)dt for all x;
(ⅶ) concave order (denoted as X≤cvY) if E[ϕ(X)]≤E[ϕ(Y)] for all concave functions ϕ:R↦R.
In finance and economics the usual stochastic order is known as the first order stochastic dominance, the increasing concave order is call as the second order stochastic dominance and the concave order is known as the mean-preserving spread. The following chain of implications is well-known.
For more on the above-mentioned stochastic orders one may refer to Müller and Stoyan (2002), Shaked and Shanthikumar (2007), Li and Li (2013).
2.6. Copula theory
Formally, for a random vector X=(X1,⋯,Xn) with distribution function F, survival function ˉF and univariate marginal distribution functions F1,⋯,Fn, if there exists some C:[0,1]n↦[0,1] and ˆC:[0,1]n↦[0,1] such that, for all xi, i∈In={1,⋯,n},
and
then C and ˆC are called as the copula and survival copula of X, respectively.
Among numerous copulas the Archimedean family is the most popular one due to the mathematical tractability and statistical applicability. For a n-monotone function ψ:[0,+∞)↦[0,1] with ψ(0)=1 and limx→+∞ψ(x)=0,
is called the Archimedean copula with generator ψ, and we denote ϕ=ψ−1 the general inverse of ψ for convenience from now on. For more on Archimedean copulas, readers may refer to Nelsen (2006), McNeil et al. (2005) and McNeil and Nešlehová (2009).
Stochastically arrangement increasing
A multivariate real function f(x) is said to be arrangement increasing (AI) if f(x)≥f(τi,j(x)) for any x∈Rn such that xi≤xj, 1≤i<j≤n. For 1≤i<j≤n, denote
and set
Shanthikumar and Yao (1991) took the first to employ the class of bivariate AI functions to generalize stochastic orders of two independent random variables to corresponding versions of statistical dependent ones. Following their ideas Cai and Wei(2014, 2015) proposed the following several notions of statistical dependence based on the above classes of multivariate functions. A random vector X is said to be
(ⅰ) stochastic arrangement increasing (SAI) if E[g(X)]≥E[g(τi,j(X))] for any 1≤i<j≤n and any g(x)∈Gi,js(n) such that the expectations exist;
(ⅱ) right tail weakly stochastic arrangement increasing (RWSAI) if E[g(X)]≥E[g(τi,j(X))] for any 1≤i<j≤n and any g(x)∈Gi,jrws(n) such that the expectations exist;
(ⅲ) left tail weakly stochastic arrangement increasing (LWSAI) if E[g(X)]≥E[g(τi,j(X))] for any 1≤i<j≤n and any g(x)∈Gi,jlws(n) such that the expectations exist;
(ⅳ) weakly stochastic arrangement increasing (WSAI) if E[g(X)]≥E[g(τi,j(X))] for any g∈Gi,jws(n) and any 1≤i<j≤n such that the expectations exist.
Denote the conditional probability
where x{i,j} is the subvector of x with the ith and jth deleted, 1≤i<j≤n. Simultaneously, Cai and Wei (2014) and Li and Li (2017a) also introduced the following three weak versions of RWSAI. X is said to be
(ⅰ) upper orthant arrangement increasing (UOAI) if its joint survival function ˉF(x) is AI;
(ⅱ) conditionally upper orthant arrangement increasing (CUOAI) if (Xi,Xj)∣X{i,j}=x{i,j} is UOAI for any fixed x{i,j} in support of X{i,j} and any 1≤i<j≤n;
(ⅲ) weak conditionally upper orthant arrangement increasing (WCUOAI) if
for all 1≤i<j≤n, t≥xj and any x(i,j) in support of X{i,j}.
As the dual, Li and Li (2016) proposed the following three dependence notions.
Definition 2.1. A random vector X is said to be
(ⅰ) lower orthant arrangement increasing (LOAI) if its joint distribution function F(x) is AI,
(ⅱ) conditionally lower orthant arrangement increasing (CLOAI) if (Xi,Xj)∣X{i,j}=x{i,j} is LOAI for any x{i,j} in support of X{i,j} and any 1≤i<j≤n,
(ⅲ) weak conditionally lower orthant arrangement increasing (WCLOAI) if
for all 1≤i<j≤n, t≤xj and any x{i,j} in support of X{i,j}.
It is easy to verify that Gi,jws(n)⊂Gijrws(n)(Gijlws(n))⊂Gi,js(n) and hence we reach the following chain of implications.
Here we remark that, an absolutely continuous random vector X is
(ⅰ) SAI if and only if it has an AI joint density function, and
(ⅱ) RWSAI/LWSAI if and only if it is upper/lower tail permutation decreasing (UTPD/LTPD), which are due to Li and You (2015).
In the literature of stochastic monotonicity of dependent random variables, many authors resorts to directly extend the classical stochastic orders between two random variables to the joint stochastic orders. For two-dimensional random vector, according to Shanthikumar and Yao (1991) and Belzunce et al. (2016) SAI, RWSAI, WSAI and UOAI are equivalent to the joint likelihood ratio order, the joint hazard rate order, the joint stochastic order, and the joint weak hazard rate order, respectively. For more on joint stochastic orders, one may refer to Righter and Shanthikumar (1992), Pellerey and Zakzadeh (2015), Pellerey and Spizzichino (2016), and Wei (2017).
3.
Allocations of insurance coverage limits and deductibles
By signing an insurance contract, a policyholder could obtain coverage from the the insurer. Two commonly-used forms of coverage are coverage limit and deductible. In the case of coverage limit, the insurer only takes care of the part below the coverage limit of the loss, and in the situation of deductible, the insurer only takes care of the part above the deductible of the full loss. For more details on insurance coverage, one may refer to Klugman et al. (2004).
Under certain circumstances, policyholders are allowed to allocate coverage limits or deductibles among multiple risks in one insurance policy. Assume one insurance policyholder faces up with nonnegative random risks X=(X1,⋯,Xn). Let T=(T1,⋯,Tn) be the vector of occurrence time of these risks, which is independent with X. For the discount rate δ≥0, denote
the vector of discount factors corresponding to time of occurrence T.
● For a total of l>0 coverage limit granted for X, let l=(l1,⋯,ln) be an allocation vector and denote
all admissible allocation vectors. Then, the policyholder gets the total discounted retained loss ∑ni=1e−δTi(Xi−li)+, where x+=max{x,0}.
● For the policyholder with a total deductible of d>0 granted for X, let d=(d1,⋯,dn) be an allocation vector and denote
all admissible allocation vectors. Then, the policyholder gets the total discounted retained loss ∑ni=1e−δTi(Xi∧di), where x∧d=min{x,d}.
Let ω>0 be the policyholder's wealth after the premium is paid and u(x) be his/her utility function. In the context of expected utility theory, the policyholders try to maximize the expected utility of ultimate wealth by allocating the coverage limits and deductibles among risks. From the viewpoint of the policyholder, the optimization allocation problem of coverage limits is formularized as
and the optimization allocation problem of deductibles is summarized as
Denote l∗=(l∗1,⋯,l∗n) and d∗=(d∗1,⋯,d∗n) the solutions to Problems (3.1) and (3.2), respectively.
3.1. Ordering optimal allocations
Due to tractability, in the related literature on the optimal allocation of coverage limits and deductibles authors usually assume independence or comonotonicity among concerned risks and independence among time of occurrence of risks. Cheung (2007) was among the first to deal with the above two optimization allocation problems, and they built the following result.
Theorem 3.1 (Cheung (2007)). For δ=0 and increasing and concave u,
(ⅰ) if X is independent and Xi≤hrXj, then l∗i≤l∗j and d∗i≥d∗j, 1≤i≠j≤n;
(ⅱ) if X is comonotonic and Xi≤stXj, then l∗i≤l∗j and d∗i≥d∗j, 1≤i≠j≤n.
Afterwards, Hua and Cheung (2008a) took the frequency effect into account in studying of the optimal allocations of coverage limits and deductibles.
Theorem 3.2 (Hua and Cheung (2008a)). For any increasing and concave u, if X is comonotonic and T is independent, then,
for any 1≤i≠j≤n.
Denote π(l) the premium for a total of l coverage limit and π(d) the premium for a total of d deductible. Hence, under the distortion risk measure ρh the optimization allocation problem of coverage limits is
and the optimization allocation problem of deductibles is summarized as
In the context of distortion risk measures Zhuang et al. (2009) also studied the ordering of the optimal allocations of coverage limits and deductibles from the viewpoint of policyholders, and they developed following results.
Theorem 3.3 (Zhuang et al. (2009)). Let l∗ and d∗ be the solution to Problems (3.3) and (3.4), respectively. For any 1≤i≠j≤n,
(ⅰ) if X is independent and δ=0, then
(ⅱ) if X is independent and δ>0, then
(ⅲ) if X is comonotonic and δ>0, then
In view of (2.3), (2.4) and (2.5), we reach the following:
● For increasing u and any distortion function h, Problems (3.1) and (3.2) coincide with Problems (3.3) and (3.4), respectively;
● For increasing concave (convex) u and concave (convex) distortion function h, Problems (3.1) and (3.2) coincides with Problems (3.3) and (3.4), respectively.
So, the result of (3.5) strengthens Theorem 3.1(ⅰ) by relaxing the hazard rate order between risks to the usual stochastic order and Theorem 3.3(ⅲ) generalizes Theorem 3.2 by relaxing the likelihood ratio order between occurrence times to the reversed hazard rate order.
Some researchers incorporated statistical dependence into either severities X or frequencies of occurrence T, and this makes the model more flexible in practical application and more general in theoretical sense.
Li and You (2012) was among the first to characterize the dependence of frequencies of occurrence by the Archimedean survival copula. Suppose Xi has survival function ˉFi and density function fi, i∈In. Denote lTi and uTi the left and right endpoints of the support of Ti and si(x)=ψ′(ˉFi(x))fi(x), i∈In.
Theorem 3.4 (Li and You (2012)). Assume that the comonotonic X satisfies X1≤st⋯≤stXn and T with T1≥lr⋯≥lrTn has Archimdean survival copula with generator ψ such that (1−t)ψ″(t)/ψ′(t) is decreasing. If sj(x)/si(x)→1 as x→uTj and lTi<uTj for all 1≤i<j≤n, then, for any permutation τ,
According to the above theorem, the worst allocation takes place if a risk-averse policyholder allocates a smaller level of coverage limits and a larger level of deductible to the risk with higher severity and frequency. Subsequently, You and Li (2016) further generalized Theorem 3.4 by relaxing the likelihood ratio order among occurrence times to the reversed hazard rate order.
Theorem 3.5 (You and Li (2016)). Assume that the comonotonic X satisfies X1≤st⋯≤stXn and T with T1≥rh⋯≥rhTn has Archimdean copula with a log-convex generator. Then, (3.7) and (3.8) both hold for any permutation τ.
On the other hand, Cai and Wei (2014) proposed several new notions of dependence, for example SAI, RWSAI, CUOAI, to model the dependence of risks and time of occurrence and extended many existing results to risks with more general dependence.
Theorem 3.6 (Cai and Wei (2014)). Assume that the utility u is increasing and concave.
(ⅰ) If X is SAI and W is SAI, then l∗1≤⋯≤l∗n.
(ⅱ) If X is CUOAI and W is SAI, then d∗1≥⋯≥d∗n.
(ⅲ) If X is comonotonic, X1≤st⋯≤stXn and W is RWSAI, then l∗1≤⋯≤l∗n and d∗1≥⋯≥d∗n.
It is worthwhile to point out the following facts:
Cai and Wei (2014, Proposition 5.2) For mutually independent X, the SAI property of X is equivalent to X1≤lr⋯≤lrXn;
Cai and Wei (2014 Proposition 5.4) For mutually independent X, the RWSAI property of X is equivalent to X1≤hr⋯≤hrXn;
Cai and Wei (2014 Proposition 5.5) For comonotonic random vector X, X1≤st⋯≤stXn is equivalent to the CUOAI or SAI property of X;
Shaked and Shanthikumar (2007, Theorem 1.B.41) For any strictly decreasing continuous function h, X≤rhY implies h(X)≥hrh(Y).
Based upon the above, one can easily verify that Theorem 3.3(ⅱ), (ⅲ) are just special cases of Theorem 3.6.
In rapid sequence, Li and You (2015) further got the following two results in the context of not considering the frequency effect.
Theorem 3.7 (Li and You (2015)). For δ=0,
(ⅰ) if X has an AI joint density, then l∗i≤l∗j and d∗i≥d∗j for any increasing u and any 1≤i<j≤n;
(ⅱ) if X has an Archimedean survival copula with a log-convex generator, then Xi≤hrXj implies l∗i≤l∗j and d∗i≥d∗j for any increasing concave u and any 1≤i≠j≤n.
Afterwards, You and Li (2017) revisited Theorem 3.7(ⅱ) in the context of the increasing utility function.
Theorem 3.8 (You and Li (2017)). For δ=0, if X has an Archimedean (survival) copula with a log-convex generator, then Xi≤rhXj(Xi≤hrXj) implies l∗i≤l∗j (d∗i≥d∗j) for any increasing u and any 1≤i<j≤n.
According to Cai and Wei(2014, 2015), a random vector X with an Archimedean (survival) copula having log-convex generator is LWSAI (RWSAI) if X1≤rh⋯≤rhXn (X1≤hr⋯≤hrXn). Naturally, one may wonder whether the following three results hold actually: for δ=0,
(ⅰ) if X is RWSAI, then l∗i≤l∗j for any increasing concave u and any 1≤i<j≤n;
(ⅱ) if X is LWSAI, then l∗i≤l∗j for any increasing u and any 1≤i<j≤n;
(ⅲ) if X is RWSAI, then d∗i≥d∗j for any increasing u and any 1≤i<j≤n.
These three conjectures can be verified by means of Theorems 3.2, 3.3 of You and Li (2015).
Recently, Li and Li (2017a) derived the optimality of the decreasing allocation of deductibles for SAI or comonotonic risks with CUOAI or WCUOAI discount factors at the cost of extra restriction on the increasing and concave u, which complements the results of Theorem 3.6.
Theorem 3.9 (Li and Li (2017a)). For any increasing and concave function u with convex u′ and concave u″, d∗1≥⋯≥d∗n holds if one of the following two conditions is fulfilled.
(ⅰ) X is SAI and W is CUOAI.
(ⅱ) X is comonotone with X1≤st⋯≤stXn and W is WCUOAI.
3.2. Comparison results of retained losses
The above-mentioned research all focus on the ordering of the optimal allocations. Some researchers studied the comparison results of retained losses when allocation vectors are ordered according to the majorization order. Also, the closed-form expression of the optimal allocation vectors of Problems (3.1) and (3.2) are built in this context as well.
Theorem 3.10 (Lu and Meng (2011)). If the independent risk vector X satisfies X1≤lr⋯≤lrXn and all marginal density functions are log-concave, then,
(ⅰ) lm⪯l′⟹∑ni=1(Xi−li)+≤st∑ni=1(Xi−l′(n−i+1))+ for l,l′∈R+n;
(ⅱ) dm⪯d′⟹∑ni=1(Xi∧di)≥st∑ni=1(Xi∧d′(n−i+1)) for d,d′∈R+n;
(ⅲ) d∗=(d,0,⋯,0) for any increasing utility u.
Along this line of research, Hu and Wang (2014) and Li and Li (2017b) discussed the closed-form optimal allocation of deductibles and the ordering of the optimal allocation of coverage limits and deductibles under more general conditions. Hu and Wang (2014) generalized Theorem 3.10 to independent X with Xi having (all even number or odd number i) log-concave densities. Then, for l,l′,d,d′∈R+n,
Li and Li (2017b) further improved the result of
● (3.9) by relaxing the reversed hazard rate order among risks to Xi≤rhYi≤rhXi+1 for some random variables Yi with DRHR, i∈In−1,
● (3.10) by relaxing the hazard rate order among risks to Xi≤hrYi≤hrXi+1 for some random variables Yi with IHR, i∈In−1, and
● (3.11) by relaxing the hazard rate order among risks to X1≤hrX≤hrXi for some random variable X with IHR, i=2,⋯,n.
Also, Li and Li (2017b) proved that (l,0,⋯,0) serves as the most unfavorable solution of the optimization Problem (3.1) for any increasing u if X1≤rhX≤rhXi for i=2,⋯,n and some random variable X with DRHR.
Open Problem 1.
As per Block et al. (1998, Corollary 2.1), a nonnegative random variable can not has log-convex distribution function. You et al. (2017) pointed out that the log-convexity assumed for Xi's distribution function is problematic in Lu and Meng (2011, Proposition 5.2) and Hu and Wang (2014, Theorem 5.1) when deriving the optimal allocation of coverage limits among risks. Although You et al. (2017) further discussed the existence of optimal allocation of coverage limits between two independent losses, from the viewpoint of policyholders with increasing utility function the optimal allocation of coverage limits of n independent risks is still an open problem.
In recent years, several researchers put their focus also on comparison of retained losses of dependent risks.
Theorem 3.11 (Manesh and Khaledi (2015)). Assume that X has componentwise decreasing joint density.
(ⅰ) If X is exchangeable, then, for l,l′∈Rn+,
(ⅱ) If X has an AI joint density, then, for l,l′∈Rn+,
As a direct consequence of Theorem 3.11(ⅰ), for exchangeable X with componentwise decreasing joint density function, the optimal allocation is l∗=(l/n,⋯,l/n).
We also obtain the following result on comparison of the retained losses, as applications of Pan et al. (2015) and You and Li (2015).
Corollary 3.12.
(ⅰ) If X is RWSAI, then, for l,l′∈Rn+,
(ⅱ) If X has an log-concave and AI joint density, then, for l,l′,d,d′∈Rn+,
(ⅲ) If X is exchangeable with a log-concave joint density, then, for l,l′∈Rn+,
(ⅳ) If X is exchangeable, then, for l,l′∈Rn+,
The most recent result in this line is due to Pan and Li (2017b), which proposes the substantial extension to the corresponding results of Hua and Cheung (2008a).
Proposition 3.13 (Pan and Li (2017b)). Suppose that X is SAI, T is SAD and they are independent. Then,
Hua and Cheung (2008b) derived closed-form of the worst allocations for the insurer in the sense that the insurer will only accept taking this risk with the highest premium. For recent studies on the worst allocations one may refer to You and Li (2017).
4.
Allocations to portfolios of assets
In financial engineering and actuarial sciences, it is one of main concerns to reasonable allocate the investor's wealth to some risk assets in the market. In tradition, the asset allocation problems are investigated under the framework of expected utility theory. Within this framework, the investors mainly concentrate on allocating the initial wealth to various assets so as to maximize the expected total potential return.
Let ω=(ω1,⋯,ωn) be an allocation vector in which the investor allocates the amount ωi of the entire wealth ω to the risk asset with nonnegative realizable return Xi, i∈In. Denote
the class of all admissible allocation vectors.
4.1. Allocations to portfolios of assets without default risks
Under the allocation ω, the return of the investor is ∑ni=1ωiXi. For the investor with utility function u, the asset allocation problem without default risk is summarized as
Denote ω∗=(ω∗1,⋯,ω∗n) the optimal allocation of Problem (4.1).
For mutually independent assets with realizable returns X=(X1,⋯,Xn), Hadar and Seo (1988) took the first to prove that the risk-averse investor would like to invest more wealth in the asset with larger realizable return in the sense of the first-order stochastic dominance, the second-order stochastic dominance or mean-preserving spread order. Specifically, their results are summarized in the following.
Theorem 4.1 (Hadar and Seo (1988)). Assume that X is mutually independent and u is increasing and concave. Then, ω∗i≤ω∗j for 1≤i≠j≤n in the following three scenarios:
(ⅰ) Xi≤stXj and xu′(x) is increasing;
(ⅱ) Xi≤icvXj, u′ is convex and xu′(x) is increasing and concave;
(ⅲ) Xi≤cvXj, u′ is convex and xu′(x) is concave.
Afterward, Landsberger and Meilijson (1990) and Kijima and Ohnishi (1996) also had a discussion on the allocation of asset with realizable return arrayed in the sense of the likelihood ratio order or the reversed hazard rate order.
Theorem 4.2 (Landsberger and Meilijson (1990), Kijima and Ohnishi (1996)). For X mutually independent, ω∗i≤ω∗j for 1≤i≠j≤n in the following two scenarios:
(ⅰ) u is increasing and X1≤lr⋯≤lrXn;
(ⅱ) u is increasing and concave and X1≤rh⋯≤rhXn.
At a later stage, Hennessy and Lapan (2002) derived the ordering property for the optimal allocation to portfolios of assets with realizable returns coupled by Archimedean dependence structures. Let Xi be of distribution function Fi and density function fi and denote ri(x)=ψ′(Fi(x))fi(x) for i∈In.
Theorem 4.3 (Hennessy and Lapan (2002)). Assume that X has Archimdean copula with generator ψ. Then, ω∗i≤ω∗j for 1≤i<j≤n whenever ri(x)≤rj(x) and u is increasing, concave and twice continuously differentiable.
Along this line of research, Li and You (2014) derived the optimal shares of assets when their realizable returns have Archimedean copula and arrayed in the sense of the likelihood ratio order. Let li and ui be the left and right endpoints of support of Xi, for i∈In, and denote lij=max{li,lj}, uij=min{ui,uj} for {i,j}⊂In.
Theorem 4.4 (Li and You (2014)). Assume that X has the Archimedean copula with (n+1)-monotone generator ψ such that (1−t)ψ″(t)/ψ′(t) is decreasing in t and ri(x)/rj(x)→1 for x→lij. If Xi≤lrXj and u is increasing, then ω∗i≤ω∗j for 1≤i≠j≤n.
Under certain conditions on the utility functions, Cai and Wei (2015) verified that the optimal allocation vector should be arrayed in the ascending order whenever the realizable returns of the assets are SAI, LWSAI and WSAI.
Theorem 4.5 (Cai and Wei (2015)). The optimal solution ω∗ satisfies ω∗1≤⋯≤ω∗n in either one of the the following scenarios:
(ⅰ) X is SAI and u is increasing;
(ⅱ) X is LWSAI and u is increasing and concave;
(ⅲ) X is WSAI, u is increasing and concave, and xu′(x) is increasing.
Note that an absolutely continuous random vector X is
● SAI if and only if it has an AI joint density function;
● LWSAI if it has one Archimedean copula with X1≤rh⋯≤rhXn.
Propositions 4.2 and 4.3 of Li and You (2014) coincide with Theorem 4.5 for absolutely continuous X.
Also, Li and Li (2016) concluded that the optimal allocation vector should be arranged in the ascending order whenever the realizable returns are CUOAI, CLOAI and WCLOAI, respectively, and these results serve as a nice complement to those of Cai and Wei (2015).
Theorem 4.6 (Li and Li (2016)). For increasing and concave u, the optimal solution ω∗ satisfies ω∗1≤⋯≤ω∗n in either one of the following scenarios:
(ⅰ) X is CUOAI, u′ is convex and xu′(x) is increasing in x≥0;
(ⅱ) X is CLOAI and u′ is convex;
(ⅲ) X is WCLOAI, u′ is convex and u″(x)>−∞ for all x≥0.
On the other hand, some researchers paid their attention to comparing the potential returns resulted from majorized allocation vectors.
Theorem 4.7 (Li and You (2014)). Assume for X the Archimedean copula with the generator ψ such that (1−t)ψ″(t)/ψ′(t) is decreasing in t and ri(x)/rj(x)→1 for x→lij and any 1≤i<j≤n. If X1≤lr⋯≤lrXn and u is increasing and concave, then
Subsequently, You and Li (2016) built the increasing concave order for potential returns with assets of realizable returns having LTPD density.
Theorem 4.8 (You and Li (2016)). The implication of (4.2) holds for any risk vector X with a LTPD probability density.
As applications of You and Li (2015) and Pan et al. (2015), we obtain the following corollary.
Corollary 4.9. The implication in (4.2) holds in the following two scenarios:
(ⅰ) X has an AI and log-concave joint density function and u is increasing.
(ⅱ) X is RWSAI and u is increasing and convex.
4.2. Allocations to portfolios of assets with default risks
It is of both practical and theoretical interest to take the default risks into account in modern insurance industry. In the literature, Cheung and Yang (2004) proposed the independence model and the threshold model to characterize the default risks of assets in the allocation problem of portfolios.
4.2.1. Independence model
For a portfolio of n assets with realizable returns X, let I=(I1,⋯,In) be indicators of their defaults, that is,
for i=1,⋯,n, and assume the independence between X and I. Then, under the framework of expected utility theory, an investor with utility function u confronts with the optimization problem
Denote ω∗=(ω∗1,⋯,ω∗n) the optimal allocation of Problem (4.3).
Let p(λ)=P(I=λ) and set, for k=0,1,⋯,n,
Denote, for 1≤i≠j≤n and k∈In−1,
Under the framework of Independence Model, Cheung and Yang (2004) was among the first to consider the optimal allocation to portfolios of assets with exchangeable realizable returns.
Theorem 4.10 (Cheung and Yang (2004)). Assume, for all 1≤i<j≤n,
If u is increasing, then ω∗1≤⋯≤ω∗n for any exchangeable X.
The exchangeability of X implies that X1,⋯,Xn are identically distributed. So, Chen and Hu (2008) focused on assets with independent realizable returns arrayed in the sense of the usual stochastic order, the concave order and the increasing concave order, respectivley.
Theorem 4.11 (Chen and Hu (2008)). Assume that (4.4) holds for all 1≤i<j≤n. If u is increasing and concave, then ω∗1≤⋯≤ω∗n holds for any independent X in either one of the following two scenarios:
(ⅰ) X1≤st⋯≤stXn and xu′(x) is increasing;
(ⅱ) X1≤icv⋯≤icvXn, u′ is convex, and xu′(x) is increasing and concave.
In Cai and Wei (2015), new dependence notions are proposed to model the dependence structure of realizable returns and the default risks. Over there they obtained the following result.
Theorem 4.12 (Cai and Wei (2015)). If X is WSAI and I is LWSAI, then ω∗1≤⋯ω∗n holds for any increasing concave u such that xu′(x) is increasing.
As is pointed out in Cai and Wei (2015), the LWSAI property of I is equivalent to (4.4). Also, the WSAI property of X implies X1≤st⋯≤stXn. So, Theorem 4.12 successfully generalized Theorem 4.11(ⅰ).
Along this stream, Li and Li (2016) utilized CUOAI, CLOAI and WCLOAI to model the dependence among realizable returns of assets, and they built the following theorem as a complement to the result of Theorem 4.12.
Theorem 4.13 (Li and Li (2016)). If (4.4) holds for all 1≤i<j≤n, then the optimal solution ω∗ of Problem (4.3) satisfies ω∗1≤⋯≤ω∗n in either one of the following three scenarios:
(ⅰ) X is CUOAI, u′ is convex, and xu′(x) increases in x≥0.
(ⅱ) X is CLOAI, u′ is convex and xu′(x) is increasing in x≥0.
(ⅲ) X is WCLOAI, u′ is convex, u″ is concave, and xu′(x) is increasing and concave in x≥0.
4.3. Threshold model
In the independence model the default is assumed to be independent of the realized return. However, this is not true in some practical situations. Hence, it is of interest to take the dependence between the realized return and the default into account. Assume that the ith asset defaults when Xi is less than some predetermined threshold level li≥0, then it realizes the return XiI(Xi>li) for i=1,⋯,n. As a result, the investor attains the potential return
For investors with utility function u, the asset allocation problem is then summarized as
For the risk-averse investors, Cheung and Yang (2004) proved that more wealth should be allocated to the asset with lower threshold in the context of exchangeable realizable returns.
Theorem 4.14 (Cheung and Yang (2004)). Assume that u is increasing and concave and X is exchangeable. Then, l∈I+n implies ω∗∈D+n.
For the risk-averse investor, Cai and Wei (2015) further proved that more wealth should be allocated to the asset with higher realizable return and lower threshold whenever the realizable returns are LWSAI.
Theorem 4.15 (Cai and Wei (2015)). Assume that u is increasing and concave and X is LWSAI. Then, l∈I+n implies ω∗∈D+n.
Lately, Li and Li (2017c) employed WSAI and CLOAI, which are strictly weaker than LWSAI in Theorem 4.15, to model the dependence among realizable returns, and their results can be summarized in the following.
Theorem 4.16 (Li and Li (2017c)). Assume that u is increasing and concave. Then, l∈I+n implies ω∗∈D+n in either of the following two situations:
(ⅰ) X is WSAI and xu′(x) is increasing in x≥0.
(ⅱ) X is CLOAI and u′ is convex.
Open Problem 2. When taking the default risks into consideration, all the existing studies on optimal allocations to the portfolio devoted to deriving the optimal ordering of the allocation vector. However, when the allocation vectors are arrayed according to the majorization order, the comparison results on the potential returns are still unknown.
5.
Capital allocation
Consider a financial institute who wishes to allocate the total capital p>0 to a portfolio of n nonnegative risks X1,⋯,Xn. Let p=(p1,⋯,pn) be an allocation vector and denote the class
of all admissible allocation vectors. Assume that the loss function is defined as ∑ni=1ϕ(Xi−pi), where ϕ is some suitable function. Let ω be the initial wealth and u be the utility function of the institute. Then, under the framework of utility theory, the optimal capital allocation problem is formulated as
Denote p∗=(p∗1,⋯,p∗n) the solution to Problem (5.1).
Xu and Hu (2012) was among the first to employ stochastic comparison to characterize loss due to the capital allocation strategy. For independent losses X1,⋯,Xn, and they built the following results.
Theorem 5.1 (Xu and Hu (2012)). Assume that X1,⋯,Xn are independent and
(ⅰ) they share with a common log-concave density function. If ϕ is convex, then
(ⅱ) and they have log-concave density functions. If X1≤lr⋯≤lrXn and ϕ is convex, then
(ⅲ) and X1≤lr⋯≤lrXn. If ϕ is convex, then
(ⅳ) u is increasing. If ϕ is convex, then
Xu and Hu (2012) also investigated the comparison results on loss functions and the ordering of the optimal capital allocation vector for comonotonic losses.
Theorem 5.2 (Xu and Hu (2012)). For comonotonic X1,⋯,Xn,
(ⅰ) if X1≤st⋯≤stXn and ϕ is convex, then (5.2) holds;
(ⅱ) if u is increasing, then Xi≤stXj implies p∗i≤p∗j, for 1≤i<j≤n.
Afterwards, researchers moved their focus to the optimal capital allocation to losses with various dependent structure other than comonotonicity. For exchangeable losses, You and Li (2014) and Manesh and Khaledi (2016) presented the following result, which generalizes and complements that of Theorem 5.1(ⅰ).
Theorem 5.3 (You and Li (2014), Manesh and Khaledi (2015)). For an exchangeable X and convex ϕ, (5.3) holds. Further, if X1,⋯,Xn have a common log-convex density function, then p∗i≤p∗j for 1≤i<j≤n.
Also, for RWSAI losses and losses with AI joint density, You and Li (2014) and Li and You (2015) developed the comparison results on losses functions along with the ordering result of the optimal allocation vector.
Theorem 5.4 (You and Li (2014), Li and You (2015)). If X
(ⅰ) has an AI joint density, ϕ is convex, and u is increasing, then, p∗i≤p∗j for 1≤i<j≤n;
(ⅱ) is RWSAI, and ϕ is increasing and convex, then (5.3) holds;
(ⅲ) is RWSAI, ϕ is increasing and convex, and u is increasing, then, p∗i≤p∗j for 1≤i<j≤n.
Much lately, Pan and Li (2017a) took the occurrence times of losses into consideration. Let δ be the discounted rate, T=(T1,⋯,Tn) be the corresponding occurrence times of the corresponding losses, which is independent of X. Since the insurer attains the total discounted loss ∑ni=1e−δTiϕ(Xi−pi), the optimal capital allocation problem is thus summarized as follows:
Let p∗ be the optimal solution to Problem (5.4), and denote W=(W1,⋯,Wn) with Wi=e−δTi for i∈In.
Theorem 5.5 (Pan and Li (2017a)). If X and W are both SAI, ϕ is increasing and convex, and u is increasing, then p∗i≤p∗j for 1≤i<j≤n.
6.
Concluding remarks
Stochastic arrangement increasing notions integrate the statistical dependence into stochastic orders and thus are especially adapted to heterogeneous risks in finance and insurance. In addition, SAI notions and their dual are also found very useful in reliability engineering, operation research and management science etc.. See for example, Feng and Shanthikumar (2017), Fang and Li(2017, 2016), You et al. (2016), and Belzunce et al.(2013, 2011). In this paper we review theoretical research results on stochastic arrangement increasing risks within several circumstances of financial and actuarial risk management. In general, we come up with the conclusions in some typical financial and actuarial situations concerned with statistically dependent risks, which serve as nice extension of those well-known results in the related literature.
(ⅰ) For multiple risks covered by one insurance policy, it is optimal to allocate larger deductible and smaller coverage limit to smaller risk associated with lower rate of occurrence if both the risk vector and the corresponding vector of occurrence rate are of some SAI properties. Such instinctively correct results underpin the rational choice of the insureds, who are naturally risk-averse in the insurance market. Due to the nonparametric joint distribution of the concerned risks, we remark that the only fly in the ointment is the lack of the closed-form of the optimal allocations of deductible and coverage limit.
(ⅱ) For portfolio asset allocation, we address the sufficient conditions on the utility function such that the optimal allocation assigns less amount of the entire asset to less profitable one in the portfolio with various SAI potential returns. These results successively generalize those classical ones on mutually independent potential returns to the context of statistically dependent ones, more pertinent to the practical scenes.
(ⅲ) As for the security capital allocation of a financial institute running multiple lines of business, our research findings propose several situations on the loss function, the utility function, SAI properties of the potential returns, and SAI properties of frequencies of occurrence so that the investor can follow the intuition to allocate more security capital to the less risky line of business.
It worth mentioning that all these research findings are about the behavior of the optimal allocations. No doubt, it is of both practical and theoretical interest to pursue the closed-form of the optimal allocations. Due to the nonlinear and nonparametric idiosyncrasy of the concerned optimization problem, we almost got no clue to locate the above-mentioned optimal allocations in the past decade. With delight we recently realize that the stochastic optimization is one feasible way to numerically identify the optimal allocations in practice. In future study we will devote to producing the algorithm leading to the optimal allocations.
Conflict of interest
The authors declare no conflicts of interest in this paper.









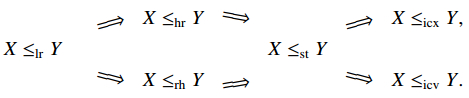



 DownLoad:
DownLoad: