1. Introduction
In nature, most of the microbial biomass is organised as sessile communities named biofilms. A biofilm can be defined as cells organised as microcolonies embedded in an organic polymer matrix of microbial origin living at an interface between two different liquids, gas and liquid, or solid and liquid, Figure 1 [1,2,3]. The biofilms at the solid-liquid interface are the most studied type of biofilm. The biofilms at solid-liquid interfaces are the major cause of biofouling and biodeterioration of materials [4,5], and a common cause of persistent infections [6]. Biofilm formation in the human gut by probiotic bacteria can also have beneficial health effects in prevention of diseases [7]. The biofilms at the liquid-liquid interface have been described mainly in aquatic environments. In marine environments, the biofilm formation at liquid-liquid interfaces results from adaptation of microorganisms to degrade insoluble hydrophobic organic compounds such as lipids and hydrocarbons present in water [1,8]. Biofilm formation in droplets of hydrophobic substances such as fuel or oil is involved in biodegradation of pollution [9,10,11]. The biofilms at the air-liquid interface form-floating structures also named pellicules [12,13]. Biofilms at the air-liquid interface are facing opposite gradients of nutrient and oxygen, with access to abundant nutrients from the solution below and oxygen from the air above [14,15]. The formation of biofilms at the air-liquid interface can require an initial first step of flocculation: during the first hours of growth in broth in static conditions, Mycobacterium smegmatis forms isolated flocs and between 18 and 30 hours, the matrix becomes rigid and pellicle forms [16].
Irrespective of the location of the biofilm, the matrix is made of extracellular polymeric substances (EPS) comprising polysaccharides, proteins, extracellular DNA, and other substances such as lipids. Extracellular polysaccharides are considered as the major structural components of the matrix [17]. Inside biofilms, matrix constituents and most of microbial cells are invisible but can be observed and characterized after staining with fluorochromes or molecules coupled to fluorochromes. Microbial cells can be stained with fluorescent DNA-binding stains like DAPI, acridine orange, SYBR green, or SYTO 9, polysaccharides can be stained with fluorescent lectins and proteins can be stained with Alexa fluor succinimidyl ester, fluoresceinisothiocyanate isomer I or SYPRO Orange [18,19,20,21]. Different biofilm components can be stained simultaneously with different fluorophores. For example, clusters of cells and matrix proteins have been studied among S. epidermidis biofilms grown in flow cell conditions [18]; biofilm flocs have been characterized either from drinking water treatment plants [22] or from wastewater treatment plants [20]; biofouling of hollow fibre ultrafiltration membranes has been studied at different operational conditions [22]. Multi-staining approaches can generate peak interference between two channels when the range of emission of two fluorochromes overlap significantly and the excitation level is different between the two [23]. Testing different combinations of fluorophores along with different mounting media, carefully selecting the excitation and emission wavelengths, and using spectral imaging rather than standard channel mode can minimize peak interference [19,24]. Among EPS, extracellular polysaccharides are probably the most studied macromolecules [17]. Fluorescently labelled lectins have been widely used to stain microbial extracellular glycoconjugates in natural and artificial environments, and to study specific bacterial species or highly complex environments. Lectins are proteins obtained from a wide variety of natural sources including seeds, plant roots, plant barks, animal, fungal and bacterial cells. The specificity and affinity of lectins for carbohydrate targets can be compared to those of antigen-antibody interactions [25].The binding specificities of several lectins used in biofilm research are presented in Table 1.
Table 1.Main lectins used in the analysis of biofilms classified by ligand specificity
|
Symbol
|
Name
|
Source
|
Ligand motif
|
Reference
|
|
Mannose Binding Lectins
|
|
|
AMA
|
Arum maculatum Agglutinin
|
Arum maculatum
|
Man
|
[26]
|
|
Con A
|
Concanavalin A
|
Canavalia ensiformis
|
Branched α-mannosidic structures; high-mannose type, hybrid type and biantennary complex type N-Glycans
|
[20,24,25,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42]
|
|
CPA
|
Pure Cicer arietinum Lectin
|
Cicer arietinum
|
Man
|
[42]
|
|
GNA
|
Snowdrop Lectin
|
Galanthus nivalis
|
α 1-3 and α 1-6 linked high mannose structures
|
[35]
|
|
HHA, HHL, AL
|
Amaryllis Lectin, Hippeastrum Hybrid Lectin
|
Hippeastrum Amaryllis
|
α-Man
|
[35]
|
|
LCH, LCA
|
Lentil Lectin
|
Lens culinaris
|
Fucosylated core region of bi- and triantennary complex type N-Glycans
|
[41]
|
|
PMA
|
Polygonatum multiflorum Agglutinin
|
Polygonatum multiflorum
|
Mannose Branched
|
[35,43]
|
|
Mannose/Galactose/N-acetylgalactosamine binding Lectins
| |
|
DGL
|
Dioclea grandiflora Lectin
|
Dioclea grandiflora
|
Man, Glc
|
[35]
|
|
LcH
|
Lens culinaris Agglutinin or Lentil Lectin
|
Lens culinaris
|
α-Man, Fucose linked to chitobiose core of oligosaccharide, α-Glc, α-GlcNAc
|
[26,44]
|
|
NI (no information)
|
Lathyrus odoratus Lectin
|
Lathyrus odoratus
|
α-Man, Glc, GlcNAc
|
[44]
|
|
PSA
|
Pisum sativum Agglutinin
|
Pisum sativum
|
α-Man, α-Glc, α-GlcNAc
|
[35,41,43]
|
|
Galactose/N-acetylgalactosamine binding Lectins
|
|
|
|
|
ACL, ACA
|
Amaranthus caudatus Lectin
|
Amaranthus caudatus
|
[gal(β1, 3) galNAc, gal(β1, 3)Neu5Ac]
|
[26,42,44]
|
|
AIA
|
Artocarpus integrifolia Lectin (Jackfruit)
|
Artocarpus integrifolia
|
Gal; GalNAc
|
[35,42]
|
|
DBA
|
Biotinylated Dolichos biflorusAgglutinin
|
Dolichos biflorus
|
α-GalNAc
|
[26,41,43,44,45]
|
|
ECA, ECL
|
Erythrina cristagalli Agglutinin, Lectin
|
Erythrina cristagalli
|
Gal, GalNAc, Lac
|
[42]
|
|
GSL, GS-I or BSL
|
Griffonia simplicifolia Lectin or Bandeiraea simplicifolia Lectin
|
Bandeiraea simplicifolia
|
α-D-Gal, N-acetyl-α-D-Gal
|
[28,35,40,41,42]
|
|
GHA
|
Glechoma hederacea
|
Glechoma hederaceaAgglutinin
|
GalNAc
|
[42]
|
|
HAA
|
Helix aspersa Agglutinin
|
Helix aspersa
|
GalNAc, GlcNAc
|
[41,42,44]
|
|
HPA
|
Helix pomatia Agglutinin
|
Helix pomatia
|
α-GalNAc
|
[26,35,42]
|
|
IAA
|
Iberis amara Agglutinin
|
Iberis amara
|
GlcNAc
|
[26,33,35]
|
|
IRA
|
lris hybrid Lectin
|
lris hybrid
|
GalNAc
|
|
|
LEL or LT, LEA
|
Lycopersicon Esculentum Lectin or Tomato Lectin
|
Lycopersicon esculentum
|
GlcNAc(β1, 4), GlcNAc oligomers
|
[26,35,42,44,46,47]
|
|
PNA
|
Peanut Agglutinin
|
Arachis hypogaea
|
Galβ1-3GalNAcα1-Ser/Thr (T-Antigen)
|
[26,28,31,32,36,39,40,41,42,44,46,47,48,49,50]
|
|
MOA
|
Marasmius oreades Agglutinin
|
Marasmius oreades
|
α 1-3-Gal homopolymers,
α-1-3-Gal-β-1-4-GlcNAc heteropolymers
|
[42,43]
|
|
MPL, MPA
|
Maclura Pomifera Lectin
|
Maclura pomifera
|
[α-Gal, α-GalNAc, Gal(β1, 3)GalNAc]
|
[35,44]
|
|
MNA-G
|
Morniga G Lectin
|
Morniga G
|
Gal
|
[35]
|
|
PHA
|
Phaseolus vulgaris
Agglutinin
|
Phaseolus vulgaris
|
GalNAc
|
[31,35,36,41,44,48]
|
|
PA-I
|
Pseudomonas aeruginosa
|
Pseudomonas aeruginosa
|
D-Gal
|
[26,33,35,48]
|
|
RCA
|
Ricinus communis Agglutinin
|
Ricinus communis (Castor Bean)
|
Glc, GalNAc
|
[41]
|
|
RTA
|
Trifolium repens Lectin
|
Trifolium repens
|
2-deoxyglucose
|
[44]
|
|
SBA
|
Soybean Agglutinin Lectin
(Glycine max)
|
Soybean
|
α-GalNAc, β-GalNAc
|
[26,32,41]
|
|
SJA
|
Sophora japonica Agglutinin
|
Sophora japonica
|
GalNAc
|
[35,41]
|
|
STA
|
Solanum tuberosum Agglutinin
|
Solanum tuberosum
|
GluNAc
|
[35]
|
|
SVAM
|
Snake Venom Agglutinin
|
Naja mossambica
|
α or βGalNAc
|
[51]
|
|
VRA
|
Vigna radiata Aglutinin
|
Vigna radiata
|
α-Gal
|
[43]
|
|
VVA
|
Vicia villosa Agglutinin
|
Vicia villosa
|
α-GalNAc
|
[26,35]
|
|
WFA
|
Wisteria floribunda Lectin
|
Wisteria floribunda
|
[terminal GalNAc(β1, 4), terminal GalNAc(β1, 3) terminal GalNAc(α1, 3)]
|
[35,42,44,52]
|
|
WGA, VGA
|
Wheat Germ Agglutinin
|
Triticum vulgaris
|
GlcNAcβ1-4GlcNAcβ1-4GlcNAc, Neu5Ac(sialic acid)
|
[25,26,28,30,34,36,39,40,41,42,43,45,46,48,49,50]
|
|
Sialic acid/N-acetylglucosamine binding Lectins
|
|
|
|
|
CCA
|
Crude Cancer antennarius
|
Cancer antennarius
|
9-O-Ac-NeuAc, 4-O-Ac-NeuAc
|
[43]
|
|
HMA
|
Homarus americanus Agglutinin
|
Homarus americanus
|
Sialic acid, N-Acetylneuraminic acid, N-Glycolyneuraminic acid
|
[26,33,42]
|
|
LFA
|
Limax flavus Lectin
|
Limax flavus
|
Sialic acid
|
[42]
|
|
Limulin
|
Horseshoe crab
|
Limulus polyphemus
|
N-acetylneuraminic acid
D-glucuronic acid
|
[28,35,48]
|
|
MAL, MAA
|
Maackia amurensis Lectin
|
Maackia amurensis
|
Neu5Ac/Glc, α2-3Galβ1-4GlcNAcβ1-R
|
[43]
|
|
Fucose/Galactose/N-acetylgalactosamine binding Lectins
|
|
|
ECorA
|
Erythrina corallodendronAgglutinin
|
Erythrina
corallodendron
|
Fuc-LacNAc, GalNAc, Gal, Lac
|
[26,43]
|
|
LBA
|
Lima Bean Agglutinin
|
Phaseolus Lunatus
|
{GalNAc(α1, 3) [L-fuc(α1, 2)Gal], GalNAc}
|
[44]
|
|
Fucose binding Lectins
| |
|
AAL
|
Aleuria aurantia Lectin
|
Aleuria aurantia
|
Fucα1-2Galβ1-4 (Fucα1-3/4)Galβ1-4GlcNAc; R2-GlcNAcβ1-4 (Fucα1-6) GlcNAc-R1
|
[26,33,35,42,43,53]
|
|
UEA-I
|
Ulex europaeus Agglutinin
|
Ulex europaeus
|
Fuc, Fucα1-2Gal-R
|
[28,32,33,36,41,46]
|
|
LTL
|
Lotus tetragonolobus Lectin
|
Lotus tetragonolobus or Tetragonolobus purpureas
|
Fuc-α-1-2-Gal-β-1-4-[Fuc(α 1)]- GlcNAc
|
[28,31,43]
|
|
Lectin with no indication of binding specificity
| |
|
RPb
|
Robinia pseudoacacia Bark
|
Robinia pseudoacacia
|
Not Indicated
|
[44]
|
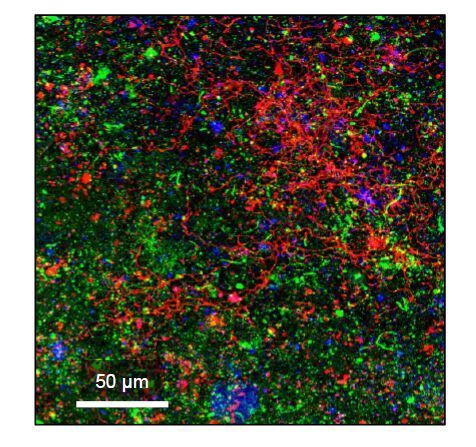
Fluorescent lectins have been used successfully to characterize mono-specific biofilms of very different bacteria like Staphylococcus epidermidis [54], Pseudomonas aeruginosa [34], Escherichia coli [55], Campylobacter jejuni [42], fresh water diatoms from epilithic biofilms [56], and also highly complex biofilms grown in natural or artificial environments [28,30,32,35,40,43,57]. An example of a highly complex biofilm formed on nanofiltration (NF) membranes during drinking water production is presented in Figure 2. Peanut agglutinin and Wheat germ agglutinin bind efficiently to extracellular substances of the NF biofilm matrix.
Concanavalin A (ConA) was shown to bind to levan, a major exopolysaccharide produced by P. syringae [51]. ConA binding in mature biofilms suggested that levan might accumulate within cell-depleted voids in the centre of microcolonies and in blebs [51]. UEA was shown to bind to a fucose-containing exopolysaccharide present in “dome” structures observed under flow conditions in Burkholderia thailandensis biofilms [41]. Different lectins have been shown to have different binding patterns inside microcolonies and/or biofilms: Among biofilms formed from the south Saskatchewan river, Triticum vulgaris and Canavalia ensiformis lectins bind to cell surfaces and/or to cell associated polysaccharides, Tetragonolobus purpureas binds to polysaccharides in the bulk of the structure, Arachis hypogea and Solanum tulerosum lectins bind to polysaccharides in the outer layer of the structure [58]. In order to stain a large part of extracellular polysaccharides in a biofilm, it is recommended to use cocktails of lectins. Nevertheless, since many lectins are glycoproteins, some lectins recognize each other; therefore possible mixtures have to be tested pairwise for precipitation before they can be used inside a cocktail. EPS of a single microcolony can be stained by at least one and up to four different lectins, each recognizing unique glycoconjugates in the microbial aggregate [58].
The “fluorescence lectin-binding analysis” can be used in combination with fluorescent in situ hybridization to correlate lectin binding with cell identification [26,42,44,48,58]. This combined method was efficient to visualize glycoconjugate components of the EPS on the single cell level inside aggregates and flocs for both procaryotic and eukaryotic cells [48]. Indeed, lectins from A. hypogaea, P. aeruginosa, and P. vulgaris stained distinct glycoconjugates originating from different eukaryotic and prokaryotic microorganisms inside lotic microbial aggregates from the Elbe river [48].
The use of fluorescent lectins is a powerful approach for qualitative and quantitative characterization of biofilms. Parts 2 and 3 are focused onto the use of fluorescent lectins to study biofouling of nanofiltration membranes in a context of drinking water production. Parts 2 and 3 constitute detailed illustrations of this particular application of fluorescent lectins that can be extrapolated to many other biofilm formation contexts.
2. Use of lectins to assess membrane biofouling during drinking water production
Drinking water requires high quality because it must meet the needs of human bodies and the corresponding requirements of hygiene and health. The definition of a drinking water is governed by standards that set maximum content limits for certain harmful substances that may be present in the water. Guidelines for Drinking-water Quality edited by the World Health Organization (WHO) are used as the scientific basis for standard setting in most countries [59]. A drinking water must be free of pathogens such as viruses or bacteria, and parasitic organisms. It must not contain certain minerals considered toxic, such as nitrates, phosphates and heavy metals, organic compounds such as hydrocarbons and pesticides. Conversely, the presence of certain substances, such as trace elements may be highly desired because regarded as essential to the human body. In this context, the treatment to clean water and make it drinkable is a major economic and health issue.
Filtration at the nanometer scale, i.e. Nanofiltration (NF), is a high technology process particularly suited to the treatment of surface waters to produce drinking water [60]. Indeed, NF provides a barrier to eliminate viruses, bacteria and parasites but also micro-pollutants such as pesticides and drug residues and therefore to obtain a water of great microbiological and chemical purity [61]. NF membranes are costly and their effectiveness and durability are limited by fouling [62].Membrane fouling is a highly complex phenomenon caused by dissolved inorganic and organic components, inert colloids, and microorganisms. Fouling means accumulation of matter on the membrane surface and decrease of filtration performance. Biofouling seems to play a major role in NF membranes fouling during drinking water production [63,64]. Biofouling is a term used to describe all instances of fouling where biologically active organisms are involved [65].
The development of strategies for fouling prevention and control requires characterizing the fouling material composition and organisation [66,67]. The use of fluorescence microscopy associated with fluorescently labelled lectins and a DNA-specific fluorescent stain like DAPI (4’, 6-diamidino-2-phenyindole dihydrochloride) has been evaluated to characterize NF membrane foulants in the drinking water plant of Méry sur Oise, France [40]. Double staining with two lectins, one FITC- and one TRITC-labelled were done with a mixture of Bandeiraea simplicifolia agglutinin (BS-1) and concanavalin A (ConA) or a mixture of peanut agglutinin (PNA) and wheat germ agglutinin (WGA). Membranes in service for at least 5 years were autopsied after extraction of filtration modules from the plant. To determine the seasonal variations of the foulants, membrane autopsies and analyses were done in March, June and September. Since the biofouling matter contains living microorganisms and active exoenzymes, it is essential to realize a fixation with paraformaldehyde as fast as possible after the membrane autopsy to avoid detachment, growth or autodigestion of the biomass. Extensive washing with filter-sterilized (0.2 mm) water is needed after fixation to remove paraformaldehyde in order to avoid not specific fixation of lectins during staining experiments. The NF200 B-400 membranes used in the plant contain an ultra-thin polypiperazine top layer (DOW, La Plaine Saint Denis, France). The NF200 B-400 membranes have a low molecular weight cut-off, high negative charge, and low hydrophobicity to efficiently remove hydrophobic natural organic matter through electrostatic repulsion/size exclusion [68]. Autofluorescence emission by polymer contents of filtration membranes can be observed after excitation at the wavelengths used in histology, Figure 3. The background level of fluorescence from polymers depends on their content in aromatic structures and conjugated double bonds in their molecular structure [69].
As shown in Figure 3, the background level of autofluorescence of the filtration membranes was easily observable but did not prevent observing the fluorescence emission by stained microbial cells and natural exopolymers. Epifluorescence observations after DAPI excitation at 364 nm showed the presence of many bacterial microcolonies interspersed at the membrane surface. The DAPI staining increased from March to September indicating that bacterial accumulation occurred at the membrane surface. Epifluorescence observations after FITC excitation at 494 nm, and TRITC excitation at 550 nm revealed the presence of polymeric carbohydrate structures located on cell surfaces and polymeric carbohydrate structures located extracellularly throughout the foulants matrix. Lectin staining was not only concentrated in areas where microcolonies were present but also extended in areas devoid of microbial cells. This binding pattern of the lectins has been previously observed with biofilms grown in vitro with river water as the sole source of microorganisms and nutrients [28]. Lectin staining increased from March to September, showing that the increase in sessile bacteria was associated with an increase in EPS production indicating biofilm accumulation. The polysaccharide composition of the fouling layer changed with time certainly as a consequence of qualitative and quantitative modifications among the populations of sessile cells. Such an analysis by epifluorescence microscopy after labelling with DAPI and fluorescent lectins is an approach that can be implemented by an industrial laboratory in a production plant. The equipment and reagents are not very expensive but it is necessary to have qualified technical personnel trained specifically. Confocal laser scanning microscopy was used to study the spatial organization and distribution of the fouling layer at the membrane surface of the same samples. Examples of these observations are shown in Figure 4.
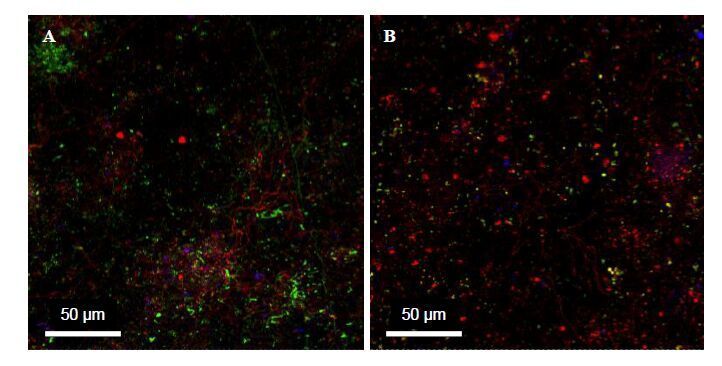
The post-acquisition Leica Confocal Software allowed the elimination of the membrane autofluorescence background. CLSM analysis confirmed that most of the stained polysaccharides were located extracellularly throughout the biofilm matrix. A high degree of spatial organization and high heterogeneity were observed within the fouling material. Depending on the lectin, stained EPS were shown as long and entangled fibres, short fibres and cloud stained areas. The dominant lectin binding was with BS-1 revealing high occurrence of galactosides residues in the polysaccharide part of the foulants. The microbial cells, mainly organized as microcolonies interspersed at the membrane surface, were localized in the superficial layer of the fouling deposit. These staining patterns suggested that the fouling layer was organized as an interpenetrated network mainly composed of exopolysaccharides supporting microbial cells adhesion and growth. The more sophisticated and expensive CLSM gave the opportunity to observe the spatial organization and 3D structure of the foulants. The fouling material exhibited the same characteristics as a biofilm. These biofilms developed at the surface of membranes in a drinking water plant may result from the presence of microbial cells and nutrients coming from feed water and also from material that has not been removed even after successive cleaning and production processes. The CLSM analysis after labelling with DAPI and fluorescent lectins is an approach that cannot be implemented by an industrial laboratory in a production plant. The equipment is very expensive and the handling of the microscope is quite complex. However, this approach can be outsourced to a specialized laboratory or analytical platform. Indeed, the realization of samples and their stabilization by treatment with paraformaldehyde are quite feasible on site, the fixed samples can then be sent to an analytical laboratory, which will perform staining and microscope observations.
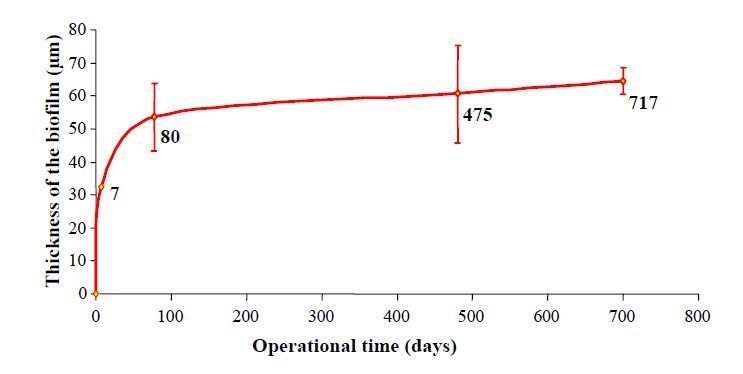
The accumulation of microorganisms on the membrane surface called biofouling results from microbial deposition and growth on the membrane [63]. During NF operation, biofilm development is made easier by bacterial trapping and nutrient concentration at the membrane surface during filtration. The development of strategies for fouling prevention and control also requires characterizing the kinetic development of biofouling [66,67]. The fluorescence lectin-binding analysis has been used to characterize the kinetic development of biofilm for two years on NF membranes at the Méry-sur-Oise plant, France [49]: the biofilm thickness, architecture and abundance were studied after CLSM and computer analyses and membrane performance was recorded over time. The membrane surface coverage rate by the biofilm was determined after conversion of colour images acquired by CLSM observation to black and white. The percentage of the area covered by the biofilm was obtained by calculating the ratio between the black and white pixels. Biofilm thickness was determined by multiplying the number of slices collected by the thickness of each slice as previously described [70]. The growth in thickness of the biofilm was greater during the first 80 days of filtration, Figure 5.
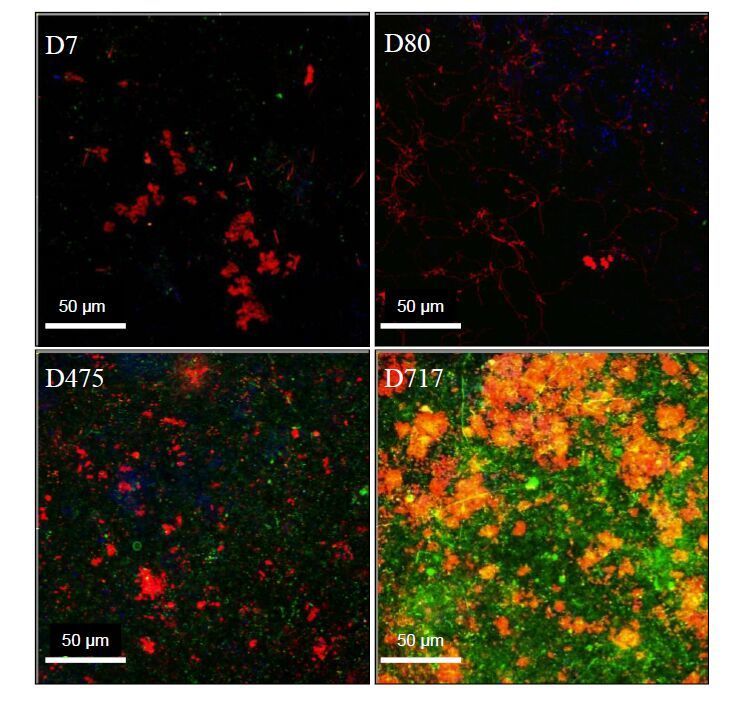
At the end of the incubation time, after 717 days, the maximum biofilm thickness was 64 ± 4 μm. A NF biofilm thickness of 20-80 μm has been also measured by confocal microscopy imaging using a pilot system fed conventionally treated Ohio River water for 15 months [62]. In this study, confocal microscopy analyses were obtained after staining the biofilm with Baclight bacterial viability kit (Molecular Probes, Inc, Eugene, OR). Thus, only the cellular part of the biofilm corresponding to viable and nonviable bacteria was taken into account. For greater thicknesses, other measurement approaches such as optical coherence tomography can be used [71]. Using this technology, penetration depths up to 1.7 mm can be observed for biofilms. Thicknesses of about 200 μm have been measured for biofilms developed on ultrafiltration membranes during gravity driven membrane filtration of water for around 50 days [71]. Three stages of biofilm growth on NF membranes were discriminated at the Méry-sur-Oise plant, Figure 6: (1) presence of relatively small sessile microcolonies embedded in an EPS matrix (after filtration for seven days); (2) microcolony growth in three dimensions but partial coverage of the membrane (filtration for up to 80 days) and (3) total coverage of the membrane and biofilm maturation by densification (filtration for 80-717 days). Blue stained cells are easily visible at day 80 and day 475 but hardly visible at day 7 and day 717. At day 7, the microcolonies are not large enough to be easily observed, and at D717, the EPS matrix masks most of the cells. The EPS content increased not linearly in the NF biofilms during the incubation period. The concomitant use of PNA and WGA lectins recognizing different saccharide residues showed that there was a modification in the lectin-staining pattern during biofilm maturation. After filtration for 475 days, there were markedly less WGA-stained carbohydrates than PNA stained polysaccharides, whilst after 717 days, the residues stained with one or the other lectin were present in similar proportions. A shift in polysaccharide composition has been previously shown during growth of mono-specific bacterial biofilms [25]. For Staphylococcus sciuri and Stenotrophomonas maltophilia, the increase in EPS production over time was different between saccharides recognized by WGA and sugars binding to concanavalin A. Thus, for different kind of biofilms, the proportions of different polysaccharides in the biofilm matrix can vary depending on the bacterial composition and the stage of maturity.
Over time, the development of biofilm on the NF membranes affected the filtration performance. Permeability was affected precociously and continuously during the experiment. The longitudinal pressure drop began to be affected from 200 days of filtration, and increased strongly after filtration for 475 days, a stage where a denser biofilm layer covering most of the membrane surface was formed. This is consistent with the previous observation that the longitudinal pressure drop can be increased by biofouling [72]. Biofilm becomes an issue only when it reaches thickness and surface coverage that cause declined flux and/or increase in pressure drops during NF operation [49,63,73].
3. Use of lectins to assess prevention and control procedures of NF membrane fouling
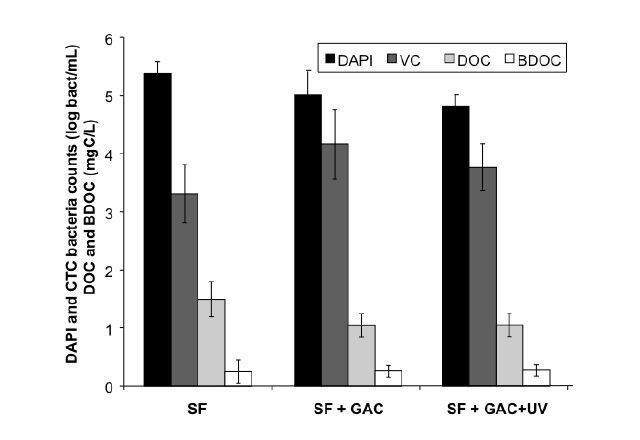
Coagulation, flocculation, settling and filtration are conventional pre-treatments upstream from NF membranes [74]. To reduce membrane biofouling, the two critical water parameters to control are the bioavailable organic matter concentration and the concentration of live bacteria. The fluorescence lectin-binding analysis was used to compare biofoulants on the surface of membranes operated in identical nanofiltration pilot units fed in parallel with the same water that has undergone different pretreatments: sand filtration (SF) with or without ozonation and granular activated carbon (GAC) adsorption (SF versus SF + GAC) or ozonation and GAC adsorption with or without UV irradiation (400 J/m2 dose) (SF + GAC versus SF + GAC + UV) [50,74].
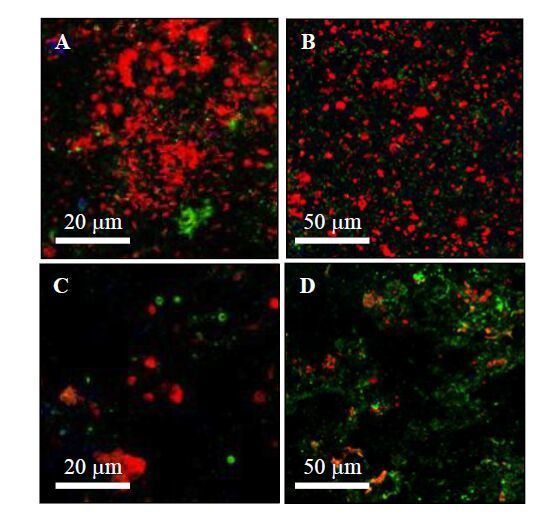
The bioavailable dissolved organic carbon (BDOC) concentration was approximately decreased by a factor 2 after the ozonation and GAC adsorption pretreatment in comparison with the sand filtration pretreatment alone, Figure 7. The viable and total bacterial counts in fed waters were not different between the two conditions. The slight differences observed were not significant. The germicide effect of UV pre-treatment was observed to range between 0.3 and 0.4 log removal of viable bacteria. For all the different feed water quality conditions, the analysis of the foulant matter after DAPI and lectin staining revealed the presence of many microorganisms organized as microcolonies embedded in exopolysaccharides, with a highly heterogeneous repartition, Figure 8. Some areas of the membrane surface were covered by significant amounts of microorganisms and polysaccharides, while others were still virgin and did not present any microbial cells. For all the pretreatments except for UV irradiation, the most intense lectin-binding signals corresponded to the PNA lectin revealing high occurrence of galactosides residues among foulants. High occurence of galactoside residues seems to be a constant characteristic of exopolysaccharides of the matrix of biofilms fed by river water [28,40]. After UV pretreatment, the most intense signal corresponded to Lycopersicon esculentum agglutinin (LEA) binding. This shift in the lectin binding pattern could be related to modifications of the biodiversity among sessile bacteria after UV irradiation: lots of filamentous bacteria were observed on the membrane without UV pretreatment, while they were scarcer on the membrane after UV irradiation [75]. CLSM observations of the foulant deposit demonstrated that the delivery of decreased amounts of nutrients or of decreased amount of live bacteria was associated with a decrease in biofilm development of the NF membranes [50,75]. This decrease in biofilm development was associated with a stabilization of the pressure drop on mid-term duration (several months).
Effective raw water pre-treatment prior to NF is essential to reduce fouling but can’t completely avoid the phenomenon. Thus, chemical cleaning is an essential step in maintaining the performance of the filtration process [64,76]. Flux recovery data are usually employed to assess the efficiency of industrial cleaning procedures but does not give any information about foulants removal from the membrane surface. The fluorescence lectin-binding analysis can give complimentary information by comparing biofoulants before and after chemical cleaning and thus can help to improve cleaning procedures. This approach applied to the cleaning in place procedures at the Méry sur Oise drinking water production plant showed that the organic fouling deposit characteristic of a microbial biofilm was only partially removed after treatment [39]. After cleaning, CLSM observations showed a general decrease of the lectin-staining pattern with differences between lectins: the decrease in lectin staining was high for some lectins (BS-1 and WGA) and weak for others (ConA and PNA). This illustrates the importance of using multiple markers with cocktails of lectins. Removal of microbial cells was revealed by the decrease of the DAPI staining. A decrease of the foulant matter thickness measured by CLSM observation was also reported indicating partial removal of the biofouling deposit. The fluorescence lectin-binding analysis is an efficient tool to assess biofouling removal, but multidisciplinary analyses are needed to take into account all the diversity of the foulant matter. Dry weight measurements, total inorganic carbon and adenosine triphosphate content measurements, inductively coupled plasma-atomic emission spectroscopy, attenuated total reflection Fourier transform infrared spectroscopy can give quantitative and/or qualitative information about foulants removal after cleaning [39,64,77,78]. Moreover, the effects of cleaning onto adhesion forces between the foulant and the membrane surface and between the bulk foulant and the fouling layer or more generally onto mechanical parameters of the foulant matter (viscosity, elasticity) can be analysed by atomic force microscopy or cone-plate rheology, respectively [76,77].
4. Conclusion
Biofilms are highly complex biological structures that form universally at wet interfaces in natural and artificial environments. Fluorescent lectins are powerful tools to characterize the extracellular polymeric substances containing sugars in biofilms. By their specificity, the lectin-binding pattern gives information about the polysaccharide content of the matrix. Fluorescent lectins can be used one by one or collection of lectins with a large panel of specificity can be tested. When the repertoire of lectins able to bind efficiently to the sample analysed is determined, it is recommended to use cocktails of lectins in order to stain a large part of extracellular polysaccharides in the biofilm. Fluorescent lectins can be used alone or with other fluorescent molecules targeting different biofilm components, like fluorescent DNA-binding stains for microbial cells, and SYPRO Orange for proteins. After staining, the biofilm samples can be observed by epifluorescence microscopy to obtain qualitative and semi-quantitative information. An industrial laboratory in a production plant or a teaching laboratory can implement this approach. The stained biofilm samples can also be observed by confocal laser scanning microscopy to obtain complimentary information such as the three-dimensional spatial organization and distribution of EPS in the biofilm structure and quantitative information like depth and biovolume. In this way, fluorescent lectins allow to study the kinetic development of a biofilm, the efficiency of different preventive or curative anti-biofilm treatments.
Conflict of interest
The author confirms that this article content has no conflicts of interest.










 DownLoad:
DownLoad: