Telomeres, species differences, and unusual telomeres in vertebrates: presenting challenges and opportunities to understanding telomere dynamics

Emory D. Ingles; Janine E. Deakin; Emory D. Ingles; Janine E. Deakin

doi:10.3934/genet.2016.1.1

AIMS Genetics

2016, Volume 3, Issue 1: 1-24. doi: 10.3934/genet.2016.1.1

Previous Article Next Article

Review

Telomeres, species differences, and unusual telomeres in vertebrates: presenting challenges and opportunities to understanding telomere dynamics

Emory D. Ingles ,
Janine E. Deakin ^,

Institute of Applied Ecology, University of Canberra, Canberra, ACT 2601, Australia

Received: 14 January 2016 Accepted: 03 March 2016 Published: 08 March 2016

There has been increasing interest in the use of telomeres as biomarkers of stress, cellular ageing and life-histories. However, the telomere landscape is a diverse feature, with noticeable differences between species, a fact which is highlighted by the unusual telomeres of various vertebrate organisms. We broadly review differences in telomere dynamics among vertebrates, and emphasize the need to understand more about telomere processes and trends across species. As part of these species differences, we review unusual telomeres in vertebrates. This includes mega-telomeres, which are present across a diverse set of organisms, but also focusing on the unusual telomeres traits of marsupials and monotremes, which have seen little to no prior discussion, yet uniquely stand out from other unusual telomere features discovered thus far. Due to the presence of at least two unique telomere features in the marsupial family Dasyuridae, as well as to the presence of physiological strategies semelparity and torpor, which have implications for telomere life-histories in these species, we suggest that this family has a very large potential to uncover novel information on telomere evolution and dynamics.
- telomere,
- mega-telomere,
- telomere length dimorphism,
- non-canonical telomere sequences,
- marsupial,
- dasyurid
Citation: Emory D. Ingles, Janine E. Deakin. Telomeres, species differences, and unusual telomeres in vertebrates: presenting challenges and opportunities to understanding telomere dynamics[J]. AIMS Genetics, 2016, 3(1): 1-24. doi: 10.3934/genet.2016.1.1

Related Papers:

Abstract

There has been increasing interest in the use of telomeres as biomarkers of stress, cellular ageing and life-histories. However, the telomere landscape is a diverse feature, with noticeable differences between species, a fact which is highlighted by the unusual telomeres of various vertebrate organisms. We broadly review differences in telomere dynamics among vertebrates, and emphasize the need to understand more about telomere processes and trends across species. As part of these species differences, we review unusual telomeres in vertebrates. This includes mega-telomeres, which are present across a diverse set of organisms, but also focusing on the unusual telomeres traits of marsupials and monotremes, which have seen little to no prior discussion, yet uniquely stand out from other unusual telomere features discovered thus far. Due to the presence of at least two unique telomere features in the marsupial family Dasyuridae, as well as to the presence of physiological strategies semelparity and torpor, which have implications for telomere life-histories in these species, we suggest that this family has a very large potential to uncover novel information on telomere evolution and dynamics.

References

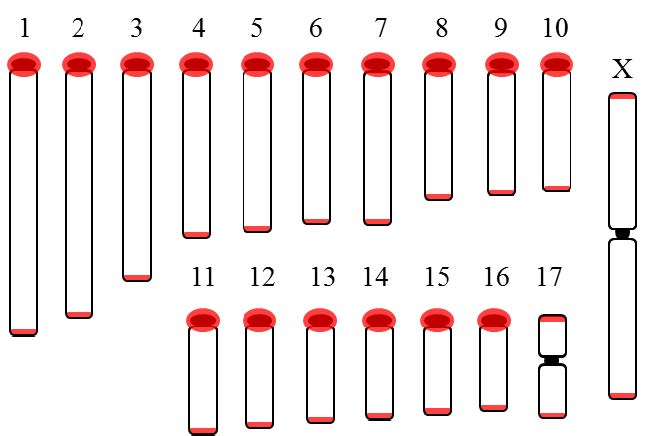
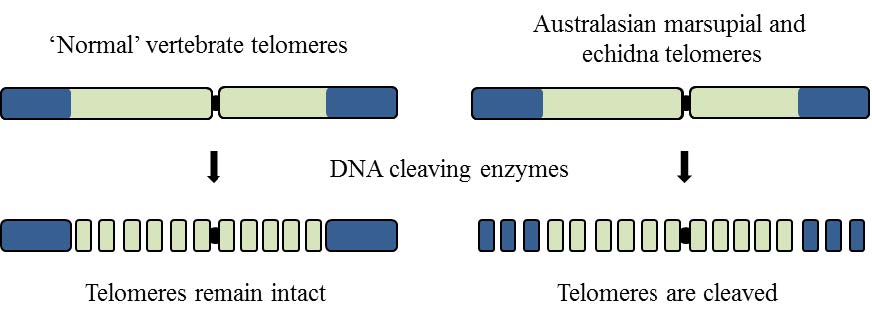
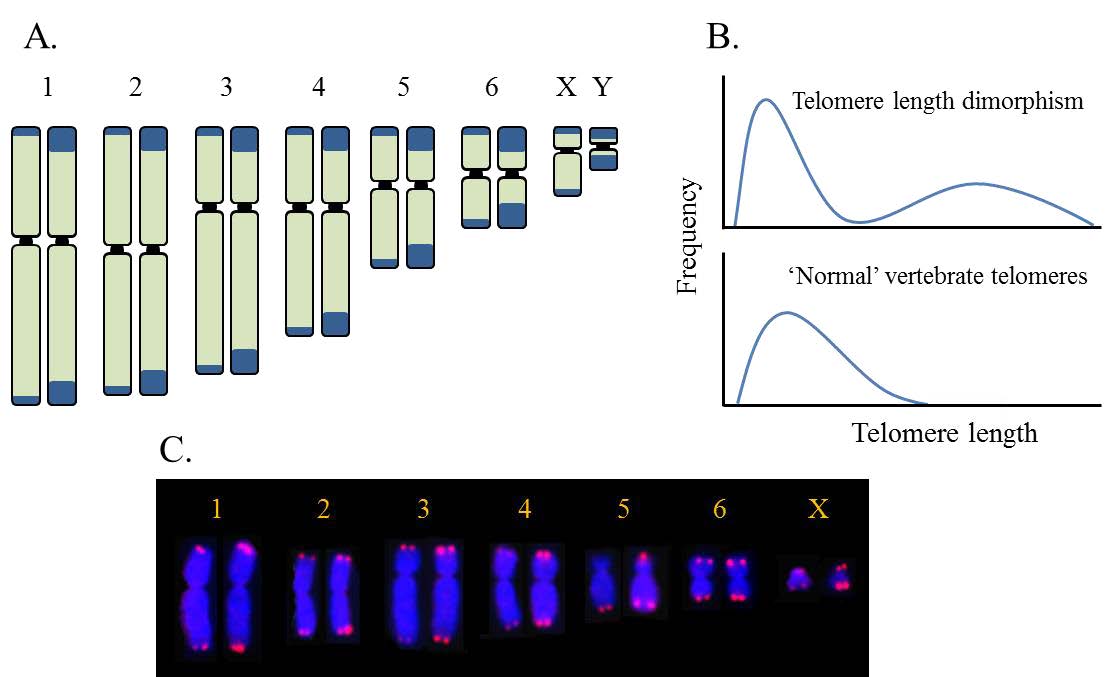
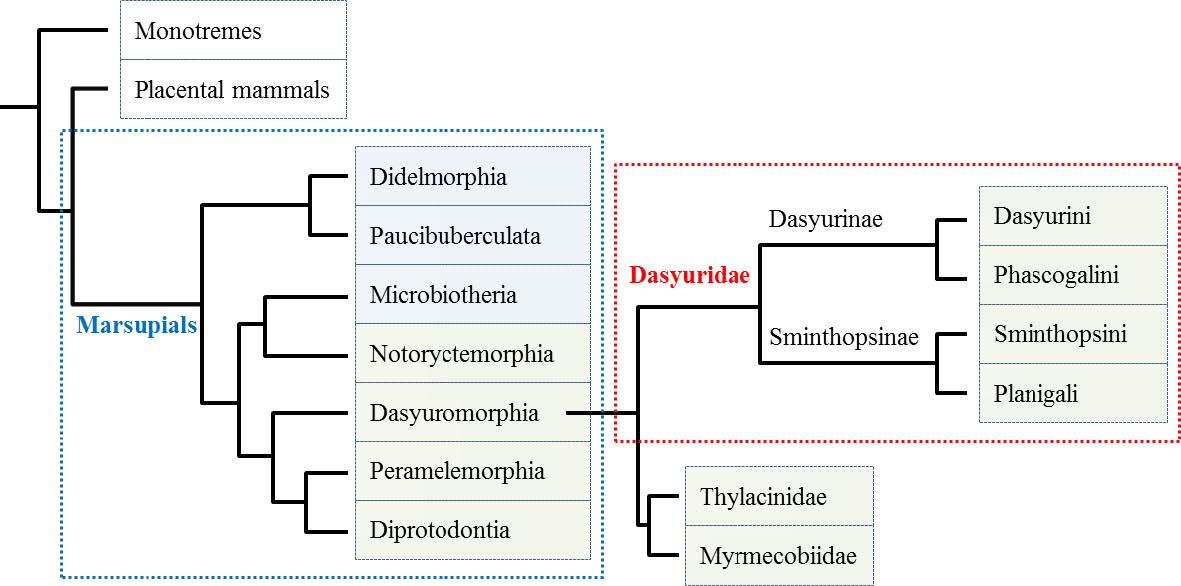
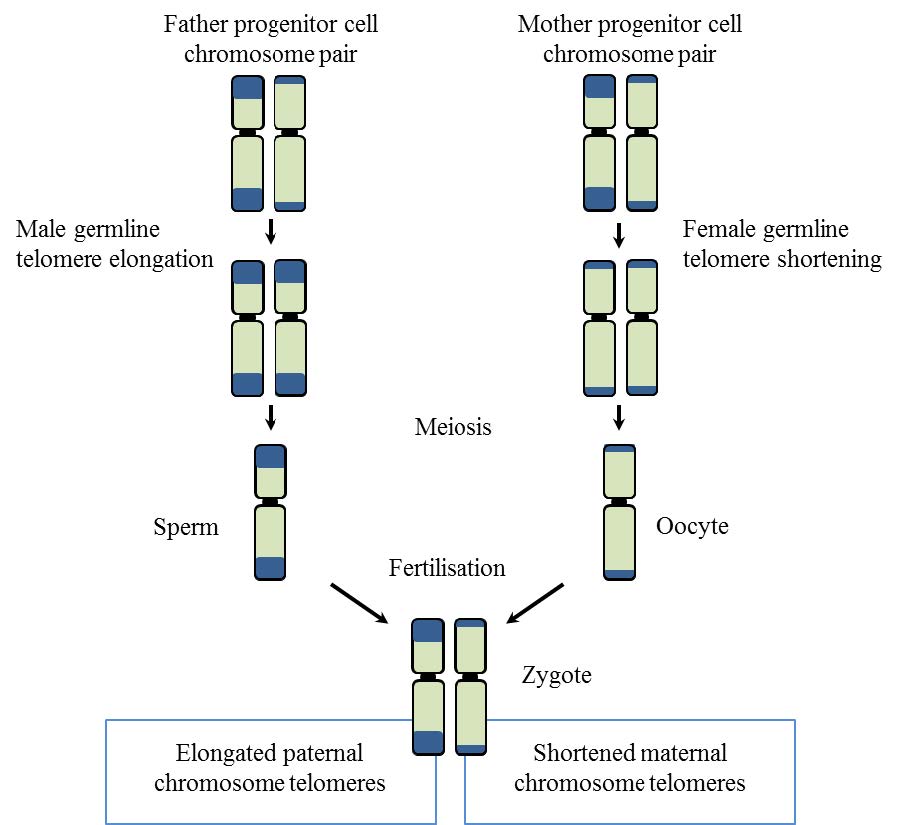
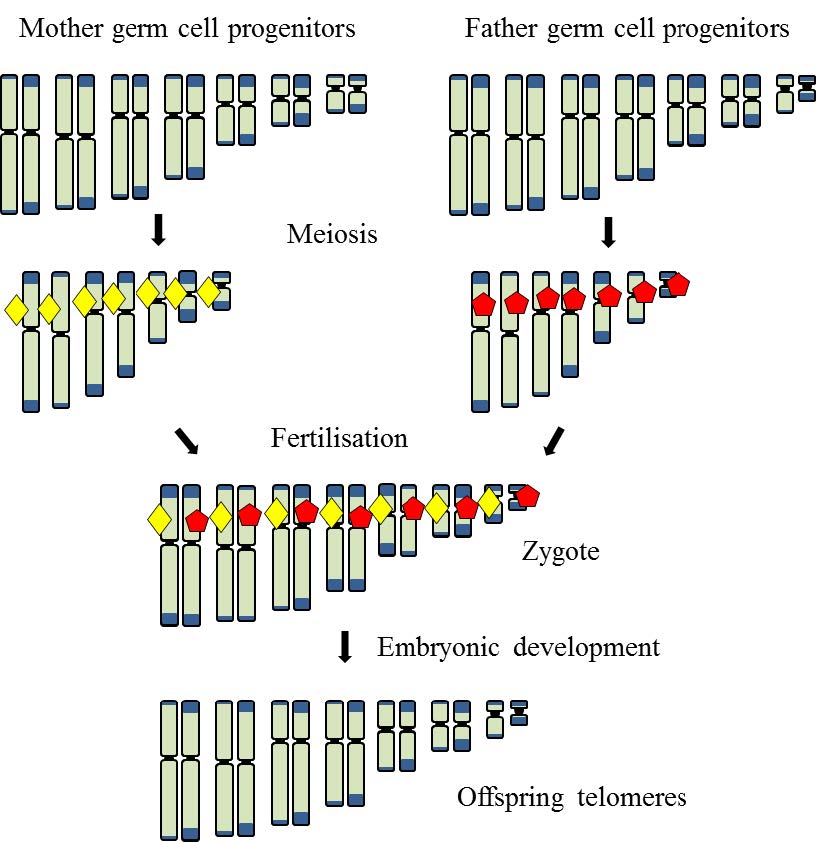
[1]	di Fagagna FD (2008) Living on a break: cellular senescence as a DNA-damage response. Nat Rev Cancer 8: 512-522. doi: 10.1038/nrc2440
[2]	Houben JMJ, Moonen HJJ, van Schooten FJ, et al. (2008) Telomere length assessment: Biomarker of chronic oxidative stress? Free Radic Biol Med 44: 235-246. doi: 10.1016/j.freeradbiomed.2007.10.001
[3]	von Zglinicki T (2002) Oxidative stress shortens telomeres. Trends Biochem Sci 27: 339-344. doi: 10.1016/S0968-0004(02)02110-2
[4]	Richter T, von Zglinicki T (2007) A continuous correlation between oxidative stress and telomere shortening in fibroblasts. Exp Gerontol 42: 1039-1042. doi: 10.1016/j.exger.2007.08.005
[5]	Artandi SE, Attardi LD (2005) Pathways connecting telomeres and p53 in senescence, apoptosis, and cancer. Biochem Biophys Res Commun 331: 881-890. doi: 10.1016/j.bbrc.2005.03.211
[6]	Haussmann MF, Marchetto NM (2010) Telomeres: Linking stress and survival, ecology and evolution. Curr Zool 56: 714-727.
[7]	Meyne J, Ratliff RL, Moyzis RK (1989) Conservation of the human telomere sequence (TTAGGG)n among vertebrates. Proc Natl Acad Sci U S A 86: 7049-7053. doi: 10.1073/pnas.86.18.7049
[8]	Moyzis RK, Buckingham JM, Cram LS, et al. (1988) A highly conserved repetitive DNA-sequence, (TTAGGG)n, present at the telomeres of human-chromosomes. Proc Natl Acad Sci U S A 85: 6622-6626. doi: 10.1073/pnas.85.18.6622
[9]	Olovnikov AM (1973) A theory of marginotomy. The incomplete copying of template margin in enzymic synthesis of polynucleotides and biological significance of the phenomenon. J Theor Biol 41: 181-190. doi: 10.1016/0022-5193(73)90198-7
[10]	Monaghan P (2010) Telomeres and life histories. the long and the short of it. Annu New York Acad Sci 1206: 130-142. doi: 10.1111/j.1749-6632.2010.05705.x
[11]	Murnane JP (2012) Telomere dysfunction and chromosome instability. Mutat Res 730: 28-36. doi: 10.1016/j.mrfmmm.2011.04.008
[12]	Hemann MT, Strong MA, Hao LY, et al. (2001) The shortest telomere, not average telomere length, is critical for cell viability and chromosome stability. Cell 107: 67-77. doi: 10.1016/S0092-8674(01)00504-9
[13]	Armanios M, Alder JK, Parry EM, et al. (2009) Short telomeres are sufficient to cause the degenerative defects associated with aging. Am J Hum Genet 85: 823-832. doi: 10.1016/j.ajhg.2009.10.028
[14]	di Fagagna FD, Reaper PM, Clay-Farrace L, et al. (2003) A DNA damage checkpoint response in telomere-initiated senescence. Nature 426: 194-198. doi: 10.1038/nature02118
[15]	Feng JL, Funk WD, Wang SS, et al. (1995) The RNA component of human telomerase. Science 269: 1236-1241. doi: 10.1126/science.7544491
[16]	Cesare AJ, Reddel RR (2010) Alternative lengthening of telomeres: models, mechanisms and implications. Nat Rev Genet 11: 319-330. doi: 10.1038/nrg2763
[17]	Kalmbach K, Robinson LG, Wang F, et al. (2014) Telomere length reprogramming in embryos and stem cells. Biomed Res Int 2014: 925121. doi: 10.1155/2014/925121
[18]	Nussey DH, Baird D, Barrett E, et al. (2014) Measuring telomere length and telomere dynamics in evolutionary biology and ecology. Methods Ecol Evol 5: 299-310. doi: 10.1111/2041-210X.12161
[19]	Salomons HM, Mulder GA, van de Zande L, et al. (2009) Telomere shortening and survival in free-living corvids. Proc Biol Sci 276: 3157-3165. doi: 10.1098/rspb.2009.0517
[20]	Bize P, Criscuolo F, Metcalfe NB, et al. (2009) Telomere dynamics rather than age predict life expectancy in the wild. Proc Biol Sci 276: 1679-1683. doi: 10.1098/rspb.2008.1817
[21]	Barrett ELB, Burke TA, Hammers M, et al. (2013) Telomere length and dynamics predict mortality in a wild longitudinal study. Mol Ecol 22: 249-259. doi: 10.1111/mec.12110
[22]	Kimura M, Hjelmborg JVB, Gardner JP, et al. (2008) Telomere length and mortality: A study of leukocytes in elderly Danish twins. Am J Epidemiol 167: 799-806. doi: 10.1093/aje/kwm380
[23]	Olsson M, Pauliny A, Wapstra E, et al. (2011) Sex differences in sand lizard telomere inheritance: paternal epigenetic effects increases telomere heritability and offspring survival. Plos One 6: 8.
[24]	Monaghan P (2014) Organismal stress, telomeres and life histories. J Exp Biol 217: 57-66. doi: 10.1242/jeb.090043
[25]	Hiyama K, Hirai Y, Kyoizumi S, et al. (1995) Activation of telomerase in human-lymphocytes and hematopoietic progenitor cells. J Immunol 155: 3711-3715.
[26]	Norrback KF, Roos G (1997) Telomeres and telomerase in normal and malignant haematopoietic cells. Eur J Cancer 33: 774-780. doi: 10.1016/S0959-8049(97)00059-2
[27]	Vera E, Blasco MA (2012) Beyond average: potential for measurement of short telomeres. Aging (Albany NY) 4: 379-392.
[28]	Delany ME, Daniels LM, Swanberg SE, et al. (2003) Telomeres in the chicken: genome stability and chromosome ends. Poult Sci 82: 917-926. doi: 10.1093/ps/82.6.917
[29]	Baird DM, Rowson J, Wynford-Thomas D, et al. (2003) Extensive allelic variation and ultrashort telomeres in senescent human cells. Nat Genet 33: 203-207. doi: 10.1038/ng1084
[30]	Gomes NMV, Ryder OA, Houck ML, et al. (2011) Comparative biology of mammalian telomeres: hypotheses on ancestral states and the roles of telomeres in longevity determination. Aging Cell 10: 761-768. doi: 10.1111/j.1474-9726.2011.00718.x
[31]	Wright WE, Shay JW (2000) Telomere dynamics in cancer progression and prevention: fundamental differences in human and mouse telomere biology. Nat Med 6: 849-851. doi: 10.1038/78592
[32]	Fick LJ, Fick GH, Li ZC, et al. (2012) Telomere length correlates with life span of dog breeds. Cell Rep 2: 1530-1536. doi: 10.1016/j.celrep.2012.11.021
[33]	Vera E, de Jesus BB, Foronda M, et al. (2012) The rate of increase of short telomeres predicts longevity in mammals. Cell Rep 2: 732-737. doi: 10.1016/j.celrep.2012.08.023
[34]	Pauliny A, Larsson K, Blomqvist D (2012) Telomere dynamics in a long-lived bird, the barnacle goose. BMC Evol Biol 12: 7. doi: 10.1186/1471-2148-12-7
[35]	Tackney J, Cawthon RM, Coxworth JE, et al. (2014) Blood cell telomere lengths and shortening rates of chimpanzee and human females. Am J Hum Biol 26: 452-460. doi: 10.1002/ajhb.22538
[36]	Bekaert S, De Meyer T, Van Oostveldt P (2005) Telomere attrition as ageing biomarker. Anticancer Res 25: 3011-3021.
[37]	Dantzer B, Fletcher QE (2015) Telomeres shorten more slowly in slow-aging wild animals than in fast-aging ones. Exp Gerontol 71: 38-47. doi: 10.1016/j.exger.2015.08.012
[38]	Nasir L, Devlin P, McKevitt T, et al. (2001) Telomere lengths and telomerase activity in dog tissues: A potential model system to study human telomere and telomerase biology. Neoplasia 3: 351-359. doi: 10.1038/sj.neo.7900173
[39]	Gomes NMV, Shay JW, Wright WE (2010) Telomere biology in Metazoa. FEBS Lett 584: 3741-3751. doi: 10.1016/j.febslet.2010.07.031
[40]	Aubert G, Lansdorp PM (2008) Telomeres and aging. Physiological Reviews 88: 557-579. doi: 10.1152/physrev.00026.2007
[41]	Armanios M, Blackburn EH (2012) The telomere syndromes. Nat Rev Genet 13: 693-704. doi: 10.1038/nrg3246
[42]	O'Hare TH, Delany ME (2011) Molecular and cellular evidence for the alternative lengthening of telomeres (ALT) mechanism in chicken. Cytogenet Genome Res 135: 65-78. doi: 10.1159/000330125
[43]	Neumann AA, Watson CM, Noble JR, et al. (2013) Alternative lengthening of telomeres in normal mammalian somatic cells. Genes Dev 27: 18-23. doi: 10.1101/gad.205062.112
[44]	Reichert S, Rojas ER, Zahn S, et al. (2015) Maternal telomere length inheritance in the king penguin. Heredity 114: 10-16. doi: 10.1038/hdy.2014.60
[45]	Njajou OT, Cawthon RM, Damcott CM, et al. (2007) Telornere length is paternally inherited and is associated with parental lifespan. Proc Natl Acad Sci U S A 104: 12135-12139. doi: 10.1073/pnas.0702703104
[46]	Barrett ELB, Richardson DS (2011) Sex differences in telomeres and lifespan. Aging Cell 10: 913-921. doi: 10.1111/j.1474-9726.2011.00741.x
[47]	Bender HS, Murchison EP, Pickett HA, et al. (2012) Extreme telomere length dimorphism in the Tasmanian devil and related marsupials suggests parental control of telomere length. Plos One 7: 10.
[48]	Delany ME, Gessaro TM, Rodrigue KL, et al. (2007) Chromosomal mapping of chicken mega-telomere arrays to GGA9, 16, 28 and W using a cytogenomic approach. Cytogenet Genome Res 117: 54-63. doi: 10.1159/000103165
[49]	Zhdanova NS, Karamisheva TV, Minina J, et al. (2005) Unusual distribution pattern of telomeric repeats in the shrews Sorex araneus and Sorex granarius. Chromosome Res 13: 617-625. doi: 10.1007/s10577-005-0988-3
[50]	Lansdorp PM, Verwoerd NP, vandeRijke FM, et al. (1996) Heterogeneity in telomere length of human chromosomes. Hum Mol Genet 5: 685-691. doi: 10.1093/hmg/5.5.685
[51]	Verhulst S, Aviv A, Benetos A, et al. (2013) Do leukocyte telomere length dynamics depend on baseline telomere length? An analysis that corrects for 'regression to the mean'. Eur J Epidemiol 28: 859-866.
[52]	Surrallés J, Hande MP, Marcos R, et al. (1999) Accelerated telomere shortening in the human inactive X chromosome. Am J Hum Genet 65: 1617-1622. doi: 10.1086/302665
[53]	Stindl R (2004) Tying it all together: telomeres, sexual size dimorphism and the gender gap in life expectancy. Med Hypotheses 62: 151-154. doi: 10.1016/S0306-9877(03)00316-5
[54]	Seluanov A, Chen ZX, Hine C, et al. (2007) Telomerase activity coevolves with body mass not lifespan. Aging Cell 6: 45-52. doi: 10.1111/j.1474-9726.2006.00262.x
[55]	Yang FT, Graphodatsky AS, O'Brien PCM, et al. (2000) Reciprocal chromosome painting illuminates the history of genome evolution of the domestic cat, dog and human. Chromosome Res 8: 393-404. doi: 10.1023/A:1009210803123
[56]	Grasman J, Salomons HM, Verhulst S (2011) Stochastic modeling of length-dependent telomere shortening in Corvus monedula. J Theor Biol 282: 1-6. doi: 10.1016/j.jtbi.2011.04.026
[57]	Sabourin M, Tuzon CT, Zakian VA (2007) Telomerase and Tel1p preferentially associate with short telomeres in S-cerevisiae. Mol Cell 27: 550-561. doi: 10.1016/j.molcel.2007.07.016
[58]	Teixeira MT, Arneric M, Sperisen P, et al. (2004) Telomere length homeostasis is achieved via a switch between telomerase-extendible and -nonextendible states. Cell 117: 323-335. doi: 10.1016/S0092-8674(04)00334-4
[59]	Bauch C, Becker PH, Verhulst S (2014) Within the genome, long telomeres are more informative than short telomeres with respect to fitness components in a long-lived seabird. Mol Ecol 23: 300-310. doi: 10.1111/mec.12602
[60]	Blasco MA, Lee HW, Hande MP, et al. (1997) Telomere shortening and tumor formation by mouse cells lacking telomerase RNA. Cell 91: 25-34. doi: 10.1016/S0092-8674(01)80006-4
[61]	Meyne J, Baker RJ, Hobart HH, et al. (1990) Distribution of non-telomeric sites of the (TTAGGG)n telomeric sequence in vertebrate chromosomes. Chromosoma 99: 3-10. doi: 10.1007/BF01737283
[62]	Nanda I, Schrama D, Feichtinger W, et al. (2002) Distribution of telomeric (TTAGGG)(n) sequences in avian chromosomes. Chromosoma 111: 215-227. doi: 10.1007/s00412-002-0206-4
[63]	McPherson MC, Robinson CM, Gehlen LP, et al. (2014) Comparative cytogenomics of poultry: mapping of single gene and repeat loci in the Japanese quail (Coturnix japonica). Chromosome Res 22: 71-83. doi: 10.1007/s10577-014-9411-2
[64]	Pokorná MJ, Rovatsos M, Kratochvíl L (2014) Sex chromosomes and karyotype of the (nearly) mythical creature, the gila monster, Heloderma suspectum (Squamata: Helodermatidae). Plos One 9: 7.
[65]	Faria KC, Marchesin SRC, Moreira PRL, et al. (2009) New insights into telomeric DNA sequence (TTAGGG)(n) location in bat chromosomes. Genet Mol Res 8: 1079-1084. doi: 10.4238/vol8-3gmr637
[66]	Andrades-Miranda J, Zanchin NIT, Oliveira LFB, et al. (2002) (T2AG3)n telomeric sequence hybridization indicating centric fusion rearrangements in the karyotype of the rodent Oryzomys subflavus. Genetica 114: 11-16. doi: 10.1023/A:1014645731798
[67]	Ventura K, Sato-Kuwabara Y, Fagundes V, et al. (2012) Phylogeographic structure and karyotypic diversity of the Brazilian shrew mouse (Blarinomys breviceps, Sigmodontinae) in the Atlantic forest. Cytogenet Genome Res 138: 19-30. doi: 10.1159/000341887
[68]	Rovatsos MT, Marchal JA, Romero-Fernández I, et al. (2011) Rapid, independent, and extensive amplification of telomeric repeats in pericentromeric regions in karyotypes of arvicoline rodents. Chromosome Res 19: 869-882. doi: 10.1007/s10577-011-9242-3
[69]	Carvalho BD, Mattevi MS (2000) (T(2)AG(3))(n) telomeric sequence hybridization suggestive of centric fusion in karyotype marsupials evolution. Genetica 108: 205-210. doi: 10.1023/A:1004157915077
[70]	Go Y, Rakotoarisoa G, Kawamoto Y, et al. (2000) PRINS analysis of the telomeric sequence in seven lemurs. Chromosome Res 8: 57-65. doi: 10.1023/A:1009279203886
[71]	Ocalewicz K (2013) Telomeres in fishes. Cytogenet Genome Res 141: 114-125. doi: 10.1159/000354278
[72]	Harley CB, Futcher AB, Greider CW (1990) Telomeres shorten during aging of human fibroblasts. Nature 345: 458-460. doi: 10.1038/345458a0
[73]	Zhdanova NS, Draskovic I, Minina JM, et al. (2014) Recombinogenic telomeres in diploid Sorex granarius (Soricidae, Eulipotyphla) fibroblast cells. Mol Cell Biol 34: 2786-2799. doi: 10.1128/MCB.01697-13
[74]	Zhdanova NS, Minina JM, Karamisheva TV, et al. (2007) The very long telomeres in Sorex granarius (Soricidae, Eulipothyphla) contain ribosomal DNA. Chromosome Res 15: 881-890. doi: 10.1007/s10577-007-1170-x
[75]	Liu WS, Fredga K (1999) Telomeric (TTAGGG)(n) sequences are associated with nucleolus organizer regions (NORs) in the wood lemming. Chromosome Res 7: 235-240. doi: 10.1023/A:1009255517764
[76]	Rakotoarisoa G, Hirai Y, Go Y, et al. (2000) Chromosomal localization of 18S rDNA and telomere sequence in the aye-aye, Daubentonia madagascariensis. Genes Genet Syst 75: 299-303. doi: 10.1266/ggs.75.299
[77]	Santani A, Raudsepp T, Chowdhary BP (2002) Interstitial telomeric sites and NORs in Hartmann's zebra (Equus zebra hartmannae) chromosomes. Chromosome Res 10: 527-534. doi: 10.1023/A:1020945400949
[78]	Supiwong W, Liehr T, Cioffi MB, et al. (2013) Karyotype and cytogenetic mapping of 9 classes of repetitive DNAs in the genome of the naked catfish Mystus bocourti (Siluriformes, Bagridae). Mol Cytogenet 6: 7. doi: 10.1186/1755-8166-6-7
[79]	Laguna MM, Amaro RC, Mott T, et al. (2010) Karyological study of Amphisbaena ridleyi (Squamata, Amphisbaenidae), an endemic species of the Archipelago of Fernando de Noronha, Pernambuco, Brazil. Genet Mol Biol 33: 57-61. doi: 10.1590/S1415-47572010005000009
[80]	Srikulnath K, Uno Y, Nishida C, et al. (2013) Karyotype evolution in monitor lizards: cross-species chromosome mapping of cDNA reveals highly conserved synteny and gene order in the Toxicofera clade. Chromosome Res 21: 805-819. doi: 10.1007/s10577-013-9398-0
[81]	Srikulnath K, Uno Y, Matsubara K, et al. (2011) Chromosomal localization of the 18S-28S and 5S rRNA genes and (TTAGGG)n sequences of butterfly lizards (Leiolepis belliana belliana and Leiolepis boehmei, Agamidae, Squamata). Genet Mol Biol 34: 582-586.
[82]	Srikulnath K, Matsubara K, Uno Y, et al. (2009) Karyological characterization of the butterfly lizard (Leiolepis reevesii rubritaeniata, Agamidae, Squamata) by molecular cytogenetic approach. Cytogenet Genome Res 125: 213-223. doi: 10.1159/000230005
[83]	Burt DW (2002) Origin and evolution of avian microchromosomes. Cytogenet Genome Res 96: 97-112.
[84]	Pokorná, M., Rens W, Rovatsos M, et al. (2014) A ZZ/ZW sex chromosome system in the thick-tailed gecko (Underwoodisaurus milii; Squamata: Gekkota: Carphodactylidae), a member of the ancient gecko lineage. Cytogenet Genome Res 142: 190-196.
[85]	Matsubara K, Uno Y, Srikulnath K, et al. (2015) No interstitial telomeres on autosomes but remarkable amplification of telomeric repeats on the W sex chromosome in the sand lizard (Lacerta agilis). J Hered 106: 753-757. doi: 10.1093/jhered/esv083
[86]	Bulazel K, Metcalfe C, Ferreri GC, et al. (2006) Cytogenetic and molecular evaluation of centromere-associated DNA sequences from a marsupial (Macropodidae : Macropus rufogriseus) X chromosome. Genetics 172: 1129-1137.
[87]	Zhdanova NS, Rogozina Iu I, Minina Iu M, et al. (2009) Telomeric DNA allocation in chromosomes of common shrew Sorex araneus, Eulipotyphla. Tsitologiia 51: 577-584.
[88]	Pellegrino KCM, Rodrigues MT, Yonenaga-Yassuda Y (1999) Chromosomal evolution in the Brazilian lizards of genus Leposoma (Squamata, Gymnophthalmidae) from Amazon and Atlantic rain forests: banding patterns and FISH of telomeric sequences. Hereditas 131: 15-21.
[89]	Foote CG, Vleck D, Vleck CM (2013) Extent and variability of interstitial telomeric sequences and their effects on estimates of telomere length. Mol Ecol Resour 13: 417-428. doi: 10.1111/1755-0998.12079
[90]	Heidinger BJ, Blount JD, Boner W, et al. (2012) Telomere length in early life predicts lifespan. Proc Natl Acad Sci U S A 109: 1743-1748. doi: 10.1073/pnas.1113306109
[91]	Angelier F, Vleck CM, Holberton RL, et al. (2013) Telomere length, non-breeding habitat and return rate in male American redstarts. Funct Ecol 27: 342-350. doi: 10.1111/1365-2435.12041
[92]	Bateson M, Brilot BO, Gillespie R, et al. (2015) Developmental telomere attrition predicts impulsive decision-making in adult starlings. Proc Biol Sci 282: 7.
[93]	Young RC, Kitaysky AS, Barger CP, et al. (2015) Telomere length is a strong predictor of foraging behavior in a long-lived seabird. Ecosphere 6: 26. doi: 10.1890/ES14-00331.1
[94]	Mizutani Y, Tomita N, Niizuma Y, et al. (2013) Environmental perturbations influence telomere dynamics in long-lived birds in their natural habitat. Biol Lett 9: 4.
[95]	Schultner J, Moe B, Chastel O, et al. (2014) Migration and stress during reproduction govern telomere dynamics in a seabird. Biol Lett 10: 4.
[96]	Pardue ML, DeBaryshe PG (2011) Retrotransposons that maintain chromosome ends. Proc Natl Acad Sci U S A 108: 20317-20324. doi: 10.1073/pnas.1100278108
[97]	Delange T, Shiue L, Myers RM, et al. (1990) Structure and variability of human-chromosome ends. Mol Cell Biol 10: 518-527. doi: 10.1128/MCB.10.2.518
[98]	Lee M, Hills M, Conomos D, et al. (2014) Telomere extension by telomerase and ALT generates variant repeats by mechanistically distinct processes. Nucl Acids Res 42: 1733-1746. doi: 10.1093/nar/gkt1117
[99]	Ujvari B, Pearse AM, Taylor R, et al. (2012) Telomere dynamics and homeostasis in a transmissible cancer. Plos One 7: 8.
[100]	Hrdličková R, Nehyba J, Lim SL, et al. (2012) Insights into the evolution of mammalian telomerase: Platypus TERT shares similarities with genes of birds and other reptiles and localizes on sex chromosomes. BMC Genom 13: 20. doi: 10.1186/1471-2164-13-20
[101]	Pagnozzi JM, Ditchfield AD, Yonenaga-Yassuda Y (2002) Mapping the distribution of the interstitial telomeric (TTAGGG)(n) sequences in eight species of Brazilian marsupials (Didelphidae) by FISH and the correlation with constitutive heterochromatin. Do ITS represent evidence for fusion events in American marsupials? Cytogenet Genome Res 98: 278-284.
[102]	Svartman M, Vianna-Morgante AM (1998) Karyotype evolution of marsupials: from higher to lower diploid numbers. Cytogenet Cell Genet 82: 263-266. doi: 10.1159/000015114
[103]	Wang X, Douglas KC, VandeBerg JL, et al. (2014) Chromosome-wide profiling of X-chromosome inactivation and epigenetic states in fetal brain and placenta of the opossum, Monodelphis domestica. Genome Res 24: 70-83. doi: 10.1101/gr.161919.113
[104]	Deakin JE, Chaumeil J, Hore TA, et al. (2009) Unravelling the evolutionary origins of X chromosome inactivation in mammals: insights from marsupials and monotremes. Chromosome Res 17: 671-685. doi: 10.1007/s10577-009-9058-6
[105]	Douglas KC, Wang X, Jasti M, et al. (2014) Genome-wide histone state profiling of fibroblasts from the opossum, Monodelphis domestica, identifies the first marsupial-specific imprinted gene. BMC Genom 15: 14. doi: 10.1186/1471-2164-15-14
[106]	Liu L, Bailey SM, Okuka M, et al. (2007) Telomere lengthening early in development. Nat Cell Biol 9: 1436-U1185. doi: 10.1038/ncb1664
[107]	Pickett HA, Reddel RR (2012) The role of telomere trimming in normal telomere length dynamics. Cell Cycle 11: 1309-1315. doi: 10.4161/cc.19632
[108]	Bryan TM, Englezou A, Gupta J, et al. (1995) Telomere elongation in immortal human-cells without detectable telomerase activity. EMBO J 14: 4240-4248.
[109]	Cerone MA, Londoño-Vallejo JA, Bacchetti S (2001) Telomere maintenance by telomerase and by recombination can coexist in human cells. Hum Mol Genet 10: 1945-1952. doi: 10.1093/hmg/10.18.1945
[110]	Grobelny JV, Kulp-McEliece M, Broccoli D (2001) Effects of reconstitution of telomerase activity on telomere maintenance by the alternative lengthening of telomeres (ALT) pathway. Hum Mol Genet 10: 1953-1961. doi: 10.1093/hmg/10.18.1953
[111]	Perrem K, Colgin LM, Neumann AA, et al. (2001) Coexistence of alternative lengthening of telomeres and telomerase in hTERT-transfected GM847 cells. Mol Cell Biol 21: 3862-3875. doi: 10.1128/MCB.21.12.3862-3875.2001
[112]	Naylor R, Richardson SJ, McAllan BM (2008) Boom and bust: a review of the physiology of the marsupial genus Antechinus. J Comp Physiol B 178: 545-562. doi: 10.1007/s00360-007-0250-8
[113]	Fisher DO, Dickman CR, Jones ME, et al. (2013) Sperm competition drives the evolution of suicidal reproduction in mammals. Proc Natl Acad Sci U S A 110: 17910-17914. doi: 10.1073/pnas.1310691110
[114]	Bradshaw SD (2015) A state of non-specific tension in living matter? Stress in Australian animals. Gen Comp Endocrinol [in press].
[115]	Weng NP (2012) Telomeres and immune competency. Curr Opin Immunol 24: 470-475. doi: 10.1016/j.coi.2012.05.001
[116]	Krajewski C, Woolley PA, Westerman M (2000) The evolution of reproductive strategies in dasyurid marsupials: implications of molecular phylogeny. Biol J Linn Soc 71: 417-435.
[117]	Barros CS, Püttker T, Pardini R (2015) Timing and environmental cues associated with triggering of reproductive activity in Atlantic forest marsupials. Mamm Biol 80: 141-147.
[118]	Leiner NO, Setz EZF, Silva WR (2008) Semelparity and factors affecting the reproductive activity of the Brazilian slender opossum (Marmosops paulensis) in southeastern Brazil. J Mammal 89: 153-158. doi: 10.1644/07-MAMM-A-083.1
[119]	Svartman M, Vianna-Morgante AM (2003) Conservation of chromosomal location of nucleolus organizer in American marsupials (Didelphidae). Genetica 118: 11-16. doi: 10.1023/A:1022986600017
[120]	Geiser F, Ruf T (1995) Hibernation versus daily torpor in mammals and birds - physiological variables and classification of torpor patterns. Physiol Zool 68: 935-966. doi: 10.1086/physzool.68.6.30163788
[121]	Giroud S, Zahn S, Criscuolo FO, et al. (2014) Late-born intermittently fasted juvenile garden dormice use torpor to grow and fatten prior to hibernation: consequences for ageing processes. Proc Biol Sci 281: 8.
[122]	Turbill C, Smith S, Deimel C, et al. (2012) Daily torpor is associated with telomere length change over winter in Djungarian hamsters. Biol Lett 8: 304-307. doi: 10.1098/rsbl.2011.0758
[123]	Turbill C, Ruf T, Smith S, et al. (2013) Seasonal variation in telomere length of a hibernating rodent. Biol Lett 9: 4.
[124]	Mitchell KJ, Pratt RC, Watson LN, et al. (2014) Molecular phylogeny, biogeography, and habitat preference evolution of marsupials. Mol Biol Evol 31: 2322-2330. doi: 10.1093/molbev/msu176
[125]	Gallus S, Janke A, Kumar V, et al. (2015) Disentangling the relationship of the Australian marsupial orders using retrotransposon and evolutionary network analyses. Genome Biol Evol 7: 985-992. doi: 10.1093/gbe/evv052
[126]	Phillips MJ, Bennett TH, Lee MSY (2009) Molecules, morphology, and ecology indicate a recent, amphibious ancestry for echidnas. Proc Natl Acad Sci U S A 106: 17089-17094. doi: 10.1073/pnas.0904649106
[127]	Nilsson MA, Arnason U, Spencer PBS, et al. (2004) Marsupial relationships and a timeline for marsupial radiation in South Gondwana. Gene 340: 189-196. doi: 10.1016/j.gene.2004.07.040
[128]	Nilsson MA, Churakov G, Sommer M, et al. (2010) Tracking marsupial evolution using archaic genomic retroposon insertions. Plos Biol 8: 9.
[129]	Griner LA (1979) Neoplasms in Tasmanian devils (Sarcophilus-harrisii). J Natl Cancer Inst 62: 589-595.
[130]	Canfield PJ, Hartley WJ, Reddacliff GL (1990) Spontaneous proliferations in Australian marsupials - a survey and review .2. dasyurids and bandicoots. J Comp Pathol 103: 147-158. doi: 10.1016/S0021-9975(08)80171-5
[131]	Canfield PJ, Cunningham AA (1993) Disease and mortality in Australasian marsupials held at London-zoo, 1872-1972. J Zoo Wildl Med 24: 158-167.
[132]	Artandi SE, DePinho RA (2010) Telomeres and telomerase in cancer. Carcinogenesis 31: 9-18. doi: 10.1093/carcin/bgp268
[133]	Lachish S, Jones M, McCallum H (2007) The impact of disease on the survival and population growth rate of the Tasmanian devil. J Anim Ecol 76: 926-936. doi: 10.1111/j.1365-2656.2007.01272.x
[134]	Ingles ED, Deakin JE (2015) Global DNA methylation patterns on marsupial and devil facial tumour chromosomes. Mol Cytogenet 8: 74. doi: 10.1186/s13039-015-0176-x
[135]	Ozturk S, Sozen B, Demir N (2014) Telomere length and telomerase activity during oocyte maturation and early embryo development in mammalian species. Mol Hum Reprod 20: 15-30. doi: 10.1093/molehr/gat055
[136]	Ozturk S (2015) Telomerase activity and telomere length in male germ cells. Biol Reprod 92: 11. doi: 10.1095/biolreprod.114.123679

Reader Comments

Your name:*

Email:*
© 2016 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)