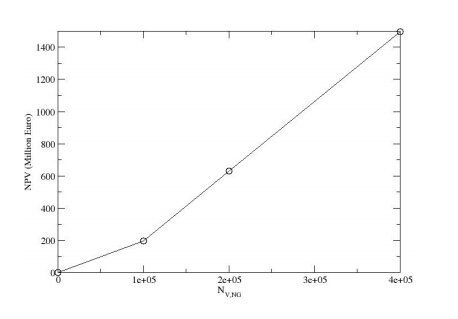
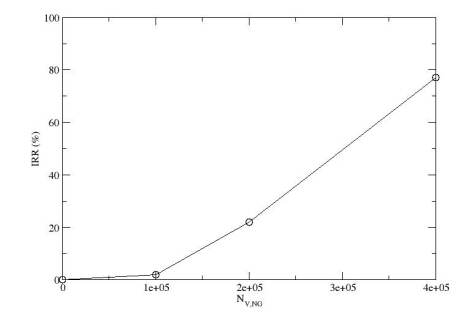
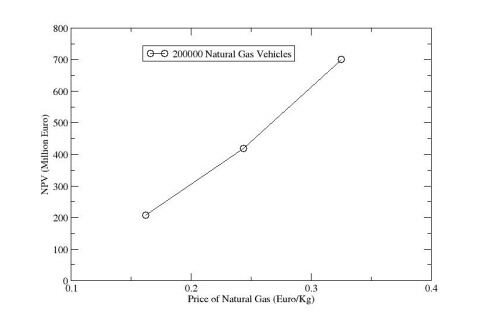
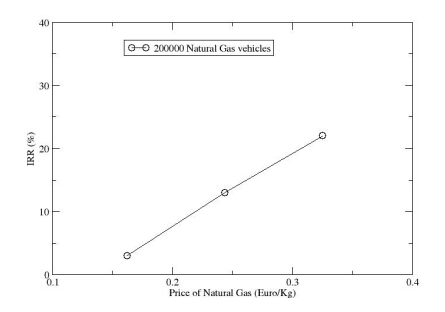
There is recent interest for the utilisation of natural gas for empowering the internal combustion engines (ICE) of vehicles. The production of novel natural gas ICE for vehicles, as well as the conversion of existing gasoline fuelled ICE of vehicles to natural gas fuelled ICE are new technologies which require to be analysed and assessed. The objective of the present study is to examine the adaptation of natural gas as vehicle fuel and carry out a technical analysis and an economical feasibility analysis of the two types of ICE vehicles, namely gasoline and natural gas fuelled vehicles. The technical model uses the physical properties of the two fuels and the performance factors of internal combustion engines including brake thermal efficiency. The resulting exhaust gas emissions are also estimated by the technical model using combustion calculations which provide the expected levels of exhaust gas emissions. Based on the analysis with the technical model, comparisons of the two types of engines are performed. Furthermore, the estimated performance characteristics of the two types of engines, along with local statistical data on annual fuel imports and annual fuel consumption for transportation and data on the vehicles fleet for the case study of Cyprus are used as input in the economical model. For the base year 2013, data of natural gas price is also used in the economical model. The economical model estimates the capital cost, the carbon dioxide emissions avoidance of fines, the net present value and the internal rate of return of the investment of large scale adaptation of natural gas fuelled vehicles for the case study. From the results and comparisons, conclusions are drawn and recommendations are provided for the adaptation of natural gas vehicles which can provide improved performance with reduced pollutant emissions.
1.
Motivations
In [1,pp. 42 and 55], we find the Maclaurin power series expansions
and
for $ x^2 < \frac{\pi^2}4 $, where $ B_{2k} $ denotes the Bernoulli numbers which can be generated by
Let
and
In the recent paper [2], Li and Qi obtained the following two results:
1. The function $ F(x) $ defined by (2) can be expanded into the Maclaurin power series expansion
for $ |x| < 2\pi $, where
2. The function $ R(x) $ defined by (3) decreasingly maps $ \bigl[0, \frac{\pi}2\bigr] $ onto $ \bigl[0, \frac{1}{6}\bigr] $.
We now introduce several new even functions as follows:
1. The first function is
2. The second function is
It is clear that $ F_1(x) = F(x) $ on $ (-2\pi, 2\pi) $.
3. Generally, the third function we are introducing is
for $ n\ge2 $.
Since the double inequality
is valid for $ n\ge2 $ and $ x\in\mathbb{R}\setminus\{0\} $, see [3,p. 326], the function $ F_n(x) $ is significantly defined for $ n\ge2 $ and $ x\in\mathbb{R} $.
As a stronger version of the double inequality (8), the following positive, nonnegative, decreasing, and concave properties of the normalized tail
for $ x\in(0, \infty) $ and $ n\ge1 $ were discovered in the paper [4]:
(a) the normalized tail $ {\rm{CosR}}_1(x) $ is nonnegative on $ (0, \infty) $ and is decreasing on $ [0, 2\pi] $;
(b) the normalized tail $ {\rm{CosR}}_n(x) $ for $ n\ge2 $ is decreasing and positive on $ (0, \infty) $;
(c) the normalized tail $ {\rm{CosR}}_1(x) $ is concave on $ (0, x_0) $, where $ x_0\in\bigl(\frac{\pi}{2}, \pi\bigr) $ is the first positive zero of the equation
and the normalized remainder $ {\rm{CosR}}_n(x) $ for $ n\ge2 $ is concave on $ (0, \pi) $.
Comparing the definition in (9) with those in (6) and (7) leads to the following conclusions:
(a) the function $ F_1(x) $ is decreasing and negative on $ (0, 2\pi) $, and is concave on $ (0, x_0) $;
(b) the function $ F_n(x) $ for $ n\ge2 $ is decreasing and negative on $ (0, \infty) $, and is concave on $ (0, \pi) $.
4. The fourth function $ R_{m, n}(x) $ for $ n > m\ge0 $ is defined
(a) when $ n > m = 0 $, by
(b) when $ n > m = 1 $, by
(c) when $ n > m\ge2 $, by
It is easy to see that $ R_{0, 1}(x) = R(x) $.
We now propose the following three problems:
1. Is the function $ F_n(x) $ for $ n\ge0 $ decreasing and concave?
2. What is the Maclaurin power series expansion of $ F_n(x) $ for $ n\ge0 $ around the origin $ x = 0 $?
3. Is the function $ R_{m, n}(x) $ for $ n > m\ge0 $ decreasing?
The first problem for the case $ n = 0 $ is immediate: the even function $ F_0(x) = \ln\cos x $ is decreasing and, by virtue of the series expansion (1), is concave in $ x\in\bigl(0, \frac{\pi}{2}\bigr) $. The first problem for the case $ n\ge1 $ was solved in the paper [4], as mentioned above. In a word, the first problem has been thoroughly solved.
The second problem for $ n = 0 $ is just the Maclaurin power series expansion (1). The second problem for $ n = 1 $ was solved by the Maclaurin series expansion (4), which was established in [2,Section 3].
The third problem for $ (m, n) = (0, 1) $ was solved in [2,Section 4], as mentioned above.
In this paper, we will give a full answer to the second problem for all cases $ n\ge2 $, solve the first problem on the interval $ \bigl(0, \frac{\pi}{2}\bigr) $ once again, and discuss the third problem for the case $ n\ge2 $.
2.
What is the Maclaurin power series expansion of $ F_n(x) $?
In this section, we solve the second problem: what is the Maclaurin power series expansion of $ F_n(x) $ for $ n\ge0 $ around the origin $ x = 0 $?
Theorem 1. For $ n\ge0 $, let
and
Then the even function $ F_n(x) $ for $ n\ge0 $ can be expanded into
Proof. Let $ u(x) $ and $ v(x)\ne0 $ be two $ n $-time differentiable functions on an interval $ I $ for a given integer $ n\ge0 $. Then the $ n $th derivative of the ratio $ \frac{u(x)}{v(x)} $ is
where the matrix
the matrix $ U_{(n+1)\times1}(x) $ is an $ (n+1)\times1 $ matrix whose elements satisfy $ u_{k, 1}(x) = u^{(k-1)}(x) $ for $ 1\le k\le n+1 $, the matrix $ V_{(n+1)\times n}(x) $ is an $ (n+1)\times n $ matrix whose elements are $ v_{\ell, j}(x) = \binom{\ell-1}{j-1}v^{(\ell-j)}(x) $ for $ 1\le \ell\le n+1 $ and $ 1\le j\le n $, and the notation $ |W_{(n+1)\times(n+1)}(x)| $ denotes the determinant of the $ (n+1)\times(n+1) $ matrix $ W_{(n+1)\times(n+1)}(x) $. This is a slight reformulation of [5,p. 40,Exercise 5].
Let
Then, straightforward differentiation yields
for $ \ell\ge0 $. Considering Expression (14) and applying the derivative formula (12) for the ratio of two differentiable functions, we acquire
for $ m\ge1 $. In other words, for $ m\ge1 $,
Consequently, the even function $ F_n(x) $ can be expanded into
The proof of Theorem 1 is completed.
□
Remark 1. When $ n = 0 $, a direct computation gives
Then, the first two terms of the Maclaurin power series expansion of the function $ \ln\cos x $ are
which coincide with the first two terms in the series expansion (1).
When $ n = 1 $, straightforward computation shows
Then, the first two terms of the Maclaurin power series expansion of the function $ F(x) $ defined by (2) are
which coincide with the first two terms in the series expansion (4).
Remark 2. Comparing the Maclaurin series expansions (1) and (4) with the series expansion (11) reveals
for $ m\ge1 $. The first formula in (13) is a new determinantal expression for the Bernoulli numbers $ B_{2m} $ with $ m\ge1 $.
Additionally, we point out that, in the papers [2,6,7,8,9,10], there have been many related results, but different from and more complicated than the first one in (13), and plenty of closely-related references on closed-form formulas and determinantal expressions for the Bernoulli numbers and polynomials $ B_{2m} $ and $ B_{m}(x) $ with $ m\in\mathbb{N} $.
3.
Is the function $ F_n(x) $ for $ n\ge0 $ decreasing and concave on $ \bigl(0, \frac{\pi}{2}\bigr) $?
In this section, we give an alternative and united proof of a modification of the first problem: is the function $ F_n(x) $ for $ n\ge0 $ decreasing and concave on $ \bigl(0, \frac{\pi}{2}\bigr) $?
Theorem 2. For $ n = 0 $ and $ n\ge2 $, the even function $ F_n(x) $ defined by (5) and (7) is decreasing and concave on $ \bigl(0, \frac{\pi}{2}\bigr) $. The even function $ F_1(x) $ defined in (6) is decreasing on $ (0, 2\pi) $ and $ (x_k, 2(k+1)\pi) $ for $ k\in\mathbb{N} $, while it is increasing on $ (2k\pi, x_k) $ for $ k\in\mathbb{N} $, where $ x_k\in(2k\pi, 2(k+1)\pi) $ for $ k\in\mathbb{N} $ is the zero of the equation $ \tan\frac{x}{2} = \frac{x}{2} $ on $ (0, \infty) $.
Proof. In the first section of this paper, it has been immediately verified that the function $ F_0(x) = \ln\cos x $ is decreasing and concave on $ \bigl(0, \frac{\pi}{2}\bigr) $.
The derivative of $ F_1(x) $ can be written as
Therefore, the derivative $ F_1'(x) $ is negative on $ (0, 2\pi) $, is positive on $ (2k\pi, x_k) $, and is negative on $ (x_k, 2(k+1)\pi) $ for $ k\in\mathbb{N} $, where $ x_k\in(2k\pi, 2(k+1)\pi) $ for $ k\in\mathbb{N} $ is the zero of the equation $ \tan\frac{x}{2} = \frac{x}{2} $ on $ (0, \infty) $. Accordingly, the function $ F_1(x) $ is decreasing on $ (0, 2\pi) $ and $ (x_k, 2(k+1)\pi) $, while it is increasing on $ (2k\pi, x_k) $ for $ k\in\mathbb{N} $.
On the interval $ \bigl(0, \frac{\pi}{2}\bigr) $ and for $ n\ge2 $, the function $ F_n(x) $ can be written as
Its first derivative is
By virtue of [11,Theorem 7.6], or in view of the results at the site https://math.stackexchange.com/a/477549 (accessed on 18 January 2024), we derive the integral representation
for $ n\ge1 $ and $ x\in\mathbb{R} $. From the integral representation (15), it follows that
and
for $ n\ge1 $, where we used the inequalities $ \cos x > 0 $ and $ x-\tan x < 0 $ in $ x\in\bigl(0, \frac{\pi}{2}\bigr) $. This means that
for $ n\ge1 $. In conclusion, the function $ F_n(x) $ for $ n\ge1 $ is decreasing on $ \bigl(0, \frac{\pi}{2}\bigr) $.
It is known that
Straightforward differentiating and simplifying give
Therefore, a direct differentiation and simplification yield
on $ \bigl(0, \frac{\pi}{2}\bigr) $ for $ n\ge1 $. Accordingly, the function $ F_n(x) $ for $ n\ge1 $ is concave on $ \bigl(0, \frac{\pi}{2}\bigr) $. The proof of Theorem 2 is thus complete. □
Remark 3. We note that a concave function must be a logarithmically concave function, but the converse is not true. However, a logarithmically convex function must be a convex function, but the converse is not true.
4.
Is the function $ R_{0, 2}(x) $ decreasing?
In [2,Section 4], the function $ R_{0, 1}(x) = R(x) $ defined by (3) or (10) for $ n = 1 $ was proved to be decreasing on $ \bigl[0, \frac{\pi}2\bigr] $ onto $ \bigl[0, \frac{1}{6}\bigr] $.
Theorem 3. The even function $ R_{0, 2}(x) $ defined by (10) for the case $ n = 2 $ is decreasing on $ \bigl[0, \frac{\pi}2\bigr] $.
Proof. For $ n\ge2 $, direct differentiation gives
and
Taking $ n = 2 $ and simplifying lead to
where
From the facts that
and, by induction,
we conclude, together with $ Q(6) = 3871296 $, that $ Q(k)\ge3871296 $ for $ k\ge6 $.
Let
The inequality
is equivalent to
for $ k\ge3 $, that is,
By virtue of the above expression for $ \mathfrak{Q}(k) $, we see that the sequence $ \mathfrak{Q}(k) $ is positive for $ k\ge13 $. On the other hand, it is straightforward that
Consequently, the sequence $ \mathfrak{Q}(k) $ is positive for all $ k\ge3 $. As a result, the sequence $ \mathcal{Q}(k) $ is increasing in $ k\ge3 $. It is immediate that $ \mathcal{Q}(3) = \frac{423}{115} = 3.678\dotsc $. Hence, we acquire
Accordingly, when
the derivative $ \Bigl[\frac{F_2'(x)}{F_0'(x)}\Bigr]' $ is negative, and then the derivative ratio $ \frac{F_2'(x)}{F_0'(x)} $ is decreasing in $ x\in\bigl(0, \frac{\pi}{2}\bigr] $.
In [12,pp. 10-11,Theorem 1.25], a monotonicity rule for the ratio of two functions was established as follows.
For $ a, b\in\mathbb{R} $ with $ a < b $, let $ p(x) $ and $ q(x) $ be continuous on $ [a, b] $, differentiable on $ (a, b) $, and $ q'(x)\ne 0 $ on $ (a, b) $. If the ratio $ \frac{p'(x)}{q'(x)} $ is increasing on $ (a, b) $, then both $ \frac{p(x)-p(a)}{q(x)-q(a)} $ and $ \frac{p(x)-p(b)}{q(x)-q(b)} $ are increasing in $ x\in(a, b) $.
With the help of this monotonicity rule and in view of the decreasing property of the derivative ratio $ \frac{F_2'(x)}{F_0'(x)} $ in $ x\in\bigl(0, \frac{\pi}{2}\bigr] $, we derive that the ratio $ \frac{F_2(x)}{F_0(x)} = R_{0, 2}(x) $ is decreasing in $ x\in\bigl(0, \frac{\pi}{2}\bigr] $. The required proof of Theorem 3 is completed. □
Remark 4. How to verify the decreasing property of the function $ R_{0, n}(x) $ for $ n\ge3 $ on $ \bigl(0, \frac{\pi}{2}\bigr] $, of the function $ R_{1, n}(x) $ on $ (0, 2\pi) $, and of the function $ R_{m, n}(x) $ for $ n > m\ge2 $ on $ (0, \infty) $? The ideas, approaches, techniques, and methods used in the proof of Theorem 3 should not be valid again, so we need to discover new ideas, approaches, techniques, and methods for verifying the decreasing property mentioned above.
Remark 5. Let
Prove that the function $ f_\alpha(x) $ is positive in $ x\in(0, \infty) $ if and only if $ \alpha > 1 $, while it is decreasing in $ x\in(0, \infty) $ if and only if $ \alpha\ge2 $.
This paper and the articles [2,13,14] are siblings, because some results in [2] have been generalized in this paper, and the results in [13,14] are about the Maclaurin power series expansions of logarithmic expressions involving normalized tails of the tangent and sine functions.
5.
Conclusions
In this paper, we presented the following results.
1. The function $ F_n(x) $ for $ n\ge0 $ was expanded into the Maclaurin power series expansion (11) in Theorem 1.
2. The function $ F_n(x) $ defined by (7) for $ n\ge0 $ was proved in Theorem 2 to be decreasing and concave on $ \bigl(0, \frac{\pi}{2}\bigr) $.
3. A new determinantal expression (13) of the Bernoulli numbers $ B_{2m} $ for $ m\ge1 $ was derived.
4. The ratio $ R_{0, 2}(x) $ was proved in Theorem 3 to be decreasing in $ x\in\bigl[0, \frac{\pi}2\bigr] $.
In order to verify the decreasing property of the function $ R_{0, n}(x) $ for $ n\ge3 $ on $ \bigl(0, \frac{\pi}{2}\bigr) $, of the function $ R_{1, n}(x) $ on $ (0, 2\pi) $, and of the function $ R_{m, n}(x) $ for $ n > m\ge2 $ on $ (0, \infty) $, we need new ideas, novel approaches, creative techniques, and innovative methods.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
This work was supported in part by the National Natural Science Foundation of China (Grant No. 12061033).
Conflict of interest
The authors declare there is no conflicts of interest.












 DownLoad:
DownLoad: