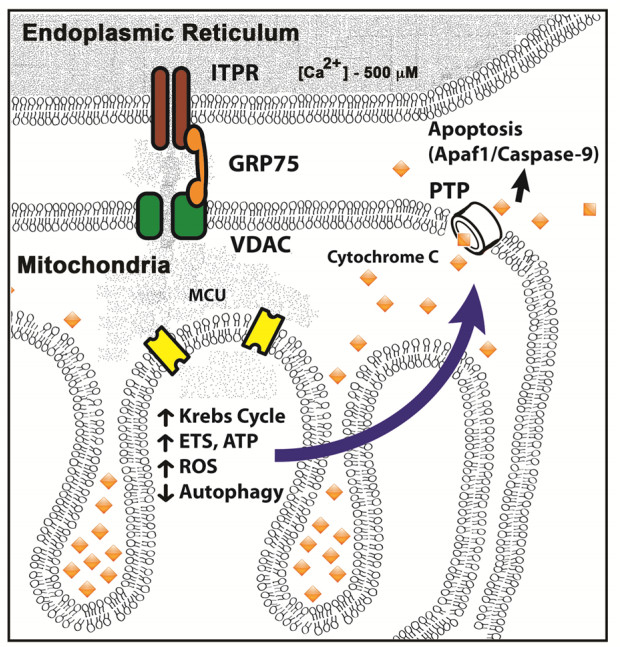
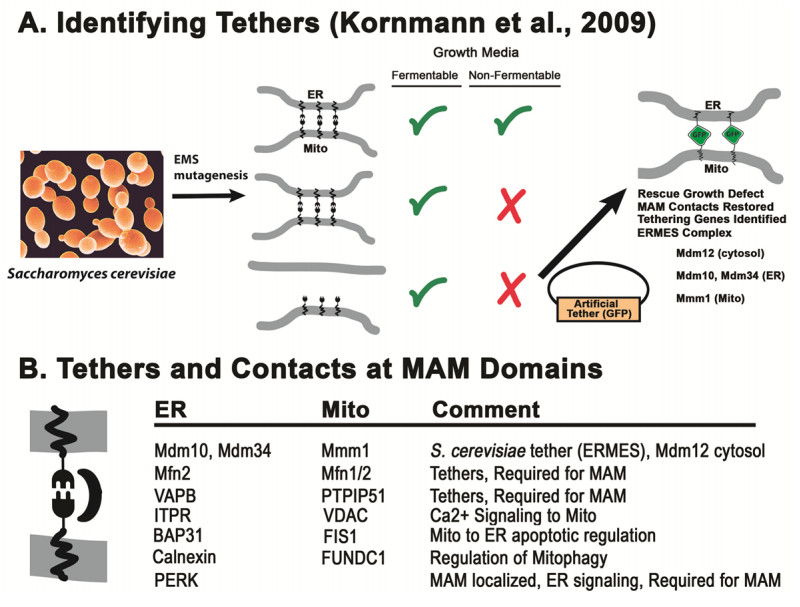
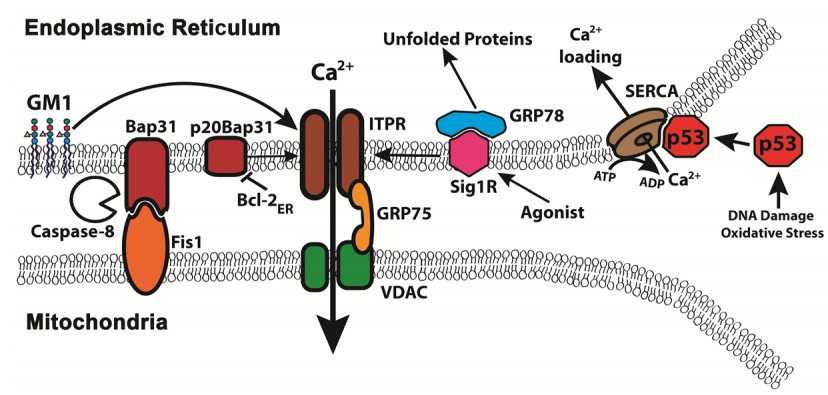
Signaling between organelles has profound implications for our understanding of organelle structural organization and regulatory processes. Close regional apposition of endoplasmic reticulum (ER) and mitochondrial membranes has been known for 50 years, but only in the past 20 years have scientists begun to unravel the nature and purpose of these quasi-synaptic contact points. At these sites of association, membranes have been shown to be of unique molecular composition, defining raft domains that are densely populated with membrane proteins, sphingolipids, and cholesterol. These associations are now referred to as mitochondrial associated membranes (MAMs). MAM domains mediate a complex array of cellular processes including; exchange of macromolecules, Ca2+ transfer, physical tethering, regulation of mitochondrial division, and signaling pathways that control autophagy and apoptosis. Dysfunction of MAM function is known to have profound cellular influence, and including the activation of several neurodegenerative disorders.
1.
Introduction
Presently, the differential systems of non-integer orders have gained wide prominence due to their great relevance in describing several real-world problems in physics, mechanics and engineering. For instance, we refer the reader to the monographs of Baleanu et al.[12], Hilfer [28], Kilbas et al. [31], Mainardi [33], Miller and Ross [34], Podlubny [37], Samko et al. [39] and the papers [22,40].
During the study of some phenomena, a number of researchers realized the importance of fractional operators with non-singular kernels which can model practical physical phenomena well like the heat transfer model, the diffusion equation, electromagnetic waves in dielectric media, and circuit model (see [7,9,23,24] and the references existing therein).
Caputo and Fabrizio in [11] studied a new kind of fractional derivative with an exponential kernel. Atangana and Baleanu [10] introduced a new operator with fractional order based upon the generalized Mittag-Leffler function. Their newly fractional operator involves kernel being nonlocal and nonsingular. The nonlocality of the kernel gives better description of the memory within the structure with different scale. Abdeljawad [4] extended this fractional derivative from order between zero and one to higher arbitrary order and formulated their associated integral operators.
On the other hand, the theory of measure of non-compactness is an essential tool in investigating the existence of solutions to nonlinear integral and differential equations, see, for example, the recent papers [6,14,20,26,38] and the references existing therein.
In [19], Benchohra et al. studied the existence of solutions for the fractional differential inclusions with boundary conditions
where CDr is the Caputo fractional derivative, G:[0,T]×E→P(E) is a multi-valued map, y0,yT∈E and (E,|⋅|) is a Banach space and P(E)={Z∈P(E):Z≠∅}.
In the present work, we are interested in studying the existence of solutions for the following nonlinear fractional differential inclusions with ABC fractional derivatives
where ABCaDα denotes the ABC fractional derivative of order α∈(1,2], (E,|⋅|) is a Banach space, P(E) is the family of all nonempty subsets of E, and F:J×E→P(E) is a given multi-valued map. We study the ABC fractional inclusion (1.2) in the case where the right hand side is convex-valued by means of the set-valued issue of Mönch fixed point theorem incorporated with the Kuratowski measure of non-compactness.
Differential inclusions play an important role as a tool in the study of various dynamical processes described by equations with a discontinuous or multivalued right-hand side, occurring, in particular, in the study of dynamics of economical, social, and biological macrosystems. They also are very useful in proving existence theorems in control theory.
Due to the importance of fractional differential inclusions in mathematical modeling of problems in game theory, stability, optimal control, and so on. For this reason, many contributions have been investigated by some researchers [1,2,3,5,8,16,17,18,25,30,35].
It is worth noting that the results included with the fractional differential inclusions with the ABC fractional derivatives in Banach spaces are rather few, so the outputs of this paper are a new addition for the development of this topic.
2.
Preliminaries
First at all, we recall the following definition of Riemann-Liouville fractional integral.
Definition 2.1. [31] Take α>0,a∈R, and v a real-valued function defined on [a,∞). The Riemann-Liouville fractional integral is defined by
Next, we present the basic definitions of the new fractional operator due to Atangana and Baleanu [10] and the extended ones due to Abdeljawad [4].
Definition 2.2. [10] Take α∈[0,1] and v∈H1(a,b),a<b, then the ABC fractional derivative is given by
where B(α)=α2−α>0 denotes the normalization function such that B(0)=B(1)=1 and Eα denotes the Mittag-Leffler function defined by
The associated Atangana-Baleanu (AB) fractional integral by
The following definitions concern with the higher order case.
Definition 2.3. [4] Take α∈(m,m+1], for some m∈N0, and v be such that v(n)∈H1(a,b). Set β=α−m. Then β∈(0,1] and we define the ABC fractional derivative by
In the light of the convention v(0)(t)=v(t), one has ABCaDαv(t)=ABCaDαv(t) for α∈(0,1].
The correspondent fractional integral is given by
Lemma 2.4. [4] For u(t) defined on [a,b] and α∈(m,m+1], for some m∈N0, we obtain that
Denote by C(J,E) the Banach space of all continuous functions from J to E with the norm ‖x‖=supt∈J|x(t)|. By L1(J,E), we indicate the space of Bochner integrable functions from J to E with the norm ‖x‖1=∫b0|x(t)|dt.
2.1. Multi-valued maps analysis
Let the Banach space be (E,|⋅|). The expressions we have used are P(E)={Z∈P(E):Z≠∅}, Pcl(E)={Z∈P(E):Z isclosed}, Pbd(E)={Z∈P(E):Z isbounded}, Pcp(E)={Z∈P(E):Z iscompact}, Pcvx(E)={Z∈P(E):Z isconvex}.
● A multi-valued map U:E→P(E) is convex (closed) valued, if U(x) is convex (closed) for all x∈E.
● U is bounded on bounded sets if U(B)=∪x∈BU(x) is bounded in E for any B∈Pbd(E), i.e. supx∈B{sup{‖y‖:y∈U(x)}}<∞.
● U is called upper semi-continuous on E if for each x∗∈E, the set U(x∗) is nonempty, closed subset of E, and if for each open set N of E containing U(x∗), there exists an open neighborhood N∗ of x∗ such that U(N∗)⊂N.
● U is completely continuous if U(B) is relatively compact for each B∈Pbd(E).
● If U is a multi-valued map that is completely continuous with nonempty compact values, then U is u.s.c. if and only if U has a closed graph (that is, if xn→x0,yn→y0, and yn∈U(xn), then y0∈U(x0).
For more details about multi-valued maps, we refer to the books of Deimling [21] and Hu and Papageorgiou [29].
Definition 2.5. A multi-valued map F:J×E→P(E) is said to be Carathéodory if
(i) t↦F(t,x) is measurable for each u∈E;
(ii) x↦F(t,x) is upper semi-continuous for almost all t∈J.
We define the set of the selections of a multi-valued map F by
Lemma 2.6. [32] Let J be a compact real interval and E be a Banach space. Let F be a multi-valued map satisfying the Carathèodory conditions with the set of L1-selections SF,u nonempty, and let Θ:L1(J,E)→C(J,E) be a linear continuous mapping. Then the operator
is a closed graph operator in C(J,E)×C(J,E).
2.2. Measure of non-compactness
We specify this part of the paper to explore some important details of the Kuratowski measure of non-compactness.
Definition 2.7. [15] Let ΛE be the family of bounded subsets of a Banach space E. We define the Kuratowski measure of non-compactness κ:ΛE→[0,∞] of B∈ΛE as
for some m∈N and Bj∈E.
Lemma 2.8. [15] Let C,D⊂E be bounded, the Kuratowski measure of non-compactness possesses the next characteristics:
i. κ(C)=0⇔C is relatively compact;
ii. C⊂D⇒κ(C)≤κ(D);
iii. κ(C)=κ(¯C), where ¯C is the closure of C;
iv. κ(C)=κ(conv(C)), where conv(C) is the convex hull of C;
v. κ(C+D)≤κ(C)+κ(D), where C+D={u+v:u∈C,v∈D};
vi. κ(νC)=|ν|κ(C), for any ν∈R.
Theorem 2.9. (Mönch's fixed point theorem)[36] Let Ω be a closed and convex subset of a Banach space E; U a relatively open subset of Ω, and N:¯U→P(Ω). Assume that graph N is closed, N maps compact sets into relatively compact sets and for some x0∈U, the following two conditions are satisfied:
(i)G⊂¯U, G⊂conv(x0∪N(G)), ¯G=¯C implies ¯G is compact, where C is a countable subset of G;
(ii) x∉(1−μ)x0+μN(x)∀u∈¯U∖U,μ∈(0,1).
Then there exists x∈¯U with x∈N(x).
Theorem 2.10. [27] Let E be a Banach space and C⊂L1(J,E) countable with |u(t)|≤h(t) for a.e. t∈J, and every u∈C; where h∈L1(J,R+). Then the function z(t)=κ(C(t)) belongs to L1(J,R+) and satisfies
3.
Main results
We start this section with the definition of a solution of the ABC fractional inclusion (1.2).
Definition 3.1. A function x∈C(J,E) is said to be a solution of the ABC fractional inclusion (1.2) if there exist a function f∈L1(J,E) with f(t)∈F(t,x(t)) for a.e. t∈J, such that ABCaDαtx(t)=f(t) on J, and the conditions x(a)=x′(a)=0 are satisfied.
Lemma 3.2. [4] For any h∈C(J,R), the solution x of the linear ABC fractional differential equation
is given by the following integral equation
Remark 3.3. The result of Lemma 3.2 is true not only for real valued functions x∈C(J,R) but also for a Banach space functions x∈C(J,E).
Lemma 3.4. Assume that F:J×E→P(E) satisfies Carathèodory conditions, i.e., t↦F(t,x) is measurable for every x∈E and x↦F(t,x) is continuous for every t∈J. A function x∈C(J,E) is a solution of the ABC fractional inclusion (1.2) if and only if it satisfies the integral equation
where f∈L1(J,E) with f(t)∈F(t,x(t)) for a.e. t∈J.
Now, we are ready to present the main result of the current paper.
Theorem 3.5. Let ϱ>0,K={x∈E:‖x‖≤ϱ},U={x∈C(J,E):‖x‖<ϱ}, and suppose that:
(H1) The multi-valued map F:J×E→Pcp,cvx(E) is Carathèodory.
(H2) For each ϱ>0, there exists a function φ∈L1(J,R+) such that
for a.e. t∈J and x∈E with |x|≤ϱ, and
(H3) There is a Carathèodory function ϑ:J×[0,2ϱ]→R+ such that
a.e. t∈J and each G⊂K, and the unique solution θ∈C(J,[a,2ϱ]) of the inequality
is θ≡0.
Then the ABC fractional inclusion (1.2) possesses at least one solution, provided that
Proof. Define the multi-valued map N:C(J,E)→P(C(J,E)) by
In accordance with Lemma 3.4, the fixed points of N are solutions to the ABC fractional inclusion (1.2). We shall show in five steps that the multi-valued operator N satisfies all assumptions of Mönch's fixed point theorem (Theorem 2.9) with ¯U=C(J,K).
Step 1. N(x) is convex, for any x∈C(J,K).
For f1,f2∈N(x), there exist w1,w2∈SF,x such that for each t∈J, we have
Let 0≤μ≤1. Then for each t∈J, one has
Since SF,x is convex (forasmuch F has convex values), then μf1+(1−μ)f2∈N(x).
Step 2. N(G) is relatively compact for each compact G∈¯U.
Let G∈¯U be a compact set and let {fn} be any sequence of elements of N(G). We show that {fn} has a convergent subsequence by using the Arzelà-Ascoli criterion of non-compactness in C(J,K). Since fn∈N(G), there exist xn∈G and wn∈SF,xn, such that
for n≥1. In view of Theorem 2.10 and the properties of the Kuratowski measure of non-compactness, we have
On the other hand, since G is compact, the set {wn(τ):n≥1} is compact. Consequently, κ({wn(s):n≥1})=0 for a.e. s∈J. Likewise,
for a.e. t,s∈J. Therefore, (3.6) implies that {fn(t):n≥1} is relatively compact in K for each t∈J.
Furthermore, For each t1,t2∈J,t1<t2, one obtain that:
As t1→t2, the right hand side of the above inequality tends to zero. Thus, {wn(τ):n≥1} is equicontinuous. Hence, {wn(τ):n≥1} is relatively compact in C(J,K).
Step 3. The graph of N is closed.
Let xn→x∗,fn∈N(xn), and fn→f∗. It must be to show that f∗∈N(x∗). Now, fn∈N(xn) means that there exists wn∈SF,xn such that, for each t∈J,
Consider the continuous linear operator Θ:L1(J,E)→C(J,E),
It is obvious that ‖fn−f∗‖→0 as n→∞. Therefore, in the light of Lemma 2.6, we infer that Θ∘SF is a closed graph operator. Additionally, fn(t)∈Θ(SF,xn). Since, xn→x∗, Lemma 2.6 gives
for some w∈SF,x.
Step 4. G is relatively compact in C(J,K).
Assume that G⊂¯U,G⊂conv({0}∪N(G)), and ¯G=¯C for some countable set C⊂G. Using a similar approach as in Step 2, one can obtain that N(G) is equicontinuous. In accordance to G⊂conv({0}∪N(G)), it follows that G is equicontinuous. In addition, since C⊂G⊂conv({0}∪N(G)) and C is countable, then we can find a countable set P={fn:n≥1}⊂N(G) with C⊂conv({0}∪P). Thus, there exist xn∈G and wn∈SF,xn such that
In the light of Theorem 2.10 and the fact that G⊂¯C⊂¯conv({0}∪P), we get
By virtue of (3.6) and the fact that wn(τ)∈G(τ), we get
Also, the function θ given by θ(t)=κ(G(t)) belongs to C(J,[a,2ϱ]). Consequently by (H3), θ≡0, that is κ(G(t))=0 for all t∈J.
Now, by the Arzelà-Ascoli theorem, G is relatively compact in C(J,K).
Step 5. Let f∈N(x) with x∈¯U. Since x(τ)≤ϱ and (H2), we have N(¯U)⊂¯U, because if it is not true, there exists a function x∈¯U but ‖N(x)‖>ϱ and
for some w∈SF,x. On the other hand, we have
Dividing both sides by ϱ and taking the lower limit as ϱ→∞, we infer that
which contradicts (3.4). Hence N(¯U)⊂¯U.
As a consequence of Steps 1–5 together with Theorem 2.9, we infer that N possesses a fixed point x∈C(J,K) which is a solution of the ABC fractional inclusion (1.2).
4.
Example
Consider the fractional differential inclusion
where α=32,a=0,b=1, and F:[0,1]×R→P(R) is a multi-valued map given by
For f∈F, one has
Thus
for t∈[0,1],x∈R. Obviously, F is compact and convex valued, and it is upper semi-continuous.
Furthermore, for (t,x)∈[0,1]×∈R with |x|≤ϱ, one has
Therefore, the condition (3.4) implies that
Finally, we assume that there exists a Carathèodory function ϑ:[0,1]×[0,2ϱ]→R+ such that
a.e. t∈[0,1] and each G⊂K={x∈R:|x|≤ϱ}, and the unique solution θ∈C([0,1],[0,2ϱ]) of the inequality
is θ≡0.
Hence all the assumptions of Theorem 3.5 hold true and we infer that the ABC fractional inclusion (4.1) possesses at least one solution on [0,1].
5.
Conclusions
In this paper, we extend the investigation of fractional differential inclusions to the case of the ABC fractional derivatives in Banach space. Based on the set-valued version of Mönch fixed point theorem together with the Kuratowski measure of non-compactness, the existence theorem of the solutions for the proposed ABC fractional inclusions is founded. An clarified example is suggested to understand the theoretical finding.
Acknowledgments
The paper is partially supported by "PIAno di inCEntivi per la RIcerca di Ateneo 2020/2022". The second author is gratefully supported by "RUDN University Strategic Academic Leadership Program".
Conflict of interest
The authors declare no conflict of interest.













 DownLoad:
DownLoad: