1.
Introduction
Psoriasis is a chronic, inflammatory skin condition driven by T-helper (Th) 1 and Th-17 pathways and is associated with increased levels of related interleukins (IL)-17A, IL-22, and IL-23 [1]. Common psoriasis triggers include drugs, physical trauma, stress, infections, and vaccination “Psoriasis Vaccinalis” (PV) [1],[2]. PV has been previously described with several vaccines, including influenza, rubella, Bacillus Calmette-Guerin (BCG), tetanus-diphtheria, COVID-19, and pneumococcal polysaccharide vaccines [2]. While the mechanism is not fully understood, the possible theories for PV include elevations in TH17, TNF-α, and IFN induced by the vaccines in a subset of genetically predisposed individuals [1].
With the emergence of the COVID-19 pandemic over the past few years, it has been estimated that COVID-19 vaccines have been administered to about 60% of the global population [3]. With this considerable coverage, physicians and patients should be aware of the possible side effects and management options. Currently, there are emerging publications that report the occurrence of new-onset psoriasis and flaring psoriasis after COVID-19 infections or vaccinations [2],[4]–[6].
However, the current reports of new-onset COVID-19 vaccine-induced psoriasis have been most likely associated with mRNA vaccines, such as Moderna® NR, BioNTech/Pfizer® vaccines, or viral vector vaccines such as the AstraZeneca vaccine [4]–[6]. In this article, we report 2 patients who developed new-onset pustular psoriasis, with one of them having the disease after an administration of the second dose of an mRNA vaccine (Pfizer®), and the second who developed PV after the first dose of a whole inactivated vaccine (Sinopharm®). PV seems to occur after any type of COVID vaccination, and awareness should be widely spread regarding this side effect.
2.
Case description
2.1. Case 1
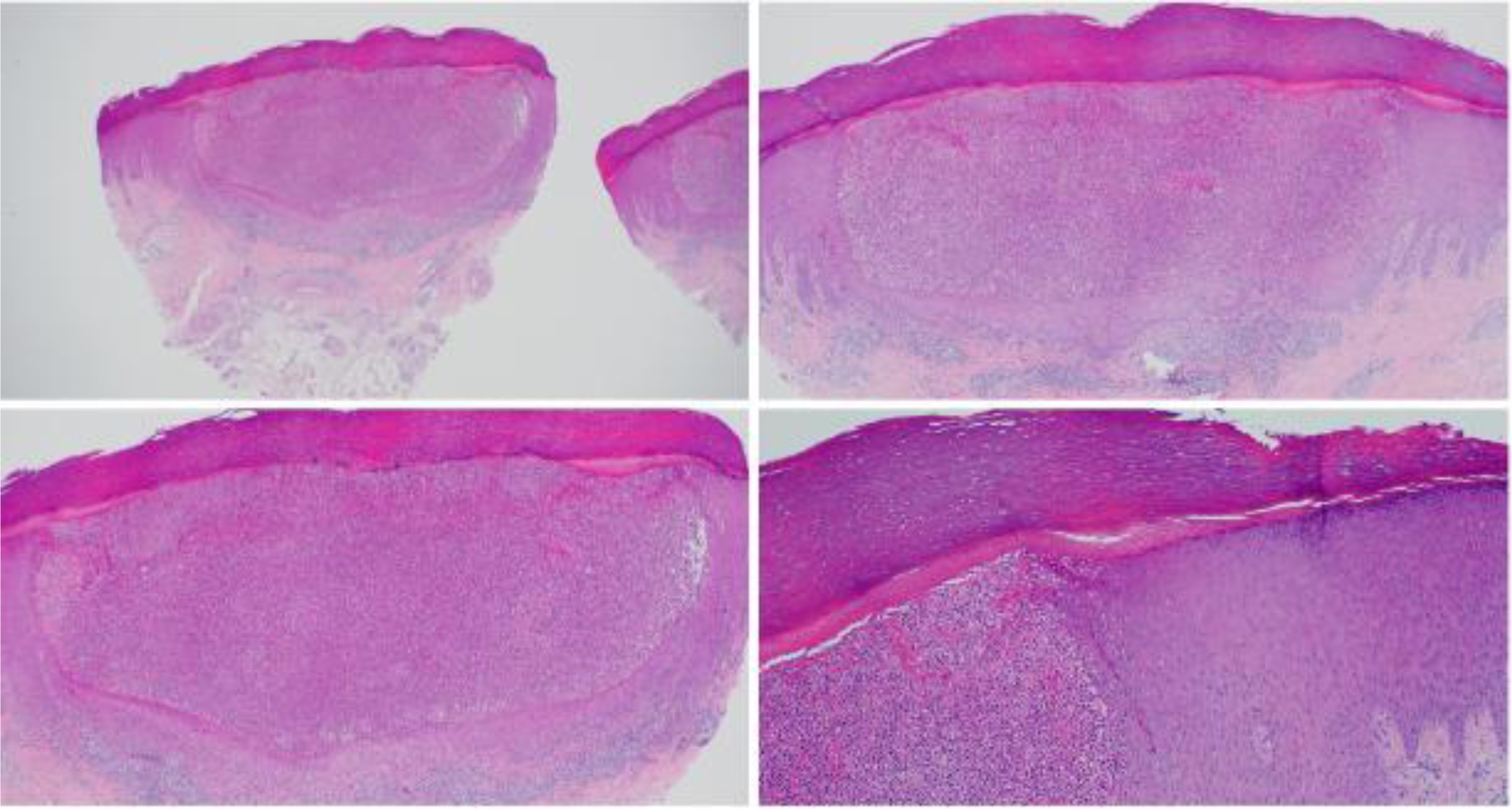
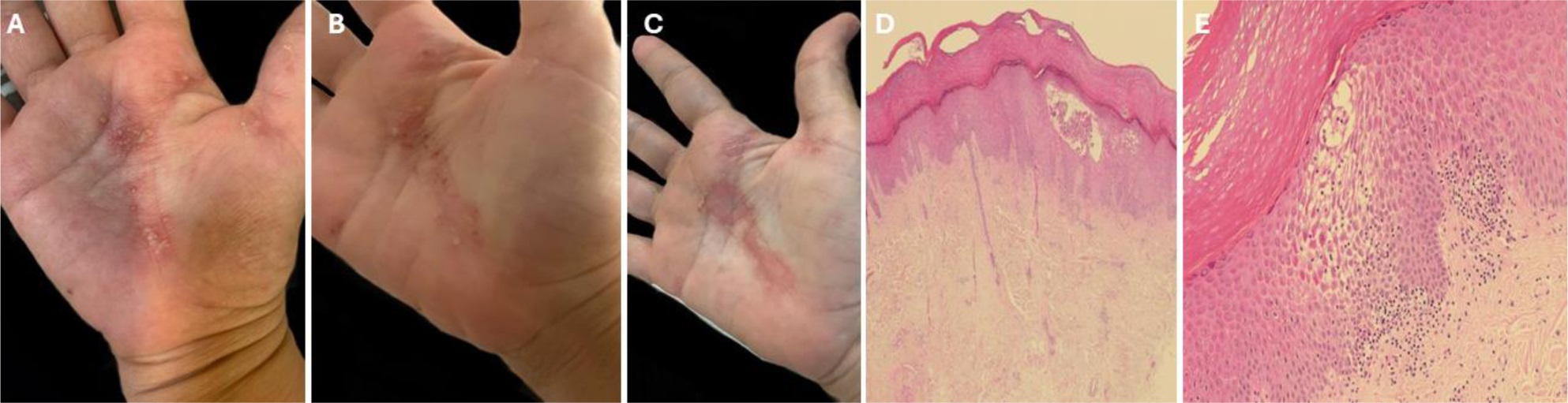
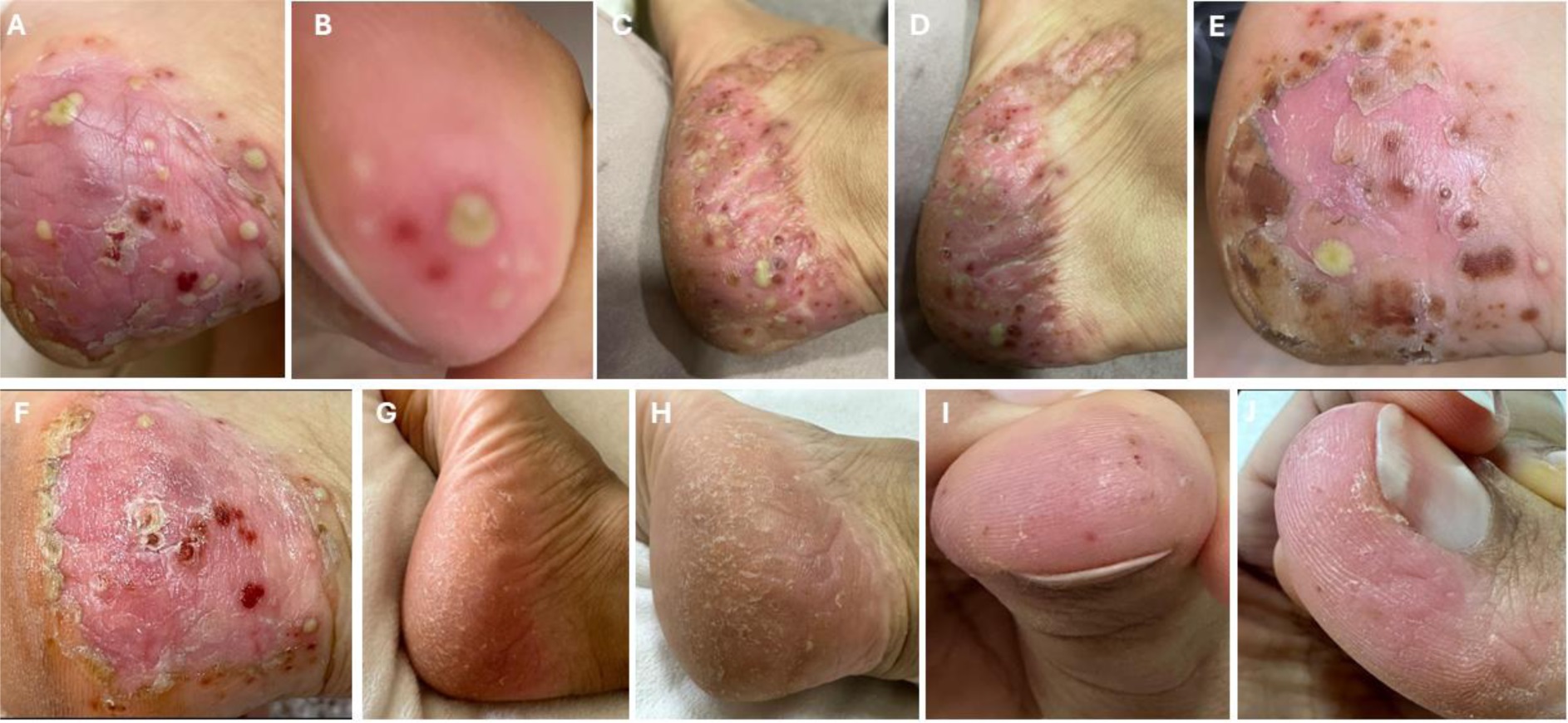
A 29-year-old female, previously healthy, presented with a 1-month history of a worsening itchy palmoplantar skin rash that was noticed two weeks after the second dose of the Pfizer® mRNA vaccine. The patient was initially diagnosed as having a skin infection in a primary care facility and received a broad-spectrum antibiotic/antifungal + corticosteroid ointment, which did not result in any improvement before her referral to a dermatologist. Upon a dermatological examination, there was a localized pinkish erythematous patch studded with a few yellowish pustules and hemorrhagic blisters on the left heel, as shown in Figure 1. Similar subtle findings were observed in the palm and the plantar aspect of the big toe (Figure 1). A punch biopsy revealed (Figure 2) a keratotic epidermis with psoriasiform blunted rete ridges with a surface parakeratosis. Numerous neutrophils were infiltrating into the epidermis and collecting subcorneally. The papillary dermis showed a mixed perivascular inflammation with scattered neutrophils. No fungal elements were seen by Grocott's Methenamine Silver stain (GMS) and a Periodic Acid-Schiff (PAS) with diastase (PAS-D) stain. A clinicopathological correlation was consistent with pustular psoriasis. The patient started a topical calcipotriol-betamethasone ointment and narrow-band ultraviolet B (NB-UVB) therapy for 6 weeks without a significant improvement, before being shifted to a Guselkumab subcutaneous injection 100mg at 0, 4 weeks, and every 8 weeks for one year, which eventually resulted in a full recovery (Figure 1). The patient remained disease-free after an additional 14-month follow-up, till the present.
2.2. Case 2
A 55-year-old female, previously healthy, presented with a 3-week history of a worsening itchy palmoplantar skin rash that was noticed one week after the first dose of a whole inactivated virus vaccine (Sinopharm®). The patient started a topical antibiotic medication by herself before seeking a dermatological consultation. Upon a dermatological examination, there was a localized pinkish erythematous patch studded with a few yellowish pustules and hemorrhagic blisters on the palms, as shown in Figure 3. A punch biopsy revealed (Figure 3) a keratotic epidermis with psoriasiform blunted rete ridges with a surface parakeratosis, which is consistent with pustular psoriasis. The patient received a topical calcipotriol-betamethasone ointment, which showed a good improvement in terms of the disappearance of the pustules, flattening of the macular erythematous lesion, and progressive healing of the skin.
3.
Discussion
This article reports the occurrence of new-onset pustular psoriasis after COVID-19 vaccination. A high index of suspicion should be taken whenever questionable skin lesions develop after vaccinations, and a specialized dermatological consultation should be timely performed to allow for early treatment before skin damage.
Psoriasis is a chronic, inflammatory skin condition driven by T-helper (Th) 1 and Th-17 pathways with increased levels of related interleukins (IL)-17A, IL-22, and IL-23. This results in red, raised patches of skin with silvery-white scales that can be itchy or painful [1],[7]. Vaccines, particularly those that effectively stimulate innate immunity, can serve as a catalyst in individuals with a genetic predisposition by boosting dendritic cell activation. This enhancement results in increased levels of IL-23 production, which supports the differentiation and longevity of Th17 cells. Then, these Th17 cells produce IL-17, which is a critical cytokine that drives the proliferation of keratinocytes and sustains inflammation in psoriatic lesions. Consequently, the ensuing cytokine cascade can reveal or worsen psoriasis after vaccination. Many vaccines and pathogens have been linked to sensitization and the activation of Th1 and Th17 cells to produce different types of interleukins and TNF-α, which are involved in the psoriasis disease onset [7]–[9]. With the overwhelming administration of COVID-19 vaccines over the past few years, several reports have described the occurrence of new-onset or flaring of psoriasis after different types of COVID-19 vaccines [6]. While flaring of Psoriasis has been reported with all types of COVID-19 vaccines, whether RNA, viral vector, or inactivated viral vaccines [6], new-onset psoriasis has solely been reported with RNA and viral vector vaccines [6]. Our case report indicates that new-onset psoriasis can occur after inactivated virus vaccine administration as well. Additionally, it emphasizes the importance of knowledge regarding PV and the importance of a full dermatological examination in any case that presents with a suspected skin infection.
While the plaque type has been the most commonly reported form of psoriasis after COVID-19 vaccinations [3],[6], other forms have also been reported, such as guttate psoriasis [1], pustular palmoplantar psoriasis [10], de novo generalized pustular psoriasis [11], and de novo nail psoriasis [12]. Our two cases had pustular palmoplantar psoriasis, which was resistant to topical corticosteroid therapy and NB-UVB treatment in the first case. Notably, other potential cutaneous side effects following COVID-19 vaccinations include delayed large local reactions, local injection site reactions, urticarial eruptions, morbilliform eruptions, pernio, cosmetic filler reactions, herpes zoster, herpes simplex flares, and pityriasis rosea-like reactions [13].
In our cases, the patients did not have a history of recent drug intake or preceding upper respiratory tract infections, nor did they have a personal or family history of psoriasis. Moreover, neither patient reported psychosocial stressors that could serve as alternative triggers, which supports a temporal link to vaccination. Notably, the interval between the COVID-19 vaccination and the disease presentation of psoriasis in our patients was 1–2 weeks. This was comparable with the published reports, which stated a range of 2–30 days for new-onset psoriasis after COVID-19 vaccination [6],[14].
In a recent review by Karampinis et al. [14], the authors identified 71 patients with plaque psoriasis flares, 12 patients with new-onset plaque psoriasis, and 17 patients with a plaque psoriasis subtype change following COVID-19 vaccination. The new onset psoriasis developed 1–30 days in the related 12 patients, while it developed 1–90 days for the flare type and 3–60 days for the plaque psoriasis subtype change. Compared to our patients who both developed new-onset pustular psoriasis after the vaccinations, Karampinis et al. found that plaque psoriasis was the only type of new-onset psoriasis, while pustular psoriasis was the predominant type of plaque psoriasis subtype change, which accounted for 52.9% of the subtype change cases. Additionally, the authors recognized the mRNA COVID-19 vaccine as the most common type in new-onset plaque Psoriasis, which accounted for 66.7% of the cases.
Although there is a plausible link between COVID-19 vaccines and psoriasis, it is crucial to follow the International Psoriasis Council (IPC) recommendation for psoriatic patients who do not have specific contraindications to receive the approved COVID-19 vaccination as soon as it becomes available to them [15]. Thus, as vaccinations against COVID-19 continue worldwide, patients should be carefully monitored if they develop any new onset or flare of skin disease once immunized.
Moreover, it is important to differentiate post-vaccination pustular psoriasis from pustular eruptions. Post-vaccination pustular psoriasis is typically characterized by sterile pustules on an erythematous base, often in individuals with a personal or family history of psoriasis. In contrast, post-vaccination pustular eruptions are a broader category of non-psoriatic pustular skin reactions that may include acute generalized exanthematous pustulosis (AGEP) or other drug-reaction-like eruptions, which typically occur without a psoriatic background and often resolve upon a withdrawal of the trigger. While both can similarly present with pustules, their underlying pathophysiology, chronicity, and patient predisposition significantly differ [16],[17].
Psoriasis flares following COVID-19 infection have continued to be reported even in the post-pandemic period. For example, Aram et al. [18] described cases of generalized pustular psoriasis in the later stages of the pandemic, mostly related to antimalarial agents that were initially used for the treatment of COVID-19, thus suggesting that the temporal association persists beyond the early pandemic era.
To note, new-onset or psoriasis flares have been sporadically documented after hepatitis B and influenza vaccines [19],[20], though COVID-19 vaccines appear to be reported more frequently, possibly due to a heightened surveillance and reporting. Other vaccines, such as the H1N1 influenza vaccine, BCG, tetanus-diphtheria, and pneumococcal polysaccharide vaccines, were also linked to cases of PV, although more research is needed to establish a definitive link between these vaccines and psoriasis [2],[21].
This study has several limitations that necessitate a careful interpretation of the presented evidence. The limited number of cases is a major limitation that restricts the generalizability. However, the goal of this report is to raise clinical awareness through the detailed documentation of rare but morbid presentations. Another limitation is the lack of a definitive causal mechanism between vaccinations and the onset of psoriasis. While definitive causality cannot be established, the temporal proximity and known immunologic effects of vaccines suggest a potential triggering role. Third, we acknowledge the presence of referral bias, as more severe or atypical cases are more likely to reach dermatology for evaluation.
4.
Conclusion
New-onset psoriasis can occur with any type of COVID-19 vaccine. Pustular psoriasis can develop after COVID-19 vaccination and may be misinterpreted early as an infection. With the tremendous administration of COVID-19 vaccination worldwide, physicians and patients should be aware of the possible side effects and treatment options for the potential complications. Clinicians, especially in primary care, should maintain a high index of suspicion for vaccine-induced psoriasis to avoid a misdiagnosis with infection and to ensure a prompt dermatologic referral.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.









 DownLoad:
DownLoad: