New iterative criteria for testing the oscillation of solutions of differential equations with distributed deviating arguments

1.   Introduction

1.1.   Overview of the study scope

Differential equations (DEs) are an essential tool in understanding and predicting many complex phenomena in science, engineering, and they are an important part of modeling and describing natural phenomena. It plays an important role in describing many physical phenomena, as in Newton's laws of motion, and can also be used in many real-life models, such as the propagation of epidemics, and the absorption of glucose by the body (see ^[1]).

There is also another type of DE called functional differential equations (FDEs), which originate from studies and reflections on dynamic phenomena that cannot be adequately modeled using traditional DEs. In the late nineteenth and early twentieth centuries, scientists began to recognize the need for models that account for both delayed and forward-time effects. In recent decades, the use of FDEs has expanded greatly in many fields, such as engineering, economics, biology, and the social sciences. These equations have become an essential tool for understanding the dynamic behavior of complex systems that contain time effects ^[2].

In the decade 1920s, delay differential equations (DDEs) began to appear in the scientific literature, where they were used to study biological systems and model the effects of temporal delays on population dynamics in various environments. The decade 1950–1960 witnessed major developments in the mathematical theory of functional differential equations, as rigorous mathematical foundations were laid for solving and studying these equations ^[3].

DDEs are a type of DE that is an equation with just one variable, typically referred to as time. It gives the function's derivative at a specific moment in terms of its values at previous times. The dependence on the past appears naturally in numerous applications in biology, electrical engineering, and physiology. A simple example in nature is reforestation, which occurs because animals must take time to digest their food before further activities and responses take place. Hence, any mathematical model of forest harvesting and regeneration has time delays built into it (see ^[4]).

Oscillation theory for ordinary DEs was developed at the beginning of the 1840s. For instance, Sturm's classical work ^[5] appeared, where oscillation theories were proven, and solutions of second-order linear homogeneous ordinary DEs were compared. In 1921, Fite ^[6] obtained the first oscillation results for DEs with a translated argument. In recent years, the number of investigations into the oscillation theory of functional DEs has considerably increased. Since then, much research has been done to progress the field of knowledge. To gain an overview of the most significant contributions, we recommend reading the monographs written by Agarwal et al. ^[7,8,9], Dosly and Rehak ^[10], and Gyori and Ladas ^[11].

Researchers have focused a lot of effort and attention on studying the oscillatory behavior of DEs. Special interest in first-order DEs was shown by Philos ^[12] and Santra et al. ^[13,14]. Even- and odd-order DEs, along with their diverse classifications, were the focus of the works in ^{[15,16,17,18]}. Examining earlier research reveals that the oscillation criteria conclusion involves three fundamental processes. All of the positive solutions to the studied equation should be categorized first. Next, a new or updated method should be developed to obtain improved relations and inequalities connecting the solution, its derivatives, and its corresponding function. Finally, the positive solutions should be excluded using the chosen technique and these improved relations.

Therefore, the purpose of this work is to establish new oscillation criteria for neutral differential equation (NDE)

where $\mu \in \left[ \mu _{0}, \infty \right)$ and $w\left(\mu \right) : = x\left(\mu \right) +p\left(\mu \right) x\left(h\left(\mu \right) \right)$. In our work, we assume the following conditions:

(A1) $\ell$ is a ratio of odd natural numbers, $\lambda \in \mathbf{C }^{1}\left(\left[ \mu _{0}, \infty \right), \left(0, \infty \right) \right)$ and

(A2) $h\in \mathbf{C}^{1}\left(\left[ \mu _{0}, \infty \right), \mathbb{R} \right) \mathbf{, \ }h\left(\mu \right) \leq \mu,$ $h^{\prime }\left(\mu \right) > 0,$ and $\lim_{\mu \rightarrow \infty }h\left(\mu \right) = \infty;$

(A3) $q\in \mathbf{C}\left(\left[ \mu _{0}, \infty \right) \times \left[ a, b\right], \left(0, \infty \right) \right),$ $p\in \mathbf{C}\left(\left[ \mu _{0}, \infty \right), \mathbb{R} \right)$ and $0\leq p\left(\mu \right) \leq p_{0};$

(A4) $\varphi \in \mathbf{C}^{1}\left(\left[ \mu _{0}, \infty \right) \times \left[ a, b\right], \left(0, \infty \right) \right),$ $\varphi \left(\mu, \varrho \right) < \mu$ for $\varrho \in \left[ a, b\right],$ and $\lim_{\mu \rightarrow \infty }\varphi \left(\mu, \varrho \right) = \infty.$

We recall the definition of solutions of (1.1), using the notations introduced earlier in $(A1)$–$(A4)$.

Definition 1. ^[19] A function $x\in \mathbf{C}\left(\left[ \mu _{0}, \infty \right), \mathbb{R} \right),$ $\mu _{x}\geq \mu _{0},$ which has the property $\lambda \left(\mu \right) \left[ w^{\prime }\left(\mu \right) \right] ^{\ell }\in \mathbf{ C}^{1}\left(\left[ \mu _{0}, \infty \right), \mathbb{R} \right)$ and satisfies Eq (1.1) on $[\mu _{x}, \infty)$, is called a solution of (1.1).

Our focus lies in the solution of Eq (1.1) that satisfy the requirement

for all $\mu > \mu _{c}$.

Definition 2 ^[19] A solution of (1.1) is called oscillatory if it is neither eventually positive nor eventually negative. Otherwise, it is said to be non-oscillatory. Equation (1.1) is said to be oscillatory if all of its solutions are oscillatory.

1.2.   Literature review

We review the most important previous works and studies that contributed to the development of the study of oscillation of DEs with neutral delay. The following discussion is a summary of some of the relationships that have been presented in the literature.

Under the canonical situation, the customary inequality

is usually used. While the inequality

is used in the non-canonical situation, see ^[20,21].

In 2007, Xu and Weng ^[22] established the criteria for oscillation of

where $\psi \in \mathbf{ C}\left(\mathbb{R}, \left[ m_{1}, m_{2}\right]\right)$, $m_{1}, m_{2} \in \mathbb{R}^+$, $w\left(\mu \right) = x\left(\mu \right) +p\left(\mu \right) \left(\mu -h_{o}\right)$ and $h_{o}\geq 0.$ They used generalized Riccati substitution and obtained criteria of Philos-type.

In 2008, Xu and Ye ^[23] studied the oscillation problem of the second order quasilinear NDE

where $0\leq p\left(\mu \right) \leq 1$ and are established under the canonical or noncanonical case. They studied the oscillation properties of Eq (1.4) by using the Riccati technique and some inequalities techniques.

In 2009, Han et al. ^[24] proved this using the following example:

that $x\left(\mu \right) = \mathrm{e}^{-\mu }$ is a positive solution of Eq (1.5). Let $x\left(\mu \right) = \mathrm{e} ^{-\mu }$ and $w\left(\mu \right) = x\left(\mu \right) +x\left(\mu -2\right) /2$. Then $w^{\prime }\left(\mu \right) < 0$ and

where

Hence, the

does not hold under the case $w^{\prime }\left(\mu \right) < 0.$ Furthermore, we have

This proves that $x\left(\mu \right) = \mathrm{e}^{-\mu }$ is a nonoscillatory solution of Eq (1.5); although Xu and Ye ^[23] proved otherwise. This confirms that there is an error in their results. Which then prompted Han et al. ^[24] to complete and correct the results obtained by Xu and Ye ^[23].

In 2010, Baculikova and Dzurina ^[25] studied the NDE of the form

The new oscillation criteria that were proposed for the situation where

and assume that the canonical case holds.

In 2014, Li et al. ^[26] studied the oscillatory properties of second-order nonlinear NDEs with distributed deviating arguments

where $\sigma \in \mathbf{ C}\left(\left[ a, b\right], \mathbb{R} \right)$. Some new criteria are offered based on less restrictive assumptions made regarding the neutral coefficient, where $p\left(\mu \right) \geq 0$. They used the Riccati substitution technique and some inequalities to establish several new oscillation criteria for (1.8), assuming that the canonical or noncanonical case holds.

In 2015, Candan ^[27] studied the oscillation of more general NDE

where $\ell \in \mathbb{R} ^{+}$, $w\left(\mu \right) = x\left(\mu \right) +\int_{a}^{d}p\left(\mu, \varrho \right) x\left(h\left(\mu, \varrho \right) \right) \mathrm{d} \varrho$ and $F\left(\mu, x\left(\varphi \left(\mu, \xi \right) \right) \right) \geq q\left(\mu, \varrho \right) \left\vert x\left(\mu \right) \right\vert ^{\ell }$. He used the Riccati method and assumed that

and considered the canonical case.

Moaaz et al. ^[28] obtained conditions for oscillation of

where $w\left(\mu \right) = x\left(\mu \right) +\int_{c}^{d}p\left(\mu, \varrho \right) x\left(h\left(\mu, \varrho \right) \right) \mathrm{d} \varrho.$ They obtained oscillation criteria that complement and enhance several results published in the literature by using an improved version of the Riccati transformations and comparison concepts.

Moaaz et al. ^[29] studied the oscillatory behavior of

As an enhancement to (1.2), they used $p\left(t\right) = \rho _{0}$

and

where $h^{\left[ h\right] }\left(\mu \right) = h\left(h^{\left[ h-1\right] }\left(\mu \right) \right)$, for $h = 1, 2, ..., 2m$.

Hassan et al. ^[30] investigated the oscillatory features of

they offered

which as enhancement to (1.3), where $\kappa \ $is odd.

Equation

has been studied by Bohner et al. ^[31]. They used

where

$h^{\left[ 0\right] }\left(\mu \right) = \mu$ and $h^{\left[ j\right] }\left(\mu \right) = h\left(h^{j-1}\left(\mu \right) \right)$ for all $j\in \mathbb{N}$, which is an enhancement of (1.3).

New better relations between the solution and its related function have been derived by a number of researchers who have lately studied the oscillatory behavior of solutions to the NDE of various orders, (see, for example, ^{[32,33,34,35]}).

1.3.   Some useful results

The following lemmas will be used in deriving our results.

Lemma 1. ^[36] Let $F,$ $H\in \left[ 0,\infty \right) .$ Then,

where

Lemma 2. ^[37] Let $\ell$ be$\ $a ratios of two odd positive integers. Then,

1.4.   Summary of the paper results

In this study, we investigate the oscillatory behavior of a neutral second-order nonlinear differential equation with distributed deviating arguments, denoted as (1.1). By employing advanced analytical techniques, we establish three significant oscillation theorems that apply to all solutions of this equation. Our findings not only generalize and extend existing results in the literature but also introduce novel oscillatory criteria based on comparison principles and Riccati-type transformations. These contributions offer a more robust and comprehensive framework for understanding the oscillatory dynamics of Eq (1.1).

Moreover, we explore the implications of these theorems in the context of fractional delay differential equations, which are particularly relevant in systems characterized by memory effects. To validate the theoretical results, we present numerical simulations (Figures 1 and 2), which demonstrate strong agreement between analytical predictions and computational outcomes, thereby confirming the effectiveness and applicability of the proposed approach.

1.5.   Paper organization

The paper is divided into four sections. In the next section, we introduce the initial lemmas, including the derivation of improved relations between the solution and its derivatives. We then derive new oscillation theorems using several approaches, and, we apply these results through a practical example to confirm their validity and applicability. In the third section, we provide a numerical analysis of the results from the previous example and schematics of the oscillatory nature of the solutions. The final section contains an analytical summary of the findings in this paper and an overview of our results in real-world applications.

2.   Results

In what follows, we derive some improved relationships between the dependent solution, its derivatives, and the corresponding function, and use them to derive our oscillation theorems. We also give several examples of the practical application of our results, emphasizing their easy applicability. For simplicity, we use the notations listed below:

Remark 1. All functional inequalities are assumed to hold for all sufficiently large $\mu$ in this section.

The following lemma provides a crucial inequality used in the proof of our main Theorems.

Lemma 3. Assume that $x\left(\mu \right)$ is an eventually positive solution of (1.1). Then, eventually

for any integer $m\geq 0$. So, Eq (1.1) became as follows:

Proof. The proof of this Lemma comes directly from the proof of Lemma 2.2 in reference ^[33]. Thus, it has been omitted. □

Theorem 1. Assume that

Then, Eq (1.1) is oscillatory.

Proof. Assume that $x(\mu)$ is a positive solution of Eq (1.1), meaning there is exists a $\mu _{0}\geq 0$ such that $x(\mu) > 0$ for $\mu \geq \mu _{0}$, and as a result, there exists a $\mu _{1}\geq \mu _{0}$ such that $x\left(h\left(\mu \right) \right) > 0$ for $\mu \geq \mu _{0}$, $x\left(\varphi \left(\mu, \varrho \right) \right)$ for $\mu \geq \mu _{o}$. This same argument can be used to show if $x(\mu)$ is an eventually negative solution. From Eq (1.1), we have

Hence, $\lambda \left(\mu \right) \left[ w^{\prime }\left(\mu \right) \right] ^{\ell }$ is decreasing. Consequently, we have two cases for $w^{\prime }(\mu)$.

(ⅰ) $w^{\prime }\left(\mu \right) < 0$ eventually.

(ⅱ) $w^{\prime }\left(\mu \right) > 0$ eventually.

First, assume that $w^{\prime }\left(\mu \right) < 0$ for $\mu \geq \mu _{1}.$ By using decreasing nature of $\lambda \left(\mu \right) \left[ w^{\prime }\left(\mu \right) \right] ^{\ell },$ we obtain

Dividing both sides of (2.3) by $\lambda (\mu)$, integrating from $\mu _{2}$ to $\mu$, and using (A1), we obtain

which contradicts the positive nature of $w(\mu)$.

Second, assume that $w^{\prime }\left(\mu \right) > 0$ for $\mu \geq \mu _{1}$. Since $w\left(\mu \right) \geq x\left(\mu \right)$ and $w\left(\mu \right)$ is increasing, we have

according to Lemma 3. Hence,

or

On the other hand, since $\lambda \left(\mu \right) \left[ w^{\prime }\left(\mu \right) \right] ^{\ell }$ is decreasing, we have

or

Let

Taking the derivative of $\omega \left(\mu \right)$, we have

or

or

Integrating (2.9) from $\mu _{3}$ to $\mu$ and using (2.6), we obtain

contradiction, since $\omega (\mu)$ is positive and decreasing. This completes the proof. □

Definition 3. We define a sequence of functions $\left\{ \digamma _{n}\left(\mu \right) \right\} _{n = 0}^{\infty }$ as

and

and $n = 1, 2, 3....$.We see that by induction

Lemma 4. Assume that $x\left(\mu \right)$ is an eventually positive solution of Eq (1.1). Then, $\digamma _{n}\left(\mu \right) \leq \omega \left(\mu \right),$ where $\omega \left(\mu \right)$ and $\digamma _{n}\left(\mu \right)$ are as defined in (2.7) and (2.11), respectively. There exists a positive function $\digamma \left(\mu \right)$ on $\left[ \mu, \infty \right)$, such that $\lim_{n\rightarrow \infty }\digamma _{n}\left(\mu \right) = \digamma \left(\mu \right)$ for $\mu \geq \mu _{1}\geq \mu _{0}$ and

Proof. By following the steps in the proof of Theorem 2.1, we arrive at (2.8). Integrating (2.8) from $\mu$ to $\mu ^{\ast }$, we get

From (2.14), it is obvious that

Then, from (2.15) we conclude the following relation

for $\mu \geq \mu _{1}$ and

we get a contradiction. Since $\omega (\mu)$ is positive and decreasing, we note that

We know that $k = 0$ by virtue of (2.16). We therefore obtain

as a consequence of (2.14), i.e.,

Furthermore, we may also observe by induction that $\omega \left(\mu \right) \geq \digamma _{n}\left(\mu \right)$ for $\mu \geq \mu _{0}$ and $n = 1, 2, 3...$.Consequently, the sequence $\digamma _{n}\left(\mu \right)$ converges to $\digamma (\mu)$ since it is monotone increasing and bounded above. Using Lebesgue's monotone convergence theorem and letting $n\rightarrow \infty$ in (2.11), we arrive at (2.13). The proof is finished. □

Theorem 2. Assume that

Then Eq (1.1) is oscillatory.

Proof. Let $x(\mu)$ be a nonoscillatory solution of Eq (1.1). By following the steps in the Lemma 4 proof, we obtain

Let

then $\beta \geq 1.$ From (2.17) and (2.18), we obtain

or

which contradicts the admissible value of $\ell$ and $\beta,$ then the proof is finished. □

Theorem 3. Let $\digamma _{n}(\mu)$ be as defined in (2.11). There exists $\digamma _{n}(\mu)$ such that

then Eq (1.1) is oscillatory.

Proof. Let $x(\mu)$ be a nonoscillatory solution of Eq (1.1) and defining $\omega (\mu)$ as in (2.7), then we have

Thus, we conclude from (2.20) that

and therefore, we have

Which contradicts (2.19) and completes the proof. □

We can derive the following corollary from the results in the previous theorem.

Corollary 1. Let $\digamma _{n}(\mu)$ be as defined in (2.12). If there exists $\digamma _{n}(\mu)$ such that either

or

Then, Eq (1.1) is oscillatory.

Proof. Let $x(\mu)$ be a nonoscillatory solution of Eq (1.1), and, therefore we may assume that $x(\mu)$ is eventually positive. Then, from (2.11), we have that

Since $\digamma _{n}\left(\mu \right) \leq \digamma \left(\mu \right),$ from (2.23), it follows that

By (2.24), we get

The above inequality follows

which contradicts with (2.21). Furthermore, define

Then, taking the derivative of (2.25) and using (2.13), we obtain

Similarly to the above, we conclude that

which contradicts with (2.22) and completes the proof. □

First, let us define

Furthermore, an additional assumption,

must be added to the fundamental assumptions (A1) through (A4) in the introduction section to achieve the following conclusions.

Theorem 4. Suppose that $\varphi \left(\mu, a\right) \in \mathbf{C}^{1}\left(\left[ \mu _{0}, \infty \right), \mathbb{R} \right),$ $\varphi ^{\prime }\left(\mu, a\right) > 0,$ and $\varphi \left(\mu, a\right) \leq h\left(\mu \right)$ for $\mu \in \left[ \mu _{0}, \infty \right)$. If there exists a real-valued function $\rho \in \mathbf{C} ^{1}\left(\left[ \mu _{0}, \infty \right), \left(0, \infty \right) \right)$ such that

then Eq (1.1) is oscillatory.

Proof. Assume that $x\left(\mu \right)$ is a nonoscillatory solution for Eq (1.1). We suppose, without losing generality, that for all $\mu \geq \mu _{1}$ and $\varrho \in \lbrack a, b]$, there exists a $\mu \in \left[ \mu _{0}, \infty \right)$ such that $x(\mu) > 0, x\left(h\left(\mu \right) \right) > 0$, and $x\left(\varphi \left(\mu, \varrho \right) \right) > 0$. Consequently, $w(\mu) > 0$. By Lemma 1, we get

By (A2) and (1.1), we have

That is,

It follows from using (1.1) and (2.28) with (2.27) that

hence,

From that fact that $w^{\prime }\left(\mu \right) > 0$ and $\varphi \left(\mu, \varrho \right) \geq \varphi \left(\mu, a\right) \,$, we have

We define a Riccati substitution:

Differentiating (2.30) and from (2.6), we get

Parallel to that, we present an additional Riccati transformation:

Similarly, by differentiating (2.32) and from (2.6), we get

Combining (2.31) and (2.33), we get

From (2.29), it is evident that

By integrating the aforementioned inequality from $\mu _{2}$ to $\mu$, we arrive at

By using the inequality (1.11) with $K = \rho ^{\prime }\left(\mu \right) /\rho \left(\mu \right)$ and $L = \ell \varphi ^{\prime }\left(\mu, \varrho \right) /\rho ^{1/\ell }\left(\mu \right) \lambda ^{1/\ell }\left(\varphi \left(\mu, \varrho \right) \right)$, we obtain

In the same way, we find that

Hence,

This contradicts with (2.26). This ends the proof. □

Theorem 5. If the first-order delay NDE

is oscillatory, then Eq (1.1) is oscillatory. Where

Proof. Continuing from (2.29), we find that

Equation (1.1) indicates that $\eta \left(\mu \right) = \lambda \left(\mu \right) \left[ w^{\prime }\left(\mu \right) \right] ^{\ell }$ is decreasing, which implies that

Consequently, from (2.36) in (2.35), we can observe that $\eta \left(\mu \right)$ is a positive solution of

Now, define a new function $\varpi (\mu)$ with

Then, by monotonicity of $\eta \left(\mu \right)$,

By replacing (2.38) with (2.37), we find that $\varpi (\mu)$ is a positive solution to the delay differential inequality

Thus, the last inequality has a positive solution. Using Theorem 1 in ^[12], we see that (2.34) also has a positive solution, which is a contradiction. The proof is complete. □

Using Theorem 2.1.1 in ^[38], we get the following corollary.

Corollary 2. If $\varphi \left(\mu, a\right) < \mu$ and

then Eq (1.1) is oscillatory.

We apply our results in the previous theories to practical examples.

Example 1. Consider

where $h_{0}, \nu \in \left(0, 1\right).$ Note that $\pi \left(\mu \right) = \mu,$

and

From Theorem 2, Eq (2.39) is oscillatory if

Applying Theorem 5 in ^[28], Eq (2.39) is oscillatory if

Remark 2. In the special case where $p_{0}$ $= 1/2,$ $h_{0} = 1/2,$ $\nu = 1/3$ and $\ell = 1$, condition (2.40) becomes $q > 0.703.$

On the other hand, using Theorem 5 in ^[28], Eq (2.39) is oscillatory if $q_{0} > 1.8635$. As a result, our findings offer an improved oscillation criterion.

The following example illustrates the sharpness of the condition (2).

Example 2. Cosider

where $\varphi \left(\mu, a\right) < \mu$ such that

and

Also,

and

By applying (2), we have

Then, all solutions of (2.42) are oscillatory. Moreover, $x\left(\mu \right) = \sin \left(\mu \right)$ is one such oscillatory solution.

3.   Numerical solutions

In this section, we present numerical solutions to show the oscillatory behavior of specific examples. These numerical simulations can then be compared with the theoretical findings obtained in previous sections.

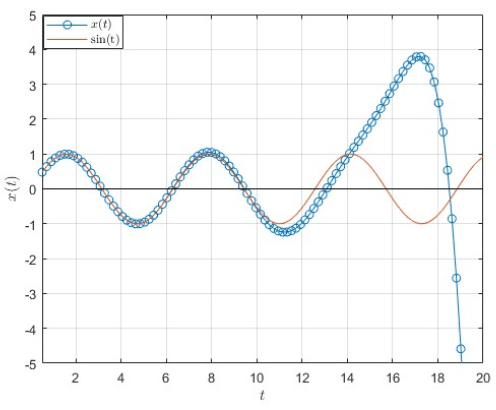
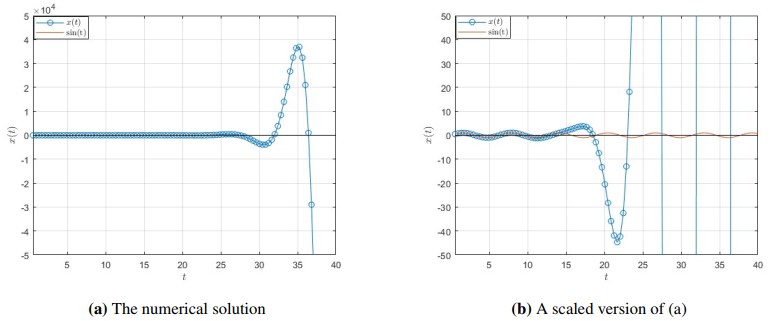
We solve Example 2 numerically, where Eq (1.1) is initially transformed to a system of first order. The system is then solved using Matlab 2024. Numerical solutions are shown in Figures 1 and 2, where $x(t) = \sin (t)$ is the history of the solution considered.

When comparing the numerical solution with the theoretical analysis, we observe a consistent oscillatory behavior in accordance with the conditions of the oscillation theorems. The mathematical analysis, based on the assumptions imposed on the coefficients and functions in the differential equation, confirms that all solutions must be oscillatory. This theoretical conclusion is supported by the numerical example given in Example 2, where the solution takes the explicit form $\sin \left(t\right)$, which clearly oscillates.

Numerically, the equation was solved using MATLAB 2024, where it was transformed into a system of first-order differential equations, and then numerical methods were applied to solve it. The numerical solutions also exhibited an oscillatory behavior consistent with the theoretical conclusions.

This agreement between the theoretical and numerical solutions indicates that the mathematical approach used in the theoretical analysis is accurate and effective in predicting oscillatory solutions. Consequently, the numerical results reinforce the validity of the theoretical proof and the approach used in the study, confirming that all solutions of the studied equation remain oscillatory over time.

4.   Conclusions

This paper investigated the oscillatory behavior of a class of second-order neutral nonlinear differential equations with distributed deviating arguments, as given in Eq (1.1). By employing the Riccati transformation and comparison principles, we established three new oscillation theorems under suitable conditions on the equation's coefficients and deviating arguments.

These results not only generalize but also extend several earlier contributions in the literature, as discussed in the introduction. Furthermore, the validity of the theoretical results has been supported by numerical examples (see Examples 1 and 2), which exhibit behaviors consistent with the predicted oscillation criteria.

Our findings provide a comprehensive analytical framework for addressing oscillatory behavior in this class of equations. In future work, it would be of interest to investigate how these results might be extended to fractional differential equations with delay, especially those involving memory effects characterized by power-law, exponential, or Mittag-Leffler kernels (see ^[39,40]).

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors gratefully acknowledge Qassim University, represented by the Deanship of Graduate Studies and Scientific Research, on the financial support for this research under the number (QU-J-PG-2-2025-53678) during the academic year 1446AH / 2024 AD.

Conflict of interest

The authors declare there is no conflict of interest.