Discontinuous Galerkin method for a three-dimensional coupled fluid-poroelastic model with applications to brain fluid mechanics

1.   Introduction

It is widely know that the spread of infectious diseases still poses a great threat to human life. For example, the H5N1 and H7N9 avian influenza viruses occasionally infect cells in the human upper respiratory tract and have the potential to transform into pandemic causing strains of influenza ^[1,2]. The outbreak of SARS (severe acute respiratory syndrom) virus in China, sent the human society into a panic ^[3,4]. The outbreak of COVID-19 has been announced as a Public Health Emergency of International Concern^[5], which brought great losses to the society and people ^[6,7,8].

As an important tool to analyze and control the spread of infectious diseases, mathematical modeling is used to predict how the disease will spread in the future, taking into account the factors that affect the spread of the disease, which is very important in the early stages of an epidemic, when no treatment or vaccination programme has been developed and therefore drug interventions are often not possible ^[9]. Mathematical models address the need for understanding the transmission dynamics and other significant factors of the disease that would aid policymakers to make accurate decisions and reduce the rate of transmission of the disease. Many authors have developed mathematical models to study the spread of COVID-19. In ^[8], Rahim ud Din et al. used an SEIR epidemic model to describe the dynamics of COVID-19 under convex incidence rate. In ^[10], Isys F. Mello et al. employed a spin $S = 1/2$ Ising-like model and a (logistic) Fermi-Dirac-like function to describe the spread of COVID-19. Especially, Hafeez Aderinsayo Adekola et al. ^[11] examined various forms of mathematical models that are relevant for the containment, risk analysis and features of COVID-19.

When a disease breaks out in a human population, people's response to the threat of the disease depends on their perception of the risk, and this perception is influenced by public and private information that is widely disseminated by the media ^[12,13,14]. Media coverage of outbreaks allows people to understand the extent of the risk and the prevention needs in the areas at risk, and encourages the public to take preventive measures such as wearing masks, avoiding public places, avoiding travel when sick and washing hands frequently. Extensive news coverage and the rapid flow of information can have a profound psychological impact on public health ^[15]. Media coverage can lower the rate of human exposure and the probability of transmission, Many researchers have used mathematical models to study the influence of media coverage ^[16,17].

In particular, novel coronavirus, which has the highest proportion of the asymptomatic among all epidemic diseases, therefore, in addition to the symptomatic, COVID-19 is likely to excrete a large amount of virus and carry out hidden transmission during the asymptomatic phase. Individuals testing positive in serological tests or blood tests for disease without symptoms is referred to as asymptomatic ^[11]. A simple SEIAR model was used to explain the transmission dynamics of the swine flu outbreak in 2009 at a residential school in Maharashtra, India ^[18]. Therefore, the recessive transmission of asymptomatic may be one of the main factors in the spread of the epidemic disease.

Besides, quarantine is essential measure in the spread of epidemic diseases. There are various forms of quarantine, such as home quarantine, quarantine of suspected infected persons and quarantine of infected persons. SARS is a good example, which effectively controlled the outbreak through quarantine ^[3,4]. The key role played by the quarantine to block the spread of COVID-19 in terms of an interacting parameter between people. In ^[10], Isys F. Mello et al. presented the key role played by the quarantine to block the spread of COVID-19 in terms of an interacting parameter between people. Therefore, we will establish an SQEIAR model considering media coverage, the asymptomatic and quarantine.

The emergence of new epidemics always imposes a certain financial burden on society, which has been widespread concerned in society. Therefore, it is of great significance to prevent and control infectious diseases at the minimum cost successfully. In this paper, we further consider the role of media coverage and quarantine in the spread of infectious diseases and establish an optimal control model. We will discuss the media coverage strategy and quarantine strategy for the optimal control problems with quadratic cost functions by applying Pontrygin maximum principle ^[19,20] and Hamilton-Jacobi-Bellman equation.

The paper is organized as follows. In the next section, an SQEIAR model is proposed and its basic properties are described. The the local and global stability of the disease-free equilibrium, as well as the local stability and uniform persistence of the endemic equilibrium are discussed in Section 3. In Section 4, threshold analysis is presented. In Section 5, the model is simulated numerically. In Section 6, the optimal control system is analyzed and simulated numerically. Lastly, the model is summarized and discussed.

2.   Model formulation and basic properties

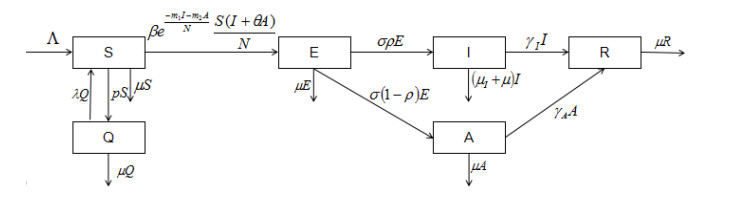
In epidemic disease models, the incidence function is extremely important as it determines the epidemic trend of the disease ^[21]. In many epidemiological models, the bilinear incidence rate $\beta S I$ and standard rates $\beta S I / N$ are the most commonly used to characterize the incidence of infectious diseases, where $\beta$ represents the transmission rate of the disease. Considering the media coverage, Cui and Zhu ^[16,22] adopted function $\beta (I) = \beta e^{-m I}$ to describe the media impact factors and proposed a new transmission rate function. Liu established the EIH model proposed in ^[12], the transmission coefficient was assumed to be $\beta e^{-(\alpha_1 E+\alpha_2 I+\alpha_3 H)}$. In ^[23], Sahu established the epidemic model and took $\beta e^{-\frac{m_1 I+m_2 H}{N}} \frac{S (I+\eta H)}{N}$ as the transmission term of the disease. In this paper, the total population at time $t$, denoted by $N (t)$, which has been sub-divided into six mutually exclusive compartments of the susceptible $S (t)$, the quarantined $Q (t)$, the exposed $E (t)$, the infectious $I (t)$, the asymptomatic $A (t)$ and the recovered $R (t)$, so that $N (t)$ = $S (t)+Q (t)+E (t) + I (t) + A (t) + R (t)$. The susceptible transforms into the quarantined, at the same time part of the quarantined backs into the susceptible, some of the susceptible gets into the exposed, at the same time part of the exposed is divided into two major categories of the symptomatic and the asymptomatic, finally some of the two classes of the infected get into the recovered. The population recruitment rate is $\Lambda$, population in all compartments decreases at rate $\mu$ due to nature death. Inspired by the literature above, in consideration of the media coverage, we adopt $\beta e^{-\frac{m_1 I+m_2 A}{N}} \frac{S (I+\theta A)}{N}$ as the transmission rate function to conduct research, where parameter $m_1$ and $m_2$ represent vector coverage coefficients for symptomatic and asymptomatic infected persons, respectively. The schematic diagram of SQEIAR is shown as following.

The following model is established based on the above assumptions

The initial conditions of system (2.1) is: $S (0) = S_0 > 0$, $Q (0) = Q_0 > 0$, $E (0) = E_0 > 0$, $I (0) = I_0 > 0$, $A (0) = A_0 > 0$, $R (0) = R_0 > 0$. The description of all the parameters is summarized in Table 1. Note that

We only consider the solutions with initial conditions in the feasible region

In the feasible region, the existence and uniqueness of the general solution and the continuation result are all valid. It can be proved that the feasible region $\Gamma$ is a positive invariant for (2.1).

Proposition 2.1. All the solution trajectories of system (2.1) initiating inside $\Gamma$ approach enter or stay within the interior of $\Gamma$.

Proof. Let $\Re^6_+ = \{(S, Q, E, I, A, R) \in \Re^6 :S\geq0, Q\geq0, E\geq0, I\geq0, A\geq0, R\geq0 \}$ denote the non-negative cone in six-dimensional Euclidean space. From the system (2.1), we observe that

Since $S(t), \, Q(t), \, E(t), \, I(t), \, A(t), \, R(t)$ are continuous with respect to $t$, and the vector field on each bounding hyperplane of $\Re^6_+$ is pointing inward direction of $\Re^6_+$, so all the solution trajectories initiating in $\Re^6_+$ will remain inside $\Re^6_+$ for all the time. Thus, the fact that $\Re^6_+$ is positively invariant for the system (2.1) is established. And the total population $N (t)$ satisfies $\frac{dN}{dt} = \Lambda-\mu N-\mu_I I$. Then, $\frac{dN}{dt}\leq \Lambda-\mu N$. Applying Birkhoff's and Rota's theorems on differential inequality ^[24,25], as $t\rightarrow \infty$, we have $0\leq N (t)\leq \frac{\Lambda}{\mu} = N_0$. Hence the solution of system (2.1) is bounded and any solution of the system which originated from $\Gamma$ remains in $\Gamma$. Thus we can find that the solution of system (2.1) is bounded and independent of the initial condition. So the feasible region $\Gamma$ is an invariant set.

Note that, $\Gamma$ is a biologically significant region for COVID-19 or other models of the same type of infectious disease. For COVID-19, as $S\geq0, Q\geq0, E\geq0, I\geq0, A\geq0, R\geq0$, i.e., the feasible region $\Gamma$ is non-negative and bounded.

Reduce the system (2.1) into non-dimensional form by using

Since $\tilde{S} = 1-\tilde{Q}-\tilde{E}-\tilde{I}-\tilde{A}-\tilde{R}$, then

The system (2.1) can be transformed the equivalent non-dimensional system

with the initial conditions:

where

In the next sections, we will study the dynamic behavior of the system (2.2) with the initial condition (2.3).

3.   The extinction and persistence of the diseases

In this section, we calculate the basic reproduction number of the system and all feasible equilibrium states. Observe that the feasible region for the non-dimensional system (2.2) is

For the system (2.2), $\Omega$ is positively invariant. We only consider the solution of the system (2.2) with initial conditions inside the feasible region $\Omega$.

3.1.   Local stability of disease-free equilibrium

The disease-free equilibrium of the system (2.2) is $E^{0} = (0, 0, 0, 0, 0, 1)$. The local stability of the disease-free equilibrium $E^{0}$ will be explored by using the basic reproduction number $\mathcal{R}_C$. The non-negative matrix $\mathcal{F}$ of the new infection terms, and the matrix $\mathcal{V}$ of the remaining terms are given by the following formula

and

The corresponding linearized matrices at the disease-free equilibrium $E^{0}$ are

and

It follows that

Then, by applying $\mathcal{R}_C = \rho (\mathrm{F} \mathrm{V}^{-1})$, where $\rho$ is the spectral radius, the basic reproduction number $\mathcal{R}_C$ is given by

where

Using Theorem 2 in ^[26], we can get the following result.

Theorem 3.1. The disease-free equilibrium $E^{0}$ of the system (2.2) is locally asymptotically stable if $\mathcal{R}_C < 1$ and $E^{0}$ is unstable if $\mathcal{R}_C > 1$.

The basic reproduction number represents the average number of people who will catch the disease from a single infected person at the beginning of the disease ^[26]. If $\mathcal{R}_C > 1$, the disease will be persistent and become endemic, otherwise, $\mathcal{R}_C < 1$, the disease will be extinct.

3.2.   Existence and local stability of endemic equilibrium

The possible positive equilibrium of the system (2.2) is obtained by solving the nonlinear equations which is obtained by equipping the derivatives of the system (2.2) to zero. The endemic equilibrium $\bar{E} = (Q^{*}, E^{*}, I^{*}, A^{*}, R^{*}, N^{*})$ of the model (2.2) is given by

where

The value of $I^{*}$ is given by

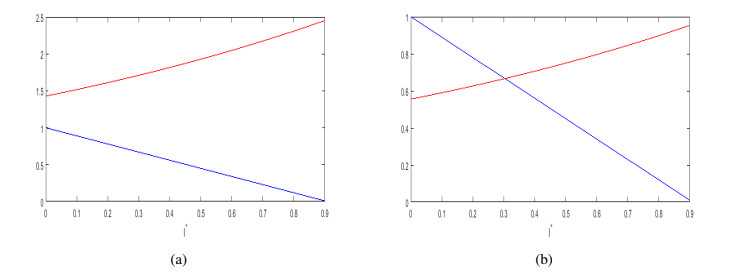
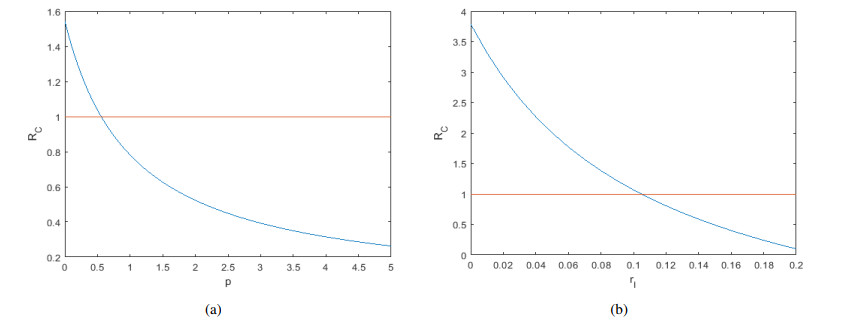
Suppose there is no media coverage, i.e., $m = 0$, we obtain $I^{*} = \frac{1}{b_5} (1-\frac{1}{\mathcal{R}_C})$. Therefore, $I^{*}$ exists in a positive value if and only if $\mathcal{R}_C > 1$, and it is the unique endemic equilibrium $\bar{E}$. Or else, the value of $I^{*}$ is given from (3.1). Now, we establish the existence of $I^{*}$ for $\mathcal{R}_C > 1$. In Figure 1, we plot the curve $\frac{e^{m I^{*}}}{\mathcal{R}_C}$ and straight line $1-b_5 I^{*}$ against $I^{*}$ in the range [0, 1]. Note that $\mathcal{R}_C < 1$, system (2.2) does not exist the endemic equilibrium. And when $\mathcal{R}_C > 1$, $I^{*}$ exists uniquely at positive level and hence the unique endemic equilibrium exists in this case (see Figure 1(b)). From the previous discussion, we can conclude the following Theorem 3.2.

Theorem 3.2. The system (2.2) has no endemic equilibrium if $\mathcal{R}_C \leq 1$. And the system (2.2) has a unique endemic equilibrium $\bar{E}$ if $\mathcal{R}_C > 1$.

In the following, we prove the local stability of the endemic equilibrium $\bar{E}$.

Theorem 3.3. The endemic equilibrium $\bar{E}$ is locally asymptotically stable if $\mathcal{R}_C > 1$, but close to 1.

Proof. The Jacobian matrix $\mathbf{J_0}$ at disease-free equilibrium is given by

Here, we establish the local stability of endemic equilibrium based on the central manifold theory and taking $\beta$ as bifurcation parameter ^[27]. A critical value of bifurcation parameter $\beta$ at $\mathcal{R}_C = 1$ is given as

Corresponding to the zero eigenvalue, the Jacobian can be easily verified $\mathbf{J_0}$ at $\tilde{\beta} = \tilde{\beta}_c$ has a right eigenvector given by $\mathbf{W} = (w_1, w_2, w_3, w_4, w_5, w_6)^T$, where

Furthermore, corresponding to the zero eigenvalue, the components of the left eigenvector, $\mathbf{V} = (v_1, v_2, v_3, v_4, v_5, v_6)$, must satisfy the equalities $\mathbf{V}\cdot\mathbf{J_0} = 0$ and $\mathbf{V}\cdot\mathbf{W} = 1$, so

where

Use the notations $x_1\equiv \tilde{Q}$, $x_2\equiv \tilde{E}$, $x_3\equiv \tilde{I}$, $x_4\equiv \tilde{A}$, $x_5\equiv \tilde{R}$, $x_6\equiv \tilde{N}$, we have

When $\beta = \beta_c$, substituting the following values of all the second order derivatives evaluated at the disease-free equilibrium $E^{0}$, we get

and

Finally, substituting the values of $\mathbf{V}$ and $\mathbf{W}$ in $\mathbf{a}$ and $\mathbf{b}$, we obtain

where

Since $\mathbf{a} < 0$ and $\mathbf{b} > 0$ at $\beta = \beta_c$, by using Theorem 4.1 and Remark 1 stated in ^[27], there is a transcritical bifurcation at $\mathcal{R}_C = 1$ and the locally asymptotically stable of the unique endemic equilibrium for $\mathcal{R}_C > 1$ is established.

3.3.   Global stability of the disease-free equilibrium $E^{0}$

We analyze the globally asymptotical stability of the disease-free equilibrium $E^0$ in this subsection.

Theorem 3.4. Suppose $\mathcal{R}_{C} < 1$ and $\tilde{\mu}_I = 0$. The disease-free equilibrium $E^{0}$ is globally asymptotically stable.

Proof. We present the global stability of the disease-free equilibrium by using the method in ^[28]. When $\tilde{\mu}_I = 0$, we have $\frac{d\tilde{N}}{d\tilde{t}} = 1-\tilde{N}$. Then $\tilde{N}\rightarrow1$ as $\tilde{t}\rightarrow \infty$. Take $\tilde{N}$ in the limiting case, i.e., $\tilde{N} = 1$, then the system (2.2) reduces to

Let $X = (\tilde{Q})$ and $Z = (\tilde{E}, \tilde{I}, \tilde{A}, \tilde{R})$, here $U_0 = (X^0, Z^0)$, where $X^0 = (\frac{\tilde{p}}{\tilde{p}+\tilde{\lambda}+1})$ and $Z^0 = (0, 0, 0, 0)$. We have

At $Z = Z^0$, $G (X, 0) = 0$. Now $\frac{dX}{d\tilde{t}} = F(X, 0) = \tilde{p}-(\tilde{p}+\tilde{\lambda}+1) X$, as $\tilde{t} \rightarrow \infty$, $X \rightarrow X^0$. Thus, $X = X^0$ $( = \tilde{Q}^0 = \frac{\tilde{p}}{\tilde{p}+\tilde{\lambda}+1})$ is globally asymptotically stable. Hence, the condition $(H_1)$ in ^[28] is satisfied. From (3.2), we get

where

and

Obviously, $B$ is an M-matrix. We have $0 < e^{-m_1 \tilde{I}-m_2 \tilde{A}}\leq1$, for $\tilde{I}\geq0$, $\tilde{A}\geq0$. Therefore, $\hat{G} (X, Z)\geq0$ since $0 \leq \tilde{S}\leq 1$. Thus both the conditions $(H_1)$ and $(H_2)$ in ^[28] are satisfied. Hence, the disease-free equilibrium $E^0$ is globally asymptotically stable if $\mathcal{R}_C < 1$.

3.4.   Uniform persistence of system (2.2)

In the next, the uniform persistence for the system (2.2) will be explored. The system (2.2) is said to be uniformly persistent if there exists a constant $c$ such that any solution $(\tilde{Q} (t), \tilde{E} (t),$ $\tilde{I} (t), \tilde{A} (t), \tilde{R} (t), \tilde{N} (t))$ satisfies

provided that $(\tilde{Q}(0), \tilde{E}(0), \tilde{I}(0), \tilde{A}(0), \tilde{R}(0), \tilde{N}(0))\in \Omega$ ^[29]. Similar as the proof of ^[30], the following theorem for persistence can be stated:

Theorem 3.5. The system (2.2) is uniformly persistent in $\Omega$ if and only if $\mathcal{R}_C > 1$.

Proof. From Theorem 3.1, the disease-free equilibrium of the model (3.2) is unstable when $\mathcal{R}_C > 1$. Applying the uniform persistence result stated in ^[29], finally it can be proved in a similar way as Proposition 3.3 in ^[31]. At the beginning, the necessity of $\mathcal{R}_C > 1$ be deduced from the result of Theorem 3.2 and the asymptotic stability of the disease-free equilibrium. The sufficiency of the condition $\mathcal{R}_C > 1$ is given by uniformly persistent results in the Theorem 4.3 in ^[29]. It can be proved that the system (3.2) satisfies the hypothesis (H) of Theorem 4.3 in ^[29]. Eventually, the proposition is proved by observing that, in (3.2), the necessary and sufficient conditions for uniform persistence in Theorem 4.3 in ^[29] is equivalent to the disease-free equilibrium is unstable. The consequence shows that in limiting case, $\tilde{Q}$, $\tilde{E}$, $\tilde{I}$ and $\tilde{A}$ of the model (3.2) will remain a positive value and the disease will persist.

4.   Threshold analysis

In this section, the quarantine parameter $\tilde{p}$, the progression rate $\tilde{\sigma}$ from the exposed to the infectious and the recovery rate for the symptomatic infectious $\tilde{\gamma}_I$ with respect to $\mathcal{R}_C$ is measured qualitatively. The threshold analysis on the parameters $\tilde{p}$ is performed by calculating the partial derivatives of the effective reproduction number $\mathcal{R}_C$. We can observe that

Hence

From the above discussion, we have the following conclusion: the larger the quarantine parameter is, the better the quarantine effect is. The basic reproduction number $\mathcal{R}_C$ decreases with the increase of the quarantine parameter $\tilde{p}$, when $\mathcal{R}_C < 1$ and the infectious disease will be extinct.

Theorem 4.1. For the model $(2.2)$, the use of quarantine of the susceptile individuals will have positive population-level impact since $\frac{\partial \mathcal{R}_C}{\partial \tilde{p}} < 0$.

In the same way, the threshold analysis respect to the parameters $(1-\tilde{\rho})$ is performed by calculating the partial derivatives of the effective reproduction number $\mathcal{R}_C$:

It follows that

where

Therefore, it can be concluded that if $\theta < \theta_{(1-\tilde{\rho})}$, the quarantine will achieve good results.

Theorem 4.2. For the model (2.2), the use of quarantine of the infectious individuals will have positive (negative) population-level impact since $\theta < \theta_{(1-\tilde{\rho})}\, \, (\theta > \theta_{(1-\tilde{\rho})})$.

5.   Numerical simulation

In this section, we provide numerical simulations to illustrate the results under the values of the biologically feasible parameters which is shown in Table 2. The system (2.1) is simulated by taking initial value $S_0 = 390, Q_0 = 58, E_0 = 245, I_0 = 95, A_0 = 45, R_0 = 160$. The initial values of the numerical simulation are arbitrary and are used only for the simulation, rather than data from a particular region. In fact, the main theoretical results in this paper are independent of the initial values, which we will also present in the subsequent numerical simulation.

Based on the form of the basic regeneration number of system (2.2) calculated in Section 3, the expression form of the basic regeneration number of system (2.1) can be obtained as follows (we also note it as $\mathcal{R}_C$):

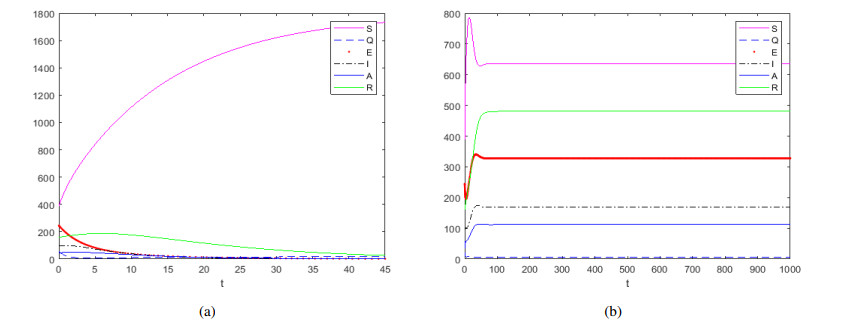
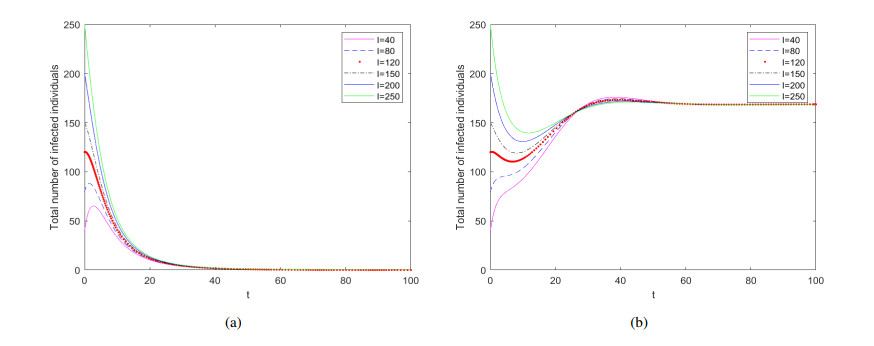
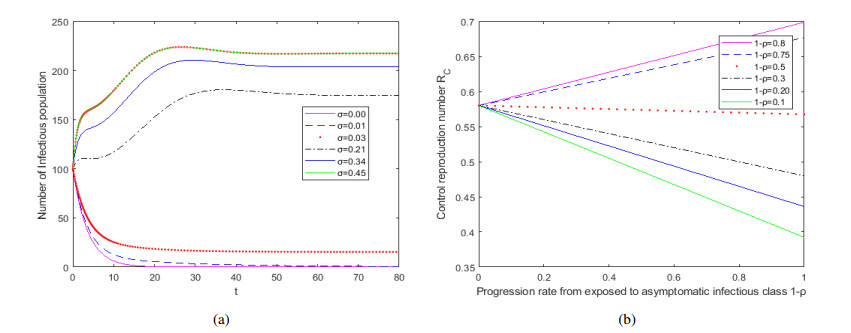
For $\beta = 0.09$, the basic reproduction number $\mathcal{R}_C = 0.3438$, the disease-free equilibrium is locally asymptotically stable, see Figure 2(a), the recovered is represented by the solid green line which is decreasing as $t$ increasing but does not go to zero. When $\beta = 0.65$, the basic reproduction number $\mathcal{R}_C = 2.4833 > 1$, the unique endemic equilibrium is locally asymptotically stable as shown in Figure 2(b), which means that the infectious increases over time but reaches a certain level after a period of time and remains stable. The fraction of the total number of infected individuals as a function of time with different initial values for $\mathcal{R}_\mathcal{C} = 0.3438 < 1$ is presented by Figure 3(a) and $\mathcal{R}_\mathcal{C} = 2.4833 > 1$ is presented by Figure 3(b), respectively. We can conclude that when the $\mathcal{R}_\mathcal{C}$ is a definite value, the trend of infected individuals has no change with the different initial values of infectious. The effect of parameter $m$ respect to infected individuals is shown separately in Figure 4, which has shown that media coverage decrease the infectious. The effect of parameter $\sigma$ on the number of the infectious is shown in Figure 5(a), when $\sigma\leq 0.03$, the number of infected individuals decrease and tend to 0, while $\sigma \geq0.21$, the number of infected individuals increase. For $1-\rho$, in Figure 6(b), $1-\rho$ has both positive and negative effects on the basic reproduction number, when $1-\rho > 0.5$, $\mathcal{R}_C$ increases, otherwise, decrease. It can be seen from Figure 6(a) that the basic reproduction number decreases as the quarantine parameter $p$ increases and $\mathcal{R}_C < 1$ if $p > 0.7$. With $\gamma_I$ increasing, the basic regenerative number is decreasing and $\gamma_I = 0.1053$ is the critical value.

6.   Optimal control strategy for disease control

From the above sections, the influence of media coverage and quarantine measures on the number of infected individuals is discussed. To ensure the effectiveness of control while minimizing the cost of various prevention measures is the top concern of the government in the face of the epidemic. Therefore, we add media coverage control and quarantine control to the system (2.1), and the model is shown as follows:

The control function $u_1(t)$ represents media coverage control for the symptomatic, $u_2(t)$ represents media coverage control for the asymptomatic and the control of the quarantine is expressed by $u_3(t)$. In order to solve $u_1(t)$, $u_2(t)$, $u_3(t)$, we construct the objective functional $J$. Then has

where $A_1$, $A_2$ represent the positive weight. We need to find an optimal control $u^*_1 (t)$, $u^*_2 (t)$ and $u^*_3 (t)$ such that

where

is the control set.

6.1.   The existence of optimal control

Optimal control existence can be demonstrated through a well known classical result: (see ^[20]), we must inspect that the following axioms are satisfied:

$(H_1)$ Controls set and set of state variables are nonempty.

$(H_2)$ The admissible control set $U$ is convex and closed.

$(H_3)$ R.H.S of state system is bounded by a linear function of the state variables and controls.

$(H_4)$ The objective functional $J$ has convex integrand on $U$ and is bounded below by $c_1(\sum _{i = 1}^{3} |u_i|^2)^\frac{\tau}{2}-c_2$, where $c_1, c_2 > 0$ and $\tau > 1$.

The existence of solutions for the system is established by using the result given by Lukes ^[32]. In this way we verify the above hypotheses. $(H_1)$ is accomplished because the coefficients are bounded. The boundedness of solutions shows that the set of controls fulfils $(H_2)$. Since the system of equations is bilinear in $u_1$, $u_2$ and solutions are bounded. So, R.H.S of system satisfies the criteria $(H_3)$. Because the integrand of objective functional is convex and the last condition is satisfied.

where $M_1$, $M_2$, $D_1$, $D_2$, $D_3$, $c_1$, $c_2 > 0$ and $\tau > 1$. Thus we have the following theorem:

Theorem 6.1. For the objective functional $J(u_1(t), u_2(t), u_3(t)) = \int_{0}^{T} (A_1 I+A_2 A+\frac{B_1}{2} u^{2}_1+\frac{B_2}{2} u^{2}_2+\frac{B_3}{2} u^{2}_3) dt$, where $U = \{(u_1(t), u_2(t), u_3(t))\mid 0\leq u_i(t)\leq1, i = 1, 2, 3, t\in [0, T]\}$ subject to system with initial conditions, there exists an optimal control $u^*_1 (t), u^*_2 (t), u^*_3 (t)$, so that $J(u^*_1(t), u^*_2(t), u^*_3(t)) = min {J(u_1(t), u_2(t), u_3(t)), (u_1(t), u_2(t), u_3(t))\in U}$.

In order to obtain an optimal control $u^*_1 (t), u^*_2 (t), u^*_3 (t)$ to make $J(u^*_1(t), u^*_2(t), u^*_3(t)) = min {J(u_1(t), u_2(t), u_3(t)), (u_1(t), u_2(t), u_3(t))\in U}$. The optimal solution can be obtained by finding the Lagrangian as well as Hamiltonian for the system. The Lagrangian is:

We need establish the Lagrangian minimum value. To achieve this goal, we construct the Hamiltonian function $H$ for the optimal problem as follows:

We can find the essential conditions for the optimal control problem by applying the Pontryagin's Maximum Principle ^[19]. For the system, the solution of optimal control problem, a non-zero vector function $\lambda (t) = (\lambda_1, \lambda_2, \lambda_3, \lambda_4, \lambda_5, \lambda_6)$ exists and the subsequent conditions is established. Then the state equation, optimality condition and adjoint equation, respectively as follows:

The essential conditions applied to the Hamiltonian $H$ give the following result:

Theorem 6.2. Given that $(S^*, Q^*, E^*, I^*, A^*, R^*)$ are optimal state solutions and $(u_1^*, u_2^*, u_3^*)$ are associated optimal control variable for the optimal control problem (6.1), then, there exists adjoint variables $\lambda_i$, for $i = 1, 2, 3, 4, 5, 6$ which satisfies

with the transversality condition $\lambda_1(T) = \lambda_2(T) = \cdot\cdot\cdot = \lambda_6(T) = 0$. Additionally, $u_1^*, u_2^*, u_3^*$ are expressed as

Proof. The adjoint equations and the conditions of transversality are obtained by the Hamilton function $H$. By putting $S = S^*, Q = Q^*, E = E^*, I = I^*, A = A^*, R = R^*$ and differentiating the Hamiltonian with respect to $S, Q, E, I, A$ and $R$ respectively, we obtain

with the transversality condition $\lambda_1(T) = \lambda_2(T) = \cdot\cdot\cdot = \lambda_6(T) = 0$. Further, by solving the equations $\frac{\partial H}{\partial u_i} = 0$, $i = 1, 2, 3$ on the interior of the control set and using the optimality condition, we obtain

Let's solve $u_1$ by using the first two equations of (6.3), thus

Hence,

Putting (6.5) in the first equation of (6.4), we get $u_1^*$. And then we can easily get $u_2^*$ and $u_3^*$ as follows

Therefore, the optimal control problem of (6.1) is finished. Furthermore, some graphs is obtained by numerical simulation.

6.2.   Numerical simulation of optimal control

In this section, we assess numerically by investigating the effect of control strategies on the transmission dynamics of disease. An iterative scheme of fourth order Runge-Kutta method is used for solving the optimality system (6.1). The common parameter values used in the computations are the same in Table 2 except $\beta$, and the initial value are $S_0 = 400, \, \, Q_0 = 200, \, \, E_0 = 300, \, \, I_0 = 50, \, \, A_0 = 60, \, \, R_0 = 35$ and $\beta = 0.26$.

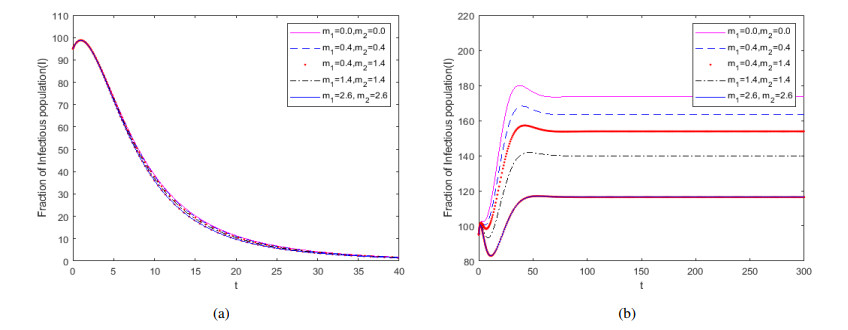
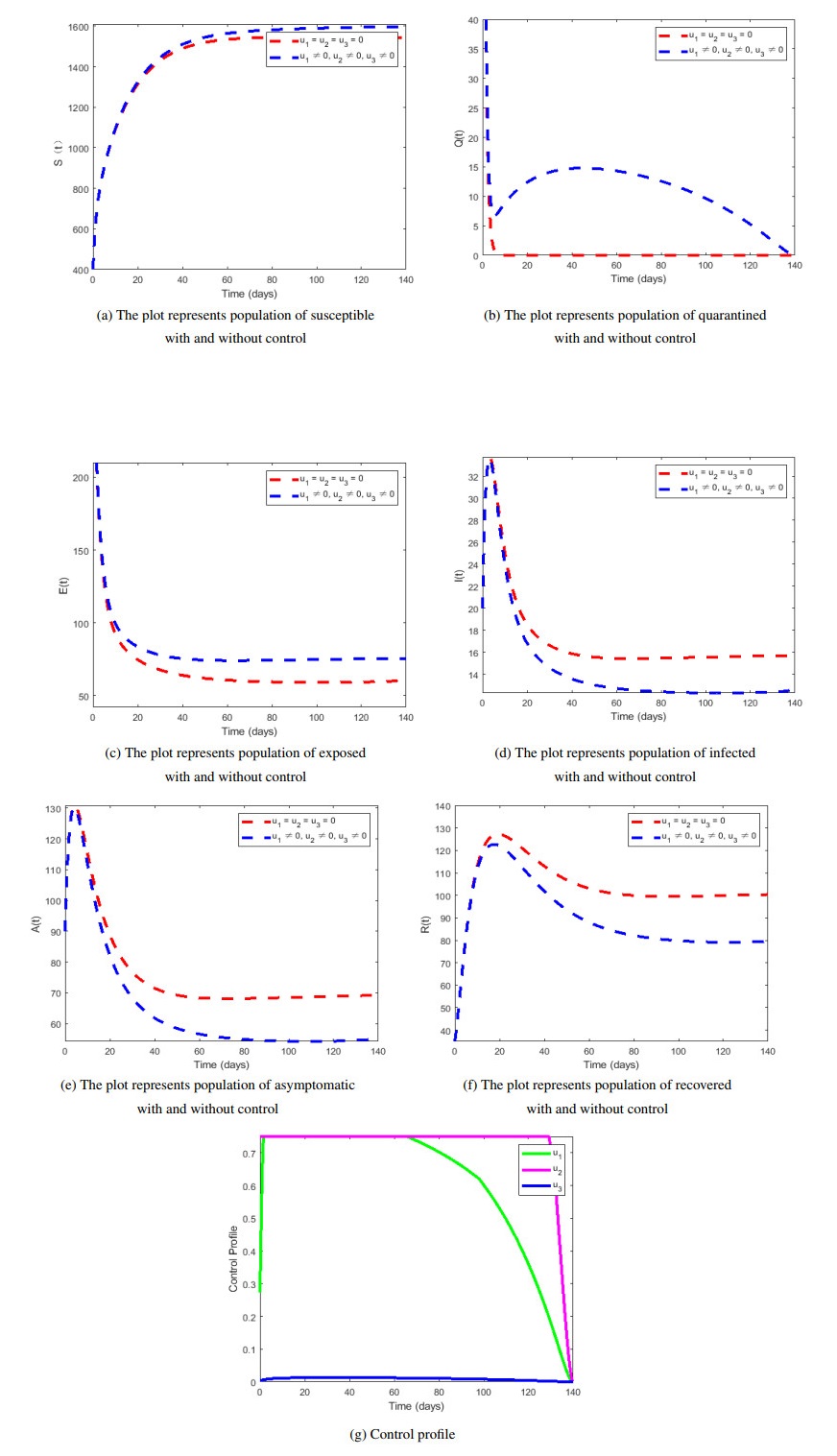
The system is numerically simulated under the control of media coverage and quarantine. When media control and quarantine control measure are used together to optimize the objection $J$, it is observed from Figure 7 that the number of symptomatic and asymptomatic individuals are both reduced, while the number of susceptible individuals will increase greatly. The upper bounds for the controls $u_1, u_2$ and $u_3$ are 140 days.

7.   Conclusions

The SQEIAR model proposed in this paper is based on the media coverage and quarantine. We discussed the dynamic behavior of the proposed model. The disease-free equilibrium of the system (2.2) is locally-asymptotically stable if $\mathcal{R}_C < 1$, and if $\mathcal{R}_C > 1$, it is unstable. Then the existence of the endemic equilibrium, the local asymptotic stability and global asymptotic stability of the equilibria of system (2.2) related to basic reproduction number are discussed and the uniformly persistent property of the system is obtained. The threshold analysis is carried out to discuss the influence of different parameters on the effective reproduction number, such as the quarantine parameter $p$, the recovery rate for symptomatic infections individuals $\gamma_I$, the progression rate parameters $\sigma$ and $1-\rho$, which have both positive and negative effects on the basic reproduction number. The increase of quarantine parameter $p$ while the effective reproduction number decrease, which indicates that quarantine measures affect the extinction rate of the disease. The recovery rate parameter $\gamma_I$ has the same effect on the basic regeneration number as the quarantine $p$. While the progression rate parameters $1-\rho$ has both positive and negative effects on the basic reproduction number, when the $1-\rho$ is greater than the threshold, $R_C$ increases, otherwise, $R_C$ decrease. The parameter $\sigma$ has both positive and negative effects on the number of the infectious, when the value of $\sigma$ is less than a certain small value, the number of infected individuals decrease and tend to 0, while $\sigma$ is bigger than a certain big value, the number of infected individuals increase.

Furthermore, the optimal control solutions are shown in Figure 7, showing media coverage and quarantine measures are simultaneously more conducive to controlling the spread of epidemic diseases in the early stages. By using the optimal control theory, we obtain the control strategy that minimizes infected and asymptomatic infected persons with the least cost of implementing control measures. Under this kinds of control, the number of symptomatic and asymptomatic individuals are both reduced, while the number of susceptible individuals will increase greatly. Therefore, the suggestion for the control of epidemic disease is to greatly reduce the number of infected persons through positive media influence and effective quarantine.

The model works well for the spread of COVID-19, based on the basic regeneration number formula given by the model, we can calculate the basic regeneration number of COVID-19 transmission in a certain region, and then predict the transmission trend of COVID-19. The impact of the analyzed model parameters on the basic regeneration number or the number of infected people can provide suggestions for the prevention and treatment of COVID-19 from media reports, quarantine, treatment and recovery. In particular, our model is able to give a control strategy that minimizes the number of COVID-19 infected and asymptomatic infected people at the least cost, which is crucial for economically underdeveloped countries to control COVID-19. Compared with other conventional COVID-19 models, such as SEIR model in the literature ^[8,33], the proposed model not only adds the category of asymptomatic infection, but also takes into account the impact of media coverage and quarantine on the transmission of COVID-19, which is more consistent with the current actual situation of COVID-19 transmission. This makes our model more practical in revealing the transmission pattern of the COVID-19.

Acknowledgments

This work is supported by the National Natural Science Foundation of China (No. 11701495), the Scientific and Technological Key Projects of Henan Province (No. 202102310631), the Key Scientific Research Project in Colleges and Universities of Henan Province of China (No. 19A110036) and Nanhu Scholars Program for Young Scholars of XYNU.

Conflict of interest

The authors declare no conflict of interest.