Complex dynamics of non-smooth pest-natural enemy Gomportz models with a variable searching rate based on threshold control

1.   Introduction

Chaotic systems exhibit intricate nonlinear dynamics, characterized by features such as pseudo-random behavior and a heightened sensitivity to initial conditions. Lur'e systems (LSs), which encompass a wide range of chaotic systems such as Chua's circuits ^[1] neural networks ^[2], and n-scroll attractors ^[3], have attracted significant research attention in the past decades. Chaos synchronization of LSs has found applications in diverse areas including image encryption ^[4,5,6], cryptography ^[7,8] and confidential communication ^[9,10,11]. The existence of time delay and stochastic perturbations are often unavoidable in a real-world control system and can cause the system to be unstable. Correspondingly, substantial efforts have been devoted to chaos synchronization of stochastic time-delay LSs, and a few results have been reported ^{[12,13,14,15]}.

When implementing chaos synchronization in a networked environment, network-induced phenomena, such as packet losses ^[16], link failures ^[17] and cyber attacks ^[18,19,20], can introduce inconsistencies between the system and the controller/filter modes ^[21]. Therefore, researchers have shown interest in studying chaos synchronization using asynchronous/mode-unmatched controllers. The hidden Markov model (HMM), proposed by Rabiner ^[22], serves as a suitable tool for describing the asynchronous phenomena. Building upon the HMM framework, Li et al. ^[23] investigated the synchronization control in Markov-switching neural networks, while Ma et al. ^[24] explored the drive-response synchronization in fuzzy complex dynamic networks. Despite these advancements, to our knowledge, there is a scarcity of research addressing chaos synchronization in stochastic time-delay LSs under asynchronous controllers.

Moreover, in networked control systems, the bandwidth of the communication network is usually limited, which can impact the control performance significantly. To eliminate unnecessary resource waste and achieve efficient resource allocation, recent studies on chaos synchronization of LSs have utilized event-triggered mechanism (ETM)-based control methods. For instance, Wu et al. ^[25] conducted research on exponential synchronization and joint performance issues of chaotic LSs by designing a switching ETM based on perturbation terms. He et al. ^[26] proposed a secure communication scheme through synchronized chaotic neural networks based on quantized output feedback ETM. Besides, several studies on memory-based ETM for chaos synchronization in LSs have been reported in ^[27,28,29]. Notably, the above literature employed fixed thresholds in the designed ETM, limiting their ability to conserve communication resources.

Motivated by the above discussion, we explore the master-slave chaos synchronization of stochastic time-delay LSs within an asynchronous and adaptive event-triggered (AAET) control framework. Unlike previous works ^{[25,26,27,28,29]}, the thresholds of the ETM used can be adjusted adaptively with real-time system states. The objective is to determine the required AAET controller gains to ensure that the synchronization-error system (SES) has both stochastic stability (SS) and $\mathcal{L}_{2}-\mathcal{L}_{\infty}$ disturbance-suppression performance (LDSP) ^[30]. The contributions of this paper are:

1) The AAET controller is first applied to tackle the chaos synchronization issue of stochastic time-delay LSs;

2) A criterion on the SS and LDSP is proposed using a Lyapunov-Krasovskii functional (LKF), a Wirtinger-type inequality, the Itô formula, as well as a convex combination inequality (CCI);

3) A method for determining the desired AAET controller is proposed by decoupling the nonlinearities that arise from the Lyapunov matrices and controller gains.

2.   Preliminaries

Throughout, we employ $\mathbb{R}^{n_1}$, $\mathbb{R}^{n_1 \times n_2}$ and $\mathbb{N}$ to stand for the $n_1$-dimensional Euclidean space, the set of all $n_1 \times n_2$ real matrices, and the set of natural numbers, respectively. The symbol $\|\cdot\|$ is the Euclidean vector norm, $(\cdot)^{T}$ represents the matrix transposition, $He(G)$ means the sum of matrix $G$ and its transpose $G^T$, $\ast$ indicates the symmetric term in a matrix and $\mathscr{E}\{\cdot\}$ and $Prob\{\cdot\}$ indicate, respectively, the expectation and probability operator. Furthermore, we utilize $col\{\cdot\}$ to denote a column vector, $diag\{\cdot\}$ to stand for a block-diagonal matrix and $\sup\{\cdot\}$ and $\inf\{\cdot\}$ to indicate the supremum and infimum of a set of real numbers, respectively.

2.1.   Physical plant

Consider the following master-slave stochastic time-delay LSs:

with $x_{m} (t) \in \mathbb{R}^{n_{x}}$ and $x_{s} (t) \in \mathbb{R}^{n_{x}}$ being the state vectors, $\xi_{m0}$ and $\xi_{s0}$ being the initial values, $y_{m} (t) \in \mathbb{R}^{n_{y}}$ and $y_{s} (t) \in \mathbb{R}^{n_{y}}$ being the output vectors, $\psi (\cdot) \in \mathbb{R}^{q}$ being the nonlinear term with all components within $[\acute{g}_{r}, \grave{g}_{r}]$ for $r = 1, 2, \cdots, q$, $u (t) \in \mathbb{R}^{q}$ being the control signal to be designed, $v (t)$ being the disturbance in $L_2[0, \, \infty)$ ^[31], one-dimension Brownian motion $\varpi (t)$ satisfying $\mathscr{E}\{d\varpi (t)\} = 0$ and $\mathscr{E}\{d\varpi^{2} (t)\} = dt$, and time-varying delay $\tau (t)$ satisfying $0 < \tau_{1} \leqslant \tau (t) \leqslant \tau_{2}$ and $\mu_{1} \leqslant \dot{\tau} (t) \leqslant \mu_{2}$, where $\tau_{1}$, $\tau_{2}$, $\mu_{1}$, and $\mu_{2}$ are constants. $\{\alpha (t), t \geqslant 0\}$ is the Markovian process and belongs to the state space $\mathscr{N} = \left\{ 1, 2, \cdots, N \right\}$. The transition rate (TR) matrix and transition probability is given by $\Pi = [\pi_{ij}]_{N \times N}$ and

with $\varsigma > 0$, $\lim_{\varsigma} \to 0 o (\varsigma)/\varsigma = 0$, $\pi_{ij} \geqslant 0$, $i \neq j$ and $\pi_{ii} = -\sum_{i = 1, i \neq j}^{N} \pi_{ij}$ ^[32,33,34]. $A_{\alpha (t)}$, $B_{\alpha (t)}$, $C_{\alpha (t)}$, $D_{\alpha (t)}$, $E_{\alpha (t)}$ and $W_{\alpha (t)}$, which can be abbreviated as $A_{i}$, $B_{i}$, $C_{i}$, $D_{i}$, $E_{i}$, and $W_{i}$ for $\alpha (t) = i \in \mathscr{N}$, are matrices with appropriate dimensions.

2.2.   Adaptive event-triggered mechanism

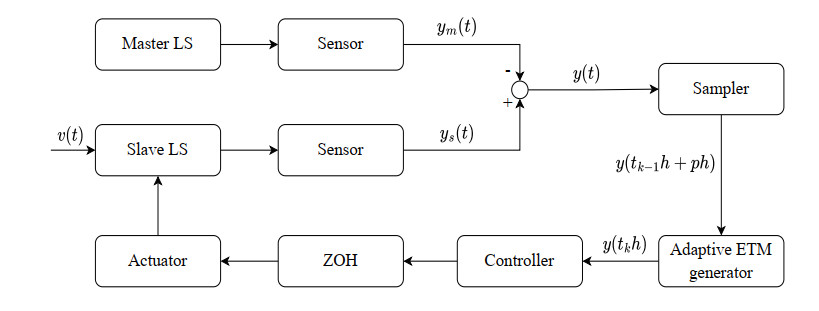
In order to minimize information transmission, the adaptive ETM is employed to determine whether the current sampled data should be transmitted to the controller, as illustrated in Figure 1. Let $t_{k}h$ denote the latest transmission time of the output signal, where $h > 0$ is the sampling period. $y (t_{k}h)$ and $y (t)$ denote the latest output signal and the current one, respectively. Defining $e (t) = y (t_{k}h) - y (t)$, the event-triggered condition is designed as follows:

where $\Psi_{i} > 0$ is the trigger matrix and $\rho (t)$ is a threshold parameter adjusted by an adaptive law as

where $\rho_{1}$ and $\rho_{2}$ are predetermined parameters with $0 < \rho_{1} \leqslant \rho_{2} < 1$, $\kappa$ is a positive scalar used to adjust the sensitivity of the function $\|e (k)\|^{2}$.

Remark 1. The value of $\rho (t)$ has a certain influence on the trigger condition (2.3). The trigger condition will be stricter with the value of $\rho (t)$ being higher, resulting in less data being transmitted to the controller. Conversely, the trigger condition will be relaxed with the value of $\rho (t)$ being lower, allowing more data to be transmitted. Furthermore, it is worth to mention that, when $\rho (t)$ takes a constant on $(0, 1]$, the adaptive ETM will be transformed into the periodic ETM (PETM); when $\rho (t)$ is set as $0$, it will be transformed into the sampled-data mechanism (SDM).

Remark 2. The $arccot$ function, incorporated in the adaptive law (2.4), enables the threshold parameter of ETM to be dynamically adjusted as the output error changes within the range of $(\rho_{1}, \rho_{2}]$. The presence of the $arccot$ function results in an inverse relationship between the threshold parameter $\rho(t)$ and the output error $e(t)$. It can be observed that $\rho(t)$ tends to $\rho_{2}$ as $\|e(t)\|^{2}$ approaches 0, and $\rho(t)$ tends to $\rho_{1}$ as $\|e(t)\|^{2}$ approaches $\infty$.

2.3.   Controller

Consider the following controller:

Unlike ^[35,36,37], the controller is based on output feedback, which is known to be more easily implemented. In the controller, we introduce another stochastic variable with state space $\mathscr{M} = \left\{ 1, 2, \cdots, M \right\}$ to describe this stochastic process $\{\beta (t), t \geqslant 0\}$. The conditional transition probability (CTP) matrix is signed as $\Phi = [\varphi_{i \iota}]_{N \times M}$ with

and $\sum_{\iota = 1}^{M} \varphi_{i \iota} = 1$. $K_{\beta (t)}$, which will be abbreviated as $K_{\iota}$, is the controller gain to be designed. Note that $\{\{\alpha (t), t \geqslant 0\} \{\beta (t), t \geqslant 0\}\}$ constitutes a HMM ^[38,39].

Define $x (t) = x_{m} (t)-x_{s} (t)$. Then, from (2.1), (2.2) and (2.5), one can establish the following SES:

where $\mathscr{F} (t) = (A_{i}-K_{\iota}C_{i})x (t) + B_{i}x (t-\tau (t)) + W_{i}\tilde{\psi} (Fx (t)) - K_{\iota}e (t) -E_{i}v (t)$, $\mathscr{G} (t) = D_{i}x (t)$, $\tilde{\psi} (Fx (t)) = \psi\left(F (x (t)+x_{s} (t))\right) - \psi (Fx_{s} (t))$ that satisfies

where $f_{r}^{T}$ indicates the r-th row of $F$. From (2.7), one can get

Remark 3. The constants $\acute{g}_{r}$ and $\grave{g}_{r}$ can be taken as positive, negative, or zero. By allowing $\acute{g}_{r}$ and $\grave{g}_{r}$ to have a wide range of values, the sector bounded nonlinearity can flexibly adapt to the needs of different systems and provide a more flexible regulation and control mechanism.

To streamline the subsequent analysis, we define

and provide two definitions and four lemmas.

Definition 1. The SES (2.6) is said to be with SS if there exists a scalar $\mathcal{M}(\alpha_{0}, \xi(\cdot))$ satisfying

when $v(t) \equiv 0$.

Definition 2. Under the zero initial condition, for a given scalar $\gamma > 0$, the SES (2.6) is said to have a LDSP if

holds for $v (t) \neq 0$.

Lemma 1. Given stochastic differential equation

where $\varpi (t)$ is one-dimension Brownian motion, for scalars $a$, $b$ $(b > a)$, and a matrix $R$, one has

where $\tilde{R} = diag\{ R, 3R \}$ and

Remark 4. Following the approaches used in ^[40,41], the Wirtinger-type inequality of Lemma 1 can be readily established. It should be noted that the integral term in $\mu (a, b)$ should be $\frac{1}{b-a} \int_{a}^{b} (b+a-2s) \mathscr{G} (s) \, d\varpi (s)$ instead of $\frac{1}{b-a} \int_{a}^{b} (b-a+2s) \mathscr{G} (s) \, d\varpi (s)$.

Lemma 2. ^[40] Consider the stochastic differential equation (2.9). For $n \times n$ real matrix $R > 0$ and the piecewise function $\tau (t)$ satisfying $0 < \tau_{1} \leqslant \tau (t) \leqslant \tau_{2}$, where $\tau_{1}$ and $\tau_{2}$ are two constants, and for $S \in \mathbb{R}_{2n \times 2n}$ satisfying $\left[\begin{array}{cc} \tilde{R} & S^{T} \\ \ast & \tilde{R} \end{array}\right] \geqslant 0$ with $\tilde{R} = diag\{ R, 3R \}$, the following CCI holds:

where

Lemma 3. ^[42] For any two matrices $\mathcal{G}$ and $\mathcal{R} > 0$ with appropriate dimensions,

holds true.

Lemma 4. ^[43] For a given scalar $\varepsilon > 0$, suppose there are matrices $\Lambda$, $U$, $V$ and $W$ ensuring

Then, one gets

3.   Main result

In contrast to the common $\mathcal{H}_{\infty}$ performance, LDSP imposes a limitation on the energy-to-peak gain from disturbance to the output signal, ensuring it does not exceed a specified disturbance-suppression index ^[44]. In this paper, we intend to develop an asynchronous controller in (2.5) with the adaptive ETM in (2.3) to guarantee the SS and LDSP of SES (2.6). First, we give a condition to ensure the SS and LDSP of SES (2.6).

Theorem 1. Given scalars $\gamma > 0$ and $\rho_2$, suppose that there exist matrices $P_{i} > 0$, $Q_{1} > 0$, $Q_{2} > 0$, $Q_{3} > 0$, $R_{1} > 0$, $R_{2} > 0$, $\Psi_{i} > 0$, diagonal matrix $L > 0$, and matrices $S$, $K_{\iota}$, for any $i \in \mathscr{N}$, $\iota \in \mathscr{M}$ satisfying

Then the SES (2.6) has the SS and LDSP, where

Proof. Select a LKF candidate as:

where

Assume that $\alpha (t) = i$, $\alpha (t+\varsigma) = j$, $\beta (t) = \iota$ and define $\mathscr{L}$ as the weak infinitesimal operator of the stochastic process $\{ x (t), \alpha (t) \}$. Then, along SES (2.6), we get

Define an augmented vector as $\tilde{\zeta} (t) = col\{ \zeta (t), \tilde{\psi} (Fx (t)), e (t) \}$. We can derive that

Based on (3.1), applying Lemmas 1 and 2 to the integral terms in (3.7) yields

where $\wp (d\varpi (t)) = \frac{\tau_{12}}{\tau (t)-\tau_{1}}\zeta^{T} (t)\mathcal{G}_{1}^{T}\tilde{R}_{2}\mu (t-\tau (t), t-\tau_{1}) + \frac{\tau_{12}}{\tau_{2}-\tau (t)} \zeta^{T} (t)\mathcal{G}_{2}^{T}\tilde{R}_{2}\mu (t-\tau_{2}, t-\tau (t))$. Recalling (3.7)–(3.10), we have

where $\tilde{\wp} (d\varpi (t)) = -2\zeta^{T} (t)\mathcal{G}_{0}^{T}\tilde{R}_{1}\mu (t-\tau_{1}, t)- 2\wp (d\varpi (t))$. It follows from (2.8) that

which means

In addition, recalling the adaptive ETM (2.3), we obtain

Combining (3.5), (3.6), (3.11), (3.12) and (3.13), we find that

Noting $\mathscr{E}\left\{ \tilde{\wp} (d\varpi (t)) \right\} = 0$, we can calculate $\mathscr{E}\left\{ \mathscr{L}V (t, x (t), i, \iota) \right\}$ by (3.14) that

Next, we discuss the SS of (2.6) under the condition of $v (t) \equiv 0$ and the LDSP of (2.6) under the condition of $v (t) \neq 0$, respectively.

i) $v (t) \equiv 0$, we can get the following inequality from (3.15):

where $\Lambda_{i}^{0} = \sum_{c = 1}^{M}\varphi_{i \iota} \left(\Lambda_{i \iota}^{1, 1} + \tilde{A}_{i \iota}^{T} \left(\tau_{1}^{2}R_{1} + \tau_{12}^{2}R_{2} \right) \tilde{A}_{i \iota} \right)$. From (3.3), we can find that there exists $a > 0$ such that for any

Utilizing the Itô formula, we obtain

which means

Thus, the SS of (2.6) is proved.

ii) $v (t) \neq 0$, under the zero initial condition, defining $J (t) = y^{T} (t)y (t) - \gamma^{2} \int_{0}^{t} v^{T} (s)v (s) \, ds$ leads to

From conditions (3.2) and (3.3), we know that $J (t) \leqslant 0$. According to Definition 2, the SES (2.6) has a LDSP $\gamma$. □

On the basis of Theorem 1, a design method of the AAET controller can be proposed.

Theorem 2. Given scalars $\varepsilon$, $\rho_{2}$ and $\gamma > 0$, suppose that there exist matrices $P_{i} > 0$, $Q_{1} > 0$, $Q_{2} > 0$, $Q_{3} > 0$, $R_{1} > 0$, $R_{2} > 0$, $\Psi_{i} > 0$, diagonal matrix $L > 0$, matrices $S$, $X_{\iota}$, $Y_{\iota}$, and $T_{i \iota}$ for any $i \in \mathscr{N}$, $\iota \in \mathscr{M}$ satisfying (3.1), (3.2), and

where

Then, AAET controller (2.5) with gains

enables the SES (2.6) to have both SS and LDSP.

Proof. According to (3.18), we have $-P_{i}K_{\iota} < T_{i \iota}$ by applying Lemma 4 to (3.16). Then, we can conclude that $P_{i}A_{i \iota} < \aleph_{i \iota}$ and $P_{i}\tilde{A}_{i \iota} < \tilde{\aleph}_{i \iota}$ lead to

where

Based on Lemma 3, we can get that $-P_{i}R_{1}^{-1}P_{i} \leqslant R_{1} - 2P_{i}$ and $-P_{i}R_{2}^{-1}P_{i} \leqslant R_{2} - 2P_{i}$, which means

where $\Lambda_{i}^{3, 3} = diag\left\{ -P_{i}R_{1}^{-1}P_{i}, \cdots, -P_{i}R_{1}^{-1}P_{i} \right\}$, $\Lambda_{i}^{4, 4} = diag\left\{ -P_{i}R_{2}^{-1}P_{i}, \cdots, -P_{i}R_{2}^{-1}P_{i} \right\}$. Due to $\varphi_{i \iota} > 0$, combining (3.19)–(3.23) yields

where

By applying Schur's complement to (3.24), we find that (3.3) can be guaranteed by (3.17). The proof is completed. □

Remark 5. The coupling between parameter $P_{i}$ and the controller gain $K_{\iota}$ in Theorem 1 is addressed by introducing a slack matrix $T_{i \iota}$. It is worth mentioning that directly setting the coupling term $K_{\iota}P_{i}^{-1}$ equal to the matrix $T_{i \iota}$ (i.e. $K_{\iota} = T_{i \iota}P_{i}$) would result in non-uniqueness of controller gains $K_{\iota}$. In this paper, we introduce $T_{i \iota}$ such that $-P_{i}K_{\iota} < T_{i \iota}$. By designing the controller gains, as given in equation (3.18), and combining it with Lemma 4, the aforementioned issue is avoided.

Remark 6. Theorem 1 provides a analysis result of the SS and LDSP for SES (2.6) based on HMM, while Theorem 2 presents a design scheme for the needed AAET controller. The proofs of these theorems involve the use of the LKF in (3.4), Itô formula, as well as the inequalities in Lemmas 1-4. To further reduce the conservatism of the obtained results, one may refer to the augmented LKFs in ^[45,46], the free-matrix-based approaches in ^[47,48,49], the refined CCIs in ^[50,51] and the decoupling methods in ^[52].

4.   Simulation example

Example 1. In this example, we consider a three-mode Chua's circuit given by

where parameters $m_{0} = -\frac{1}{7}$, $m_{1} = \frac{2}{7}$, $m_{3} = 0.1$, and $a_{i}$, $b_{i}$, $c_{i}$, $d_{i}$ $(i = 1, 2, 3)$ are listed in Table 1. The nonlinear characteristics $\psi_{1} (x_{1} (t)) = \frac{1}{2} (|x_{1} (t)+1|-|x_{1} (t)-1|)$ belonging to sector $[0, 1]$, and $\psi_{2} (x_{2} (t)) = \psi_{3} (x_{3} (t)) = 0$. The circuit model can be re-expressed as LS (2.1) with

The delay parameters are specified as $\tau_{1} = 0.1$, $\tau_{2} = 0.18$, $\mu_{1} = 0.1$ and $\mu_{2} = 0.26$, the parameters related to the adaptive law are given by $\rho_{1} = 0.1$, $\rho_{2} = 0.9$, $\kappa = 0.5$ and the TR and CTP matrices are chosen as

By solving the LMIs in Theorem 2, the optimal LDSP is found to be $\gamma^{\ast} = 0.0553$, and the controller gains and adaptive ETM weight matrices are calculated as

We set the initial states as $x_{m} (t) = \left[\begin{array}{ccc} -0.2 & -0.3 & 0.2 \end{array}\right]^{T}$, $x_{s} (t) = \left[\begin{array}{ccc} 0.25 & 0.35 & 0.35 \end{array}\right]^{T}$ $(t \in [-\tau_{2}, 0])$ and the disturbance as $v (t) = 0.1sint (t)$. The sampling period is chosen to be $h = 0.05s$. A possible mode evolution of system and AAET controller is drawn in Figure 2. When there is no controller applied, we can find from Figure 3 that the system is unstable. By utilizing the devised AAET controller shown in Figure 4, the state response curves of the SES (2.6) are exhibited in Figure 5. It can be seen that the synchronization error between the master and slave LSs approaches zero over time, indicating that the master and slave LSs can successfully achieve synchronization under the presented AAET controller. The trajectory of the adaptive law and release time intervals between two trigger moments are depicted in Figures 6 and 7, respectively. Based on the simulation results, it can be observed that as the SES (2.6) stabilizes, the threshold function gradually converges to a fixed value. Define the function $\gamma(t) = \sqrt{\mathscr{E} \left\{\sup_{t \geqslant 0} \{ \| y (t) \|^{2} \}\right\} / \mathscr{E} \left\{\int_{0}^{t} \| v (s) \|^{2} ds\right\}}$ for LDSP. Then the trajectory of $\gamma(t)$ under zero initial condition is depicted in Figure 8. It is evident from Figure 8 that the maximum value of $\gamma(t)$ is $0.0047$, which is lower than $\gamma^{\ast} = 0.0553$.

Table 2 presents the data transmission rates under different triggering mechanisms in the same conditions. The comparison demonstrates that the adaptive ETM employed in this study can effectively reduce data transmission to achieve the goal of conserving channel resources.

5.   Conclusions

The master-slave chaos synchronization of stochastic time-delay LSs (2.1) and (2.2) within a networked environment has been considered. To tackle the challenges posed by potential mode-mismatch behavior and limited networked channel resources, the AAET controller in (2.5) has been employed. A criterion on the SS and LDSP of the SES (2.6) has been proposed in Theorem 1 using a LKF, a Wirtinger-type inequality, the Itô formula, as well as a CCI. Then, a method for determining the desired AAET controller gains has been proposed in Theorem 2 by decoupling the nonlinearities that arise from the Lyapunov matrices and controller gains. Finally, simulation results have confirmed that the designed controller can achieve chaos synchronization between the master LS (2.1) and slave LS (2.2), while significantly reducing data transmission.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by the Key Research and Development Project of Anhui Province (Grant No. 202004a07020028).

Conflict of interest

All authors declare no conflicts of interest in this paper.