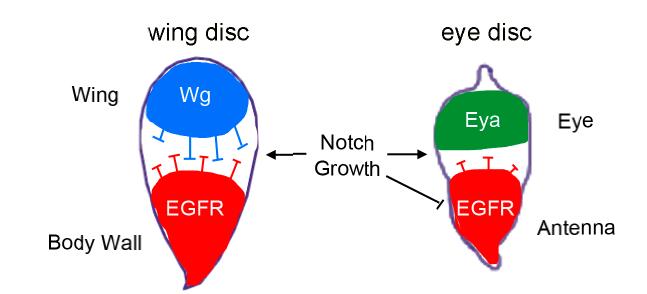
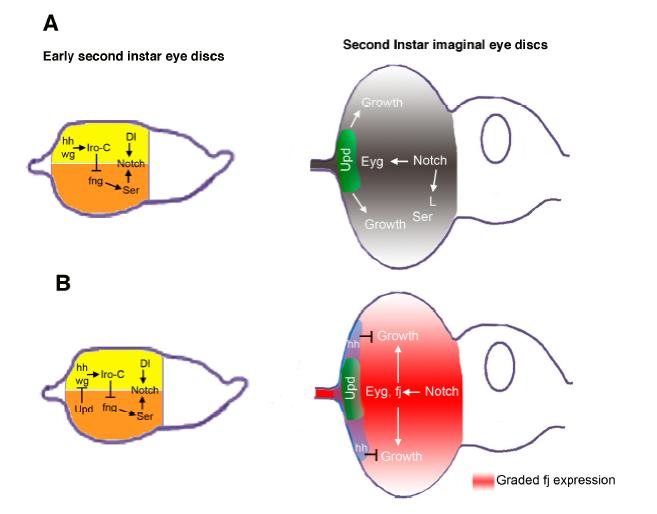
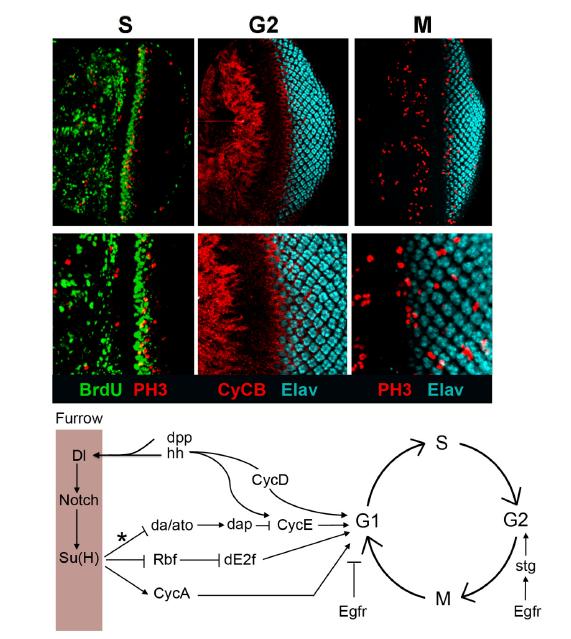
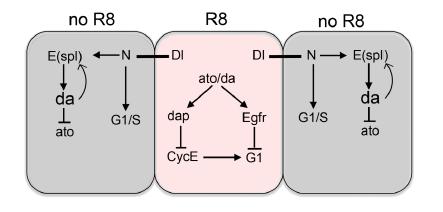
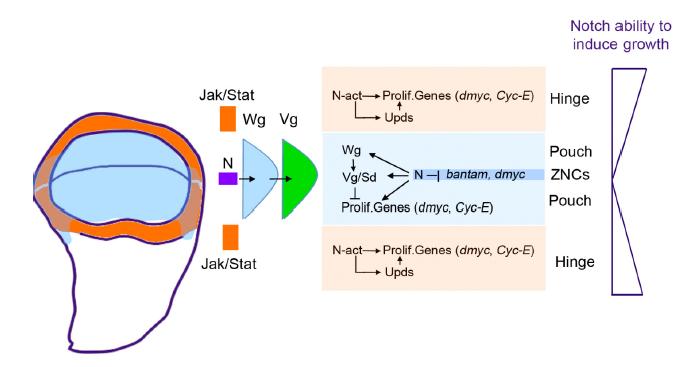
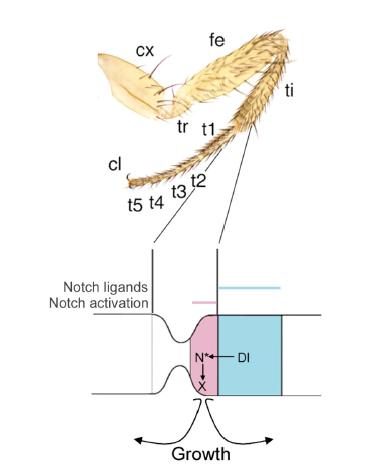
The Notch signalling pathway is evolutionary conserved and participates in numerous developmental processes, including the control of cell proliferation. However, Notch signalling can promote or restrain cell division depending on the developmental context, as has been observed in human cancer where Notch can function as a tumor suppressor or an oncogene. Thus, the outcome of Notch signalling can be influenced by the cross-talk between Notch and other signalling pathways. The use of model organisms such as Drosophila has been proven to be very valuable to understand the developmental role of the Notch pathway in different tissues and its relationship with other signalling pathways during cell proliferation control. Here we review recent studies in Drosophila that shed light in the developmental control of cell proliferation by the Notch pathway in different contexts such as the eye, wing and leg imaginal discs. We also discuss the autonomous and non-autonomous effects of the Notch pathway on cell proliferation and its interactions with different signalling pathways.
1.
Introduction
The resource allocation problem is an important and challenging issue and has attracted a lot of attention with interests for practitioners and researchers [1]. Effective (added) resource allocation can improve the efficiency of operation. However, the usage of the resource, especially abundant usage, will create extra costs and result in pollution. Therefore, how to manage and utilize resources efficiently has become an important issue. Nowadays, low carbon, high efficiency and high customer satisfaction have become crucial factors for companies to gain competitiveness. Manufacturers not only need to maximize profits (i.e., reduce time-dependent measure criterion) but also need to control the extra resource input. Although the stated objectives are often conflicting, a resource allocation scheduling approach that increases revenue and optimizes resources provides an additional chance that can facilitate improvements.
Scheduling problems with resource allocation mean that the job processing times can be controlled by changing the allocation of resources to jobs. Many researchers have expended vast amounts of effort on this vivid area of scheduling research from JIT [2,40], maintenance activity [3], agent scheduling [4], batch scheduling [5]. A comprehensive discussion on scheduling problems with resource allocation (controllable processing times) is provided by Shabtay et al. [6] and Shioura et al. [7]. In such problem, job scheduling and resource allocation decisions should be coordinated carefully to achieve the most efficient system performance. Therefore, the quality of a solution is measured by two criteria: scheduling criterion and resource consumption cost. Recent studies of resource allocation scheduling problems include Low et al. [8], Shioura et al. [9], Yin et al. [10] and Shabtay et al. [11]. Yin et al. [10] study the single-machine due-window assignment with common flow allowances and resource-dependent processing times. They consider two criteria: one is an integrated cost consisting of job earliness, weighted number of tardy jobs, and due-window assignment cost, and the other is the resource consumption cost. Based on the two criteria, they analyze four different models and provide the algorithm to obtain pareto-optimal schedules. Shabtay et al. [11] study a single-machine scheduling problem with resource allocation and due date assignment. They provide a bicriteria analysis. For the limited total weighted resource consumption, they develop a pseudo-polynomial algorithm and fully polynomial time approximation scheme to minimize the total weighted number of tardy jobs plus due date assignment cost. Recently, Yepes et al. [38] consider the unrelated parallel machine scheduling problem with setup times and additional resources in the setups. Yepes et al. [39] study a bi-objective parallel machine scheduling problem with additional resources during setups. They propose a new multi-objective algorithm.
In many realistic situations, the processing times of jobs is easily affected by many other factors such as worker's experience or fatigue, task's waiting time, machine abrasion. Related examples can be found in steel production [12], electronics manufacturing [13], pollution containment [14], and so on. In the literature, the studies are commonly known as scheduling with learning effect or deteriorating jobs. For the comprehensive literature reviews on both study categories, the readers may refer to Cheng et al. [15], Biskup [16], Gawiejnowicz [17], and Wang et al. [18]. Sometimes, we cannot obtain the specific function expression of learning/deteriorating effect. Therefore, researchers have recently considered scheduling problems with general learning/deteriorating effect functions. Gordon and Strusevich [19] study two due date assignment and single machine scheduling problems with positionally dependent processing times. They give polynomial-time dynamic programming algorithms for the studied problems. Zhao et al. [20] consider a slack due window assignment and single machine scheduling with position effect and deterioration effect. Yin et al. [21] investigate a due-date assignment and single-machine scheduling with generalized position-dependent deteriorating jobs and deteriorating multi-maintenance activities. Rustogi et al. [22] present polynomial-time algorithms for single machine problems with generalized positional deterioration effects and machine maintenance. Rustogi et al. [23] further study a general model for single machine scheduling problems with time and position dependent effects. They provide solution algorithms for minimizing the makespan and the sum of completion times. Rudek [24] study a parallel machine scheduling problem with varying processing times to minimize the makespan. They present an arbitrary monotonic function dependent on the number of previously processed jobs to describe the actual job processing time.
In order to be more realistic in modelling a production system, researchers have recently considered scheduling problems with variable processing times and resource allocation simultaneously. Oron [14] describes a real application of scheduling to deal with accidents that involve pollution or contamination. The case is modeled as a single-machine scheduling model with convex resource function and general linear deterioration. They develop a polynomial-time solution for minimizing the makespan. Moreover, they compute the optimal resource allocation policy for a given job instance to minimize the total flowtime. Rudek et al. [25] investigate the scheduling problems with the aging effect and additional resource allocation. They describe an example of a deteriorating system and model it as a single-machine scheduling model. Rudek et al. [26] study the flowshop scheduling problem with the aging effect and additional resource allocation. They provide optimal polynomial time solution algorithms for their special cases of the considered problems. Ji et al. [27] consider slack (SLK) due date assignment and single machine scheduling problem with aging effect, resource allocation and a rate-modifying activity. They provide a polynomial-time algorithm to solve it. Sun et al. [28] study three due date assignment methods for single machine scheduling problems with convex resource allocation and variable job processing times. They show that three versions of the problem can be solved in polynomial time. Lu et al. [29] consider the unrelated parallel-machine resource allocation scheduling problem with deteriorating jobs and learning effect. They prove that the problem is polynomial time solvable for minimizing the weighted sum of the total load, the total completion time, the total absolute deviation of completion time and the total resource cost. Wang et al. [30] consider a single machine scheduling with job-dependent learning effect and convex resource-dependent processing times. They provide the polynomial time algorithms for all studied objective functions. Zhao et al. [31] introduce a unified approach to single-machine scheduling problems with deterioration effect and convex resource allocation subject to an upper bound on the total resource consumption. They show that this unified model can be useful in solving scheduling problems under due date assignment and some scheduling problems that do not involve due dates. Tian et al. [32] study the two-machine no-wait flowshop scheduling with learning effect and resource allocation. They show that some cases including makespan, total completion time and total absolute differences in completion times are all polynomially solvable.
In the paper, we investigate the resource allocation scheduling model of deterioration effect and general positional effect, which is the general and extensional case of existing research. Moreover, we further study the criterion of minimizing total weighted resource consumption subject to an upper bound on scheduling costs. Two unified models for solving single machine scheduling problems with the deterioration effect, general positional effect and convex resource allocation are presented. And we show that the two unified models can be applied to solve various due window assignment problems. At the same time, our study also indicates that a large set of scheduling problems that have the common feature can be expressed as positional penalties function can be solved by using the unified approach.
The rest of this paper is organized as follows. The following section gives the problem statements formally. In section 3, two unified models are presented and analyzed. Section 4 is the applications of unified models for solving due-window assignment problems. The last section concludes the paper and suggests topics for future research.
2.
Problem description
In this section, we define our problems formally. Consider a production system that consists of $n$ independent jobs, $N = \{ {J_1}, {J_2}, \ldots , {J_n}\} $, that are to be processed without preemption on a single machine at time zero. The machine can process at most one job at a time. In this paper, we propose a more general scheduling model that stems from Rudek et al. [25,26], Sun et al. [28], Wang et al. [30], Zhao et al. [31], and so on. In the model, ${p_j}$ is actual processing times of job ${J_j}$ which is determined simultaneously by resource allocation, starting time ${S_j}$ and processing position $r .$ The actual job processing times are given as follows:
where ${w_j}$ is a positive parameter representing the workload of job ${J_j} $, ${u_j}$ is the amount of resource allocated to job ${J_j} $, $k$ and $b$ are positive constant, and $g(r)$ is a function that specifies a job-independent positional effect. In earlier papers, the focus has been on particular functions that define the positional factors $g(r) $, e.g., ${r^c}$ ($c \geqslant 0$ or $c \leqslant 0$) [13,16] or $cr$ ($c \geqslant 0$) [16], and so on.
Let $U$ be the total available amount of resources, $R$ be a certain threshold. A solution for the studied problem is defined by a schedule $\pi $ and by a resource allocation vector $[{u_1}, \ldots , {u_n}] .$ The quality of a solution is measured by two different criteria. The first is the scheduling criterion $f$ and the second is the total resource consumption cost which is given by $\sum\nolimits_{j = 1}^n {{b_j}{u_j}} .$ One of our objectives is to determine the optimal job sequence and resource allocation policy to minimize the scheduling criterion $f .$ And another objective is to minimize the total weighted resource consumption cost under a certain threshold $R .$ Therefore, our general problems are given by
and
3.
The unified models
In this section, we present the unified models respectively for solving the problems (1) and (2).
First, we study problem (1) and consider the following optimization problem (P1).
where ${a_j}(j = 1, 2, ..., n), {b_j}(j = 1, 2, ..., n), U$ and $k$ are positive parameters.
Lemma 1. For the problem (P1), the optimal values of that minimize the function are ${x_j} = U\frac{{{{(\frac{{{a_j}}}{{{b_j}}})}^{\frac{1}{{k + 1}}}}}}{{\sum\nolimits_{j = 1}^n {{{({a_j}{b_j})}^{\frac{1}{{k + 1}}}}} }}, j = 1, 2, ..., n .$ The optimal value of $f$ is ${f^ * } = \frac{1}{{{U^k}}}{\left[ {\sum\nolimits_{j = 1}^n {{{({a_j}{b_j})}^{\frac{1}{{k + 1}}}}} } \right]^{k + 1}} .$
Proof. It is obviously that we only need to consider the case ${b_1}{x_1} + {b_2}{x_2} + ... + {b_n}{x_n} = U .$
Because $\sum\nolimits_{j = 1}^n {{b_j}{x_j}} = U $, ${x_1} = \frac{{U - \sum\nolimits_{j = 2}^n {{b_j}{x_j}} }}{{{b_1}}} .$ Therefore, we can get
Note that $f$ is a convex function of ${x_j} $, and it follows that $\frac{{\partial f}}{{\partial {x_j}}} = 0$ provide necessary and sufficient conditions for optimality.
Taking the first derivative of $f$ with respect to ${x_j} $, we have
Let $\frac{{\partial f}}{{\partial {x_j}}} = 0 $, then ${x_j} = {(\frac{{{a_j}}}{{{a_1}{b_j}b_1^k}})^{\frac{1}{{k + 1}}}}(U - \sum\nolimits_{j = 2}^n {{b_j}{x_j}} ) .$ Therefore,
This can be further written as $\sum\nolimits_{j = 2}^n {{b_j}{x_j}} = U\frac{{\sum\nolimits_{j = 2}^n {{{(\frac{{{a_j}b_j^k}}{{{a_1}b_1^k}})}^{\frac{1}{{k + 1}}}}} }}{{1 + \sum\nolimits_{j = 2}^n {{{(\frac{{{a_j}b_j^k}}{{{a_1}b_1^k}})}^{\frac{1}{{k + 1}}}}} }} .$
By substituting the above relationship into ${x_1} = \frac{{U - \sum\nolimits_{j = 2}^n {{b_j}{x_j}} }}{{{b_1}}}$ and solving for ${x_1} $, we obtain
It follows that ${x_j} = U\frac{{{{(\frac{{{a_j}}}{{{b_j}}})}^{\frac{1}{{k + 1}}}}}}{{\sum\nolimits_{j = 1}^n {{{({a_j}b_j^k)}^{\frac{1}{{k + 1}}}}} }}, j = 2, ..., n .$
Consequently, we have ${f^ * } = \frac{1}{{{U^k}}}{\left[ {\sum\nolimits_{j = 1}^n {{{({a_j}b_j^k)}^{\frac{1}{{k + 1}}}}} } \right]^{k + 1}} .$
For the problem $1|{p_j} = \left( {{{\left( {\frac{{{w_j}}}{{{u_j}}}} \right)}^k} + b{S_j}} \right)g(r), \sum {{b_j}{u_j}} \leqslant U|f $, it is obvious that for any given feasible resource allocation, our problem is reduced to determining a job sequence that minimizes the scheduling criterion $f .$ In the following, we show that the same techniques used to solve single-machine scheduling with fixed job processing times ${p'_j}$ can be incorporated into the model with the actual job processing times ${p_j} = \left( {{{\left( {\frac{{{w_j}}}{{{u_j}}}} \right)}^k} + b{S_j}} \right)g(r) .$
Given the problem $1|{p_j} = \left( {{{\left( {\frac{{{w_j}}}{{{u_j}}}} \right)}^k} + b{S_j}} \right)g(r), \sum {{b_j}{u_j}} \leqslant U|f $, there is a corresponding problem $1|{p'_j}|f$ with fixed job processing times. For a given schedule $\pi = \left[ {{J_{\left[ 1 \right]}}, {J_{\left[ 2 \right]}}, ..., {J_{\left[ n \right]}}} \right] $, we assume that the objective function of the problem $1|{p'_j}|f$ can be expressed as $f\left( \pi \right) = \sum\limits_{j = 1}^n {{\xi _j}{p_{[j]}}} $, where ${\xi _j}$ are position-dependent parameters. In the following, we will give the expression of the objective function for the problem $1|{p_j} = \left( {{{\left( {\frac{{{w_j}}}{{{u_j}}}} \right)}^k} + b{S_j}} \right)g(r)$, $\sum {{b_j}{u_j}} \leqslant U|f .$ The actual processing times of jobs can be expressed as follows:
Therefore, for the problem $1|{p_j} = \left( {{{\left( {\frac{{{w_j}}}{{{u_j}}}} \right)}^k} + b{S_j}} \right)g(r), \sum {{b_j}{u_j}} \leqslant U|f $, we have
where,
Note that for a given schedule $\pi = \left[ {{J_{\left[ 1 \right]}}, {J_{\left[ 2 \right]}}, ..., {J_{\left[ n \right]}}} \right] $, ${\varphi _j}, {w_{[j]}}$ $(j = 1, 2, \ldots , n)$ are constants. Let ${a_{\left[ j \right]}} = {\varphi _j}w_{\left[ j \right]}^k$ and ${x_{\left[ j \right]}} = {u_{\left[ j \right]}} $, then $f\left( \pi \right) = \sum\nolimits_{j = 1}^n {\frac{{{a_{\left[ j \right]}}}}{{x_{\left[ j \right]}^k}}} .$ Because the objective function can be written in the format shown in (P1), by Lemma 1, the optimal resource allocation for a given sequence is
Thus, we obtain that the function $f\left( \pi \right) $, under an optimal resource allocation, can be expressed as $f\left( \pi \right) = \frac{1}{{{U^k}}}{\left[ {\sum\nolimits_{j = 1}^n {{{({\varphi _j}w_{\left[ j \right]}^kb_{[j]}^k)}^{\frac{1}{{k + 1}}}}} } \right]^{k + 1}} .$
Due to $U$ and $k$ are positive constants, minimizing the function $f(\pi )$ is equivalent to minimizing the function $y = \sum\nolimits_{j = 1}^n {{{({\varphi _j}w_{\left[ j \right]}^kb_{[j]}^k)}^{\frac{1}{{k + 1}}}}} = \sum\nolimits_{j = 1}^n {\varphi _j^{\frac{1}{{k + 1}}}w_{\left[ j \right]}^{\frac{k}{{k + 1}}}b_{[j]}^{\frac{k}{{k + 1}}}} .$
We denote $\varphi _j^{\frac{1}{{k + 1}}}$ as ${\xi _j}$ and $w_{\left[ j \right]}^{\frac{k}{{k + 1}}}b_{[j]}^{\frac{k}{{k + 1}}}$ as ${p_{[j]}} $, then $y$ is of the form $\sum\nolimits_{j = 1}^n {{\xi _j}{p_{[j]}}} .$ This means that the functions of the problems $1|{p_j} = \left( {{{\left( {\frac{{{w_j}}}{{{u_j}}}} \right)}^k} + b{S_j}} \right)g(r), \sum {{b_j}{u_j}} \leqslant U|f$ and $1|{p'_j}|f$ have the same form.
Theorem 1. When $f$ is of the form $\sum\nolimits_{j = 1}^n {{\xi _j}{p_{[j]}}} $, the problem $1|{p_j} = \left( {{{\left( {\frac{{{w_j}}}{{{u_j}}}} \right)}^k} + b{S_j}} \right)g(r)$, $\sum {{b_j}{u_j}} \leqslant U|f$ is polynomially solvable if the corresponding problem $1|{p'_j}|f$ is polynomially solvable.
Proof. Because the objective functions of the problems $1|{p'_j}|f$ and $1|{p_j} = \left( {{{\left( {\frac{{{w_j}}}{{{u_j}}}} \right)}^k} + b{S_j}} \right)g(r)$, $\sum {{b_j}{u_j}} \leqslant U|f$ have the same form, the correctness of the theorem follows.
In the following, we study problem (2) and consider the following optimization problem (P2).
Lemma 2. For the problem (P2), the optimal values of ${x_j}$ that minimize the function $h$ is ${x_j} = {R^{ - \frac{1}{k}}}b_j^{ - \frac{1}{{k + 1}}}a_j^{\frac{1}{{k + 1}}}(\sum\limits_{j = 1}^n {a_j^{\frac{1}{{k + 1}}}b_j^{\frac{k}{{k + 1}}}{)^{\frac{1}{k}}}} $, $j = 1, 2, \ldots , n .$ The optimal value of $h$ is ${h^ * } = {R^{ - \frac{1}{k}}}{(\sum\limits_{j = 1}^n {a_j^{\frac{1}{{k + 1}}}b_j^{\frac{k}{{k + 1}}}} )^{\frac{1}{k} + 1}} .$
Proof. It is obvious that we only need to consider the case $\frac{{{a_1}}}{{x_1^k}} + \frac{{{a_2}}}{{x_2^k}} + \cdots + \frac{{{a_n}}}{{x_n^k}} = R .$
Because $\sum\limits_{j = 1}^n {\frac{{{a_j}}}{{x_j^k}} = R} $ and $\frac{{{a_1}}}{{x_1^k}} = R - \sum\limits_{j = 2}^n {\frac{{{a_j}}}{{x_j^k}}} .$ Therefore, we can get
Note that $h$ is a convex function of ${x_j} $, and it follows that $\frac{{\partial h}}{{\partial {x_j}}} = 0$ provide necessary and sufficient conditions for optimality.
Taking the first derivative of $h$ with respect to ${x_j} $, we obtain
Let $\frac{{\partial h}}{{\partial {x_j}}} = 0 $, then we have ${x_j} = \frac{{{{({b_1}{a_j})}^{\frac{1}{{k + 1}}}}a_1^{\frac{1}{{k(k + 1)}}}}}{{b_j^{\frac{1}{{k + 1}}}{{(R - \sum\limits_{j = 2}^n {\frac{{{a_j}}}{{x_j^k}}} )}^{\frac{1}{k}}}}} .$
By substituting ${(R - \sum\limits_{j = 2}^n {\frac{{{a_j}}}{{x_j^k}}} )^{\frac{1}{k}}} = \frac{{a_1^{\frac{1}{k}}}}{{{x_1}}}$ into ${x_j} = \frac{{{{({b_1}{a_j})}^{\frac{1}{{k + 1}}}}a_1^{\frac{1}{{k(k + 1)}}}}}{{b_j^{\frac{1}{{k + 1}}}{{(R - \sum\limits_{j = 2}^n {\frac{{{a_j}}}{{x_j^k}}} )}^{\frac{1}{k}}}}} $, $j = 2, ..., n $, we can get ${x_j} = \frac{{{{({b_1}{a_j})}^{\frac{1}{{k + 1}}}}a_1^{\frac{1}{{k(k + 1)}}}{x_1}}}{{b_j^{\frac{1}{{k + 1}}}a_1^{\frac{1}{k}}}} = \frac{{{{({b_1}{a_j})}^{\frac{1}{{k + 1}}}}{x_1}}}{{b_j^{\frac{1}{{k + 1}}}a_1^{\frac{1}{{k + 1}}}}} .$
In order to eliminate the variable ${x_1}$ in the above equation, we have $x_j^k = \frac{{{{({b_1}{a_j})}^{\frac{k}{{k + 1}}}}x_1^k}}{{b_j^{\frac{k}{{k + 1}}}a_1^{\frac{k}{{k + 1}}}}} $, $\frac{{{a_j}}}{{x_j^k}} = \frac{{a_j^{\frac{1}{{k + 1}}}b_j^{\frac{k}{{k + 1}}}a_1^{\frac{k}{{k + 1}}}}}{{b_1^{\frac{k}{{k + 1}}}x_1^k}} $, $\sum\limits_{j = 2}^n {\frac{{{a_j}}}{{x_j^k}}} = {(\frac{{{a_1}}}{{{b_1}}})^{\frac{k}{{k + 1}}}}x_1^{ - k}\sum\limits_{j = 2}^n {a_j^{\frac{1}{{k + 1}}}b_j^{\frac{k}{{k + 1}}}} .$ Based on $\sum\limits_{j = 2}^n {\frac{{{a_j}}}{{x_j^k}}} $ $ = R - \frac{{{a_1}}}{{x_1^k}} $, we can obtain
Therefore, we have
It follows that
Consequently, we can obtain
For the problem $1|{p_j} = \left( {{{\left( {\frac{{{w_j}}}{{{u_j}}}} \right)}^k} + b{S_j}} \right)g(r), f \leqslant R|\sum {{b_j}{u_j}} $, it is obvious that for any given schedule, our problem is reduced to determining the optimal resource allocation that satisfies the scheduling criterion $f \leqslant R$ and minimizes the total weighted resource allocation costs. In the following, we will show that the function expressions of the problems $1|{p_j} = \left( {{{\left( {\frac{{{w_j}}}{{{u_j}}}} \right)}^k} + b{S_j}} \right)g(r), f \leqslant R|\sum {{b_j}{u_j}} $ and $1|{p'_j}|f$ have the same form. Similarly, for a given schedule $\pi = \left[ {{J_{\left[ 1 \right]}}, {J_{\left[ 2 \right]}}, ..., {J_{\left[ n \right]}}} \right] $, it is assumed that the objective function of the problem $1|{p'_j}|f$ can be expressed as $f\left( \pi \right) = \sum\limits_{j = 1}^n {{\xi _j}{p_{[j]}}} $, where ${\xi _j}$ are position-dependent parameters.
Based on Eq (3), let ${a_{\left[ j \right]}} = {\varphi _j}w_{\left[ j \right]}^k$ and ${x_{\left[ j \right]}} = {u_{\left[ j \right]}} $, then $f\left( \pi \right) = \sum\nolimits_{j = 1}^n {\frac{{{a_{\left[ j \right]}}}}{{x_{\left[ j \right]}^k}}} .$ Therefore, the problem $1|{p_j} = \left( {{{\left( {\frac{{{w_j}}}{{{u_j}}}} \right)}^k} + b{S_j}} \right)g(r), f \leqslant R|\sum {{b_j}{u_j}} $ can be written in the format shown in (P2). By Lemma 2, the optimal resource allocation for a given sequence is ${u_{[j]}} = {R^{ - \frac{1}{k}}}b_{[j]}^{ - \frac{1}{{k + 1}}}{({\varphi _j}w_{[j]}^k)^{\frac{1}{{k + 1}}}}(\sum\limits_{j = 1}^n {{{({\varphi _j}w_{[j]}^k)}^{\frac{1}{{k + 1}}}}b_j^{\frac{k}{{k + 1}}}{)^{\frac{1}{k}}}} .$ Thus, the objective function can be expressed as $\sum {{b_j}{u_j}} = {R^{ - \frac{1}{k}}}{(\sum\limits_{j = 1}^n {{{({\varphi _j}w_{[j]}^k)}^{\frac{1}{{k + 1}}}}b_{[j]}^{\frac{k}{{k + 1}}}} )^{\frac{1}{k} + 1}}$ $ = {R^{ - \frac{1}{k}}}{(\sum\limits_{j = 1}^n {\varphi _j^{\frac{1}{{k + 1}}}{{({w_{[j]}}{b_{[j]}})}^{\frac{k}{{k + 1}}}}} )^{\frac{1}{k} + 1}} .$
Due to $R$ and $k$ are positive constants, minimizing the function $\sum {{b_j}{u_j}} $ is equivalent to minimizing the function $y' = \sum\limits_{j = 1}^n {\varphi _j^{\frac{1}{{k + 1}}}{{({w_{[j]}}{b_{[j]}})}^{\frac{k}{{k + 1}}}}} .$ Denote $\varphi _j^{\frac{1}{{k + 1}}}$ as ${\xi _j}$ and $w_{\left[ j \right]}^{\frac{k}{{k + 1}}}b_{[j]}^{\frac{k}{{k + 1}}}$ as ${p_{[j]}} $, then $y' = \sum\limits_{j = 1}^n {{\xi _j}{p_{[j]}}} .$ This means that the objective functions of the problems $1|{p_j} = \left( {{{\left( {\frac{{{w_j}}}{{{u_j}}}} \right)}^k} + b{S_j}} \right)g(r)$, $f \leqslant R|\sum {{b_j}{u_j}} $ and $1|{p'_j}|f$ have the same form.
Theorem 2. When $f$ is of the form $\sum\nolimits_{j = 1}^n {{\xi _j}{p_{[j]}}} $, the problem $1|{p_j} = \left( {{{\left( {\frac{{{w_j}}}{{{u_j}}}} \right)}^k} + b{S_j}} \right)g(r)$, $f \leqslant R|\sum {{b_j}{u_j}} $ is polynomially solvable if the corresponding problem $1|{p'_j}|f$ is polynomially solvable.
Proof. Because the objective functions of the problems $1|{p'_j}|f$ and $1|{p_j} = \left( {{{\left( {\frac{{{w_j}}}{{{u_j}}}} \right)}^k} + b{S_j}} \right)g(r)$, $f \leqslant R|\sum {{b_j}{u_j}} $ have the same form, the correctness of the theorem follows.
4.
Applications for solving due-window assignment problems
Due window assignment is the most common and significant problem in modern manufacturing and supply chain management. Integrated due windows assignment and production scheduling has received considerable attention from both practitioners and researchers [33]. There are three main categories of due window assignment models (CON/SLK/DIF due window) in the literature. Common due window (denoted by CON) denotes all jobs have the same due window, that is, a time window $[{d_1}, {d_2}] .$ Slack due window (denoted by SLK) denotes all jobs have the common flow allowances. The due window starting time for the job ${J_j}$ is defined as $d_j^1 = {p_j} + {q_1} .$ Similarly, the due window completion time for the job ${J_j}$ is defined as $d_j^2 = {p_j} + {q_2}$ $({q_2} \geqslant {q_1}) .$ The window size ${D_j} = d_j^2 - d_j^1$ is identical for all the jobs. Different due window (denoted by DIF) denotes each job can be assigned a different due window with no restrictions.
We begin by considering the common due window assignment model. Let $D = {d_2} - {d_1}$ denote the size of the common window. Both ${d_1}$ and $D$ are decision variables. The objective is to minimize the cost function $Z = \sum\nolimits_{j = 1}^n {(\alpha {E_j} + \beta {T_j} + \gamma {d_1} + \delta D)} $, where ${E_j} = \max \{ 0, {d_1} - {C_j}\} $ is the earliness for job ${J_j}$; ${T_j} = \max \{ 0, {C_j} - {d_2}\} $ is the tardiness for job ${J_j}$; $\alpha , \beta , \gamma , \delta $ are the positive weight factor.
For the fixed job processing times, the following results for CON due window assignment problem are given by Liman et al. [34]. It can be easily showed that the results also hold for our problem.
Lemma 3. For the problem $1|CON|\sum {(\alpha {E_j} + \beta {T_j} + \gamma {d_1} + \delta D)} $, there exists an optimal schedule for which both the due window starting time ${d_1}$ and the due window completion time ${d_2}$ coincide with the job completion times, i.e., ${d_1} = {C_{[l]}}$ and ${d_2} = {C_{[l + m]}} $, respectively, where $l = \max \left\{ {\left\lceil {\frac{{n(\delta - \gamma )}}{\alpha }} \right\rceil , 0} \right\}$ and $l + m = \max \left\{ {\left\lceil {\frac{{n(\beta - \delta )}}{\beta }} \right\rceil , 0} \right\} .$
Moreover, $Z = \sum\nolimits_{j = 1}^n {(\alpha {E_j} + \beta {T_j} + \gamma {d_1} + \delta D)} = \sum\nolimits_{j = 1}^n {{\xi _j}{p_{[j]}}} $, where
Consequently, the objective function of the problem (PC1) $1|{p_j} = \left( {{{\left( {\frac{{{w_j}}}{{{u_j}}}} \right)}^k} + b{S_j}} \right)g(r)$, $\sum {{b_j}{u_j}} \leqslant U, CON|\sum {(\alpha {E_j} + \beta {T_j} + \gamma {d_1} + \delta D)} $ can be expressed as $Z = \sum\nolimits_{j = 1}^n {{\varphi _j}{{(\frac{{{w_{[j]}}}}{{{u_{[j]}}}})}^k}} $, where,
Let ${a_{\left[ j \right]}} = {\varphi _j}w_{\left[ j \right]}^k$ and ${x_{\left[ j \right]}} = {u_{\left[ j \right]}} $, then $f\left( \pi \right) = \sum\nolimits_{j = 1}^n {\frac{{{a_{\left[ j \right]}}}}{{x_{\left[ j \right]}^k}}} .$ According to Lemma 1, we can obtain $f\left( \pi \right) = \frac{1}{{{U^k}}}{\left[ {\sum\nolimits_{j = 1}^n {{{({\varphi _j}w_{\left[ j \right]}^kb_{[j]}^k)}^{\frac{1}{{k + 1}}}}} } \right]^{k + 1}} .$
Because the problem $1|CON|\sum {(\alpha {E_j} + \beta {T_j} + \gamma {d_1} + \delta D)} $ can be solved in $O(n\log n)$ time and $\varphi _j^{^{\frac{1}{{k + 1}}}}$ are job-independent position weights, from Theorem 1, the problem $1|{p_j} = \left( {{{\left( {\frac{{{w_j}}}{{{u_j}}}} \right)}^k} + b{S_j}} \right)g(r), \sum {{b_j}{u_j}} \leqslant U, CON|\sum {(\alpha {E_j} + \beta {T_j} + \gamma {d_1} + \delta D)} $ can be solved in $O(n\log n)$ time.
Similarly, according to Theorem 2, the problem (PC2) $1|{p_j} = \left( {{{\left( {\frac{{{w_j}}}{{{u_j}}}} \right)}^k} + b{S_j}} \right)g(r), CON$, $\sum {(\alpha {E_j} + \beta {T_j} + \gamma {d_1} + \delta D)} \leqslant R|\sum {{b_j}{u_j}} $ can be solved in $O(n\log n)$ time.
The formal statement of the solution is provided in the following algorithm.
Theorem 3. The problems PC1 and PC2 can be solved in $O(n\log n)$ time.
Proof. The correctness of Algorithm 1 follows from the above analysis. Step 1, step 2 and step 3 require $O(n)$ time, step 4 requires $O(n\log n)$ time, and step 5 requires $O(n)$ time. Thus, the overall computational complexity of the algorithm is $O(n\log n) .$
Example 1. There are $n = 5$ jobs. Let $\alpha = 10 $, $\beta = 18 $, $\gamma = 2 $, $\delta = 6 $, $U = 50 $, $b = 0.1$ and $k = 1 .$ Job parameters are given in Table 1. Without loss of generality, we assume that $g(r) = {r^a}$ and $a = - 0.1 .$ According to Algorithm 1, we first obtain that $l = 2$ and $l + m = 4 .$ The values of ${({\varphi _j})^{\frac{1}{{k + 1}}}}$ and ${({w_j}{b_j})^{\frac{k}{{k + 1}}}}$ are presented in Table 2. According to the HLP rule, we can get the optimal sequence $[{J_4}, {J_2}, {J_5}, {J_1}, {J_3}] .$ Based on step 5, the optimal resources are ${u_4} = 3 $, ${u_2} = 2.5 $, ${u_5} = 11.35 $, ${u_1} = 5 $, ${u_3} = 1.75 .$ At last, we can figure out that ${d_1} = 6.45 $, ${d_2} = 10.30$ and ${f^ * } = 362.18$ for the problem PC1. Similarly, the problem PC2 can be solved by Algorithm 1.
Next, we show that slack due window and different due window assignment problems also can be solved by using the unified models. The results of lemma 4 and lemma 5 are proved by Wu et al. [35] and Yue et al. [36] for the fixed job processing times, respectively.
Lemma 4. For the problem $1|SLK|\sum {(\alpha {E_j} + \beta {T_j} + \gamma d_j^1 + \delta ({q_2} - {q_1}))} $, there exists an optimal schedule satisfies the following properties:
1) prior to a certain position in the sequence, all the jobs are early, and starting from a certain position in the sequence, all the jobs are tardy, i.e., ${C_j} \leqslant d_j^1$ implies ${C_{j - 1}} \leqslant d_{j - 1}^1$ and ${C_j} \geqslant d_j^2$ implies ${C_{j + 1}} \geqslant d_{j + 1}^2 .$
2) the optimal values of ${q_1}$ and ${q_2}$ are equal to ${C_{[l]}}$ and ${C_{[m]}} $, respectively, where $l = \max \left\{ {\left\lfloor {\frac{{n(\delta - \gamma )}}{\alpha }} \right\rfloor , 0} \right\}$ and $m = \max \left\{ {\left\lfloor {\frac{{n(\beta - \delta )}}{\beta }} \right\rfloor , 0} \right\} .$
Moreover, $Z = \sum\nolimits_{j = 1}^n {(\alpha {E_j} + \beta {T_j} + \gamma d + \delta ({q_2} - {q_1}))} = \sum\nolimits_{j = 1}^n {{\xi _j}{p_{[j]}}} $, where
Lemma 5. For the problem $1|DIF|\sum {(\alpha {E_j} + \beta {T_j} + \gamma d_j^1 + \delta {D_j})} $, there exists an optimal schedule that satisfies the optimal due window starting time $d_j^1$ and the optimal due window completion time $d_j^2$ for job ${J_j}$ is no greater than its completion time ${C_j} $, i.e., $d_j^1 \leqslant d_j^2 \leqslant {C_j} .$
Moreover, $Z = \sum\nolimits_{j = 1}^n {(\alpha {E_j} + \beta {T_j} + \gamma {d_j} + \delta {D_j})} = \sum\nolimits_{j = 1}^n {\xi (n - j + 1){p_{[j]}}} $, where $\xi = \{ \beta , \gamma , \delta \} .$
It is also worth noting that Lemma 4 and Lemma 5 also hold for our problems. According to Theorem 1, Theorem 2 and the results above, we can immediately get the following theorem.
Theorem 4. The problem $1|{p_j} = \left( {{{\left( {\frac{{{w_j}}}{{{u_j}}}} \right)}^k} + b{S_j}} \right)g(r), \sum {{b_j}{u_j}} \leqslant U, X|$ $\sum {(\alpha {E_j} + \beta {T_j} + \gamma d_j^1 + \delta {D_j})} $ and problem $1|{p_j} = \left( {{{\left( {\frac{{{w_j}}}{{{u_j}}}} \right)}^k} + b{S_j}} \right)g(r), X$, $\sum {(\alpha {E_j} + \beta {T_j} + \gamma d_j^1 + \delta {D_j})} \leqslant R|\sum {{b_j}{u_j}} $ for $X \in \{ SLK, DIF\} $ can be solved in $O(n\log n)$ time.
Remark. It is very obvious to see that the unified models can be applied to some scheduling problems, which can be solved by a slightly modified Algorithm 1. Those scheduling problems have the common feature that the scheduling objective function can be expressed as a positional penalties function [37]. For example, the makespan, the sum of completion times, various due dates assignment, and so on.
5.
Conclusions
In this paper, we study single machine scheduling problems with resource allocation, deterioration and general positional effect. The actual processing time of a job is the function of the amount of resource allocation, starting time and the position. We present two unified models and show that the unified models can be applied to solve various due window assignment problems. Two unified models can describe the general scheduling criterion under the total weighted resource consumption constrain and the total weighted resource allocation costs under the scheduling costs constrain. We show that some scheduling problems can be reduced to the unified models and solved in polynomial time. Identifying the set of Pareto optimal schedules or considering the linear resource consumption functions in the setting is interesting and significant work for future research.
Acknowledgments
The authors thank the editor and the reviewers for their useful comments to improve the paper. This work was supported by the National Natural Science Foundation of China under Grant No.71901084, Zhejiang Provincial Natural Science Foundation of China under Grant No. LQ19G020010 and MOE (Ministry of Education of China) Project of Humanities and Social Sciences under Grant No. 19YJC630099.
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: