On the stability analysis of numerical schemes for solving non-linear polynomials arises in engineering problems

1.   Introduction

One of the most critical areas of applied mathematics are iterative techniques to solve nonlinear equations. Their importance is due to their wide applications in different fields, such as engineering, computer science, physics, biology, chemistry, banking, business, digital signal processing, control theory, insurance, social science, and many others. For instance, ^[1,2,3,4] evidence some of these applications. Computer visual representation, which converts numerical data into 2D or 3D images, unquestionably offers a modern and unconventional solution to some mathematical topics. It gives a fresh perspective and provides a deep knowledge of the characteristics and behavior of iterative processes for finding polynomial roots and allocating them (e.g., ^{[5,6,7,8,9,10,11]}). The development of digital computer hardware and software has substantially impacted many scientific disciplines and is frequently utilized in almost all scientific domains, including mathematics. The usage of advanced computational tools, such as symbolic computation and computer graphics, is necessary to tackle many complex problems in applied mathematics and other scientific disciplines. Thanks to the rapid development of computer graphics over the past 20 years, scientists from various fields can now use cutting-edge computer techniques to study and visualize phenomena that are not easily observable. Architecture and engineering, biomedical applications (X-ray computed tomography (CT), magnetic resonance imaging (MRI), mathematics, physics, business and management graphics, education and learning, user interface design, image syntheses, mapping and cartography, video and multimedia technology (animation, move, etc.), and business are just a few examples where high-quality computer visualization provides new and remarkable insights. Many problems in the areas above remain unsolvable by humans. Computer graphics allow a quick and practical link between machines and people. The technology and mathematics that computer graphics provide to a wide range of applications in theory and practice, and they indeed have great potential in the future (see e.g., ^{[12,13,14,15,16]}). The initial guess value affects the classical Newton-like method's performance, particularly for large-scale nonlinear problems. For this reason, many iterations of Newton's technique have been devised. For example, Knoll et al. ^[17] suggested the arc-length approaches, and Lemieux et al. ^[18] offered the Jacobian-Free Newton-Krylov method. Wu et al. ^[19] provided novel contributions to Newton's research. Qureshi et al. ^[20] presents the trapezoidal second-order Newton's, He et al. ^[21] presented the variational Newton-type scheme, Saheya et al. ^[22] employed the rational approximation function to suggest a Newton-like method, Abbasbandy ^[23] proposed an improved version of Newton's scheme by using a modified Adomian decomposition technique. Motivated by the above mentioned work, this study develops a novel family of Newton-type iterative algorithms using a single parameter for locating the simple root of nonlinear equations. The parameter value influences the newly developed family. The best parameter value for that family of methods should be chosen based on the method that has a larger region of convergence at starting points where the classical methods diverge. To achieve this aim, we deal with the corresponding complex dynamical system, determining fixed and critical points, analyzing asymptotic convergence, and identifying values that decompose the corresponding rational function. The main contribution of this work is reflected as follows:

● Construction of a family of numerical schemes for finding roots of scalar nonlinear equations.

● Using CAS-Maple to verify the convergence order of the proposed method.

● Finding fixed and critical points utilizing complex dynamical analysis.

● Dynamical and parametric planes are generated using critical points.

● Computational tools are used to analyze the proposed technique's convergence rate, efficiency, stability, and applicability.

● Analyzing how the suggested technique can be applied in various research disciplines.

Some engineering applications are considered to show improved efficiency and stability compared to other classical techniques discussed in the literature. This research aims to construct a novel family of iterative methods using the computer algebra system CAS-Maple, Mathematica, MATLAB, Scilab, GNU Octave, Python, and many others (see e.g., ^[24,25]). It uses parameter and dynamical planes to apply these techniques for picking the best parameter value for the iterative scheme. This paper is organized as follows: In section 2, the proposed method is introduced. In section 3, the stability of the proposed method using complex dynamical analysis is discussed. In section 4, the efficiency of this method is illustrated by applications. The last section is the conclusion of this article.

2.   Construction of numerical methods and their convergence analysis

This section discusses some well-known methods in the literature. One of the most ancient and popular numerical methods for approximating single roots of a nonlinear equation

is Newton's method ^[26] (NM), which has local quadratic convergence.

Kou et al. ^[27] presents an optimal 2nd-order iterative method (abbreviated as YO) as follows:

where $\lambda _{n} = \alpha = 1$ and $\alpha _{1} = 0.$

Chicharro et al. ^[28] give the optimal local second-order iterative method (abbreviated as AC) as follows:

We suggested the following optimal family of numerical iterative schemes abbreviated as BB1:

where $u = \frac{f(x^{(t)})(f^{\prime }(x^{(t)}))^{\beta }}{(f^{\prime }(x^{(t)}))^{2}}, \beta, \alpha \in \mathbb{R}.$

The convergence order of iteration scheme Eq (2.5) is found by using CAS-Maple 18 in the form of the following theorem:

Theorem 1. Let $I$ an open interval and $\zeta \in I$ be a simple root of a sufficiently differential function $f:I\subseteq \Re \longrightarrow \Re$. For a real valued function $\vartheta (u)$ and $x^{(0)}$ sufficiently close to $\zeta$ with $\vartheta (0) = 0,$ and $\vartheta ^{\prime }(0) < \infty$ then iterative scheme (2.5) has local quadratic convergence, satisfying the error equation:

where $c_{m} = \frac{f^{m}(\zeta)}{m!f^{\prime }(\zeta)}; m\geq 2.$

Proof. Let $f(x)$ have a simple root $\zeta$ and $e^{(t)} = x^{(t)}-\zeta$. By a Taylor series expansion of $f(x^{(t)})$ around $x^{(t)} = \zeta,$ taking $f(\zeta) = 0,$ we get

and

Dividing (2.7) by (2.8), we have

Thus, using the Taylor series, we have

and putting $\vartheta (0) = 0$ in (2.14), we have

This proves second-order convergence. □

Special cases:

Now we construct some special cases of the family of methods described by (2.5). We construct the following numerical schemes by choosing $\beta = 2$ in (2.5).

Method-1 (abbreviated as BB1): Take the function $\vartheta$$($$u$$)$ defined as {$\vartheta$}$($$u$$) = \frac{u}{1+u}$ which satisfies the condtion of Theorem 1, i.e., $\vartheta ^{\prime }(0) < \infty$. Then, we have the following optimal family of iterative methods:

Method-2 (abbreviated as BB2): Take the function $\vartheta$$($$u$$)$ defined as {$\vartheta$}$($$u$$) = \frac{u}{1+\gamma u^{2}}$ which satisfies the condtion of Theorem 1, i.e., $\vartheta ^{\prime }(0) < \infty$. Then, we have the following optimal family of iterative methods:

Method-3 (abbreviated as BB3): Take the function $\vartheta$$($$u$$)$ defined as {$\vartheta$}$($$u$$) = \frac{u}{1+\gamma u}$ which satisfies the condtion of Theorem 1, i.e., $\vartheta ^{\prime }(0) < \infty$. Then, we have the following optimal family of iterative methods:

where $\alpha, \gamma \in \Re.$

2.1.   Complex dynamical analysis of the family of numerical methods

This section discusses the stability of the numerical scheme Eq (2.16) against the backdrop of the complex dynamics. Iterative method Eq (2.16) leads to the following rational map:

Recalling some basic concepts of this theory (detailed information can be found in ^{[29,30,31,32,33,34,35,36,37,38]}). Taking a rational function $\Re _{f}: \mathbb{C} \longrightarrow \mathbb{C}$, $\mathbb{C}$ denotes the Riemann sphere. The orbit $s_{0}\in \mathbb{C}$ defines a set $orb(x) = \{x_{0}, \Re _{f}(x_{0}), \Re _{f}^{2}(x_{0}), ..., \Re _{f}^{m}(x_{0}), ...\}.$ A point $x_{0}\in \mathbb{C}$ is called a fixed point if $\Re _{f}(x_{0}) = x_{0}$. A particular fixed point $x_{0}$ is called a strange fixed point if $f(x^{r}) = 0$ when $x_{0}\neq x^{r}.$ A T-periodic point is defined as the point $x_{T}\in \mathbb{C}$ satisfying $\Re ^{T}(x_{T}) = s_{T}$ with $\Re ^{\prime }(x_{T})\neq x_{T}$ for $x < T.$ If $x_{0\text{ }}$ is a fixed point of $\Re$, then it is:

● Super attracting if $\left\vert \Re _{f}^{\prime }(x_{0})\right\vert = 0$.

● Attracting if $\left\vert \Re _{f}^{\prime }(x_{0})\right\vert < 1$.

● Repulsive if $\left\vert \Re _{f}^{\prime }(x_{0})\right\vert > 1$.

● Neutral if $\left\vert \Re _{f}^{\prime }(x_{0})\right\vert = 1$.

● A strange fixed point if it not associated to any root of non-linear equation (2.1).

An attracting point $x^{\ast }\in \mathbb{C}$ defines a basin of attraction $\Re (x^{\ast })$ as the set of starting points whose orbit tends to $x^{\ast }.$

The iterative method BB1 holds the scaling theorem which allows a suitable change of co-ordinate to reduce of dynamics of iteration of general maps to the study of a specific family of iteration of similar maps. The one point iterative method (2.16) has a universal Julia set if a rational map exist which conjugates by the Mobius transformation.

Theorem 2. A rational map $f_{g}(x)$ arising from (2.16) applied to $f(x) = (x-a)(x-b)$, where $a, b\in \Re, f_{g}(x)$ is conjugate via the Mobius transformation by $M(v) = \frac{v-a}{v-b}$ to

Proof. Let $f(x) = (x-a)(x-b),$ where $a, b\in \Re.$ The Möbius transformation given by:

with inverse

which we consider as a map from $\mathbb{C} \cup \infty.$

Then, we have

□

Similarly, we can get the following conclusions.

Theorem 3. A map $f_{g}(x)$ (rational) arising from BB2, BB3, AC, NM, and YO applied to $f(x) = (x-a)(x-b)$, where $a, b\in \Re, f_{g}(x)$ is conjugate via the Mobius transformation by $M(v) = \frac{v-a}{v-b}$ to

The fixed points of (2.22) are $x = -1, x = 0, x = 1$, and $x = \infty$. We calculate $f_{g}^{\prime }(x, \alpha)$ for the stability of fixed points of BB1 as:

From (2.28) it is clear that $x = 0$ and $\infty$ are always super attractive fixed points but the stability of other fixed points are depends on $\alpha,$ which we present here. The operator $f_{g}^{\prime }(x, \alpha)$ for $x = -1$ gives

Analyzing (2.29), as $\alpha \longrightarrow \pm \infty$ we obtain horizontal asymptotes for $\left\vert f_{g}^{\prime }(-1, \alpha)\right\vert = 1$ and vertical asymptotes for $\alpha = 0$ (Newton method).

Theorem 4. The strange point $x = -1$ is known as:

(i) If $\Re _{e}(\alpha) < \frac{1}{4},$ then $x = -1$ is an attractor and it can be super attractor for $\alpha = -1$.

(ii) When $\Re _{e}(\alpha) = \frac{1}{4}$, is a parabolic point for $x = -1.$

(iii) If $\alpha \neq 0$ and $\Re _{e}(\alpha) > \frac{1}{4},$ is a repulsive for $x = -1$.

Proof. As

then,

Let us consider $\alpha = a+ib \; \in \; \mathbb{C}.$

Then,

Thus,

Finally, if $a\neq 0$ and $\Re _{e}(\alpha) > \frac{1}{4}$, then $\left\vert f_{g}^{\prime }(-1, \alpha)\right\vert \geqslant 1.$ □

The operator $f_{g}^{\prime }(1, \alpha)$ gives

By analyzing (2.34), as $\alpha \longrightarrow \pm \infty$ we obtain horizontal asymptotes in $\left\vert f_{g}^{\prime }(1, \alpha)\right\vert = 1.$

Theorem 5. The character of the strange point $x = 1$ is as follows:

(i) If $\Re _{e}(\alpha) > -\frac{3}{4},$ it is an attractor for $x = 1$.

(ii) When $\Re _{e}(\alpha) = -\frac{3}{4}$, it is a parabolic point for $x = 1$.

(iii) If $\alpha \neq 0$ and $\Re (\alpha) < -\frac{3}{4},$ then $x = 1$ a repulsive.

Proof. As

then,

Consider $\alpha = a+ib\in \mathbb{C}.$

Then,

Thus,

Finally, if $a\neq 1$and $\Re _{e}(\alpha) > -\frac{3}{4}$, then $\left\vert f_{g}^{\prime }(1, \alpha)\right\vert < 1$ □

The stability functions of the iterative schemes BB1 are as follows:

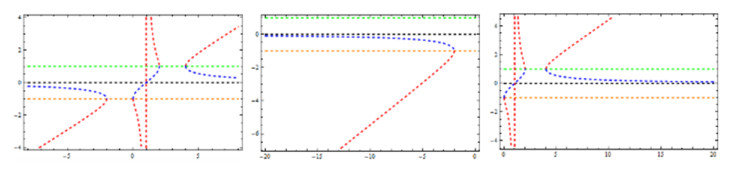
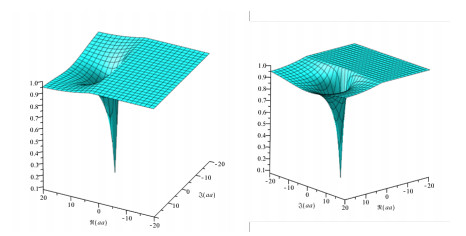
Figure 1 represents the region of stability of strange fixed points. Left: Figure $f_{g}^{\prime }(1, \alpha)$. Right: Figure $f_{g}^{\prime }(-1, \alpha)$.

Analysis of Critical Points:

The critical points of BB1 satisfy $f_{g}^{\prime }(-1, \alpha) = 0$ i.e., $x = 0, x = \infty$ and

If $\alpha \neq 1, 1/4,$ then observe that $cr1 = \frac{1}{cr2}$ and $cr1 = cr2 = 1$ only when $\alpha = -1$, while $cr1 = cr2 = -1$ only when $\alpha = 0.$ Figure 2 presents the behavior of the fixed and critical points for real of $\alpha$. Fixed points $-1, 0$, and $1$ are represented by orange, black, and green dotted lines, while critical points $(cr1, cr2)$ are represented by red and blue lines, respectively.

Figure 3: The union of respective stability function of the all strange fixed points of BB1-BB3, AC, and YO, respectively, from left to right.

Theorem 6. The only member of BB1 whose operator is always conjugated to the rational map $x^{2}$ is the element corresponding to $\alpha = 0.$

Proof. From (2.22), we represent $nn(x) = x^{2}((4\alpha +x+1)$ in the numerator and $dd(x) = (4\alpha +1)x+1$ denominator of (2.22). Then, for $\alpha = 0$, we get $nn(x) = dd(x)$. □

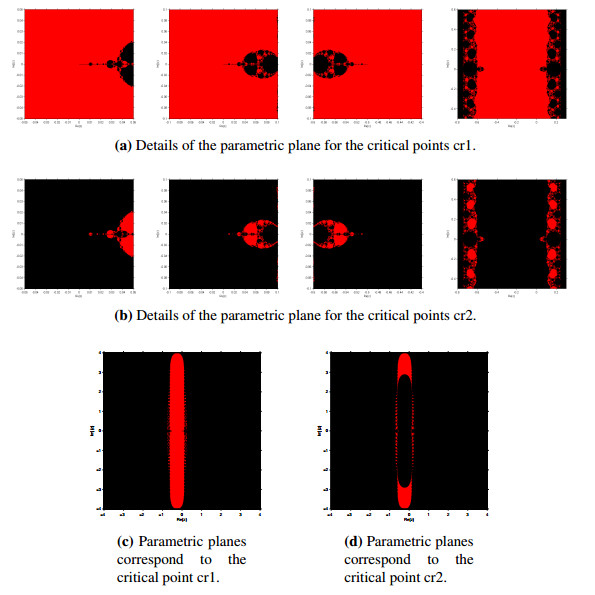
Parametric planes:

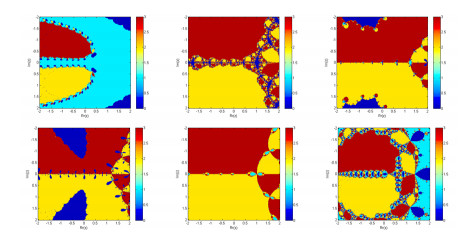
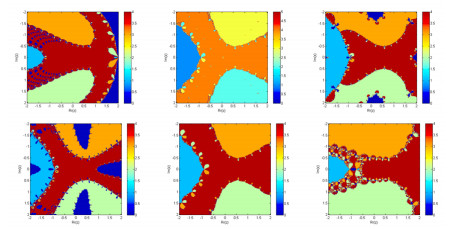
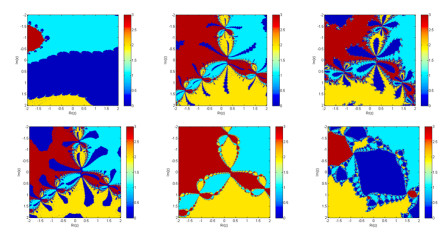
We generate a parametric plane by taking $\alpha$ over a mesh of $250,000$ points in a complex plane. Critical points are chosen as initial guessed values and then iterate until it converges to any fixed points. Taking $10^{-3}$ as a tolerance. We paint the complex parameter value in red if it converges, and black in other cases. The parametric planes for the critical points are shown in Figure 4.

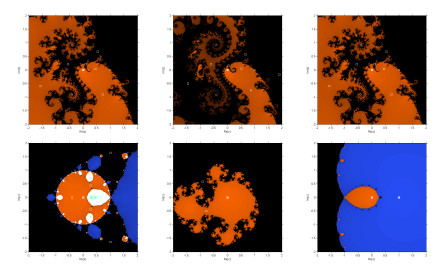
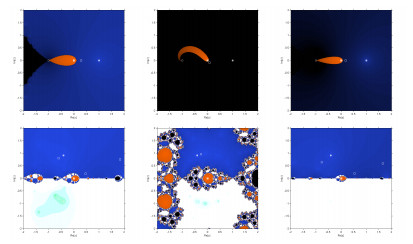
Dynamical planes:

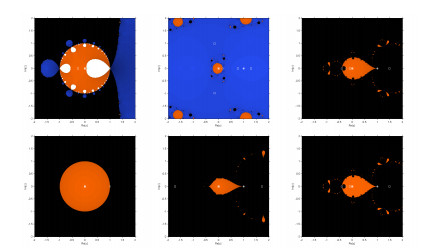
Dynamical planes are generated as parametric planes. To generate them, the real and imaginary parts of the starting estimations are represented as two axes over a mesh of $250\times 250$, and the same stopping criteria as in the parametric plane. The study assigns different colors to indicate which root the method converges to, and black in other cases. The dynamical planes of the iterative scheme BB1, YO, NM, and AC for different parametric values are shown in Figures 5–7.

In Table 1, Els-Time denotes the amount of time in seconds that has passed, Start-Points denotes the number of starting points (62500.00 in a square), Average-It denotes the average number of iterations, C-Points denotes the number of converging points, and D-Points denotes the number of diverging points utilized to form dynamical planes (the basins of attractions ^[39,40]). Table 1 clearly shows that our recently developed methods BB1–BB3 outperform the existing iterative methods in terms of CPU-Time, Average-It, T-Points, C-Points, and D-Points.

In Table 2, Els-Time denotes the amount of time in seconds that has passed, Start-Points denotes the number of starting points (62500.00 in a square), Average-It denotes the average number of iterations, C-Points denotes the number of converging points, and D-Points denotes the number of diverging points utilized to form dynamical planes (the basins of attractions). Table 2 clearly shows that our recently developed methods BB1–BB3 outperform existing iterative methods in terms of CPU-Time, Average-It, T-Points, C-Points, and D-Points.

In Table 3, Els-Time denotes the amount of time in seconds that has passed, Start-Points denotes the number of starting points (62500.00 in a square), Average-It denotes the average number of iterations, C-Points denotes the number of converging points, and D-Points denotes the number of diverging points utilized to form dynamical planes (the basins of attractions). Table 3 clearly shows that our recently developed methods BB1-BB3 outperform the existing iterative methods in terms of CPU-Time, Average-It, T-Points, C-Points, and D-Points.

2.2.   Engineering applications

This section discusses an engineering application to check the efficiency and performance of the newly developed methods compared to existing methods, i.e., the AC, YO, and NM methods.

Example 1. Current-Voltage Diode ^[41]

A manufacturing company provided a tunnel diode with voltage-current output:

The tunnel diode is connected with resistor R and voltage source E. By applying Kirchhoff's voltage law, we find a relation for the steady current as follows:

For a given E = 1.4 and R = 19, we find x by setting f(x) = 0,

The exact roots of (2.41) are

The initial estimates of $f_{1}(x)$ have been taken as

Table 4 clearly shows the dominance behavior of BB1–BB3 over the AC, YO, and NM iterative methods in approximated absolute error on various number of iterations $n$ for the non-linear function $f_{1}(x)$. Various initial guess values are used in order to approximate all roots of $f_{1}(x)$.

Example 2. Mass-Spring system ^[42]

A spring develops a non-linear restoring force given by

where F represents force in kg force and x is displacement in cm. Using value of constants $r_{1} = 5.25kg/cm, \; r_{3} = 0.60kg/cm, \; r_{5} = 0.0118kg/cm$ in (2.42), we get a non-linear equation in terms of the displacement $x$

The exact roots of (2.43) are

The initial estimates for simultaneous determination of all roots of non-linear function $f_{2}(x)$ has been taken as:

Table 5 clearly shows the dominance behavior of BB1–BB3 over the AC, YO, and NM iterative methods in approximated absolute error on various number of iterations $n$ for the non-linear function $f_{2}(x)$. Various initial guess values are used in order to approximate all roots of $f_{2}(x)$.

Example 3. Fractional conversion of magnesium hydroxide in hydrochloric acid: ^{[43,44,45,46]}.

The acidity of a saturated solution of magnesium hydroxide MgOH in hydrochloric acid HCl is given by

for the hydronium ion concentration $\left[ H_{3}O^{+}\right].$ If we set $x = 10^{4}\left[ H_{3}O^{+}\right],$ we obtain the following non-linear equation

with exact roots $2.4$, $-3.0\pm 2.3i$ up-to one decimal place. The initial estimates of (2.45) have been taken as:

Table 6 clearly shows the dominance behavior of BB1–BB3 over the AC, YO, and NM iterative methods in approximated absolute error on various number of iterations $n$ for the non-linear function $f_{3}(x)$. Various initial guess values are used in order to approximate all roots of $f_{3}(x)$.

3.   Conclusions

We developed a family of iterative techniques with two parameters for locating the roots of nonlinear equations. Due to the lengthy and complicated mathematical formulas used in the convergence study, we used symbolic computation utilizing several programs created in the Mathematica computer system. We implemented a different method to evaluate the root solver efficiency utilizing parametric planes (Figures 1–4) and dynamical planes (Figures 5–7) to select the best parameter value. The stability region and dynamical behavior of the strange fixed points were discussed. Root-finding methods can be analyzed graphically using this approach concerning various starting points. Well-built software will offer a visual knowledge of the convergence behavior of iterative methods for establishing comparison standards to show the basins of attraction (Figures 8–10). However, it will also consider various qualitative factors, such as CPU time and the convergence region. The numerical results show that the newly developed technique outperforms the current method regarding the residual error, CPU-time, and iterations. In the future, we will construct higher-order efficient, optimal, and stable iterative methods for finding simple as well as all distinct and multiple roots of Eq (2.1). We may explore the applications of these results in other areas. For example, the dynamics nonlinear inventory management system, numerical solution of fractional SIR epidemiological model, stability and optimal control strategies for a novel epidemic model of COVID-19.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

All authors declare no conflicts of interest in this paper.