Factors influencing secondary school teachers' usage behavior of dynamic mathematics software: A partial least squares structural equation modeling (PLS-SEM) method

1.   Introduction

Education is experiencing a profound digital transformation in the era of the relentless pursuit of technological advancement ^{[1,2,3,4,5,6]}, and the importance of integrating information technology into mathematics teaching has been widely recognized by educational systems around the world ^[7,8]. Technology-based models for mathematics teaching have received considerable critical attention, and they can help teachers create engaging mathematics classrooms that are more effective for teaching and learning ^{[9,10,11,12,13,14,15,16]}. Applying digital technologies in the mathematics classroom has been recognized as a high-potential teaching pattern ^[17,18,19], and dynamic mathematics software, as a kind of subject-specific digital technology, is vitally important for mathematics teaching and learning ^{[20,21,22,23]}.

Dynamic mathematics software, such as The Geometer's Sketchpad, GeoGebra, Desmos, Netpad, Cabri 3D and Fathom dynamic data software, is a kind of subject-specific digital tool used for enabling users to create mathematical objects and operate them dynamically and interactively ^{[24,25,26,27]}. The use of dynamic mathematics software is a key issue in mathematics education. Relevant national and international studies have shown that at the secondary school level, the use of dynamic mathematical software helps students achieve individual and collective understanding of mathematics ^[28,29], make connections between mathematical objects and graphical representations ^[30,31], and explore real-world mathematical problems ^[32,33]. It has the ability to make active constructions of mathematical knowledge in a dynamic learning environment ^[34,35], and it facilitates students' mathematical problem-solving ^{[36,37,38,39,40,41]}. Thus, it improves mathematical learning performance ^[42,43]. In a word, dynamic mathematics software is necessary for effective mathematics teaching and learning, so it needs further in-depth research.

Although there have been many previous studies conducted on dynamic mathematics software, most of the studies in this field focus on its concrete use in teaching and learning ^{[32,36,44,45,46,47,48]}, its effects on students' mathematics learning ^{[10,11,12,13,14,15,16,49,50]}, its influence on the professional development of mathematics teachers ^{[51,52,53,54,55,56]}, and so on. Several literature reviews and a meta-analysis ^{[18,25,57,58]} also confirmed that the existing studies overlooked the importance of teachers' acceptance and adoption of dynamic mathematics software ^[27,59]. The factors that influence secondary school mathematics teachers' behavioral intentions and usage behavior of dynamic mathematics software and the method applied in research remain unclear. Therefore, this study aimed to address these gaps in the existing literature through a quantitative approach based on the extended UTAUT model and the PLS-SEM method. The following two research questions were investigated.

1) What factors positively affect secondary school teachers' behavioral intentions and usage behavior of dynamic mathematics software based on an extended unified theory of acceptance and use of technology (UTAUT) model?

2) Does gender, teaching experience, major, or training moderate each relationship in the extended UTAUT model?

In the following sections, most related previous studies on dynamic mathematics software are described first. Then, a secondary school teachers' dynamic mathematics software usage conceptual model is proposed based on the UTAUT model and integrated with the concept of self-efficacy, along with the relevant hypotheses. In the methodology section, the method and process for instrument development, data collection and data analysis are described in detail. After that, the results are shown based on the standard procedure on how to report the results of partial least squared structural equation modeling, and the main findings are interpreted and highlighted. Finally, the implications, limitations and future research are discussed.

2.   Literature review and hypothesis development

2.1.   Dynamic mathematics software at the secondary school level

Dynamic mathematics software is suitable for teaching and learning at the secondary school level. Owing to the various affordances, such as calculating, generating accurate diagrams, making measurements, and dragging elements of a drawing ^[60,61], dynamic mathematics software can be used in arithmetic, algebra, geometry, functions, probability, statistics, calculus and so forth ^[62,63]. It provides opportunities for positive changes to teaching and learning ^[64]. Principally, dynamic mathematics software can support the creation of meaningful learning environments that allow problem-solving and cultivation of creativity, thus aiding in a better understanding of mathematics. For instance, Oner ^[29] analyzed the mathematical discourse of a group of middle school students within a virtual collaborative dynamic mathematics environment (GeoGebra), finding that students gradually moved from a visual discourse to a more formal discourse, which is beneficial to construct geometric dependencies. Dogru and Akyuz ^[28] explored the mathematical practices of eighth grade students' learning about prisms, cylinders and their surface areas with the help of dynamic mathematics software (GeoGebra), which enriches the instruction by assisting students in visualizing and reasoning about 3D shapes, and the results revealed that students' understanding improved. In addition, there were some systematic reviews and meta-analyses indicating that the instruction by use of dynamic mathematics software can effectively improve students' mathematics achievement, compared with traditional instruction ^[18,42,43]. This is probably because dynamic mathematics software states or verifies conjectures much more easily than in other computational environments or in the more traditional setting of paper and pencil in mathematics class ^[65]. Overall, dynamic mathematics software can not only help secondary school mathematics teachers to discern, discuss and reason with the invariant properties of mathematics objects ^[66], but also have a positive effect on secondary school students' mathematical reasoning ^[13], helping them develop academic achievement and ensuring the survival of the learning impact of mathematics ^[67].

2.2.   UTAUT and digital teaching

Several models were put forward to investigate individuals' behavioral intention and usage behavior of new technology. For example, Davis et al. ^[68,69] proposed the first-generation technology acceptance model (TAM) in 1989, which was designed to predict new technology acceptance and usage on the job and suggested two main cognitive beliefs that influence users' technology acceptance: perceived usefulness and perceived ease of use. Venkatesh and Davis ^[70] proposed the second-generation technology acceptance model (TAM2) in 2000, which explored the influence of factors such as social and cognitive processes on the perceived usefulness, behavioral intention and usage behavior of specific technologies. Since then, Venkatesh and his colleagues continually explored better models to improve the explanatory power. After reviewing some popular models and theoretical frameworks related to technology acceptance, such as the technology acceptance model ^[69,70], theory of planned behavior ^[71] and innovation diffusion theory ^[72], they found that none of the models involved in the research had more than 50% explanatory power for the user's behavior. Based on these theories and models, the unified theory of acceptance and use of technology (UTAUT) model was proposed ^[73].

The UTAUT model involves four main factors that influence users' acceptance and use of technology: performance expectancy (PE), effort expectancy (EE), social influence (SI) and facilitating conditions (FC). It also includes four moderators involving individual differences: gender, age, experience and voluntariness of use. This model is widely used because its explanatory power for the user's behavior far exceeds that of other technology acceptance models. Besides, Venkatesh et al. ^[74] pointed out that adding new constructs can help expand the theoretical horizon of the UTAUT model. To compensate for the lack of focus in the UTAUT model on specific tasks, some researchers would use it in conjunction with the task-technology fit model ^[75,76]. From previous literature reviews, it is evident that self-efficacy is the most frequently added external variable ^[77]. Some researchers believe that self-efficacy may influence teachers' use of technology while teaching ^[78,79]. Therefore, this study adds self-efficacy to the original UTAUT model to explore its influence on secondary school mathematics teachers' intentions and behavior toward the use of dynamic mathematics software.

The success of digital teaching and learning largely depends on its acceptance and use by teachers ^[80]. The UTAUT model can be an important theoretical framework for assessing the acceptance and use of digital teaching tools. Several studies have used the UTAUT model to investigate the adoption of digital technologies, such as the use of digital mathematics textbooks ^[81] and interactive whiteboards ^[82]. At the same time, digital technology is not only a tool for teaching and learning but also for teacher education, so the results of research based on the UTAUT model can provide guidance for the development and implementation of digital teaching and learning. For example, if teachers have low performance expectancy for digital teaching, the usefulness and effectiveness of digital teaching can be improved by enriching the content and enhancing the affordance of the tools, thereby increasing teacher satisfaction and usage behavior. Thus, digital teaching and learning have the potential to change the way of teaching and provide new ideas for teaching and learning for teachers. The UTAUT model can help us better understand teachers' acceptance and use of digital technologies, thus improving the usefulness and effectiveness of digital teaching and learning.

2.3.   Formulation of hypothesis

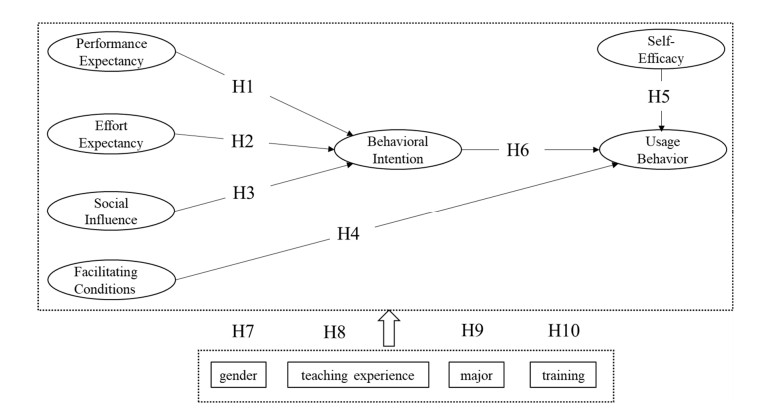
In this study, the UTAUT model was chosen as the grounded model for developing a conceptual model to investigate the factors that influence secondary school teachers' usage behavior of dynamic mathematics software. In this conceptual model, self-efficacy was added as a new construct, which may influence the usage behavior of teachers. In order to analyze the individual differences in how to moderate the path relationships in the model, this study retained gender as a moderating variable, removed voluntariness of use, replaced age with teaching experience, replaced experience with training, and added major as a new moderating variable. Figure 1 illustrates this conceptual model.

2.3.1.   Performance expectancy

Performance expectancy (PE) is defined as "the degree to which an individual believes that using the system will help him or her to attain gains in job performance" ^[73] (pp. 447). This definition implies that if a system component were not useful, the user would not have any motivation to use that part of the system. Therefore, performance expectancy often appears as perceived usefulness in the TAM model ^[68,69,83]. In the context of this study, performance expectancy is regarded as the teachers' belief that dynamic mathematics software can improve teaching quality at the secondary school level. Research relating to performance expectancy for digital technologies has indicated that it can positively affect the user's adoption of new technology ^[84,85]. Accordingly, the following hypothesis is formulated:

H1: Performance expectancy affects secondary school teachers' behavioral intentions of dynamic mathematics software.

2.3.2.   Effort expectancy

According to UTAUT, effort expectancy (EE) is interpreted as "the degree of ease associated with the use of the system" ^[73] (pp. 450). This definition implies that when users feel that a system is easy to use and does not require much effort, they will have a high intention of using it to acquire the expected performance. Therefore, effort expectancy often appears as perceived ease of use in the TAM model ^[68,69,83]. In this study, effort expectancy represents teachers' belief about the ease of use of dynamic mathematics software. Previous studies have demonstrated that effort expectancy is a vital factor and significantly affects the users' adoption of new technology ^[85,86]. Therefore, this study proposes the following hypothesis:

H2: Effort expectancy affects secondary school teachers' behavioral intentions of dynamic mathematics software.

2.3.3.   Social influence

Social influence is defined as "the degree to which an individual perceives that important others believe he or she should use the new system" ^[73] (pp. 451), which is similar to subjective norms of the theory of reasoned action ^[87]. In the context of this study, social influence stands for teachers' perceptions about how school leaders, colleagues, and students believe they should use dynamic mathematics software. Venkatesh et al. ^[73] stated that social influence was a significant determinant of behavioral intention. Moreover, several empirical studies showed that social influence greatly affects someone to adopt new tools ^[88,89]. Accordingly, the following hypothesis is proposed:

H3: Social influence affects secondary school teachers' behavioral intentions of dynamic mathematics software.

2.3.4.   Facilitating conditions

Facilitating conditions are interpreted as "the degree to which an individual believes that an organizational and technical infrastructure exists to support the use of the system" ^[73] (pp. 453). According to the UTAUT model, facilitating conditions have an influence on usage behavior, and several articles related to technology acceptance also show that facilitating conditions significantly influence people's adoption of new technologies ^[27,90,91]. In this study, facilitating conditions are defined as hardware and software facilities of the classroom, curriculum resources related to dynamic mathematics software, and on-time professional support when secondary school teachers have trouble in using dynamic mathematics software. Therefore, this study makes the following hypothesis:

H4: Facilitating conditions affect secondary school teachers' usage behavior of dynamic mathematics software.

2.3.5.   Self-efficacy

According to the study conducted by Bandura ^[92], self-efficacy is people's judgments of their capabilities to organize and execute courses of action required to attain designated types of performances (pp. 391), which is concerned not with the skills one has but with judgments of what one can do with whatever skills one possesses. Based on the concept of dynamic mathematics software, self-efficacy is regarded as the individual's judgmental analysis of the use of dynamic mathematics software to accomplish a specified type of task. Moreover, self-efficacy and usage behavior have been empirically supported based on causal interlinks between them ^[78,79]. Therefore, the following hypothesis is formulated by this research:

H5: Self-efficacy affects secondary school teachers' usage behavior of dynamic mathematics software.

2.3.6.   Behavioral intention and usage behavior

Behavioral intention (BI) is defined as "the extent to which individuals are willing to use the new system in the future" ^[73] (pp. 456). Usage behavior (UB) refers to the patterns, habits, and actions of users when interacting with a system, which is usually measured using their duration and frequency of using a target system ^[93]. Now, there is a growing corpus of research suggesting that behavioral intention predicts the actual usage behavior with regard to technology use ^[94]; for example, Sumak et al.'s study ^[89] found that the usage behavior is positively affected by behavioral intention. Therefore, this study will also test the effect of behavioral intention on usage behavior, as suggested by the original UTAUT model.

H6: Secondary school teachers' behavioral intentions of dynamic mathematics software affect their usage behavior.

2.3.7.   Gender as a moderating variable

Venkatesh et al. ^[73] reported that gender can play a moderating role in the path relationships in the UTAUT model. Recent studies continue to confirm this finding ^[95,96]. In the educational context, male teachers typically master computer-based instructional media more quickly and use subject-specific tools more frequently in their teaching than female teachers ^[97]. Therefore, this study hypothesizes that gender is a potential moderating variable in the secondary school teachers' dynamic mathematics software usage conceptual model.

H7: Gender moderates all relationships in the secondary school teachers' dynamic mathematics software usage conceptual model.

2.3.8.   Teaching experience as a moderating variable

A teacher with more years of teaching experience may have a unique perspective on a certain technology. In the original UTAUT model, the variable of age is used as a moderating factor. However, in the context of education, age does not reflect a person's work experience as a teacher. Therefore, this study introduced the variable of teaching experience and divided it into three groups according to the years of teaching, namely, less than 5 years, 6-15 years, and over 15 years. Hu et al.'s study ^[98] showed that years of teaching positively moderate the acceptance of emerging mobile technologies among academic faculties. Therefore, the study proposes that teaching experience is a potential moderating variable in the secondary school teachers' dynamic mathematics software usage conceptual model.

H8: Teaching experience moderates all relationships in the secondary school teachers' dynamic mathematics software usage conceptual model.

2.3.9.   Major as a moderating variable

Considering China's teacher education system, it is hypothesized that teachers who graduated from a mathematics major are more receptive to dynamic mathematics software than those who graduated from a non-mathematics major. When pre-service mathematics teachers study in a teacher training program, they learn not only subject knowledge, pedagogical knowledge and pedagogical content knowledge, but also the knowledge on how to use subject-specific digitalization tools ^[99], which leads them to exposure to dynamic mathematics software much earlier. Therefore, the potential moderating variable of major is introduced. In summary, the study hypothesizes that the major is a potential moderating variable in the secondary school teachers' dynamic mathematics software usage conceptual model.

H9: Major moderates all relationships in the secondary school teachers' dynamic mathematics software usage conceptual model.

2.3.10.   Training as a moderating variable

People's perspectives can be influenced by training ^[100,101]. The original UTAUT model considered experience as the key moderating variable, while this study argues that trained teachers, who can gain insight into dynamic mathematics software, increase their proficiency in its use, which will influence teachers' actual usage behavior of dynamic mathematics software. Therefore, training is substituted for the original experience, and the study hypothesizes that the training is a potential moderating variable in the secondary school teachers' dynamic mathematics software usage conceptual model.

H10: Training moderates all relationships in the secondary school teachers' dynamic mathematics software usage conceptual model.

3.   Methodology

This study used a quantitative method to explore factors that positively affect secondary school teachers' usage behavior of dynamic mathematics software. It also examined the moderating effects of gender, teaching experience, major and training on all relationships in the secondary school teachers' dynamic mathematics software usage conceptual model. With six constructs, namely, performance expectancy, effort expectancy, social influence, facilitating conditions, behavioral intention and usage behavior in a standard UTUAT model, self-efficacy was also added to the model. Based on the conceptual model developed from a literature review, the data were collected by a self-designed questionnaire. Three hundred ninety-three secondary school mathematics teachers in Hunan, a south-central province of China, provided valid questionnaire data. The PLS-SEM method ^{[102,103,104,105,106,107,108,109]} was used to analyze these data.

3.1.   Instrument development

The instrument in this study is a questionnaire on secondary school teachers' usage behavior of dynamic mathematics software, which contains two parts. One part is the personal information of secondary school teachers, including gender, nationality, professional title, level of education, major, teaching experience, school location, school level, training on dynamic mathematics software and dynamic mathematics software mastery, etc. The other part is the factors that may influence secondary school teachers' usage behavior of dynamic mathematics software, which involves 24 items that focused on performance expectancy, effort expectancy, social influence, facilitating conditions, self-efficacy, behavioral intention and usage behavior. These items were adopted from the relevant instruments of acceptance and use of technology ^[27,73,74], combined with the characteristics of dynamic mathematics software ^{[110,111,112]}. Particularly, the items that measure performance expectancy were designed according to the affordances of dynamic mathematics software ^[113,114].

Two pilot studies were conducted before the final version of the questionnaire was obtained. One was conducted in a group of secondary school mathematics teachers from a western province of China on August 5, 2022, and the other was also conducted in a group of secondary school mathematics teachers on August 11, 2022, but these teachers came from an eastern province of China. The structure and several items were modified according to the results of the pilot studies. Then, the questionnaire items were considered by three professors and four other researchers for the assessment of content validity. The final version of the questionnaire was obtained after being revised due to suggestions for improvement.

All measurement items used a 5‑point Likert scale ranging from strongly disagree (1 point) to strongly agree (5 points). The 0-1 coding scheme was used for gender (male: 0, female: 1), major (non-mathematics: 0, mathematics: 1) and training on dynamic mathematics software (training_no: 0, training_yes: 1), and the 0-1-2 coding scheme was used for teaching experience (less than 5 years: 0; 6-15 years: 1; over 15 years: 2). The specific items are shown in Table 1. In addition, an open-ended question was set: Could you talk about the factors that influence secondary school mathematics teachers' usage behavior of dynamic mathematics software according to your experience?

3.2.   Data collection

The questionnaire was first shown onsite to a group of secondary school mathematics teachers from rural areas in the Hunan province of China using a 2-dimensional bar code created by the Wenjuanxing application (https://www.wjx.cn) on August 22, 2022. A total of 62 responses were collected. The instrument had a good reliability and validity according to the initial analysis. Then, the 2-dimensional bar code of the questionnaire was sent to many secondary school mathematics teachers by WeChat with the help of several leaders of master teachers' studios and leaders of teaching research groups in Hunan province. The questionnaire was anonymous, and the respondents didn't have to provide names and contact information. Data were collected using a convenient sampling technique. In the preface of the questionnaire, we announced that this study aimed to explore factors that may affect secondary school teachers' usage behavior of dynamic mathematics software. We also announced that this study was voluntary and would not have any negative influences on the respondents. All data that were collected were used only for this study.

A total of 393 secondary school mathematics teachers (128 males and 265 females) provided valid data. These teachers are distributed in 13 of 14 prefecture-level cities of Hunan, China. Most of them (244) come from the capital city, Changsha, of Hunan province. More than 90% of them are Han nationality. Over half (50%) of them have an intermediate professional title. There are 352 and 41 teachers with undergraduate and master's degrees, respectively. More than four fifths of the teachers graduated from a mathematics major, while less than one fifth of them graduated from a non-mathematics major. Most teachers have rich teaching experience; for example, 45% of them have taught for more than 15 years. A total of 227 and 166 teachers work in cities and villages, respectively. More than 85% of them were teaching in junior high school when the study was conducted. More than 70% of the teachers do not experience systematic training on dynamic mathematics software. About one third of the teachers do not know how to use any kind of dynamic mathematics software. Table 2 shows the demographics of the teachers in more detail. The average time for completing the questionnaire was 7 minutes, indicating that these teachers had a good attitude and took the questionnaire seriously.

3.3.   Data analysis

SPSS 26 and SmartPLS 4 were used to analyze the quantitative data. First, SPSS 26 was used for the preliminary analysis of the data. The specific steps are as follows: (1) data clearing; (2) using the Kolmogorov-Smirnov test ^[115] to examine the normality of each item of the instrument, where the results showed that all data were not normally distributed. It can be concluded that the evaluation of the conceptual model is not appropriate to use the covariance-based structural equation modeling (CB-SEM) approach ^[116] but should use the PLS-SEM approach ^[105,106]. This approach has limited restrictions on sample size and distributional assumptions, which is suitable for non-normal data and small sample size ^{[108,117,118,119,120]}. In addition, PLS-SEM is suitable for explanation and prediction, which are the objects of this study. Next, the conceptual model was assessed by using the SmartPLS 4 in two stages: (1) executing the PLS-SEM algorithm, Bootstrapping, and PLSpredict algorithm to obtain the results of the measurement model evaluation and structural model evaluation; (2) using the Bootstrap multigroup analysis to test whether teachers' gender, teaching experience, major and training have moderating effects on all path relationships in the conceptual model.

Since a reflective measurement model was used in this study, the evaluation of this model involves four aspects, namely, indicator reliability, internal consistency reliability, convergent validity and discriminant validity ^[106] (pp. 116-126). The specific methods are as follows: (1) evaluating the indicator reliability by calculating the outer loadings and the t value of each indicator; (2) evaluating the internal consistency reliability by calculating the values of Cronbach's Alpha ^[121], exact reliability coefficient (ρ_A) ^[122] and composite reliability (ρ_C) ^[123] of each construct; (3) evaluating the convergent validity by calculating the values of average variance extraction (AVE) ^[124] of each construct; (4) evaluating the discriminant validity by using the Fornell-Larcker criterion ^[124] and the Heterotrait-Monotrait (HTMT) ratio of correlations ^[125].

Henseler et al. ^[126] argued that the overall goodness of fit of the model should be considered as a starting point in the structural model evaluation, which is especially necessary when the measurement model is reflective. The standardized root mean square residual (SRMR) ^[127] and the normed fit index (NFI) ^[128] are commonly used to assess the suitability and robustness of the structural models ^[129]. Hair et al. ^[106] (pp. 187-205) argued that the structural model evaluation should focus on the model's capability to explain and predict one or more target constructs. The specific steps are as follows: (1) assessing the structural model for collinearity by examining the variance inflation factor (VIF) values of all sets of predictor constructs in the structural model; (2) assessing the significance and relevance of the structural model relationships by calculating the path coefficients (β), t values, p values, 95% confidence intervals and total effects; (3) assessing the model's explanatory power by calculating the coefficients of determination (R²) and the f² effect sizes; (4) assessing the model's predictive power by using the PLSpredict procedure ^[130].

The analysis of moderating effects of categorical variables can be implemented through several approaches ^[106] (pp. 287-290). Since the partial least squares structural equation modeling method does not rely on distribution assumptions, two non-parametric approaches, the PLS‑MGA ^[131], and the permutation test ^[132], are often used in research. Although the permutation test is recommended by Hair et al. ^[106] (pp. 289), the application of this approach may be influenced by highly unequal group-specific sample sizes, which is the fact in this study. Therefore, the PLS-MGA approach was used to implement multi-group analysis. This approach derives a probability value for a one-tailed test. If the one-tailed p value is less than 0.05, or larger than 0.95, the parameter values of two groups of data will have statistically significant differences, which means the moderating effect exists in this path relationship. For the situation that needs to compare a parameter across more than two groups, the omnibus test of group differences (OTG) ^[133] was often recommended. However, the OTG approach has not yet been included in SmartPLS4. Considering this fact, the moderating effect of teaching experience was analyzed by conducting three pairwise comparisons: over 15 years vs. 1-5 years, 6-15 years vs. 1-5 years and over 15 years vs. 6-15 years. The Bonferroni correction approach ^[134] was used to control for the familywise error rate. The significance level of 0.05/3≈0.017 instead of 0.05 was used. For a one-tailed test, if the p value is less than 0.017, or larger than 0.983, the parameter values of two groups of data will have statistically significant differences.

According to Hair et al. ^{[105,106,135]} and Henseler et al. ^[126], the reflective measurement model and structural model evaluation criteria for this study are presented in Table 3.

4.   Results

The results are divided into three parts. First, the reflective measurement model evaluation showed indicator reliability, internal consistency reliability, convergent validity and discriminant validity. Second, the structural model evaluation showed the overall goodness of fit of the model, the result of examining collinearity, the significance and relevance of the structural path relationships, the coefficients of determination (R²), the f² effect sizes and the PLSpredict results. Finally, the partial least squares multi-group analysis (PLS-MGA) showed the results of the moderating effect analysis of gender, teaching experience, major and training on all relationships in the secondary school teachers' dynamic mathematics software usage conceptual model.

4.1.   Measurement model evaluation

The evaluation of a reflective measurement model consists of four dimensions, namely, indicator reliability, internal consistency reliability, convergent validity and discriminant validity. The standardized outer loadings of all indicators were between 0.789 and 0.949, which were greater than the critical value of 0.708. The smallest t value of 28.729 was bigger than the critical value of 2.57, indicating that the outer loadings of all indicators were statistically significant at the 0.01 level. The values of Cronbach alpha of all constructs ranged from 0.838 to 0.935, and the values of the composite reliability (ρ_C) of all constructs were between 0.902 and 0.958, while those of the exact reliability coefficient (ρ_A) were between 0.842 and 0.935. Since Cronbach's alpha was too conservative, and the composite reliability (ρ_C) was too liberal, the exact reliability coefficient (ρ_A) was typically viewed as the constructs' true reliability ^[106] (pp. 119), and all were greater than the critical value of 0.7 and smaller than the value of 0.95. These showed the measurement model had a good indicator reliability and a high internal consistency reliability. The values of average variance extracted (AVE) of all constructs were between 0.686 and 0.885, which were larger than the critical value of 0.5. Therefore, the measurement model had a good convergent validity (Table 4).

The discriminant validity of the model was evaluated mainly based on the Fornell-Larcker criterion and the Heterotrait-Monotrait (HTMT) ratio of correlations. The Fornell-Larcker criterion requires that the square root of each construct's average variance extracted (AVE) should be greater than its highest correlation with any other construct. As shown in Table 5, the values of the square root of the AVE of each construct for the bold marked on the diagonal were greater than all other values in the same row and column. Namely, each of them was greater than the correlation between this construct and the other constructs, indicating that the measurement model had a good discriminant validity.

The Heterotrait-Monotrait (HTMT) ratio of correlations is defined as the ratio of the mean of all correlations of indicators across constructs measuring different constructs (i.e., the heterotrait-heteromethod correlations) relative to the geometric mean of the average correlations of indicators measuring the same construct (i.e., the monotrait-heteromethod correlations). In short, HTMT is the ratio of the between-trait correlations to the within-trait correlations ^[106] (pp. 122). In principle, the HTMT value should be less than 0.85. If there are similar constructs in the model, the corresponding HTMT value cannot exceed 0.9. As shown in Table 6, the biggest HTMT value was 0.808, which failed to exceed the critical value of 0.85. This further confirmed that the measurement model had undoubted discriminant validity.

4.2.   Structural model evaluation

The starting point of the structural model assessment is to examine the overall goodness of fit of the model in this study. The overall model had a good fit and robustness because the SRMR (standardized root mean square residual) value was 0.056 < 0.08, and the NFI (normed fit index) value was 0.835 > 0.8. As can be seen in Table 7, the VIF (variance inflation factor) values of all sets of predictor constructs in the structural model were clearly below the threshold of 3, which meant the structural model did not have a collinearity problem.

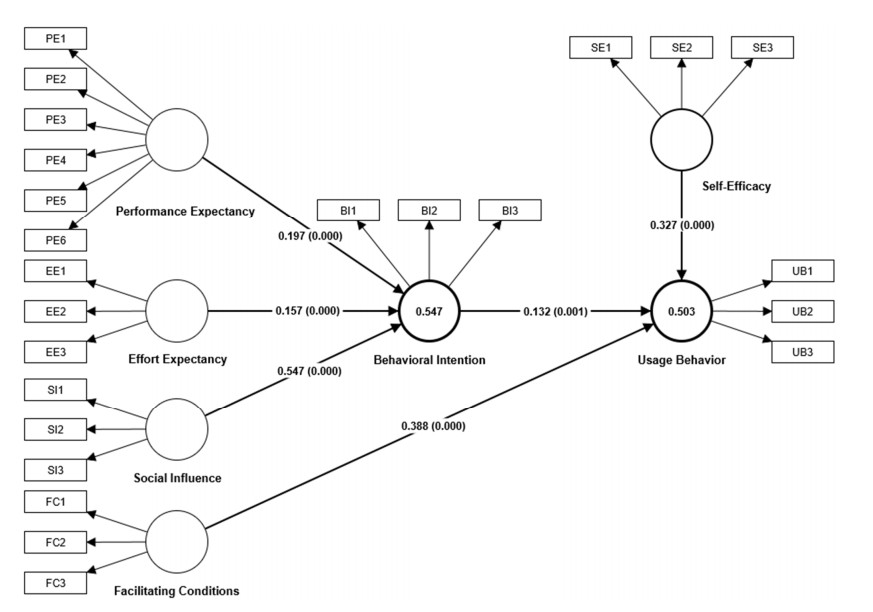
After using the Bootstrap technique with 5000 samples in SmartPLS4, the path coefficients, t values, p values, 95% confidence intervals and total effects were obtained, which indicated that all hypothesized path relationships were supported (Table 8). Specifically, social influence was the most important factor that affected secondary school mathematics teachers' behavioral intentions of dynamic mathematics software (β = 0.547, p < 0.001), followed by performance expectancy (β = 0.197, p < 0.001) and effort expectancy (β = 0.157, p < 0.001). Facilitating conditions greatly affected secondary school mathematics teachers' usage behavior of dynamic mathematics software (β = 0.388, p < 0.001), followed by self-efficacy (β = 0.327, p < 0.001) and behavioral intention (β = 0.132, p = 0.001). In addition, performance expectancy (β = 0.026, p = 0.017), effort expectancy (β = 0.021, p = 0.011), and social influence (β = 0.072, p = 0.001) significantly and indirectly affected secondary school mathematics teachers' usage behavior of dynamic mathematics software via behavioral intention. The significance testing results of the total effects are showed in Table 9.

The explanatory power of a model relates to its ability to fit the data at hand by quantifying the strength of association indicated by the PLS path model. The most commonly used measure to evaluate the structural model's explanatory power is the coefficient of determination (R²) value, which represents the amount of variance in the endogenous construct explained by all of the exogenous constructs linked to it ^[106] (pp. 195). The R² values of behavioral intention and usage behavior were 0.547 and 0.503, respectively, which means the model had a moderate explanatory power for these two endogenous constructs. The f² effect size expresses the change in the R² value when a specific predecessor construct is omitted from the model. As can be seen in Table 10, social influence (f² = 0.464) had a large effect size on behavioral intention, and performance expectancy (f² = 0.062) and effort expectancy (f² = 0.047) had small effect sizes on behavioral intention. Facilitating conditions (f² = 0.162) had a medium effect size on usage behavior, and self-efficacy (f² = 0.108) and behavioral intention (f² = 0.031) had small effect sizes on usage behavior.

According to Hair et al. ^[106] (pp. 196-205), the best approach for assessing the predictive power of a PLS path model is by means of Shmueli et al.'s ^[130] PLSpredict procedure. After running the PLSpredict algorithm with 10 folds and 10 repetitions in SmartPLS4, the Q_predict² values, the RMSE values of PLS-SEM analysis and the naïve linear regression model (LM) benchmark for all indicators of the endogenous constructs were obtained (Table 11). Since all indicators got negative values after calculating the differences of PLS-SEM_RMSE and LM_RMSE, the model had high predictive power.

The final model with R², path coefficients and p values is shown in Figure 2.

4.3.   Multi-group analysis

Multigroup analysis allows testing whether differences between group-specific path coefficients are statistically significant. This study used a nonparametric multigroup analysis approach, the partial least squares multi‑group analysis (PLS‑MGA), to examine whether gender, teaching experience, major and training can moderate the path relationships in the secondary school teachers' dynamic mathematics software usage conceptual model. An outline of the steps is given here: (1) generating data groups, (2) evaluating categorical moderator variable by Bootstrap multiple group analysis procedure, and (3) analyzing different groups' path coefficients (β) and p values.

In turn, the groups of gender (female vs. male), teaching experience 1 (over 15 years vs. 1-5 years), teaching experience 2 (6-15 years vs. 1-5 years), teaching experience 3 (over 15 years vs. 6-15 years), major (mathematics vs. non-mathematics) and training (training_yes vs. training_no) were set up, and the results of the analysis of moderating effects were obtained by a Bootstrap multiple group analysis procedure (Tables 12-17). The results suggested that gender and teaching experience did not have moderating effects on all path relationships in the conceptual model. This means that the hypotheses H7 and H8 were rejected.

However, different types of majors of secondary school mathematics teachers had a moderating effect on "H5: self-efficacy (SE)→usage behavior (UB)" (Δβ = 0.461, p = 0.001). Specifically, self-efficacy had a positive direct effect on the dynamic mathematics software's usage behavior of secondary school mathematics teachers who graduated from a mathematics major (β = 0.406, p < 0.001), while it had no direct effect for those who graduated from a non-mathematics major (β = -0.055, p = 0.727) (Table 16). Therefore, it could be noted that self-efficacy may lead to the active use of dynamic mathematics software, and the effect of self-efficacy is more salient for teachers who graduated from a mathematics major.

There was also a moderating effect of major on "H6: behavioral intention (BI)→usage behavior (UB)" (Δβ = -0.326, p = 0.999). There was no direct effect of behavioral intention on the usage behavior of dynamic mathematics software of secondary school mathematics teachers who graduated from a mathematics major (β = 0.066, p = 0.089), while there was a positive direct effect for those who graduated from a non-mathematics major (β = 0.392, p < 0.001) (Table 16). Therefore, it could be noted that teachers who graduated from a non-mathematics major were more influenced by behavioral intention to usage behavior.

In addition, there was a moderating effect of training on "H3: social influence (SI)→behavioral intention (BI)" (Δβ = -0.184, p = 0.959). Specifically, social influence had a positive direct effect on behavioral intention of secondary school mathematics teachers who have been trained for using dynamic mathematics software (β = 0.406, p < 0.001). Meanwhile, social influence had a larger positive direct effect on behavioral intention of those who did not get a chance for training (β = 0.589, p < 0.001) (Table 17). Therefore, teachers who have not been trained were more influenced by social influence to behavioral intention.

5.   Discussion

Dynamic mathematics software, such as GeoGebra, is a kind of subject-specific digital tool used for enabling users to create mathematical objects and operate them dynamically and interactively. Using dynamic mathematics software to teach and learn can be highly effective for a lot of content of mathematics at the secondary school level. Although this kind of software has been used to teach by many secondary school mathematics teachers, and some researchers have paid attention to its application, few researchers have explored the factors influencing secondary school teachers' usage behavior of dynamic mathematics software. This study performed this task by using a PLS-SEM method. This study proposed a conceptual model to explore the factors influencing secondary school teachers' usage behavior of dynamic mathematics software, which was generated by adding self-efficacy to the original UTAUT model. The results of the measurement model evaluation and structural model evaluation showed that this conceptual model was very plausible. The path relationships in the empirical model remained consistent with the conceptual model.

The results of the quantitative analysis indicated that performance expectancy (β = 0.197, p < 0.001) and effort expectancy (β = 0.157, p < 0.001) significantly affected secondary school teachers' behavioral intentions of dynamic mathematics software. Previous studies showed that these two variables affected the desire and willingness to use new technology ^[75,86]. Therefore, if secondary school teachers can perceive the usefulness and master the basic functions of dynamic mathematics software, they may have intentions to use it in their classroom. Even so, these two independent variables were not the most important factors. Instead, social influence had the greatest impact on secondary school mathematics teachers' behavioral intentions of dynamic mathematics software (β = 0.547, p < 0.001), which was consistent with the findings of some previous studies. Lai ^[88] used a structural equation modeling method based on the UTAUT model and found that performance expectancy, social influence and facilitating conditions positively and significantly affected older adults' intention to use mobile devices, and that social influence was the most significant factor. In a study exploring teachers' acceptance and use of interactive whiteboards, social influence was found to be the greatest predictor of behavioral intention ^[89]. It indicated that teachers' behavioral intentions to adopt a new technological tool for teaching and learning was largely influenced by the school climate and surrounding people.

Facilitating conditions strongly influenced secondary school mathematics teachers' usage behavior of dynamic mathematics software (β = 0.388, p < 0.001). Some research had shown that facilitating conditions were truly important factors influencing teachers' adoption and use of information technology ^[90,91]. This finding was completely aligned with our previous study ^[27], which found that facilitating conditions were the biggest factor influencing elementary school teachers' usage behavior of dynamic mathematics software. Therefore, a good technology environment is important, and appropriate curriculum resources and expert teachers' support are also very important for using dynamic mathematics software.

Self-efficacy also played an important role in determining secondary school mathematics teachers' usage behavior of dynamic mathematics software (β = 0.327, p < 0.001). Self-efficacy had a direct positive effect on the usage behavior in this study, which meant that high levels of self-efficacy may enhance teachers' usage behavior of dynamic mathematical software. This finding confirmed the outcomes of previous similar studies ^[79]. It suggested that when secondary school mathematics teachers have sufficient self-efficacy in using dynamic mathematics software during their pedagogical activities, they may actually use it.

It is worth noticing that the strength of the relationship between behavioral intention and usage behavior of dynamic mathematics software, although statistically significant (β = 0.132, p = 0.001), was the weakest path relationship in this model. It was very different from the findings of Wijaya et al.'s study ^[86] on micro-lecture, in which the path coefficient from behavioral intention to usage behavior was the largest one. The possible reason may be because dynamic mathematics software is a kind of subject-specific teaching software. More than 70% of secondary school mathematics teachers in this study claimed that they had not learned dynamic mathematics software systematically, and one third of the teachers declared that they were unfamiliar with any kind of dynamic mathematics software. Under this situation, even if these secondary school mathematics teachers are willing to use dynamic mathematics software, it is difficult for them to produce actual usage behavior.

By using the NVivo software, this study created a word cloud based on the open-ended question in the instrument. It was found that the most important influencing factors mentioned by secondary school mathematics teachers were the lack of hardware facilities and poor personal computer skills, which meant they felt a lack of facilitating conditions and self-efficacy. It further confirmed the results of the quantitative analysis.

In addition to the analysis of the path relationships between the independent variables and dependent variables, this study also analyzed how individual differences among teachers affect the relationships between the variables. It has been identified in some studies, such as Jang et al.'s study ^[97] on elementary school teachers' using interactive whiteboards, that gender may moderate the path relationships in the model. For a teacher, the years of teaching are more important than the age when we talk about his/her teaching. Therefore, teaching experience was used as the moderating variable instead of age. At the same time, systematic training on dynamic mathematics software is a very important experience in professional development, which may influence teachers' behavioral intentions and usage behavior. Since most teachers who graduated from a mathematics major may have an opportunity to learn a course of technologies in mathematics education, and those who graduated from a non-mathematics major may not have this opportunity, the major was also used as a moderating variable in this study. The results of the multi-group analysis on the teachers' gender and teaching experience revealed that none of these variables was able to moderate the path relationships between the independent variables and dependent variables. However, the major will moderate the path relationship between self-efficacy and usage behavior, and between behavioral intention and usage behavior. The training will also moderate the path relationship between social influence and behavioral intention. Our findings may shed some light on the fact that teachers who graduated from a mathematics major do have an advantage in the acceptance and use of dynamic mathematics software. The teachers who got training on dynamic mathematics software may not be too ready to change their intentions by other peoples' opinions. Therefore, it is necessary to make sure all pre-service mathematics teachers have opportunities to learn how to use dynamic mathematics software (such as GeoGebra).

6.   Implications

6.1.   Theoretical implications

Based on the original UTAUT model, this study developed a conceptual model by adding a self-efficacy construct. First, the model distinguished three independent variables (namely, performance expectancy, effort expectancy and social influence) that can significantly influence behavioral intention, as well as two independent variables (namely, facilitating conditions and self-efficacy) that can significantly influence usage behavior, and the behavioral intention can significantly influence secondary school teachers' usage behavior of dynamic mathematics software. This is the first quantitative study on the factors influencing secondary school teachers' usage behavior of dynamic mathematics software, and the conceptual model has more than 50% explanatory power for both behavioral intention and usage behavior, which means it is a good theoretical model. Second, the PLS-SEM method was proven to be valid to explore the influential factors of secondary school teachers' usage behavior of dynamic mathematics software, which is different from the method used by previous studies, for example, the pretest-posttest design method. Finally, this conceptual model can be applied to explore the influential factors of the behavioral intention or usage behavior of other digital technologies at K-12 school levels.

6.2.   Practical implications

This study showed that the factors influencing secondary school mathematics teachers' behavioral intentions of dynamic mathematics software were social influence, performance expectancy and effort expectancy, from the largest to the smallest, and the factors influencing the usage behavior were facilitating conditions, self-efficacy and behavioral intention. Among them, social influence, facilitating conditions and self-efficacy deserved our special attention.

The implications to improve secondary school mathematics teachers' behavioral intentions and usage behavior of dynamic mathematics software consist of the following: (1) offering a course based on dynamic mathematics software during pre-service or in-service teacher training, which can improve teachers' self-efficacy, performance expectancy and effort expectancy; (2) providing good hardware and software facilities for using dynamic mathematics software at secondary schools, which can improve facilitating conditions; (3) creating an atmosphere to encourage teachers to use dynamic mathematics software, for example, organizing various forms of competition activities, which can improve social influence; (4) developing some curriculum resources related to dynamic mathematics software; and (5) fostering some master teachers who are good at using dynamic mathematics software, which can also improve facilitating conditions for teachers to use dynamic mathematics software.

7.   Conclusions

By using the PLS-SEM method, this study analyzed the factors influencing secondary school mathematics teachers' usage behavior of dynamic mathematics software based on an extended UTAUT model. It was found that social influence, performance expectancy and effort expectancy significantly and positively affected secondary school mathematics teachers' behavioral intentions of dynamic mathematics software, and social influence was the greatest influential factor. In addition, facilitating conditions, self-efficacy and behavioral intention had significant and positive effects on secondary school mathematics teachers' usage behavior of dynamic mathematics software, and facilitating conditions were the greatest influential factors. There were no significant moderating effects of gender and teaching experience on all relationships in the dynamic mathematics software usage conceptual model, while major had a moderating effect on the relationship between self-efficacy and usage behavior, as well as the relationship between behavioral intention and usage behavior. Training also had a moderating effect on the relationship between social influence and behavioral intention. This study aimed at figuring out the important factors that need to be observed for the adoption of dynamic mathematics software at the secondary school level, which benefits the government, schools, and universities in enhancing teachers' digital teaching competencies. In order to improve secondary school mathematics teachers' usage behavior of dynamic mathematics software, the government should provide sufficient funds to make sure the schools have appropriate hardware and software facilities. The schools should develop more curriculum resources related to dynamic mathematics software, and the universities should provide appropriate courses to help pre-service and in-service mathematics teachers to grasp dynamic mathematics software.

8.   Limitations and future research

This study had several limitations that needed to be considered with caution. First, it used a non-random sample. Although the sample covered almost all prefecture-level cities of Hunan, China, most of them came from the capital city of this province. The regional and cultural characteristics may also have significant differences. Therefore, another examination is needed to confirm the results of this study. Second, the predictor constructs in this study can only explain the variance of the usage behavior construct up to 50.3%, indicating that some other factors still affect secondary school mathematics teachers' usage behavior of dynamic mathematics software. Thus, further study may need to include other factors, such as technological pedagogical content knowledge (TPACK), or engagement. Finally, some qualitative methods like in-depth interviews should be included in future research.

Use of AI tools declaration

The authors declare they have not used artificial intelligence (AI) tools in the creation of this article.

Acknowledgments

This study was funded by the Young Scholar Fund of Humanities & Social Science of Chinese Ministry of Education, grant number 18YJC880115. The authors extend their thanks to all secondary school mathematics teachers in the Hunan province of China who supported this study.

Conflict of interest

The authors declare there is no conflict of interest.