Histologic and histomorphometric evaluation of minicono abutment on implant surrounding tissue healing and bone resorption on implants placed in healed bone. An experimental study in dogs

1.   Introduction

Graph plays a dynamic role in various sciences such as physics, biology, chemistry, and computer science ^[2,3,4,5,8]. It is used in various frameworks related to social and information systems ^[4] and also solves many issues related to everyday life. In physics, there are various circuits constructed by considering different graphs ^[5]. The atomic number of many molecules is evaluated by using group symmetry graphs that are still unknown a few years ago ^[3]. In computer science, many problems have been discussed using graphs that were not easy to visualize earlier. For discrete mathematics and combinatorics, the applications of number theory and graph theory are of crucial importance. In this work, we employ number theory to investigate the special classes of graphs.

Rogers ^[18] discussed the action of a quadratic map on multiplicative groups under modulo a prime $p$ by using the associated directed graph for which there is an edge from each element to its image. He established a formula to decompose a graph into cyclic components with their attached trees. The necessary and sufficient conditions for the existence of isolated fixed points have also been established. Somer and Krizek ^[19] studied the structures of graphs of quadratic congruences for composite modulus. Mahmood and Ahmad ^[10,11] proposed many new results of graphs over residues modulo prime powers. Haris and Khalid ^{[12,13,14,15]} investigated the structure of power digraphs associated with the congruence $x^{n}\equiv y\; (mod\; m)$. Meemark and Wiroonsri ^[9] discussed the structure of $G(R, k)$ using a quadratic map, where $R$ is the quotient ring of polynomials over finite fields and $k$ is the modulus. Wei and Tang ^[20] introduced the concept of square mapping graphs of the Gaussian ring $Z_{m}[i]$. Ali et al. ^[21,22] introduced new labeling algorithm on various classes of graphs with applications. Some basic and useful result discussed in ^{[1,6,7,16,23,24]} as well.

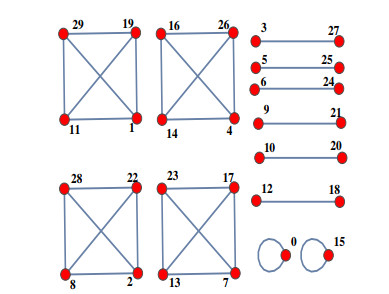
Let $p$ be a prime and $a$ an integer coprime to $p$. Then $a$ is called a quadratic residue $\; (\text{mod}\; p)$ if and only if the congruence $x^{2}\equiv a\; (\text{mod}\; p)$ has a solution. Otherwise, $a$ is called quadratic non-residue $\; (\text{mod}\; p)$. Two non-zero integers $x$ and $y$ are called zero divisors in the ring $Z_{m}$ if and only if $xy\equiv 0\; (\text{mod}\; m)$ ^[17]. Recall that a graph $\overbrace{G}(2, m)$, whose vertices are elements of ring $Z_{m}$ and there will be an edge between $\overline{x}$ and $\overline{y}$ $(\overline{x}\neq \overline{y})$ if $\overline{x}^{2}\equiv \overline{y}^{2}\; (\text{mod}\; m)$ then, $\overbrace{G}(2, m)$ is termed as a quadratic graph. For $m = 30$ vertex set is

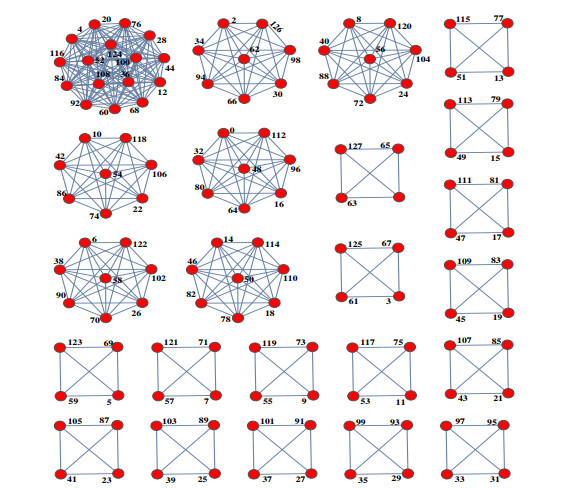
$Z_{n} = \{\overline{0}, \overline{1}, \overline{2}, \overline{3}, \overline{4}, \overline{5}, \overline{ 6}, \overline{7}, \overline{8}, \overline{9}, \overline{10}, \overline{11}, \overline{12}, \overline{13}, \overline{14}, \overline{15}, \overline{16}, \overline{17}, \overline{18}, \overline{19}, \overline{20}, \overline{ 21}, \overline{22}, \overline{23}, \overline{24}, \overline{25}, \overline{26}, \overline{27},$ $\overline{28}, \overline{29} \}$, by solving the congruences $\overline{x}^{2}\equiv \overline{y}^{2}\; (\text{mod}\; 30)$ for each $\overline{x},$ $\overline{y}\in Z_{n}$ then, there are 2, 4, 6 copies of $K_{1}$, $K_{4}$ and $K_{2}$, respectively as shown in Figure 1. We note that each copy of $K_{2}$ and $K_{4}$ has equal sum 30 and 60, respectively. Here $K_{n}$ is a complete graph obtained if each node connected with every other node except itself ^[4].

Theorem 1.1. ^[17] Let $p$ be an odd prime, $k$ be a positive integer, and $a$ an integer such that $(a, p) = 1$. Then

1. The congruence $x^{2}\equiv a\; ({mod}\; p^{k})$ has either no solution or exactly two incongruent solutions modulo $p^{k}.$

2. The congruence $x^{2}\equiv a\; ({mod}\; p^{k})$ has no solution if $a$ is quadratic non-residue of $p$ and exactly two incongruent solutions modulo $p$ if $a$ is quadratic residue of $p$.

Theorem 1.2. ^[17] Let $a$ be an odd number. Then we have the following:

1. The congruence equation $x^{2}\equiv a\; ({mod}\; 2)$ has the unique solution if and only if $x\equiv 1 \; ({mod}\; 2).$

2. The congruence equation $x^{2}\equiv a \; ({mod}\; 4)$ either has no solution if $a\equiv 3\; \; {mod}\; 4)$ or has two solutions $x \equiv 1, 3 \; \; ({mod}\; 4)$ if $a\equiv 1 \; ({mod}\; 4)$.

3. When $k\geq 3,$ the equation $x^{2}\equiv a \; ({mod}\; 2^{k})$ either has no solution if $a\not\equiv 1\; ({mod}\; 8)$; or has four solutions $x_{1}, -x_{1}, x_{1}+2^{k-1}, -(x_{1}+2^{k-1})$ if $a \equiv 1 \; ({mod}\; 8)$.

2.   Quadratic residues graphs over $Z_{2^{\beta}}$ and $Z_{q^{\beta}}$

In this section, we characterize quadratic residue graphs for some well-known classes of integers $2^{\beta}$ and $q^{\beta},$ for each positive integer $\beta$ and odd prime $q$.

Theorem 2.1. Let $m = 2^{\beta}$ be an integer. Then

Proof. We discuss two cases to prove this theorem, the zero-divisors and unit elements of the ring $Z_{m}$. Firstly, we discuss zero-divisors, let $S = \{2m | m = 0, 1, 2, \cdots, 2^{\beta-1}~~-1\}$ be the set of all zero-divisors of $Z_{2^{\beta}}$ with including zero for each positive integer $\beta$. To find the number of solutions of $\eta^{2}\equiv \beta^{2}\; (\text{mod} \; 2^{\beta})$, we start from $\eta^{2}\equiv \beta^{2}\; (\text{mod} \; 2)$, in this case just $S = \{0\}$. Therefore, $\eta^{2}\equiv 0\; (\text{mod} \; 2)$ has only one solution which is zero, but by the definition of quadratic zero-divisors graph there will be a no loop, so $\overbrace{G}(2, 2) = K_{1}$. For $\beta = 2$, $\eta^{2}\equiv 0\equiv2^{2}\; (\text{mod} \; 2^{2})$ has two solution namely $\eta = 0, 2$, then $\overbrace{G}(2, 2^{2}) = K_{2}$. If $\beta = 3$, then there are two congruences

The roots of these congruences are $\eta = 0, 4$, and $\eta = 2, 6,$ respectively. Thus, there exist two copies of $K_{2}$. For $\beta = 4$, we have

The corresponding roots of congruence are $\{0, 4, 8, 12\}$ and $\{2, 6, 10, 14\},$ respectively. Therefore, $\overbrace{G}(2, 2^{4}) = 2K_{4}$. There are three congruences for $\beta = 5$

The solution sets of these congruences are $\{0, 8, 16, 24\}$, $\{2, 6, 10, 14, 18, 22, 26, 30\}$, and $\{4, 12, 20, 28\},$ respectively. Therefore, there are two copies of $K_{4}$ and one copy of $K_{8}$. For $\beta = 6$, we have

The zeros of these congruences are $\{0, 8, 16, 24, 32, 40, 48, 54\}$, $\{2, 18, 34, 50\}\bigcup\{ 62, 46, 30, 14\},$ $\{4, 12, 20, 28, 36, 44, 52, 60\}$, and $\{6, 22, 38, 54\}\bigcup\{ 58, 42, 26, 10\},$ respectively. For $\beta = 7$, there are 7 different congruences. We have

Roots of these congruences are $\{ 2t+16m | m = 0, 1, 2\cdots 2^{3}-1\}$, $\{ 2t+32m | m = 0, 1, 2\cdots 2^{2}-1\}\bigcup\{ 2^{7}-32m-2t| m = 0, 1, 2\cdots 2^{2}-1\}$, $t = 1, 3, 4, 5, 7$, $\{ 4+8m | m = 0, 1, 2\cdots 2^{4}-1\}$. Hence, there are six copies of $K_{8}$ and one copy of $K_{16}$. For $\beta = 8$, there are 12 congruences. We have

Zeroes of these congruences are $\{ 2+4t+64m | m = 0, 1, 2\cdots 2^{2}-1\}\bigcup\{ 2^{8}-64m-4t-2| m = 0, 1, 2\cdots 2^{2}-1\}$, $t = 0, 1, \cdots, 2^{3}-1$, $\{ 4t+32m | m = 0, 1, 2\cdots 2^{4}-1\}$, $\{4t+32m | m = 0, 1, 2\cdots 2^{3}-1\}\bigcup\{ 2^{8}-32m-4t| m = 0, 1, 2\cdots 2^{3}-1\}$, $t = 1, \cdots, 2^{2}-1$. Thus, we have $\overbrace{G}(2, 2^{8}) = 8K_{4}\bigoplus4K_{16}$. For $\beta = 9$, there are 23 different congruences. We have

Solutions of congruences (2.5)$-$(2.7) are $\{ 2+4t+128m | m = 0, 1, 2\cdots 2^{2}-1\}\bigcup\{ 2^{9}-128m-4t-2| m = 0, 1, 2\cdots 2^{2}-1\}$, $t = 0, 1, \cdots, 2^{6}-1$, $\{ 4t+32m | m = 0, 1, 2\cdots 2^{4}-1\}$, $\{ 4t+64m | m = 0, 1, 2\cdots 2^{3}-1\}\bigcup\{ 2^{9}-64m-4t| m = 0, 1, 2\cdots 2^{3}-1\}$, $t = 1, 3, 4, 5, 7$, $\{ 8+16m | m = 0, 1, 2\cdots 2^{5}-1\}$. That is, $\overbrace{G}(2, 2^{9}) = 16K_{8}\bigoplus 6K_{16}\bigoplus K_{32}$. For $\beta = 10$, there are 44 different congruences. We have

Sequences of roots of congruences (2.8)$-$(2.10) are $\{ 2+4t+256m | m = 0, 1, 2\cdots 2^{2}-1\}\bigcup\{ 2^{10}-256m-4t-2| m = 0, 1, 2\cdots 2^{2}-1\}$ $t = 0, 1, \cdots, 2^{5}-1$, $\{ 4+8t+128m | m = 0, 1, 2\cdots 2^{3}-1\}\bigcup\{ 2^{10}-128n-8t-4| m = 0, 1, 2\cdots 2^{3}-1\}$, $t = 0, 1, \cdots, 2^{3}-1$, $\{ 8t+64m | m = 0, 1, 2\cdots 2^{5}-1\}$, $\{ 8t+64m | m = 0, 1, 2\cdots 2^{4}-1\}\bigcup\{ 2^{10}-64m-8t| m = 0, 1, 2\cdots 2^{4}-1\}$, $t = 1, \cdots, 2^{2}-1$. That is, $\overbrace{G}(2, 2^{10}) = 32K_{8}\bigoplus 8K_{16}\bigoplus 4K_{32}$. For $\beta = 11$,

Zeroes of congruences (2.11)$-$(2.14) are $\{ 2+4t+512m | m = 0, 1, 2\cdots 2^{2}-1\}\bigcup\{ 2^{11}-512m-4t-2| m = 0, 1, 2\cdots 2^{2}-1\}$, $t = 0, 1, \cdots, 2^{6}-1$, $\{ 4+8t+256m | m = 0, 1, 2\cdots 2^{3}-1\}\bigcup\{ 2^{11}-256m-8t-4| m = 0, 1, 2\cdots 2^{3}-1\}$, $t = 0, 1, \cdots, 2^{4}-1$, $\{ 8t+64m | m = 0, 1, 2\cdots 2^{5}-1\}$, $\{ 8t+128m | m = 0, 1, 2\cdots 2^{4}-1\}\bigcup\{ 2^{11}-128m-8t| m = 0, 1, 2\cdots 2^{4}-1\}$, $t = 1, 3, 4, 5, 7$, $\{ 16+32m | m = 0, 1, 2\cdots 2^{6}-1\}$.

Therefore, we have $\overbrace{G}(2, 2^{11}) = 64K_{8}\bigoplus 16K_{16}\bigoplus 6K_{32}\bigoplus K_{64}$. For $\beta = 12$, there are 172 congruences. We have

Sets of roots of congruences (2.15)$-$(2.18) are $\{ 2+4t+1024m | m = 0, 1, 2\cdots 2^{2}-1\}\bigcup\{ 2^{12}-1024m-4t-2| m = 0, 1, 2\cdots 2^{2}-1\}$, $t = 0, 1, \cdots, 2^{7}-1$, $\{ 4+8t+512m | m = 0, 1, 2\cdots 2^{3}-1\}\bigcup\{ 2^{12}-512m-8t-4| m = 0, 1, 2\cdots 2^{3}-1\}$, $t = 0, 1, \cdots, 2^{5}-1$, $\{ 8t+256m | m = 0, 1, 2\cdots 2^{4}-1\}\bigcup\{ 2^{12}-256m-8t| m = 0, 1, 2\cdots 2^{4}-1\}$, $t = 0, 1, \cdots, 2^{3}-1$, $\{ 16t+128m | m = 0, 1, 2\cdots 2^{6}-1\}$, $\{ 16t+128m | m = 0, 1, 2\cdots 2^{5}-1\}\bigcup\{ 2^{12}-128m-8t| m = 0, 1, 2\cdots 2^{5}-1\}$, $t = 1, \cdots, 2^{2}-1$. That is, $\overbrace{G}(2, 2^{12}) = 128K_{8}\bigoplus 32K_{16}\bigoplus 8K_{32}\bigoplus 4K_{64}$.

The generalize sequence for $\beta \geq 9,$ where $\beta$ is an odd number, there are $\frac{2^{4}(2^{\beta-7}-1)+21}{3}$ number of congruences. we have

Sequences of roots of congruences (2.19)$-$(2.21) are $\{ 2^{i}+2^{i+1}t+2^{\beta-i-1}m | m = 0, 1, 2\cdots 2^{i+1}-1\}\bigcup\{ 2^{\beta} -2^{\beta-i-1}m-2^{i+1}t-2^{i}| m = 0, 1, 2\cdots 2^{i+1}-1\}$, $t = 0, 1, \cdots, 2^{\beta-2i-3}-1$, $i = 1, 2, 3, \cdots, \frac{\beta-7}{2}$, $\{ 2^{\frac{\beta-5}{2}}t+2^{\frac{\beta+1}{2}}m | m = 0, 1, 2, \cdots 2^{\frac{\beta-1}{2}}-1\},$ $\{ 2^{\frac{\beta-5}{2}}t+2^{\frac{\beta+3}{2}}m | m = 0, 1, 2, \cdots 2^{\frac{\beta-3}{2}}-1\} \bigcup\{ 2^{\beta}-2^{\frac{\beta+3}{2}}m-2^{\frac{\beta-5}{2}}k| m = 0, 1, 2, \cdots 2^{\frac{\beta-3}{2}}-1\}$, $t = 1, 3, 4, 5, 7$, $\{2^{\frac{\beta-3}{2}}+2^{\frac{\beta-1}{2}}m | m = 0, 1, 2\cdots 2^{\frac{\beta+1}{2}}-1\}$. That is, $\overbrace{G}(2, 2^{\beta}) = \bigoplus\limits_{i = 1}^{\frac{\beta -7}{2}}2^{\beta-5-2(i-1)}K_{2^{3+(i-1)}} ~~~\bigoplus 6K_{2^{(\beta-1)/2}}~~ \bigoplus K_{2^{(\beta+1)/2}}$.

For second case when $\beta$ is an even number and $\beta\ge10$, we have $\frac{2^{5}(2^{\beta-8}-1)+36}{3}$ congruences as follows

Sequences of zeroes of congruences (2.22)$-$(2.23) are $\{ 2^{i}+2^{i+1}t+2^{\beta-i-1}m | m = 0, 1, 2\cdots 2^{i+1}-1\}\bigcup\{ 2^{\beta}-2^{\beta-i-1}m-2^{i+1}t-2^{i}| m = 0, 1, 2\cdots 2^{i+1}-1\}$, $t = 0, 1, \cdots, 2^{\beta-2i-3}-1$, $i = 1, 2, 3, \cdots, \frac{\beta-6}{2}$, $\{ 2^{\frac{\beta-4}{2}}t+2^{\frac{\beta+2}{2}}m | m = 0, 1, 2\cdots, 2^{\frac{\beta}{2}}-1\}$, $\{ 2^{\frac{\beta-4}{2}}t+2^{\frac{\beta+2}{2}}m | m = 0, 1, 2\cdots, 2^{\frac{\beta-2}{2}}-1\} \bigcup\{ 2^{\beta}-2^{\frac{\beta+2}{2}}m-2^{\frac{\beta-4}{2}}t| m = 0, 1, 2^{\frac{\beta-2}{2}}-1\}$, $t = 1, \cdots, 2^{2}-1$.

Thus, $\overbrace{G}(2, 2^{\beta}) = \bigoplus\limits_{i = 1}^{\frac{\beta -6}{2}}2^{\beta-2i-3}K_{2^{2+i}} \bigoplus 2^{2}K_{2^{\beta/2}}$.

Now, we discuss the unit elements of $Z_{m}.$ For $m = 2, 4$, the result is straightforward. For $\beta\ge3$, the graph $\overbrace{G}(2, m)$ contains $\phi(2^{\beta}) = 2^{\beta-1}~~$ number of vertices. We calculate the least positive residues of the square of the integers, which are smaller than and relatively prime with $m.$ Hence, there are $\phi(2^{\beta}) = 2^{\beta-1}~~$ obtained. By Theorem 1.2, the congruence $x^{2}\equiv a \; (\text{mod}\; 2^{\beta})$ has either no solution or exactly four incongruent solutions. This implies that, there are always $\frac{\phi(m)}{4} = \frac{\phi(2^{\beta-1}~~)}{4} = 2^{\beta-3}$ quadratic residues among all the vertices. Thus $\overbrace{G}(2, m) = 2^{\beta-3}K_{4}$. By combining both cases, we get the desired result. The quadratic residues graph for $n = 128$ is shown in Figure 2.

Theorem 2.2. Let $q$ be an odd prime. Then $\overbrace{G}(2, q^{\beta})$

Proof. To prove this theorem first we assume zero-divisors of the ring $Z_{m}$. Let $q$ is an odd prime and $S = \{ tq^{\beta} | t = 0, 1, 2, \cdots, q^{\beta-1}~~-1 \}$ be zero-divisors including zero of $q^{\beta}$ for each positive integer $\beta$. To solve congruence $\eta^{2}\equiv \beta^{2} \; (\text{mod}\; q^{\beta})$ for each $\beta\geq1$, we start with $\eta^{2}\equiv \beta^{2} \; (\text{mod}\; q)$. In this case, $0$ is only root of this congruence, but there is no edge between two vertices when they are same, so $\overbrace{G}(2, q) = K_{1}$. For $\beta = 2$, there is only one congruence namely $\eta^{2}\equiv 0 \; (\text{mod}\; q^{2})$, roots of this congruence are $\eta = 0, q, 2q, \cdots, (q-1)q$. There are $q$ solutions and will be complete graph of order $q$. For $\beta = 3,$ there are $\frac{q+1}{2}$ congruences. We have

Zeros of these congruences are $\{\eta = q^{2}(m-1) | m = 1, 2, \cdots, q \}$, and $\{\eta = q^{2}(m-1)+qt |\; t = 1, 2, \cdots, \frac{q-1}{2}, \; \; m = 1, 2, \cdots, q \}$$\bigcup \{\eta = q^{3}-q^{2}(m-1)-qt |\; t = 1, 2, \cdots, \frac{q-1}{2}, \; \; m = 1, 2, \cdots, q \},$ respectively. For $\beta = 4$, the number of distinct congruences is $(q^{2} - q + 1)/2.$ These are

Sequences of roots of these congruences are $\{\eta = q^{2}(m-1) | m = 1, 2, \cdots, q^{2} \}$, and $\{\eta = q^{3}(m-1)+qt |\; t = 1, 2, \cdots, \frac{q^{2}-1}{2}, {\rm\; but\; } t\neq ql, \; \; l = 1, 2, \cdots, \frac{q-1}{2}, \; \; m = 1, 2, \cdots, q \}$$\bigcup \{\eta = q^{4}-q^{3}(-1)-pt |\; t = 1, 2, \cdots, \frac{p^{2}-1}{2}, {\rm\; but\; } t\neq pl, \; \; l = 1, 2, \cdots, \frac{q-1}{2}, \; \; m = 1, 2, \cdots, q \},$ respectively.

For $\beta = 5$, we have

Zeroes of these congruences are $\{\eta = q^{3}(m-1) | m = 1, 2, \cdots, q^{2} \}$, $\{\eta = q^{3}(m-1)+q^{2}t |\; t = 1, 2, \cdots, \frac{q-1}{2}, \; \; m = 1, 2, \cdots, q^{2} \}$$\bigcup \{\eta = q^{5}-q^{3}(m-1)-q^{2}t |\; t = 1, 2, \cdots, \frac{q-1}{2}, \; \; m = 1, 2, \cdots, q^{2} \}$, and $\{\eta = q^{4}(m-1)+qt |\; t = 1, 2, \cdots, \frac{q^{3}-1}{2}, {\rm\; but\; } t\neq ql, \; \; l = 1, 2, \cdots, \frac{q^{2}-1}{2}, \; \; m = 1, 2, \cdots, q \}$$\bigcup \{\eta = q^{5}-q^{4}(m-1)-qt |\; t = 1, 2, \cdots, \frac{q^{3}-1}{2}, {\rm\; but\; } t\neq ql, \; \; l = 1, 2, \cdots, \frac{q^{2}-1}{2}, \; \; m = 1, 2, \cdots, q \},$ respectively.

If $\beta = 6$, then we have

Sequences of roots of congruences (2.31)$-$(2.33) are $\{\eta = q^{3}(m-1) | m = 1, 2, \cdots, q^{3} \}$, $\{\eta = q^{4}(m-1)+q^{2}t |\; t = 1, 2, \cdots, \frac{q^{2}-1}{2}, \; {\rm\; but\; } t\neq ql, \; \; l = 1, 2, \cdots, \frac{q-1}{2}, \; \; m = 1, 2, \cdots, q^{2} \}$$\bigcup \{\eta = q^{6}-q^{3}(m-1)-q^{2}t |\; t = 1, 2, \cdots, \frac{q^{2}-1}{2}, \; {\rm\; but\; } t\neq ql, \; \; l = 1, 2, \cdots, \frac{q-1}{2}, \; \; m = 1, 2, \cdots, q^{2} \}$, and $\{\eta = q^{5}(m-1)+qt |\; t = 1, 2, \cdots, \frac{q^{4}-1}{2}, {\rm\; but\; } t\neq ql, \; \; l = 1, 2, \cdots, \frac{q^{3}-1}{2}, \; \; m = 1, 2, \cdots, q \}$$\bigcup \{\eta = q^{6}-q^{5}(m-1)-qt |\; t = 1, 2, \cdots, \frac{q^{4}-1}{2}, {\rm\; but\; } t\neq ql, \; \; l = 1, 2, \cdots, \frac{q^{3}-1}{2}, \; \; m = 1, 2, \cdots, q \},$ respectively.

Now we are going to derive generalize sequence for both odd and even distinct congruences for $\beta\geq5$ and $\beta \equiv 1\; (\text{mod}\; 2)$. These are

Sequences of roots are $\bigcup\limits _{i = 1}^{\frac{\beta-1}{2}}{\{}\{\eta = q^{\beta-i}(m-1)+q^{i}t |\; t = 1, 2, \cdots, \frac{q^{\beta-2i}-1}{2}, {\rm\; but\; } l\neq ql, \; \; l = 1, 2, 3, \cdots, \frac{q^{\beta-2i-1}-1}{2}, m = 1, 2, \cdots, q^{i} \}$, $\bigcup \{\eta = q^{\beta}-q^{\beta-i}(m-1)-q^{i}t |\; t = 1, 2, \cdots, \frac{q^{\beta-2i}-1}{2}, {\rm\; but\; } t\neq ql, \; \; l = 1, 2, \cdots, \frac{q^{\beta-2i-1}-1}{2}, \; \; m = 1, 2, \cdots, q^{i} \} \Big{\}}$ and $\{\eta = q^{\frac{\beta+1}{2}}(m-1) | m = 1, 2, \cdots, q^{\frac{\beta-1}{2}} \},$ respectively. Therefore, for every positive integer $\beta \geq 5$ with $\beta\equiv 1\; (\text{mod} \; 2)$, $\overbrace{G}(2, q^{\beta}) = \bigoplus\limits_{i = 1}^{\frac{\beta -1}{2}}\Big{(}\frac{q^{\beta-2i}-q^{\beta-2i-1}}{2}\Big{)}K_{2q^{i}}\bigoplus K_{q^{(\beta -1)/2}}$. In second case, when $\beta\geq6$ and $\beta \equiv 1\; (\text{mod}\; 2)$, the number of distinct congruences is $\frac{q^{\beta-1}~~+q+2}{2(q+1)}$. We have

Zeroes of congruences $(2.36)$ and $(2.37)$ are $\bigcup\limits _{i = 1}^{\frac{\beta-2}{2}}{\{}\{\eta = q^{\beta-i}(m-1)+q^{i}t | \; t = 1, 2, \cdots, \frac{q^{\beta-2i}-1}{2}, {\rm\; but\; } t\neq ql, \; \; l = 1, 2, 3, \cdots, \frac{q^{\beta-2i-1}-1}{2}, \; m = 1, 2, \cdots, q^{i} \}$$\bigcup \{\eta = q^{\beta}-q^{\beta-i}(m-1)-q^{i}t |\; t = 1, 2, \cdots, \frac{q^{\beta-2i}-1}{2}, {\rm\; but\; } t\neq ql, \; \; l = 1, 2, \cdots, \frac{q^{\beta-2i-1}-1}{2}, \; \; m = 1, 2, \cdots, q^{i} \} \Big{\}}$, and $\{\eta = q^{\frac{\beta}{2}}(m-1) | m = 1, 2, \cdots, q^{\frac{\beta}{2}} \}$, respectively. Thus, for $\beta\equiv6$ with $\beta\equiv 0\; (\text{mod} \; 2)$, $\overbrace{G}(2, q^{\beta}) = \bigoplus\limits_{i = 1}^{\frac{\beta -2}{2}}\Big{(}\frac{q^{\beta-2i}-q^{\beta-2i-1}}{2}\Big{)}K_{2q^{i}}\bigoplus K_{q^{\beta/2}}.$

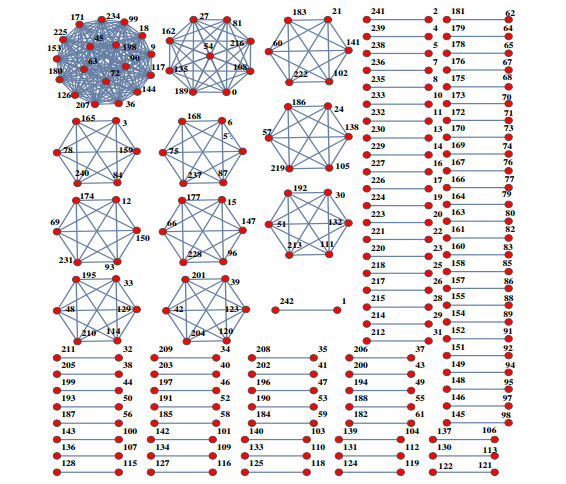
Now, we assume the set of unit elements of $Z_{m}.$ The graph $\overbrace{G}(2, m)$ contains $\phi(q^{\beta}) = q^{\beta-1}~~(q-1),$ vertices, where $\beta\geq1$. We determine the least positive residue of the square of the integers which are less than and relatively prime with $m.$ Because, there are $\phi(q^{\beta}) = q^{\beta-1}~~(q-1)$ squares to be found. By Theorem 1.1, the congruence $x^{2}\equiv a \; (\text{mod}\; q^{\beta})$ has either no solution or exactly two incongruent solutions. This implies, there are always $\frac{\phi(q^{\beta})}{2} = \frac{(q^{\beta-1}~~(q-1))}{2}$ quadratic residues among all the vertices. Thus, $\overbrace{G}(2, q^{\beta}) = \frac{(q^{\beta-1}~~(q-1))}{2}K_{2}$. By combining both cases, we get the desired result. Quadratic graph for $m = 162$ is shown in Figure 3.

3.   Quadratic residues graphs over $Z_{2^{\beta}q},$ $Z_{qp}$ and $Z_{2q^{\beta}}$

In this section, we characterize quadratic residues graphs for $n = 2^{\beta}q, 2q^{\beta}, qp$.

Theorem 3.1. Let $q$ be an odd prime. Then $\overbrace{G}(2, 2^{\beta}q)$

Proof. Let $n = 2^{\beta}q$ be an integer, where $q$ is an odd prime. For $\beta = 1$, $S = \{ 2m|\; m = 0, 1, 2, \cdots q-1\}\bigcup\{q\}$ is set of zero-divisors of $Z_{2q}$ including $0$. There are $\frac{q+1}{2}$ distinct congruences. We have

$\gamma = 0$, $\gamma = q$, and $\gamma = 2t, \; 2q-2t, \; \; t = 1, 2, 3, \cdots, \frac{q-1}{2}$ zeroes of congruences, respectively. When $\beta = 2$, there exit following congruences given as

Sets of roots of these congruence are $\{ 0, 2q \}$, $\{ q, 3q \}$, $\{ 2t, 2q-2t\}\bigcup\{2^{2}q-2t, 2^{2}q-2q+2t\}, \; \; \; t = 1, 2, \cdots, \frac{q-1}{2},$ respectively. There are $q+2$ congruences for $\beta = 3$. They are $\eta^{2} \equiv 0\; (\text{mod} \; 2^{3}q), \; \eta^{2} \equiv (2 q)^{2}\; (\text{mod} \; 2^{3}q), \; \; \eta^{2} \equiv q^{2}\; (\text{mod} \; 2^{3}q), \; \; \text{and}\; \eta^{2}\equiv (2t)^{2}\; (\text{mod} \; 2^{3}q), \; \; \;$$t = 1, 2, \cdots, q-1.$ The zeroes of these congruences are $\{ 0, 2^{2}q \}$, $\{ 2q, 2^{3}q-2q \}$, $\{ q, 3q, 5q, 7q \}$ and $\{ 2t, 2^{2}q-2t\}\bigcup\{2^{3}q-2t, 2^{3}q-2^{2}q+2t\}, \; \; \; t = 1, 2, \cdots, q-1$, respectively. For $\beta = 4$, there are $q + 3$ congruences. We have

zeroes are $\{ 0, 2^{2}q, 2^{3}q, 2^{2}q+ 2^{3}q \}$, $\{ q, 7p, 9p, 15q\}$, $\{ 2q, 6q, 10q, 14q\}$, $\{ 3q, 5q, 11q, 13q\}$ and $\{ 2t, 2^{2}q-2t, 2^{2}q+2t, 2^{3}q-2t \}\bigcup\{2^{4}q-2t, 2^{4}q-2^{2}q+2t, 2^{4}q-2^{2}q-2t, 2^{4}q-2^{3}q+2t \}, \; \; \;$$t = 1, 2, \cdots, q-1$, respectively.

For $\beta = 5$, there are $(3q+11)/2$ congruences

Zeroes of congruences (3.1)$-$(3.6) are $\{0, 2^{3}q, 2^{4}q, 2^{3}q+2^{4}q \}$, $\bigcup \limits_{t\in \{1, 3, 5, 7\}} \{ qt, 2^{4}q+qt \}\bigcup \{2^{5}q-qt, 2^{5}q-2^{4}q- qt\}$, $\{4q, 12q, 20q, 28q \}$, $\{2q, 6q, 10q, 14q, 18q, 22q, 26q, 30q \}$, $\bigcup_{\substack{t = 2l, \\1 \leq l \leq q-1}}\Big{\{}\{ 2^{3} q j + 2t, \; \; j = 0, 1, 2, \cdots, 2^{2}-1 \}\cup \{ 2^{5}q-2^{3} q j - 2t, \; \; j = 0, 1, 2, \cdots, 2^{2}-1\} \Big{\}},$ $\bigcup \limits_{ l = i}^ {\frac{q-1}{2} }\Big{\{}\{ 2^{2} q i + 4l-2, \; \; i = 0, 1, 2, \cdots, 2^{3}-1 \}\cup \{ 2^{5}q-2^{2} q i - 4l+2, \; \; i = 0, 1, 2, \cdots, 2^{3}-1\} \Big{\}}.$

For $\beta = 6$, we have

Solution sets of congruences (3.7)$-$(3.10) are

$\bigcup \limits_{1\leq i\leq \lfloor \frac{3q}{4} \rfloor, j = 0}^{\lfloor \frac{3q-4i}{q}\rfloor} \{ 2^{4}ql+6p-8i-2qj, \; l = 0, 1, \cdots, 2^{2}-1 \}$$\bigcup \{ 2^{6}q-2^{4}ql-6q+8i+2qj, \; l = 0, 1, \cdots, 2^{2}-1\}$$\bigcup \{ 2^{4}ql+ 2^{4}+6q-8i-2qj, \; l = 0, 1, \cdots, 2^{2}-1 \}\bigcup \{ 2^{6}q-2^{4}ql- 2^{4}-6q+8i+2qj, \; l = 0, 1, \cdots, 2^{2}-1\}.$

For $\beta = 7$, we obtain

Zeroes of congruences (3.11)$-$(3.16) are

For $\beta = 8,$ the following congruence equations turning out to be

Zeroes of congruences (3.17)$-$(3.22) are

For $\beta = 9,$ we have

Sets of solution of congruences (3.23)$-$(3.30) are

For $\beta = 10,$ we get

Zeroes of congruences (3.37)$-$(3.44) are

For $\beta = 11,$ we obtain

Sets of solution of congruences (3.45)$-$(3.54) are

For $\beta\geq10$ with $\beta\equiv 0\; (\text{mod}\; 2)$, there are $2^{\beta-5}5+\frac{(2^{\beta-8}-1)2^{\beta-5}}{3\cdot2^{\beta-8}}(2q-1)+6q-2$ congruences. We have

For $\nu = 1, 2, 3, \cdots, \frac{\beta-8}{2},$

Zeroes of congruences (3.55)$-$(3.62) are

For $\nu = 1, 2, 3, \cdots, \frac{\beta-8}{2},$

where $A = \lfloor \frac{2^{\beta-5+\nu}~~-2^{\nu-1}~~q}{2^{\beta-5+\nu}~~} \rfloor$, $B = \lfloor \frac{(2^{\beta-5+\nu}~~-2^{\nu-1}~~)q-(2^{\beta-5+\nu}~~)i}{2^{\nu}q} \rfloor$, $C = 2^{7}q+2^{6}q+2^{3}q+2^{2}q$ and $t = \Big{(}2^{\beta-5+\nu}~~-2^{\nu-1}~~\Big{)}q- (2^{\beta-5+\nu}~~)i-2^{\nu}qj$.

where $D = \frac{(2^{\frac{\beta}{2}}-2^{\frac{\beta-8}{2}})q}{2^{\frac{\beta}{2}}}$, $E = \frac{(2^{\frac{\beta}{2}}-2^{\frac{\beta-8}{2}})q-2^{\frac{\beta}{2}}i}{2^{\frac{\beta-6}{2}}q}$, $F = 2^{4}q+2^{3}q$ and $t = (2^{\frac{\beta}{2}}-2^{\frac{\beta-8}{2}})q-2^{\frac{\beta}{2}}i-2^{\frac{\beta-6}{2}}qj$.

where $G = \frac{(2^{\frac{\beta-2}{2}}-2^{\frac{\beta-6}{2}})q}{2^{\frac{\beta-2}{2}}}$, $H = \frac{(2^{\frac{\beta-2}{2}}-2^{\frac{\beta-6}{2}})q-2^{\frac{\beta-2}{2}}i}{2^{\frac{\beta-6}{2}}q}$ and $t = (2^{\frac{\beta-2}{2}}-2^{\frac{\beta-6}{2}})q-2^{\frac{\beta-2}{2}}i-2^{\frac{\beta-6}{2}}qj$.

For $\beta\geq11$ with $\beta\equiv 1\; (\text{mod}\; 2),$ there are $2^{\beta-5}5+\frac{(2^{\beta-8}-1)2^{\beta-5}}{3\cdot2^{\beta-8}}(2q-1)+ \frac{23q-9}{2}$ congruences. We have

For $\nu = 1, 2, 3, \cdots, \frac{\beta-9}{2},$

Zeroes of congruences (3.63)$-$(3.72) are

For $\nu = 1, 2, 3, \cdots, \frac{\beta-9}{2},$

where $A = \lfloor \frac{2^{\beta-5+\nu}~~-2^{\nu-1}~~q}{2^{\beta-5+\nu}~~} \rfloor$, $B = \lfloor \frac{(2^{\beta-5+\nu}~~-2^{\nu-1}~~)q-(2^{\beta-5+\nu}~~)i}{2^{\nu}q} \rfloor$, $C = 2^{7}q+2^{6}q+2^{3}q+2^{2}q$ and $t = \Big{(}2^{\beta-5+\nu}~~-2^{\nu-1}~~\Big{)}q- (2^{\beta-5+\nu}~~)i-2^{\nu}qj$.

where $L = \frac{2^{\frac{\beta+1}{2}}-2^{{\frac{\beta-9}{2}}})q}{2^{\frac{\beta+1}{2}}}$, $M = \frac{(2^{\frac{\beta+1}{2}}-2^{{\frac{\beta-9}{2}}})q-2^{\frac{\beta+1}{2}}i}{2^{\frac{\beta-7}{2}}q}$, $N = 2^{7}q+2^{4}q+2^{3}q$ and $t = (2^{\frac{\beta+1}{2}}-2^{{\frac{\beta-9}{2}}})q-2^{\frac{\beta+1}{2}}i-2^{\frac{\beta-7}{2}}qj$.

where $Q = \frac{(2^{\frac{\beta-1}{2}}-2^{\frac{\beta-7}{2}})q}{2^{\frac{\beta-1}{2}}}$, $R = \frac{(2^{\frac{\beta-1}{2}}-2^{\frac{\beta-7}{2}})q-2^{\frac{\beta-1}{2}}i}{2^{\frac{\beta-5}{2}}q}$, $S = 2^{5}q+2^{4}q$ and $t = (2^{\frac{\beta-1}{2}}-2^{\frac{\beta-7}{2}})q-2^{\frac{\beta-1}{2}}i-2^{\frac{\beta-5}{2}}qj$.

Now, we consider the set of unit elements of $Z_{m}$. The $x^{2}\equiv a$ $\; (\text{mod}\; 2)$ has one solution and $x^{2}\equiv a \; (\text{mod}\; 2^{2})$ has two solution. By Theorem 1.2, if $\beta \geq 3,$ the congruence $x^{2}\equiv a \; (\text{mod}\; 2^{\beta})$ has either no solution or exactly 4 incongruent solutions. Furthermore, again by Theorem 1.1, for an odd prime the congruence $x^{2}\equiv a \; (\text{mod}\; q)$ has either no solution or exactly 2 incongruent solutions. By using Chinese remainder theorem, if $\beta = 0\; \text{or}\; 1$ then, $x^{2}\equiv a \; (\text{mod}\; 2^{\beta})$ has either no solution or exactly 2 incongruent solutions. If $\beta = 2$ then, $x^{2}\equiv a \; (\text{mod}\; 2^{\beta})$ has either no solution or exactly 4 incongruent solutions. Lastly, if $\beta \geq 3$, then $x^{2}\equiv a\; (\text{mod}\; 2^{\beta})$ has either no solution or exactly 8 incongruent solutions. Hence, $\overbrace{G}(2, 2^{\beta}q) = \frac{\phi(n)}{8}K_{8}, \beta\geq3$. We achieve the desired outcome by combining both cases.

Proposition 3.2. If $q$ and $p$ are odd primes, then $\overbrace{G}(2, qp) = K_{1}\bigoplus\frac{q+p-2}{2}K_{2}\bigoplus \frac{(q-1)(p-1)}{4}K_{4}.$

Proof. To prove this first we discuss the zero-divisors elements of ring $Z_{m}.$ Let $\{ 0, nq, yp | n = 1, 2, 3, \cdots, p-1, y = 1, 2, 3, \cdots, q-1\}$ be a set of zero-divisors of $Z_{qp}$ with zero. There are $\frac{q+p}{2}$ distinct congruences. We have

Zeroes of these congruences are $\eta = 0$, $\eta = qt, qp-qt, \; \; t = 1, 2, 3, \cdots, \frac{p-1}{2},$ and $\eta = pt, qp-pt, \; \; t = 1, 2, 3, \cdots, \frac{q-1}{2}.$ Thus, $\overbrace{G}(2, qp) = K_{1}\bigoplus\frac{q+p-2}{2}K_{2}.$ Now we discuss the unit elements of $Z_{m}$. By Theorem 1.1, for distinct odd primes $q$ and $p$, the congruence $x^{2}\equiv a \; (\text{mod}\; q)$ has either no solution or exactly 2 incongruent solutions. Similarly, the congruence $x^{2}\equiv a \; (\text{mod}\; p)$ has either no solution or exactly 2 incongruent solutions. By using Chines remainder theorem we have, $x^{2}\equiv a \; (\text{mod}\; q^\beta)$ has either no solution or exactly 4 solutions. Thus, $\overbrace{G}(2, qp) = \frac{\phi(qp)}{4}K_{4} = \frac{\phi(q-1)(p-1))}{4}K_{4}$. We get the desired outcome by combining both cases.

Theorem 3.3. Let $q$ be an odd prime. Then, $\overbrace{G}(2, 2q^{\beta})$

Proof. The proof is on similar lines as illustrated in the proof of Theorem 3.1.

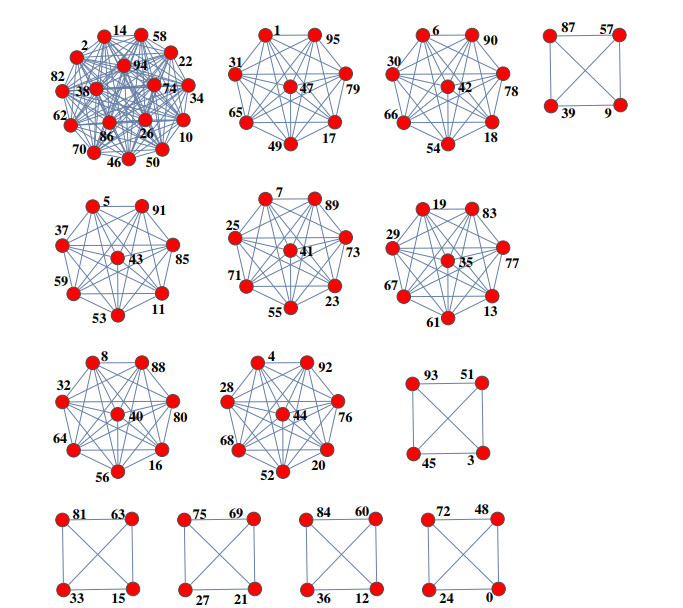
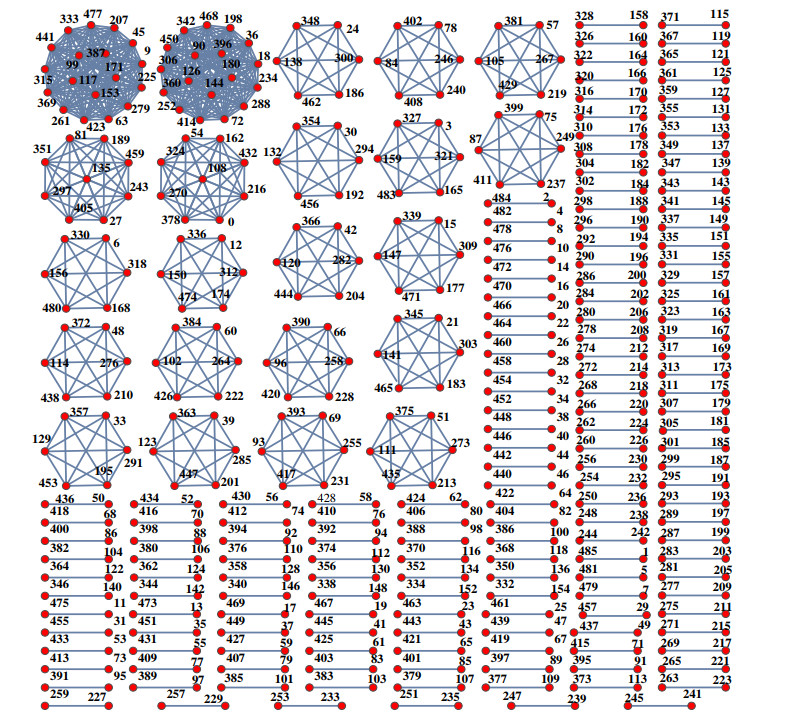
Figures 4 and 5 reflect Theorems 3.1 and 3.3, respectively.

4.   Conclusions

In this article, we investigated the mapping $x^{\alpha}\equiv y^{\alpha}, \; \; (\text{mod}\; m)$ for $\alpha = 2$ over the ring of integers. A problem of partitions of a given set into the form of subsets with equal sums is NP problem. A paradigmatic approach was introduced to find equal sum partitions of quadratic maps via complete graphs. Moreover, we characterized quadratic graphs associated with the mapping $x^{\alpha}\equiv y^{\alpha}, \; \; (\text{mod}\; m),$ $\alpha = 2$ for well-known classes $m = 2^{\beta}, q^{\beta}, 2^{\beta}q, 2q^{\beta}, qp,$ in terms of complete graphs, where $q, p$ is an odd prime. Later on, we intend to extend our research to higher values of $\alpha$ over various rings. We hope that this work will open new inquiry opportunities in various fields for other researchers and knowledge seekers.

Acknowledgment

This work was funded by the Deanship of Scientific Research (DSR) at King Abdulaziz University, Jeddah. The authors, therefore, acknowledge with thanks DSR for technical and financial support.

Conflict of interest

The authors declare that they have no conflict of interest regarding the publication of the research article.